Introduction

Companies are continuously facing the resistance to settle into the ever changing technological environment. Six Sigma has been recognized for many years as an efficient strategy and has helped several companies to rise to this challenge. This is one of the most important and popular developments in the field of process improvement. It has saved large amounts of money and improved the processes for a large number of manufacturing organizations worldwide (Neuman and Cavanagh 2000; Snee and Hoerl 2003; Harry and Schroeder 2005). Six Sigma has gone through a considerable evolution since the early exposition. Initially it was a quality improvement methodology based on statistical concepts. Then it transformed to a disciplined process improvement technique. In its current existence; it is commonly presented as ‘a breakthrough strategy’ of best in class. It is accepted that in current scenario Six Sigma is applicable to various environments such as service, manufacturing, process, software industry regardless of the size of the business, and, if successfully implemented, it may lead to nearly perfect solutions and services (Banuelas et al. 2005; Antony et al. 2006; Chakrabarty and Tan 2007). Six Sigma has enormous potential to reduce breakdown costs, improve performance, grow revenue, strengthen focus, and empower resources (Snee and Hoerl 2004). It is a commanding strategy that employs a regimented approach to undertake process variability using the application of statistical and non‐statistical tools and techniques in an accurate way (Jiju 2004). This teaches everyone in the organization to become more effective and efficient (Eckes 2003). Business leaders must be aware that successful implementation of Six Sigma requires not only technical understanding, but also behavioral awareness (Linderman et al. 2003). Most of the SMEs (Small and medium-sized enterprises) are not aware of Six Sigma and many not have the proper resources to execute Six Sigma projects (Jiju et al. 2005). In comparison with conventional approaches of quality and process improvement, Six Sigma is the most effective approach because of the interrelation between planning, organizational structures, measures, tools and techniques (Tilo et al. 2004; Zu et al. 2008). Six Sigma is a process improvement strategy which includes various phases logically related with each other acronym DMAIC methodology (define, measure, analyze, improve and control) is used for continuous improvement in any system or processes (Amer et al. 2008). It is the strategy of achieving key improvements in the process by applying DMAIC methodology through elimination of causes. Manufacturing units can put into action such strategies to enhance productivity of their manufacturing processes (Singh and Singh 2014).

In this case study, we are focusing on the analysis phase of DMAIC methodology through which all Six Sigma projects are executed. In the analysis phase, all measurements will be analyzed by understanding them and to make basic problem easier. The idea is to search for the factors having the biggest impact on process performance and determine the roots causes. In this case we have identified various factors for breakdown/failure in center less grinding section of machine shop in an automotive industry. The aim of study is to prioritize the critical breakdown factors in CLG section for further improvement. In this context, the key attributes/impacts were identified that depended on the views of various decision makers (such as machine operators, maintenance experts, production manager, technical and financial experts, etc.) and there are no crystalline themes among the views of these decision makers. Therefore it turned out to be necessary to forecast the excellent solution in terms of selecting critical factors for such problems using a decision-making technique. Such problems can be attempted with multiple attribute decision making (MADM) approach. MADM models are used to select best alternative from the large number of alternatives for a set of selection criteria. This approach has been effectively applied in broad range of decision-making problems in engineering and scientific fields (Perego and Rangone 1998; Pahlavani 2010). A variety of methods are reported under MADM category in literature (Chen et al. 1992; Tönshoff et al. 2007). MADM approach includes analytic hierarchy process (AHP) (Saaty 2014), graph theory and matrix approach (GTMA) (Rabbani et al. 2014), VlseKriterijumska Optimisacija I Kompromisno Resenje (VIKOR) (Liu et al. 2014; Singh and Kumar 2014), technique for order preference by similarity to ideal solution (TOPSIS) (Chu 2002; Chu and Lin 2003; Khanna et al. 2011; Dey et al. 2014), simple additive weighting (SAW) (Afshari et al. 2010) multiplicative analytical hierarchy process (MAHP) (Cheng and Mon 1994), weighted product method (WPM), Group decision making (GDM) (Chen 2000) and many others. These techniques have been successfully applied to various fields of engineering and among these, VIKOR and TOPSIS are outstanding multiple attribute decision making (MADM) approaches. These have been applied to various problems ranging from advanced manufacturing (Kulak and Kahraman 2005), production planning (Chen and Liao 2003), supplier selection (Azar et al. 2011), decision making (Sanayei et al. 2010), machine tool selection (Nguyen et al. 2014), supply chain management (Wei et al. 2007) and many more (Vats and Vaish 2013; Ding and Kamaruddin 2014; Tahriri et al. 2014; Tiwary et al. 2014; Vats and Vaish 2014a, b). These approaches work on crisp value of attributes/impacts. The aim of present study is to select critical factors for breakdown/failure in CLG section under fuzzy environment using fuzzy VIKOR and fuzzy TOPSIS methodology using AHP weights. The present study is one of the first efforts to evaluate failure parameters using fuzzy MADM approach in Six Sigma analysis phase in Indian automotive sector.

Evaluation criteria

Six attributes have been identified for evaluation of the critical breakdown factors in center less grinding section of the selected automotive industry. These are based on the discussion with various technical experts, machine operators, production manager, maintenance manager and studies conducted by various researchers (Ayağ and Özdemir 2011; Nguyen et al. 2014).

Attributes/impact

Symbol

Depiction

Ease of maintenance

C 1

It describes the ease with which a machine can be maintained in order to correct defects or their causes. Ease of Maintenance is the means whereby the Project Team confirms whether equipment can be maintained in-service and meets the maintainability and ease of maintenance criteria within the maintenance strategy

Safety

C 2

There are common hazards associated with the use of machine shop equipment and tools. Working safely is the first thing because the safe way is the correct way. The costs of accidents and ill health to engineering machine shops may be disproportionately high. Many employees are ‘key’ workers whose losses through injury or ill health severely disrupt production and lowers productivity and profitability

MTBF

C 3

It is the prime factor for selecting critical reasons of breakdown in machine shops. MTBF is stated as the average time between system failures of the entire machine shop. It defines of how reliable a component is. It shows the failure rate of each parameter responsible for breakdown in CLG section

Cost

C 4

It is also a key factor for investigating critical reasons of breakdown. It includes the cost of breakdown, maintenance, repair and all activities necessary to meet all its functional requirements throughout the service life. This becomes a critical to estimate such costs

Green effect

C 5

Green Effects go beyond just energy efficiency and attempt to rate an effort with regard to the total environmental stewardship of a machine shop. It includes minimum wastage, low energy consumption and user friendly environment. In this regard green effects are significantly more encompassing than just energy. An energy efficient shop floor may not be a green shop floor, but a true shop floor will be energy efficient

Repair time

C 6

It is the Portion of breakdown time during which one or more experts are working on a system to effect a repair. Repair time includes preparation time, fault detection time, fault correction time and final bind up time

Methods

As discussed in previous section, the present study emphasizes on finding out critical factors responsible for breakdown time in CLG’s to improve their availability and to enhance company profit. This is done by first optimizing the parameters using AHP and then using VIKOR and TOPSIS with fuzzy logic to sum up the result.

Analytical hierarchy process (AHP)

Analytic hierarchy process is a decision making model that aids us in making decision in our complex world, developed by Satty (1980, 1988). AHP provides a framework to cope with multiple criteria situations involving intuitive, rational, qualitative and quantitative aspects. It has been one of the most widely used techniques for complex decision found especially suitable for planning at strategic level. It is a three part process which includes, identifying and organizing decision objectives, criteria constraints and alternatives into a hierarchy. The process requires the decision‐maker to develop a hierarchical structure of the factors in the given problem and to provide judgments about the relative importance of each of these factors and ultimately to specify a preference for each decision alternative with respect to each factor (Bhutta and Huq 2002). The elements of the hierarchy are related to an aspect of the decision problem which can be carefully measured or roughly estimated anything at all that applies to the decision making. Generally hierarchy has three levels; the goal, the criteria, the alternatives. The levels of hierarchy describe a system from the lowest level (sets of alternatives), through the intermediate levels (sub criteria and criteria), to the highest level (general object) (Liu and Hai 2005). It is the essence of the AHP that human judgments, and not just the underlying information, can be used in performing the evaluations. In order to compare distinct attributes, numeric priority values are assigned to the attributes on the scale of 1–9 (Saaty 1990). AHP is used as a framework to formulize the evaluation of trade‐offs between the conflicting selections criteria associated with the various suppliers’ offers (Nydick and Hill 1992; Radcliffe and Schniederjans 2003). The comparison is based on expert opinion, some inconsistency may occur in the system. The consistency of system can be checked by the consistency ratio (CR):

$${\text{CR}} = \frac{\text{CI}}{\text{RI}}$$
(1)

where CI is the consistency index which can be written as:

$$CI = \frac{{\lambda_{\hbox{max} } - m}}{m - 1}$$
(2)

The random consistency index (R.I.) is the predefined value (Satty 1994).

Fuzzy logic

Fuzzy approach was introduced to undertake the problem where there are no clear edges between the two parameters (Azar et al. 2011). It deals with the problems where it is hard to differentiate between members and non-member objects of a set. Fuzzy approach was used for multiple criteria decision making where the stress is on likelihood rather than probability (Wei et al. 2007). Fuzzy logic is based on a set theory and contains a membership function within the interval (0, 1) which depicts the extent of significance of an element for being the member of the set (Bevilacqua et al. 2006). Linguistic variables are used for all the assessments, in which numerical values are assigned without any riddle. A linguistic variable is a variable whose value is denoted in words or sentences in a natural or artificial language (Zadeh 1975). For example, if the values of quality are presumed to be the fuzzy variables marked as good, bad and worst in place of actual numbers, then quality is a linguistic variable. Fields of artificial intelligence, linguistics, pattern recognition, human decision processes, psychology, economics etc. have origin in the linguistic approach (Bellman and Zadeh 1970). Different fuzzy numbers are used depending on their situation. In present case we use trapezoidal fuzzy numbers (b 1, b 2, b 3, b 4) for {b 1, b 2, b 3, b 4 ∊ R; b 1 ≤ b 2 ≤ b 3 ≤ b 4} as in Fig. 1. Because of its simplicity and information processing in a fuzzy environment; it is often suitable to work with trapezoidal fuzzy numbers. The membership function µ b (x) of trapezoidal fuzzy number is defined as

$$\mu_{b} \left( x \right) \, = \left\{ {\begin{array}{*{20}l} {\frac{{x - b_{1} }}{{b_{2} - b_{1} }},} \hfill & {\quad x \in \left[ {b_{1} ,b_{2} } \right]} \hfill \\ {1,} \hfill & {\quad x \, \in \left[ {b_{2} ,b_{3} } \right]} \hfill \\ {\frac{{b_{4} - x}}{{b_{4} - b_{3} }},} \hfill & {\quad x \in \left[ {b_{3} ,b_{4} } \right]} \hfill \\ {0,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(3)
Fig. 1
figure 1

Trapezoidal fuzzy number

Full size image

VIKOR

Opricovic (2011) developed VIKOR, the Serbian name: VlseKriterijumska Optimizacija I Kompromisno Resenje; method to determine the compromise solution for a set of alternatives. Compromise solution is a feasible solution closest to the ideal solution for a MADM problem. The compromise solutions could be the basis for agreements, involving the decision maker’s preferences by criteria weight. This method focuses on ranking and selecting from a set of alternatives, and determines compromise solutions for a problem with conflicting criteria, which can help the decision makers to reach a final decision (Sanayei et al. 2010). VIKOR algorithm determines the weight stability intervals for the obtained compromise solution with the input weights given by the experts.

TOPSIS

TOPSIS (Technique for order preference by similarity to an ideal solution) method was presented by Hwang and Yoon (Yoon and Hwang 1995). TOPSIS uses different weighting schemes and distance metrics to compares results of different sets of weights applied to set of multiple criteria data (Olson 2004; Önüt and Soner 2008). The basic principle is that the chosen alternative should have the shortest distance from the ideal solution and the farthest distance from the negative ideal solution. The ideal solution is a solution that maximizes the benefit criteria and minimizes the cost criteria, whereas the negative ideal solution maximizes the cost criteria and minimizes the benefit criteria. Benefit criteria is for maximization, while the cost criteria is for minimization. The best alternative is the one, which is closest to the ideal solution and farthest from the negative ideal solution (Wang and Elhag 2006).

Methodology used

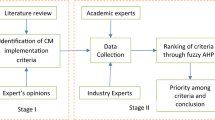
This section explains the steps involved in the proposed subjective fuzzy VIKOR and Fuzzy TOPSIS approach for calculation of critical factors responsible for breakdown in CLG’s. The approach utilizes AHP weights for inter-comparison among all criteria followed by fuzzy logic approach with VIKOR and TOPSIS methods. Figure 2 shows the flow chart of proposed methodology used in present study and make clears how the views of the decision makers are quantitatively compiled. It includes following steps:

Fig. 2
figure 2

Flow chart for methodology used

Full size image
Step 1 :

Calculation of AHP weights.

As discussed in “Analytical hierarchy process (AHP)” section, AHP weights (W j ) are calculated for all breakdown parameters. This provides the weights of different criteria.

Step 2 :

Define linguistic terms, relevant membership function and corresponding fuzzy numbers.

A set of fuzzy rates is required in order to compare all the alternatives for each criterion. These fuzzy terms are assigned by the decision makers and responsible for intra criterion comparisons of the alternatives.

Step 3 :

Decision matrix formation.

Let p be the parameters and q be the alternative. For k number of decision makers in the proposed model for the aggregated fuzzy rating for C j criterion is represented as x ijk = {x ijk1 , x ijk2 , x ijk3 , x ijk4}. For i = 1, 2,… p; j = 1,2,… q; k = 1,2,… k, x ijk is calculated as (Kahraman et al. 2003; Kwong and Bai 2003):

$$\left\{ \begin{aligned} x_{ij1} = \mathop {\hbox{min} }\limits_{k} \left\{ {b_{ijk1} } \right\} \hfill \\ x_{ij2} = \frac{1}{k}\sum {b_{ijk2} } \hfill \\ x_{ij3} = \frac{1}{k}\sum {b_{ijk3} } \hfill \\ x_{ij4} = \mathop {\hbox{max} }\limits_{k} \left\{ {b_{ijk4} } \right\} \hfill \\ \end{aligned} \right.$$
(4)

Thus the obtained decision matrix (M) is shown as:

$$M = \left[ {\begin{array}{*{20}l} {x_{11} } \hfill & {x_{12} } \hfill & \cdots \hfill & {x_{1p} } \hfill \\ {x_{21} } \hfill & {x_{22} } \hfill & \cdots \hfill & {x_{2p} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {x_{q1} } \hfill & {x_{q2} } \hfill & \cdots \hfill & {x_{qp} } \hfill \\ \end{array} } \right]$$
Step 4 :

Defuzzification.

Defuzzification is performed to obtain the crisp values for each criterion corresponding to each alternative. This provides a quantitative value for the linguistic variables and fuzzy numbers assigned based on the verbal reasoning of the decision makers. Following equation lead to the crisp values:

$$\begin{aligned} f_{ij} & = {\text{Defuzz}}\left( {x_{ij} } \right) \, = \frac{{\int {\mu \left( x \right) \cdot x{\text{d}}x} }}{{\int {\mu (x) \cdot {\text{d}}x} }} \\ & = \frac{{\int_{{x_{ij1} }}^{{x_{ij2} }} {\left\{ {\left( {x - x_{ij1} } \right)/(x_{ij2} - x_{ij1} )} \right\} \cdot x{\text{d}}x} + \int_{xij2}^{{x_{ij3} }} {x{\text{d}}x} + \int_{{x_{ij3} }}^{{x_{ij4} }} {\left\{ {(x_{ij4} - x)/(x_{ij4} - x_{ij3} )} \right\} \cdot x{\text{d}}x} }}{{\int_{{x_{ij1} }}^{{x_{ij2} }} {\left\{ {(x - x_{ij1} )/(x_{ij2} - x_{ij1} )} \right\}{\text{d}}x + \int_{xij2}^{{x_{ij3} }} {{\text{d}}x} + \int_{{x_{ij3} }}^{{x_{ij4} }} {\left\{ {(x_{ij4} - x)/(x_{ij4} - x_{ij3} )} \right\} \cdot x{\text{d}}x} } }} \\ & = \frac{{ - x_{ij1} x_{ij2} + x_{ij3} x_{ij4} + (1/3)(x_{ij4} - x_{ij3} )^{2} + (1/3)(x_{ij2} - x_{ij1} )^{2} }}{{ - x_{ij1} - x_{ij2} - x_{ij3} + x_{ij4} }} \\ \end{aligned}$$
(5)

The crisp values, thus obtained are integrated with AHP weights to calculate final ranking using-VIKOR and TOPSIS approach as discussed below.

VIKOR approach steps

Step 5 :

Determination of ideal and negative ideal solutions;

The ideal solution f* and negative ideal solution f − are determined as

$$f^{*} = \, \{ \hbox{max} f_{ij} \}$$
(6)
$$f^{ - } = \left\{ {\hbox{min} f_{ij} } \right\}$$
(7)
Step 6 :

Calculation of utility and regret measures

$$S_{i} = \sum\limits_{j = 1}^{n} {W_{j} \frac{{\left( {f_{j}^{*} - f_{ij} } \right)}}{{\left( {f_{j}^{*} - f_{j}^{ - } } \right)}}} ;\quad \forall i$$
(8)
$$R_{i} = {\text{Max}}_{j} \left[ {W_{j} \frac{{\left( {f_{j}^{*} - f_{ij} } \right)}}{{\left( {f_{j}^{*} - f_{j}^{ - } } \right)}}} \right];\quad \forall i$$
(9)

where S i and R i represent the utility and regret measures, respectively and W j is the relative weight assigned to the jth parameter using AHP.

Step 7 :

Calculation of VIKOR index

$$Q_{i} = v\left[ {\frac{{S_{i} - S^{*} }}{{S^{ - } - S^{*} }}} \right] + \left( {1 - v} \right)\left[ {\frac{{R_{i} - R^{*} }}{{R^{ - } - R^{*} }}} \right];\quad \forall i$$
(10)

where Q i represents ith alternatives VIKOR value, v is the group utility weight, it is generally considered as 0.5 (unsupervised) and;

$$S^{*} = \min_{i} \left( {S_{i} } \right);$$
(11)
$$S^{ - } = \max_{i} \left( {S_{i} } \right);$$
(12)
$$R^{*} = \, \min_{i} \left( {R_{i} } \right);$$
(13)
$$R^{ - } = \max_{i} \left( {R_{i} } \right);$$
(14)

Breakdown factor with least value of VIKOR index Q i is preferred.

TOPSIS approach steps

Step 5 :

Normalized the matrix as given below:

$$r_{ij} = \frac{{f_{ij} }}{{\sqrt {\sum\nolimits_{i = 1}^{m} {\left( {f_{ij} } \right)^{2} } } }};\quad \forall_{j}$$
(15)
Step 6 :

Calculate the weighted normalized decision matrix as given:

$$V_{ij} = \left[ {r_{ij} } \right]_{ \, m \times n} \times \left[ {W_{j} } \right]_{ \, n \times m}^{\text{diagonal}}$$
(16)
Step 7 :

Calculate the positive ideal and negative ideal solution:

The positive ideal solution V + j and negative ideal solution V − j are as given below:

$$V_{j}^{ + } = \left\{ {\left( {\hbox{max} V_{ij} ,j \in J_{1} } \right),\left( {\hbox{min} V_{ij} ,j \in J_{2} } \right),i = 1,2,3 \ldots m} \right\};\quad \forall j$$
(17)
$$V_{j}^{ - } = \left\{ {\left( {\hbox{min} V_{ij} ,j \in J_{1} } \right),\left( {\hbox{max} V_{ij} ,j \in J_{2} } \right),i = 1,2,3 \ldots m} \right\};\quad \forall j$$
(18)

where J 1 and J 2 represents higher best and lower best criteria respectively.

Step 8 :

Calculate the distance d + i and d − i from the positive ideal solution and negative ideal solution respectively

$$d_{i}^{+} = \left[{\sum\limits_{j = 1}^{n} {\left({V_{ij} - V_{j}^{+}} \right)^{2}}} \right]^{0.5},\quad i = 1,2,3, \ldots m$$
(19)
$$d_{i}^{-} = \left[{\sum\limits_{j = 1}^{n} {\left({V_{ij} - V_{j}^{-}} \right)^{2}}} \right]^{0.5},\quad i = 1,2,3,\ldots m$$
(20)
Step 9 :

Calculation of TOPSIS rank index:

$$C_{i}^{ + } = \frac{{d_{i}^{ - } }}{{d_{i}^{ - } + d_{i}^{ + } }}$$
(21)

Breakdown factor with highest rank index C + i are preferred.

Results and discussion

The hierarchical structure for the selection of critical breakdowns factors in CLG’s is demonstrated in Fig. 3. Level A specifies our goal on selection of the critical factors that have to be selected from the identified thirteen important factors of failure indicated in level B. Further, in brainstorming session with decision makers like machine operators, maintenance experts, production manager, technical and financial experts etc.; we concluded that selection of the critical factors of breakdowns in CLG’s depends on six criteria as discussed in “Evaluation criteria” section and these are illustrated in level C of the Fig. 3 as attributes/impacts. Breakdown parameters are fully interdependent on these attributes and it shows the intricacy of the problem. Moreover, this is a time consuming process and significant knowledge of both technological as well as economic aspects is needed in this case. After the attributes are identified, the next issue is to prioritize these attributes, as to which one has more impact on the identified breakdown reasons. AHP approach is used to prioritize these attributes and in order to compare these distinct attributes, numeric priority values are assigned to the attributes on a scale of 1–9 and pair-wise comparison is made. Table 1 shows the relative decision matrix formed on the basis of pair-wise comparison (AHP approach) and the weights calculated for all the considered criteria. MTBF appease as the most dominant attribute for the selection of these critical reasons of breakdown; while green effect is found to be the least dominant factor. Figure 4 shows contribution of all these dominating attributes towards selection of these critical breakdown factors. It is clearly observed that contributions of these attributes vary from shop floor of company to company.

Fig. 3
figure 3

The hierarchical structure for the selection of the critical factors of Breakdowns in CLG’s

Full size image
Table 1 Subjective weights of the evaluation criteria calculated using AHP
Full size table
Fig. 4
figure 4

Contribution of all dominating attributes about selection of critical factors for breakdown in CLG’s

Full size image

In next step, fuzzy hypothesis analysis is performed on conclusions of the decision makers for comparison of all alternatives for each attribute. Fuzzy logic approach dealt well with such problems. Linguistic variables were used for selection of the critical factors of breakdowns. These were further converted into fuzzy numbers as shown in Table 2 for the current study. The highest range is termed absolutely high (AH) and the least is termed as absolutely poor (AP). Table 3 demonstrates the linguistic decision matrix filled during brainstorming session with decision makers. Here a single decision matrix has been formed rather than having a separate decision matrix for each decision maker. However, it is clearly known that final decision matrix can change as per the requirements and existing conditions. Further, fuzzy values are finally transformed into crisp values as shown in Eq. (5). Table 4 shows the calculated crisp values obtained from aggregated fuzzy ratings. Calculated crisp values are used with VIKOR approach as shown in Eqs. (6)–(14) and these values are used with TOPSIS approach, using Eqs. (15)–(21) to obtain the rank indices of all alternatives. Table 5 shows corresponding rank indices and ranks for the factors of breakdowns in CLG’s. The ranking of alternatives obtained by VIKOR and TOPSIS approach are exactly same. This shows the robustness of the results used. Our computation shows that conveyor malfunction is the prime factor for breakdown in CLG section. Other main reasons for breakdown are slide failure, CWD unit fault, coolant pump malfunction and hydraulic oil leakage, respectively (refer Table 5). It is also observed that sensor faults are having least effect on failure of this section. Improper lubrication and grinding wheel fault and electrical faults are also rarely responsible for failure. We found that our results are in good agreement with long term perceptions of auto companies under normal working conditions. These critical causes of capacity waste need immediate monitoring, so that productivity loss could be checked for future.

Table 2 Linguistic variables and corresponding fuzzy numbers
Full size table
Table 3 Linguistic decision matrix of factors for breakdown in CLG’s for all evaluation criteria
Full size table
Table 4 Calculated crisp values for assigned fuzzy rates
Full size table
Table 5 Calculated VIKOR and TOPSIS ranking
Full size table

Conclusions

Fuzzy MADM method has been used for the selection of the critical factors of breakdown in CLG section of an automotive industry. Analytical Hierarchy Process (AHP) method is used to calculate weights of all persuasive attributes for selection of the failure parameters. MTBF has been found to be the most serious and green effect as least critical attribute. Further priority order of critical breakdown factors in CLG’s is determined using fuzzy VIKOR and fuzzy TOPSIS approach with AHP weights. Conveyor malfunction, slide not working, and CWD unit fault, coolant pump malfunction and hydraulic oil leakage are found to be the critical factors of breakdowns in CLG section. This study explores the feasibility of fuzzy VIKOR and fuzzy TOPSIS methods in Six Sigma analysis phase for selection of the breakdown/failure parameters. Briefly, the main features of this study are summarized as follows:

  1. (a)

    The study helps to highlight the importance of ‘Analysis Phase’ for successful implementation of Six Sigma project.

  2. (b)

    The study has also helped to prove that Fuzzy-MADM approach can be effectively used to select most critical CTQs, which can be further improved to achieve better sigma rating.

  3. (c)

    Within MADM, the study has successfully explored the efficacy of AHP, VIKOR and TOPSIS methods to prioritize the CTQs which are highly important for execution of Six Sigma project.

  4. (d)

    The study will help the managers and practitioners to implement Six Sigma more effectively and more scientifically, using MADM approaches instead of using conventional statistical tools.