Introduction and literature review

Market power as the principal companies’ success factors is a primitive and important challenge to which companies are faced. The companies, which are competing in the same market, are attempting to increase own market penetrations by using different implements to achieve the more market power than the other rivals. The market power leads to enhance the penetrability of companies so that the market would be handled by the powerful firms (Wei et al. 2013; Zhao et al. 2014). One of the practical and the efficient implements which cause to improve the companies’ revenue and also their power market is presenting an optimal price where the same products are launched to the market. So, pricing policy as the useful tool which can solve this imperative problem is recognized by enterprises for decades. In fact, the companies attempt to optimize their selling prices to acquire the more market demand.

Recently, many researchers are focused on the pricing policies. For instance, Starr and Rubinson (1978) proposed a model to survey the relation between the demand of product and its prices. Dada and Srikanth (1987) studied pricing policies under quantity discounts. Kim and lee (1998) employed pricing and ordering strategies for a single item with fixed or variable capacity to maximize the profit of firm faced to price-sensitive and deterministic demand over a planning horizon. Boyaci and Gallego (2002) considered joint pricing and ordering decisions in a supply chain consisting of a wholesaler and one or several retailers. A complete review of dynamic pricing models was presented by Elmaghraby and Keskinocak (2003). Several studies applied pricing policy with coordination mechanisms under different assumptions (Chen and Simchi-Levi 2004a, b, 2006; Chen et al. (2006); Xiao et al. (2010); Wei and Zhao (2011); Yu and Ma (2013); Maihami and Karimi (2014); Taleizadeh and Noori-daryan (2014)). Sinha and Sarmah (2010) studied pricing decisions in a distribution channel under the competition and coordination issues in which two competitive vendors sell products to a common retailer in the same market. A comprehensive review of pricing models for a multi-product system is performed by Soon (2011). Shavandi et al. (2012) presented a new constrained pricing and inventory model for perishable products which those are classified to complementary, substitutable and independent products. Their aim is to optimize the prices, inventory and production decisions such that the total profit is maximized. Mahmoodi and Eshghi (2014) presented three algorithms to obtain the optimal pricing decisions in a duopoly supply chain. Taleizadeh et al. (2014) developed a vendor managed inventory (VMI) model in a two-level supply chain including a vendor and multiple retailers to survey the optimal pricing and inventory policies such that the total profit of the chain is maximized.

The concept of complementary products is suggested when the customer has to purchase more than one product at the same time so that the products could have the required efficiency (Yue et al. 2006). For an instance, software and hardware systems of a computer are two complementary products and should be purchased together to have the required efficiency for the customer. But, if a customer is not satisfied enough with a purchased product and purchases a similar product, then these two products will be substitutable products. For example; different marks of software or hardware systems of a computer may be considered as substitutable products. Several researchers examine the effects of complementary and substitutable products on the profit of inventory systems. For example, the pricing decisions of two complementary products as the bundle policy is studied by Yue et al. (2006) where the products are produced by two separate firms. Mukhopadhyay et al. (2011) considered a duopoly market where two independent firms offer complementary goods under information asymmetry. The Stackelberg game-theoretic model to solve the proposed model is utilized. Yan and Bandyopadhyay (2011) proposed a profit-maximization model and applied a bundle pricing policy for complementary items. Wei et al. (2013) examined the pricing problem under the different market powers structures between members of a supply chain with two manufacturers and one retailer for two complementary products. Wang et al. (2014) employed pricing policy for two complementary products in a fuzzy environment and they survey the changes of the optimal retail prices of two complementary products under two different scenarios. Wei et al. (2015) presented joint optimal pricing and warranty period of two complementary products in a supply chain with two manufacturers and one common retailer under horizontal firm’s cooperation/noncooperation strategies.

Tang and Yin (2007) extended the Starr and Rubinson (1978)’s work for two substitutable products under the fixed and variable pricing strategies. The goal of this paper is to jointly determine optimal order quantity and retail price. Hsieh and Wu (2009) and Gurler and Yilmaz (2010) employed coordinating mechanisms for substitutable products under various assumptions. Then two problems are carried out by Zhao et al. (2012a, b) such that in the first one, a pricing problem of substitutable products in a fuzzy environment is discussed. In the second one, a pricing policy in a supply chain including one manufacturer and two competitive retailers for substitutable products where the customers’ demand and the manufacturing costs are non-deterministic is employed. Chen et al. (2013) discussed pricing problem for substitutable products under traditional and online channels in a two-stage supply chain including a manufacturer and a retailer where the manufacturer sells a product to a retailer and also sells directly to customers through an online channel. Hsieh et al. (2014) surveyed pricing and ordering decisions of partners of a supply chain including multiple manufacturers and a retailer under demand uncertainty where each manufacturer produces a different substitutable product which is sold through the retailer. Zhao et al. (2014) developed a pricing model for substitutable products under the different market power of firms in a supply chain with two competitive manufacturers and a retailer. Fei et al. (2015) considered a price model for one supplier and multiple retailers under different product substitution degrees. In this article, the authors studied the effect of sub-packaging cost on the retail price.

Panda et al. (2015) studied joint pricing and replenishment policies in a dual-channel supply chain where the manufacturer is the leader of Stackelberg model. Zhang et al. (2014) developed a dynamic pricing model in a competitive supply chain under deterministic demand function to optimize the benefits of supply chain members. Also, they analyzed the profit sensitivity with respect to various factors. Giri and Sharma (2014) developed pricing model under cooperative and non-cooperative advertising in a supply chain with a single manufacturer and two competitive retailers. Consumer demand function depends on price and advertising. They show that cooperative advertising policy is more beneficial.

After reviewing comprehensively pricing problems of complementary and substitutable products, we found although several pricing models are developed to optimize the profit or cost of the inventory systems for complementary and substitutable products, the pricing problem of both complementary and substitutable products in a two-echelon supply chain with market power and demand leakage considerations is not discussed.

In this paper, a pricing model of complementary and substitutable products in a two-echelon supply chain in which each echelon including two manufacturers and one retailer under demand leakage is developed, where the different market powers are assumed for the chain members. Two different game-theoretic approaches including MS-Stackelberg and MS-Bertrand are employed to examine the pricing decisions of the chain members when the market power is different and subsequently demand leaks from one echelon to the second one.

The rest of the paper is organized as follows. The problem is described in Sect. 2. The model is formulated in Sect. 3. Section 4 provides solution methods under MS-Stackelberg and MS-Bertrand game-theoretic approaches. Sections 5 and 6 contain a numerical example, sensitivity analysis and conclusion as a summary of findings and some future researches.

Problem description

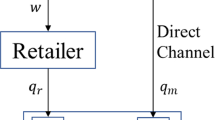
Consider a two-echelon supply chain including one retailer and two manufacturers in every echelon where each echelon supplies two complementary products. In the first echelon, manufacturers 1 and 2, respectively, produce two complementary products 1 and 2 and wholesale the products to retailer 1. Then retailer 1 sells the products 1 and 2 to the customers. In the second one, manufacturers 3 and 4 produce two complementary products 3 and 4 and wholesale them to retailer 2. Therefore, retailer 2 sells the products 3 and 4 to the customers. We assume two complementary products produced in each echelon of supply chain are the same such that products 1 and 3 and products 2 and 4 are the same.

In other words, based on Fig. 1 in which the schema of the supply chain is shown, the manufacturer i produces product i at unit manufacturing cost \(C_{i}\) and sells it to retailer j at unit wholesale price \(W_{i}\). Afterward, the retailer j sells the product i to end users at unit retail price \(P_{i}\) where in the first echelon \(i = 1,2 \, j = 1\) and in the second echelon \(i = 3,4 \, j = 2\). Moreover, we assume that if the unit manufacturing cost \(C_{i}\) is different in each echelon of supply chain, the demand leakage from the echelon with the higher unit manufacturing cost to the echelon with lower unit manufacturing cost occurs. Therefore, the products 1 and 3 and also the products 2 and 4 will be transacted in the market as the substitutable products. This scheme can be used for software and hardware systems of a computer as described in previous section. These products are complementary and are produced by manufacturers 3 and 4, as different brands, respectively. So, if a customer is not satisfied enough from the purchased products of manufacturer 1 and 2, then products 1 and 3 and products 2 and 4 will be substitutable products.

Fig. 1
figure 1

A two-echelon supply chain

Full size image

The assumptions utilized to model the discussed problem are as follows.

  1. 1.

    Demand is deterministic and price-sensitive.

  2. 2.

    The same complementary products are produced in each echelon.

  3. 3.

    In the first model, the same unit manufacturing costs are considered for each echelon.

  4. 4.

    In the second model, different unit manufacturing costs are assumed for each echelon which is caused demand leakage between two echelons of the chain. So, the product with the higher unit manufacturing cost will be substituted by the products with the lower unit manufacturing cost.

  5. 5.

    The higher market power is assumed for the manufacturers than the retailer in each echelon so that the market is managed by the manufacturers.

  6. 6.

    Shortage is not allowed.

  7. 7.

    All the parameters are deterministic and positive.

The main aim of this paper is to study the optimal pricing policies in a two-echelon supply chain for two complementary products under two scenarios with the different market powers of each echelon partners. Two manufacturers and one retailer are the partners of each echelon and the problem is to determine the optimal values of wholesale prices of the manufacturers and the selling prices of the retailers to maximize the profit of the chain.

The following notations are used to develop the problem.

\(C_{i}\) :

The unit manufacturing cost of product i;

\(A_{i}\) :

The primary demand of customers for product i;

\(\beta_{ii}\) :

The self-price sensitivity for the demand of ith product respect to its own price;

\(\beta_{ij}\) :

The cross price sensitivities for the demand of ith product respect to the price of jth product j, \(\beta_{ii} > \beta_{ij}\);

\(L_{1}\) :

The factor of demand leakage between products 1 and 3;

\(L_{2}\) :

The factor of demand leakage between products 2 and 4;

\(D_{i}\) :

The demand rate of customers for product i under the first scenario;

\(D^{\prime}_{i}\) :

The demand rate of customers for product i under the second scenario;

\(\pi_{mi}\) :

The profit function of manufacturer i under the first scenario;

\(\pi^{\prime}_{mi}\) :

The profit function of manufacturer i under the second scenario;

\(\pi_{rj}\) :

The profit function of retailer j under the first scenario;

\(\pi^{\prime}_{rj}\) :

The profit function of retailer j under the second scenario;

\(W_{i}\) :

The wholesale price of product i per unit, ($);

\(P_{i}\) :

The retail price of product i per unit, ($)

The optimal values of the decision variables of the models under the both scenarios are shown by sign (*). In addition, some notations utilized to model the first and the second models are defined in Appendices 1 and 2, respectively.

Mathematical model

In this section, two pricing models for the complementary products with and without demand leakage considerations in a two-echelon supply chain are developed where two manufacturers and one retailer are the partners of each echelon.

The first model: without demand leakage

In this model, the same unit manufacturing costs are considered for the manufacturers of each echelon. So, the demand leakage between two echelons is not occurred. Thus, the demand functions of complementary products 1, 2, 3, and 4 are formulated as follows.

$$D_{1} = A_{1} - \beta_{11} P_{1} - \beta_{12} P_{2}$$
(1)
$$D_{2} = A_{2} - \beta_{22} P_{2} - \beta_{21} P_{1}$$
(2)
$$D_{3} = A_{3} - \beta_{33} P_{3} - \beta_{34} P_{4}$$
(3)
$$D_{4} = A_{4} - \beta_{44} P_{4} - \beta_{43} P_{3}$$
(4)

And the profit functions of the manufacturers and the retailers are represented as follows.

$$\pi_{m1} \left( {W_{1} } \right) = \left( {W_{1} - C_{1} } \right)\left[ {A_{1} - \beta_{11} P_{1} - \beta_{12} P_{2} } \right]$$
(5)
$$\pi_{m2} \left( {W_{2} } \right) = \left( {W_{2} - C_{2} } \right)\left[ {A_{2} - \beta_{22} P_{2} - \beta_{21} P_{1} } \right]$$
(6)
$$\pi_{r1} \left( {P_{1} ,P_{2} } \right) = \left( {P_{1} - W_{1} } \right)\left[ {A_{1} - \beta_{11} P_{1} - \beta_{12} P_{2} } \right] + \left( {P_{2} - W_{2} } \right)\left[ {A_{2} - \beta_{22} P_{2} - \beta_{21} P_{1} } \right]$$
(7)
$$\pi_{m3} \left( {W_{3} } \right) = \left( {W_{3} - C_{3} } \right)\left[ {A_{3} - \beta_{33} P_{3} - \beta_{34} P_{4} } \right]$$
(8)
$$\pi_{m4} \left( {W_{4} } \right) = \left( {W_{4} - C_{4} } \right)\left[ {A_{4} - \beta_{44} P_{4} - \beta_{43} P_{3} } \right]$$
(9)
$$\pi_{r2} \left( {P_{3} ,P_{4} } \right) = \left( {P_{3} - W_{3} } \right)\left[ {A_{3} - \beta_{33} P_{3} - \beta_{34} P_{4} } \right] + \left( {P_{4} - W_{4} } \right)\left[ {A_{4} - \beta_{44} P_{4} - \beta_{43} P_{3} } \right]$$
(10)

The second model with demand leakage

In this case, a symmetrical demand leakage between two echelons of supply chain due to the different unit manufacturing costs of two echelons is considered. The demand leakage occurs between products 1 and 3 and also between products 2 and 4. As a result, products 1 and 3 and products 2 and 4 can be traded as the substitutable products. So, the demand functions of products 1, 2, 3, and 4 are obtained as follows:

$$D^{\prime}_{1} = A_{1} - \beta_{1} P_{1} - L_{1} \left( {P_{1} - P_{3} } \right)$$
(11)
$$D^{\prime}_{2} = A_{2} - \beta_{2} P_{2} - L_{2} \left( {P_{2} - P_{4} } \right)$$
(12)
$$D^{\prime}_{3} = A_{3} - \beta_{3} P_{3} + L_{1} \left( {P_{1} - P_{3} } \right)$$
(13)
$$D^{\prime}_{4} = A_{4} - \beta_{4} P_{4} + L_{2} \left( {P_{2} - P_{4} } \right)$$
(14)

Meanwhile, the following relationships are established between \(\beta_{ii}\),\(\beta_{ij}\), and \(L_{i}\)

$$\beta_{ii} = \beta_{i} + L_{i}$$
(15)
$$\beta_{ij} = L_{i}$$
(16)

Hence, the profit functions of the manufacturers and retailers are represented as follows:

$$\pi^{\prime}_{m1} \left( {W_{1} } \right) = \left( {W_{1} - C_{1} } \right)\left[ {A_{1} - \beta_{1} P_{1} - L_{1} \left( {P_{1} - P_{3} } \right)} \right]$$
(17)
$$\pi^{\prime}_{m2} \left( {W_{2} } \right) = \left( {W_{2} - C_{2} } \right)\left[ {A_{2} - \beta_{2} P_{2} - L_{2} \left( {P_{2} - P_{4} } \right)} \right]$$
(18)
$$\pi^{\prime}_{r1} \left( {P_{1} ,P_{2} } \right) = \left( {P_{1} - W_{1} } \right)\left[ {A_{1} - \beta_{1} P_{1} - L_{1} \left( {P_{1} - P_{3} } \right)} \right] + \left( {P_{2} - W_{2} } \right)\left[ {A_{2} - \beta_{2} P_{2} - L_{2} \left( {P_{2} - P_{4} } \right)} \right]$$
(19)
$$\pi^{\prime}_{m3} \left( {W_{3} } \right) = \left( {W_{3} - C_{3} } \right)\left[ {A_{3} - \beta_{3} P_{3} + L_{1} \left( {P_{1} - P_{3} } \right)} \right]$$
(20)
$$\pi^{\prime}_{m4} \left( {W_{4} } \right) = \left( {W_{4} - C_{4} } \right)\left[ {A_{4} - \beta_{4} P_{4} + L_{2} \left( {P_{2} - P_{4} } \right)} \right]$$
(21)
$$\pi^{\prime}_{r2} \left( {P_{3} ,P_{4} } \right) = \left( {P_{3} - W_{3} } \right)\left[ {A_{3} - \beta_{3} P_{3} + L_{1} \left( {P_{1} - P_{3} } \right)} \right] + \left( {P_{4} - W_{4} } \right)\left[ {A_{4} - \beta_{4} P_{4} + L_{2} \left( {P_{2} - P_{4} } \right)} \right]$$
(22)

Solution method

For solving the on hand problem, the MS game-theoretic approach is applied, in which the followers first make decision about their decision variables and then the leaders determine the optimal values of own decision variables according to the best reaction of the followers. Here, we consider the manufacturers as the Stackelberg leaders and the retailers as Stackelberg followers where the wholesale prices of the manufacturers and the retail prices of the retailers are the decision variables of the introduced model. So, the manufacturers have more market powers than the retailers and also the market is leaded by the manufacturers. Meanwhile, the theory of MS game consists of two practical approaches which are known as the MS-Bertrand and the MS-Stackelberg models. In this section, we intend to obtain the optimal values of the decision variables by employing the MS-Bertrand and the MS-Stackelberg models under both scenarios.

The MS-Bertrand model

Based on the MS-Bertrand approach, although the manufacturers as the leader have more market power than the retailers as the followers, in each echelon of supply chain the manufacturers have the same power and they move, simultaneously. The solution algorithm of MS-Bertrand model is presented in Fig. 2.

Fig. 2
figure 2

The MS-Bertrand algorithm

Full size image

The first model under the MS-Bertrand approach

According to the MS-Bertrand solution algorithm, the optimal values of selling prices of four products versus the wholesale prices are obtained as follows:

$$P_{1}^{ * } \left( {W_{1} ,W_{2} } \right) = F_{1} + F_{2} W_{1} + F_{3} W_{2}$$
(23)
$$P_{2}^{ * } \left( {W_{1} ,W_{2} } \right) = F_{4} + F_{5} \,W_{1} + F_{6} \,W_{2}$$
(24)
$$P_{3}^{ * } \left( {W_{3} ,W_{4} } \right) = U_{1} + U_{2} \,W_{3} + U_{3} W_{4}$$
(25)
$$P_{4}^{ * } \left( {W_{3} ,W_{4} } \right) = U_{4} + U_{5} \,W_{3} + U_{6} \,W_{4}$$
(26)

Substituting Eqs. (23)–(26) into the manufacturer’s profit function, the optimal values of wholesale prices of products are acquired as follows:

$$W_{1}^{*} = \frac{{E_{1} E_{6} - E_{2} E_{3} }}{{E_{4} E_{6} - E_{5} E_{3} }}$$
(27)
$$W_{2}^{*} = \frac{{E_{2} E_{4} - E_{1} E_{5} }}{{E_{4} E_{6} - E_{5} E_{3} }}$$
(28)
$$W_{3}^{*} = \frac{{G_{1} G_{6} - G_{2} G_{3} }}{{G_{4} G_{6} - G_{5} G_{3} }}$$
(29)
$$W_{4}^{*} = \frac{{G_{2} G_{4} - G_{1} G_{5} }}{{G_{4} G_{6} - G_{5} G_{3} }}$$
(30)

Then, by substituting Eqs. (27)–(30) into Eqs. (23)–(26), the independent optimal selling prices can be obtained as:

$$P_{1}^{*} = F_{1} + F_{2} \left( {\frac{{E_{1} E_{6} - E_{2} E_{3} }}{{E_{4} E_{6} - E_{5} E_{3} }}} \right) + F_{3} \left( {\frac{{E_{1} E_{6} - E_{2} E_{3} }}{{E_{4} E_{6} - E_{5} E_{3} }}} \right)$$
(31)
$$P_{2}^{*} = F_{4} + F_{5} \left( {\frac{{E_{1} E_{6} - E_{2} E_{3} }}{{E_{4} E_{6} - E_{5} E_{3} }}} \right) + F_{6} \left( {\frac{{E_{2} E_{4} - E_{1} E_{5} }}{{E_{4} E_{6} - E_{5} E_{3} }}} \right)$$
(32)
$$P_{3}^{*} = U_{1} + U_{2} \left( {\frac{{G_{1} G_{6} - G_{2} G_{3} }}{{G_{4} G_{6} - G_{5} G_{3} }}} \right) + U_{3} \left( {\frac{{G_{2} G_{4} - G_{1} G_{5} }}{{G_{4} G_{6} - G_{5} G_{3} }}} \right)$$
(33)
$$P_{4}^{*} = U_{4} + U_{5} \left( {\frac{{G_{1} G_{6} - G_{2} G_{3} }}{{G_{4} G_{6} - G_{5} G_{3} }}} \right) + U_{6} \left( {\frac{{G_{2} G_{4} - G_{1} G_{5} }}{{G_{4} G_{6} - G_{5} G_{3} }}} \right)$$
(34)

The second model under the MS-Bertrand approach

According to the MS-Bertrand solution algorithm, the optimal retail prices of four products versus the wholesale prices of the manufacturers are obtained as follows:

$$P_{1}^{ * } \left( {W_{1} ,W_{3} } \right) = K_{1} + K_{2} W_{3} + K_{3} W_{1}$$
(35)
$$P_{2}^{ * } \left( {W_{2} ,W_{4} } \right) = K_{4} + K_{5} W_{4} + K_{6} W_{2}$$
(36)
$$P_{3}^{ * } \left( {W_{1} ,W_{3} } \right) = K_{7} + K_{8} W_{1} + K_{3} W_{3}$$
(37)
$$P_{4}^{ * } \left( {W_{2} ,W_{4} } \right) = K_{9} + K_{10} W_{2} + K_{6} W_{4}$$
(38)

Substituting Eqs. (35)–(38) into the profit functions of manufacturers, the optimal values of wholesale prices are acquired as follows:

$$W_{1}^{*} = \frac{{N_{1} N_{6} - N_{2} N_{3} }}{{N_{4} N_{6} - N_{5} N_{3} }}$$
(39)
$$W_{2}^{*} = \frac{{N_{7} N_{12} - N_{8} N_{9} }}{{N_{10} N_{12} - N_{11} N_{9} }}$$
(40)
$$W_{3}^{*} = \frac{{N_{2} N_{4} - N_{1} N_{5} }}{{N_{4} N_{6} - N_{5} N_{5} }}$$
(41)
$$W_{4}^{*} = \frac{{N_{8} N_{10} - N_{7} N_{11} }}{{N_{10} N_{12} - N_{11} N_{9} }}$$
(42)

Therefore, by substituting Eqs. (39)–(42) into Eqs. (35)–(38), the optimal retail prices can be obtained independently as:

$$P_{1}^{*} = K_{1} + K_{2} \left( {\frac{{N_{2} N_{4} - N_{1} N_{5} }}{{N_{4} N_{6} - N_{5} N_{3} }}} \right) + K_{3} \left( {\frac{{N_{1} N_{6} - N_{2} N_{3} }}{{N_{4} N_{6} - N_{5} N_{3} }}} \right)$$
(43)
$$P_{2}^{*} = K_{4} + K_{5} \left( {\frac{{N_{8} N_{10} - N_{7} N_{11} }}{{N_{10} N_{12} - N_{11} N_{9} }}} \right) + K_{6} \left( {\frac{{N_{7} N_{12} - N_{8} N_{9} }}{{N_{10} N_{12} - N_{11} N_{9} }}} \right)$$
(44)
$$P_{3}^{*} = K_{7} + K_{8} \left( {\frac{{N_{1} N_{6} - N_{2} N_{3} }}{{N_{4} N_{6} - N_{5} N_{3} }}} \right) + K_{3} \left( {\frac{{N_{2} N_{4} - N_{1} N_{5} }}{{N_{4} N_{6} - N_{5} N_{3} }}} \right)$$
(45)
$$P_{4}^{*} = K_{9} + K_{10} \left( {\frac{{N_{7} N_{12} - N_{8} N_{9} }}{{N_{10} N_{12} - N_{11} N_{9} }}} \right) + K_{6} \left( {\frac{{N_{8} N_{10} - N_{7} N_{11} }}{{N_{10} N_{12} - N_{11} N_{9} }}} \right)$$
(46)

The MS-Stackelberg model

Under this approach, the manufacturers, because of the more market powers, are considered as the leaders of Stackelberg and the retailers are considered as the followers. Moreover, in each echelon of supply chain, the manufacturers don’t have the similar powers and they sequentially make decisions about own decision variables. Also the Stackelberg game is current between them such that one of the manufacturers plays the role of the Stackelberg leader and the other one is the follower of Stackelberg. The figurative MS-Stackelberg solution algorithm is indicated in Fig. 3 in which manufacturer i is the leader and manufacturer j is the follower.

Fig. 3
figure 3

The MS-Stackelberg algorithm

Full size image

The first model under the MS-Stackelberg approach

Based on the MS-Stackelberg algorithm, the optimal values of selling prices of four products versus the wholesale prices of manufacturers are obtained, similar to the MS-Bertrand model, as follows:

$$P_{1}^{ * } \left( {W_{1} ,W_{2} } \right) = F_{1} + F_{2} W_{1} + F_{3} W_{2}$$
(47)
$$P_{2}^{ * } \left( {W_{1} ,W_{2} } \right) = F_{4} + F_{5} W_{1} + F_{6} W_{2}$$
(48)
$$P_{3}^{ * } \left( {W_{3} ,W_{4} } \right) = U_{1} + U_{2} W_{3} + U_{3} W_{4}$$
(49)
$$P_{4}^{ * } \left( {W_{3} ,W_{4} } \right) = U_{4} + U_{5} W_{3} + U_{6} W_{4}$$
(50)

Since in the first echelon manufacturer 1 is the leader and manufacturer 2 is the follower, so by substituting Eqs. (47) and (48) into the profit functions of manufacturer 1 and 2, the optimal wholesale price of the manufacturer 1 is obtained as:

$$W_{2} = \frac{{E_{2} }}{{E_{6} }} - \frac{{E_{5} }}{{E_{6} }}W_{1}$$
(51)
$$W_{1}^{ * } = \frac{{E_{7} }}{{E_{8} }}$$
(52)

Then by substituting Eq. (52) into Eq. (51), the optimal wholesale price of manufacturer 2 is obtained as follows:

$$W_{2}^{ * } = \frac{{E_{2} }}{{E_{6} }} - \frac{{E_{5} }}{{E_{6} }}\left( {\frac{{E_{7} }}{{E_{8} }}} \right)$$
(53)

In the second echelon of supply chain, manufacturer 3 is the leader and manufacturer 4 is the follower. Afterward, by substituting Eqs. (49) and (50) into the profit functions of the second echelon manufacturers, the optimal wholesale price of manufacturers 3 is obtained, so we have:

$$W_{4} = \frac{{G_{2} }}{{G_{6} }} - \frac{{G_{5} }}{{G_{6} }}W_{3}$$
(54)
$$W_{3}^{ * } = \frac{{G_{7} }}{{G_{8} }}$$
(55)

Hence, the optimal value of manufacturer 4 is derived by substituting Eq. (55) into Eq. (54) as follows:

$$W_{4}^{ * } = \frac{{G_{2} }}{{G_{6} }} - \frac{{G_{5} }}{{G_{6} }}\left( {\frac{{G_{7} }}{{G_{8} }}} \right)$$
(56)

Therefore, by substituting Eqs. (52)–(56) into Eqs. (47)–(50), the independent retailers’ optimal retail prices are obtained which are:

$$P_{1}^{*} = F_{1} + F_{2} \left( {\frac{{E_{7} }}{{E_{8} }}} \right) + F_{3} \left( {\frac{{E_{2} }}{{E_{4} }} - \frac{{E_{5} }}{{E_{6} }}\left( {\frac{{E_{7} }}{{E_{8} }}} \right)} \right)$$
(57)
$$P_{2}^{*} = F_{4} + F_{5} \left( {\frac{{E_{7} }}{{E_{8} }}} \right) + F_{6} \left( {\frac{{E_{2} }}{{E_{6} }} - \frac{{E_{5} }}{{E_{6} }}\left( {\frac{{E_{7} }}{{E_{8} }}} \right)} \right)$$
(58)
$$P_{3}^{*} = U_{1} + U_{2} \left( {\frac{{G_{7} }}{{G_{8} }}} \right) + U_{3} \left( {\frac{{G_{2} }}{{G_{6} }} - \frac{{G_{5} }}{{G_{6} }}\left( {\frac{{G_{7} }}{{G_{8} }}} \right)} \right)$$
(59)
$$P_{4}^{*} = U_{4} + U_{5} \left( {\frac{{G_{7} }}{{G_{8} }}} \right) + U_{6} \left( {\frac{{G_{2} }}{{G_{6} }} - \frac{{G_{5} }}{{G_{6} }}\left( {\frac{{G_{7} }}{{G_{8} }}} \right)} \right)$$
(60)

The second model under MS-Stackelberg approach

Based on the MS-Stackelberg algorithm, the optimal selling prices of four products versus the wholesale prices, which are obtained as the MS-Bertrand model, are as follows.

$$P_{1}^{ * } \left( {W_{1} ,W_{3} } \right) = K_{1} + K_{2} W_{3} + K_{3} W_{1}$$
(61)
$$P_{2}^{ * } \left( {W_{2} ,W_{4} } \right) = K_{4} + K_{5} W_{4} + K_{6} W_{2}$$
(62)
$$P_{3}^{ * } \left( {W_{1} ,W_{3} } \right) = K_{7} + K_{8} W_{1} + K_{3} W_{3}$$
(63)
$$P_{4}^{ * } \left( {W_{2} ,W_{4} } \right) = K_{9} + K_{10} W_{2} + K_{6} W_{4}$$
(64)

According to the assumptions, a symmetrical demand leakage occurs between two echelons of supply chain on the same products because of different unit manufacturing costs in the echelons. The demand leakage occurs between products 1 and 3 and also products 2 and 4. Here, we assume that the unit manufacturing costs of manufacturers 1 and 2 are larger than manufacturers 3 and 4. So, the manufacturers 1 and 2 lost their demand and the manufacturers 3 and 4 against earn more demands due to their lower unit manufacturing costs.

Therefore, manufacturers 3 and 4 handle the market owing to having the more powers than the other ones. As a result, manufacturers 3 and 4 are the Stackelberg leaders and manufacturers 1 and 2 are the Stackelberg followers. Thus, by substituting Eqs. (61) and (63) into the profit functions of manufacturers, the optimal wholesale price of manufacturer 1 is derived as follows:

$$W_{1} = \frac{{N_{1} }}{{N_{4} }} - \frac{{N_{3} }}{{N_{4} }}W_{3}$$
(65)
$$W_{3}^{ * } = \frac{{N_{13} }}{{N_{14} }}$$
(66)

Then, the optimal value of unit wholesale price of manufacturer 1is obtained by substituting Eq. (66) into Eq. (65) which is:

$$W_{1}^{ * } = \frac{{N_{1} }}{{N_{4} }} - \frac{{N_{3} }}{{N_{4} }}\left( {\frac{{N_{13} }}{{N_{14} }}} \right)$$
(67)

Furthermore, by substituting Eqs. (62) and (64) into the objective functions of manufacturers 2 and 4, the optimal unit wholesale price of manufacturer 4 is:

$$W_{2} = \frac{{N_{7} }}{{N_{10} }} - \frac{{N_{9} }}{{N_{10} }}W_{4}$$
(68)
$$W_{4}^{ * } = \frac{{N_{15} }}{{N_{16} }}$$
(69)

In addition, the optimal unit wholesale price of manufacturer 2 is obtained by substituting Eq. (69) into Eq. (68) which is:

$$W_{2}^{ * } = \frac{{N_{7} }}{{N_{10} }} - \frac{{N_{9} }}{{N_{10} }}\left( {\frac{{N_{15} }}{{N_{16} }}} \right)$$
(70)

Eventually, by substituting Eqs. (66)–(70) into Eqs. (61)–(64), the retailers’ optimal unit retail prices can be obtained independently, as follows:

$$P_{1}^{*} = K_{1} + K_{2} \left( {\frac{{N_{13} }}{{N_{14} }}} \right) + K_{3} \left( {\frac{{N_{1} }}{{N_{4} }} - \frac{{N_{3} }}{{N_{4} }}\left( {\frac{{N_{13} }}{{N_{14} }}} \right)} \right)$$
(71)
$$P_{2}^{*} = K_{4} + K_{5} \left( {\frac{{N_{15} }}{{N_{16} }}} \right) + K_{6} \left( {\frac{{N_{7} }}{{N_{10} }} - \frac{{N_{9} }}{{N_{10} }}\left( {\frac{{N_{15} }}{{N_{16} }}} \right)} \right)$$
(72)
$$P_{3}^{*} = K_{7} + K_{8} \left( {\frac{{N_{1} }}{{N_{4} }} - \frac{{N_{3} }}{{N_{4} }}\left( {\frac{{N_{13} }}{{N_{14} }}} \right)} \right) + K_{3} \left( {\frac{{N_{13} }}{{N_{14} }}} \right)$$
(73)
$$P_{4}^{*} = K_{9} + K_{10} \left( {\frac{{N_{7} }}{{N_{10} }} - \frac{{N_{9} }}{{N_{10} }}\left( {\frac{{N_{15} }}{{N_{16} }}} \right)} \right) + K_{6} \left( {\frac{{N_{15} }}{{N_{16} }}} \right)$$
(74)

Numerical example and sensitivity analysis

In this section, a numerical example for a two-echelon supply chain including two manufacturers and one retailer in each echelon is presented. According to the assumption, the model is developed for two complementary products and price-sensitive demand. In addition, the discussed problem is formulated under two different scenarios where the MS-Stackelberg and the MS-Bertrand solution algorithms are employed to solve them. In this example, we consider \(A_{1} = A_{2} = 180\), \(A_{3} = A_{4} = 220\), \(C_{1} = C_{2} = 25\), \(C_{3} = C_{4} = 20\), \(\beta_{11} = \beta_{33} = 0.5\), \(\beta_{22} = \beta_{44} = 0.6\), \(\beta_{12} = \beta_{21} = 0.3\), \(\beta_{34} = \beta_{43} = 0.35\), \(\beta_{13} = \beta_{31} = 0.3\), \(\beta_{24} = \beta_{42} = 0.35\) and the results are shown in Tables 1 and 2.

Table 1 Optimal decision of retail prices and wholesale prices under different decision scenarios
Full size table
Table 2 Maximum profits of the total system and for every firm under different decision scenarios
Full size table

The findings obtained from Table 1 are summarized as follows.

  • According to the obtained results of the first model, retailers 1 and 2 achieve their highest optimal retail prices for products 1 and 3 under the MS-Stackelberg approach and also for products 2 and 4 under the MS-Bertrand approach.

  • The highest optimal wholesale prices of products 1 and 3 are acquired under the MS-Stackelberg approach and also for products 2 and 4 under the MS-Bertrand approach in the first model. About the second model, the highest optimal wholesale prices and optimal retail prices of products 1, 2, 3, and 4 are achieved under the MS-Stackelberg approach.

From Table 2, the following results can be obtained too.

  • In the first model, manufacturers 1 and 3 achieve their highest profits under the MS-Stackelberg approach and the manufacturers 2 and 4 achieve their highest profits under the MS-Bertrand approach. In the second model, all the manufacturers achieve their highest profits under the MS-Stackelberg approach.

  • The retailers 1 and 2 achieve their highest profits using MS-Bertrand game-theoretic approach in the first model, and in the second model retailer 1 achieves his highest profit applying MS-Stackelberg game and retailer 2 achieves his highest profit using MS-Bertrand game.

  • The whole supply chain achieves the maximum profit under the MS-Bertrand game-theoretic approach in the first and the second models.

To study the effect of changing the parameter values on the optimal values of the decision variables for this paper, a sensitivity analysis is performed. The sensitivity analysis for the first model is done only at the first echelon of supply chain and for the second model is done only between products 1 and 3. Tables 3, 4, 5 and 6 show the results of the first model under MS-Bertrand and MS-Stackelberg policies, respectively.

Table 3 The sensitivity analysis for the first model in first echelon of supply chain under MS-Bertrand policy
Full size table
Table 4 The sensitivity analysis for the first models profit functions in first echelon of supply chain under MS-Bertrand policy
Full size table
Table 5 The sensitivity analysis for the first model in first echelon of supply chain under MS-Stackelberg policy
Full size table
Table 6 The sensitivity analysis for the first models profit functions in first echelon of supply chain under MS-Stackelberg policy
Full size table

The findings obtained from Tables 3 and 4 are summarized as follows.

  • \(W_{1}^{ * }\), \(W_{2}^{ * }\), \(P_{1}^{ * }\), \(P_{2}^{ * }\), \(D_{1}\), \(D_{2}\), \(\pi_{m1}\), \(\pi_{m2}\) and \(\pi_{r1}\) are consumedly sensitive respect to the changes in parameters \(A_{1}\) and \(A_{2}\). When \(A_{1}\) and \(A_{2}\) are decreased by 25 and 50 %, all of decision variables decrease and vice versa.

  • \(W_{1}^{ * }\), \(W_{2}^{ * }\), \(P_{1}^{ * }\), \(P_{2}^{ * }\), \(\pi_{m1}\) and \(\pi_{m2}\) are consumedly sensitive respect to the changes in parameters \(\beta_{11}\) and \(\beta_{22}\), while \(D_{1}\), \(D_{2}\) and \(\pi_{r1}\) are moderately sensitive respect to the changes in value of \(\beta_{11}\) and \(\beta_{22}\). When \(\beta_{11}\) and \(\beta_{22}\) are decreased by 25 and 50 %, \(D_{1}\) and \(D_{2}\) decrease, while \(W_{1}^{ * }\), \(W_{2}^{ * }\), \(P_{1}^{ * }\), \(P_{2}^{ * }\), \(\pi_{m1}\), \(\pi_{m2}\) and \(\pi_{r1}\) increase and vice versa.

  • \(W_{1}^{ * }\), \(W_{2}^{ * }\), \(P_{1}^{ * }\), \(P_{2}^{ * }\), \(D_{1}\), \(D_{2}\), \(\pi_{m1}\), \(\pi_{m2}\) and \(\pi_{r1}\) are moderately sensitive respect to the changes in \(\beta_{12}\) and \(\beta_{21}\). When \(\beta_{12}\) and \(\beta_{21}\) are decreased by 25 and 50 %, all of the decision variables increase and vice versa.

  • \(W_{1}^{ * }\), \(W_{2}^{ * }\), \(P_{1}^{ * }\) and \(P_{2}^{ * }\) are slightly sensitive respect to the changes in parameters \(C_{1}\) and \(C_{2}\), while \(D_{1}\), \(D_{2}\), \(\pi_{m1}\), \(\pi_{m2}\) and \(\pi_{r1}\) are moderately sensitive respect to the changes in value of \(C_{1}\) and \(C_{2}\). When \(C_{1}\) and \(C_{2}\) are decreased by 25 and 50 %, \(W_{1}^{ * }\), \(W_{2}^{ * }\), \(P_{1}^{ * }\) and \(P_{2}^{ * }\) decrease while \(D_{1}\), \(D_{2}\), \(\pi_{m1}\), \(\pi_{m2}\) and \(\pi_{r1}\) increase and vice versa.

The results of Tables 5 and 6 are similar to the results of Tables 3 and 4, except for sensitivity analysis of \(\beta_{11}\) and \(\beta_{22}\). We assume manufacture 1 is the leader and manufacturer 2 is the follower. The results show \(W_{1}^{ * }\), \(P_{1}^{ * }\) and \(\pi_{m1}\) are consumedly sensitive respect to the changes in parameters \(\beta_{11}\) and \(\beta_{22}\), while \(W_{2}^{ * }\), \(P_{2}^{ * }\) and \(\pi_{m2}\) are slightly sensitive respect to the changes in value of \(\beta_{11}\) and \(\beta_{22}\). When \(\beta_{11}\) and \(\beta_{22}\) are decreased by 25 and 50 %, \(W_{1}^{ * }\), \(P_{1}^{ * }\) and \(\pi_{m1}\) increase while \(W_{2}^{ * }\), \(P_{2}^{ * }\) and \(\pi_{m2}\) decrease. Also, sensitivity analysis is performed on the second model under MS-Bertrand policy and its results are shown Tables 7 and 8. Moreover the results of sensitivity analysis of the second model under MS-Stackelberg are shown in Tables 9 and 10.

Table 7 The sensitivity analysis for the second model between products 1 and 3 under MS-Bertrand policy
Full size table
Table 8 The sensitivity analysis for the second models profit functions between products 1 and 3 under MS-Bertrand policy
Full size table
Table 9 The sensitivity analysis for the second model between products 1 and 3 under MS-Stackelberg policy
Full size table
Table 10 The sensitivity analysis for the second models profit functions between products 1 and 3 under MS-Stackelberg policy
Full size table

The findings obtained from Tables 7 and 8 are summarized as follows.

  • \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\), \(D^{\prime}_{1}\), \(D^{\prime}_{3}\), \(\pi^{\prime}_{m1}\), \(\pi^{\prime}_{m3}\), \(\pi^{\prime}_{r1}\) and \(\pi^{\prime}_{r2}\) are moderately sensitive respect to the changes in parameters \(A_{1}\) and \(A_{3}\). When \(A_{1}\) and \(A_{3}\) are decreased by 25 and 50 %, all of decision variables decrease and vice versa.

  • \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\), \(D^{\prime}_{1}\), \(D^{\prime}_{3}\), \(\pi^{\prime}_{m1}\), \(\pi^{\prime}_{m3}\), \(\pi^{\prime}_{r1}\) and \(\pi^{\prime}_{r2}\) are consumedly sensitive respect to the changes in parameters \(\beta_{1}\) and \(\beta_{3}\). When \(\beta_{1}\) and \(\beta_{3}\) are decreased by 25 and 50 %, all of the decision variables increase and vice versa.

  • \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\), \(D^{\prime}_{1}\) and \(D^{\prime}_{3}\) are moderately sensitive respect to the changes in parameters \(\beta_{13}\) and \(\beta_{31}\), while \(\pi^{\prime}_{m1}\), \(\pi^{\prime}_{m3}\), \(\pi^{\prime}_{r1}\) and \(\pi^{\prime}_{r2}\) are slightly sensitive respect to the changes in parameters \(\beta_{13}\) and \(\beta_{31}\). When \(\beta_{13}\) and \(\beta_{31}\) are decreased by 25 and 50 %, \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\) and \(P_{3}^{ * }\) increase, while \(D^{\prime}_{1}\), \(D^{\prime}_{3}\), \(\pi^{\prime}_{m1}\), \(\pi^{\prime}_{m3}\), \(\pi^{\prime}_{r1}\) and \(\pi^{\prime}_{r2}\) decrease and vice versa.

  • \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\), \(D^{\prime}_{1}\), \(D^{\prime}_{3}\), \(\pi^{\prime}_{m1}\), \(\pi^{\prime}_{m3}\), \(\pi^{\prime}_{r1}\) and \(\pi^{\prime}_{r2}\) are slightly sensitive respect to the changes in value of \(C_{1}\). When \(C_{1}\) is decreased by 25 and 50 %, \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\), \(D^{\prime}_{3}\), \(\pi^{\prime}_{m3}\) and \(\pi^{\prime}_{r2}\) decrease, while \(D^{\prime}_{1}\), \(\pi^{\prime}_{m1}\) and \(\pi^{\prime}_{r1}\) increase and vice versa.

  • \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\), \(D^{\prime}_{1}\), \(D^{\prime}_{3}\), \(\pi^{\prime}_{m1}\), \(\pi^{\prime}_{m3}\), \(\pi^{\prime}_{r1}\) and \(\pi^{\prime}_{r2}\) are slightly sensitive respect to the changes in value of \(C_{3}\). When \(C_{3}\) is decreased by 25 and 50 %, \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\), \(D^{\prime}_{1}\), \(\pi^{\prime}_{m1}\) and \(\pi^{\prime}_{r1}\) decrease, while \(D^{\prime}_{3}\), \(\pi^{\prime}_{m3}\) and \(\pi^{\prime}_{r2}\) increase and vice versa.

The results of Tables 9 and 10 are similar to the results of Tables 7 and 8, except for the sensitivity analysis of \(\beta_{13}\) and \(\beta_{31}\). \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\), \(D^{\prime}_{1}\) and \(D^{\prime}_{3}\) are moderately sensitive respect to the changes in parameters \(\beta_{13}\) and \(\beta_{31}\), while \(\pi^{\prime}_{m1}\), \(\pi^{\prime}_{m3}\), \(\pi^{\prime}_{r1}\) and \(\pi^{\prime}_{r2}\) are slightly sensitive respect to the changes in parameters \(\beta_{13}\) and \(\beta_{31}\). When \(\beta_{13}\) and \(\beta_{31}\) are decreased by 25 and 50 %, \(W_{1}^{ * }\), \(W_{3}^{ * }\), \(P_{1}^{ * }\), \(P_{3}^{ * }\) and \(\pi^{\prime}_{r2}\) increase, while \(D^{\prime}_{1}\), \(D^{\prime}_{3}\), \(\pi^{\prime}_{m1}\), \(\pi^{\prime}_{m3}\) and \(\pi^{\prime}_{r1}\) decrease and vice versa.

Some of the sensitivity analyses in Tables 3, 4, 5, 6, 7, 8, 9 and 10 are illustrated by Figs. 4, 5, 6, 7, 8, 9, 10, 11 and 12. Figures 4, 5, 6, 7, 8, 9, 10, 11 and 12 show the effect of some key parameters on optimal wholesale and retail prices and also on the profit of the chain.

Fig. 4
figure 4

Changes of optimal prices with respect to \(A_{1} = A_{2}\) for the first model under MS-Bertrand policy

Full size image
Fig. 5
figure 5

Changes of optimal prices with respect to \(\beta_{11} = \beta_{22}\) for the first model under MS-Bertrand policy

Full size image
Fig. 6
figure 6

Changes of maximum profits with respect to \(A_{1} = A_{2}\) for the first model under MS-Bertrand policy

Full size image
Fig. 7
figure 7

Changes of optimal prices with respect to \(\beta_{12} = \beta_{21}\) for the first model under MS-Stackelberg policy

Full size image
Fig. 8
figure 8

Changes of optimal prices with respect to \(C_{1} = C_{2}\) for the first model under MS-Stackelberg policy

Full size image
Fig. 9
figure 9

Changes of optimal prices with respect to \(A_{1}\) for the second model under MS-Bertrand policy

Full size image
Fig. 10
figure 10

Changes of optimal prices with respect to \(\beta_{1} = \beta_{3}\) for the second model under MS-Bertrand policy

Full size image
Fig. 11
figure 11

Changes of maximum profits with respect to \(C_{1}\) for the second model under MS-Stackelberg policy

Full size image
Fig. 12
figure 12

Changes of maximum demands with respect to \(C_{3}\) for the second model under MS-Stackelberg policy

Full size image

Conclusion

We discussed the pricing problem of two complementary and substitutable products in a two-echelon supply chain under two scenarios where two manufacturers and one retailer are the members of each echelon. Under the first scenario, which leads to develop the first model, the same unit manufacturing costs for both echelons are supposed and in the second one we assume that the unit manufacturing costs of echelons are different which causes to leak demand from the echelon with higher unit manufacturing cost to the lower one. Two same complementary products are supplied to the market by each echelon of chain to satisfy the customers’ demand. The model is developed under price-sensitive and deterministic demand.

The main aim of this research is to analyze the pricing decisions of the members of chain for complementary and substitutable products with the different market powers under two scenarios. In this research, two solution algorithms including MS-Bertrand and MS-Stackelberg game-theoretic approaches are presented to survey the effects of the different market powers on the optimal value of decision variables and also the total profit of the supply chain where the whole sale prices of manufacturers and the retail prices of retailers are the decision variables of the proposed models. Finally, a numerical example to show the applicability of the proposed models is presented and we found that the maximum profit of the whole supply chain is obtained under MS-Bertrand approach in both proposed models. For future works, the model can be extended under stochastic demand and also considering competing retailers can develop and enhance our models.

Funding

The first author would like to thank the financial support of the University of Tehran for this research under Grant Number 30015-1-02.