Abstract
The growing interest in technicians’ workloads research is probably associated with the recent surge in competition. This was prompted by unprecedented technological development that triggers changes in customer tastes and preferences for industrial goods. In a quest for business improvement, this worldwide intense competition in industries has stimulated theories and practical frameworks that seek to optimise performance in workplaces. In line with this drive, the present paper proposes an optimisation model which considers technicians’ reliability that complements factory information obtained. The information used emerged from technicians’ productivity and earned-values using the concept of multi-objective modelling approach. Since technicians are expected to carry out routine and stochastic maintenance work, we consider these workloads as constraints. The influence of training, fatigue and experiential knowledge of technicians on workload management was considered. These workloads were combined with maintenance policy in optimising reliability, productivity and earned-values using the goal programming approach. Practical datasets were utilised in studying the applicability of the proposed model in practice. It was observed that our model was able to generate information that practicing maintenance engineers can apply in making more informed decisions on technicians’ management.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Maintenance workload optimisation scheduling problem has witnessed the application of different modelling approaches in improving equipment availability (Safaei et al. 2008). Performance metrics, methodologies and tools used to ascertain the control of technicians’ workload during the plant’s operating hours have evolved for decades. The pressure and growing interest in technicians’ workload practices and research seems to be associated strongly with the recent surge in competition globally. It was also triggered by the increasingly difficulty in economic growth of industries. Current research trends in this area therefore match technicians’ characteristics with workloads and other considerations. There are immense benefits in understanding the reliability of technicians (Gregoriades and Sutcliffe 2008). This will help in the integration of technicians’ reliability into technicians’ work performance evaluation. All these efforts are to minimise maintenance job rework and reduce overtime. It also aids making the overhaul activity more effective and reduce equipment breakdown to an acceptable level. This study is motivated by lack of information on how to optimise the technicians’ costs, workloads, sizes and reliability of technicians. Most theoretical accounts of reliability have been skewed towards machines.
An organisation with an effective and efficient group of technicians experiences several benefits. These benefits are improved productivity, elevated sales, enhanced customer service, reduced labour costs, improved employee engagement and satisfaction (Bartels and Richey 2008). Focusing on the maintenance department as a major area for driving the above-mentioned benefits is important because of its interrelationships with other departments. Maintenance problems in manufacturing systems are diverse. Technicians’ workload and reliability problems, which are key problems in solving other problems in maintenance system, are least considered in literature. Several contributions on spare parts management, machine availability (Safaei et al. 2008) and maintenance budget (Mansour 2011; Ighravwe and Oke 2014; Ighravwe et al. 2015) have been documented. Within the last few decades, researchers and industrial practitioners have started considering human factors in maintenance systems with a view of ensuring robust maintenance management systems.
Dealing with the maximisation of a multi-objective problem that is nonlinear in formulation, a single objective model with weights for each objective was considered. Such a model can be solved easily using metaheuristics (evolutionary algorithms and swarm algorithms) in order to generate compromise solutions. Currently, there exists sparse documentation on big-bang–big-crunch (BB–BC) and EP algorithms as solution methods for technicians’ parameters optimisation.
Studying fatigue during the design of technicians’ workload and reliability for planned operations will help in improving work-plans. Another aspect of technician’s problem, which has been sparingly considered in the literature, is experiential knowledge of the technicians who engage in rework activities.
The objective of this study was to develop a mixed-integer optimisation model that optimises technicians’ sizes, workloads (service times), reliability, availability, performance (efficiency) and quality of workdone. A performance comparative analysis of EP and BB–BC algorithms when used in solving the proposed model was also carried out. The selection of these algorithms was motivated by their low computation time.
Literature review
Maintenance system operations are often executed using maintenance teams (Hedjazi 2015). These teams are formed based on the skills of technicians (Hedjazi 2015) and the types of maintenance activities (Ighravwe and Oke 2014; Ighravwe et al. 2015) in an organisation. Tohidi and Tarokh (2005) reported that when forming teams, there is the need to ensure proper communication systems. These help in improving the productivity of teams. Thus, the interest of researchers and practitioners in maintenance systems is on the analysis of types of maintenance activities, policies, technicians’ attributes (productivity, service time and skills) and cost of operating maintenance systems (Lai et al. 2015). The core reason for studying maintenance departmental performance is to improve organisation’s profitability (Alsyouf 2007). This has stimulated different scientific methods in analysing maintenance systems.
Maintenance workload management helps in determining equipment downtime. When workload is optimally shared among the team members, low amounts of equipment downtime will be experienced. For example, the concern of Oladokun et al. (2006) was how to predict equipment downtime. In their study, a predictive model was designed to predict equipment downtime using machine breakdown periods and maintenance repair time as dependent variable. The issue of how to determine maintenance repair times was not exhaustively addressed in their study. Rana and Purohit (2012) investigated the application of critical path method in addressing the problems of technician’s productivity, maintenance time and tasks balancing. One drawback of their study is the assumption that technicians are capable of doing any maintenance work in an organisation. In practice, this assumption is feasible for small-scale organisations. However, for large-scale systems, the assumption may be violated. This study relaxed the assumption of Rana and Purohit (2012) by considering technicians for different sections (mechanical, electrical and instrumentation). The scope of Ighravwe and Oke’s (2014) study limited maintenance activities to routine maintenance. Ighravwe and Oke (2014) modelled maintenance time utilisation problem by considering the allocated and actual maintenance time used by technicians. No mention of technician’s training and fatigue experienced during the execution of maintenance activities was mentioned in their work. In the work of He et al. (2014), the issue of technician’s reliability and cost were addressed using nonlinear programming techniques. Their proposed model can be applied in a maintenance system. However, consideration was not given to the impact of technician’s fatigue, experiential knowledge and training on technician’s reliability.
Huge amount of funds are usually invested in maintenance systems of organisations. This is necessary avert machine breakdowns, which could be more costly. Fajardo and Drekic (2015) pointed out that cost-effective maintenance checks could be achieved during close-down periods. The problem of technician cost and equipment availability was studied by Safaei et al. (2008). The application of simulated annealing as a solution method for handling multi-objective technicians’ problem was demonstrated. They considered the management of regular, outsourcing and overtime maintenance activities. Mansour’s (2011) studied maintenance cost minimisation problem by proposing a mixed-integer programming model that incorporates equipment complexity. Their work investigated the suitability of genetic algorithm as a solution method for technicians’ parametric optimisation.
Kaufman and Lewis (2007) considered the application of repair and replacement models for maintenance workload management. In their study, information on service rates and failures, fixed maintenance times and random replacement times was generated. A model that minimised the total cost of technicians used for maintenance activities was developed by De Bruecker et al. (2015) using mixed-integer programming approach. In their study, a model enhancement heuristic was proposed as solution method for their model. The heuristic considered stochastic service levels.
Knapp and Mahajan (1998) conducted a comparative analysis between centralised and decentralised organisational structure as it affects maintenance systems. Consideration was given to technician-type (in-house and sub-contracted technicians) and training levels of technicians. The results of their study demonstrated how optimal allocation of technicians can be achieved. A study which considered organisational policies on technicians’ capacity was presented by Mjema (2002). The challenge of managing the switches of technicians for mechanical and electrical workloads was considered. Their analysis was based on the technicians’ utilisation and through-put time, work-order requirement and prioritisation rules.
Manzini et al. (2015) presented a nonlinear model which minimises cost of preventive and corrective maintenance as well as technicians’ workload and spare parts cost. These maintenance costs were optimised under total expected and probabilistic costs. Hervet and Chardy (2012) reported the use of mixed-integer programming approach in addressing the problem of preventive maintenance workforce needs during the design of passive optical network. Jarugumill (2011) studied workforce problem by considering regular and overtime activities as well as workers’ skills.
Research methodology
This section presents the proposed model (“Model formulation” section) and discussed the solution methods used in solving the proposed model (“Solution methods” section). The development of the proposed model was based on the following assumptions:
-
1.
Technicians in the same group can be categorised differently, and these categories are known in advance;
-
2.
Available maintenance work is carried out by in-house maintenance crew only; and
-
3.
Inventories for maintenance work are available and released when needed.
Some of the notations used in formulating the proposed model are given as follows:
- i :
-
Maintenance activity
- j :
-
Maintenance section
- k :
-
Technicians category
- t :
-
Planning period
- M :
-
Total number of types of maintenance activities
- N :
-
Total number of maintenance sections
- K :
-
Total number of technicians categories
- T :
-
Total number of sub-planning periods
- x ijkt :
-
Number of technicians required for maintenance activity i from maintenance section j belonging to technician category k at period t
- R ijkt :
-
Reliability of a technician required for maintenance activity i from maintenance section j belonging to technician category k at period t
- δ ijkt :
-
Amount of maintenance time required by technician to carry out maintenance activity i from maintenance section j belonging to technician category k at period t (h)
- v ijkt :
-
Earned-value of a technician that carries out maintenance activity i from maintenance section j belonging to technician category k at period t (
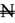 )
) - c ijkt :
-
Unit cost of technician that carries out maintenance activity i from maintenance section j belonging to technician category k at period t (
 )
) - r it :
-
Expected value of technicians’ reliability for maintenance activity i at period t
- \( \chi_{it} \) :
-
Total cost of technicians required to carry out maintenance activity i at period t (
 )
) - \( \chi_{t} \) :
-
Total cost of technicians required to carry out available maintenance activities at period t (
 )
) - a ijt :
-
Actual number of days a technician in section j from technicians category k at period t is available in a maintenance system (days)
- p ijt :
-
Actual performance of a technician in section j from technician’s category k at period t
- q ijt :
-
Actual quality of workdone by a technician in section j from technician’s category k at period t (kg)
- \( \hat{a}_{ijt} \) :
-
Expected days a technician in section j from technician’s category k at period t is available at a maintenance system (days)
- \( \hat{p}_{ijt} \) :
-
Expected performance of a worker in section j from technician’s category k at period t
- \( \hat{q}_{ijt} \) :
-
Expected quality of workdone by a technicians in section j from technician’s category k at period t (kg)
- \( b_{ijk\;1} \) :
-
The minimum value of fatigue experienced during maintenance activity i by a technician from maintenance section j belonging to technicians’ category k (h)
- \( b_{ijk\;2} \) :
-
The maximum value of fatigue experienced during maintenance activity i by a technician from maintenance section j belonging to technicians’ category k (h)
- \( c_{jk\;1} \) :
-
The minimum value of extra fatigue on technicians for overtime activities by technicians from maintenance section j belonging to technician’s category k (h)
- \( c_{jk\;2} \) :
-
The maximum value of extra fatigue on technicians for overtime activities by technicians from maintenance section j belonging to technician’s category k (h)
- \( e_{jk\;1} \) :
-
The minimum value of experiential on technicians for reworked activities by technicians from maintenance section j belonging to technician’s category k (h)
- \( e_{jk\;2} \) :
-
The maximum value of experiential on technicians for reworked activities by technicians from maintenance section j belonging to technician’s category k (h)
- \( V_{ijk\;2} \) :
-
The minimum value of training impact on technicians for maintenance activity i by technicians from maintenance section j belonging to technician’s category k (h)
- \( V_{ijk\;2} \) :
-
The maximum value of training impact on technicians for maintenance activity i by technicians from maintenance section j belonging to technician’s category k (h)
- \( f\left( b \right) \) :
-
Probability density function of fatigue on technicians for maintenance activities
- \( f\left( v \right) \) :
-
Probability density function of training impact on technicians service times
- \( f\left( e \right) \) :
-
Probability density function of extra fatigue experience by technicians during overtime maintenance activity
- \( f\left( c \right) \) :
-
Probability density function of experience gain by technicians during reworked maintenance activity
Model formulation
This study presented two technicians’ objectives (earned-value and reliability) which were subjected to technician’s cost, service time, reliability, availability, performance and quality of workdone.
The cost of keeping a particular level of technician in a system depends largely on the expected contributions from the technicians. Using the concept of earned-value from engaging technicians in planned and unplanned maintenance activities in an organisation, the total earned-value from scheduling the different technicians for stochastic maintenance activities in a maintenance system was expressed as Eq. (1). The technician’s earned-value is a function of the size of technicians assigned to carry out maintenance activities \( (x_{ijkt} ), \) time spent on maintenance activities \( (\delta_{ijkt} ) \) and the unit earned-value expected from each technician \( (v_{ijkt} ). \) Technician’s earned-value could be defined as a measure of the value of utilising a technician for maintenance activities with respect to maintenance time.
By looking beyond the concept of earned-value of technicians, technicians scheduling analysis may be improved on using the average expected technician reliability \( (R_{ijk} ) \) over a planning period. The study of technician’s reliability provides a means of estimating the degree to which the expected earned-value of technicians will be achieved. Since technicians work in groups, we considered their reliability as being parallel. The expected average technicians’ reliability is expressed as Eq. (2).
The volume of maintenance work from overtime, overtime and rework maintenance activities in a system varies from one period to another. This variation may be attributed to equipment usage, equipment age, organisation’s maintenance policy and quantity of spare parts used. Furthermore, factors such as fatigue, training and experiential knowledge affect technicians performance when restoring equipment to acceptable functional state.
The issue of routine maintenance activities has been studied in the literature (Mansour 2011). However, the concerns of researchers have been on equipment. Information on factors which affect technicians’ performance is sparse in maintenance literature. This study considered the issue of fatigue and training on technician’s service time. Since it is often difficult to measure fatigue in qualitative terms, a continuous function was used to capture the amounts of fatigue a technician experience during the maintenance activities. This is possible by considering two extreme values for technician’s fatigue for a particular kind of maintenance activity. The expected reduction in maintenance time of technicians in a section is expressed as Eq. (3).
where \( L_{1\,jt} \) and \( \bar{L}_{1\,jt} \) are the minimum and maximum amounts of routine maintenance tasks available for maintenance section j at period t, respectively.
The extension of production activities beyond the scheduled periods makes it necessary for technicians to be on ground. The technicians are expected to carry out maintenance activities that are required during overtime production activities. The need for overtime activities may be attributed to a change in production volume and maintenance-related problems. Shiftan and Wilson (1994) considered this problem under a deterministic condition. This study deviated from Shiftan and Wilson (1994) approach by introducing stochastic element into overtime maintenance activities. These stochastic elements involve the fatigue experienced during normal and overtime periods as well as reduction in maintenance time as a result of training technicians (Eq. 4). The determination of the number of overtime technicians will improve technicians’ cost control in systems (Aghdaghi and Jolai 2008).
where \( L_{2\,jt} \) and \( \bar{L}_{2\,jt} \) are the minimum and maximum amounts of overtime maintenance tasks available for maintenance section j at period t, respectively.
The failures of machines to produce the expected number of defective products after maintenance often result in re-maintenance (rework) of such machines. This problem results from poor diagnosis of the causes of breakdown of installed machines or the use of inferior spare parts. Whenever this problem occurs, technicians who are responsible for the initial maintenance of such machines could have gained experience on the possible causes of the poor machine performance. By the combining experiential knowledge, training and fatigue, the constraint for the expected time for sectional rework activities is given as Eq. (5).
where \( L_{3\,jt} \) and \( \bar{L}_{3\,jt} \) are the minimum and maximum amounts of rework maintenance tasks available for maintenance section j at period t, respectively.
Using the expected value and standard deviation of technician in a unit for the classes of technicians in each section, the minimum number of technicians required for each class under the various units in a maintenance department can be expressed as follows:
where \( \mu_{{x_{ijkt} }} \) is mean value of maintenance task i from maintenance section j for technician k at period t. \( P(x_{ijkt} ) \) is the probability of occurrence of maintenance task i from maintenance section j for technician k at period t and \( \alpha_{{r_{{}} }} \) contribution of variance in maintenance tasks to \( \mu_{{x_{ijkt} }} . \)
The average number of technicians required in a planning horizon should not be less than the specified number of technicians (Eq. 7). This allows variations in the number of technicians in a section from one period to another.
where \( x_{{ijk,{\text{ave}}}} \) is the average number of technicians expected to be scheduled to carried out maintenance task i from maintenance section j belonging to technician’s category i at period t.
The sum of technicians in each period is expected to be within a specified range. This constraint helped in controlling the amount of technicians within a particular category (Eq. 8).
In Ighravwe et al. (2015), technicians’ overall effectiveness (TOE) was considered. To control the expected value of TOE, there is the need to consider constraining the minimum values for sectional technicians’ availability, quality of workdone and performance. The expected performance of each section in a maintenance department could be considered as the expected technician’s efficiency. We applied uniform distribution concept (Wu 2008) to estimate the expected technicians’ availability, quality of workdone and performance. Technicians’ availability is expressed as Eq. (9), while technicians’ performance was expressed as Eq. (10). The quality of workdone constraints is expressed as Eq. (11).
where \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a}_{j} \) and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{b}_{j} \) are the minimum and maximum values of technicians’ performance for maintenance task i from technicians in section j at period t, respectively. \( \bar{a}_{j} \) and \( \bar{b}_{j} \) are the minimum and maximum values of technicians’ availability for maintenance task i from technicians in section j at period t, respectively. \( \tilde{a}_{j} \) and \( \tilde{b}_{j} \) are the minimum and maximum values of technicians’ quality of work for maintenance task i from technicians in section j at period t, respectively. \( \bar{a}_{j} \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a}_{j} \) and \( \tilde{a}_{j} \) are the confident levels for technicians’ availability, performance and quality of workdone for maintenance task i expected from technicians in section j.
We relaxed the expression for TOE as defined by Ighravwe et al. (2015), to a stochastic constraint using the concept of normal distribution (Wu 2008) as Eq. (12).
where \( \mu_{i} ,\,\sigma_{i} \) and \( \alpha_{i} \) are the mean, standard deviation and confident level for TOE expected for maintenance task i from the technicians in a maintenance system, respectively.
Beyond specifying the expected TOE of technicians, there is the need for the cost implication consideration that will be associated with scheduling a particular level of technicians for each maintenance task at the different planning periods. The expression of the cost for each maintenance activity is considered (Eq. 13). The total cost of technicians required for the maintenance activities at each period is expressed as Eq. (14).
To further constraint the proposed model, the issue of the expected reliability from each maintenance section is considered. The reliability of each section in a maintenance department is expressed as Eq. (15).
Solution methods
The handling of the multi-objective is carried out using the weights of each of the objectives and deviational variables for the objective functions (Wu 2008). The new objective function is given as Eq. (16).
where f 1,max and f 2,max are the maximum values for the technicians earned-value and reliability, respectively.
The summary of the proposed mixed-integer programming model is presented as follows:
Subject to the following constraints:
Non-negativity constraints
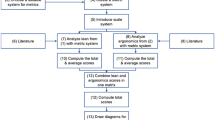
The flow chart for the evolutionary programming and big-bang–big-crunch algorithms is depicted in Fig. 1. The termination of each of these algorithms was taken as the maximum epoch. EP algorithms are different from other evolutionary algorithms (genetic algorithm, differential evolution and genetic programming) because it does not require crossover operation. The first EP algorithm was proposed by Fogel (1962). The quest to improve the mutation operation in EP algorithms has led to different versions of the EP algorithms.
The potentials of EP and BB–BC algorithms in generating optimal solution for computational problems are due to their stochastic-populate-based capacity. For the EP algorithm, the mutation introduced randomness into a current solution. In the BB–BC algorithm (Osman and Eksin 2006), randomness to current solution is introduced through the generation of centre of mass (big-crunch) and the new variable (big-bang). In Fig. 1, \( z_{ij}^{g} \) is the value of solution i decision variable j at epoch g and \( z_{j}^{g} \) the centre of mass for decision variable j at epoch g. The variable \( z_{gj}^{{}} \) is the value of global solution variable j in a current epoch. Some authors have considered \( z_{gj}^{{}} \) as the centre of mass during the implementation of BB–BC algorithm. The variable \( f_{i}^{g} \) is the quality of solution i at epoch g. In the EP section, \( \psi_{1} \) is a uniform random number which lies between (0, 1). This variable helps in controlling the influence of the difference between current global and local optimal solutions in a population at a particular epoch g. The variable \( \psi_{2} \) in the BB–BC algorithm is a random variable which lies at ±1, and \( \vartheta \) is a constant parameter that helps in controlling the search capacity of the BB–BC algorithm. The variables \( z_{{j, {\rm min} }} \) and \( z_{{j, {\rm }}} \) are the minimum and maximum values of decision variable j.
Model application
The proposed model and algorithms (BB–BC and EP) were coded using C# programming language on a Windows 8 computer with installed memory (RAM) of 4.00 GB, 1.80 GHz processor and 64 bit operating system. To demonstrate the applicability of the proposed model, datasets from Ighravwe and Oke (2014) were used and complemented with simulated data. The datasets that were simulated are technician’s reliability, earned-value, quality of workdone, availability and performance as well as the amount of rework and overtime maintenance activities. The amount planned maintenance work in Ighravwe and Oke (2014) was increased by 20 %. This enables us to generate upper bounds for the various planned maintenance activities.
The minimum value for the amounts of overtime was about 40 % of minimum planned maintenance workload. We considered the amount of rework maintenance activities as 30 % of the amounts of minimum planned maintenance workload. Table 1 shows the amount of planned, rework and overtime maintenance activities for the system. By observing the total amounts of workloads for the different sections, available maintenance time and technician’s categories, the bounds for the numbers of technicians in the different maintenance sections were estimated. The unit cost for overtime maintenance activities was about 110 % of unit cost of engaging them in normal maintenance activities. The unit cost of rework maintenance activities was about 30 % of the unit cost of engaging them in normal maintenance activities.
The proposed model was solved using pre-emptive goal programming approach. This enabled us to determine the bounds for the objective functions. We considered the technicians’ earned-valued goal as being a higher priority than the technicians’ reliability goal. However, some organisations may consider the technicians’ reliability goal as being a higher priority than the technicians’ earned-valued goal. To address priority determination, priority scored performance measurement can be used (Tarokh and Nazemi 2006). The minimum value of the expected reliability of the total scheduled technicians was 85 %. During the testing of the proposed model, the minimum acceptable reliability of the technicians was 60 %. The maximum acceptable reliability of the technicians was 95 %.
For the EP algorithm, the selection between parents and off-springs was based on Boltzmann–Gibbs approach in simulated annealing (Engelbrecht 2007). The total number of epochs for the EP and BB–BC algorithms was 200. The limiting parameter \( (\psi ) \) for the BB–BC algorithm was 0.2. The Pareto solutions obtained for at the initial implementation of EP and BB–BC algorithms are in Table 2.
Based on the objective functions results in Table 2, the differences between the upper and lower bounds for the technicians’ earned-value objective are  54,264.00 and
54,264.00 and  71,990.22 for the EP and BB–BC algorithms, respectively. For the reliability objective, the differences between the upper and lower bounds for the EP and BB–BC algorithms are 0.1 and 0.3, respectively. Equal importance was given to the objective functions (i.e. w
1 = 0.5 and w
2 = 0.5). The values of the Pareto solutions obtained for the objective functions are in Table 3.
71,990.22 for the EP and BB–BC algorithms, respectively. For the reliability objective, the differences between the upper and lower bounds for the EP and BB–BC algorithms are 0.1 and 0.3, respectively. Equal importance was given to the objective functions (i.e. w
1 = 0.5 and w
2 = 0.5). The values of the Pareto solutions obtained for the objective functions are in Table 3.
From the values for the two objective functions obtained from the two solution methods presented in Table 2, the differences between the upper and lower bounds for the maintenance technicians’ earned-value objective are  54,264.00 and
54,264.00 and  71,990.22, for the EP and BB–BC algorithms, respectively. For the reliability objective, the differences between the upper and lower bounds for the EP and BB–BC algorithms are 0.1 and 0.3, respectively. To obtain optimal solution from the proposed model using the EP and BB–BC algorithms, equal importance was assigned to maintenance technicians earned-value and reliability objectives (i.e. w
1 = 0.5 and w
2 = 0.5). By using Eq. (16) as objective function for the proposed model and Eqs. (17) and (18) as soft constraints, the values of the Pareto solutions obtained for the two objective functions are presented in Table 3.
71,990.22, for the EP and BB–BC algorithms, respectively. For the reliability objective, the differences between the upper and lower bounds for the EP and BB–BC algorithms are 0.1 and 0.3, respectively. To obtain optimal solution from the proposed model using the EP and BB–BC algorithms, equal importance was assigned to maintenance technicians earned-value and reliability objectives (i.e. w
1 = 0.5 and w
2 = 0.5). By using Eq. (16) as objective function for the proposed model and Eqs. (17) and (18) as soft constraints, the values of the Pareto solutions obtained for the two objective functions are presented in Table 3.
Based on the information in Table 3, the BB–BC algorithm performed better than the EP algorithm. By using the BB–BC algorithm as solution method for the proposed model, the number of maintenance technicians required to be scheduled to carry out the available maintenance work are shown in Table 4. In addition, the breakdown of maintenance time and reliability associated with each scheduled technicians for the various maintenance activities are in Table 4.
Discussion of results
The total number of technicians required for routine maintenance was 121 technicians, while 101 technicians were required for overtime maintenance activities. Rework maintenance activities required 84 technicians (Table 3). For routine maintenance activities, the system required 66 mechanical technicians and 32 electrical technicians. A total of 23 instrumentation technicians were required for routine maintenance activities. During the scheduling of technicians for overtime maintenance activities, the required mechanical technicians were 50. A total of 19 instrumentation technicians were required for overtime maintenance activities. The number of electrical technicians required for overtime electrical maintenance activities was 32 technicians.
The number of instrumentation technicians required for rework maintenance activities was the same as the number of workers for overhaul maintenance (19 technicians). The number of technicians for rework mechanical maintenance was 41 technicians. The company’s electrical section required about 24 technicians for rework maintenance activities.
The importance of this information is that it will assist maintenance managers in preparing logistics required to carry out successful maintenance tasks. For instance, in situations where production facilities are not on the same site, adequate arrangement for technician and spare parts transportation logistics will be made (Yuceer 2013). Another benefit of the above information is that business owners will have the opportunity to know how much of their working capital will be devoted to technicians’ expenses. For instance, the highest number of technicians required for the routine and the overtime maintenance tasks was at period 3. For the routine maintenance tasks, 31 technicians are required, while 26 technicians are required to cover the available overtime maintenance tasks. The highest number of technicians for rework maintenance tasks was at periods 1 and 2.
To further simplify the above analysis, the pattern for the average number of the different categories of technicians is shown in Fig. 2. This provides an overview of the trend of the required average number of the technicians for the system.
The organisation will need about  107, 694,516 for the technicians’ expense for four periods. The total amount of funds required to cater for the technicians’ expenses at period 1 was
107, 694,516 for the technicians’ expense for four periods. The total amount of funds required to cater for the technicians’ expenses at period 1 was  8, 274,106, while a sum of
8, 274,106, while a sum of  8, 212,776 was required at period 2. At period 3,
8, 212,776 was required at period 2. At period 3,  8, 322,675 was required for technicians’ expenses. The technicians’ expense at period 4 was less than that of period 3 with about 4 % (
8, 322,675 was required for technicians’ expenses. The technicians’ expense at period 4 was less than that of period 3 with about 4 % ( 335, 716). The company’s management can decide to budget funds for each period or for all the periods. Since resources are scare, the decision markers will prefer to plan for technicians’ expenses at each period.
335, 716). The company’s management can decide to budget funds for each period or for all the periods. Since resources are scare, the decision markers will prefer to plan for technicians’ expenses at each period.
Beyond the issue of cost management, how the allocated time for maintenance activities (time management) will be utilised is equal of importance to the decision markers. The amounts of maintenance time for rework maintenance activities are relative the same for the maintenance sections (Fig. 3). There are differences in the amounts of maintenance times for routine and overtime maintenance activities required for the maintenance sections (Fig. 3). The combination of the different maintenance times will help in analysing production line availability whenever there is fluctuation in product demand. At period 1, the unavailability of the production line was 3704 h, while the production line was unavailable for 3702 h at period 2. The amount of time of the production line unavailability for period 3 was the same as that of period 2 (3704 h). Period 4 had the least production line unavailability (3680 h).
The question of how reliable the scheduled technicians are when carrying out assignment based on the allocated maintenance times is displayed in Table 3. By providing answer to this question, the problem of how to manage a maintenance system will be reduced to other areas such as spare management and design of technicians’ motivational schemes. A summary of the average technician’s reliability for the different technician’s categories is in Table 4. The average reliability expected from the technicians during routine maintenance is relatively stable when compared with the average reliability during rework activities (Fig. 4).
Conclusions
This study has succeeded in proposing a multi-objective technician’s scheduling model using mixed-integer programming approach. The integer aspect of the proposed model deals with the technicians’ size and time, while the technicians’ reliability is considered as a real-value decision variable. We demonstrated how the proposed model can be used in obtaining Pareto solutions for technicians’ earned-value and reliability. Also, the proposed model results for different planning periods technicians size, maintenance time and reliability for the different kinds of maintenance task and technician’s categories are presented. The computational results from EP and BB–BC algorithms as solution methods are compared, and the suitability of these algorithms has been shown from the results obtained. It was observed that the BB–BC algorithm performed better than the EP algorithm. The value of Pareto optimal solution obtained using the BB–BC algorithm from is  1, 415,878.40 and 98 % for the total technicians earned-value and reliability.
1, 415,878.40 and 98 % for the total technicians earned-value and reliability.
The main benefit of the proposed model is that it can be used to select technicians’ matrix for the different kinds of maintenance tasks in a system. Another benefit of the model is that the information it generates can be used in estimating the productivity of technicians assigned for the different maintenance activities.
The contributions of this study are as follows: First, the introduction of training, fatigue and experimental knowledge in designing technicians’ schedule plan is presented. Second, an integrated platform for determining the number of technicians for routine, rework and overtime maintenance tasks was contributed to technicians’ allocation literature. Third, the use of technicians’ earned-value in a technician’s optimisation was added to literature. Lastly, the application of BB–BC algorithm as a promising solution method for technician’s optimisation models has been explored.
However, we acknowledge some limitations of the proposed model. The proposed model lacks the capacity to deal with the problem of technician’s transfers from one section to another. Also, our model cannot be used to address workers’ preferences for particular types of maintenance activities and the effects of technician’s absenteeism on work-plans.
The use of swarm algorithm in obtaining Pareto solution when applying the proposed model can be investigated as a further study. Also, the application of system dynamic modelling approach in establishing the interrelations among technicians’ variables (time, size and reliability) and other maintenance parameters (spare parts) can be investigated as a further study.
References
Aghdaghi M, Jolai F (2008) A goal programming model for vehicle routing problem with backhauls and soft time windows. J Ind Eng Int 4(6):7–18
Alsyouf I (2007) The role of maintenance in improving companies’ productivity and profitability. Int J Prod Econ 105(1):70–78
Bartels S, Richey J (2008) Workforce management—impacting the bottom-line, an oracle white paper. Oracle Corporation, Redwood Shores, CA, pp 1–10
De Bruecker P, Van den Bergh J, Belien J, Demeulemeester E (2015) A model enhancement heuristic for building robust air craft maintenance personnel rosters with stochastic constraints. Eur J Oper Res 246:661–673
Engelbrecht AP (2007) Computational intelligence: an introduction. Wiley, London
Fajardo VA, Drekic S (2015) Controlling the workload of M/G/1 queues via the q-policy. Eur J Oper Res 243:607–617
Fogel LJ (1962) Autonomous automata. Ind Res Mag 4(2):14–19
Gregoriades A, Sutcliffe A (2008) Workload prediction for improved design and reliability of complex systems. Reliab Eng Syst Saf 93:530–549
He M, Hu Q, Wu X, Jing P (2014) A combination algorithm for selecting functional logistics service vendors based on SQP and BNB. J Chem Pharm Res 6(5):2013–2018
Hedjazi D (2015) Scheduling a maintenance activity under skills constraints to minimise total weighted tardiness and late tasks. Int J Ind Eng Comput 6:135–144
Hervet C, Chardy M (2012) Passive optical network design under operations administration and maintenance considerations. J Appl Oper Res 4(3):152–172
Ighravwe DE, Oke SA (2014) A non-zero integer non-linear programming model for maintenance workforce sizing. Int J Prod Econ 150:204–214
Ighravwe DE, Oke SA, Adebiyi KA (2015) Maintenance workload optimisation with accident occurrence considerations and absenteeism from work using genetic algorithms. Int J Manag Sci Eng Manag. doi:10.1080/17509653.2015.1065208
Jarugumill S (2011) Integrated workforce planning considering regular and overtime decisions. In: Doolen T, Van Aken E (eds) Proceedings of the 2011 industrial engineering research conference
Kaufman DL, Lewis ME (2007) Machine maintenance with workload considerations. Naval Res Logist 54(7):750–766
Knapp GM, Mahajan M (1998) Optimisation of maintenance organisation and manpower in process industries. J Qual Maint Eng 4(3):168–183
Lai Y-C, Fan D-C, Huang K-W (2015) Optimising rolling stock assignment and maintenance plan for passenger railway operations. Comput Ind Eng 85:284–295
Mansour MAA-F (2011) Solving the periodic maintenance scheduling problem via genetic algorithm to balance workforce levels and maintenance cost. Ame J Eng Appl Sci 4(2):223–234
Manzini R, Accorsi R, Cennerazzo T, Ferrari E, Maranesi F (2015) The scheduling of maintenance. A resource-constraints mixed integer linear programming model. Comput Ind Eng 87:561–568
Mjema EAM (2002) An analysis of personnel capacity requirement in maintenance department by using simulation method. J Qual Maint Eng 8(3):253–273
Oladokun VO, Charles-Owaba OE, Nwaouzru CS (2006) An application of artificial neural network to maintenance management. J Ind Eng Int 2(3):19–26
Osman KE, Eksin I (2006) New optimisation method: big-bang big-crunch. Adv Eng Softw 37:106–111
Rana RS, Purohit R (2012) Balancing of maintenance task during maintenance of four wheeler. Int J Eng Res Appl 2(3):496–504
Safaei N, Banjevic D, Jardine AKS (2008) Multi-objective simulated annealing for a maintenance workforce scheduling problem: a case study. In: Tan CM (ed) Simulated annealing. I-Tech Education and Publishing, Vienna, pp 27–48
Sakthivel S, Mary D (2013) Big bang-big crunch algorithm for voltage stability limits improvement by coordinated control of svc settings. Res J Appl Sci Eng Technol 6(7):1209–1217
Shiftan Y, Wilson NHM (1994) Absence, overtime, and reliability relationships in transit workforce planning. Transp Res Part A: Policy and Pract 28(3):245–258
Tarokh MJ, Nazemi E (2006) Performance measurement in industrial organisations case study: Zarbal Complex. J Ind Eng Int 2(3):54–69
Tohidi H, Tarokh MJ (2005) Team size effect on teamwork productivity using information technology. J Ind Eng Int 1(1):37–42
Wong KP, Yuryevich PD (1997) Evolutionary programming-based algorithms for environmentally-constrained economic dispatch. IEEE Trans Power Syst 13(2):301–316
Wu Z (2008) Hybrid multi-objective optimisation models for managing pavement assets. Ph.D. Thesis, Virginia Polytechnic Institute and State University
Yuceer U (2013) An employee transporting problem. J Ind Eng Int 9:3
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ighravwe, D.E., Oke, S.A. & Adebiyi, K.A. A reliability-based maintenance technicians’ workloads optimisation model with stochastic consideration. J Ind Eng Int 12, 171–183 (2016). https://doi.org/10.1007/s40092-015-0134-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-015-0134-6



 )
) )
) )
) )
)


