Introduction

Banks, as one of the most complex industries in this rapidly changing high-tech world of computers and telecommunications, need to be flexible enough to respond rapidly to change and also to keep up with stiff competition. In such competitive environment, continuous improvement is critical for any successful organization. Therefore, improving performance is widely recognized as essential to gaining an extra competitive edge. Due to working in a competitive business environment, banking chain has a multi-dimensional and complex structure. Banking chain plays an important role in the economic cycle of each country, so to gain/remain on sustainable competitive edge performance evaluation has become a critical role which management of every financial institution may play. In this regard, bank branch performance, as the focus of empirical application in this paper, has become more difficult due to size variety, offering different services to different costumers, and multi-dimensional structure. Generally two methods are used to measure bank branch operational efficiency; parametric and non-parametric. The drawback of parametric techniques is a number of inherent limitations which make them unsuitable for fully reflecting the increasingly complex nature of banking chains. For example, regression analysis as one of the best parametric techniques is a central tendency method and is only suitable for modeling single input-multiple outputs or multiple inputs-single output systems. Data envelopment analysis (DEA), as a non-parametric method, is an excellent efficiency analysis tool that creates efficient production frontier to compare the DMU under evaluation relative to the best decision making units (DMUs) if they are operating under the same conditions. Dealing with multiple inputs and multiple outputs is an appealing feature which gives DEA an edge over other analytical tools. Standard DEA evaluates the relative efficiency of DMUs in presence of multiple inputs and multiple outputs, but it does not provide sufficient details for managerial decisions. In real world scenarios, companies (DMUs) are mainly comprised of various divisions/levels that are linked together and have a great deal of interactions between them and follow multi-level Stackelberg relationships. Complex hierarchical structure of banking chains makes their managers deal with many challenges. The most important challenges that managers should cope with are: variable costs and demand under the multi-level Stackelberg relationships with interactions among levels, and coordinating these relationships to provide high quality services for customers. Bank managers can improve their cost efficiency through remaining or improving the quality of their services in order to create competitive advantage. Banking chain cost efficiency evaluates the ability of banks in producing current outputs at minimal level of cost which provides managers some insights behind the total cost in operations. The problems in the way of evaluation of banking branch performance naturally exhibit a multi-level decision making models which are connected in a hierarchical way. Since in the multi-level decentralized decision companies the individual set of decision variables is often controlled by each level which have their own, often mutually conflicting, objectives the evaluation of banking chain performance is based on multi-perspective. Therefore, performance evaluation in such particular multi-level decentralized decision structures can be modeled by bi-level programming DEA approach. Bi-level programming data envelopment analysis (BLPDEA) approach goes to the black box and embodies internal structure and interior interactions of system when it has a hierarchical structure. BLPDEA also can provide a valuable insight and detailed information to manager when evaluating the performance of a system with Stackelberg-game relationships (Wu 2010). The main purpose of this paper is to illustrate a seldom utilized non-parametric analysis technique called BLPDEA which addresses the problem of cost efficiency evaluation under the Stackelberg leader–follower relationships in the context of banking. Bi-level DEA model is a NP-hard nonlinear programming. Since nonlinear models are reducing the validity of the model, in this paper, we recommended the Mixed integer programming method which converts the bi-level mathematical programming to a linear mathematical programming and significantly improves the process to achieve the optimum solution.

The remainder of this paper is organized as follows: In the next section, “Literature review” section, literature is reviewed. Section “Fundamentals of DEA, DEA cost efficiency and bi-level programming” introduces the concepts of cost efficiency DEA and bi-level programming. In “Proposal model” section bi-level programming DEA model proposed by Wu (2010) is presented. In “The framework of the efficiency evaluation of the banks” section, we demonstrate empirical use of bi-level programming DEA model in the form of a case study (Iranian bank). Conclusions are presented in “Empirical study” section.

Literature review

In comparison with techniques of assessing organization performance, the method of DEA proposed by Charnes et al. (1978) is a better way to organize and analyze data because it allows efficiency to change over time and requires no prior assumption on the specification of the efficient frontier. Thus, DEA is an excellent approach for the performance analysis of banking industry. In many real world scenarios, DMUs have a two-stage network process and due to this reason, DEA has been extended to examine the efficiency of two-stage processes, where all of the outputs from the first stage are intermediate measures that make up the inputs of the second stage. Wang (1997) present a two-stage process in the banking industry where the banks use inputs (of the first stage) including fixed assets, labor, and information technology (IT) investments to generate deposits. The banks then use the deposits (intermediate measure) to generate loans and profits (as the outputs). Momen et al. (2012) measured the operational risk of Iranian banks based on Loss Distribution Approach. Bhattacharya et al. (1997) used a two-stage DEA approach to examine the impact of liberalization on the efficiency of the Indian banking industry. In the first stage, a technical efficiency score was calculated, whereas in the second stage a stochastic frontier analysis was used to attribute variation in efficiency scores of three sources: temporal, ownership and noise component. Seiford and Zhu (1999) examined the performance of the top 55 US banks using a two-stage DEA approach. Results indicated that relatively large banks exhibit better performance on profitability, whereas smaller banks tend to perform better with respect to marketability. Sexton and Lewis (2003) proposed a two-stage process for evaluating Major League Baseball performance. Khalili-Damghani and Taghavifard (2012) proposed a generic process in which just-in-time (JIT) practices are changed into agility indices, and agility indices are converted into performance measurement in supply chain in form of a conceptual model. Then, a three-stage data envelopment analysis (TSDEA) model proposed to measure the relative efficiency of aforementioned process and sub-processes. Babazadeh et al. (2012) designed a network and applied a mixed integer linear programming to evaluate supply chain efficiency. Khalili-Damghani and Tavana (2013) proposed a new network DEA (NDEA) model for measuring the performance of agility in supply chains. Their proposed fuzzy NDEA model was linear and independent of the α-cut variables. Sanieemonfared and Safi (2013) applied a novel DEA network structure to measure relative efficiency of academic colleges in both teaching quality and research productivity. Kao and Hwang (2008) developed a different approach where the entire two-stage process can be decomposed into the product of the efficiencies of the two sub-processes. As a result, both the overall efficiency and each stage’s efficiency are obtained. Tone and Tsutsui (2009) extended the SBM model into a network framework to deal with intermediate products formally. Avkiran (2009), as the first empirical study of NSBM, relies on actual aggregate data of domestic commercial banks in the UAE, and applied the non-oriented network slacks-based measure for evaluating the profit efficiency. Fukuyama and Weber (2010) extended the slacks-based inefficiency measure for evaluating a two-stage system with bad outputs in a Japanese bank. Paradi et al. (2011) developed a two-stage DEA approach for simultaneously benchmarking the performance of operating units. Li et al. (2012) extended the findings of Liang et al. (2008) and proposed a centralized and non-cooperative model to evaluate the efficiency of two-stage process to further decompose the overall efficiency for complex network structure. Khalili-Damghani and Hosseinzadeh Lotfi (2012) developed a fuzzy two-stage data envelopment analysis (FTSDEA). In this paper, each decision making unit supposed to make up of two serially connected sub-DMUs. Tavana and Khalili-Damghani (2014), proposed an efficient two-stage fuzzy DEA model to calculate the efficiency scores for a DMU and its sub-DMUs. They used the Stackelberg (leader–follower) game theory approach to prioritize and sequentially decompose the efficiency score of the DMU into a set of efficiency scores for its sub-DMUs.

Bi-level decision making or bi-level programming techniques, first introduced by Von Stackelberg (1952), have been developed for mainly solving decentralized decision process with decision makers in a hierarchical organization. Decision maker at the upper level is termed as the leader, and in the lower level, the followers which have their own and perhaps mutually conflicting objective. Bi-level programming has been applied in a great deal of fields. Ryu et al. (2004) presented a bi-level programming framework to capture conflicting interests of multiple elements in the context of supply chain planning problems. Huijun et al. (2008) proposed a bi-level programming model to describe and solve the location problem in which both the benefits of costumers and logistics planers are taken into account. Sakawa et al. (2002) dealt with a transportation problem in a housing material manufacturer and derived a satisfactory solution to the problem. Roghanian et al. (2007) considered a probabilistic bi-level linear multi-objective programming problem and its application in enterprise-wide supply chain planning problem. Arora and Gupta (2009) presented an interactive fuzzy goal programming approach for bi-level programming problem with the characteristics of dynamic programming. Hongjie et al. (2011) established two inventory control models of deteriorating items respectively according to time-based and the quantity-based integrated delivery strategies for suppliers under VMI model based on bi-level programming. Lachhwani and Poonia (2012) developed a procedure for solving multilevel fractional programming problems in a large hierarchical decentralized organization by fuzzy goal programming approach. In this paper, fuzzy goal programming approach is used for achieving the highest degree of each of the membership goal by minimizing negative deviational variables. Alimardani et al. (2013) developed a continuous review policy for inventory control in a three-echelon supply chain including retailers, a central warehouse with limited storage space, and two independent manufacturing plants which offer two kinds of product to the customer. Arianezhad et al. (2013) presented a new two-echelon model to control the inventory of perishable goods. The main purpose of the model is to minimize the maintenance cost of the entire chain. Due to the complexity of the model, they used genetic algorithm under MATLAB to solve and confirm the accuracy of the model’s performance.

Cost efficiency model is used to show the ability of DMUs to produce current outputs at minimal level of cost and how DEA can be used to identify types of inefficiency, which can emerge for treatment when information on costs is known exactly (Cooper et al. 2007). Tohidi and Khodadadi (2013) introduced a new model to evaluate cost efficiency of DMUs with negative data. They also demonstrated that proposed cost efficiency is a product of a locative and range directional measure efficiencies. Bahri and Tarokh (2012) focused on “seller–buyer” supply chain model with exponential distribution lead time and showed that their method can minimize the costs compared with systems that ignore the relation between seller and buyer.

Wu (2010) developed an innovative quantitative approach to evaluate the performance of multi-level decision network structure by integrating cost DEA into the bi-level programming framework and create bi-level programming DEA model. To show applicability of bi-level programming DEA model, Wu (2010) have demonstrated applications of the model in two practical examples: a banking chain and a manufacturing supply chain.

Fundamentals of DEA, DEA cost efficiency and bi-level programming

Data envelopment analysis

DEA is a linear programming based methodology which can calculate multiple inputs and outputs and can also evaluate DMUs both qualitatively and quantitatively. DMU, which can be related to different firms or the condition of the same firm over time, stands for decision making unit.

DEA was first proposed by Charnes et al. (1978). The evolutionary form of CCR model was suggested in 1984 by Banker et al. In subsequent years, several models were developed by a large number of researchers. Orientation, disposability, diversification, and return to scale are different aspects that can be seen in these models.

There are numerous studies on efficiency evaluation with the DEA model in several filed. For example, in banking such as Elyasiani and Mehdian (1990), Kao and Liu (2004), Camanho and Dyson (1999, 2005), and Cook and Hababou (2001). In supply chain efficiency evaluation, such as Khalili-Damghani and Sadi-Nezhad (2014), Khalili-Damghani and Hosseinzadel Lofit (2012), Khalili-Damghani and Taghavifard (2012, 2013), Abtahi and Khalili-Damghani (2011), Khalili-Damghani and Tavana (2013), and Khalili-Damghani et al. (2011, 2012). In other companies such as Tavana et al. (2014), Khalili-Damghani et al. (2015), Khalili-Damghani and Taghavifard (2012) and Tavana et al. (2013).

DEA cost efficiency

Many different types of DEA models with different aims have been developed. The aim of the majority of DEA models is focused on the technical-physical aspects of production for use in situations with unknown unit price and cost information, or where their uses are limited because of variability in the prices and costs that might need to be considered. Cost efficiency model is used to show the ability of DMUs to produce current outputs at minimal level of cost and how DEA can be used to identify types of inefficiency which can emerge for treatment when information on costs is known exactly (Cooper et al. 2007).

Suppose there are \(n\) DMUs under evaluation, each indexed by \(\left( {j = 1, \ldots ,n} \right)\), and \(X = \left( {x_{1} , \ldots ,x_{m} } \right)^{T}\) is the input vector which produces the output vector \(Y = \left( {y_{1} , \ldots ,y_{s} } \right)^{T}\) under the production possibility set. Then, the DEA cost efficiency model of 0th DMU, \(( 0 \in \{ 1, \ldots ,n\} )\), can be formulated as following linear programming:

$$\begin{aligned} & \varvec{cx}^{*} = \varvec{min}\mathop \sum \limits_{{\varvec{i} = {\mathbf{1}}}}^{\varvec{m}} \varvec{c}_{i} \varvec{x}_{i } \\ & \varvec{s}.\;\varvec{to} \\ & \mathop \sum \limits_{{\varvec{ j} = 1}}^{\varvec{n}} \varvec{x}_{{\varvec{ij}}}\varvec{\lambda}_{\varvec{j}} \le \varvec{x}_{\varvec{i}} ,\quad \varvec{i} = 1, \ldots ,\varvec{m}; \\ & \mathop \sum \limits_{{\varvec{ j} = 1}}^{\varvec{n}} \varvec{y}_{{\varvec{rj}}}\varvec{\lambda}_{\varvec{j}} \ge \varvec{ y}_{{\varvec{r}0}} ,\quad \varvec{r} = 1, \ldots ,\varvec{s}; \\ &\varvec{\lambda}_{\varvec{j}} \ge 0,\;\varvec{x}_{\varvec{i}} \ge 0. \\ \end{aligned}$$
(1)

where \((x_{i} ,\lambda_{j} )\) are decision variables and \((c_{i} )\) is the unit cost of input i which may vary from one DMU to another. This model allows substitutions in inputs. The objective function of model is to minimize the total cost of 0th DMU.

Based on an optimal solution \((x^{*} ,\lambda^{*} )\) of the above LP, the cost efficiency of \({\text{DMU}}_{0}\) is defined as:

$$\varvec{E}_{{\varvec{c }}} = \varvec{ }\frac{{\varvec{CX}^{\varvec{*}} }}{{\varvec{CX}_{{{\mathbf{0 }}}} }}$$
(2)

where \(X_{0}\) is the existing input vector of \({\text{DMU}}_{0}\).

Bi-level programming

Bi-level programming which is motivated by Von Stackelberg’s game theory (1952) refers to situations where there are two decision makers in an organization which are inter-connected in a hierarchical structure. In such situations, the decision maker who first makes decision is termed as the leader and the other who knows the decision of opponent then makes a decision is termed as the follower. These two decision makers have independent, perhaps mutually conflicting, objectives. In the context of bi-level programming, the leader first specifies a decision and then the follower with the full knowledge of the leader’s decision determines a decision so as to optimize his/her objective function. Accordingly, the leader also makes a decision so as to optimize his/her objective function. The obtained solution of the above mentioned procedure is a Stackelberg equilibrium solution (Sakawa and Nishizaki 2009). A bi-level linear programming problem for obtaining the Stackelberg solution is formulated as follows:

$$\begin{aligned} & \mathop {\varvec{minimize}}\limits_{\varvec{x}} \varvec{z}_{1} \left( {\varvec{x},\varvec{y}} \right) = \varvec{c}_{1} \varvec{x} + \varvec{d}_{1} \varvec{y} \\ & \varvec{where }\;\varvec{y}\;\varvec{ solves} \\ & \mathop {\varvec{minimize}}\limits_{\varvec{y}} \varvec{z}_{2} \left( {\varvec{x},\varvec{y}} \right) = \varvec{c}_{2} \varvec{x} + \varvec{d}_{2} \varvec{y} \\ & \varvec{subject}\;\varvec{to}\quad \varvec{Ax} + \varvec{By} \le \varvec{b}; \\ & \varvec{x} \ge 0,\varvec{ y} \ge 0. \\ \end{aligned}$$
(3)

where \(c_{i} \;i = 1,2\) are \(n_{1}\)-dimensional row coefficient vector, \(d_{i} ,\;i = 1,2\) are \(n_{2}\)-dimensional row coefficient vector, \(A\) is an \(m \times n_{1}\) coefficient matrix, \(B\) is an \(m \times n_{2}\) coefficient matrix, \(b\) is an \(m\)-dimensional column constant vector. \(z_{1} \left( {x,y} \right)\) and \(z_{2} \left( {x,y} \right)\) are the objective function of the leader and the follower, respectively. x and y are a set of decision variables which are controlled by the leader and follower, respectively (Sakawa and Nishizaki 2009).

Sakawa and Nishizaki (2009) gave the following definitions on basis of bi-level programming:

Definition 1

(Sakawa and Nishizaki 2009) \(S\) is the feasible region of the bi-level linear programming problem:

$$S = \left\{ {\left( {x,y} \right) |Ax + By \le b, x \ge 0, y \ge 0} \right\}.$$

Definition 2

(Sakawa and Nishizaki 2009) \(S\left( x \right)\) is the decision space of the follower after \(x\) is specified by the leader:

$$S\left( x \right) = \left\{ {y \ge 0 |By \le b - Ax, x \ge 0} \right\}.$$

Definition 3

(Sakawa and Nishizaki 2009) \(S_{X}\) is the decision space of the leader:

$$S_{X} = \left\{ {x \ge 0|{\text{there}}\;{\text{is}}\;{\text{a}}\;y\;{\text{such}}\;{\text{that}}\;Ax + By \le b, y \ge 0} \right\}.$$

Definition 4

(Sakawa and Nishizaki 2009) \(R\left( x \right)\) is the set of rational responses of the follower for \(x\) specified by the leader:

$$R(x) = \left\{ {y \ge 0 |y \in { \arg }\mathop { \hbox{min} }\limits_{y \in S(x)} z_{2} \left( {x,y} \right)} \right\}.$$

Definition 5

(Sakawa and Nishizaki 2009) Inducible region:

$${\text{IR}} = \left\{ {\left( {x,y} \right) |\left( {x,y} \right) \in S, y \in R(x)} \right\}.$$

Definition 6

(Sakawa and Nishizaki 2009) Stackelberg solution:

$$\left\{ {\left( {x,y} \right) |\left( {x,y} \right) \in { \arg }\mathop { \hbox{min} }\limits_{{\left( {x,y} \right) \in {\text{IR}}}} z_{1} \left( {x,y} \right)} \right\}.$$

In the bi-level programming, follower optimization problem is considered as one of the constraints of a bi-level optimization problem. So, by applying the Kuhn–Tucker approach as a popular way in solving BLP, the follower’s problem can be replaced by the Kuhn–Tucker conditions of the follower’s problem. Then the leader’s problem with constraints involving the optimality conditions of the follower’s problem is solved (Sakawa and Nishizaki 2009). Using Kuhn–Tucker conditions, the bi-level linear programming problem (3) can be rewritten as the following equivalent single-level nonlinear programming problem:

$$\begin{aligned} & \varvec{minimize}\quad \varvec{z}_{1} \left( {\varvec{x},\varvec{y}} \right) = \varvec{c}_{1} \varvec{x} + \varvec{d}_{1} \varvec{y} \\ & \varvec{subject }\;\varvec{to}\quad \varvec{uB} - \varvec{v} = - \varvec{d}_{2} ; \\ & \varvec{u}\left( {\varvec{Ax} + \varvec{By} - \varvec{b}} \right) - \varvec{vy} = 0; \\ & \varvec{Ax} + \varvec{By} \le \varvec{b}; \\ & \varvec{x} \ge 0,\varvec{ y} \ge 0,\varvec{ u}^{\varvec{T}} \ge 0,\varvec{ v}^{\varvec{T}} \ge 0, \\ \end{aligned}$$
(4)

where u is an m-dimensional row vector and v is an n 2-dimensional row vector. u and v are the dual variable associated with constraints \(Ax + By \le b\) and \(y \ge 0\), respectively.

By introducing zero-one vectors \(w_{1} = (w_{11} , \ldots ,w_{1m} )\) and \(w_{2} = (w_{21} , \ldots ,w_{{2n_{2} }} )\), the non-linear programming problem (4) is transformed into a following linear mixed zero-one programming problem, and it can be solved by a zero-one mixed integer solver:

$$\begin{aligned} & \varvec{minimize}\quad \varvec{z}_{1} \left( {\varvec{x},\varvec{y}} \right) = \varvec{c}_{1} \varvec{x} + \varvec{d}_{1} \varvec{y} \\ & \varvec{subject }\;\varvec{to }\quad \varvec{ }0 \le \varvec{u}^{\varvec{T}} \le \varvec{Mw}_{1}^{\varvec{T}} ; \\ & 0 \le \varvec{b} - \varvec{Ax} - \varvec{By} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{1}^{\varvec{T}} } \right); \\ & 0 \le \left( {\varvec{uB} + \varvec{d}_{2} } \right)^{\varvec{T}} \le \varvec{Mw}_{2}^{\varvec{T}} ; \\ & 0 \le \varvec{y} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{2}^{\varvec{T}} } \right); \\ & \varvec{x} \ge 0, \\ \end{aligned}$$
(5)

where e is an m-dimensional vector of ones, and M is a large positive constant. The readers who are interested in bi-level programming may refer to Sakawa and Nishizaki (2009).

Proposal model

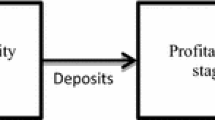
Banking branch performance evaluation problems naturally exhibit a two-level decision modeling which are connected in a hierarchical way. In a bank chain structure, the funds from costumers in the form of deposits are collected within the first level and in the second level the deposits from previous level are taken to make profit. Since the funds collected from the first level determines on the investment decision in the second level, the banking branch performance evaluation problem can be modeled as a leader-follower Stackelberg problem (Wu 2010). The conceptual bi-level DEA model with shared resource is depicted in Fig. 1.

Fig. 1
figure 1

Bi-level programming DEA model with shared resource (Wu 2010)

Full size image

Consider the n banking branch, which was indexed by \(\left( {j = 1, \ldots ,n} \right)\), is involving two levels \(L_{1}\), and \(L_{2}\). This \(L_{1}\)–\(L_{2}\) chain has been addressed using bi-level programming structure, where the first level is termed as a leader and the second level as a follower. These two bank branch chains performance evaluation problem for specific \({\text{DMU}}_{0}\) can be mathematically modeled in the bi-level programming DEA model, which considers the hierarchical structure of the bank branch including decision maker in each level who makes a decision to control a set of decision variables independently, as follows:

$$\begin{aligned} & \mathop {\varvec{Min}}\limits_{{\overline{\varvec{X}}^{{\mathbf{1}}} ,\overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}}} ,\varvec{\lambda}}} \varvec{ }\left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\mathbf{1}}} + \varvec{C}^{{{\mathbf{2}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}}} } \right) + \varvec{ }\left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\mathbf{2}}} + \varvec{ D}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}}} \varvec{ } + \varvec{ D}^{{{\mathbf{2}}^{\varvec{T}} }} \overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}}} } \right) \\ & \varvec{s}.\;\varvec{to} \\ & \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{X}_{\varvec{j}}^{{\mathbf{1}}}\varvec{\lambda}_{\varvec{j}} \le \overline{\varvec{X}}^{{\mathbf{1}}} ; \\ & \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{X}_{\varvec{j}}^{{\varvec{D}{\mathbf{1}}}}\varvec{\lambda}_{\varvec{j}} \le \overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}}} ; \\ & \mathop \sum \limits_{{\varvec{ j} = 1}}^{\varvec{n}} \varvec{Y}_{\varvec{j}}^{{\mathbf{1}}}\varvec{\lambda}_{\varvec{j}} \ge \varvec{Y}_{{\mathbf{0}}}^{{\mathbf{1}}} ; \\ & \mathop \sum \limits_{{\varvec{j} = {\mathbf{1}}}}^{\varvec{n}} \varvec{Y}_{\varvec{j}}^{{\varvec{I}{\mathbf{1}}}}\varvec{\lambda}_{\varvec{j}} \ge \varvec{Y}_{{\mathbf{0}}}^{{\varvec{I}{\mathbf{1}}}} ; \\ & \overline{\varvec{X}}^{{\mathbf{1}}} \varvec{ } + \varvec{ }\overline{\varvec{X}}^{{\mathbf{2}}} \le \varvec{E }\left( {\varvec{const}.} \right); \\ \end{aligned}$$
(6)
$$\begin{aligned} & \mathop {\varvec{Min}}\limits_{{\overline{\varvec{X}}^{{\mathbf{2}}} ,\overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}}} ,\overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}}} ,\varvec{\pi}}} \varvec{ }\left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\mathbf{2}}} + \varvec{ D}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}}} \varvec{ } + \varvec{ D}^{{2^{\varvec{T}} }} \overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}}} } \right) \\ & \varvec{s}.\;\varvec{to} \\ & \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{X}_{\varvec{j}}^{{\mathbf{2}}}\varvec{\pi}_{\varvec{j}} \le \overline{\varvec{X}}^{{\mathbf{2}}} ; \\ & \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{X}_{\varvec{j}}^{{\varvec{D}2}}\varvec{\pi}_{\varvec{j}} \le \overline{\varvec{X}}^{{\varvec{D}2}} ; \\ & \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{Y}_{\varvec{j}}^{{\varvec{I}{\mathbf{1}}}}\varvec{\pi}_{\varvec{j}} \le \overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}}} ; \\ & \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{Y}_{\varvec{j}}^{{\mathbf{2}}}\varvec{\pi}_{\varvec{j}} \ge \varvec{ Y}_{{\mathbf{0}}}^{{\mathbf{2}}} ; \\ & \overline{\varvec{X}}^{{\mathbf{1}}} \varvec{ },\overline{\varvec{X}}^{{\mathbf{2}}} ,\overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}}} ,\overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}}} \varvec{ },\varvec{ }\overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}}} \varvec{ },\;\varvec{\lambda },\varvec{ \pi } \ge {\mathbf{0}}, \\ \end{aligned}$$

where the \(X^{1}\) and \(X^{2}\) are \(m_{1}\)-dimensional row vectors of the shared input of the leader and the follower, respectively, \(X^{D1}\) is an \(m_{2}\)-dimensional row vector of the direct input of the leader, \(X^{D2}\) is the \(m_{3}\)-dimensional row vector of the direct input to the follower, \(Y^{I1}\) is an \(m_{4}\)-dimensional row vector which is the intermediate output to the leader and the intermediate input to the follower, \(Y^{1}\) is an \(m_{5}\)-dimensional row vector of the direct output of the leader, and \(Y^{2}\) is an \(m_{6}\)-dimensional row vector of the direct output to the follower. \(C^{1T} , C^{2T} , D^{1T} , D^{2T}\) are the input unit cost vectors associated with the shared input, the direct input to the leader, the direct input to the follower, and the intermediate input to the follower, respectively. \(\lambda\) and \(\pi\) are the nonnegative multiplier used to aggregate existing leader and follower activities, respectively (Wu 2010).

To solve the bi-level model problem Wu (2010) converts bi-level mathematical programming to a non-linear mathematical programming and then uses trial and error process to achieve the optimum solution, which makes the process lengthy and time-consuming. Since nonlinear models are reducing the validity of the model, in this paper, we recommended the Mixed integer programming method, which converts the bi-level mathematical programming to a linear mathematical programming and significantly improves the process to achieve the optimum solution.

The bi-level programming DEA model (6) is transformed into the mixed integer single-level linear programming DEA model as follows:

$$\begin{aligned} & \varvec{min }\left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{{\mathbf{1}}^{\varvec{T}} }} \varvec{ } + \varvec{ C}^{{{\mathbf{2}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}^{\varvec{T}} }} } \right) + \varvec{ }\left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{2} + \varvec{ D}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}}} \varvec{ } + \varvec{ D}^{{{\mathbf{2}}^{\varvec{T}} }} \overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}^{\varvec{T}} }} } \right) \\ & {\varvec{s}}.\;{\varvec{to}} \\ & \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{X}_{\varvec{j}}^{{\mathbf{1}}}\varvec{\lambda}_{\varvec{j}} \le \overline{\varvec{X}}^{{\mathbf{1}}} ; \\ & \mathop \sum \limits_{{\varvec{ j} = 1}}^{\varvec{n}} \varvec{X}_{\varvec{j}}^{{\varvec{D}{\mathbf{1}}}}\varvec{\lambda}_{\varvec{j}} \le \overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}}} ; \\ & \mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{Y}_{\varvec{j}}^{{\mathbf{1}}}\varvec{\lambda}_{\varvec{j}} \ge \varvec{Y}_{0}^{{\mathbf{1}}} ; \\ & 0 \le \overline{\varvec{X}}^{{\mathbf{2}}} - \left( {\mathop \sum \limits_{{\varvec{j} = 1}}^{\varvec{n}} \varvec{X}_{\varvec{j}}^{{\mathbf{2}}}\varvec{\pi}_{\varvec{j}} } \right) \le \varvec{Mw}_{{\mathbf{1}}}^{\varvec{T}} ; \\ & 0 \le \varvec{U}^{{\mathbf{1}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{1}}}^{\varvec{T}} } \right); \\ & 0 \le \overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}}} - \left( {\mathop \sum \limits_{{\varvec{j} = {\mathbf{1}}}}^{\varvec{n}} \varvec{X}_{\varvec{j}}^{{\varvec{D}{\mathbf{2}}}}\varvec{\pi}_{\varvec{j}} } \right) \le \varvec{Mw}_{{\mathbf{2}}}^{\varvec{T}} ; \\ & 0 \le \varvec{U}^{{\mathbf{2}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{2}}}^{\varvec{T}} } \right); \\ & 0 \le \overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}}} - \left( {\mathop \sum \limits_{{\varvec{ j} = {\mathbf{1}}}}^{\varvec{n}} \varvec{Y}_{\varvec{j}}^{{\varvec{I}{\mathbf{1}}}}\varvec{\pi}_{\varvec{j}} } \right) \le \varvec{Mw}_{{\mathbf{3}}}^{\varvec{T}} ; \\ & 0 \le \varvec{U}^{{\mathbf{3}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{3}}}^{\varvec{T}} } \right); \\ & 0 \le \mathop \sum \limits_{{\varvec{j} = {\mathbf{1}}}}^{\varvec{n}} \varvec{Y}_{\varvec{j}}^{{\mathbf{2}}}\varvec{\pi}_{\varvec{j}} - \varvec{Y}_{0}^{{\mathbf{2}}} \le \varvec{Mw}_{{\mathbf{4}}}^{\varvec{T}} ; \\ \end{aligned}$$
(7)
$$\begin{aligned} & 0 \le \varvec{U}^{{\mathbf{4}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{4}}}^{\varvec{T}} } \right); \\ & 0 \le \varvec{E} - \overline{\varvec{X}}^{{\mathbf{1}}} - \overline{\varvec{X}}^{{\mathbf{2}}} \varvec{ } \le \varvec{Mw}_{{\mathbf{5}}}^{\varvec{T}} ; \\ & 0 \le \varvec{U}^{{\mathbf{5}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{5}}}^{\varvec{T}} } \right); \\ & \varvec{U}^{{\mathbf{1}}} - \varvec{U}^{{\mathbf{5}}} + \varvec{V}^{{\mathbf{1}}} = \varvec{C}^{{\mathbf{1}}} ; \\ & \varvec{U}^{{\mathbf{2}}} + \varvec{V}^{{\mathbf{2}}} = \varvec{D}^{{\mathbf{1}}} ; \\ & \varvec{U}^{{\mathbf{3}}} + \varvec{V}^{{\mathbf{3}}} = \varvec{D}^{{\mathbf{2}}} ; \\ & - \varvec{X}_{\varvec{j}}^{{\mathbf{2}}} \varvec{U}^{{\mathbf{1}}} - \varvec{X}_{\varvec{j}}^{{\varvec{D}{\mathbf{2}}}} \varvec{U}^{{\mathbf{2}}} - \varvec{Y}_{\varvec{j}}^{{\varvec{I}{\mathbf{1}}}} \varvec{U}^{{\mathbf{3}}} + \varvec{Y}_{\varvec{j}}^{{\mathbf{2}}} \varvec{U}^{{\mathbf{4}}} + \varvec{V}^{{\mathbf{4}}} = {\mathbf{0}}; \\ & 0 \le \overline{\varvec{X}}^{{\mathbf{2}}} \le \varvec{Mw}_{{\mathbf{6}}}^{\varvec{T}} ; \\ & 0 \le \varvec{V}^{{\mathbf{1}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{6}}}^{\varvec{T}} } \right); \\ & 0 \le \overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}}} \le \varvec{Mw}_{{\mathbf{7}}}^{\varvec{T}} ; \\ & 0 \le \varvec{V}^{{\mathbf{2}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{7}}}^{\varvec{T}} } \right); \\ & 0 \le \overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}}} \le \varvec{Mw}_{{\mathbf{8}}}^{\varvec{T}} ; \\ & 0 \le \varvec{V}^{{\mathbf{3}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{8}}}^{\varvec{T}} } \right); \\ & 0 \le\varvec{\pi}_{\varvec{j}} \le \varvec{Mw}_{{\mathbf{9}}}^{\varvec{T}} ; \\ & 0 \le \varvec{V}^{{\mathbf{4}}} \le \varvec{M}\left( {\varvec{e} - \varvec{w}_{{\mathbf{9}}}^{\varvec{T}} } \right); \\ & \overline{\varvec{X}}^{{\mathbf{1}}} \varvec{ },\overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}}} ,\varvec{\lambda } \ge 0\varvec{ }, \\ \end{aligned}$$

where the \(U^{1}\) and \(V^{1}\) are the \(m_{1}\)-dimensional dual vectors correspond to shared input constraints and variables to the follower, respectively, \(U^{2}\) and \(V^{2}\) are the \(m_{3}\)-dimensional dual vectors associated with direct input constraints and variables to the follower, respectively, \(U^{3}\) and \(V^{3}\) are the \(m_{4}\)-dimensional dual vectors correspond to the intermediate input constraints and variables of the follower, respectively, \(U^{4}\) and \(V^{4}\) are the \(n\)-dimensional dual vectors, and \(U^{5}\) is an \(m_{1}\)-dimensional dual vectors correspond to the constrained resources. Correspondingly, \(W_{i}^{T} , \;i = 1, \ldots ,9\), are the zero-one vectors. \(e\) and \(M\) are the vector of ones and the large positive constant, respectively.

By solving the bi-level programming DEA model, the optimal solution of \(\left( {\overline{X}^{1*} ,\overline{X}^{2*} ,\overline{X}^{D1*} ,\overline{X}^{D2*} ,\overline{Y}^{I1*} ,\lambda_{j}^{*} ,\pi_{j}^{*} } \right)\) are obtained. Based on optimal solution, the cost efficiency of the leader of \({\text{DMU}}_{0}\) is defined as:

$$\varvec{CE}_{{\mathbf{0}}}^{\varvec{L}} = \frac{{\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{{\mathbf{1}}\varvec{*}}} + \varvec{C}^{{{\mathbf{2}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}\varvec{*}}} }}{{\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \varvec{X}_{{\mathbf{0}}}^{{\mathbf{1}}} + \varvec{C}^{{{\mathbf{2}}^{\varvec{T}} }} \varvec{X}_{{\mathbf{0}}}^{{\varvec{D}{\mathbf{1}}}} }}$$
(8)

and the cost efficiency of the follower of \({\text{DMU}}_{0}\) is defined as:

$$\varvec{CE}_{{\mathbf{0}}}^{\varvec{F}} = \frac{{\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{{\mathbf{2}}\varvec{*}}} + \varvec{D}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}\varvec{*}}} + \varvec{D}^{{2^{\varvec{T}} }} \overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}\varvec{*}}} }}{{\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \varvec{X}_{{\mathbf{0}}}^{{\mathbf{2}}} + \varvec{D}^{{{\mathbf{1}}^{\varvec{T}} }} \varvec{X}_{{\mathbf{0}}}^{{\varvec{D}{\mathbf{2}}}} + \varvec{D}^{{{\mathbf{2}}^{\varvec{T}} }} \varvec{Y}_{{\mathbf{0}}}^{{\varvec{I}{\mathbf{1}}}} }}$$
(9)

and the total cost efficiency of \({\text{DMU}}_{0}\) is defined as:

$$\varvec{CE}_{{\mathbf{0}}}^{\varvec{S}} = \frac{{\left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{{\mathbf{1}}\varvec{*}}} + \varvec{C}^{{{\mathbf{2}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{1}}\varvec{*}}} } \right) + \left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{{\mathbf{2}}\varvec{*}}} + \varvec{D}^{{{\mathbf{1}}^{\varvec{T}} }} \overline{\varvec{X}}^{{\varvec{D}{\mathbf{2}}\varvec{*}}} + \varvec{D}^{{{\mathbf{2}}^{\varvec{T}} }} \overline{\varvec{Y}}^{{\varvec{I}{\mathbf{1}}\varvec{*}}} } \right)}}{{\left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \varvec{X}_{{\mathbf{0}}}^{{\mathbf{1}}} + \varvec{C}^{{{\mathbf{2}}^{\varvec{T}} }} \varvec{X}_{{\mathbf{0}}}^{{\varvec{D}{\mathbf{1}}}} } \right) + \left( {\varvec{C}^{{{\mathbf{1}}^{\varvec{T}} }} \varvec{X}_{{\mathbf{0}}}^{{\mathbf{2}}} + \varvec{D}^{{{\mathbf{1}}^{\varvec{T}} }} \varvec{X}_{{\mathbf{0}}}^{{\varvec{D}{\mathbf{2}}}} + \varvec{D}^{{2^{\varvec{T}} }} \varvec{Y}_{{\mathbf{0}}}^{{\varvec{I}{\mathbf{1}}}} } \right)}}.$$
(10)

The framework of the efficiency evaluation of the banks

After analyzing the previous literature review, the efficiency of the banks which was proposed throughout this research was shown in Fig. 2. The analytical processes were divided and carried out in six steps: (1) in the first step the efficiency measurements of the bank were determined by reviewing literature and expert ideals; (2) in the second step the hierarchical structure of the bank was determined and the measurements were divided into two levels namely leader and follower levels; (3) in the third step the relationships between the leader and the follower were determined; (4) in the fourth step the main bi-level DEA model of the bank was created; (5) in the fifth step the created bi-level model was converted into a single linear model using mixed integer programming; (6) and finally in the sixth step the efficiency of the bank was obtained and the its ranking was recognized.

Fig. 2
figure 2

Proposed performance evaluation model of bank

Full size image

Empirical study

Banks are financial institutions that gather their assets from different resources and they made available for the sections that need liquidity. Therefore, banks are considered critical currents for each nation. Along with the emergence of private banks in the financial markets, Demand has dramatically increased for variety of banking services. Banks are looking for different procedures of functional improvement to attract customers, since they overtake one another to increase their contribution in market and Profitability; performance evaluation of banks is significantly considered among them and it is become one of the main bank manager activities.

Growth and economic development of every country requires moving additional funds of saver to the investors in a proper way. Availability of an extensive and efficient financial market which in financial resources is directed toward the best investment opportunities is critical. On the other hand, the maximum turnover in Iran is achieved through banking system. In addition, desired functioning of the banking system plays an important role to improve the economic actions.

However, it can be used the most traditional factors of an enterprise performance to evaluate a bank performance with modern procedures. One of the institutions investigating function of banking system is Iran Banking education Institute. Most performance evaluation criteria of it is quantitative, in addition it is considered financial standards. It investigates banks based on Liabilities, Assets, Number of bank branches, international and exchange Activities, The combination of human resources, profits and losses, facilities, overdue demands and the benefit of electronic banking technology. In this study, first it is determined the indicators through bank experts interview and library studies and criteria are extracted. These include: fixed assets, space, non-invest deposits, IT cost, profit, Deposit, Marketability employees and profitability employees. Usually the bank performance evaluation process involves the measurement of the performance of bank through its profitability levels. There are some other factors, in addition to profitable activities, that play an important role in bank performance evaluation process, including: bank location (ratio of residential to commercial region of the banks), cultural context of the region (whatever people tend to deposit their money as long term or current deposit), the services bank provides to compete with other banks and attract customers. These factors affect bank’s performance indirectly, and usually are ignored in performance evaluation. So, in addition to the bank’s profitability, intangible factors that indirectly affect bank’s performance should also be taken into account while measuring the performance of banks. Thus, to measure all aspects of bank performance, the banks were evaluated in two levels so that all activities that affect the performance of banks would be taken into consideration.

Each bank studied in this research considers certain strategies according to the needs of people and market traction due to the geographic location of each region in terms of area, culture, population density, the ratio of commercial to residential area, etc. The banks offer different services to their clients by hiring the required number of employers, and with the deployment of fixed assets such as office supplies, computers, desks, chairs, banking software, IT costs, storage systems, and data protection. Banks collect their resources by attracting deposits from clients, and they begin profiting by investing those resources on various projects and giving loans.

As mentioned, banks can be viewed as an entity in which two decision makers in a hierarchical structure make decisions in turn so as to optimize their performance. Based on the proposal model in the previous section, the bi-level programming DEA model was applied to evaluate the performance of 15 branches of Iranian banks in 2011. Each branch had a certain amount of marketability and profitability level, where the marketability played as a leader and the profitability level served as a follower. Marketability level indicates the ability of the branch in marketing to collect funds from costumer in form of deposit by consuming the bank’s resources. Profitability level indicates the ability of the branch to make profit by investing the deposits in other activities. The evaluation index system of bank branch performance evaluation problem is shown in Table 1.

Table 1 Evaluation index system
Full size table

The performance of each branch is characterized by seven variables where fixed assets \((X^{D11} )\), space \((X^{D12} )\), and non-invest deposits \((Y^{1} )\) are associated with leader level, while IT cost \((X^{D2} )\) and profit \((Y^{2} )\) are associated with the follower level. Deposit \((Y^{I1} )\) from leader to follower level is intermediate variable. Marketability employees \((X^{1} )\) and profitability employees \((X^{2} )\) are resource shared variables. The data related to these variables are presented in Table 2. Shared employees and the space costs are also given in Table 2 and due to cost nature of fixed assets, deposits, IT costs, and the correspond costs are assumed to be unit.

Table 2 Data
Full size table

The first column of Table 3 depicts the results of performance evaluation using the CCR model, where each unit is as a black box with only a few input and output while the relationships between the elements are not considered. To calculate the performance of the banks in this way, four inputs (Employee, Fixed asset, Space, and IT Cost) are used to obtain one output (Profit). (these inputs and outputs belong to leader and follower levels.)

Table 3 Cost efficiency and reference set unit
Full size table

At this stage we ignored the intermediate variables that exist between the leader and follower. The results showed that three out of the 15 banks were efficient, and the other 12 banks had high performance compared to the performance of the bi-level models. This experiment shows how weak the DEA’s classic model is in regards to separation ability. Compared to classic DEA models, bi-level DEA model has higher separation ability, mainly because it provides a tool to reveal the internal activities and relationships between activities within the black box and provides a detailed assessment of the existing subsystem performance.

Based on mixed integer single-level linear programming DEA model (7), cost efficiency scores for the bank branches and the followers and the leaders are obtained. Cost efficiency scores and the reference units correspond to the leader and the follower are given in following Table 3.

According to Table 3, there are no cost efficient banks, because banks are not performing efficiently at both decision levels. The tenth and eleventh banks are cost efficient at the leader, and the first and third banks are cost efficient at the follower level, and because the other player in these banks is inefficient, these banks systematically are termed as inefficient. Table 3 also indicates that the second bank is more efficient than the third, tenth, and eleventh banks which are only efficient in one level, so that, it can be the advantages of coordination between players. In addition, the classic DEA efficiency score and reference set for the leader and follower are shown in the Table 3. DMU 1, 3 and 7 are efficient in classic DEA model, DMU 10 and 11 are reference for the leader and DMU 1 and 3 are reference for the follower.

Conclusion

In the real world, banks have a decentralized structure in which multi decision makers in a hierarchical structure makes decision in turn or at the same time to optimize their objective function. In this rapidly changing world, responding to change needs the ability of management to identify the location of inefficiency. Thus, efficiency analysis can be a source of competitive advantages (Avkiran 2009). DEA is a better way to measure efficiency since it requires no prior assumption on the specification of the efficient frontier. In this paper, we applied bi-level programming DEA model with two inter-related decision makers in a decentralized decision structure to evaluate the performance of 15 Iranian bank branches with one level correspond to a leader while the other a follower. Bi-level programming DEA model proposed by (Wu 2010) can provide insight and detailed information to bank managers when measuring the efficiency of a bank with Stackelberg-game relationships. The results obtained from bi-level programming DEA model have a strong discriminating power due to considering internal operations in the banking chain.

Further researchers can develop our model in the three-level or multi-level. Since the multi-level DEA models are NP-hard problem, we proposed to use heuristic model to solve them. Finally, we propose to further researcher to create a benchmark unit in bi-level DEA model and determine VRS in efficiency model.