Abstract
Cross-docking is a logistic concept, which plays an important role in supply chain management by decreasing inventory holding, order packing, transportation costs and delivery time. Paying attention to these concerns, and importance of the congestion in cross docks, we present a mixed-integer model to optimize the location and design of cross docks at the same time to minimize the total transportation and operating costs. The model combines queuing theory for design aspects, for that matter, we consider a network of cross docks and customers where two M/M/c queues have been represented to describe operations of indoor trucks and outdoor trucks in each cross dock. To prepare a perfect illustration for performance of the model, a real case also has been examined that indicated effectiveness of the proposed model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In the competitive environment, companies must satisfy more complicated demands with less response time. Cross-docking is a relatively new warehousing strategy in logistic that involves moving products directly from the receiving dock to the shipping dock (Bellanger et al. 2013). It can be defined as a transshipment platform which receives flows from various suppliers and consolidates them with other flows for a common final delivery to a destination (Kinnear 1997). Also the efficiency of cross-docking will influence the lead time, inventory level and response time to the costumer (Kuo 2013).
In the literature, there are some researchers who considered cross-docking problem. For instance, Bellanger et al. (2013) dealt with the problem of finding optimal schedule in cross-docking, where the main goal was to minimize the completion time of the latest order. In their paper, cross-docking was modeled as a three-stage hybrid flow shop, and for obtaining good feasible solutions, they have developed several heuristic schemes. They also proposed a branch-and-bound algorithm to evaluate the heuristics. Chen and Song (2009) considered two-stage hybrid cross-docking scheduling problem, where the objective was minimizing the make span. To do so, a mixed-integer programming and four heuristics were presented.
Kuo (2013), considered another interesting aspect in optimization of cross-docking; he presented a model for optimizing both inbound and outbound truck sequencing and both inbound and outbound truck dock assignment. Jayaraman and Ross (2003) considered supply chain design problem which incorporates cross-docking into a supply chain environment. Agustina et al. (2010) provide a literature review of mathematical models in cross-docking, where the models were classified into three levels of operational, tactical and strategic.
In recent years, Santos et al. (2013) dealt with pickup and delivery in cross docks, and proposed an integer programming model and a Branch-and-price for the problem. Liao et al. (2012) considered problem of inbound and outbound truck sequencing for cross docks, and proposed two new hybrid differential evolution algorithms for the problem. Agustina et al. (2014) considered perishable food products, and proposed a mixed-integer model to minimize earliness, tardiness, inventory holding, and transportation cost.
Location analysis and network design are two major research areas in supply chain optimization, location problems deal with the decisions of where to optimally locate facilities whereas network design involves activating optimal links (Contreras and Fernández 2012). In this area, Ross and Jayaraman (2008) studied location planning for the cross docks and distribution centers in supply chains. Later, Babazadeh et al. (2012) proposed a new network design mathematical model for an agile supply chain.
Lüer-Villagra and Marianov (2013) considered price and location; they proposed a competitive hub location and pricing problem for the air passenger industry. Mousavi and Tavakoli-Moghaddam (2013) considered location and routing scheduling problems with cross-docking, and present a two-stage mixed-integer programming model.
Tavakkoli-moghaddam et al. (2013) considered a network design problem for a three level supply chain, and proposed a new mathematical model, where their aims were to determine the number of located distribution centers, their locations, capacity level, and allocating customers to distribution centers.
One of the most important factors in supply chain management is response time, which consists of production, handling and waiting times (Vis and Roodbergen 2011). Some researchers modeled response time in stochastic environment, and some of them used queuing theory to represent a mathematical model. Some researchers believe that it makes the problem hard to solve, and some suggest cutting planes for obtaining optimal solutions in small and medium-sized problem instances (Karimi-Nasab and Seyedhoseini 2013).
In this area, Ha (1997) considered Poisson demand and exponential production times for a single item make-to-stock production system. He proposed an M/M/1/S queuing system for modeling the system. Later, Karimi-Nasab and Fatemi Ghomi (2012) argued that it is not a practical assumption that production times are fixed input data of the problem. They proposed that in many cases the production time of the item may be considered as either a decision variable or an uncertain input data other than a fixed value. Nonetheless, many operational managers believe that making decisions with minimal total costs is of crucial importance (Karimi-Nasab and Sabri-Laghaie 2014).
Kerbache and Smith (2004) proposed context of supply chain and application of queue approach. They modeled supply chain network as a queuing system and analyzed it, in particular, they used queuing network methods to evaluate the performance measures of a supply chain. In this research, queuing theory has been used to describe stock control system of retailers and response of suppliers, where each retailer has been assumed to be an M/M/1 queue with balk arrival, and each supplier has been assumed to be an M/M/1 queue.
In summary, it is clear that despite of the many contributions in the location problems, there is little consideration due to cross dock location problem, which considers stochastic waiting time for cross docks. In this paper, cross dock location problem has been considered, where the primary goal is to develop a rich model to represent following key questions:
-
Where cross docks should be located?
-
What is the optimal number of indoor trucks and outdoor trucks?
-
How customers should be allocated to cross docks?
These questions are obviously interconnected, for example location and numbers of cross docks affect interval flows for each cross dock and consequently it would influence number of trucks, for that matter, a mixed-integer model has been presented. The main contributions of this paper can be summarized as follows:
-
Location problem of cross docks has been considered in an uncertainty environment
-
A mathematical model has been developed which simultaneously optimizes location of cross docks, number of indoor trucks and outdoor trucks.
-
A congestion constraint has been considered in the model which restricts waiting time of customers to not be more than tI, and another constraint has been considered that restricts waiting time of shipments in cross docks to not be more than tI.
The reminder of this paper is organized as follows: section two provides a brief definition of the problem, and also represents a mathematical model and a linearization approach to solve the problem. Section three is for computational results which consist of an example and a real case. Section four concludes the paper.
Problem definition
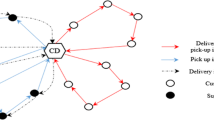
The basic supply chain elements considered in this paper consist a network with some cross docks and some customers, where each customer sends shipments to the other customers, and cross docks transport the shipments for customers. Material flow in which network implemented is illustrated in Fig. 1. In this Figure, dotted lines demonstrate flows that distribute shipments for customers, and connection lines are for flows which collect shipments from customers. The considered problem deals with two types of decisions, the primary decisions are where to optimally locate cross docks and how to allocate customers to cross docks, and the secondary decision is determining the optimal truck number which needs to be allocated to each cross dock. The objective of the model consists of costs related to transportation costs, establishing costs and operation costs of trucks.
This problem entails the following assumptions:
-
1.
Demand size for each customer is less than size of a truck, and each truck can give service to n customers.
-
2.
Each truck gives service to exactly n customers, and if number of customers be lesser than n, then truck waits to service with full capacity.
-
3.
Location of customers is fixed.
-
4.
Between each pair of nodes—customers and cross docks—at most one link can be constructed.
-
5.
Candidate nodes for cross docks are fixed.
-
6.
Demand of customer k has been assumed Poisson distribution with rate of \( \lambda_{\text{k}} \).
-
7.
Service time for each truck has been assumed exponentially distribution with mean value of \( \frac{1}{\mu } \).
-
8.
Waiting time for each shipment in cross dock must not be more than tI.
-
9.
Waiting time for customers that are ready to get service must not be more than tI.
Considering following assumption, all n customers get service together. Consequently, a Markov process would occur for a shipment with size of n customers, which could be transported by a truck. Figure 2 depicts this Markov process, where each state, number of customers for a specific shipment, has been represented by i. In this Markov, when n−1 customers are in the system and a new customer arrives, then a new shipment becomes ready for transportation. As probabilities of all the states are equal, rate of truck demands is Poisson distribution with value of \( \frac{{ \lambda_{\text{j}} }}{n} \), where \( \lambda_{\text{j}} \) is demand rate for all costumers that allocated to cross dock j.
In this queue each customer has some waiting time but as \( \lambda_{\text{j}} \) is a big amount for cross docks, waiting time in this queue could be ignorable. For that matter only waiting time for trucks are considered in this paper.
Considering following assumption, an M/M/c queue occurs in each cross dock for outdoor shipments and an M/M/c queue occurs in each cross dock for indoor shipments. For this queue, probability of zero waiting time in queue is equal to Eq. 1.
Also probability of t waiting time in queue is equal to Eq. 2.
In other words, W s (t) can be expressed as follows:
Model development
Objective
St:
Objective function has composed of five sections. First section is for transportation costs, second section relates to costs of establishing cross docks, and the other three sections are for operating indoor and outdoor trucks.
Constraint five calculates indoor flows for cross dock t, constraint six calculates outdoor flows that need to be transported from cross dock t to another cross dock, and constraint seven calculates outdoor flows go through cross dock t and customers. Constraints eight and nine ensure that between each pair of customers, only one path be constructed. Constraint 10 states that a path goes through a cross dock only if it is established. Constraints 11, 12 and 13 states that no truck can be allocated to a cross dock unless it has been established. Constraints 14, 15 and 16 ensure that waiting time of customer for indoor trucks or outdoor trucks not to be more than tIt, where constraint 14 is for indoor trucks, constraint 16 is for outdoor trucks which give service to shipments between two cross docks and constraint 15 is for outdoor trucks which goes through cross docks and customers.
Solving approach
Using Eq. 3, constraint 14 is equal to constraint 17.
where λ is equal to λ It. Similar to constraint 14, constraints 15 and 16 can be described in order to W s (t), which are some nonlinear constraints. To conquer nonlinearity of the model, it has been proposed to replace constraints 14, 15 and 16 with Eqs. 18, 19, and 20.
where λ max,Im, λ max,1Om and λ max,2Om are the maximum arrival rate for each of the queues that constraints 14, 15 and 16 would be satisfied. For this reason, to solve the model, λ max,Im and λ max,1Om and λ max,2Om must be defined for each possible number of indoor or outdoor trucks.
Computational result
In this paper, using a numerical example, performance of the proposed model has been evaluated, and then efficiency of the model has been examined by a real case.
Numerical result
In this section, the model has been coded with Gams software, and an example has been produced in “Appendix” A. We analyzed the model due to flow rate in Fig. 3, where ρ is considered as a coefficient for flow rate between each pair of nodes. As demonstrated in this figure, flow rate has a concave relation with optimal costs. This pattern has been affected by two reasons: the first reason is change in trucks and operating costs of trucks, and the second reason is change in transportation costs.
Mousavi and Tavakoli-Moghaddam (2013) proposed a two-stage model for cross-docking problem, where the first stage aims to find location of cross docks and the second stage aims to find optimal scheduling of trucks. For the first stage they considered fixed costs of establishing cross docks and transportation costs. Ross and Jayaraman (2008) also considered same costs and examined two location problem of cross docks. Using queuing theory, we proposed three waiting time constraints for shipments in cross docks and customers, and also considered costs related to operation of trucks. Differences between results of our model and previous models occur because of tIt and δ, which affect transportation costs also. As tIt be bigger, our model becomes more similar to the previous models. To prepare a better description among models, previous example has been considered and three values of tIt have been considered and sensitivity of the objective value due to operating cost of each truck has been analyzed in Fig. 4. As demonstrated in this figure, when tIt becomes lesser, sensitivity due to truck costs increases.
Case study
In this section, we represent a case study, which is for Dried fruit products in Iran. In this case, we only considered two major products of raisin and pistachios. Based on information of 2012, Iran is capable to produce 154,000 tons of raisin and 192,000 tons of pistachios per year. Where it exports 138,000 tons of raisin and 150,000 tons of pistachios. These two products need to be gathered from farmers or factories that pack the products, then transfer them to wholesalers.
There are five wholesalers in countries of Qatar, Iraq, Russia, Azerbaijan and Turkey which consist of major exports of these products, and also more than 15 wholesalers are existing in different cities of Iran. Also there are 14 cities which produce major raisins of Iran and 30 cities which produce major pistachios of Iran. In these cities, Ghazvin produces with 50,000 tons of raisin is the most capable producer of raisin, and Rafsanjan with 21,000 tons of pistachios is the most capable producer of pistachios.
Production rate of raisin and pistachios for different cities in year of 2012, and also products flow rate between each pair of cities for both of the products have been presented in “Appendix” B. In this case, it has been assumed that all the cross docks must be established in the Iran. Consequently, transportation of the exports out of the Iran can be ignored, and only it be considered in Iran. Another reason for this is for different transportation types which could be used out of the Iran. For instance, if a shipment wants to go Qatar, it must go to Bandarabas dock, and then it goes to Qatar.
Experts defined 16 potential locations for cross docks. This case has been solved under two scenarios: the first one is when raisin products and pistachios products need to be transported separately, and the second one is when they could be transported together. For this case, Figs. 5 and 6 demonstrate optimal solution of the case for the first scenario, and Fig. 7 demonstrates optimal solution for the second scenario.
For this case, Table 1 prepares a brief description of optimal solution for both of the scenarios.
As it is demonstrated in Table 1, if raisin and pistachios could be transported together, optimal costs would plunge. For this scenario, costs are 720 million Tomans, which is significantly lesser than when these products need to be transported separately. Because of consolidation of raisin and pistachios, numbers of trucks and cross docks have been decreased. In this case, 64 trucks and seven cross docks are needed for the first scenario and 56 trucks and four cross docks are needed for the second scenario.
Conclusion
In this paper, we considered the problem of cross-docking, and proposed a mathematical model to simultaneously optimize location of cross docks and number of trucks. Assigning optimal trucks, and sequencing of trucks in cross docks are some historical problems, but considering location of cross docks with variable number of trucks is a new problem.
In this model, we used one of the most important concepts of cross docks, which state that no shipment in cross docks can wait more than a specific time. Some of the researchers state that this waiting time is equal to 12 h and some defined 24 h. For this reason we proposed two stochastic constraints. We also improved the model by considering another waiting time constraint for shipments in customer nodes. Consequently, to satisfy these constraints, numbers of indoor trucks and outdoor trucks in each cross dock have been considered variable.
In this paper, the model has been examined due to different parameters of the model, and differences among our model and previous models have been analyzed. We also prepared a real case to illustrate performance of the model, which is for products of raisin and pistachios in Iran. For this case, two scenarios have been considered and proposed model has been analyzed.
For future studies this research can be extended by considering scheduling of trucks, this may increase complexity of the problem but the model would become more realistic. Another extension of this research is possible by considering rate of corruption for perishable inventories. Another aspect which is of further interest is to consider waiting time costs in objective, although it may be expected that this will lead to intractable formulations.
Abbreviations
- flij :
-
Rate of flow goes to customer j from customer i
- \( {\text{C}}_{\text{ijtl }} \) :
-
Transportation cost between customer i and j where flow goes through cross docks of t and l
- C 1mt :
-
Costs of allocating m outdoor trucks to cross dock t for transportation between cross docks
- C 2mt :
-
Costs of allocating m indoor trucks or outdoor trucks to cross dock t for transporting for customers
- Ft :
-
Establishing cost of cross dock t
- M I :
-
Highest possible Number of indoor trucks
- M 1O :
-
Highest possible Number of outdoor trucks for transportation between cross docks
- M 2O :
-
Highest possible Number of outdoor trucks for a cross dock to transport goods for customers
- N :
-
Number of candidate nodes for cross docks
- L :
-
Number of customers
- x ijt1 :
-
\( 1 {\text{ if there is any way from customer i to customer j which uses cross dock t and }}\,0\,{\text{otherwise}} \)
- y mt :
-
1 if m indoor truck be allocated to cross dock t \( {\text{and}}\,0\,{\text{otherwise}} \)
- z mt :
-
1 if m outdoor truck be allocated to cross dock t to transport goods for customers \( {\text{and}}\,0\,{\text{otherwise}} \)
- lmt :
-
1 if m outdoor truck be allocated to cross dock t for transportation to other cross docks \( {\text{and}}\,0\,{\text{otherwise}} \)
- N t :
-
\( 1 {\text{ if cross dock j establish and}}\,0\,{\text{otherwise}} \)
- λ It :
-
Rate of indoor demand for cross dock t
- λ O1t :
-
Rate of outdoor flows that need to be transported from cross dock t to another cross dock
- λ O2t :
-
Outdoor flows go through cross dock t and customers
References
Agustina D, Lee CKM, Piplani R (2010) A review : mathematical models for cross docking planning. Int J Eng Bus Manag 2(2):47–54
Agustina D, Lee CKM, Piplani R (2014) Vehicle scheduling and routing at a cross docking center for food supply chains. Int J Prod Econ 152:29–41
Babazadeh R, Razmi J, Ghodsi R (2012) Supply chain network design problem for a new market opportunity in an agile manufacturing system. J Ind Eng Int. doi:10.1186/2251-712X-8-19
Bellanger A, Hanafi S, Wilbaut C (2013) Three-stage hybrid- flow shop model for cross-docking. Comput Oper Res 40:1109–1121
Chen F, Song K (2009) Minimizing make span in two-stage hybrid cross docking scheduling problem. Comput Oper Res 36:2066–2073
Contreras I, Fernández E (2012) General network design: a unified view of combined location and network design problems. Eur J Oper Res 219(3):680–697
Ha AY (1997) Stock-rationing policy for a make-to-stock production system with two priority classes and backordering. Nav Res Logist (NRL) 44(5):457–472
Jayaraman V, Ross A (2003) A simulated annealing methodology to distribution network design and management. Eur J Oper Res 144:629–645
Karimi-Nasab M, Fatemi Ghomi SMT (2012) Multi-objective production scheduling with controllable processing times and sequence-dependent setups for deteriorating items. Int J Prod Res 50(24):7378–7400
Karimi-Nasab M, Sabri-Laghaie K (2014) Developing approximate algorithms for EPQ problem with process compressibility and random error in production/inspection. Int J Prod Res 52(8):2388–2421
Karimi-Nasab M, Seyedhoseini SM (2013) Multi-level lot sizing and job shop scheduling with compressible process times: a cutting plane approach. Eur J Oper Res 231(3):598–616
Kerbache L, Smith JM (2004) Queueing networks and the topological design of supply chain systems. Int J Prod Econ 91(3):251–272
Kinnear E (1997) Is there any magic in cross-docking? Supply Chain Manag Int J 2:49–52
Kuo Y (2013) Optimizing truck sequencing and truck dock assignment in a cross docking system. Expert Syst Appl 40:5532–5541
Liao TW, Egbelu PJ, Chang PC (2012) Two hybrid differential evolution algorithms for optimal inbound and outbound truck sequencing in cross docking operations. Appl Soft Comput 12:3683–3697
Lüer-Villagra A, Marianov V (2013) A competitive hub location and pricing problem. Eur J Oper Res 231:734–744
Mousavi SM, Tavakoli-Moghaddam R (2013) A hybrid simulated annealing algorithm for location and routing scheduling problems with cross-docking in the supply chain. J Manuf Syst 32:335–347
Ross A, Jayaraman V (2008) An evaluation of new heuristics for the location of cross-docks distribution centers in supply chain network design. Comput Ind Eng 55:64–79
Santos FA, Mateus GR, da Cunha AS (2013) The pickup and Delivery problem with cross-docking. Comput Oper Res 40:1085–1093
Vis IFA, Roodbergen KJ (2011) Layout and control policies for cross docking operations. Comput Ind Eng 61:911–919
Tavakkoli-moghaddam R, Forouzanfar F, Ebrahimnejad S (2013) Incorporating location, routing, and inventory decisions in a bi-objective supply chain design problem with risk-pooling. J Ind Eng Int 9:19
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
Appendix B
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Seyedhoseini, S.M., Rashid, R. & Teimoury, E. Developing a cross-docking network design model under uncertain environment. J Ind Eng Int 11, 225–236 (2015). https://doi.org/10.1007/s40092-014-0088-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-014-0088-0