A modified NSGA-II solution for a new multi-objective hub maximal covering problem under uncertain shipments

Abstract

Hubs are centers for collection, rearrangement, and redistribution of commodities in transportation networks. In this paper, non-linear multi-objective formulations for single and multiple allocation hub maximal covering problems as well as the linearized versions are proposed. The formulations substantially mitigate complexity of the existing models due to the fewer number of constraints and variables. Also, uncertain shipments are studied in the context of hub maximal covering problems. In many real-world applications, any link on the path from origin to destination may fail to work due to disruption. Therefore, in the proposed bi-objective model, maximizing safety of the weakest path in the network is considered as the second objective together with the traditional maximum coverage goal. Furthermore, to solve the bi-objective model, a modified version of NSGA-II with a new dynamic immigration operator is developed in which the accurate number of immigrants depends on the results of the other two common NSGA-II operators, i.e. mutation and crossover. Besides validating proposed models, computational results confirm a better performance of modified NSGA-II versus traditional one.

Introduction

There are three major decisions in a supply chain design: location, routing and inventory decisions (Tavakkoli-Moghaddam et al. 2013). Hub location is one of the most appealing fields in facility location which attracted many researchers in recent years. Hub location problems have many applications in areas such as postal delivery systems, telecommunication networks, airline networks, and other delivery systems with numerous demand and supply nodes. Hubs are facilities which collect the flows from several origin centers, then rearrange and distribute them to their destinations. The effective use of hub nodes decreases the number of required links for connecting origins to destinations and helps to benefit the economies of scale. Hub location problem was first introduced by O’Kelly (1986). Afterwards, O’Kelly (1987) proposed the first mathematical model for hub location problem. Hub location problem consists of subcategories such as hub median, hub center, and hub covering problems (Alumur et al. 2012). This paper focuses on hub covering problems. The interested reader is advised to review the papers by Campbell and O’Kelly (2012) and Farahani et al. (2013) to study the other subcategories.

Hub covering problems, as location-allocation problems, consist of two sub problems namely hub set covering problem (HSCP) and hub maximal covering problem (HMCP). While HSCP is aimed at minimizing the transportation and hub establishment costs without any limitation on the number of established hubs, a hub maximal covering problem is constrained by the number of established hubs as an exogenous parameter. The hubs should be located in such a way that the total utility gained from all the covered origin/destination (O/D) pairs is maximized. Campbell (1994) introduced hub covering problems and proposed mathematical models for both HSCP and HMCP. Kara and Tansel (2003) developed a non-linear model for the single allocation HSCP. They proved NP hardness of the problem and linearized it in three different ways. Wagner (2008) formulated a new mathematical model for HSCP, in which the cost discount factor is independent from the number of transmitted commodities. Tan and Kara (2007) used hub covering problem in the Turkish cargo delivery system including 81 cities with expert-based weights. Calık et al. (2009) studied a single allocation hub covering problem with an incomplete hub network. They proposed an efficient heuristic algorithm based on Tabu Search. Qu and Weng (2009) employed a path re-linking approach to solve HMCP. Karimi and Bashiri (2011) proposed models for HSCP and HMCP under a different coverage type and developed two heuristic algorithms to solve them. Fazel Zarandi et al. (2012) investigated a multiple allocation HSCP. What they assumed is that a node will be covered if there are at least a given number of paths to satisfy its demand. Furthermore, to consider the dispersion among hubs, they forced a lower bound on the distance between the established hubs. Hwang and Lee (2012) proposed two heuristics for HMCP and implemented them on the CAB dataset. The results confirmed satisfying performance of the heuristics in terms of both the solution quality and the computational time. In this paper, to mitigate the complexity of models for single and multiple allocation HMCPs, new mathematical formulations with fewer constraints and variables than the existing ones are proposed.

As mentioned earlier, most of the existing hub location models have been formulated in deterministic environments leading to invalid results for implementation; because, in practice, many problem parameters are characterized with high uncertainty. To face such uncertainty, some efforts have been made. Some of the major extensions to hub location problems under uncertainty are summarized in Table 1. As observed, demand, transportation time, customer’s entrance rate to hubs, fixed costs of establishing hubs, covering radius and location of demand nodes were assumed to be uncertain in previous researches. Notably, in previous researches, uncertainty in the links among node pairs due to disruption has not been investigated. So, we study the effect of disruption in the links transmitting loads among node pairs in a hub network. Sometimes, to model the hub networks, it is critical to take into account link failure probability. For example, in martial distribution systems, there is usually a disruption probability for the transmitted cargos in war. According to some factors like airplane specifications as well as geographical and weather conditions of the path in air transportation systems, there are always some risks for flight. Also, when a massage is transmitted across different stations in a telecommunication system, it may be altered or destructed due to an interaction or crosstalk. Therefore, we develop a bi-objective HMCP model in which besides the coverage, safety of the weakest path in the obtained network is also maximized. Noteworthy, the safety of shipment through each link follows, as usual, a Bernoulli distribution independently from the other ones.

Table 1 Major contributions to hub location problems under uncertainty

Based on the above explanations, main contributions of this paper are as follows:

• 1. Proposing new efficient mathematical formulations for single and multiple allocation HMCPs.

• 2. Investigating HMCPs under uncertain shipments by developing a bi-objective model maximizing safety of the paths in designed network.

• 3. Modifying the traditional NSGA-II to obtain a better performance in solving the HMCP problems.

The rest of the paper is organized as follows. In Sect. 2, we present the proposed mathematical formulations. To solve the proposed model efficiently, a modified version of NSGA-II is proposed in Sect. 3. Computational results to validate the models and analyze performance of the proposed algorithm are provided in Sect. 4. Finally, concluding remarks and some guidelines for further research are provided in Sect. 5.

Proposed mathematical model

In this section, mathematical formulations are developed for single and multiple allocation HMCPs as well as bi-objective HMCPs under uncertain shipments. Consider $N=\left\{1,2,\dots ,n\right\}$ as the set of nodes, i and j as indices for origins (O) and destinations (D), respectively, and k and l as indices for hubs. Each node is a potential candidate for establishing a hub. Each O/D pair can be connected only through hubs. It is assumed that hub network is complete, and an O/D pair may be connected through one or two hubs. Hence, if at least one of the origin or destination nodes is a hub, it is possible to connect them directly. Moreover, it is assumed that traveling times among the nodes are symmetric and follow the triangle inequality (e.g., for i, k, j: $t_{ij}\le t_{ik}+t_{kj}$).

We assume that safety of the transmitted load between nodes i and j, independent of the other links, follows a Bernoulli distribution with parameter $p_{ij}$. Therefore, if it is planned to transmit load from origin i to hub k ($x_{ik}=1$), hub k to hub l ($x_{kl}=1$) and hub l to destination j ($x_{jl}=1$), safety for transmitting the load between origin i and destination j will be equal to $p_{ik}.p_{kl}.p_{lj}$.

As special facilities are employed for transportation among the hubs, a cost discount factor $\mathit{\alpha }$ is introduced. Campbell (1994) suggested that O/D pair i–j will be covered through hubs k and l in the following three ways:

• 1. Total transportation cost (time or distance) from origin i to destination j via hubs k and l is less than a predetermined amount T ($c_{ik}+c_{kl}+c_{lj}\le T$). In this paper, this rule is used for covering an O/D pair.

• 2. Transportation cost (time or distance) for each link in the path from i to j via hubs k and l is less than a predetermined amount θ ($c_{ik}\le \mathit{\theta },c_{kl}\le \mathit{\theta },c_{lj}\le \mathit{\theta }$).

• 3. Transportation cost (time or distance) from origin i to hub k and hub l to destination j is less than a predetermined amount Δ ($c_{ik}\le \mathit{\Delta },c_{lj}\le \mathit{\Delta }$).

Model parameters

$w_{ij}$ :

Importance of covering O/D pair i–j

$C_{ik}$ :

Traveling time (cost or distance) from node i to k

T :

Maximum permissible transportation cost (time or distance) for covering O/D pairs

P :

Number of hubs to be established

$p_{ik}$ :

Safety for the link transmitting loads between nodes i and k

$M$ :

A big number

Model variables

$x_{ik}$ :

Binary variable which is equal to 1 if node i is connected to hub k

$y_{ij}$ :

Binary variable which is equal to 1 if O/D pair i, j are connected to the hub network

$s$ :

Safety of the weakest path in the designed hub network

Single allocation HMCP model

In the following, the proposed model is presented for single allocation HMCPs:

$$\text{max}\sum _i\sum _j\sum _k\sum _l{w}_{ij}{x}_{ik}{x}_{lj}$$

(1)

$$x_{ik}\le x_{kk};\forall i,k$$

(2)

$$\sum _k{x}_{kk}=P$$

(3)

$$\sum _k{x}_{ik}\le 1;\forall i$$

(4)

$$(c_{ik}+\mathit{\alpha }{c}_{kl}+c_{lj})x_{ik}{x}_{jl}\le T;\forall i,j,k,l$$

(5)

$$x_{ik}\in \left\{0,1\right\}\forall i,k$$

(6)

Expression (1), as the common objective of HMCPs, maximizes total utility of the hub network as sum of importance of the covered nodes. Constraint (2) ensures that non-hub nodes are only connected to hub nodes. Equation (3) guarantees that exactly P hubs are established in the network. Equation (4) confirms that a non-hub node may be connected to only one hub. Constraint (5) is suggested for covering an O/D pair. Regarding the first rule of covering, variables can simultaneously be equal to 1 only if the total transportation costs from origin i to hub k, hub k to hub l considering the discount factor and hub l to destination j are less than the given threshold T. To linearize the proposed non-linear model, binary variable y and constraint (7) are added to the model.

$$2y_{ij}\le \sum _k{x}_{ik}+\sum _l{x}_{jl}\forall i,j$$

(7)

$$y_{ij}\in \left\{0,1\right\}$$

(8)

In constraint (7), binary variable $y_{ij}$ is allowed to be 1 if both i and j are connected to the hub network simultaneously; otherwise, this variable is forced to be 0. Thereupon, non-linear objective function (1) can be substituted with (9).

$$\text{max}\sum _i\sum _j{w}_{ij}{y}_{ij}$$

(9)

Using Lemma 1, constraint (5) can be linearized with no excess variables.

Lemma 1

Linear constraint (10) can be used instead of non-linear constraint (5).

$$(c_{ik}+\mathit{\alpha }{c}_{kl}+c_{lj}).(x_{ik}+x_{jl}-1)\le T;\forall i,j,k,l$$

(10)

Proof

Generally there are four possible cases for binary variables $x_{ik},x_{jl}$. (1) $x_{ik}=x_{jl}=0$: constraint (5) changes to $0\le T$ and constraint (10) to $\left(-1\right)\left(c_{ik}+\mathit{\alpha }{c}_{kl}+c_{lj}\right)\le T$. $T$ is a nonnegative parameter; so, both equations are obvious; (2) $x_{ik}=0,x_{jl}=1$: both equations change to $0\le T$; (3) $x_{ik}=1,x_{jl}=0$: this case is similar to 2; (4) $x_{ik}=x_{jl}=1$: both equations change to $\left(c_{ik}+\mathit{\alpha }{c}_{kl}+c_{lj}\right)\le T$. Since both constraints work similarly in all possible cases, we can use them interchangeably.

To the best of our knowledge, there are two distinct formulations for HMCPs presented in Campbell (1994) and Karimi and Bashiri (2011). The proposed non-linear model consists of $n^2$ variables and $n^4+n^2+n+1$ constraints and the linearized version has $2n^2$ binary variables and $n^4+2n^2+n+1$ constraints. However, the formulation proposed by Campbell (1994) has $n^4+n^2+n$ variables with $2n^4+n^2+1$ constraints and the model proposed by Karimi and Bashiri (2011) has $2n^2+n$ variables with $n^4+2n^2+n+1$ constraints (using the same coverage type).

Multiple allocation HMCP model

To formulate multiple allocation HMCP, constraints (4) and (7) are omitted, and (11) and (12) are added.

$$y_{ij}\le \sum _k{x}_{ik}\forall i,j$$

(11)

$$y_{ij}\le \sum _l{x}_{jl}\forall i,j$$

(12)

These constraints allow upper bound of the binary variable to be 1 if both the origin and destination nodes are connected to hub network; otherwise, this equation is forced to be 0. This formulation for multiple allocation HMCPs has $2n^2$ binary variables and $n^4+3n^2+1$ constraints. Whereas the formulation proposed by Campbell (1994) has $n^4+n^2+n$ variables with $2n^4+1$ constraints and the model proposed by Karimi and Bashiri (2011) has $2n^2+n$ variables with $n^4+2n^2+n+1$ constraints (using the same coverage type).

Bi-objective HMCPs

To increase safety of paths in the designed network, expressions (13), (14), (15) are added to proposed HMCP formulations.

$$\text{Max}s$$

(13)

$$s\le x_{ik}{x}_{jl}(p_{ik}{p}_{kl}{p}_{jl})+M(1-x_{ik}{x}_{jl});\forall i,j,k,l$$

(14)

$$s\ge 0$$

(15)

The second objective as expression (13) tries to maximize safety of the weakest path in the network considering the uncertainty in transmitting load to its destination. Constraint (14) provides an upper bound for safety of the weakest path in network. For O/D pair (i, j), the upper bound is equal to safety of established path i toward j via hubs k and l. Noteworthy, if the aforementioned path is not established, expression (14) is converted to an unnecessary constraint. Lemma 2 proposes a linear equivalent to non-linear constraint (14).

Lemma 2

Linear constraint (16) and non-linear constraint (14) may be used interchangeably.

$$s\le \frac{x_{ik}+x_{jl}}{2}{p}_{ik}{p}_{kl}{p}_{lj}+M(1-\frac{x_{ik}+x_{jl}}{2});\forall i,j,k,l$$

(16)

Proof

There are four possible cases for binary variables $x_{ik}$, $x_{jl}$. (1) $x_{jl}=x_{ik}=0$: right-hand side of both constraints equals $M$; (2) $x_{jl}=1,x_{ik}=0$: right-hand side of constraint (14) equals $M$ and right side of constraint (16) equals $\frac{p_{ik}.p_{kl}.p_{jl}}{2}+\frac{M}{2}$ and considering $M$ is a large number they work similarly; (3) $x_{jl}=0,x_{ik}=1$: this case is analyzed similar to 2; (4) $x_{jl}=x_{ik}=1$: right-hand side of both equations equals $p_{ik}.p_{kl}.p_{jl}$. The two constraints work similarly in all possible cases so they might be used alternatively.

Solution algorithm: modified NSGA-II

In multi-objective models, existing constraints frequently prevent achieving a solution in which all the objective functions are optimal (Ghane and Tarokh 2012). In this situation, the set of Pareto optimal solutions, i.e. the solutions none of which is utterly better than the others, is the best choice. Classical optimization methods convert a given multi-objective problem to a single-objective one by different approaches. When the obtained single-objective problem is solved, in fact, one of the solutions in the set of Pareto optimal solutions is found. To map the whole Pareto optimal frontier, this procedure should be repeated many times, which is a time-consuming process (Deb et al. 2002). Furthermore, considering the complexity of real-world problems, a good approximation of Pareto optimal frontier is generally acceptable (Coello Coello 2007). This leads to the use of evolutionary algorithms to solve multi-objective problems. Early analogies between the mechanism of natural selection and learning or optimization process have been led to development of so-called evolutionary algorithms whose main goal is to simulate the evolutionary process on a computer (Coello Coello and Lamont 2004). A key benefit of multi-objective evolutionary algorithms is to attain a set of Pareto solutions. Such algorithms try to improve quality of the first-frontier members in consecutive generations. Initially, Schaffer (1985) applied a genetic algorithm (GA) to solve a multi-objective problem and proposed a vector-evaluated GA. After that, numerous multi-objective versions of evolutionary algorithms were proposed. Non-dominated sorting genetic algorithm (NSGA) is one of the most efficient and commonly used versions of multi-objective GA offered by Srinivas and Deb (1994). To resolve some shortcomings of NSGA, Deb et al. (2002) proposed an improved version called NSGA-II which in most multi-objective optimization problems is capable of converging to high-quality solutions with a better spread of solutions in the obtained frontier than the previous evolutionary algorithms (Noori-Darvish and Tavakkoli-Moghaddam 2012). In this paper, a modified version of NSGA-II is developed for solving the proposed multi-objective single allocation HMCP model. The modified NSGA-II differs in three ways from traditional one: (1) improved operators are designed to adapt to the problem, (2) an immigration operator is introduced for a better search in the solution space, and (3) a new mechanism is designed for adding individuals to the population. The following subsections are devoted to explain the proposed algorithm.

Chromosome structure

Besides simplicity, chromosome structure should contain all the information required to solve the problem. The most important features of problem are (a) ordinary nodes must be connected to hubs, (b) each ordinary node is allowed to connect only into one hub, (c) P hubs are established and (d) to cover an O/D pair, length of established path must be smaller than the specified covering radius.

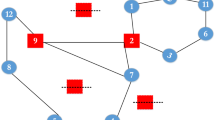
In the proposed structure, each allele is denoted as a node, and number in it refers to the hub number to which the node is allocated (feature b). Hence, if a node’s position is equal to the hub number allocated to it, the considered node is a hub. Figure 1 demonstrates the proposed structure for a problem with seven nodes. As alleles 2 and 5 are allocated to themselves, they are denoted as hubs. To create each chromosome in the initial population, P nodes are selected randomly to be hubs (feature c) and each one of the remaining nodes is assigned to only one hub randomly (feature a). Considering the covering constraint, for a specified O/D pair, if the total transportation cost in a given path is less than the determined covering radius it will be covered. For example, in the network designed in Fig. 1, ordinary nodes 4 and 6 are assigned to hubs 2 and 5, respectively. Thus, the considered path is 4–2–5–6. If the total transportation cost in this path ($c_{42}+\mathit{\alpha }{c}_{25}+c_{56}$) is less than the covering radius, O/D pair (4, 6) is covered and the associated utility ($w_{ij}$) is taken into account. Safety of the covered path 4–2–5–6 is $p_{42}{p}_{25}{p}_{56}$. This probability for the uncovered paths is not calculated.

Fig. 1

Chromosome structure for a problem with seven nodes

Non-dominated sorting

Sorting and selecting the best individuals for the next generation are the most important differences between NSGA-II and the other multi-objective evolutionary algorithms. Initially, each solution is allocated a rank according to the number of times dominated by the other solutions. The rank of a solution determines the frontier in which it is located; therefore, the solutions with rank 1 are those in the first frontier. Actually, the first-frontier members are the algorithm’s approximation of Pareto optimal frontier. Then, algorithm tries to improve them in iterative generations. The solutions located in a less crowded area are the more favorable solutions in the same frontier because of clarifying shape of the Pareto frontier.

To sort solutions of the same frontier, crowding distance measure is used (Deb et al. 2002). For each objective function, the solutions within the same frontier are sorted in ascending order. Based on the distance between two consecutive solutions for each objective function, the crowding distance measure is calculated as follows:

$${\text{CD}}_i=\sum _{m=1}^M\frac{f_m^{i+1}-f_m^{i-1}}{f_m^{\text{max}}-f_m^{\text{min}}}$$

(17)

where M is the number of objectives, $f_{\text{m}}^{\text{max}}$ and $f_{\text{m}}^{\text{min}}$ are the maximum and minimum amounts of objective m among frontier members, and $f_{\text{m}}^{\text{i + 1}}$ and $f_{\text{m}}^{\text{i - 1}}$ are the amounts of objective function m for the subsequent and precedent solutions in the sorted frontier population.

Due to the importance of boundary solutions of a frontier in detecting its shape, the first and the last solution crowding distances are set to be infinite. Finally, to select the best individuals for the next generation, the solutions are sorted in an ascending order according to their rank. Among the solutions with the same rank, those with higher crowding distance are preferred.

Genetic operators

Genetic operators are tools for better search, i.e. exploration and exploitation, in the solution space. As a result of mating, new offsprings are involved in population whose features are a mixture of parents’ specifications. This process is simulated with a crossover operator in GA. Seldom abnormalities in the genetic structure of some individuals in the population cause salient differences in their specifications, called mutation operator in GA. The mutation operator plays an important role as it helps to escape local optima. Another phenomenon which human societies are faced is entrance of some foreign individuals into the existing population, called immigration, used as another genetic operator here.

Among various crossover techniques, we apply the simple single-point crossover. However, if we select a cut point randomly and interchange corresponding parts of chromosomes, infeasible solutions like those in Fig. 2 may be generated. As shown in Fig. 2, first offspring has four hubs including nodes 2, 3, 6, and 7 while second one has nodes 5 and 6 as hubs. Furthermore, in second offspring, the second and the forth nodes are allocated to non-hub nodes 7 and 2, respectively, which are as unacceptable allocations.

Fig. 2

Crossover with an infeasible solution

To resolve this problem, a modified single-point crossover is proposed. At first, the set of hub nodes in each parent, called h₁ and h₂, with cardinality of P are derived. Cut point Q is randomly selected from [1, P−1]. Then, the first Q members of h₁ and the last P−Q members of h₂ are joined, and the set of hubs in first offspring c₁ is created. Similarly, the first Q members of h₂ and the last P−Q members of h₁ make the set of hubs in second offspring c₂. If there are duplicates in each of the aforementioned sets, one of non-hub nodes is randomly replaced with one of repetitive hub nodes. After determining the set of hubs in each offspring, non-hub nodes are allocated to hubs randomly to create the complete offsprings. Figure 3 shows implementation of the proposed single-point crossover on Fig. 2.

Fig. 3

Modified crossover performed on h1 and h2

To mutate a given chromosome, after random selection of a hub and non-hub node, non-hub node is altered to a hub and vice versa. Also, all the nodes allocated to the previous hub, including the hub node, are assigned to the new hub. To do mutation on the chromosome in Fig. 4, non-hub node 3 and hub node 2 are selected at random.

Fig. 4

A mutation example

The third operator introduced here is called immigration. As it happens in most societies, a set of individuals, called immigrants, are added to the existing population periodically. Immigrants are created randomly and cause a better search in the solution space. In the proposed algorithm, set of immigrants consists of two parts. The first part is a fixed number of immigrants called ‘basic number of immigrants’ or BIN, and the second one varies in sequential iterations called ‘variable number of immigrants’ or VIN. After crossover and/or mutation, if the offspring dominates any of the parents, the operation is considered successful. The exact value of VIN is equal to number of unsuccessful crossover/mutation operations. In NSGA-II, results of two operators (crossover and mutation) are directly added to populations while, in the modified NSGA-II, only the successful offsprings will be added to population, and the others will be replaced with immigrants.

Accordingly, in each iteration of NSGA-II, number of offsprings and mutants added to population is more than (or equal to) the modified NSGA-II; however, sum of the offsprings, mutants, and immigrants in the modified NSGA-II is, as BIN value, more than sum of the offsprings and mutants in the traditional NSGA-II. The offsprings and immigrants are added to the main population, and after using non-dominated sorting algorithm, better individuals, considering the population size, move to the next generation. The pseudo code of modified NSGA-II is provided in Fig. 5.

Fig. 5

Pseudo code of modified NSGA-II

Computational results

In this section, first the proposed formulations are validated and their efficiencies are proved using some numerical examples extracted from the Turkish data set (Tan and Kara 2007) and effect of the second objective function is evaluated using a weighting method on a small-sized HMCP. Then, multi-objective metrics are introduced and after parameters setting, performance of the modified NSGA-II is studied versus the traditional algorithm.

Model validation and efficiency

In numerical examples, we have 10, 20, 30, 35 nodes and the number of established hubs are 1 and 2. Covering threshold (T) equals to average distance among nodes and discount factor $\mathit{\alpha }$ is 0.5. GAMS 22.2 with CPLEX solver is used to solve the experimental problems.

To validate the proposed linear formulations for single and multiple allocation HMCPs, they are compared to the formulations proposed in Karimi and Bashiri (2011) in terms of required computational time and relative gap (using the same coverage type). In Table 2, we compare the single allocation model with the one in Karimi and Bashiri (2011). In all experiments, the solution obtained by both formulations is the same which corroborates validity of the proposed model. The relative gap in the proposed model is always less than that in Karimi and Bashiri (2011). Average relative gap for the proposed model is 0.042 whereas in Karimi and Bashiri (2011) it is 0.067. Also, computational time for the proposed model is less than that of Karimi and Bashiri (2011) for all experimental problems.

Table 2 Validating the proposed model for single allocation HMCP

Similar experiments for the proposed model in multiple allocation case result to the same solutions for both formulations. Table 3 shows that average relative gap for the proposed model is 0.021 whereas in Karimi and Bashiri (2011) it is 0.065. Also, computational time in all experiments is always less than that in Karimi and Bashiri (2011).

Table 3 Validating the proposed model for multiple allocation HMCPs

Effects of the second objective

We involve a second objective to force the model to choose safer paths for connecting all O/D pairs. To represent optimum results of the proposed multi-objective model for a small-sized instance, a weighting method is applied for obtaining Pareto solutions. Consider a problem with seven nodes in which two hubs must be established. The covering radius and discount factor are assumed to be 300 and 0.5, respectively. Table 4 presents utility of covering and safety probability of each O/D pair. Each time a given weight is allocated to each objective, and GAMS22.2 is used to solve the resulting single-objective problem.

Table 4 Utility and safety probability for each O/D pair

Figure 6 demonstrates the optimal solutions from four different weighting preferences. Case (a) shows optimal solution when the only criterion is maximizing the total utility ($w_1=1,w_2=0$). In this case, nodes 5 and 7 are hubs, total covering utility is 3,796 and the path from 2 to 3 via hubs 5 and 6 is the weakest one with safety 0.003. In case (b), the associated weights for both objectives are 0.5 ($w_1=w_2=0.5$). Accordingly, nodes 4 and 6 are hubs, total covering utility is 3,796 and the path from 2 to 7 via hub 4 is the weakest one with safety 0.353. In case (c), $w_1=0.4$ and $w_2=0.6$. As a result, total covering utility is 2,723, node 2 is not connected to network, and the weakest path is the one from 5 to 7 via hub 6 with safety 0.521. Finally, in case (d), the only criterion is maximizing safety of weakest path ($w_1=0,w_2=1$). Consequently, nodes 5 and 6 are hubs with safety 0.988, the other nodes are not connected to network, and total covering utility is 72.

Fig. 6

Optimal results of multi-objective model for different weighting preferences

The above results clearly show effects of the second objective on forming the hub network (i.e. selecting hub nodes and paths for linking non-hub nodes). Obviously, an increase in the importance of second objective causes selection of more reliable paths although the total covering utility may be decreased.

Multi-objective metrics

Quality of solutions and their relative dispersion in Pareto frontier are the most important properties of an evolutionary algorithm. To compare modified versus traditional NSGA-II, five multi-objective metrics are introduced.

• 1. Quality metric (QM) More solutions in Pareto frontier imply better performance of the algorithm (Schaffer 1985).

• 2. Best frontier members (BFM) Solutions with the best fitness for each objective in Pareto frontier.

• 3. Average frontier fitness (AFF) Average fitness of solutions in first frontier for each objective.

• 4. Mean ideal distance (MID) Average distance among solutions in Pareto frontier and a hypothetical ideal solution (Zitzler and Thiele 1998). Lower value of MID shows better performance of the algorithm.

  $$\text{MID}=\frac{{\sum }_{i=1}^n\sqrt{{(\frac{f_{1i}-f_1^{\text{best}}}{f_{1,g}^{\text{max}}-f_{1,g}^{\text{min}}})}^2+{(\frac{f_{2i}-f_2^{\text{best}}}{f_{2,g}^{\text{max}}-f_{2,g}^{\text{min}}})}^2}}{n}$$

  (18)

  where n is the number of Pareto solutions, f _ji is value of jth objective for ith solution in Pareto frontier, and $f_{i,g}^{\text{max}},f_{i,g}^{\text{min}}$are maximum and minimum amounts of ith objective among solutions in Pareto frontier. Notably, coordinates of the ideal solution in all problems are assumed to be $(f_1^{\text{best}},f_2^{\text{best}})=({\sum }_{i,j}{w}_{ij},1).$

• 5. Spacing metric (SM) Distribution of solutions in Pareto frontier as denoted in (19). Lower SM signs better dispersion of the solutions in the frontier (Srinivas and Deb 1994).

  $$\text{SM}=\frac{{\sum }_{i=1}^{n-1}\left|d_i-\overline{d}\right|}{(n-1)\overline{d}}$$

  (19)

  where d _i is Euclidean distance between solutions i and i+1 in sorted Pareto solutions and $\overline{d}$ is average Euclidean distance.

Parameter tuning

Parameter tuning has a salient effect on quality of solutions and computational time of evolutionary algorithms. To set parameters, Taguchi method is applied which is a fractional factorial experiment design. Compared to the full factorial experiments, fractional approaches focus on the orthogonal arrays of data to analyze different levels of factors which lead to a considerable reduction in number of conducted experiments. For a comprehensive review on the Taguchi approach, one may refer to Roy (2001).

As mentioned earlier, speed of convergence to actual Pareto frontier and diversity of solutions in obtained frontier are the main criteria in analyzing evolutionary algorithms. Rahmati et al (2013) incorporate these parameters and propose a single response metric for Taguchi method namely multi-objective coefficient of variation (MOCV).

$$\text{MOCV}=\frac{\text{QM}}{\text{SM}}$$

(20)

There are five parameters in NSGA-II that need to be tuned, each of which is assigned four initial values as Table 5 based on the previous experiments. At last, the mentioned factors are analyzed with an L₁₆ design. Larger values of response are more desirable. Each experiment is done four times and average response levels are given in Table 6. Given the response levels, parameter levels are provided in Table 5.

Table 5 Desired levels for parameters and selected values

Table 6 L₁₆ design and related response levels

Performance of modified NSGA-II

To assess performance of the proposed NSGA-II, it is compared with the traditional one. They are compared regarding the multi-objective metrics introduced in 4.3. Generally, hub location problems are among NP-hard ones and they have a high computational complexity. Due to the size of numerical examples in other papers (for a comprehensive list of instances, one may refer to Tables 1, 2 in (Farahani et al. 2013)), we have divided our experiments into small, medium, and large-sized problems. Small-size instances have 20, 40, and 50 nodes, medium-sized problems have 70, 100, 150, and 200 nodes, and the large-sized ones consist of 300, 400, 500 and 1,000 nodes. The experiments were done on a PC with Core 2 Duo, CPU2.4 GHs and RAM 1 GB. MATLAB R2011b was used to code both the traditional and modified NSGA-II. The number of hubs in each experimental problem is randomly selected from the number of nodes. The nodes are scattered on a plane according to problem size, and Euclidian distance is calculated for them. Hence, the distances among the nodes satisfy triangle inequality. For problems of less than 100 nodes, between 100 and 500 nodes, and more than 500 nodes, coordinates of the network planes are selected at random from [0,100], [0,300], and [0,500], respectively. Also, the distance matrix is symmetric. Covering each node in HMCPs creates a certain utility according to some properties of that node. Utility is selected randomly from [0,350]. Comparative results on traditional and modified NSGA-II algorithms for all multi-objective metrics are provided in Tables 7 and 8.

Table 7 Computational results for the QM₁ and QM₂

Table 8 Computational results for QM, SM and MID metrics

It is obvious that modified NSGA-II surpasses the traditional one according to BFM metric in all experimental problems. For first objective, the most deviation of traditional NSGA-II from modified one is 24.21 % for problems of size 150, and the average deviation is 9.58 %. For second objective, corresponding most deviation is 2.29 % for problems of size 150, and the average is 0.5 %.

AFF in modified NSGA-II surpasses that of traditional one which shows better performance of proposed algorithm. Considering Table 7 for the first objective, the most and mean AFF deviation of traditional NSGA-II from the modified one are 5.85 % (problem of size 300) and 3.2 %, respectively. The corresponding deviations for second objective are 1.23 % (problem of size 500) and 0.38 %, respectively.

Table 8 summarizes the values of QM, SM and MID in experimental problems. As mentioned earlier, larger values for QM and smaller values for SM and MID are more desirable. In all experimental problems, QM and SM in modified NSGA-II are better than those in traditional algorithm. This is also evident in Figs. 7 and 8. For MID metric, except problems with 100 and 300 nodes, modified NSGA-II shows a better performance than NSGA-II. Figure 9 compares MID metric of NSGA-II with that of modified NSGA-II.

Fig. 7

QM in NSGA-II versus modified NSGA-II

Fig. 8

SM in NSGA-II versus modified NSGA-II

Fig. 9

MID in NSGA-II versus modified NSGA-II

Results of ANOVA established for two algorithms in terms of QM, SM and MID are provided in Table 9. Null hypothesis is that there is no significant deviation among the three metric values of two algorithms. According to Table 9 with a 5 % significance level, null hypothesis is rejected for QM and SM which means that modified NSGA-II outperforms NSGA-II. Although in most cases MID in the proposed algorithm is less than the original one, but the respective gap is not significant. As a sample, Pareto frontiers of problem with 20 nodes for both algorithms are displayed in Fig. 10. Horizontal and vertical axes stand for first and second objectives, respectively. The diagram confirms the monotony and higher quality of Pareto frontier of the modified NSGA-II.

Table 9 ANOVA results in 5 % risk level

Fig. 10

Pareto frontier of problem with 20 nodes

Concluding remarks and directions for future research

In this paper, we proposed new formulations for single and multiple allocation hub maximal covering problems. It was shown that proposed non-linear model and linearized versions outperform the existing formulations from the literature. Also, the considered problems were investigated under uncertainty in transmitted loads to destinations via a bi-objective mixed-integer model. Such models are applied in martial transportation networks, message delivery in telecommunication systems and air transport systems. Along with maximization of coverage, selecting safer paths for transmitting loads was considered as another objective. To solve the proposed model, a modified version of NSGA-II was developed in which new crossover and mutation operators are introduced to adapt with structure of the considered problem. Moreover, a new immigration operator was involved. The modified NSGA-II and NSGA-II were compared using five multi-objective metrics, four of which proved the supremacy of the proposed algorithm. In this paper, the probability of disruption in a link was investigated; however, an interesting direction for future research is addressing probability of disruption for nodes.