Abstract
Roof shape and slope are both important parameters for the safety of a structure, especially when facing wind loads. The present study demonstrates the pressure variations due to wind load on the pyramidal roof of a square plan low-rise building with 15% wall openings through CFD (Computational Fluid Dynamics) simulation. Many studies on roofed structures have been performed in the past; however, a detailed review of the literature indicates that the majority of these studies focused on flat, hip, gable and spherical roofs only. There is a lack of research that analyses these effects on pyramidal roof buildings. ANSYS (Analysis System) ICEM (Integrated Computer Engineering and Manufacturing)-CFD and ANSYS Fluent commercial packages have been used for modelling and simulation, respectively, and ANSYS CFD Post was used to obtain the results. A realizable k–ε turbulent model was used for the pressure distribution on the roof of the building model. In the present study, twenty-four models with different roof slopes (α), i.e. 0°, 10°, 20°, and 30°, with various wind incidence angles (ϴ), i.e. 0°, 15°, 30°, 45°, 60° and 75° were investigated. The influence of roof slope and wind incidence angle are analysed in this study. Results have been represented through pressure coefficient (Cp) contours on the roof surface and velocity streamlines of the flow field of the different cases. The optimization of the roof slope may be achieved by considering different wind incidence angles for buildings so that they may better withstand wind force in a specific area. When wind pressure coefficients from building models with openings were compared with pressure coefficients from building models without openings, it was found that the pressure coefficients for building models without openings are almost twice or three times that of the pressure coefficients for models with openings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
From an aerodynamic engineering point of view, a pyramidal-shaped building has its own interesting characteristics. However, in spite of its specific features, very limited research work has been carried out in this specific area of wind load on pyramidal roof buildings (Roy et al. 2018b; Roy et al. 2018a). Maximum studies in this field are concerned with low-rise buildings with canopy roof (Roy 2010, a) gable roof, hip roof (Ahmad and Kumar 2001; Irtaza et al. 2015; Tecle et al. 2015; Habte et al. 2017), isolated pitched roof (Bourabaa et al. 2015), tall chimney (Verma et al. 2015; Khan and Roy 2017) and tall structures (Paul and Dalui 2008; Amin and Ahuja 2014; Kar and Dalui 2016; P. Martinez-Vazquez 2016; Sanyal and Kumar 2018), and aim to provide information about the consistency of performance and the upgrading of design economy (Isyumov 1999). Moreover, the technical layout of pyramidal buildings with respect to wind load norms is generally not listed in standard tables (Wind codes). Therefore, it is essential to study the flow and pressure on pyramidal roof buildings.
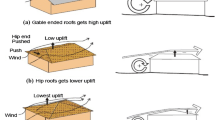
Definitely geometry of building has a significant effect on distribution of wind pressure on surface of roof and walls of building. A pyramidal roof was found with lowest uplift when compared with gable roof and hip roof and is shown in Fig. 1 (Shreyas Ashok Keote 2015).
Flow over gable roof, hip roof and pyramidal roof (Shreyas Ashok Keote 2015)
In a study of design guiding principles for community housing for extreme events, it was found that destruction of the cladding is often the beginning of structure failure and inhabitant injury during an extreme wind event (Coulbourne et al. 2002). In a study of wind load on roof tiles, the vulnerability analysis indicated that the net wind uplift loading on tiles caused an increase in tile destruction rather than the external surface pressures (Li et al. 2014). Thus, for the structure’s design, along with other loads, wind load must also be considered. In old-fashioned roofing systems, high wind-induced suctions can cause major damage which can lead to subsequent rain intrusion and loss of interior substances (Mintz et al. 2016).
When a building is subjected to wind load, then wind load has mainly two components, i.e. drag force and lift force and both may be positive or negative wind pressures. In a study of tension leg platform superstructure, it was found that drag force used to increase in surge and heave reactions, but generally the influence of the current drag is determined by the extent of the wave energy spectrum (Oyejobi et al. 2016). Extreme wind conditions are the reason behind different types of losses and one of them is broken window frame/glass and damaging of building envelop, which causes water infiltration inside the building (De Leon and Lazcano 2018).
Wind load on a building is also highly affected by its surrounding, which may be the shape of nearby buildings, height of buildings or distance of surrounding buildings from the principal building. A significant change in pressure coefficients on the building was found due to variations in the distance of interfering walls; this may be explained by the fact that shielding occurs (John et al. 2012). The coefficient of pressure in some specific interfering situation was found to be larger than that in isolated case which evidences that the presence of the interfering buildings does not always contribute to the reduction of wind load on the principal building (Kar and Dalui 2016).
Different codes such as IS 875 (Part 3): Indian Standard Design Loads (IS 875 (Part 3) 2015), Australian/New Zealand Standard (AS/NZS)—Structural Design Action, Part Wind Action (AS/NZS 1170.2:2011 2016) and ASCE/SEI: 7-10, Minimum Design Loads for Buildings and Other Structures (ASCE/SEI: 7-10 2010) are used worldwide for accessing the wind loads. Wind codes also categorise the buildings on the basis of their height and a building less than 18 m and 20 m height is known as low-rise building as per American wind code and Indian wind code, respectively (ASCE/SEI: 7-10 2010; IS 875(Part 3) : 2015 2015). The normative methodologies which are recommended by different wind codes of different countries seem to be very conservative in some cases and they might not be a good depiction of the demands gained from experimental tests (Tapia-Hernández and Cervantes-Castillo 2018). In existing building codes and standards, however, the design specifications regarding wind loads acting on roof edge metal systems were found inadequate (Baskaran et al. 2018).
Wind direction also has a significant effect on pressure magnitude. The wind load on a structure is proportional to the square of the wind speed (Sarkar et al. 2014). And for correct assessment of wind power potential both wind speed and wind direction are equally important and for wind direction analysis, finite mixture of two von Mises distributions has proved to be a suitable candidate for Indian climatology (Gugliani et al. 2017; Gugliani et al. 2018b). Extreme Value Analysis (EVA) of hourly mean wind speed data approach is the most suitable for the region of varied wind climate (Gugliani et al. 2018a).
A full-sized wind testing facility known as the Wall of Wind (WOW) was used to investigate wind generated internal and external pressures and pressure coefficients on the eaves of hip roofs which were found to be significantly lower than gable roofs (Tecle et al. 2015). The largest suction was found close to corner edges and near the ridgeline in the case of low-rise canopy roofs (Roy et al. 2010b, 2007); similar results were noticed on roofs of other types of low-rise buildings.
CFD simulation is a multifunctional and extremely useful tool (Blocken 2014), and is thus ideal for evaluating the unsteady aerodynamic loads on the vibrant roofs in a wider reduced frequency range (Ding et al. 2014). CFD reduces both time and cost in design and research, and provides detailed and visualized information (Canonsburg 2013). While wind tunnel testing is one way to investigate structures for wind loading, but this is a cumbersome process as it needs extensive effort and is also time consuming; moreover, it is an expensive process.
A lot of work has already been done on CFD simulation of buildings. Computational Fluid Dynamics study is helpful in determining magnitude of pressure coefficients, velocity streamline, velocity vector, numbers of correlated constraint variables, etc. through the model surface (Verma et al. 2015a). CFD simulations are helpful in the investigation of boundary layer separation and wake formation (Verma et al. 2015b). As an alternative to wind tunnel testing, CFD simulation is used nowadays to determine the effects of wind on structures. A fair number of studies have been carried out through the CFD simulation instead of wind tunnel testing and the results obtained from CFD simulations are adequately consistent with experimental results (Bhattacharyya et al. 2014). In experimental and numerical investigations of flat, conical and hemispherical roof models, the hemispherical roof was found to have the most critical pressure field and a good agreement was seen between experimental and numerical outcomes and same was found for the design of API pump (Ayremlouzadeh and Ghafouri 2016; Sajjadi and Sarkardeh 2016; Ozmen and Aksu 2017). Also, CFD simulations have been used to test different aerodynamic mitigation techniques (Aly and Bresowar 2016). In a study of scour process about single and compound bridge piers, CFD results were found under-predicted and over-predicted when two different CFD codes have been used (Alemi and Maia 2016).
Therefore, in this paper, the impact of the roof inclination angle on pyramidal roof of low-rise buildings is analysed using Computational Fluid Dynamics (CFD). A hip roof is found safer than a gable roof in a study, while the pyramidal roof had the lowest uplift among the three roof shapes, i.e. gable roof, hip roof and pyramidal roof (Shreyas Ashok Keote 2015). Thus, the pyramidal roof low-rise building was considered for this study.
A CFD analysis is required for this study since the performance assessment of the different roof geometries is not only based on the inclination of the roof surface and wind direction, but also on the airflow pattern (velocities) around the building resulting from different vertical exposed area. In the past 50 years, CFD has evolved into a powerful tool for research works in urban physics and building aerodynamics (Blocken 2014). In this paper, the simulations are performed using realizable k–ε turbulent model by considering grid-sensitive analysis and validation with previously published wind tunnel experimental measurements. The detailed analysis of the flow field, performing CFD simulation, is modelled simultaneously in the same computational domain. The wind tunnel velocity and turbulence intensity measurements used in this study are from the experimental wind tunnel study on wind loads on different types of building carried out by Chand and Bhargava (1992); Chand et al. (1995); Chad and Bhargava (1997); Chand et al. (1998). CFD simulation study on pyramidal roof buildings with different wind incident angles carried out by Roy et al. (2012) is used for CFD model validation in the present study.
CFD simulation of the wind tunnel experimental study
In the present study, the wind load investigation for pyramidal roof of a square plan low-rise building has been carried out through CFD modelling and simulation. Different types of wind tunnel experimental study at CSIR-CBRI, Roorkee, India, have been conducted by Roy et al. (2012b) and Chand et al. (1992, 1995, 1997, 1998). Roy et al. (2012a, b) carried out the wind load investigation for pyramidal roof of a square plan low-rise building. The information here has been used to validate the velocity and turbulence intensity profile and the model dimension was kept the same to have the comparisons of the different parameters. ANSYS tool ICEM CFD has been used for modelling, while ANSYS Fluent has been used for simulation. The results have been extracted using CFD Post. The model is divided into finite number of volumes (cells) using hexahedral mesh in ICEM CFD. Governing equations are solved by ANSYS Fluent using finite-volume method and realizable k–ε turbulent model has been used for the simulation in Fluent. Results are extracted in CFD Post, which includes contours of wind pressure coefficients mainly.
Computational settings in CFD simulation
Four pyramidal roof building models are created in ICEM CFD with roof slopes of 0°, 10°, 20°, and 30°. The plan area and height of the pyramidal roof building model were collected from a study conducted at The Central.
Building Research Institute, Roorkee (India) (Roy et al. 2012b) and the domain specifications for the present study are as per the study conducted by Revuz et al. (2012) and both domain specifications and building model dimensions are shown in Fig. 2. Measurements are taken with the scale of 1/25. In Fig. 2b, the building model with dimensions and opening dimensions and position are shown, another opening considered as shown in Fig. 2c, in the opposite wall C is also placed at the same position, i.e. vertically 36 mm above (full scale 0.9 m) from the bottom and horizontally it is centrally placed 72.5 mm (1.8 m) from corners. Both the openings have same size, i.e. 80 mm × 40 mm (2 m × 1 m).
Meshing of CFD domain and of building model
The building models are created in ICEM CFD as shown in Fig. 2. Since the simulation processing and result accuracy depend upon mesh quality, a fine mesh is required around the building model. A structural hexahedral grid was used for meshing. As shown in Fig. 3a, fine meshing was used on the pyramidal roof building faces and near the bottom area around the model.
The quality of mesh should be checked for every model. In this study, the quality of mesh is above 0.6 in each model as shown in Fig. 3b. In ANSYS tool ICEM CFD can be used to check the mesh quality. A quality of 0.5 (in a range which goes from 0.0 to 1.0) or higher is classified as good meshing ideal for the converged solution (Ansys 2007).
Boundary conditions
For the real physical demonstration of the fluid flow, appropriate boundary conditions that really simulate the actual flow are necessary. Defining the detail boundary conditions at the inlet and outlet of the flow domain, which is essential for a precise solution, is always problematic. With the following expressions for the along-wind component of velocity, a velocity inlet was used at the windward boundary. Velocity, U, which is varying with eight of the inlet domains, is similar to the experimental study conducted by Roy et al. (2012) and Chand and Bhargava (1992, 1995, 1997, 1998). Standard depiction of the velocity profile in the atmospheric boundary layer (ABL) is as shown below:
It was deemed necessary to validate the numerical results using experimental results. To do this, the validation of velocity profile and turbulence intensity has been shown in Fig. 4 (Roy et al. 2012b).
In the present work, the values of the parameters z0 and u* are as follows: \(z_{0} = 0.0001\) m and \(u_{*} = 0.11\) m/s.
The measured longitudinal turbulence intensity (\(I\)) is transformed into turbulent kinetic energy \(k\) as input for the simulations using Eq. (2), assuming that \(\sigma_{\text{v}} < < \sigma_{\text{u}}\) and \(\sigma_{\text{w}} < < \sigma_{\text{u}}\). It is observed that with a greater value of \(k\), a small inconsistency is found in the results in the order of a few percentage points (< 5%) in the magnitude of amplification factors:
The inlet turbulence dissipation rate profile ε mentioned by Richards and Hoxey (1993) is given by
where \(z\) is the height co-ordinate, \(\kappa\) the von Karman constant (~ 0:42), \(z_{0}\) the scaled aerodynamic roughness length corresponding to a power-law exponent of 0.15 (here \(z_{0} = 0.03/25 = 0.0012\;{\text{m}}\)) and \(u_{ *}\) the friction velocity associated with horizontally homogeneous (stable) ABL flow. The top and the sides of the computational domain are displayed as slip walls (zero normal velocity and zero normal gradients of all variables). At the outlet, zero static pressure is stated.
Solver settings
The finite-volume method in ANSYS Fluent is used for resolving governing equations and related case-specific boundary conditions. The basic principle of using finite element method is that the body is divided into subdivisions or small isolated areas which are known as finite elements. Size of the stiffness matrix be determined by the number of nodes and the results are amended by increasing the number of nodes and collocation points (Jabbari 2016). Each element has governing equations in Fluent and these elements are accumulated into a global matrix.
As stated previously, the clarifications were steady state. Second-order differencing was used for the momentum, pressure and turbulence equations and the “coupled” pressure–velocity coupling method due to its forcefulness for steady-state, single-phase flow problems.
The residuals fell below the generally applied criteria of dropping to 10−4 of their initial values after more than a few hundred iterations. However, this was not the single check for convergence—the drag, lift and side forces and the moments subjected to the pyramidal roof building model were also examined throughout the simulation and only when they attained fixed values were the simulations supposed to have converged. Although the simulations were steady state, there was some variation (< 1%) in the “steady” values of the various monitoring values.
Results and discussion
In present study, CFD simulation is carried out for the different models of pyramidal roof buildings with similar plan shape but dissimilar roof angles and varying wind directions. The prime objective of this study is to observe the change in wind-induced pressure distribution on roof surfaces with varying slopes in pyramidal roof buildings.
Horizontal homogeneity of the velocity profile in CFD simulation
Horizontal homogeneity of the velocity profile is the variation of velocities in domain on the windward side of the building model placed inside the domain. From line numbers 22–30, a total of nine numbers of vertical locations were created at a distance of 100 mm each to observe the horizontal homogeneity of the velocity profile as shown in Fig. 5a. In Fig. 5b, the velocity profiles along the height of the domain on different locations are shown. It is observed that at the top of the building, the wind velocity is almost 11 m/s, validating the velocity profile of the CFD simulation.
It is further observed that at line 29, which is close to the building placed in the domain, the velocity profile is lower than that at line 28. This is because of the obstruction caused by the building position, which causes the velocity streamlines to merge with one another.
The velocity profile of the vertical locations near the building model on the windward side is seen to decrease gradually compared to the lines near the inlet location as shown in Fig. 5. The velocity profile represented in white is at the inlet location and the yellow is near the building model. At the building height, the velocity magnitude is 15% lower than the inlet velocity. As the height from bottom increases, velocity magnitude is similar with other velocity profiles.
Pressure coefficients on roof surface of the building
To analyse the effect of the roof inclination on the pressure coefficient on the roof surface of the building in more detail, Fig. 6 a–d shows the contours of the pressure coefficient (Cp). The pressure coefficient is calculated as
where P is the static pressure, P0 the reference static pressure, ρ = 1.225 kg/m3 is the air density and Uref is the approach-flow wind speed at building height (Uref = 9.81 m/s at z = 0.11 m). Pressure coefficient contours for different roof slopes and for different wind directions were plotted using Ansys Fluent. For roof slopes 0°, 10°, 20° and 30°, and for wind incidence angle 0°, 15°, 30°, 45°, 60° and 75°, contours are shown in Fig. 6a–d. The roof has been divided into four parts, i.e. face A, face B, face C and face D. Face A is in the windward direction while face C is opposite to face A and is on the leeward side, case 0˚ wind incidence angle. Face B and face D are side faces of the roof and are parallel to wind flow when the wind incidence angle is 0˚.
In Fig. 6a, the roof is flat and out of all the incident wind angle the maximum pressure coefficient is found to be as − 0.4 which is less than the maximum pressure coefficient of − 0.9 by wind tunnel experimental study and the maximum pressure coefficient of − 0.98 by CFD simulation study on flat roof without opening as described by Roy et al. (2012a, 2012b) and the maximum pressure coefficient of − 0.8 on the windward roof surface, of the flat roof building with \(\frac{h}{w} \le \frac{1}{2}\) as mentioned in IS: 875 (part-3) (2015).
In Fig. 6b, the roof is of 10° roof slope and out of all the incident wind angles, the maximum pressure coefficient is found to be as − 0.57 which is less than the maximum pressure coefficient of − 0.98 by wind tunnel experimental study and the maximum pressure coefficient of − 0.91 by CFD simulation study on pyramidal roof of 10° roof slope without opening as described by Roy et al. (2012a, b) and the maximum pressure coefficient of − 1.4 on the windward roof surface, of the 10° gable roof building with \(\frac{h}{w} \le \frac{1}{2}\) as mentioned in IS: 875 (part-3) (2015).
In Fig. 6c, the roof is of 20° roof slope and out of all the incident wind angles, the maximum pressure coefficient is found to be as − 1.5 which is more than the maximum pressure coefficient of − 1.1 by wind tunnel experimental study and less than the maximum pressure coefficient of −1.6 by CFD simulation study on pyramidal roof of 20° roof slope without opening as described by Roy et al. (2012a, b) and the maximum pressure coefficient of − 1.2 on the windward roof surface, of the 20° gable roof building with \(\frac{h}{w} \le \frac{1}{2}\) as mentioned in IS-875(Part-3):2015(IS: 875 (part-3) 2015).
In Fig. 6d, the roof is of 30° roof slope and out of all the incident wind angles, the maximum pressure coefficient is found to be as − 1.5 which is more than the maximum pressure coefficient of − 1.1 by wind tunnel experimental study and less than the maximum pressure coefficient of − 1.6 by CFD simulation study on pyramidal roof of 20° roof slope without opening as described by Roy et al. (2012b) and the maximum pressure coefficient of − 1.2 on the windward roof surface, of the 20° gable roof building with \(\frac{h}{w} \le \frac{1}{2}\) as mentioned in IS: 875 (part-3) (2015).
From Fig. 6a–d, it is observed that wind pressure coefficients are changing from negative pressure coefficient to positive pressure coefficient as the roof slope is increasing from 0° to 30°. The roof with 0˚ roof slope has negative pressure coefficients because of its flat shape. The roof with roof slope 10° and 20° also has negative pressure coefficients on most of the surface as they also resemble a flat roof. In Fig. 6d, positive pressure coefficients of maximum value 0.3 is observed for 30° roof slope at 45° wind directions but it is 0 for 30° gable roof building and 0.3 for 45° gable roof building with \(\frac{h}{w} \le \frac{1}{2}\) as mentioned in IS: 875 (part-3) (2015).
From Fig. 7, where area weighted pressure coefficients have been represented graphically, it can be noticed that magnitude of negative pressure or suction is continuously changing with wind direction. From all the graphs, it is clear that when a face will be perpendicular to the wind direction, there will be higher pressure coefficients as compared to the pressure coefficients on parallel faces.
It is also noticeable that when joint of two faces will be perpendicular to the wind direction, then the whole roof surface will have low wind pressure, it is because of the wind distribution, as the joint of two faces divide the wind into two parts and effect of wind on roof surface becomes less.
Detailed variation of pressure coefficients with values, on all four roof faces, i.e. face A, face B, face C and face D, for wind direction 0°–75° at an interval of 15° for all roof slopes, i.e. 0°, 10°, 20° and 30° is shown in Fig. 8.
From Fig. 8, it can be seen that area weighted pressure coefficients change continuously with changes in wind incidence angles. In most cases, the face perpendicular to wind direction on windward side experiences the highest negative pressure or suction. The highest negative pressure coefficient was found to be − 0.540, for the 10° roof slope with a 0° wind incidence angle on face A.
To know the pressure variation with change in roof slope, a comparison has been carried out among mean pressure coefficients (area weighted average) and Fig. 9 shows this comparison of overall maximum area weighted pressure coefficients for different roof slopes.
From Fig. 9, it is clear that the highest maximum negative area weighted pressure coefficient is for roof slope 10°. For roof slopes 0° and 30°, it is approximately the same while for 20° roof slope, the maximum area weighted pressure coefficient is the lowest.
Comparison between pressure coefficients on pyramidal roof building with and without openings
Openings in a building have a significant effect on wind pressure coefficients. To study this effect in detail, pressure coefficients from our present study were compared with the results of Roy et al. (2012a) as shown in Fig. 10 a, b. In their study, they have carried out the study on pyramidal building model with roof slopes in between 0° and 30° @ 5° interval up to 20° roof slopes and for building models in between 15° and 20° roof slopes have been considered @ 1°, because of its less suction effect on the roof slope 15° to 20°. The pressure variation on the roof (named as A, B, C and D) has been observed and the maximum suction values have been considered which may guide the design of the roofing elements. The maximum suction values have been shown and it is to have some understanding of the nature of wind effects on the roof with change in the roof slope and wind incident angles.
a Variation of maximum area weighted mean pressure coefficients (Cp) on pyramidal roof without openings with roof slope from 0° to 30° for wind incidence angle of 0° to 45°, @15° increments (Roy et al. 2012b) and b comparison between area weighted mean pressure coefficients for wind direction 15° with and without openings
With these comparisons of pressure values it can be concluded that the pyramidal building model with roof slopes in between 15° and 20° roof slopes is having a better chance of survival than the other roof slopes.
Openings in a building affect the wind pressure distribution on its walls and roof. Our present study found a large difference in pressure coefficients for building models with openings and those without openings. These findings are shown in Fig. 10. It is observed that the pressure coefficients for building models, without openings are almost twice or three times the pressure coefficients of models with openings.
Velocity streamlines
Accurate modelling of wind field around building roof and understanding of bluff body aerodynamics assure structural safety and reliability under wind loads (Fernando 2013; Li et al. 2018). Melbourne (1980) has provided some background concerned with the fluid mechanics of turbulent flows, with applications to the field of wind engineering. He has reviewed the effects of turbulence, including the effects of scale on the flow over bluff bodies and the resultant pressures and forces.
A velocity streamline is the path traced by a moving particle in a flow of fluid. Figure 11 shows a section of a bluff body (i.e. buildings and other civil engineering structures immersed in the atmospheric boundary layer) immersed in a flow of velocity V. The flow will develop local pressures P over the body in accordance with the Bernoulli equation and remain constant along a streamline.
Bernoulli’s equation and wind flow around a rectangular building (Stathopoulos and Baniotopoulos 2007)
As per the ideal conditions of stagnation V1 = 0; P1 = P + 1/2 ρV2 and if V2 < V, P2 > P; this implies inward-acting pressure (called as overpressure or simply pressure). However, if V2 > V, P2 < P, i.e. outward-acting pressure, it is known as suction. Pressures are usually expressed in a dimensionless form which is independent of velocities. This dimensionless form is called pressure coefficient (CP) and is defined as per Eq. 4. The basic characteristics of steady flow around a simple rectangular building or tower are shown in Fig. 11. The presence of the bluff bodies causes the wind flow to separate and formed the wake zone in the leeward direction. The wind flow separates from the body at the two upstream edges and forms two regions: an outer flow, where there is no viscosity effect and an inner flow, i.e. the wake region. The outer flow is separated by the inner flow by an area of high vorticity, called as “shear layer”.
Flow separation and wake regions for square and rectangular cylinders immersed in a flow field are shown in Fig. 12a, b.
Bernoulli’s equation and wind flow around a rectangular building (Simiu and Yeo 2019)
The incorporation of the pressures over the body results in a net force and moment. As per Fig. 12c, the components of the force in the along-wind and across-wind directions are called drag and lift, respectively. The drag, lift, and moment are affected by the shape of the body, the Reynolds number, and the incoming flow turbulence (Simiu and Yeo 2019). For horizontal flows, considering Bernoulli’s equation, the airflow velocity (V) produces a local pressure (P) which can be written as
where the second term is called dynamic pressure and ρ is the air density.
The net aerodynamic lift and drag forces per unit span FL and FD in the across-wind and along-wind directions, respectively, can be rendered dimensionless and expressed in terms of lift and drag coefficients, CL and CD (Simiu and Yeo 2019):
where B is some typical reference dimension of the structure. For the net flow-induced moment M about the elastic centre the corresponding coefficient is
Figure 13 shows the velocity streamlines in the XY plane at eave height as shown in Fig. 5, of 0° roof slope, i.e. flat roof models with various wind directions. As the building models are square in plan and are modelled for low-rise buildings, flow field around them with streamline separation and reattachment point is to be expected as per the pattern shown in Fig. 11. However, due to the presence of openings in building model the variation in the flow patterns is significant and varies with the change in wind directions.
It has been observed from Figs. 7 and 8 that the maximum area weighted averaged mean pressure coefficients (Cp) are higher for the wind incident angles 0°, 15° and 30° due to the simple reattachments of the velocity streamlines observed in the leeward side whereas in case of wind incident angles 45°, 60° and 75°, significant recirculation zone is visible on the leeward side. Face A and Face B are affected by higher area weighted pressure coefficients (suction) in comparison with the other faces.
Figure 14 shows the velocity streamlines in the XZ plane at the centreline of the building as shown in Fig. 5, of 0° roof slope, i.e. flat roof models with various wind directions. It has been observed that the stagnation zone is more in case of wind incident angles 0°, 15° and 30° in comparison to the wind incident angles of 45°, 60° and 75°. Further the recirculation zone is gradually increasing for wind incident angles 0° and reaches the maximum at 75°.
Figure 15 shows the velocity streamlines in the XY plane at eave height as mentioned in Fig. 5, of 10° roof slope models with various wind directions.
Once again, openings cause reduction in the wake zone formation compared to the buildings without openings as mentioned in Fig. 11. Except for the 0° wind incidence angles, all other wind angles show formation of recirculation zone in the leeward side.
Figure 16 shows the velocity streamlines in the XZ plane at the centreline of the building as shown in Fig. 5, of 10° roof slope with various wind directions. It has been observed that the stagnation zone is more in case of wind incident angles 0° and 75° in comparison to the wind incident angles of 15°, 30°, 45° and 60°. Further the recirculation zone is same for wind incident angles 0° and 75° and higher for the wind incident angles 15°, 30°, 45° and 60°. This observation is also reflected by higher area weighted pressure coefficients (suction) on Face A and Face B for wind incident angles 0° and 75°. Again for this roof model also Face A and Face B are affected by higher area weighted pressure coefficients (suction) in comparison with the other faces as shown in Figs. 7 and 8.
The velocity streamlines in the XY plane at eave height as mentioned in Fig. 5, with various wind directions of 20° roof slope models, are shown in Fig. 17. Similar to the 10° models, in this model also except 0° wind incidence angles, all other wind angles shows formation of recirculation zone in the leeward side. The area weighted pressure coefficients (suction) on Face A for the 0° wind incidence angle is higher as there is no recirculation zone formation on the leeward surface as it is visible for all other wind incident angles.
Recirculation zone appears near Face D for wind incidence angles of 15°, 30° and 45° and it is observed near Face C for wind incidence angle 60° and 75°. This may lead to the increased suction on the adjoining wall. The very sudden change in flow pattern of streamlines may be because of openings, as the openings receive the wind flow differently for different wind directions.
Figure 18 shows the velocity streamlines in the XZ plane at the centreline of the building as shown in Fig. 5, of 20° roof slope with various wind directions. It has been observed that the stagnation zone is more in case of wind incident angles 0° only in comparison to the other wind incident angles of 15°, 30°, 45° and 60°. Further the recirculation zone is smaller for wind incident angles 0° and higher for the other wind incident angles. This observation is also reflected by higher area weighted pressure coefficients (suction) on Face A only for wind incident angles 0°. In this roof model, only Face A is affected by higher area weighted pressure coefficients (suction) in comparison with the other faces as shown in Figs. 7 and 8.
The velocity streamlines in the XY plane at eave height as mentioned in Fig. 5, with various wind directions of 30° roof slope models, are shown in Fig. 19.
Significant change in the recirculation zone is visible in comparison to the other roof models. In this models also 30° and 45° wind incidence angles experiencing the 2–3 numbers of larger recirculation zones in comparison to the other wind angles in the leeward side near Faces C and D.
The area weighted pressure coefficients (suction) on Faces C and D for the 30° and 45° wind incidence angles are higher as shown in Figs. 7 and 8. Recirculation zone appears near Face D for wind incidence angles of 60° and it is observed near Face C for wind incidence angle 75°. This may lead to the higher suction on the roof surfaces Faces D and C.
Figure 20 shows the velocity streamlines in the XZ plane at the centreline of the building as shown in Fig. 5, of 30° roof slope with various wind directions. It has been observed that the stagnation zone is visible above the roof surface Face C in all the wind incident angles. Further the recirculation zone is higher for wind incident angles 30° and 45°. This observation is also reflected by higher area weighted pressure coefficients (suction) on Face C for these wind incident angles as shown in Figs. 7 and 8.
After going through the discussion on the velocity streamlines for different roof slopes and for various wind angles, it has been observed that the recirculation zone and stagnation zone are important parameters while considering the pressure coefficient on the roof surfaces.
Limitations and future research
The two main goals of this study of pyramidal roofed buildings were
(1) To evaluate the impact of the roof inclination angle and (2) to evaluate the impact of the wind incident angles.
Openings were present in the walls of the building, both for a normal wind incidence angle (α = 0°). Four roof inclination angles were evaluated (0°, 10°, 20° and 30°). It is essential to mention the limitations of the current study, which may be addressed in future research work:
-
This study considers a simplified single zone building. The impact of other building parameters such as eaves and internal layout must be investigated.
-
This study is performed for an isolated building. Interference effects should be considered to have a better understanding of the pressure variations on the roof.
-
The study focuses on wind incidence angles as direction 0°–75° at an interval of 15°.
-
In this study, all cases have the same building height and the height to width ratio of the building is as mentioned in IS-875(Part-3):2015[60].
-
Additional research is needed to study the effect of wall area above and below the inlet opening, and to better understand its effect on the wake zone, recirculation zone and stagnation zones created at different locations of the building due to the incoming flow.
-
From all contours of pressure coefficients and velocity streamlines, effects of roof slope, wind direction and opening were analysed. The effects of openings on wind pressure distribution and on wind flow behaviour around building models were found to be greater than the wind direction and roof slope. The present study may be taken further by analysing the building models for other roof slopes and for other types of openings.
Conclusions
This paper presents the impacts of roof slope and wind direction on wind pressure distribution over pyramidal roof of low-rise buildings of square plan. Ansys Fluent was used to generate the results which were presented by the contours of pressure coefficients and graphs. It is found that the variation of wind pressure coefficients depends upon the location of point of observation and evolution of general rule of thumb for predicting the influence of roof slope is difficult. However, peak values of pressure coefficients, pressure difference across different roofing elements and other information about wind pressure on pyramidal roofs of different slopes oriented in different directions with respect to the wind can be derived from these data. The main conclusions derived from the study are given below:
-
The validation study shows that the realizable k–ε turbulence model provides the most accurate results and capable of simulation horizontal homogeneous velocity profiles.
-
A face perpendicular to the wind direction will have the higher pressure coefficients as compared to the pressure coefficients on parallel faces. It is also noticeable that when the joint of two faces is perpendicular to the wind direction, then the whole roof surface will have low wind pressure.
-
Wind induces suction almost over the entire pyramidal roof of square plan building models for all roof slopes, i.e. 0°, 10°, 20° and 30° and the highest negative area weighted pressure coefficient was found to be − 0.540, for 10° roof slope with 0°-wind incidence angle on face A.
-
Wind incident angle is the important parameter and a deciding factor while considering the area weighted pressure coefficient on the roof surfaces.
-
The highest maximum negative pressure coefficient is for roof slope 10°, and for roof slope 0° and 30°, it is approximately same while for 20° roof slope, the maximum pressure coefficient is the lowest.
-
When there are openings in a building, the wind pressure distribution on walls and roof are significantly affected. Our study showed a considerable difference in pressure coefficients for building models with openings and those without.
-
The openings in building models with varying wind directions experienced significant differences in the flow field, with respect to the building without opening.
-
The recirculation zone and stagnation zone formation in the velocity streamlines for different roof slopes and for various wind angles are important parameters while considering the pressure coefficient on the roof surfaces.
References
Ahmad S, Kumar K (2001) Interference effects on wind loads on low-rise hip roof buildings. Eng Struct 23:1577–1589
Alemi M, Maia R (2016) Numerical Simulation of the Flow and Local Scour Process around Single and Complex Bridge Piers. Int J Civ Eng. https://doi.org/10.1007/s40999-016-0137-8
Aly AM, Bresowar J (2016) Aerodynamic mitigation of wind-induced uplift forces on low-rise buildings: a comparative study. J Build Eng 5:267–276. https://doi.org/10.1016/j.jobe.2016.01.007
Amin JA, Ahuja AK (2014) Characteristics of wind forces and responses of rectangular tall buildings. Int J Adv Struct Eng 6:1–14. https://doi.org/10.1007/s40091-014-0066-1
Ansys Inc. (2015) Ansys Fluent 16.2 user guide
AS, NZS 1170.2:2011 (2016) Australian/New Zeeland standard—structural design action, part 2: wind action. SAl Global Limited under licence from Standards Australia Limited, Sydney and by Standards New Zealand
ASCE, SEI: 7–10 (2010) Minimum design loads for buildings and other structures. American Society of Civil Engineering, Reston, Virginia, Structural Engineering Institute
Ashok S, Keote DK (2015) Construction of low rise buildings in cyclone prone areas and modification of cyclone construction of low rise buildings in cyclone prone areas and modification of cyclone. J Energy Power Sources 2:247–252
Ayremlouzadeh H, Ghafouri J (2016) Computational fluid dynamics simulation and experimental validation of hydraulic performance of a vertical suspended API pump. Int J Eng 29:1612–1619
Baskaran A, Molleti S, Martins N (2018) Development of wind load criteria for commercial roof edge metals. J Archit Eng 24:1–18. https://doi.org/10.1061/(asce)ae.1943-5568.0000308
Bhattacharyya B, Dalui SK, Ahuja AK (2014) Wind induced pressure on ‘E’ plan shaped tall buildings. Jordan J Civ Eng 8:120–134
Blocken B (2014) 50 years of computational wind engineering: past, present and future. J Wind Eng Ind Aerodyn 129:69–102. https://doi.org/10.1016/j.jweia.2014.03.008
Bourabaa N, Delacourt E, Menet JL (2015) Wind potential evaluation around isolated pitched roof buildings. J Renew Sustain Energ 10(1063/1):4915288
Chad I, Bhargava PK (1997) Laboratory studies on the effect of external projections on wind pressure distribution on low- rise buildings laboratory studies on the effect of external projections on wind pressure distribution on low-rise buildings. Archit Sci Rev 40:133–137. https://doi.org/10.1080/00038628.1997.9696823
Chand I, Bhargava PK (1992) Studies on the effect of mean wind speed profile on the height of air layer affected by buildings. Renew Energy 2:507–512
Chand I, Sharma VK, Bhargava PK (1995) Effect of Neighbouring Buildings on Mean Wind Pressure Distribution on a Flat Roof. Archit Sci Rev 38:29–36. https://doi.org/10.1080/00038628.1995.9696773
Chand I, Bhargava PK, Krishak NLV (1998) Effect of balconies on ventilation aeromotive force on low-rise buildings. Build Environ 33:385–396
Coulbourne WL, Tezak ES, McAllister TP (2002) Design guidelines for community shelters for extreme wind events. J Archit Eng 8:69–77. https://doi.org/10.1061/1076-0431
De Leon D, Lazcano G (2018) Impact of two connection types on the behavior and losses of a steel hotel building under strong winds in Mexico. Int J Civ Eng 16:905–916. https://doi.org/10.1007/s40999-017-0238-z
Ding W, Uematsu Y, Nakamura M, Tanaka S (2014) Unsteady aerodynamic forces on a vibrating long-span curved roof. Wind Struct 19:649–663
Fernando HJS (2013) Handbook of environmental fluid dynamics. CRC Press, Boca Raton, pp 33487–33742
Gugliani GK, Sarkar A, Mandal S, Agrawal V (2017) Location wise comparison of mixture distributions for assessment of wind power potential: a parametric study Location wise comparison of mixture distributions for assessment of wind power. Int J Green Energy 14:737–753. https://doi.org/10.1080/15435075.2017.1327865
Gugliani GK, Sarkar A, Bhadani S, Mandal S (2018a) A novel approach for accurate assessment of design wind speed for variable wind climate. KSCE J Civ Eng 23(2):608–623
Gugliani GK, Sarkar A, Ley C, Mandal S (2018b) New methods to assess wind resources in terms of wind speed, load, power and direction. Renew Energy 129:168–182. https://doi.org/10.1016/j.renene.2018.05.088
Habte F, Asghari Mooneghi M, Baheru T, Zisis I, Gan Chowdhury A, Masters F, Irwin P (2017) Wind loading on ridge, hip and perimeter roof tiles: a full-scale experimental study. J Wind Eng Ind Aerodyn 166:90–105. https://doi.org/10.1016/j.jweia.2017.04.002
Irtaza H, Javed MA, Jameel A (2015) Effect on wind pressures by variation of roof pitch of low-rise hip-roof building. Asian J Civ Eng 16:869–889
IS 875 (Part 3) (2015) Indian standard design loads (Other than Earthquake) for buildings and structures—code of practice, part 3 wind loads, 3rd edn. Bureau of Indian Standards, New Delhi
Isyumov N (1999) Overview of wind action on tall buildings and structures. In: Wind Engineering into 21st Century. Rotterdam, pp 15–28
Jabbari MNMLE (2016) Numerical Simulation of Turbulent Flows Using a Least Squares Based Meshless Method. Int J Civ Eng. https://doi.org/10.1007/s40999-016-0087-1
John AD, Roy AK, Gairola A (2012) Wind Loads on Walls of Low-Rise Building. 6th National Conference on Wind Engineering (NCWE). The Indian Society of Wind Engineering (ISWE), India, CRRI, New Delhi, pp 449–456
Kar R, Dalui SK (2016) Wind interference effect on an octagonal plan shaped tall building due to square plan shaped tall buildings. Int J Adv Struct Eng 8:73–86. https://doi.org/10.1007/s40091-016-0115-z
Khan M, Roy AK (2017) CFD Simulation of Wind Effects on Industrial RCC Chimney. Int J Civ Eng Technol 8:1008–1020
Li R, Chowdhury AG, Asce M, Bitsuamlak G, Gurley KR, Asce M (2014) Wind effects on roofs with high-Pro fi le tiles: experimental Study. J Archit Eng 20:1–11. https://doi.org/10.1061/(asce)ae.1943-5568.0000156
Li T, Yang Q, Ishihara T (2018) Unsteady aerodynamic characteristics of long-span roofs under forced excitation. J Wind Eng Ind Aerodyn 181:46–60. https://doi.org/10.1016/j.jweia.2018.08.005
Martinez-Vazquez P (2016) Wind-induced vibrations of structures using design spectra. Int J Adv Struct Eng 8:379–389. https://doi.org/10.1007/s40091-016-0139-4
Melbourne W (1980) Turbulence, bluff body aerodynamics and wind engineering. 7th Australas. Hydraul. Fluid Mech. 9–14
Mintz B, Mirmiran A, Suksawang N, Gan Chowdhury A (2016) Full-scale testing of a precast concrete supertile roofing system for hurricane damage mitigation. J Archit Eng 22:1–12. https://doi.org/10.1061/(asce)ae.1943-5568.0000209
Oyejobi DO, Jameel M, Ramli Sulong NH (2016) Nonlinear response of tension leg platform subjected to wave, current and wind forces. Int J Civ Eng 14:521–533. https://doi.org/10.1007/s40999-016-0030-5
Ozmen Y, Aksu E (2017) Wind pressures on different roof shapes of a finite height circular cylinder. Wind Struct 24:25–41
Paul R, Dalui SK (2008) Wind effects on ‘Z’ plan-shaped tall building: a case study. Int J Adv Struct Eng 8:319–335. https://doi.org/10.1007/s40091-016-0134-9
Revuz J, Hargreaves DM, Owen JS (2012) On the domain size for the steady-state CFD modelling of a tall building. Wind Struct An Int J 15:313–329. https://doi.org/10.12989/was.2012.15.4.313
Richards PJ, Hoxey RP (1993) Appropriate boundary conditions for computational wind engineering models using the k-ϵ turbulence model. J Wind Eng Ind Aerodyn 46–47:145–153. https://doi.org/10.1016/0167-6105(93)90124-7
Roy AK (2010) Wind Loads on Canopy Roofs. Ph D Thesis, IIT Roorkee, Uttarakhand, India
Roy AK, Ahuja AK, Gupta VK (2007) Wind pressure distribution on flat canopy roofs. In: Recent advances in civil engineering (RACE-07). Civil Engineering Department, College of Engg. & Tech., B.P.U.T., Bhubaneswar
Roy AK, Ahuja AK, Gupta VK (2010) Variation of wind pressure on canopy-roofs. Int J Earth Sci Eng 3:19–30
Roy AK, Babu N, Bhargava PK (2012a) Atmospheric Boundary Layer Airflow Through CFD Simulation on Pyramidal Roof of Square Plan Shape Buildings. VI Natl Conf Wind Eng 291–299
Roy AK, Bhargava PK, Babu N (2012b) Atmospheric boundary layer airflow through CFD simulation on pyramidal roof of square plan shape buildings. 6th National Conference on Wind Engineering (NCWE). The Indian Society of Wind Engineering (ISWE), CRRI, New Delhi, India, pp 291–299
Roy AK, Singh J, Sharma SK, S.K. Verma (2018a) Wind pressure variation on pyramidal roof of rectangular and pentagonal plan low rise building through CFD simulation. Int Conf Adv Constr Mater Struct 1–10. https://doi.org/10.13140/rg.2.2.10167.42401
Roy AK, Singh J, Sharma SK, Verma SK (2018b) Wind pressure variation on pyramidal roof of rectangular and pentagonal plan low rise building through CFD simulation. In: International conference on advances in construction materials and structures (ACMS-2018). IIT Roorkee, Roorkee, Uttarakhand, India
Sajjadi SSS, Sarkardeh H (2016) Accuracy of numerical simulation in asymmetric compound channels. Int J Civ Eng. https://doi.org/10.1007/s40999-016-0113-3
Sanyal P, Kumar S (2018) Effects of courtyard and opening on a rectangular plan shaped tall building under wind load. Int J Adv Struct Eng 10:169–188. https://doi.org/10.1007/s40091-018-0190-4
Sarkar A, Kumar N, Mitra D (2014) Extreme wind climate modeling of some locations in india for the specification of the design wind speed of structures. J Civil Eng 18:1496–1504. https://doi.org/10.1007/s12205-014-0428-z
Simiu E, Yeo DH (2019) Wind effects on structures modern: structural design for wind. Wiley, Hoboken
Stathopoulos T, Baniotopoulos CC (2007) Wind effects on buildings and design of wind-sensitive structures. Springer, New York
Tapia-Hernández E, Cervantes-Castillo JA (2018) Influence of the drag coefficient on communication towers. Int J Civ Eng 16:499–511. https://doi.org/10.1007/s40999-017-0157-z
Tecle AS, Bitsuamlak GT, Chowdhury AG (2015) Opening and compartmentalization effects of internal pressure in low-rise buildings with gable and hip roofs. J Archit Eng 21:04014002. https://doi.org/10.1061/(asce)ae.1943-5568.0000101
Verma SK, Roy AK, Lather S, Sood M (2015) CFD simulation for wind load on octagonal tall buildings. Int J Eng Trends Technol 24:211–216. https://doi.org/10.14445/22315381/ijett-v24p239
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Singh, J., Roy, A.K. Effects of roof slope and wind direction on wind pressure distribution on the roof of a square plan pyramidal low-rise building using CFD simulation. Int J Adv Struct Eng 11, 231–254 (2019). https://doi.org/10.1007/s40091-019-0227-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-019-0227-3