Abstract
A quadrilateral and a triangular element based on the strain approach are developed for static, free vibration and buckling analyses of Reissner–Mindlin plates. The four-node triangular element SBTP4 has the three essential external degrees of freedom at each of the three corner nodes and at a mid-side node; whereas the quadrilateral element SBQP has the same degrees of freedom at each of the four corner nodes. Both elements use the same assumed strain functions which are in the linear variation where bending and transverse shear strains are independent and satisfy the compatibility equations. The use of the strain approach allows obtaining elements with higher-order terms for the displacements field. The formulated elements have been proposed to improve the strain-based rectangular plate element SBRP previously published. Several numerical examples demonstrate that the present elements are free of shear locking and provide high-accuracy results compared to the available published numerical and analytical solutions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Analyses of static, buckling and free vibration of plate structures play a large role in structural engineering applications. Considerable research works on analysis of plates are still being conducted (Mackerle 1997, 2002; Leissa 1969, 1987; Liew et al. 1995, 2004).
Designers prefer low-order Reissner–Mindlin plate elements due to their simplicity and efficiency. However, for thin plates, these elements often suffer from the shear locking phenomenon when dealing with thin plates. To overcome shear locking, many research works have been undertaken where the use of the selective reduced integration was first intervened (Zienkiewicz et al. 1971; Hughes et al. 1978; Malkus and Hughes 1978). The formulation procedure used is to divide the strain energy into two parts, one of bending and the other of shear. Then, two different integration rules for these two parts are used. For low-order polynomial elements based on displacement model, such as the four-node classical bilinear element, an exact integration (two Gauss points in each direction) is taken for the bending strain energy; whereas a reduced integration (one Gauss point) is used for the shear strain energy. This selective integration can be provided with a more efficient element but often leads to numerical instability. Considerable investigations have been oriented to develop robust elements using different improved formulations and numerical techniques to avoid shear locking such as mixed formulation, enhanced assumed strain methods, assumed natural strain methods, discrete shear gap method and smoothed finite element method (Lee and Wong 1982; Ayad et al. 1998; Lovadina 1998; César de Sá and Natal Jorge 1999; César de Sá et al. 2002; Cardoso et al. 2008; MacNeal 1982; Bathe and Dvorkin 1985, 1986; Zienkiewicz et al. 1990; Batoz and Katili 1992; Bletzinger et al. 2000; Nguyen-Xuan et al. 2008; Liu and Nguyen-Thoi 2010).
The strain approach has been employed as an alternative to formulate robust plate elements (Belarbi and Charif 1999; Belounar and Guenfoud 2005; Belounar and Guerraiche 2014; Guerraiche et al. 2018; Belounar et al. 2018) to increase the accuracy and stability of the numerical solutions as well as to eliminate shear locking phenomena. The use of the strain approach (Belarbi and Charif 1999; Belounar and Guenfoud 2005; Belounar and Guerraiche 2014; Guerraiche et al. 2018; Belounar et al. 2018; Djoudi and Bahai 2004a, b; Rebiai and Belounar 2013; 2014) has several advantages where it enables to obtain efficient elements with high-order polynomial terms for the displacement functions without the need of including internal nodes. The first developed strain-based Mindlin plate element SBRP (Belounar and Guenfoud 2005) has been adopted for the linear analysis of plates having only rectangular shapes. However, this element suffers from shear locking for very thin plates (Belounar et al. 2018). Then, the formulation of a new three-node strain-based triangular Mindlin plate element SBTMP (Belounar et al. 2018) has been developed for static and free vibration of plate bending. The assumed curvatures and transverse shear strains for the SBRP element (Belounar and Guenfoud 2005) are coupled and contain quadratic terms. The key idea used in this paper is to formulate new elements to overcome shear locking for very thin plates and to improve the accuracy for plates with regular and distorted shapes.
In this paper, a quadrilateral and a triangular strain-based plate element have been formulated for static, free vibration and buckling analyses of plates using Reissner–Mindlin theory. The opportunity is taken to explore the displacements field obtained from the strain-based quadrilateral plate element (SBQP) by applying it to a four-node triangular element strain-based triangular plate with four nodes (SBTP4) having the same degrees of freedom (W, βx, and βy) at each of the three corner nodes and a mid-side node. In the process of formulation, these elements are based on linear variation for the five strain components where bending and transverse shear strains are independent and satisfying the compatibility equations. The numerical study shows that the SBQP and SBTP4 elements pass the patch test, are free of shear locking, and can be found numerically more efficient than the SBRP element (Belounar and Guenfoud 2005).
Formulation of the proposed elements
Derivation of the displacements field
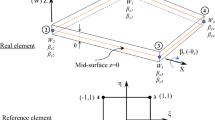
For Reissner–Mindlin plate elements (Fig. 1), the strains in terms of the displacements are given as:
In matrix form, it can be given as
The five strains, bending (κx, κy and κxy) and transverse shear (γxz and γyz), given in Eq. (1a) cannot be considered independent, for they are in terms of the displacements W, βx and βy and therefore, they must satisfy the compatibility equations (Belounar and Guenfoud 2005) given as:
The field of displacements due to the three rigid body modes is obtained by having Eq. (1a) equal to zero and the following results are obtained:
The proposed quadrilateral and triangular elements (SBQP and SBTP4) have three degrees of freedom (W, βx and βy) at each of the four nodes. Therefore, the displacements field should contain twelve independent constants and having used three (α1, α2, α3) for the representation of the rigid body modes, the remaining nine constants (α4, α5, …, α12) are to be apportioned among the five assumed strains of the two elements.
The interpolation of the assumed strains field for the present elements (SBQP and SBTP4) is given as:
Assumed bending (κx, κy and κxy) and transverse shear (γxz and γyz) strains given in Eq. (4) of the proposed elements are independent and have only linear terms contrarily for the SBRP element (Belounar and Guenfoud 2005), where bending and transverse shear strains are coupled and quadratic terms are included in the assumed shear strain components.
The bracketed terms of the assumed strains (Eq. 4) are added to have the compatibility equations (Eq. 2) to be satisfied. The strain functions (κx, κy, κxy, γxz, γyz) given by Eq. (4) are substituted into Eq. (1a) and after integration, we obtain:
The displacement functions obtained from Eq. (5a) are summed to the displacements of rigid body modes given by Eq. (3) to obtain the final displacement shape functions:
The displacement functions of Eq. (5b) and the strain functions of Eq. (4) can be given in matrix form, respectively, as:
And the matrices [P] and [Q] are given as:
And the displacements field, the strains field, and constant parameters vectors are:
The geometrical strains can be expressed as:
We substitute Eq. (6) into Eq. (12), we obtain:
And the matrix [G] is given as:
The transformation matrix [C] which relates the element nodal displacements ({qe}T = (W1, βx1, βy1, …, W4, βx4, βy4)) to the 12 constants ({α}T = (α1, …, α12)) can be given as:
The constant parameters vector {α} can be derived from Eq. (16a) as follows:
The matrices [N] (Eq. 8), [B] (Eq. 8) and [Bg] (Eq. 14) are obtained, respectively, by substituting Eq. (16b) into Eqs. (6), (7) and (13):
And the matrix [Pi] calculated from Eq. (9) for each of the four element nodes coordinates (xi, yi), (i = 1, 2, 3, 4) to obtain:
Element matrices
The standard weak form for free vibration and buckling can, respectively, be expressed as:
By substituting Eqs. (6), (7) and (13) into Eqs. (19) and (20), we obtain:
Where the element stiffness, mass and geometrical stiffness matrices ([Ke], [Me], \([K_{\text{g}}^{\text{e}} ]\)), are, respectively, as:
The stress–strain relationship is given by:
where \(\{ \sigma \} = \{ M_{x} ,M_{y} ,M_{xy} ,T_{x} ,T_{y} \}^{T} ,\) \(\{ \varepsilon \} = \{ \kappa_{x} ,\kappa_{y} ,\kappa_{xy} ,\gamma_{xz} ,\gamma_{yz} \}^{T} .\)
where [D], [D]b, [D]s are, respectively, rigidity, bending rigidity, shear rigidity matrices and [T] is the matrix containing the mass material density:
where \(\sigma_{x}^{0}\), \(\sigma_{y}^{0}\) and \(\sigma_{xy}^{0}\) are the in-plane stresses.
The matrices [K0], [M0] and [Kg0] given in Eqs. (23), (24) and (25) are numerically computed with exact Gauss and Hamer rule integration, respectively, for quadrilateral and triangular elements (SBQP and SBTP4). The element stiffness, mass and geometrical matrices ([Ke], [Me] and \([K_{\text{g}}^{\text{e}} ]\)) can then be obtained. These are assembled to obtain the structural stiffness, mass and geometrical matrices ([K], [M] and [Kg]).
For static analysis, we use
For free vibration, we use
For the buckling analysis, we use
Numerical validation
To validate the accuracy and efficiency of the formulated quadrilateral and triangular elements (SBQP and SBTP4), several numerical examples have been investigated for static, free vibration and buckling analysis of isotropic plates where the patch test of rigid body modes and the mechanic patch test are first carried out. The obtained results of the SBQP and SBTP4 elements are compared with other numerical and analytical solutions available in the literature.
Patch test of rigid body modes
To verify that both SBQP and SBTP4 elements pass the patch test of rigid body modes, the eigenvalues of the stiffness matrix for a single element are computed for various shapes and different aspect ratio. The only three zero eigenvalues obtained correspond to the three rigid displacement modes for a plate.
Mechanic patch test
In this patch test, a rectangular plate of (L = 2a = 40) length and (2b = 20) width simply supported at the three corner 1,2 and 3 (W1 = W2 = W3 = 0) is considered where the plate is modeled by several elements as shown in Fig. 2 (Batoz and Dhatt 1990) for various side–thickness L/h ratio (10,100 and 1000). The plate boundaries are subjected to solicitations that produce the state of constant moments (or stresses). For the case of Mn = 1 applied on all sides (Fig. 2), the obtained results are Mx = My = 1 everywhere in the plate (Table 1). Whereas for the case of Mns = 1 applied on all sides (Fig. 2), the obtained results at any points of the plate are Mxy = 1 (Table 1). The results given in Table 1 confirm that both SBQP and SBTP4 elements fulfill the mechanic patch test.
Square plates
A classical benchmark is first studied of square plate bending problem (Fig. 3) with different boundary conditions and various thickness–side (h/L) ratios subjected to a uniform load (q = 1), where the shear locking free test and convergence investigation of central deflection are considered in this study.
Shear locking free test is considered for a clamped square plate with several values of ratios (L/h = 10–1,000,000) using a mesh of 12 × 12. The central deflection results of the plate illustrated in Table 2 and Fig. 4, confirm that the new formulated elements (SBQP and SBTP4) are able to solve the shear locking problem when the plate thickness becomes gradually small. However, it is observed that the SBRP element (Belounar and Guenfoud 2005) exhibits from shear locking phenomena for (L/h > 100).
Now, convergence tests of a square plate are investigated with three cases of boundary conditions [clamped, soft simply supported SS1 (W = 0), and hard simply supported SS2 (W = βs = 0)]. Various values of h/L ratios of 0.1, 0.01, and 0.001 are considered for thick, thin and very thin plates, respectively. The obtained results of the vertical displacement at the center of the plate are presented in Tables 3, 4 and 5 and Figs. 5, 6 and 7, which show that:
-
Faster convergence towards analytical solutions (Taylor and Auricchio 1993) is obtained using only a small number of elements for all cases of ratios (h/L = 0.1, 0.01, and 0.001) and boundary conditions.
-
The SBQP and SBTP4 elements have similar behaviors for thin and very thin plates (h/L = 0.01, 0.001); whereas, for thick plates (h/L = 0.1), the SBTP4 element is a little better than the SBQP element.
-
Both proposed elements are free from shear locking phenomena where they are able to provide excellent results for thin and very thin plates (h/L = 0.01, 0.001).
-
Slow convergence to analytical solutions (Taylor and Auricchio 1993) is obtained using the SBRP element (Belounar and Guenfoud 2005) for thick and thin plates (h/L = 0.1, 0.01) and suffers from shear locking for very thin plates (h/L = 0.001).
Skew plates
To show the performance of the present elements to the sensitivity of mesh distortion, two examples of thin skew plates subjected to a uniform load (q = 1) are considered which are known in the literature as severe tests and studied by many researchers (Razzaque 1973; Morley 1963). The first is concerned with Razzaque’s skew plate (Razzaque 1973) (β = 60°) with simply supported on two sides and free on the other sides (Fig. 8). The results of the vertical displacement at the center of the plate using uniform meshes N = 2, 4, 8, 12 and 16 are given in Table 6 and Fig. 9 for (h/L = 0.001). The obtained results for both elements (SBQP and SBTP4) are in quite a good agreement with the reference solution given by Razzaque (1973). But it can be seen that the SBTP4 element is a little better than the SBQP and MITC4 (Nguyen-Xuan et al. 2008) elements.
The second example treated by Morley (β = 30°) (Morley 1963) is simply supported (W = 0) on all sides (Fig. 8). Using meshes of N = 4, 8, 16 and 32, the obtained vertical displacement at the center of the plate are presented in Table 7 and Fig. 10 for h/L = 0.01 and 0.001. It can be observed that for h/L = 0.01, the results of the SBTP4 and SBQP elements are in good agreement with the reference solution (Morley 1963); whereas, for h/L = 0.001, the SBTP4 element is more efficient than the SBQP and MITC4 (Chen and Cheung 2000) elements.
Free vibration of square plates
Convergence tests of the formulated quadrilateral and triangular elements are first undertaken for simply supported (W = βs = 0) and clamped plates with two thickness–side ratios (h/L = 0.005 and 0.1) (Fig. 3). The results of the first six non-dimensional frequencies (λ = (ω2ρL4h/D)1/4) using the SBQP and SBTP4 elements with four regular meshes (N = 4, 8, 16 and 22) are presented in Tables 8, 9, 10 and 11 and Figs. 11 and 12 together with the four-node mixed interpolation of tensorial component MITC4 (Nguyen-Thoi et al. 2012), the discrete shear gap triangle DSG3 (Nguyen-Thoi et al. 2012) and the edge-based smoothed discrete shear gap triangular ES-DSG (Nguyen-Thoi et al. 2012) elements. It can be demonstrated that:
-
Both elements (SBQP and SBTP4) agree well with analytical solutions (Abbassian et al. 1987) and other elements (MITC4, DSG3, and ES-DSG) (Nguyen-Thoi et al. 2012).
-
Figures 11 and 12 show that the SBQP and SBTP4 elements produce more accurate results than those given by other elements (MITC4, DSG3, and ES-DSG) (Nguyen-Thoi et al. 2012) when few elements are employed (4 × 4 mesh).
Having verified the convergence rate of the formulated elements, thin square plates (h/L = 0.005) with five different kinds of boundary conditions (SSSF, SFSF, CCCF, CFCF, and CFSF) for a 22 × 22 mesh are considered. The results of the four non-dimensional frequencies (λ = ωL2(ρh/D)1/2) are presented in Table 12 and the first four mode shapes of SSSF and CFCF plates are plotted in Figs. 13 and 14. For all cases of boundary condition, the following can be concluded:
-
The present results are very close to analytical solutions (Leissa 1969) and are more accurate than those of the MITC4, DSG3 and ES-DSG elements (Nguyen-Thoi et al. 2012).
-
The two elements (SBQP and SBTP4) have similar behavior, are shear locking free and their accuracy is insensitive to boundary conditions.
Free vibration of parallelogram plates
A cantilever parallelogram plate of skew angle = 60° with two h/L ratios (0.001 and 0.2) is studied (Fig. 15) using 22 × 22 mesh. The computed six non-dimensional frequencies (λ = ωL2/π2(ρh/D)1/2) and the mode shapes are illustrated in Table 13 and Fig. 16, respectively. These results are compared with other numerical (DSG3, ES-DSG3, and MITC4) (Nguyen-Thoi et al. 2012) and analytical solutions (Karunasena et al. 1996). It can be seen that the SBQP and SBTP4 elements have a good accuracy compared to exact solutions (Karunasena et al. 1996) and are good competitors to ES-DSG3 and MITC4 (Nguyen-Thoi et al. 2012) and better than DSG3 (Nguyen-Thoi et al. 2012).
Buckling of square plates subjected to uniaxial compression
Square plates subjected to uniaxial compression (Fig. 17) with h/L of 0.01 is analyzed for both simply supported (SSSS) and clamped (CCCC). The buckling load factor is defined as Kh = λcrL2/(π2/D). The results of the buckling load factor for the SBQP and SBTP4 elements using 4 × 4, 8 × 8, 12 × 12, 16 × 16 and 20 × 20 meshes are presented in Table 14 and Fig. 18. For all cases of boundary condition, the two elements (SBQP and SBTP4) have similar results and converge to analytical solutions (Timoshenko and Gere 1970). In addition, these elements have excellent accuracy compared to other elements (DSG3 and ES-DSG3) (Nguyen-Xuan et al. 2010a, b).
The results of the buckling load factor (Kh) and the relative error using 20 × 20 mesh are presented in Table 15. Numerical results of the SBQP and SBTP4 elements are in good agreement with analytical solutions (Timoshenko and Gere 1970) and other numerical solutions (Nguyen-Xuan et al. 2010a, b; Tham and Szeto 1990; Vrcelj and Bradford 2008; Liew and Chen 2004).
Buckling of square plates subjected to biaxial compression
Square plate subjected to biaxial compression (Fig. 19) with three essential boundary conditions (SSSS, CCCC, SCSC) is considered for h/L = 0.01 using a mesh of 16 × 16. The buckling load factor results (Kh = λcrL2/(π2/D)) of the proposed elements are presented in Table 16 with analytical (Timoshenko and Gere 1970) and other numerical solutions (Nguyen-Xuan et al. 2010a, b; Tham and Szeto 1990; Vrcelj and Bradford 2008). It can be seen that both elements (SBQP and SBTP4) provide results which agree well with analytical solutions (Timoshenko and Gere 1970) and other solutions (Nguyen-Xuan et al. 2010a, b; Tham and Szeto 1990; Vrcelj and Bradford 2008) for all cases of boundary condition.
Conclusion
A simple and efficient quadrilateral and triangular strain-based finite elements have been presented for static, free vibration and buckling analyses of Reissner–Mindlin plates. The four-node strain-based triangular element SBTP4 has the three engineering external degrees of freedom at each of the three corner nodes and one mid-edge point, while the quadrilateral element SBQP has the same engineering degrees of freedom at each of the four corner nodes. These developed elements passed successfully both patch and benchmark tests for plate bending problems. Numerical results show that the SBQP and SBTP4 elements are shear locking free, stable and superior to the original strain-based rectangular plate element (SBRP) (Belounar and Guenfoud 2005) which suffers from shear locking when the plate thickness becomes progressively very thin and has less rate of convergence to analytical solutions for thick and thin plates. The obtained results using both strain-based elements (SBQP and SBTP4) show that a rapid convergence to analytical solutions can be achieved with relatively coarse meshes compared with other robust elements based on different methods. In perspective, these elements can be superposed with membrane robust elements to construct shell elements for the analysis of complex shell structures.
Abbreviations
- L :
-
Length of plate
- k :
-
Shear correction factor
- ρ :
-
Material density
- ν :
-
Poisson’s ratio
- E :
-
Young’s modulus
- h :
-
Thickness of plate
- β :
-
Angle of the skew plate
- D :
-
Flexural rigidity of plate = Eh3/[12(1 − v2)]
- G :
-
Shear modulus = E/[2(1 + v)]
- λ :
-
Non-dimensional frequency parameter
- ω :
-
Angular frequency
- λ cr :
-
Critical buckling load
- α i :
-
Constants in displacement fields
- W :
-
Displacement in the z-direction
- β x, β y :
-
Rotations about y and x axes, respectively
- x, y, z :
-
Co-ordinates system
- [K e]:
-
Element stiffness matrix
- [M e]:
-
Element mass matrix
- \([K_{\text{g}}^{\text{e}} ]\) :
-
Element geometrical matrix
- [K]:
-
Structural stiffness matrix
- [M]:
-
Structural mass matrix
- [K g]:
-
Structural geometrical matrix
- [C]:
-
Transformation matrix
- [P]:
-
Displacement matrix
- [Q]:
-
Strain matrix
- [G]:
-
Geometrical strain matrix
- {F}:
-
Structural nodal force vector
- {q}:
-
Structural nodal displacements vector
- {q e}:
-
Element nodal displacements vector
References
Abbassian F, Dawswell DJ, Knowles NC (1987) Free vibration benchmarks. Atkins engineering sciences. Softback, Glasgow
Ayad R, Dhatt G, Batoz JL (1998) A new hybrid-mixed variational approach for Reissner–Mindlin plate. The MiSP model. Int J Numer Methods Eng 42(7):1149–1179
Bathe KJ, Dvorkin EN (1985) A four-node plate bending element based on Mindlin/Reissener plate theory and a mixed interpolation. Int J Numer Methods Eng 21(2):367–383
Bathe KJ, Dvorkin EN (1986) A formulation of general shell elements, the use of mixed interpolation of tensorial components. Int J Numer Methods Eng 22(3):697–722
Batoz JL, Dhatt G (1990) Modélisation des structures par éléments finis. Volume 2 poutres et plaques. Hermes, Paris
Batoz JL, Katili I (1992) On a simple triangular Reissner/Mindlin plate element based on incompatible modes and discrete constraints. Int J Numer Methods Eng 35(8):1603–1632
Belarbi MT, Charif A (1999) Développement d’un nouvel élément hexaédrique simple basé sur le modèle en déformation pour l’étude des plaques minces et épaisses. Revue européenne des éléments finis 8(2):135–157
Belounar L, Guenfoud M (2005) A new rectangular finite element based on the strain approach for plate bending. Thin Walled Struct 43(1):47–63
Belounar L, Guerraiche K (2014) A new strain based brick element for plate bending. Alex Eng J 53(1):95–105
Belounar A, Benmebarek S, Belounar L (2018) Strain based triangular finite element for plate bending analysis. Mech Adv Mater Struct. https://doi.org/10.1080/15376494.2018.1488310
Bletzinger KU, Bischoff M, Ramm E (2000) A unified approach for shear-locking free triangular and rectangular shell finite elements. Comput Struct 75(3):321–334
Cardoso RPR, Yoon JW, Mahardika M, Choudhry S, Alves de Sousa RJ, Fontes Valente RA (2008) Enhanced assumed strain (EAS) and assumed natural strain (ANS) methods for one-point quadrature solid-shell elements. Int J Numer Methods Eng 75(2):156–187
César de Sá JMA, Natal Jorge RM (1999) New enhanced strain elements for incompatible problems. Int J Numer Methods Eng 44(2):229–248
César de Sá JMA, Natal Jorge RM, Fontes Valente RA, Areias PMA (2002) Development of shear locking-free shell elements using an enhanced assumed strain formulation. Int J Numer Methods Eng 53(7):1721–1750
Chen WJ, Cheung YK (2000) Refined quadrilateral element based on Mindlin/Reissner plate theory. Int J Numer Methods Eng 47(1–3):605–627
Djoudi MS, Bahai H (2004a) A cylindrical strain-based shell element for vibration analysis of shell structures. Finite Elem Anal Des 40(13–14):1947–1961
Djoudi MS, Bahai H (2004b) Strain-based finite element for vibration of cylindrical panels with openings. Thin Walled Struct 42(4):575–588
Guerraiche K, Belounar L, Bouzidi L (2018) A new eight nodes brick finite element based on the strain approach. J Solid Mech 10(1):186–199
Hughes TJR, Cohen M, Haroun M (1978) Reduced and selective integration techniques in finite element method of plates. Nucl Eng Des 46(1):203–222
Karunasena W, Liew KM, Al-Bermani FGA (1996) Natural frequencies of thick arbitrary quadrilateral plates using the pb-2 Ritz method. J Sound Vib 196(4):371–385
Lee SW, Wong C (1982) Mixed formulation finite elements for Mindlin theory plate bending. Int J Numer Methods Eng 18(9):1297–1311
Leissa AW (1969) Vibration of plates: NASA, SP-160, Washington DC
Leissa AW (1987) Plate vibration research: 1981–1985: classical theory. Shock Vib Digest 19(2):11–18
Liew KM, Chen XL (2004) Buckling of rectangular Mindlin plates subjected to partial in-plane edge loads using the radial point interpolation method. Int J Solids Struct 41(5–6):1677–1695
Liew KM, Xiang Y, Kitipornchai S (1995) Research on thick plate vibration: a literature survey. J Sound Vib 180(1):163–176
Liew KM, Wang J, Ng TY, Tan MJ (2004) Free vibration and buckling analyses of shear-deformable plates based on FSDT meshfree method. J Sound Vib 276(3–5):997–1017
Liu GR, Nguyen-Thoi T (2010) Smoothed finite element methods. CRC Press, London
Lovadina C (1998) Analysis of a mixed finite element method for the Reissner–Mindlin plate problems. Comput Methods Appl Mech Eng 163(1–4):71–85
Mackerle J (1997) Finite element linear and nonlinear, static and dynamic analysis of structural elements: a bibliography (1992–1995). Eng Comput 14(4):347–440
Mackerle J (2002) Finite element linear and nonlinear, static and dynamic analysis of structural elements: a bibliography (1999–2002). Eng Comput 19(5):520–594
MacNeal RH (1982) Derivation of element stiffness matrices by assumed strain distribution. Nucl Eng Des 70(1):3–12
Malkus DS, Hughes TJR (1978) Mixed finite element methods-reduced and selective integration techniques: a unification of concepts. Comput Methods Appl Mech Eng 15(1):63–81
Morley LSD (1963) Skew plates and structures. Pergamon Press, Oxford
Nguyen-Thoi T, Phung-Van P, Nguyen-Xuan H, Thai-Hoang C (2012) A cell-based smoothed discrete shear gap method using triangular elements for static and free vibration analyses of Reissner Mindlin plates. Int J Numer Methods Eng 91(7):705–741
Nguyen-Xuan H, Rabczuk T, Bordas S, Debongnie JF (2008) A smoothed finite element method for plate analysis. Comput Methods Appl Mech Eng 197(13–16):1184–1203
Nguyen-Xuan H, Liu GR, Thai-Hoang C, Nguyen-Thoi T (2010a) An edge-based smoothed finite element method (ES-FEM) with stabilized discrete shear gap technique for analysis of Reissner-Mindlin plates. Comput Methods Appl Mech Eng 199(9–12):471–489
Nguyen-Xuan H, Rabczuk T, Nguyen-Thanh N, Nguyen-Thoi T, Bordas S (2010b) A node-based smoothed finite element method with stabilized discrete shear gap technique for analysis of Reissner-Mindlin plates. Comput Mech 46(5):679–701
Razzaque A (1973) Program for triangular bending elements with derivative smoothing. Int J Numer Methods Eng 6(3):333–343
Rebiai C, Belounar L (2013) A new strain based rectangular finite element with drilling rotation for linear and nonlinear analysis. Arch Civ Mech Eng 13(1):72–81
Rebiai C, Belounar L (2014) An effective quadrilateral membrane finite element based on the strain approach. Measurement 50:263–269
Taylor RL, Auricchio F (1993) Linked interpolation for Reissner-Mindlin plate element: Part II—a simple triangle. Int J Numer Methods Eng 36(18):3057–3066
Tham LG, Szeto HY (1990) Buckling analysis of arbitrary shaped plates by spline finite strip method. Comput Struct 36(4):729–735
Timoshenko SP, Gere JM (1970) Theory of elastic stability, 3rd edn. McGraw-Hill, New York
Vrcelj Z, Bradford MA (2008) A simple method for the inclusion of external and internal supports in the spline finite strip method (SFSM) of buckling analysis. Comput Struct 86(6):529–544
Zienkiewicz OC, Taylor RL, Too JM (1971) Reduced integration technique in general analysis of plates and shells simple and efficient element for plate bending. Int J Numer Methods Eng 3(2):275–290
Zienkiewicz OC, Taylor RL, Papadopoulos P, Onate E (1990) Plate bending elements with discrete constraints: new triangular elements. Comput Struct 35(4):505–522
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Belounar, A., Benmebarek, S., Houhou, M.N. et al. Static, free vibration, and buckling analysis of plates using strain-based Reissner–Mindlin elements. Int J Adv Struct Eng 11, 211–230 (2019). https://doi.org/10.1007/s40091-019-0226-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-019-0226-4