Shear strength and stiffness enhancement of cross-stiffened steel plate shear walls

Abstract

Nowadays, the use of steel plate shear walls, as an effective seismic resisting system, has been of great interest in enhancing the lateral strength and stiffness of buildings both in renovation and seismic rehabilitation of existing concrete and steel structures. In the present research, the shear strength and stiffness of steel plate shear walls in various configurations of stiffeners, including horizontal, vertical, and horizontal–vertical, were investigated by finite element method and finally semi-empirical relations were presented in this regard. The results indicated that the shear strength and stiffness of stiffened SPSWs were well predicted by the proposed relations, but increasing the number of stiffeners above a certain range will not have a significant effect on enhancing the stiffness and strength.

Introduction

In recent years, extensive experimental investigations have been conducted under cyclic and monotonic loads on steel plate shear walls (SPSWs) to ensure the seismic performance of the system. The results have revealed high stiffness, sufficient strength, excellent ductility, and high energy absorption of this seismic resisting system. The researchers have been analytically interested in steel plate shear walls as the steel plate shear walls are used in seismic rehabilitation of existing structures in addition to newly constructed structures.

Alinia and Dastfan compared the behavior of unstiffened (thin) and stiffened panels in 2006 and 2007. In this numerical study, the effect of stiffening was investigated on the ultimate strength and cyclic behavior of stiffened and unstiffened panels. They found that the optimal number of stiffeners should be used to achieve sufficient rigidity and ductility (Alinia and Dastfan 2006, 2007). Sabouri ghomi et al. conducted studies to improve the stability and prevent the early elastic buckling of the wall using horizontal and vertical stiffeners. They also observed that the proper application of stiffeners would enhance the energy absorption and stiffness of the system (Sabouri-Ghomi et al. 2008).

Alinia and Sarraf Shirazi provided a practical design method for stiffening thin SPSWs (Alinia and Sarraf Shirazi 2009). Sabouri-Ghomi and Sajjadi proposed a method to determine the minimum moment of inertia for stiffeners to prevent the global buckling of the plate (Sabouri-Ghomi and Sajjadi 2012). The values resulting from this method were compared with the tests conducted by Takahashi et al. (1973) where a good agreement was reached.

They also studied the performance of unstiffened panel between two openings in stiffened steel walls by finite element methods. The results of their research suggested that there will be limitations on the dimensions of the cross-section of stiffener, as well as the height–width ratio of intermediate panel such that intermediate thin steel plate is yielded sooner than the dual stiffeners on both sides (Sabouri et al. 2013).

Nie et al. recommended a design method for calculating the lateral resistance capacity of stiffened SPSWs based on the experimental research (Nie et al. 2013). Machaly et al. numerically investigated the ultimate shear strength of SPSWs (Machaly et al. 2014). Brando and De Matteis provided design curves for low strength-high hardening metal multi-stiffened shear plates, based on both experimental tests and parametric numerical analyses (Brando and De Matteis 2014). Sabouri-Ghomi and Mamazizi conducted an experimental investigation of stiffened SPSWs with two rectangular openings (Sabouri-Ghomi and Mamazizi 2015).

Zirakian and Zhang studied the buckling and yielding behavior of unstiffened slender, moderate and stocky low yield point SPSWs with various support and loading conditions (Zirakian and Zhang 2015). Guo et al. explored the influence of hinged, rigid, and semi-rigid connection joints on the behavior of stiffened and unstiffened SPSWs using experimental test and finite element analysis (Guo et al. 2015). Rahmzadeh et al. described the effect of the rigidity and arrangement of stiffeners on the buckling behavior of plates (Rahmzadeh et al. 2016). Jin et al. investigated the stability of buckling-restrained SPSWs with inclined-slots (Jin et al. 2016). Guo et al. analyzed the failure mode, energy dissipation mechanism, and the influence of joint connecting forms and arrangement of stiffeners on the seismic performance of cross-stiffened SPSWs with a semi-rigid connected frame (Guo et al. 2017).

Haddad et al. experimentally investigated the cyclic performance of stiffened steel plate shear walls with three configurations including cross-stiffened, circular-stiffened, and diagonally stiffened SPSWs (Haddad et al. 2018). Afshari and Gholhaki proposed an equation for shear strength degradation of unstiffened steel plate shear walls with optional located opening (Afshari and Gholhaki 2018).

Despite many studies performed on the stiffened steel plate shear walls by various researchers, these walls require time-consuming and expensive non-linear static and dynamic analyses to capture the strength and stiffness of the system. On the other hand, almost all classical and theoretical relations associate with unstiffened steel plate shear walls, and there is no definite relation to estimate the strength and stiffness of the stiffened panel compared to the unstiffened panel. Accordingly, the purpose of this paper is to achieve simple relations computing the strength and stiffness of the stiffened panel based on the number of vertical and horizontal stiffeners converting the global buckling mode of the plate to the local buckling mode in sub-panels.

Accordingly, after modeling validation, unstiffened shear wall was stiffened by 4 horizontal and vertical stiffeners. Based on the results obtained by the analysis of the aforementioned models, the proposed equations were extracted to estimate the strength and stiffness of the models. Then, based on these relations, the strength and stiffness of the stiffened panels were predicted with a higher number of stiffeners. The accuracy of predictive values was examined by re-modeling with a larger number of stiffeners and, if appropriate, the proposed relations were confirmed and presented. At the end, the number of stiffeners was introduced in which the proposed relations were valid. The flowchart of the process is displayed in Fig. 1.

Fig. 1

Modelling flowchart

Validation of mesh sensitivity and modeling

An experimental stiffened specimen of Takahashi (Takahashi et al. 1973) was selected for modelling and validation purposes, which is a steel plate shear wall of 2.1 m wide, 0.9 m high, 3.2 mm thick, and with a yield stress of 232 MPa and ultimate stress of 380 MPa. The experimental model has six vertical and two horizontal stiffeners in the same spaces on both sides of the plate with a cross-section of 60 × 4.5 mm. The above model has a simple surrounding hinge frame. Thereupon, in finite element method, the simple connection of beam–column was modelled by triangulation of the beam web at the column flange junction, with this method used to simulate simple connection of column base to deep beam as well (Fig. 2). The 4-node Shell element (SHELL181) was used in finite element modeling (Software 2012) of the surrounding frame and plate. In addition, the profiles of type IPB300 and IPB400 were used for surrounding beams and columns and deep beam, respectively.

Fig. 2

Finite element model under lateral load

To perform mesh sensitivity analysis, different mesh sizes were considered in accordance with Fig. 3, with the model undergoing monotonic lateral load.

Fig. 3

Force–displacement (push over) curve of experimental specimen and the finite element models with different mesh sizes

Figure 3 reveals the comparison of the modeling and laboratory results suggesting the proper adaptation of simulation to experimental results. In this figure, the finite element model with a mesh size of 15 mm by 15 mm had the minimum error (1.2%) compared to the experimental results. At the same time, it has claimed the longest analysis time (Table 1). The use of the finite element model with a 60 mm by 60 mm mesh size resulted in an ignorable increase in average error percentage of up to 2.1% compared to the experimental results, but at the same time, it reduced the analysis time to more than one-tenth of the time required for a 15 mm mesh. Therefore, it can be used as an appropriate mesh size for future modeling.

Table 1 Results of mesh sensitivity analysis

Considering the aspect ratio of the shear panels of the present study with the above-mentioned experimental test and given the scale of the models of the present research, the 150 mm by 150 mm mesh size was selected for all of the subsequent modellings.

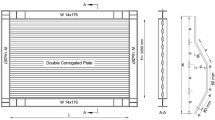
The experimental model of Sabouri and Sajjadi (2008) was selected as the second specimen for the modeling validation. The bilinear kinematic stress–strain curve was employed in finite element modeling of the infill plate, stiffeners, and the frame members. The elastoplastic tangent of the strain hardening part and the Poisson’s ratio were considered as 2% of the young’s modulus and 0.3, respectively. Geometric specifications and mechanical properties of the above-mentioned specimen are given in Fig. 4 and Table 2.

Fig. 4

Specification of Sabouri & Sajjadi’s specimen

Table 2 Mechanical properties of steel material used in the finite element modeling

Comparison of the analytical results of finite element model and laboratory specimen as shown in Fig. 5 confirms the accuracy of the modeling with 15 × 15 cm mesh size. Hence, this size is used for the upcoming modelling process.

Fig. 5

Force–displacement curve of experimental specimen and the finite element model

Modeling of studied specimens

To achieve simple relations representing the increase in the percentage of strength and stiffness of the stiffened panel with stiffener compared to the same model without stiffener, a panel without stiffener should first be modeled. Concerning common bay length of buildings, a steel plate shear wall 5000 mm wide, 3000 mm high and 2.5 mm thick was considered with a simple connection surrounding frame. Stiffness of the beam and column is such that the plate is completely under pure shear.

To select proper sections for the surrounding elements with sufficient rigidity, the specifications of AISC341-16 (AISC 2016a) were used. The preliminary design of surrounding columns and the connecting beam, given its simple connections to adjacent columns, was performed using Eqs. (1) and (2), respectively (AISC 2016b).

$$I_{c} \ge 0.0031(t_{w} d^{4} /b)$$

(1)

$$M_{\text{pb}} > (\sigma_{\text{ty}} t_{w} b^{2} \cos^{2} \alpha )/8$$

(2)

where I_c, t_w, d, b, and M_pb are column moment of inertia, plate thickness, plate height, plate width, and plastic moment capacity of the beam, respectively. α represents the diagonal tension field angle as shown in Relation (3). In addition, the stress of tension field at the yielding time (σ_ty) is obtained by solving Eq. (4) (AISC 2016b).

$$\tan^{4} \alpha = \left( {1 + \frac{{t_{w} b}}{{2A_{c} }}} \right)/\left[ {1 + t_{w} d\;\left( {\frac{1}{{A_{b} }} + \frac{{d^{3} }}{{360I_{c} b}}} \right)} \right]$$

(3)

$$\sigma_{\text{ty}}^{2} + 3\tau_{\text{cr}} \sigma_{\text{ty}} \,\sin \,(2\alpha ) + 3\tau_{cr}^{2} - F_{y}^{2} = 0$$

(4)

In above equations, A_c, A_b and τ_cr denote the column cross-sectional area, beam cross-sectional area, and the critical buckling shear stress of steel plate, respectively. τ_cr can be determined in accordance with classical stability Equation (Timoshenko and Gere 1961) as follows:

$$\tau_{\text{cr}} = \frac{{k\pi^{2} E}}{{12(1 - \nu^{2} )}} \cdot \left( {\frac{{t_{\text{w}} }}{b}} \right)^{2} \le \tau_{y} = \frac{{F_{y} }}{\sqrt 3 }$$

(5)

where ν, E, τ_y, and F_y are Poisson’s ratio (0.3), elasticity modulus, shear yielding stress, and uniaxial tensile yielding stress of the plate, respectively. The shear buckling factor k which depends on the steel plate aspect ratio and boundary conditions, which is equal to 18.861 for the simple supported plate of the present research. Accordingly, for the wall with the mentioned sizes, beams and columns of type IPB300 were designed and modeled as displayed in Fig. 6.

Fig. 6

Dimensions and specifications of the shear panel

ST37 with modulus of elasticity of 205.94 GPa and yield stress of 235.36 MPa was utilized in all members with ideal bilinear stress–strain curve without hardening (elastic-perfectly plastic). Since removal of the bottom beam will reduce time of analyses, bottom beam was removed in all simulations and simple boundary condition was applied on column base and wall directly. According to theoretic relations based on classical stability equation (AISC 2016a) and also considering the insignificant value of τ_cr (0.878 MPa ≈ 0) obtained from Eq. (5), σ_ty is almost equal to specified minimum yield stress (uniaxial yield stress, F_y) of infill plate. Hence, the shear strength of the steel plate shear wall is obtained by Relation (6).

$$V_{y} = 0.5F_{y} bt_{w} \sin (2\alpha )$$

(6)

Concerning the value of α (42.7°) which was obtained by Eq. (3), theoretical shear strength of the wall was 1466.27 kN. Based on finite element model analysis of unstiffened panel, shear strength of the plate was 1425.89 kN, indicating 2.8% error compared to analytical value of 1466.27 kN. This demonstrates the proper accuracy of mesh sizes and modeling process.

An introduction to arrangement and dimensions of stiffeners

To investigate the behavior of stiffened panels under various arrangements of stiffeners, 25 models with different horizontal and vertical spacings of stiffeners were prepared according to Fig. 7, which underwent the lateral load.

Fig. 7

Arrangements selected for stiffeners to study the shear panel capacity

The sizes and moment of inertia of stiffeners should be such that the global buckling of the plate is prevented and, in accordance with Fig. 8, the global buckling mode should be converted to a local buckling mode in sub-panels. In other words, in case of choosing inappropriate dimensions and thickness for the stiffener, global buckling of the plate, as well as the stiffeners definitely occurs and the steel plate capacity will not be fully utilized.

Fig. 8

The effect of sizes and geometrical specifications of the stiffener in the buckling mode of shear panel, a improper global buckling of the panel with inappropriate stiffener, b proper local buckling of sub-panels with appropriate stiffeners

To convert the global buckling of the plate to the local buckling mode in each sub-panel, the relation provided by Timoshenko for orthotropic plates must be satisfied in accordance with Relation (7) (Timoshenko and Gere 1961).

$$\left( {\frac{{I_{x} }}{{S_{x} }} + \frac{{t_{w}^{3} }}{{12 - 12\nu^{2} }}} \right)^{0.75} + \left( {\frac{{I_{y} }}{{S_{y} }} + \frac{{t_{w}^{3} }}{{12 - 12\nu^{2} }}} \right)^{0.25} \ge \frac{{t_{w}^{3} }}{{12 - 12\nu^{2} }}\left( {\frac{d}{{S_{x} }}} \right)^{2} \left( {\frac{{k_{L} }}{{k_{G} }}} \right)$$

(7)

where k_G is the global buckling coefficient of the plate, calculated as 3.64 in terms of the simple connection of the plate to the surrounding members, and k_L is the local buckling coefficient of the plate obtained from Relation (8).

$$\left\{ \begin{aligned} k_{L} = 5.35 + \frac{4}{{(S_{y} /S_{x} )^{2} }}\quad \quad \quad \frac{{S_{y} }}{{S_{x} }} \ge 1 \hfill \\ k_{L} = 4 + \frac{5.35}{{(S_{y} /S_{x} )^{2} }}\quad \quad \quad {\kern 1pt} \,\quad \frac{{S_{y} }}{{S_{x} }} < 1 \hfill \\ \end{aligned} \right.$$

(8)

Other parameters of relation (7) are shown in Fig. 9.

Fig. 9

Geometrical specifications of the panel and stiffeners

According to Fig. 9, if the same thickness and dimensions are used for horizontal and vertical stiffeners (I_x= I_y), and by replacing I_s with I_x and I_y in Relation (7), and with respect to S_x and S_y values obtained from arrangements of stiffeners based on Fig. 7, the moment of inertia value (I_s) is calculated for the horizontal and vertical stiffeners of the examined models, with the highest value of (30.16 × 10⁴ mm⁴) for the model 0v4h. Therefore, by choosing stiffeners with 10 mm width (b_s= 100 mm) and 10 mm thickness (t_s= 10 mm), according to Relation (9), the moment of inertia corresponding to the chosen dimensions is equal to 33.33 × 10⁵ mm⁴ which is higher than the highest value required for the 0v4h model. Therefore, the moment of inertia required for stiffeners of all models is provided to supply the local buckling of sub-panels.

$$I_{s} = \frac{1}{3}t{}_{s}b_{s}^{3} .$$

(9)

Also, the width–thickness ratio of the selected stiffeners to control stiffener slenderness is equal to 10, which according to Relation (10), is lower than the maximum allowed value (16.56) (AISC 2016b), and therefore, the dimensions of stiffeners are appropriate.

$$\frac{{b_{s} }}{{t_{s} }} < 0.56\sqrt {\frac{E}{{F_{ys} }}}$$

(10)

In the above relation, F_ys is the yield stress of stiffening materials.

Analysis and study of results

Determination of the empirical relation, which indicates the percentage enhancement of shear strength and stiffness of the models compared to the thin model without stiffener, requires the definition of the yield point of the model. In the present study, based on the concept of plastic energy equilibrium (FEMA-356 2000), an idealized bilinear force–displacement curve replaces the actual pushover curve assuming elastic-perfectly plastic behavior (without hardening or softening). For this purpose, the point B, as revealed in Fig. 10, must be chosen using an iterative graphical procedure so that the areas enclosed by the idealized bilinear curve and nonlinear push over curve are balanced below and above the idealized bilinear curve.

Fig. 10

Behavioral model selected to study the shear panel capacity

In Fig. 10, V_y is the effective shear yield strength (shear strength), V_u, is the ultimate lateral load carrying capacity of the shear panel, K_e represents the effective shear stiffness, δ_y shows the limiting elastic shear displacement, and δ_u is displacement at the moment of the ultimate load carrying capacity.

Analysis of the displacement–force curves obtained from model’s analysis

The ultimate strength (V_u), the limiting elastic strength (V_y), and the panel stiffness (K_e) are expected to increase, while the ultimate shear displacement of the structure (δ_u) is expected to diminish due to adding the stiffener to the shear panel. Figures 11, 12, 13, 14 and 15 present the effect of enhancing the strength and stiffness and reducing ultimate displacement of the structure after addition of stiffeners. In these figures, changes in shear panel force–displacement curve without vertical stiffeners are observed after adding only the horizontal stiffener from zero to four stiffeners (Fig. 11). The process of adding horizontal stiffener from 0 to 4 for a panel with one vertical stiffener up to 4 vertical stiffeners is demonstrated in Figs. 12, 13, 14 and 15, respectively.

Fig. 11

The effect of adding horizontal stiffener on the changes in pushover curves for 0v models

Fig. 12

The effect of adding horizontal stiffener on the changes in pushover curves for 1v models

Fig. 13

The effect of adding horizontal stiffener on the changes in pushover curves for 2v models

Fig. 14

The effect of adding horizontal stiffener on the changes in pushover curves for 3v models

Fig. 15

The effect of adding horizontal stiffener on the changes in pushover curves for 4v models

As revealed in Figs. 11, 12, 13, 14 and 15, raising the number of stiffeners increased the stiffness and strength of the specimens and decreased the ultimate shear displacement of the structure. Figure 16 indicates the position of formation of the diagonal tension field in each of the models.

Fig. 16

Distribution of 1st principle stress in each specimen at the moment of the diagonal tension field formation

As can be observed, the global buckling mode has been prevented and the local buckling has formed on each of the sub-panels by choosing the appropriate stiffener. The effective shear yield strength and stiffness of all models have been calculated using an idealized bilinear model with the results presented in Tables 3 and 4, respectively.

Table 3 Effective shear yield strength of the studied models

Table 4 Effective shear stiffness of the studied models

Determination of semi-empirical relations for estimating the model’s strength

According to the results of Table 3, we can determine the semi-empirical relationship between the increase in the percentage of the strength of models with stiffeners compared to those without stiffeners according to the number of horizontal (n_h) and vertical (n_v) stiffeners added to the shear panel. Accordingly, Fig. 17 shows the average percentage of variations in the strength of the models compared to unstiffened thin panel for two modes of increase in vertical stiffeners (n_v), regardless of the number of horizontal stiffeners as well as the increase in the horizontal stiffener (n_h), irrespective of the number of vertical stiffeners. The best curves passing through each of data categories with different equations are fitted in two precise and approximate states according to Fig. 17. Finally, Relation (11) presents the percentage of changes in the strength based on the number of horizontal and vertical stiffeners.

Fig. 17

Percentage increase of shear strength based on the number of a vertical stiffeners, b horizontal stiffeners

$$\Delta V_{y} (\% ) = \frac{{23.57n_{v}^{1.22} }}{{4.56 + n_{v}^{1.22} }} + \frac{{26.68n_{h}^{1.59} }}{{7.26 + n_{h}^{1.59} }}.$$

(11)

In which, ΔV_y is the percentage increase of the shear strength of the stiffened panel compared to unstiffened panel. To simplify the above relation, we used power fitness as depicted in Fig. 17 to obtain a simple as Relation (12).

$$\Delta V_{\text{y}} (\% ) = 4.66\;n_{\text{v}}^{0.69} + 3.97\;n_{\text{h}}^{0.89}$$

(12)

Determination of semi-empirical relation for estimating the model’s stiffness

Using the results of Table 4 and the curves of Fig. 18, the semi-empirical relation can be achieved to calculate the percentage increase of the stiffened panels compared to the unstiffened panel in terms of adding the number of horizontal and vertical stiffeners. As presented in Fig. 18a, the trend of stiffness elevation, unlike strength, is not the same in both manners of adding horizontal and vertical stiffeners (values in columns and rows of Table 4, respectively). For example, the ascending stiffness trend due to addition of vertical stiffeners in the panels without horizontal stiffener (0h) has been greater than that in panels with one horizontal stiffener (1h).

Fig. 18

Increasing trend of stiffness for various additions of stiffeners. a The percentage of increase of stiffness in terms of the number of vertical stiffeners, b curve fitting of coefficients, c curve fitting of powers, d the percentage of increase of stiffness in terms of the number of horizontal stiffeners

This trend in (1h) is also greater than in (2h) and the aforementioned course decreases after adding the number of horizontal stiffeners. Therefore, unlike the trend mentioned for the strength of specimens, use of mean of variations in this case will yield a considerable error. Therefore, to minimize the calculation error and provide a simple empirical relation for increasing the stiffness of specimens, it is necessary to use the fitting functions (B and C) of Fig. 18b, c respectively in relation to the coefficients along with the power of resulting equations of Fig. 18a.

Accordingly, an exact relation suggesting the percentage of increase in the stiffness due to the effect of adding vertical stiffeners is achieved separately for any particular number of horizontal stiffeners while not using the average variation. The above process takes into account the trend of increase of stiffness of the values of the row in Table 4 in the given relation.

To apply the columnar values of increase in the stiffness in Table 4, the column (0v) should be studied in accordance with Fig. 18d to obtain the desired relation. The mentioned relation is associated with a quantitative error due to the simultaneous effect of increased horizontal and vertical stiffeners and can be presented as Relation (13) for the percentage increase of the model stiffness in terms of the number of stiffeners.

$$\begin{aligned} \Delta K_{e} = [(A + B\;.\;n_{v}^{C} )/120720.5] \times 100\; \hfill \\ \left\{ \begin{aligned} A = \frac{{2.44 \times 10^{5} }}{{1 + 25.34\exp ( - 1.38n_{h} )}} \hfill \\ B = \frac{{4.12 \times 10^{4} }}{{1 + \exp ( - 2.12 + n_{h} )}} \hfill \\ C = \frac{1}{{1.11 + 4.16 \times 10^{ - 4} \times n_{h}^{5.34} }} \hfill \\ \end{aligned} \right.\; \hfill \\ \end{aligned}$$

(13)

ΔK_e is the increasing percentage of shear stiffness of stiffened panel compared to the unstiffened panel. Another remarkable point in this section, as seen in Table 4, is the greater effect of horizontal stiffener on the elevation of stiffness of stiffened panel compared to vertical stiffener. Comparing any arbitrary couples of models of the studied panels whose total stiffeners are equal, but the number of their horizontal and vertical stiffeners are exactly opposite, it is observed that a model with a higher number of horizontal stiffeners will have greater stiffness. The reason may be the ratio of (S_y/S_x), which ultimately leads to a more uniform tension field between the beams. The above issue is not the case for increased strength of the panels, and the effect of horizontal and vertical stiffeners on the panel’s strength rise is almost the same. In other words, if the goal is only to enhance the stiffness of the panel with one stiffener, then this stiffener should be used horizontally.

Verification of the proposed relation

The prediction of the strength and stiffness of the panels based on the proposed Relations (11) and (13) is presented in Tables 5 and 6, respectively. To verify the relations provided, other models with horizontal and vertical stiffeners greater than 4 (models 5v0h, 0v5h,1v5h, and 4v6h) have been modeled by finite element software. Further, their stiffness and strength and corresponding values obtained by the proposed relations have been compared in Figs. 19, 20, 21, and 22, respectively.

Table 5 Prediction of models’ strengths using the proposed Relation (11)

Table 6 Prediction of models’ stiffness using the proposed Relation (13)

Fig. 19

Results of finite element analysis for validation of 5v0h model; a proper placement of force–displacement curve of 5v0h model, b shear strength and stiffness of 5v0h model

Fig. 20

Results of finite element analysis for validation of 0v5h model; a proper placement of force–displacement curve of 0v5h model, b shear strength and stiffness of 0v5h model

Fig. 21

Results of finite element analysis for validation of 1v5h model; a proper placement of force–displacement curve of 1v5h model, b shear strength and stiffness of 1v5h model

Fig. 22

Results of finite element analysis for validation of 4v6h model; a distribution of Von Mises stress and deformation of 4v6h, b shear strength and stiffness of 4v6h model

The proper congruence between the results of the finite element modeling for the validation specimens and the values of the proposed relation confirm the validity of the relations. The results suggest that maximum 7 horizontal and vertical stiffeners provide the maximum strength and stiffness of the panel. This specific bound is exactly the boundary, after which the diagonal tension field will not completely form in all sub-panels.

By comparing the shear strength values given in Table 5 obtained using the proposed Relation (11), with the corresponding values included in Figs. 19, 20, 21 and 22 derived from the finite element modeling of the verification models, it can be observed that the error rate due to application of the proposed Relation (11) instead of the time-consuming finite element analysis for verification models 5v0h, 0v5h, 1v5h, and 4v6h, was 0.30, 0.76, 0.43, and 0.51%, respectively. This indicates the high accuracy of the proposed Relation (11) in the estimation of shear strength of stiffened panels. Similarly, the comparison of the predicted stiffness values for the four above-mentioned validation models (Table 6) and the corresponding values obtained from finite element analysis indicated an error rate of 3.05, 0.61, 0.39, and 0.55%, respectively, due to applying the proposed Relation (13). This clearly confirms the accuracy of the proposed relation in the estimation of the stiffness of the stiffened models.

In addition to verifying the proposed relations through finite element re-modeling, as discussed for the 5v0h, 0v5h, 1v5h, and 4v6h validation models, the validity of the proposed relations in terms of estimating the percentage increase of the strength of stiffened panels has been measured with three experimental studies in accordance with Table 7.

Table 7 Verification of the proposed Relation (11) with experimental tests

The results clearly indicate the high accuracy of the proposed relations regarding the increasing rate in the strength of the stiffened shear panel with the arbitrary number of horizontal or vertical stiffeners.

Conclusions

The results indicated that the unstiffened thin steel plate shear wall possessed a high ductility. Also, the lateral load-carrying capacity of the wall increased due to adding stiffeners and limiting different displacements and out-of-plane deformations, as well as the enhanced stiffness of the structure. The results indicated that there is a special upper bound for the number of horizontal and vertical stiffeners in the stiffening process of a specific panel. Addition of stiffeners beyond the allowed value had no significant effect on enhancing the stiffness and strength of the panel, and only increased the weight of the panel and executive problems. Investigations of the present paper introduced the number 7 for horizontal and vertical stiffeners, as the valid range for using the proposed relation for the percentage increase in strength and stiffness. The results revealed that horizontal stiffener was more effective in enhancing the stiffness of the panel than vertical stiffener was. However, the effect of adding whether horizontal and vertical stiffeners on the strength rise was almost the same. In other words, if the goal is to enhance the stiffness of the panel with a stiffener, this should be horizontal. The results also suggested that achieving simple relations is possible to calculate the stiffness and strength of a stiffened panel from an unstiffened panel. Comparison of the error rate obtained using the simplified relations of the percentage increase in strength (Relation 12) instead of the corresponding exact relation (Relations 11) indicated that the use of the simplified relation was very useful where the recorded error was negligible (less than 2.65%) in all models.