Short-term deflection of RC beams using a discrete rotation approach

Abstract

Quantifying the deflection of RC beams has been performed traditionally using full-interaction moment–curvature methods without considering the slip that takes place between the reinforcement and the surrounding concrete. This was commonly carried out by deriving empirically based flexural rigidities and using elastic deflection equations to predict the deformation of RC structures. However, as flexural and flexural/shear cracks form in RC beams with increase in applied load, the reinforcement steel begins to slip against the surrounding concrete surface causing the cracks to widen and ultimately increasing the deflection at mid-span. Current design rules cannot cope directly with the deformation induced by the widening of cracks. Because of that, this study focused on predicting the non-time dependent deflection of RC beams at both service and ultimate limit states using a mechanics-based discrete rotation approach. The mechanics-based solution was compared with experimental test results and well-established code methods to which a good agreement between the results was observed. The method presented accounts for the non-linear behavior of the concrete in compression, the partial-interaction behavior of the reinforcement, and the deflection was computed while considering the rotation of discrete cracks. Due to its generic nature, the method presented does not require any calibration with experimental findings on the member level, which makes it appropriate to quantify the deflection or RC structures with different types of concrete and novel reinforcement material.

Introduction

The deflection of RC structures is an important part of the serviceability design as it often controls member sizes. Furthermore, the determination of the non-linear deflection is an important indication to the ductility of RC structures and their ability to absorb energy. Much of the previous work on calculating the deformation of RC beams and slabs have adopted full-interaction moment–curvature methods (Branson 1965; Bischoff 2005; Castel et al. 2006; Bischoff 2007; Gilbert 2007); that is, they did not consider the slip between the reinforcement bars and the surrounding concrete surface. The moment–curvature analysis was used to derive cracked and uncracked flexural rigidities which were later calibrated with test data (Branson 1965, 1977). This full-interaction approach has been used as the basis for measuring the deformation of RC members in many design codes (CEN 1992; ACI (American Concrete Institute) 2005). Being empirically based, the method does not account for the deflection associated with crack widening; therefore, predicting the deformation of RC members with new reinforcement materials using Branson’s approach will require the calibration of a large number of laboratory tests before being used with confidence. This could prove to be both time consuming and very costly, and hence could halt the development of novel materials in the construction industry.

With the formation of cracks in RC structures, sliding or slip between the reinforcement bars and surrounding concrete surface takes place to release strain concentrations at the crack (Oehlers et al. 2005, 2014a, b, 2017; Ayesha Siddika et al. 2019). These cracks continue to widen through slip, and the widening of individual cracks in RC flexural members causes the mid-span deflection to increase (Bachmann 1970). Significant research on the topic has followed to quantify the deflection induced by flexural and flexural/shear cracks in RC structures. For example, the tensile region of the beam was idealized by an RC prism subjected to tensile force at the center and the bondstress–slip behavior between the steel reinforcement bars and adjacent concrete was subsequently quantified (CEB 1992; Haskett et al. 2008). The concrete prism was examined both experimentally (Tastani and Pantazopoulou 2010) and theoretically (Yankelevsky et al. 2008). This has allowed researchers to quantify tension stiffening behavior of the reinforcement steel (Haskett et al. 2009b; Muhamad et al. 2011, 2012). This progress in research has inspired several researchers to quantify the deflection associated with the discrete rotation of cracks using a rigid-body moment-rotation analysis at a crack (Haskett et al. 2009a; Muhamad et al. 2013; Oehlers et al. 2013) and using a segmental moment-rotation analysis (Visintin et al. 2013, 2016; El-Zeadani et al. 2019a, b). In all these mechanics-based approaches, the deflection was measured under service loads and the concrete in compression was idealized as linear elastic.

Consider the unconfined concrete cylinder of length L_pr and width d_pr subjected to compressive axial stress, σ_ax, shown in Fig. 1. Initially, the concrete cylinder behaves elastically and the stress–strain curve follows the elastic line depicted in Fig. 2, which is a material property independent of the size of the concrete cylinder. However, after the strain in the concrete reaches ε_mat at point A in Fig. 2, gradual sliding and crack widening of the potential wedge in Fig. 1 take place. This causes divergence from the elastic line as the stress increases indicating the beginning of softening and which continues until reaching the maximum unconfined concrete strength, f_co, at point B. After that, greater softening takes place as the stress–strain relationship follows the linear descending branch. Moreover, it is well recognized that the concrete’s stress–strain behavior under compression is affected by the method of measuring the strain, and the shape of the concrete cylinder (Jansen and Shah 1997; Chen et al. 2013, 2015), given as

Fig. 1

Unconfined concrete cylinder in compression

Fig. 2

Concrete stress–strain relationship

$$\mu = \frac{{L_{\text{pr}} }}{{d_{\text{pr}} }}.$$

(1)

Furthermore, the concrete’s stress–strain behavior depends on the size of the specimen as well, defined as the ratio of the prism lengths, given as:

$$\eta = \frac{{L_{{{\text{pr}} - 1}} }}{{L_{{{\text{pr}} - 2}} }},$$

(2)

where L_pr−1 and L_pr−2 are the lengths of cylinders 1 and 2, respectively. For instance, it has been shown that when is greater than 2, the concrete strength f_c hardly varies with increase in length and the strength can be considered independent of the size factor. However, as the length of the concrete specimen increases, the strain corresponding to the peak stress and the concrete strain on the descending branch of the stress–strain relationship reduce; that is, the strain of the concrete in compression is affected by the size factor, (Chen et al. 2013). This made it clear that various zones control the behavior of concrete in compression, and both energy methods (Shah and Sankar 1987; Jansen and Shah 1997) and shear friction methods (Haskett et al. 2010, 2011) were developed to quantify the compression behavior in large deformation zones.

The overall contraction of the cylinder D_ax in Fig. 1 is attributable to: (1) the elastic material strain, ε_mat, which does not depend on the size factor; and (2) the effective strain, ε_eff, caused by the sliding of the concrete wedge shown as H_wdg in Fig. 1. It is the effective strain that causes the strain to be size-dependent, and, therefore, should be incorporated in the design of reinforced concrete structures. Using shear-friction theory, Chen et al. (2013, 2015) developed strain adjustment factors for directly converting the strain of a particular test specimen of length L_pr−1 to that of length L_pr−2, and it is given by following expression:

$$\varepsilon_{{{\text{axgl}} - 2}} = \left[ {\varepsilon_{{{\text{axgl}} - 1}} - \varepsilon_{\text{mat}} } \right]\frac{{L_{{{\text{pr}} - 1}} }}{{L_{{{\text{pr}} - 2}} }} + \varepsilon_{\text{mat}} ,$$

(3)

where ε_axgl−1 and ε_axgl−2 are the axial global strain for concrete cylinders 1 and 2, respectively. Equation (3) can be plotted as in Fig. 3 where L_pr−1/L_pr−2 represents the size factor . For instance, L_pr−1 could be the size of a standard 200 mm cylinder (shape factor μ > 2) of which the stress–strain relationship is shown by the stress–strain curve marked η = 1 in Fig. 3. Doubling the length of the cylinder to say 400 mm (L_pr−1 = 200 mm and L_pr−2 = 400 mm) gives a shape factor η = 1/2 and from Fig. 3, it can be seen that despite having the same strength f_c, the ductility of the 400 mm cylinder is much lower than the 200 mm one. Further doubling the cylinder again to 800 mm would give the stress–strain curve marked η = 1/4.

Fig. 3

Concrete size-dependent stress–strain relationship

With all that in mind, the aim of this study is to present a generic mechanics-based discrete rotation approach for predicting the non-time dependent mid-span deflection of RC beams in bending at all limit states (both service and ultimate). This is carried out by first performing a segmental moment-rotation analysis that incorporates the size-dependent stress–strain relationship of concrete, the softening of the concrete in compression, and the slip between the reinforcement steel and adjacent concrete. After that, the discrete rotation of individual cracks is determined and used to compute the deflection at mid-span. The deflection results obtained from the discrete-rotation mechanics-based approach are then compared with experimental test results and well-established code methods for steel-reinforced RC beams (CEN 1992; ACI (American Concrete Institute) 2005). The approach presented here does not require calibration with empirical findings; thus, it may be used to predict the deflection of RC structures with new types of reinforcement material or refine existing design rules and methods.

Segmental moment-rotation analysis

The first step to determine the non-time-dependent deflection is to perform a segmental moment-rotation analysis as depicted in Fig. 4. A moment M causes the sides of the segment to rotate from G–G to H–H by an angle θ as given in Fig. 4a. The stress–strain relationship for the concrete in compression can be predicted using Popovics (1973) expression given as

Fig. 4

Segmental moment-rotation analysis: a segment of an RC beam subjected to a constant moment; b RC beam section; c concrete prism

$$\sigma_{\text{ax}} = \frac{{f_{\text{co}} \left[ {\frac{{\left( {\varepsilon_{\text{ax}} } \right)_{200} }}{{\varepsilon_{\text{co}} }}} \right]r}}{{r - 1 + \left[ {\frac{{\left( {\varepsilon_{\text{ax}} } \right)_{200} }}{{\varepsilon_{\text{co}} }}} \right]^{r} }},$$

(4)

where σ_ax is the axial stress, f_co is the unconfined compressive strength, ε_co is the concrete strain corresponding to the peak stress of unconfined concrete determined as (Chen et al. 2013)

$$\varepsilon_{\text{co}} = 4.76 \times 10^{ - 6} f_{\text{co}} + 2.13 \times 10^{ - 3} ,$$

(5)

where f_co is in MPa. Furthermore, (ε_ax)₂₀₀ in Eq. (4) is the axial strain of a 100 × 200 mm cylinder, and r is a ductility factor taken as

$$r = \frac{{E_{\text{c}} }}{{E_{\text{c}} - \frac{{f_{\text{co}} }}{{\varepsilon_{\text{co}} }}}},$$

(6)

where E_c is the concrete’s elastic modulus. Equation (4) applies to a concrete segment where L_pr is equal to 200 mm. However, when the size of the concrete segment is greater or less than 200 mm, the size-dependent strain can be computed using Eq. (3) which can be rewritten as follows where L_pr−1 = 200 mm:

$$\varepsilon_{\text{axgl}} = \left[ {\left( {\varepsilon_{\text{ax}} } \right)_{200} - \varepsilon_{\text{mat}} } \right]\frac{100}{{L_{\text{def}} }} + \varepsilon_{\text{mat}} ,$$

(7)

of which, L_def is half the length of the RC beam segment depicted in Fig. 4a. If stirrups are present in the RC beam, the confinement effect can be determined in line with Chen et al. (2015). For example, the peak concrete stress, f_cc, and the strain corresponding to the peak concrete stress, ε_cc, for a confined concrete segment can be computed as follows:

$$f_{\text{cc}} = f_{\text{co}} \left[ {1 + 3.65 \left( {\frac{{\sigma_{\text{con}} }}{{f_{\text{co}} }}} \right)^{0.82} } \right],$$

(8)

$$\varepsilon_{\text{cc}} = \varepsilon_{\text{co}} \left[ {1 + 14.74 \left( {\frac{{\sigma_{\text{con}} }}{{f_{\text{co}} }}} \right)^{1.03} } \right],$$

(9)

where σ_con is the confinement stress provided by stirrups given as:

$$\sigma_{\text{con}} = \frac{{n_{\text{leg - link}} (f_{\text{y - link}} )(A_{\text{link}} )}}{{b \left( {S_{\text{link}} } \right)}},$$

(10)

of which, f_y-link is the yield stress of the steel links, A_link is the sectional area of the links, b is the width of the beam, S_link is the spacing between links and n_leg-link is the number of legs of the steel link (e.g. 2 legs or 3 legs). Similarly, the stress–strain relationship for a 200-mm confined concrete segment can be plotted using Popovics’ (1973) expression given by Eq. (4) and the size-dependent strain can be determined using Eq. (7).

As for the reinforcement steel, the stress–strain relationship can be idealized as given in Fig. 5. The behavior initially follows an elastic response with a Young’s modulus E_r up to the yield stress f_y at a strain ε_y. For strains greater than ε_y, the stress in the steel reinforcement follows a strain hardening modulus E_sh up to the fracture stress σ_fract. Furthermore, to represent the local deformations of the steel reinforcement, the ascending branch of the CEB-FIP bondstress–slip model depicted in Fig. 6 (CEB 2010) can be used.

Fig. 5

Idealized bi-linear stress–strain relationship

Fig. 6

CEB-FIP bondstress–slip relationship for steel reinforcement

The steel reinforcement’s tension stiffening behavior can be determined from a concentrically loaded concrete prism of width b and height 2c as shown in Fig. 4c. The area of the reinforcement in the concrete prism, A_r, is equivalent to total area of the reinforcement steel in the tensile region of the RC beam shown in Fig. 4b. In a similar way, the perimeter of the reinforcement bar in the concrete prism, L_p, is equivalent to the total perimeter of all the reinforcement bars in the tensile region of the RC beam (El-Zeadani et al. 2019a, c). This assumption gives fairly accurate results as long as all the tension reinforcements in the beam have the same bondstress–slip properties (Oehlers et al. 2015). A span of the prism in Fig. 4c is illustrated in Fig. 7a where the position of the initial crack occurs at the left of the prism, while the full-interaction boundary occurs slightly to the right at a distance S_p from the crack face. As the load P_r increases, the concrete tensile stress increases as well until the concrete tensile strength f_ct is reached at a distance S_p from the initial crack by which a new crack forms. After that, the behavior of the concrete prism shifts to that of a prism with multiple cracks (Fig. 7b) such that zero slip is presumed to take place mid-way between the cracks.

Fig. 7

Tension stiffening mechanism

The moment-rotation analysis is performed on a segment of length, L_pr, equal to 2S_p as given in Fig. 4a. The primary crack spacing distance S_p is determined using the following closed-form solution given by Muhamad et al. (2012) which was derived following the CEB-FIP bondstress–slip model shown in Fig. 6:

$$S_{\text{p}} = \left[ {\frac{{\left( {1 + \varphi } \right)f_{\text{ct}} A_{\text{c}} \delta_{1}^{\varphi } }}{{\tau_{\hbox{max} } L_{\text{p }} \left( {\sqrt {2C_{9} } } \right)^{\varphi } }}} \right]^{{\frac{1}{1 + \varphi }}} ,$$

(11)

where

$$C_{9} - \frac{{\sqrt {2C_{9} } f_{\text{ct}} A_{\text{c}} \lambda_{2} \delta_{1}^{\varphi } }}{{\tau_{\hbox{max} } L_{\text{p }} }} = - 0.5 \left( {\frac{{f_{\text{ct}} }}{{E_{\text{c}} }} + \frac{{f_{\text{ct}} A_{\text{c}} }}{{A_{\text{r}} E_{\text{r}} }}} \right)^{2} ,$$

(12)

$$\lambda_{2} = \frac{{\beta_{2} \tau_{\hbox{max} } }}{{\delta_{1}^{\varphi } }},$$

(13)

$$\beta_{2} = \frac{{L_{\text{p}} }}{{A_{\text{r}} }} \left( {\frac{1}{{E_{\text{r}} }} + \frac{{A_{\text{r}} }}{{E_{\text{c}} A_{\text{c}} }}} \right),$$

(14)

and φ can be as taken as 0.4 (Muhamad et al. 2012) and A_c is the concrete prism cross-sectional area. The segmental moment-rotation analysis is performed as follows while considering the formation of cracks.

Uncracked segmental analysis

Before applying any moment M, the RC segment is uncracked. Only half of the RC segment of length L_def is considered in ensuring analysis due to symmetry (Fig. 8). The first step is to fix the rotation θ; then, the neutral axis depth, d_NA, is guessed. The concrete segment’s curvature, χ, can be computed as follows:

$$\chi = \frac{\theta }{{L_{\text{def}} }},$$

(15)

where the angle θ is in radians. The strains at the outer most compression and tension fibres are determined, respectively, as follows;

Fig. 8

Uncracked concrete segmental analysis

$$\varepsilon_{{{\text{c}} - {\text{c}}}} = \chi d_{\text{NA}} ,$$

(16)

$$\varepsilon_{{{\text{c}} - {\text{t}}}} = \chi (h - d_{\text{NA}} ).$$

(17)

As for the strain in the compressive and tensile reinforcement, they are given by

$$\varepsilon_{\text{rc}} = \chi d_{\text{rc}} ,$$

(18)

$$\varepsilon_{\text{rt}} = \chi d_{\text{rt}} ,$$

(19)

where d_rc and d_rt are as shown in Fig. 8.

The concrete in compression tends to behave elastically at the start of loading and a triangular stress distribution as illustrated in Fig. 8d can be assumed to take place. Similarly, a triangular stress distribution can be assumed for the concrete in tension and the forces acting across the section can be computed accordingly. The concrete compressive force P_cc occurs at 1/3 d_NA from the top compression fibre, while the concrete tensile force P_ct occurs at 1/3 (h − d_NA) from the bottom tensile fibre. The force profile is given in Fig. 8e. The value of d_NA is guessed until force equilibrium is achieved for a particular rotation θ. After that, the moment of the section can be computed from the force profile. The procedure is then repeated for a different rotation, θ, and when the concrete tensile strength, f_ct, is first achieved in the bottom tensile fibre of the concrete segment, a crack forms as shown in Fig. 9a. The moment at which the tensile strength is first achieved is known as the full-interaction cracking moment, M_cr-FI.

Fig. 9

Single crack concrete segmental analysis

Single crack segmental analysis

After the formation of the first crack, partial-interaction (slip) takes place such that the tensile part of the concrete segment can be idealized as an infinitely long prism (Fig. 7a). The slip of the reinforcement steel can be calculated as follows:

$$\Delta_{\text{r}} = \theta d_{\text{rt}} .$$

(20)

Partial-interaction closed-from solutions can be used to determine the load in the reinforcement for a given reinforcement slip Δ_r. For instance, while still elastic, the force in the reinforcement steel is given by (Muhamad et al. 2012)

$$P_{\text{r}} = A_{\text{r}} E_{\text{r}} \sqrt {\frac{{2 \lambda_{2} \Delta_{\text{r}}^{1 + \varphi } }}{1 + \varphi }} .$$

(21)

However, when the reinforcement steel yields, the force can be determined using the following expression:

$$P_{\text{r}} = A_{\text{r}} E_{\text{sh}} \sqrt {\frac{{2 \lambda_{\text{sh}} \left( {\Delta_{\text{r}} - \Delta_{\text{y}} } \right)^{1 + \varphi } }}{1 + \varphi }} + A_{\text{r}} f_{\text{y}} ,$$

(22)

where

$$\lambda_{\text{sh}} = \frac{{\beta_{\text{sh}} \tau_{\rm{max} } }}{{\delta_{1}^{\varphi } }},$$

(23)

$$\beta_{\text{sh}} = \frac{{L_{\text{p}} }}{{A_{\text{r}} }} \left( {\frac{1}{{E_{\text{sh}} }} + \frac{{A_{\text{r}} }}{{E_{\text{c}} A_{\text{c}} }}} \right),$$

(24)

and Δ_y in Eq. (22) can be determined using the following expression:

$$\frac{{\lambda_{2} \Delta_{\text{y}}^{1 + \varphi } }}{1 + \varphi } = 0.5 \left( {\frac{{f_{\text{y}} }}{{E_{\text{r}} }}} \right)^{2} .$$

(25)

As for the concrete in compression and prior to softening, a triangular stress distribution applies (Fig. 9d). The concrete compressive force, P_cc, occurs at a distance 1/3 d_NA from the top compression fibre and the force profile is similar to that in Fig. 9e. On the other hand, when the concrete in compression softens, Simpson’s rule for determining the area and centroid of an irregular shape can be used to compute the force exerted by the softened concrete. First of all, the area under the stress diagram that is within the softening zone is divided into an even number of segments of width s as shown in Fig. 10b. The strain at the end of each segment is determined by simply multiplying the curvature χ by the distance from the neutral axis for the respective segment end. Next, using the concrete’s size-dependent stress–strain relationship, obtained from Eqs. (4) and (7), the stress at the end of each segment can be measured. After that, the force due to the softened concrete can be computed as follows assuming that the softening zone in Fig. 10b has been divided into six segments:

$$P_{\text{soft}} = b \times \frac{s}{3} \times \left[ {\left( {\sigma_{6} + \sigma_{\text{mat}} } \right) + 4\left( {\sigma_{1} + \sigma_{3} + \sigma_{5} } \right) + 2\left( {\sigma_{2} + \sigma_{4} } \right)} \right],$$

(26)

which acts at a distance d_soft from the neutral axis equal to

Fig. 10

Simpson’s rule for determining the softening force

$$\begin{aligned} d_{\text{soft}} &= \frac{b \times s}{{3 P_{\text{soft}} }} \times \left[ {\left( {\sigma_{6} d_{6} + \sigma_{\text{mat}} d_{\text{mat}} } \right) }\right.\\&\quad\left.{+ 4\left( {\sigma_{1} d_{1} + \sigma_{3} d_{3} + \sigma_{5} d_{5} } \right) + 2\left( {\sigma_{2} d_{2} + \sigma_{4} d_{4} } \right)} \right]. \end{aligned}$$

(27)

As for the concrete in the elastic zone (below the softening zone), a triangular stress distribution is assumed and the force P_mat acts at 2/3 d_mat from the neutral axis. The force profile when softening occurs is shown in Fig. 9j. Again, force equilibrium is first determined for a particular rotation θ by guessing d_NA; after which, the moment M is calculated. Consequently, the rotation θ is altered and the whole procedure is repeated again. The single crack segmental analysis is continued until the force in the reinforcement, P_r, exceeds the force to cause additional primary cracks, $F_{{{\text{r}}\_{\text{cr}}\_{\text{p}}}}$ given as (Muhamad et al. 2012)

$$F_{{{\text{r}}\_{\text{cr}}\_{\text{p}}}} = \frac{{f_{\text{ct}} }}{{E_{\text{c}} }}A_{\text{r}} E_{\text{r}} + f_{\text{ct}} A_{\text{c}} .$$

(28)

At this point, a new crack forms at a distance S_p as shown in Fig. 11a and the tensile region of the concrete segment is idealized as that in Fig. 7b. The analysis is continued as follows.

Fig. 11

Multiple crack concrete segmental analysis

Multiple crack segmental analysis

When multiple cracks form, the total displacement of the RC beam segment is as given in Fig. 11b. The total rotation θ of the segment is nθ_i, where n is the number of crack faces and θ_i is the rotation of each individual crack face. In Fig. 11a, the total number of crack faces is 2 (n = 2). The total reinforcement pull-out Δ_r is equal to nΔ_r−p where Δ_r−p is the pull-out at each crack face. Again, partial-interaction closed-form solutions can be established for the prism in Fig. 7b to determine the load–slip relationship based on the appropriate boundary conditions. For example, prior to yielding, the force in the reinforcement steel can be computed using the following expression:

$$P_{{{\text{r}}\_ {\text{p}}}} = A_{\text{r}} E_{\text{r}} \sqrt {\frac{{2 \lambda_{2} \Delta_{{{\text{r}}\_{\text{p}}}}^{1 + \varphi } }}{1 + \varphi } + \left( {\frac{{\Delta_{{{\text{r}}\_ {\text{p}}}} }}{{S_{\text{s}} }}} \right)^{2} } ,$$

(29)

where S_s is S_p/2. When yielding of the reinforcement takes place, the force is determined by

$$P_{{{\text{r}}\_ {\text{p}}}} = A_{\text{r}} E_{\text{sh}} \sqrt {\frac{{2 \lambda_{\text{y}} \left( {\Delta_{{{\text{r}}\_ {\text{p}}}} - \Delta_{{{\text{y}}\_{\text{p}}}} } \right)^{1 + \varphi } }}{1 + \alpha } + \left( {\frac{{\Delta_{{{\text{r}}\_ {\text{p}}}} - \Delta_{{{\text{y}}\_{\text{p}}}} }}{{S_{\text{s}} }}} \right)^{2} } + A_{\text{r}} f_{\text{y}} ,$$

(30)

where

$$\frac{{\lambda_{2} \Delta_{{{\text{y}}\_{\text{p}}}}^{1 + \varphi } }}{1 + \alpha } + 0.5\left( {\frac{{\Delta_{{{\text{y}}\_{\text{p}}}} }}{{S_{\text{s}} }}} \right)^{2} = 0.5 \left( {\frac{{f_{\text{y}} }}{{E_{\text{r}} }}} \right)^{2} .$$

(31)

As for the concrete in the compression zone, the analysis follows as before; that is, if the concrete has not softened yet, the force profile is similar to that displayed in Fig. 11d, and similar to that in Fig. 11f if the concrete has already softened. Furthermore, the moment M for a particular rotation θ is determined when force equilibrium is achieved.

Limits to the moment-rotation analysis

The moment-rotation analysis is stopped when either (a) the concrete in compression reaches its sliding capacity, S_slide, (b) the reinforcement debonds when the slip exceeds the maximum debonding slip, δ_max or (c) the reinforcement fractures when the strain in the reinforcement reaches the fracture strain, ε_fract, whichever occurs first. The moment M at which one of these limits is achieved is the ultimate moment capacity of the RC beam segment.

Sliding of the concrete in compression, Δ_wdg, can be determined from the size-dependent stress–strain relationship and is given as follows:

$$\Delta_{\text{wdg}} = \varepsilon_{\text{wdg}} L_{\text{def}} ,$$

(32)

where

$$\varepsilon_{\text{wdg}} = \varepsilon - \varepsilon_{\text{mat}} .$$

(33)

Both Mattock and Hawkins (1972) and Martinez et al. (1984) have suggested that the sliding capacity, S_slide for unconfined concrete is approximately 0.4 mm. However, confinement due to stirrups further increases the sliding capacity of concrete wedges and Haskett et al. (2009a) give the sliding capacity as

$$S_{\text{slide}} = 2.51 \frac{{\sigma_{\text{con}} }}{{f_{\text{co}} }} + 0.61.$$

(34)

Discrete rotation deflection analysis

Under the discrete rotation approach, the RC beam is separated into two regions: (a) an uncracked region of length 2L_u and (b) a cracked region of length L_cr as illustrated in Fig. 12b (Muhamad et al. 2013; Oehlers et al. 2013; El-Zeadani et al. 2019a, b). The deflection of the beam due to the uncracked region is determined by integrating the curvature along L_u, where full interaction can be expected to take place. Meanwhile, the deflection caused by the cracked portion of the beam can be computed by considering the discrete rotation of each individual crack.

Fig. 12

Discrete rotation deflection: a moment; b crack formation; c deflection due to a single crack

Deflection due to discrete rotation

At the start of loading, the beam is uncracked; however, once the moment in the beam reaches M_cr-FI determined from the uncracked segmental analysis, a crack forms (shown by the initial crack in Fig. 12b. Subsequent cracks at distance S_p from the previous crack continue to take place once the moment reaches M_cr-FI. Now, consider crack B in Fig. 12c subjected to moment M_B. The rotation of each crack face can be determined from the appropriate M–θ relationship. The sum of both crack face rotations gives the total rotation of crack B shown as 2θ_B in Fig. 12c. The mid-span deflection caused by crack B can be predicted from the geometry of the shape in Fig. 12c and is given as follows:

$$\delta_{\text{mid}} = \, L_{\text{L}} \theta_{\text{B}} .$$

(35)

The procedure described for crack B needs to be repeated for each individual crack to determine the contribution of each discrete crack to the total deflection of the beam. An important thing to note while computing the rotation of the flexural cracks is to use the correct M–θ relationship. For instance, consider crack A shown in Fig. 12b, which has no cracks to its left; henceforth, the left face of the crack is idealized as an infinitely long prism with a single crack and its rotation, that is θ_A−L, is determined from a M–θ relationship developed using a concrete segment with a single crack. Meanwhile, crack B is present to the right of crack A; hence, the rotation of the right face of crack A, that is θ_A−R, is determined from a M–θ relationship developed from a multiple crack segmental analysis. As for crack C, and since cracks are present to its right and left, the rotation of both crack faces can be determined from a M–θ relationship developed using a concrete segment with multiple cracks. Therefore, it might be convenient to plot the M–θ relationships for a segment with a single crack and multiple cracks separately.

Deflection due to curvature

The deflection of the uncracked portions of the beam can be visualized as that in Fig. 13c and can be determined by simply integrating the curvature along L_u. For a beam subjected to the loading shown in Fig. 13a, the uncracked deflection can be solved using elastic bending theory as follows:

Fig. 13

Deflection due to curvature: a applied load; b RC beam; c curvature deflection

$$\delta_{{\chi_{\text{u}} }} = \frac{w}{{24{\text{EI}}_{\text{uncr}} }} \left( {2LL_{\text{u}}^{3} - L_{\text{u}}^{4} - L^{3} L_{\text{u}} } \right) + \frac{P}{{48{\text{EI}}}} \left( {4L_{\text{u}}^{3} - 3L^{2} L_{\text{u}} } \right).$$

(36)

Validation with experimental results

Three reinforced concrete beams that included both longitudinal and shear reinforcement were casted and tested in the laboratory until failure to determine the load–deflection response and to validate the results from the discrete rotation approach. Furthermore, an additional six reinforced concrete beams having different dimensions and different material properties as reported by previous researchers were also used to validate the deflection results obtained from the discrete rotation approach.

Beam specimen details

The RC beams tested in this study, named RC-B1, RC-B2 and RC-B3, were chosen as in Fig. 14. The width of the beams, b, was set to 200 mm and the height of the beams, h, was kept at 300 mm. The distance between the supports was 3500 mm and the total length of the beams was 3600 mm. The beams had both tensile and compressive steel reinforcement. The tensile reinforcement bars were 16 mm in diameter, while the compressive reinforcement bars were 12 mm in diameter. Furthermore, to tie the longitudinal reinforcement together and to resist the shear force, 8 mm diameter mild-steel shear links with two legs were spaced at 150 mm along the length of the beam. The cover to the shear links was set to 30 mm.

Fig. 14

RC-B1, RC-B2, RC-B3 details: a section; b test setup

In addition, four simply supported reinforced concrete beams tested by Gilbert and Nejadi (2004) were also considered. Two of the beams, named B1-a and B1-b, had cross-sectional dimensions as depicted in Fig. 15a where the width, b, was 250 mm and the height, h, was 348 mm. Both B1-a and B1-b had two 16 mm diameter tensile reinforcement where the concrete cover was maintained at 40 mm. Meanwhile, the other two beams, named B2-a and B2-b, had cross-sectional dimensions as given in Fig. 15b, where the width, b, was 250 mm and the height, h, was 333 mm. The diameter of the tensile reinforcement was kept the same at 16 mm, while the concrete cover was set to 25 mm. The four beams had an effective span of 3500 mm as shown in Fig. 15c.

Fig. 15

Gilbert and Nejadi (2004) RC beam details: a B1-a, B1-b; b B2-a, B2-b; c test setup

Lastly, two ordinary RC beams tested by Alagusundaramoorthy et al. (2003) were also taken into account for the purpose of comparison and validation. The beams, named CB1 and CB2, are depicted in Fig. 16a, where the cross-sectional dimensions were set as 230 × 380 mm (b × h). The reinforcement steel consisted of two 25 mm diameter rebars in the tensile region, and two 9 mm diameter rebars in the compression region. The beams had 9 mm diameter shear links spaced at 150 mm as given in Fig. 16b. The concrete cover to the tensile and compressive rebars were 38 mm and 25 mm, respectively. The overall length of the beams was 4880 mm, while the span between the supports was kept at 4576 mm.

Fig. 16

Alagusundaramoorthy et al. (2003) RC beam details: a section; b test setup

Material properties

The concrete material properties were determined using concrete cylindrical specimens with a diameter-to-height ratio of 1:2. The mean unconfined concrete compressive strength, f_co, was determined in accordance with ASTM C39/C39M standard, while the elastic modulus of concrete, E_c, and the splitting tensile strength, f_tsp, were determined in line with ASTM C469/C469M and ASTM C496/C496M test methods, respectively. The unconfined mean concrete cylinder strength, f_co, was 22.7 MPa, the elastic modulus of concrete, E_c, was 22,717 MPa, while the splitting tensile strength, f_tsp, was 2.8 MPa. As for the reinforcement steel, the mechanical properties were determined in the laboratory using a rebar tensile test in accordance with ASTM A370 test procedure. The elastic modulus, E_r, was 154 GPa, while the strain hardening modulus, E_sh, was 1.57 GPa. The yield strength, f_y, for the steel reinforcement was 535 MPa, while the fracture tensile strength σ_fract was 615 MPa. As for the shear links, the yield strength, f_y-link, was given by the supplier as 250 MPa.

As for B1-a, B1-b, B2-a and B2-b tested by Gilbert and Nejadi (2004), the unconfined compressive strength, f_co, was 36.3 MPa, the splitting tensile strength, f_tsp, was 3.06 MPa, the elastic modulus of concrete, E_c, was 26,930 MPa and the elastic modulus of the reinforcement steel, E_r, was 200 GPa. As for CB1 and CB2 reported by Alagusundaramoorthy et al. (2003), the concrete compressive strength, f_co, was 31 MPa, the yield strength of the reinforcement steel, f_y, was 414 MPa and the elastic modulus of the reinforcement steel, E_r, was 200 GPa.

Experimental setup

RC-B1, RC-B2 and RC-B3 were simply supported as depicted in Fig. 17a–c. A hydraulic jack was used to apply a point load at mid-span as shown in Fig. 17d, where for the first 10 kN, the load was applied in 2 kN increments, after that, the load was applied in 5 kN increments until failure. To measure the deflection, a linear variable differential transducer (LVDT) was placed at mid-span under the applied load as shown in Fig. 17e. In addition, two strain gauges were fixed to the tensile steel reinforcement at the center of the beam as depicted in Fig. 14b to record the strains as the test proceeded. Meanwhile, for B1-a, B1-b, B2-a and B2-b, the beams were subjected to a four-point flexural bending and the load was applied at 1167 mm from the support as shown in Fig. 15c. Similarly, CB1 and CB2 were tested under four-point flexural bending with the applied load being 1830 mm away from the supports as illustrated in Fig. 16b. The deflection of the beams was recorded using an LVDT placed at mid-span.

Fig. 17

RC-B1, RC-B2 and RC-B3 experimental setup

Test results and discussion

The experimental results for the beams considered in this study are reported here and compared with those derived from the mechanics-based approach.

Mid-span reinforcement steel strain results

For RC-B1, RC-B2 and RC-B3, the reinforcement bars strain results against the applied mid-span load, P, are shown in Fig. 18. For each beam, the tensile reinforcement had two strain gauges fixed at mid-span, and the experimental results were recorded by the strain gauges marked SG1 and SG2 in Fig. 18; whereas the theoretical strain results were derived using the segmental moment-rotation analysis. From Fig. 18a, c, a significant agreement between the experimental and the theoretical strains was observed. The reinforcement bars yielded at an applied load, P, of approximately 55 kN, and the slope of the elastic response and the strain hardening response from the experimental and theoretical results were almost identical. RC beam 2 was an anomaly as yielding occurred at a higher applied load of about 61 kN as illustrated in Fig. 18b.

Fig. 18

Strain in reinforcement steel: a RC-B1; b RC-B2; c RC-B3

Crack spacing

As the discrete rotation approach accounts for the formation of additional flexural cracks while computing the deflection of the beams, a comparison between the experimental and theoretical crack spacing values would be helpful to ensure the validity of the proposed approach. During testing of the RC beams, flexural cracks were marked after each load increment until failure of the beams took place. After unloading the beams, the distance between two consecutive primary cracks was measured in the laboratory from center-to-center of the crack opening at the level of the reinforcement. The primary crack spacing results are given in Table 1, while the development of cracks and the crack patterns in RC-B1, RC-B2 and RC-B3 as the load on the beams increased are given in Figs. 19, 20, and 21, respectively.

Table 1 RC beams primary crack spacing values

Fig. 19

RC-B1 crack development pattern

Fig. 20

RC-B2 crack development pattern

Fig. 21

RC-B3 crack development pattern

Furthermore, Table 2 highlights the number of cracks that took place in the beams together with the minimum crack spacing, S_exp-min, maximum crack spacing, S_exp-max, mean crack spacing, S_exp-mean and theoretical crack spacing, S_p, given by Eq. (11). Apparently, the experimental mean crack spacing results for the RC beams were slightly higher than the theoretically predicted crack spacing values. However, the difference was not significant and it can be deduced that Eq. (11) gives a good approximation of the spacing of cracks in RC beams.

Table 2 Summary of crack spacing results for RC-B1, RC-B2 and RC-B3

Mid-span deflection

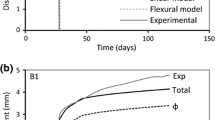
The beams’ short-term discrete rotation deflection results together with the experimental results are given in Fig. 22. The deflection results for RC-B1, RC-B2, RC-B3, CB1 and CB2 were considered until failure, while for the remaining beams, the results were stopped just prior to yielding of the reinforcement steel. Furthermore, the mid-span deflection results obtained from ACI-318 code of practice effective moment of inertia method (ACI (American Concrete Institute) 2005) and EC 2 code deflection prediction technique (CEN 1992) were also considered and are shown in Fig. 22.

Fig. 22

Mid-span deflection results

From the discrete rotation analysis, only primary cracks took place for all the beams considered and the step changes in the load–deflection response indicate the formation of additional primary cracks. This is illustrated clearly in Fig. 23 which gives the discrete rotation deflection results for RC-B1, RC-B2 and RC-B3 up to a load of 15 kN. The horizontal portions on the load–deflection response in Fig. 23 are caused by the slip induced when new cracks form; whereas, the rising portions of the load–deflection response indicate the increase in deflection with increase in load. Furthermore, if the RC beams were cracked before loading due to damage or shrinkage, the load–deflection response follows line O–B–C in Fig. 23 when one crack is present and line O–D–E if three cracks are present prior to loading. This explains the early discrepancy between the theoretical and experimental results seen in RC-B1, RC-B2 and RC-B3 as seen in Fig. 22a, b, which could be due to the presence of small cracks prior to loading. This discrepancy is almost eliminated for the other beams considered in this study.

Fig. 23

Development of cracks in the discrete rotation approach for RC-B1, RC-B2 and RC-B3

Table 3 displays the experimental and theoretical failure loads and their corresponding mid-span deflection for RC-B1, RC-B2, RC-B3, CB1 and CB2. The theoretical failure load, P_u-theo, was determined from the moment-rotation segmental analysis as described in “Limits to the moment-rotation analysis” when one of the limits was first achieved. In all of the beams considered, tension failure by excessive yielding of the steel reinforcement took place and Fig. 24 shows RC-B1, RC-B2 and RC-B3 at failure. From Table 3, it is apparent that the mechanics-based approach presented here gives a fairly good estimate of the failure load. Moreover, a significant agreement between the experimental and theoretical mid-span deflection results exists at failure load as shown in Table 3 for all the beams considered. This further shows the suitability of the discrete rotation approach in predicting the deflection of the beams at failure loads.

Table 3 Mid-span deflections and failure loads of RC beams

Fig. 24

Failure of RC beams: a RC-B1; b RC-B2; c RC-B3

It can be concluded that the discrete rotation approach presented here provides accurate predictions of the deflection of the RC beams at both service and ultimate limit states, and even when the reinforcement steel yields as shown in Fig. 22a, e. In addition, the discrete rotation approach correlates well with existing code methods, especially EC2 code method where the results were often almost identical. In some cases, as in Fig. 22c, d, the discrete rotation approach provided significantly better predictions of the deflection than the ACI code which underestimated the deflection of B1-a, B1-b, B2-a and B2-b. Furthermore, unlike the discrete rotation approach where the formation of cracks was reflected in the load–deflection response, the ACI and EC2 codes deflection results were smooth and did not incorporate the formation and widening of flexural cracks.

Conclusion

This paper presents the results of the application of a discrete rotation approach to predict the load–deflection behavior of RC beams in bending. The approach is based on a segmental moment-rotation analysis that accounts for the slip between the tensile reinforcement bars and the surrounding concrete surface, the softening of the concrete in compression and the size and shape effect of the concrete stress–strain relationship. The mid-span deflection was computed following a discrete rotation approach where the deflection of the beams due to the cracked portion was determined by considering the rotation of each individual crack, whereas the deflection contribution of the uncracked portions was calculated by integrating the curvature along the uncracked length following a full-interaction analysis.

From the findings of this study, it is seen that the discrete rotation approach gives good prediction of the deflection of the beams at all limit states including the post yield deformations. The approach simulates the behavior that is seen in practice as can be seen from the step changes in the load–deflection response when new cracks form. Furthermore, the mechanics-based discrete rotation approach considers the bondstress–slip relationship of the reinforcement steel in the analysis. This makes the solution conducive for different types of bondstress–slip relationships and thereby different reinforcement materials. Moreover, the approach can be used to refine existing design rules by investigating the factors that affect the deformation of RC members.