Free vibration analysis of functionally graded doubly curved shell panels resting on elastic foundation in thermal environment

Abstract

The purpose of the paper is to develop an analytical investigation on free vibration of a simply supported functionally graded (FG) doubly curved shell panels resting on elastic foundation in thermal environment. Heat conduction and temperature-dependent material properties are both taken into account. The temperature field considered is assumed to be a uniform distribution over the shell surface and varied in the thickness direction only. Material properties are assumed to be temperature dependent and graded in the thickness direction according to a simple power law distribution in terms of the volume fractions of the constituents. Based on the first-order shear deformation theory and applying the Hamilton’s principle, governing equations of motion are derived. The results of the study are compared with the available published literature. The numerical results obtained reveal that the material volume fraction index, geometrical parameters and temperature change have significant effects on natural frequencies of the FG doubly curved shell panels.

Introduction

Functionally graded materials (FGMs) have been used in various engineering applications because of their distinctive material properties, which can be altered to satisfy different working environments. Typically, these materials are made from a mixture of ceramic and metal or a combination of different metals. The ceramic constituent provides the high-temperature resistance due to its low thermal conductivity. The ductile metal constituent, on the other hand, prevents fracture caused by stresses due to high-temperature gradient in a very short period of time. Numerous studies on thermo-mechanical characteristics of FGM structures have been carried out to date.

Static and dynamic analyses of functionally graded shells in thermal environment are well established in the existing literature. Kadoli and Ganesan (2006) presented linear thermal buckling and free vibration analysis for functionally graded cylindrical shells with clamped–clamped boundary condition with temperature-dependent material properties. First-order shear deformation theory along with Fourier series expansion of the displacement variables in the circumferential direction are used to model the FGM shell. Shen and Wang (2010) investigated thermo-elastic vibration and buckling characteristics of the functionally graded piezoelectric cylindrical shell using Maxwell equation with a quadratic variation of the electric potential along the thickness direction of the cylindrical shells and the first-order shear deformation theory. Based on Love’s shell theory and the von Karman–Donnell type of kinematic nonlinearity, free vibration analysis of simply supported functional graded cylindrical shells for four sets of in-plane boundary conditions is performed by Haddadpour et al. (2007) using Galerkin’s method. The free vibration analysis of rotating functionally graded (FG) cylindrical shells subjected to thermal environment is investigated based on the first-order shear deformation theory of shells and was reported in the work of Malekzadeh and Heydarpour (2012). Pradyumna and Bandyopadhyay (2010) investigated the free vibration and buckling behavior of functionally graded singly and doubly curved shell panels. A higher-order shear deformation theory is used and the shell panels are subjected to a temperature field. Bhangale et al. (2006) used the first-order shear deformation theory to study the thermal buckling and vibration behavior of truncated functionally graded conical shells in a high-temperature environment by finite element method. Temperature-dependent material properties are considered to carry out a linear thermal buckling and free vibration analysis. Zhao et al. (2009) studied static response and free vibration characteristic of metal and ceramic functionally graded shells using the element-free kp-Ritz method. The displacement field is expressed in terms of a set of mesh-free kernel particle functions according to Sander’s first-order shear deformation shell theory. Wattanasakulpong and Chaikittiratana (2015) presented an investigation of free vibration of stiffened functionally graded doubly curved shallow shells under thermal environment. Two types of temperature rise throughout the shell thickness: linear temperature rise and nonlinear temperature rise are considered. Alijani et al. (2011) studied geometrically nonlinear vibrations of functionally graded doubly curved shells subjected to thermal variations and harmonic excitation via multi-modal energy approach.

However, studies on thermal vibration analyses of functionally graded doubly curved shell panels resting on elastic foundation are very rare in the existing literature. Thus, in this paper, the vibration analysis of simply supported functionally graded doubly curved shells resting on Winkler–Pasternak elastic foundation including thermal effects is performed. The material properties are assumed to be temperature dependent and graded in the thickness direction according to a simple power law function. A first-order shear deformation theory is used for the analysis of two FG panels, namely, cylindrical, spherical, and as special case of plate.

Theoretical formulation

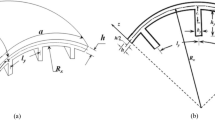
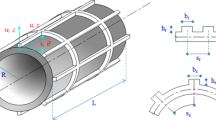
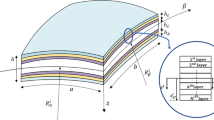
Consider a functionally graded doubly curved panel with length a, width b, and thickness h, referred to an orthogonal curvilinear coordinate system (x, y, z), as shown in Fig. 1. R₁ and R₂ are the radii of principal curvatures of the middle surface in the x-direction and the y-direction, respectively. The elastic material properties vary through the shell thickness according to a simple power law distribution in terms of the volume fractions of the constituents. The top surface (z = h/2) of the shell is assumed to be ceramic rich, whereas the bottom surface (z = − h/2) is assumed to be metal rich. The effective properties of the functionally graded material at any thickness of coordinate z can be expressed by the following power law distribution:

$$P\left( {z,T} \right) = \left( {P_{\text{c}} - P_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} + P_{\text{m}} ,$$

(1)

where p is the volume fraction exponent, P_m and P_c represent the properties of the metal and the ceramic, respectively. The properties of the temperature-dependent constituents of an FGM shell can be expressed as (Bhangale et al. 2006):

$$P\left( T \right) = P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} } \right),$$

(2)

where $P_{0} ,\;P_{ - 1} ,\;P_{1} ,\;P_{2}$ and $P_{3}$ are the coefficients of temperature T(K) and are unique to the constituent materials.

Fig. 1

Coordinate system and geometry of an in-contact doubly curved FGM panel

In this study, Poisson ratio ν is assumed to be constant, Young’s modulus E and thermal expansion coefficient α are assumed to be temperature dependent, whereas the mass density ρ and thermal conductivity $\kappa$ are independent of the temperature (Huang and Shen 2004):

$$E\left( {z,T} \right) = E_{\text{m}} \left( T \right) + \left[ {E_{\text{c}} \left( T \right) - E_{\text{m}} \left( T \right)} \right]\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} ;\quad \kappa \left( z \right) = \kappa_{\text{m}} + \left( {\kappa_{\text{c}} - \kappa_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} ;$$

(3)

$$\alpha \left( {z,\; \, T} \right) = \alpha_{\text{m}} \left( T \right) + \left[ {\alpha_{\text{c}} \left( T \right) - \alpha_{\text{m}} \left( T \right)} \right]\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} ;\quad \rho \left( z \right) = \rho_{\text{m}} + \left( {\rho_{\text{c}} - \rho_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} .$$

It is assumed that temperature variation occurs in the thickness direction only and one-dimensional temperature field is assumed to be constant in the x–y surface of the shell. In such case, the temperature distribution through the thickness of the functionally graded shell can be obtained by solving a steady-state heat transfer equation as follows (Wattanasakulpong and Chaikittiratana 2015):

$$- \frac{\text{d}}{{{\text{d}}z}}\left[ {\kappa_{\text{f}} \frac{{{\text{d}}T}}{{{\text{d}}z}}} \right] = 0.$$

(4)

This equation is solved by imposing boundary conditions of T = T_c at z = h/2 and T = T_m at z= − h/2. The solution of this equation, by means of polynomial series as (Javaheri and Eslami 2002):

$$T\left( z \right) = T_{\text{m}} + \left( {T_{\text{c}} - T_{\text{m}} } \right)\eta \left( z \right),$$

(5)

$${\text{with}}\;\;\eta \left( z \right) = \frac{1}{C}\left[ {\begin{array}{*{20}l} {X - \frac{{\kappa_{\text{cm}} }}{{\left( {p + 1} \right)\kappa_{\text{m}} }}X^{p + 1} + \frac{{\kappa_{\text{cm}}^{2} }}{{\left( {2p + 1} \right)\kappa_{\text{m}}^{2} }}X^{2p + 1} } \hfill \\ { - \frac{{\kappa_{\text{cm}}^{3} }}{{\left( {3p + 1} \right)\kappa_{\text{m}}^{3} }}X^{3p + 1} + \frac{{\kappa_{\text{cm}}^{4} }}{{\left( {4p + 1} \right)\kappa_{\text{m}}^{4} }}X^{4p + 1} - \frac{{\kappa_{\text{cm}}^{5} }}{{\left( {5p + 1} \right)\kappa_{\text{m}}^{5} }}X^{5p + 1} } \hfill \\ \end{array} } \right],$$

(6a)

$$\left\{ {\begin{array}{*{20}l} {X = \left( {\frac{z}{h} + \frac{1}{2}} \right);\quad \kappa_{\text{cm}} = \kappa_{\text{c}} - \kappa_{\text{m}} } \hfill \\ {C = 1 - \frac{{\kappa_{\text{cm}} }}{{\left( {p + 1} \right)\kappa_{\text{m}} }} + \frac{{\kappa_{\text{cm}}^{2} }}{{\left( {2p + 1} \right)\kappa_{\text{m}}^{2} }} - \frac{{\kappa_{\text{cm}}^{3} }}{{\left( {3p + 1} \right)\kappa_{\text{m}}^{3} }} + \frac{{\kappa_{\text{cm}}^{4} }}{{\left( {4p + 1} \right)\kappa_{\text{m}}^{4} }} - \frac{{\kappa_{\text{cm}}^{5} }}{{\left( {5p + 1} \right)\kappa_{\text{m}}^{5} }},} \hfill \\ \end{array} } \right.$$

(6b)

According to the first-order shear deformation shell theory, the displacement field can be expressed as (Wattanasakulpong and Chaikittiratana 2015):

$$\begin{aligned} u\left( {x,y,z,t} \right) & = u_{0} \left( {x,y,t} \right) + z\phi_{x} \left( {x,y,t} \right), \\ v\left( {x,y,z,t} \right) & = v_{0} \left( {x,y,t} \right) + z\phi_{y} \left( {x,y,t} \right), \\ w\left( {x,y,z,t} \right) & = w_{0} \left( {x,y,t} \right). \\ \end{aligned}$$

(7)

where u₀, v₀ and w₀ are the displacement at the mid-surface of the shell in the x, y and z directions, respectively; and $\phi_{x}$ and $\phi_{y}$ are the rotations of the transverse normal about the y and x axes, respectively.

The linear strains are defined as:

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{xy} } \\ \end{array} } \right\}\text{;}\quad \left\{ {\begin{array}{*{20}c} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\phi_{y} + \frac{{\partial w_{0} }}{\partial y} - \frac{{v_{0} }}{{R_{2} }}} \\ {\phi_{x} + \frac{{\partial w_{0} }}{\partial x} - \frac{{u_{0} }}{{R_{1} }}} \\ \end{array} } \right\}\text{,}$$

(8)

where

$$\begin{aligned} \varepsilon_{x}^{0} & = \frac{{\partial u_{0} }}{\partial x} + \frac{{w_{0} }}{{R_{1} }}\text{;}\;\;\varepsilon_{y}^{0} = \frac{{\partial v_{0} }}{\partial y} + \frac{{w_{0} }}{{R_{2} }}\text{;}\;\;\gamma_{xy}^{0} = \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}\text{,} \\ \kappa_{x} & = \frac{{\partial \phi_{x} }}{\partial x}\text{;}\;\;\kappa_{y} = \frac{{\partial \phi_{y} }}{\partial y}\text{;}\;\;\kappa_{xy} = \frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}\text{.} \\ \end{aligned}$$

(9)

Then, the linear constitutive relations are expressed as,

$$\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\},$$

(10)

where

$$Q_{11} = Q_{22} = \frac{E(z,T)}{{1 - \nu^{2} }};\quad Q_{12} = \frac{\nu E(z,T)}{{1 - \nu^{2} }};\quad Q_{44} = Q_{55} = Q_{66} = \frac{E(z,T)}{{2\left( {1 + \nu } \right)}}.$$

(11)

The force and moment resultants and are defined by:

$$\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\tau_{xy} } \\ \end{array} } \right\}{\text{d}}z} ;\quad \left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {z\sigma_{xx} } \\ {z\sigma_{yy} } \\ {z\tau_{xy} } \\ \end{array} } \right\}{\text{d}}z} ;\quad \left\{ \begin{aligned} Q_{yz} \hfill \\ Q_{xz} \hfill \\ \end{aligned} \right\} = k_{s} \int\limits_{ - h/2}^{h/2} {\left\{ \begin{aligned} \sigma_{yz} \hfill \\ \sigma_{xz} \hfill \\ \end{aligned} \right\}{\text{d}}z} ,$$

(12)

$$\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 \\ {A_{12} } & {A_{22} } & 0 & {B_{12} } & {B_{22} } & 0 \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 \\ {B_{12} } & {B_{22} } & 0 & {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {B_{66} } & 0 & 0 & {D_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{xy} } \\ \end{array} } \right\};\quad \left\{ {\begin{array}{*{20}c} {Q_{yz} } \\ {Q_{xz} } \\ \end{array} } \right\} = k_{s} \left[ {\begin{array}{*{20}c} {A_{44} } & 0 \\ 0 & {A_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\},$$

where

$$\left( {A_{ij} ,B_{ij} ,D_{ij} } \right) = \int\limits_{ - h/2}^{h/2} {Q_{ij} \left( {1, \, z, \, z^{2} } \right){\text{d}}z} \quad {\text{with}}\;(ij) = (11, \, 12, \, 21, \, 22, \, 66),$$

(13)

and,

$$A_{ij} = \int\limits_{ - h/2}^{h/2} {Q_{ij} {\text{d}}z} \quad {\text{with}}\;(ij) = (44,\,55),$$

and k_s is shear correction coefficient (k_s = 5/6). The temperature is assumed to only vary along the thickness direction of the shell; thus, $\tau_{xy}^{{}} = 0$. The thermal stresses for the functionally graded shell in the x, y directions are expressed as follows:

$$\sigma_{xx}^{\left( T \right)} = \sigma_{yy}^{\left( T \right)} = - \frac{{E\left( {z,T} \right)\alpha \left( {z,T} \right)}}{1 - \nu }\Delta T,$$

(14)

where $\Delta T = T\left( z \right) - T_{0}$ is temperature rise from the reference temperature T₀ at which there are no thermal strain.

Using the Hamilton’s principle, we can obtain the equations of motion as (Wattanasakulpong and Chaikittiratana 2015):

$$\begin{aligned} \frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} + \frac{{Q_{xz} }}{{R_{1} }} & = A_{11}^{T} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + A_{22}^{T} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + B_{11}^{T} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + B_{22}^{T} \frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }} + I_{0} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }}, \\ \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{yy} }}{\partial y} + \frac{{Q_{yz} }}{{R_{2} }} &= A_{11}^{T} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + A_{22}^{T} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + B_{11}^{T} \frac{{\partial^{2} \phi_{y} }}{{\partial x^{2} }} + B_{22}^{T} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} + I_{0} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }}, \\ \frac{{\partial Q_{xz} }}{\partial x} + \frac{{\partial Q_{yz} }}{\partial y} - \frac{{N_{xx} }}{{R_{1} }} &- \frac{{N_{yy} }}{{R_{2} }} + K_{\text{g}} \nabla^{2} w_{0} - K_{\text{w}} w_{0} = A_{11}^{T} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + A_{22}^{T} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + I_{0} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }}, \\ \frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial M_{yy} }}{\partial y} - Q_{xz} & = B_{11}^{T} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + B_{22}^{T} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + D_{11}^{T} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + D_{22}^{T} \frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }} + I_{1} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }}, \\ \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{yy} }}{\partial y} - Q_{yz} & = B_{11}^{T} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + B_{22}^{T} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + D_{11}^{T} \frac{{\partial^{2} \phi_{y} }}{{\partial x^{2} }} + D_{22}^{T} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} + I_{1} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }}, \\ \end{aligned}$$

(15)

where

$$\left\{ {\begin{array}{*{20}l} {\left( {A_{11}^{T} , \, B_{11}^{T} , \, D_{11}^{T} } \right) = \int\limits_{ - h/2}^{h/2} {\sigma_{xx}^{(T)} (1, \, z, \, z^{2} ){\text{d}}z,} } \hfill \\ {A_{22}^{T} = A_{11}^{T} ;\;\;B_{22}^{T} = B_{11}^{T} ;\;\;D_{22}^{T} = D_{11}^{T} ,} \hfill \\ {I_{i} = \int\limits_{ - h/2}^{h/2} {\rho (z)\, \cdot \,z^{i} \,{\text{d}}z\quad i = ( 0 , { 1, 2),}} } \hfill \\ {\nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }},} \hfill \\ \end{array} } \right.$$

(16)

and K_w is the Winkler’s elastic foundation coefficient and K_g is a constant showing the effect of the shear interaction of vertical elements.

The internal moment and force resultants are expressed in displacement terms using Eqs. (7)–(13) and then substituting into Eq. (15), we get the equations of motion expressed to the displacement components (u₀, v₀, w₀, $\phi_{x} ,\phi_{y}$).

Solution procedures

Based on the Navier’s approach, the displacement unknowns satisfying the simply supported boundary conditions for the FG doubly curved shell are assumed in the following forms:

$$\left\{ \begin{aligned} u_{0} (x,y,t) \hfill \\ v_{0} (x,y,t) \hfill \\ w_{0} (x,y,t) \hfill \\ \phi_{x} (x,y,t) \hfill \\ \phi_{y} (x,y,t) \hfill \\ \end{aligned} \right\} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left\{ \begin{aligned} u_{mn} e^{i\omega t} \cos (\alpha x)\sin (\beta y) \hfill \\ v_{mn} e^{i\omega t} \sin (\alpha x)\cos (\beta y) \hfill \\ w_{mn} e^{i\omega t} \sin (\alpha x)\sin (\beta y) \hfill \\ \phi_{xmn} e^{i\omega t} \cos (\alpha x)\sin (\beta y) \hfill \\ \phi_{ymn} e^{i\omega t} \sin (\alpha x)\cos (\beta y) \hfill \\ \end{aligned} \right\}} } ,$$

(17)

where $u_{mn} , \, v_{mn} , \, w_{mn} , \, \phi_{xmn} , \, \phi_{ymn}$ are the coefficients; i is the imaginary unit (i² = − 1); ω is the natural frequency; $\alpha = m\pi /a$; $\beta = n\pi /b$.

The final form of equations of motion can be obtained by substituting Eq. (17) in the equations of motion expressed to the displacement components of Eq. (15) and conceded as.

$$\left( {\left[ K \right]_{5 \times 5} - \omega^{2} \left[ M \right]_{5 \times 5} } \right)\left\{ \Delta \right\}_{5 \times 1} = \left\{ 0 \right\}_{5 \times 1} ,$$

(18)

where $\left[ K \right]_{5 \times 5}$ and $\left[ M \right]_{5 \times 5}$ are the stiffness matrix and the mass matrix, respectively. With $K_{ij}$, $M_{ij}$ are the elements which can be obtained by Symbolic Toolbox of the MATLAB software. $\left\{ \Delta \right\}_{5 \times 1} = \left\{ {u_{mn} \, v_{mn \, } w_{mn} \, \phi_{xmn} \, \phi_{ymn} } \right\}^{T}$ is the displacement vector.

The natural frequency $\omega_{mn}$ can be obtained by solving the above eigenvalue-type equation (Eq. 18). With each pair of m and n, there is a corresponding unique mode shape of the natural frequency for the FG doubly curved shell panel.

Results and discussion

Validation study

To verify the accuracy of the presented solutions, two examples have been analyzed for free vibration of the simply supported FG shell panels and the values of the fundamental frequencies are compared with those in existing literature. It is noted that the doubly curved shell panels can be flexible and degenerated into the different structures by setting these quantities:

• $\frac{a}{{R_{1} }} = \frac{b}{{R_{2} }} = 0$ for the plate structures;

• $\frac{a}{{R_{1} }} = 0$ for the cylindrical panel; $\frac{a}{{R_{1} }} = \frac{b}{{R_{2} }}$ for the spherical panel.

According to Reddy and Chin (1998), the effective material properties used in the present study are listed in Table 1.

Table 1 Temperature-dependent coefficients of the FGM shell panel

Example 1

We first consider the FG doubly curved shell panels resting on elastic foundation under ambient temperature with geometrical parameters: a/b = 1, a/h = 10, power law index p = 0.5 and various curvatures (a/R₁, b/R₂)

The non-dimensional natural frequencies for two types of curved panel (spherical panel and cylindrical panel) and the associated plate are calculated for various values of foundation parameters and displayed in Table 2. A comparison is made by comparing with those given by Kiani et al. (2012). The non-dimensional frequency parameter is defined as: $\varOmega_{1} = \frac{{a^{2} }}{h}\, \cdot \,\omega \, \cdot \,\sqrt {\rho_{\text{c}} /E_{\text{c}} }$. According to Kiani et al. (2012), the non-dimensional Winkler and Pasternak coefficients are $K_{0} = \frac{{K_{\text{w}} \, \cdot \,a^{4} }}{{D_{\text{m}} }}$; $J_{0} = \frac{{K_{\text{g}} \, \cdot \,b^{2} }}{{D_{\text{m}} }}$ with $\left( {D_{\text{m}} = E_{\text{m}} h^{3} /12/(1 - \nu^{2} )} \right)$. The material properties of ceramic and metal are as follows:

Table 2 Comparison of non-dimensional frequencies $\varOmega_{1}$ for FG square doubly curved shells resting on elastic foundation (under ambient temperature)

• Ceramic (Al₂O₃): E_c = 380 GPa; ρ_c = 3800 kg/m³; ν = 0.3.

• Metal (Al): E_m = 70 GPa; ρ_m = 2707 kg/m³; ν = 0.3.

As shown in Table 2, a good agreement between the results is accomplished.

Example 2

In this example, the vibration analysis of FG plates (a/R₁ = b/R₂=0) in the thermal environment not resting on elastic foundation (K₀ = J₀ = 0) is investigated.

The FG plate is made of SUS304 and Si₃N₄ and the material properties are assumed to be dependent of temperature as listed in Table 1. Geometrical parameters of the plate are: h = 0.025 (m); a = b = 0.2 (m); a/h = 8. The non-dimensional frequency parameter is used in the form: $\varOmega_{2} = \frac{{a^{2} }}{h}\, \cdot \,\omega \, \cdot \,\sqrt {\rho_{{0{\text{m}}}} \left( {1 - \nu^{2} } \right)/E_{{0{\text{m}}}} }$ with E_0m and ρ_0m as the reference values of E_m and ρ_m at T₀ = 300 K. Table 3 shows the calculated non-dimensional frequencies parameters in a comparison with those given by Shen and Wang (2012) using higher-order shear deformation plate theory. It can be seen clearly that the results obtained are in very good agreement. The biggest difference are 1.18% for T_c = 600 K, T_m = 600 K, mode (2, 2) and p = 1 and 1.17% for T_c = 400 K, T_m = 300 K, mode (2, 2) and p = 0.5.

Table 3 Comparison of non-dimensional frequencies for the FG plates under thermal environment

These two comparisons show that the presented results match very well with the established ones. It can be seen that the maximum difference of the fundamental frequency between present solution and Shen and Wang’s solution is only about 1.20% at T_c = T_m = 600 K and p = 1, mode (2, 2).

Parametric study

Next, the following parametric studies are carried out to analyze the free vibration of FG doubly curved shell panels in the case of resting on elastic foundation (K₀ = 100 and J₀ = 10) or without contacting with elastic foundation (K₀ = J₀ = 0) in thermal environment. The FG material type used is SUS304/Si₃N₄ in the following investigation with the material properties as in the Table 1. The non-dimensional frequency parameter is defined as $\varOmega_{3} = 100\, \cdot \,\omega \, \cdot \,h\, \cdot \,\sqrt {\rho_{{0{\text{c}}}} /E_{{0{\text{c}}}} }$ with E_0c and ρ_0c as the reference values of E_c and ρ_c at T₀ = 300 K. The geometrical parameters of the shell panels are: a/b = 1; a/h = 20; for spherical shell (a/R₁ = b/R₂ = 0.5) and for cylindrical shell (a/R₁ = 0; b/R₂ = 0.5). The temperature at the metal-rich surface is T_m = 300 K and the temperature at the ceramic-rich surface is T_c.

For illustration purpose, on the plot graph, the non-dimensional frequencies of shell panels resting on elastic foundation are depicted by solid lines whereas the dash lines are for the case of shell panels not resting on elastic foundation.

Effect of the temperature on the fundamental natural frequency

The temperature variation refers to the case when the metal temperature is kept constant while the ceramic surface is heated; so there is a temperature difference ΔT between the top and bottom shell surfaces. The variation of the non-dimensional fundamental frequencies of the spherical and cylindrical FG shell panels (p = 1) versus the temperature is shown in Fig. 2. It is observed that the trend of the non-dimensional fundamental frequency changes of the cylindrical panel and spherical panel are the same. The non-dimensional fundamental frequencies decrease when the temperature of the ceramic surface (T_c) increases. The reduction of the non-dimensional fundamental frequencies is due to the decreasing of panel’s stiffness when the temperature increases. The non-dimensional fundamental frequency of FG shell panels with the elastic foundation is higher than that without elastic foundation.

Fig. 2

Variation of the non-dimensional fundamental frequency of the FG panel with the temperature (T_c)

Effect of the power law index on the fundamental frequency

Figure 3 shows the effect of the power law index (p) on non-dimensional fundamental frequencies of cylindrical and spherical panels. The temperatures are T_m = 300 K, T_c = 400 K. It can be seen that the non-dimensional natural frequency decreases with increasing value of power law index (p). It is basically due to the fact that Young’s modulus of ceramic is higher than metal. Figure 3 also shows that the non-dimensional natural frequency decreases significantly when p is small.

Fig. 3

Variation of the non-dimensional fundamental frequency of the FG panel with the power law index (p)

Effect of geometrical parameters on the fundamental frequency

Figure 4 and 5 depict the variation for the non-dimensional fundamental frequency of spherical panel and cylindrical panel versus the side-to-thickness (a/h) and side-to-radius ratios (b/R₂). Note that: p = 1, T_m = 300 K, T_c = 400 K. It can be seen clearly from Fig. 4 that the dimensionless frequencies of these shell panels decrease dramatically with the increase of the side-to-thickness ratio.

Fig. 4

Variation of the non-dimensional fundamental frequency of the FG panel with a/h ratio

Fig. 5

Variation of the non-dimensional fundamental frequency of the FG panel with b/R₂ ratio

To study the effect of the variation of the fundamental frequency versus side-to-radius ratio of shell panels (b/R₂), the geometric and material properties and the temperature used for investigation in Fig. 5 are: a/b = 1, a/h = 20, p = 1, T_m = 300 K, T_c = 400 K and with varying ratio of b/R₂. For spherical panel, a/R₁ = b/R₂ and for cylindrical panel, a/R₁ = 0. Figure 5 shows that the non-dimensional fundamental frequency increases with increasing of side-to-radius ratio. This means that the rising of the curvature of the shell causes an increase in the stiffness, which causes a rapid increase of the non-dimensional fundamental frequency of the panel.

Table 4 and Fig. 6 show an observation concerning the effect of foundation parameters K₀, J₀ on the variation of non-dimensional fundamental frequency $\varOmega_{3}$ of FG panel with a/b = 1, p = 1, a/h = 20, T_m = 300 K and T_c = 400 K. These results indicate that the non-dimensional fundamental frequency $\varOmega_{3}$ increases with increasing of foundation parameters K₀, J₀, and the shear Pasternak parameter J₀ has more significant effect than the Winkler parameter K₀ in causing an increase of the non-dimensional fundamental frequency.

Table 4 Variation of the non-dimensional fundamental frequency of the FG panel with various foundation parameters (K₀ and J₀)

Fig. 6

Effect of foundation parameters K₀ and J₀ on non-dimensional fundamental frequency $\varOmega_{3}$ of the FG panel

Based on the presented theory, it is clearly shown that the effect of foundation parameters K₀, J₀ plays an important role in the increase of the non-dimensional fundamental frequency of the FG panel. The non-dimensional fundamental frequencies of shell panels resting on elastic foundation are always bigger than those without elastic foundation.

Conclusion

In this paper, a solution for vibration analysis of simply supported FG doubly curved shell panels based on the first-order shear deformation theory is formulated. The Pasternak-type elastic foundation is in contact with the FG shell panels in thermal environment. The accuracy of numerical solutions has been validated against existing results in available literature. The numerical results show a significant impact of foundation parameters, thermal environment (T_c, T_m), power law index (p), side-to-thickness ratio (a/h) and side-to-radius ratio (b/R₂) on non-dimensional fundamental frequency of the FG shell panels. We hope that the presented analytical solution could be useful references for future researches which relate to the mechanical behaviors of FG doubly curved shell panel structures.