Introduction

The ASCE 2017 report card listed that about 9% of bridges in the USA are classified structurally deficient and each year more than 3000 new bridges are being constructed (Bhide 2008). It has been always a challenge for the bridge engineers to find new ways to build better bridges with reduced construction time. So far, significant efforts have been provided in developing innovative ways to increase the long-term structural performance, and currently, the use of UHPC has becoming more popular in the construction industry for its superior properties such as its early very high strength that might reach 96 MPa (14,000 psi) in 3 days, its promising toughness, and long-term steadiness. The term UHPC is classified as innovative cementitious composite materials, where ground-breaking technology of cement and concrete industry grouped together (Graybeal 2010).

In fact, the concept of using UHPC for connection between precast concrete panels started in the mid 90s. At that time, a building was being constructed at Aalborg University using UHPC as a closure pour material, and additional project was completed, where UHPC was used for slab-column connections and its bond characteristics, (Aarup et al. 2009; Hansen and Jensen 1999; Nielsen et al. 1996; Aarup and Jensen 1998). Additional research, was completed at Chalmers University focusing on the application of UHPC as closure material (Broo and Broo 1997; Harryson 1999, 2000). Simplicity in construction and outstanding performance made UHPC connection more popular than conventional modular-component connections, where conventional concrete connections require post-tensioning, complex confinement reinforcement, large volume of concrete, etc., (Graybeal 2010). An ample amount of studies has been conducted to investigate the bond strength between UHPC and various materials. Perry and Seibert (2012) reported on applications related to precast joints of UHPC. The bond characteristics between timber and UHPC were studied by Schäfers and Seim (2011). The interfacial behavior of hollow glass fiber-reinforced plastic beams having a UHPC filled compressive zone was examined by El-Hacha and Chen (2012). Graybeal and Swenty (2012) investigated the performances of precast deck joints with variable cross sections. More research has been conducted on developing analytical models to predict that the compressive and tensile strength are also conducted. As this is not always feasible to conduct large-scale test of UHPC connection of bridge deck elements, a need for developing dependable 3D finite-element model is now time worthy. Graybeal (2006a, b, 2008, 2009a, b), performed comprehensive experimental tests on UHPC characterization, full-scale flexural and shear of I-girders, and pi-girders.

Numerical modeling of UHPC connected deck panels has been always challenging due to non-availability of post-peak behavior of UHPC either under compression or tension loads. The post-peak behavior is very important to predict the damage parameters needed for numerical modeling (Chen and Graybeal 2012). Different modeling approaches considering diverse assumptions have been proposed, but sensitivity analyses are needed for identifying the major parameters affecting the numerical results. In this paper, an effort has been made to develop a finite-element model that can be applied for a variety of UHPC bridge connections subjected to monotonic loading. It is needed to recognize the major factors which affects the numerical results and evaluate the sensitivity of the material input parameters on the variability and response of the models.

Experimental program

Two full-scale experimentally tested deck panels were selected from Graybeal (2010). The two specimens had two different UHPC connections, where straight and headed bars were used. Table 1 provides the details of the two test specimens.

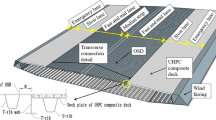
Table 1 Test specimen (Graybeal 2010)
Full size table

The details for each of the specimens, the location of UHPC filled connection, and normal strength concrete deck panels are provided in Figs. 1 and 2. In all cases, the size of the test specimens was 2400 × 2152 mm (94.5 × 84.7 inch). The diamond shape UHPC connection runs parallel to the length of the slab specimen with a 152 mm (6 inch) nominal width, as shown in Fig. 1. No post-tensioning was included in the test panels and the connection reinforcements were extended from the adjacent precast slabs into the UHPC connection, (Graybeal 2010).

Fig. 1
figure 1

Reinforcement details for panel 8H (Graybeal 2010)

Full size image
Fig. 2
figure 2

Reinforcement details for panel 8G (Graybeal 2010)

Full size image

Finite-element modeling

The modeling UHPC connected bridge deck panels under monotonic loading using computer-aided program is needed to broaden the current knowledge and provide some reliable results, especially with the high cost of experimental testing of UHPC connections. The numerical simulations were conducted using the ABAQUS (ABAQUS Inc. 2016) code, which is a general FE analysis software for modeling the nonlinear material behavior, interaction between different materials, heat transfer, fluid dynamics problem, etc. Both implicit and explicit numerical methods are available in ABAQUS for solving problems associated with large deformation and multi-loading environments. ABAQUS/explicit method was used for simulating the FE models as it can effectively handle severely nonlinear behavior.

Precast panels

To model the concrete material in ABAQUS, various models are available in the software library. The “concrete damaged plasticity” model is used in this paper and was developed by Lubliner et al. (1989) and then elaborated by Lee and Fenves (1998). The constitutive relationship requires the following material input parameters:

  • uniaxial stress–strain constitutive relation under compressive and tensile loading;

  • damage parameters \( d_{\text{c}} \) and \( d_{\text{t}} \) for compressive and tensile load, respectively.

These parameters are used to identify and validate damage and crack patterns of the developed model and compare it with experimental results. Three different concrete constitutive models were adopted in this study to identify the most suitable concrete model for this study. These models were only used to predict the behavior of the precast concrete panels.

Concrete model proposed by Hsu and Hsu (1994)

The concrete model derived by Hsu and Hsu (1994) is limited to a concrete compressive strength of 62 MPa. For other concrete grades, modifications should be made by referring to the original work reported by Hsu and Hsu (1994). This model assumes a linear stress–strain relationship up to 50% of the ultimate compressive strength (σcu) in the ascending portion. The model was only used to predict the compressive stresses from 0.5σcu to 0.3σcu in the descending portion:

$$ \sigma_{\text{c }} = \left( {\frac{{\beta \left( {\frac{{\varepsilon_{\text{c}} }}{{\varepsilon_{0} }}} \right)}}{{\beta - 1 + \left( {\frac{{\varepsilon_{\text{c}} }}{{\varepsilon_{0} }}} \right)^{\beta } }}} \right)\sigma_{\text{cu }} , $$
(1)

where the parameter β depends on the shape of the stress–strain diagram and is given by

$$ \beta = \frac{1}{{1 - \left[ {\frac{{\sigma_{cu} }}{{\varepsilon_{0} E_{0} }}} \right]}} , $$
(2)
$$ \varepsilon_{0} = 8.9 \times 10^{ - 5 } \sigma_{\text{cu}} + 2.114 \times 10^{ - 3} . $$
(3)

The initial tangential modulus, E0, is given by

$$ E_{0} = 1.243 \times 10^{2 } \sigma_{\text{cu}} + 3.28312 \times 10^{3} . $$
(4)

Concrete model proposed by Park and Paulay (1975)

This model considers concrete as an elastic–plastic and strain hardening material. The constitutive relation in compression is assumed to follow the expression given below:

$$ f_{\text{c}} = f^{'} \left[ {\frac{{2\varepsilon_{\text{c}} }}{{\varepsilon_{0} }} - \left( {\frac{{\varepsilon_{\text{c}} }}{{\varepsilon_{0} }}} \right)^{2} } \right] , $$
(5)

where f’ is the cylinder compressive strength of concrete in MPa. ε0 is the strain at peak stress, and εcu is the crushing strain.

Concrete model proposed by Saenz (1964)

The uniaxial compressive stress–strain relationship proposed by Saenz (1964) is as follows:

$$ \sigma_{\text{C}} = \frac{{E_{\text{C}} \varepsilon_{\text{C}} }}{{1 + \left( {R + R_{\text{E}} - 2} \right)\left( {\frac{{\varepsilon_{\text{C}} }}{{\varepsilon_{0} }}} \right) - \left( {2R - 1} \right) \left( {\frac{{\varepsilon_{\text{C}} }}{{\varepsilon_{0} }}} \right)^{2} + R \left( {\frac{{\varepsilon_{\text{C}} }}{{\varepsilon_{0} }}} \right)^{3} }} , $$
(6)

where

$$ R = \frac{{R_{\text{E}} \left( {R_{\sigma } - 1} \right)}}{{(R_{\varepsilon } - 1)^{2} }} - \frac{1}{{R_{\varepsilon } }} ,\quad R_{\text{E}} = \frac{{E_{\text{C}} }}{{E_{0} }},\quad E_{0} = \frac{{f'_{\text{C}} }}{{\varepsilon_{0} }}, $$

where \( R_{\text{E}} = 4\;{\text{and}}\;R_{\sigma } = 4 . \)

Concrete compression and tension damage parameters were calculated using the following equations which were proposed by Birtel and Mark (2006)

$$ d_{\text{c}} = 1 - \frac{{\sigma_{\text{c}} E_{\text{c}}^{ - 1} }}{{\varepsilon_{\text{c}}^{\text{pl}} \left( {\frac{1}{{b_{\text{c}} }} - 1} \right) + f_{\text{c}} E_{\text{c}}^{ - 1} }} , $$
(7)

where \( d_{\text{c}} = \) concrete compression damage parameter, \( f_{\text{c}} = \) compressive stress, \( E_{\text{c}} = \) modulus of elasticity of concrete, \( \varepsilon_{\text{c}}^{\text{pl}} = \) plastic strain corresponding to compressive strength, and \( b_{\text{c}} = \) constant ranges 0 < \( b_{\text{c}} \) < 1:

$$ d_{\text{t}} = 1 - \frac{{\sigma_{\text{t}} E_{\text{c}}^{ - 1} }}{{\varepsilon_{\text{t}}^{\text{pl}} \left( {\frac{1}{{b_{\text{t}} }} - 1} \right) + f_{t} E_{\text{c}}^{ - 1} }}, $$
(8)

where \( d_{\text{t}} = \) concrete tension damage parameter, \( f_{\text{t}} = \) tensile stress, \( E_{\text{c}} = \) modulus of elasticity of concrete, \( \varepsilon_{\text{t}}^{\text{pl}} = \) plastic strain corresponding to tensile strength, and \( b_{\text{t}} = \) constant ranges 0 < \( b_{\text{t}} \) < 1.

The concrete parameters used in the plastic damage model are shown in Table 2.

Table 2 Concrete parameters used in the plastic damage model
Full size table

UHPC

Very limited analytical model has been developed for predicting the compressive and tensile behavior of UHPC up to the knowledge of the authors. The UHPC compressive strength was 210 MPa and the tensile strength was taken as 6.40 MPa (Graybeal 2006a). Figure 3 shows the stress–strain history of the UHPC used in this study and provided as input in ABAQUS. Concrete compression damage parameter that was used based on Eqs. (7) and (8) (Birtel and Mark 2006). Table 3 shows the input parameters used in the damage model.

Fig. 3
figure 3

Axial stress–strain behavior for UHPC (a) in compression and (b) in tension (Graybeal 2006a)

Full size image
Table 3 Ultrahigh-performance concrete parameters used in the plastic damage model (Chen and Graybeal 2012)
Full size table

Reinforcing steel

Reinforcing steel has been modeled using a 2-noded linear 3D truss element (T3D2); however, solid elements were used to model the headed end. The reinforcing bars within the concrete slab were simulated using the embedded element technique available in ABAQUS. Both elastic-perfectly plastic and bilinear stress–strain curves are tested for the simulation. The other parameters used to define the behavior of reinforcing steel are shown in Table 4.

Table 4 Parameters of reinforcing steel
Full size table

Panel 8H has been reinforced at the connection using headed bars of 16M (#5) as normal reinforcement, whereas panel 8G was reinforced by straight, lapped bars of 16M (#5). The thickness of the headed bars was 12.7 mm (0.5 in) and a diameter of 50.5 mm (1.987 in.). For panel 8H and 8G, the minimum lap length in the connection was 90 mm (3.54 inch) and 150 mm (5.9 inch), respectively. Two additional 16M (#5) bars were provided along the length of the connection between the top and bottom layers. Steel reinforcement is assumed to have perfect bond with concrete as an embedded element in ABAQUS. The mesh configuration and reinforcement details are shown in Fig. 5a. A displacement controlled loading was applied to the panels through a rigid steel plate placed on the top of the panels until the failure occurs as reported in the test program which is shown in Fig. 4. In the experiment, the deck panels were supported by elastomeric pads on the top of steel plates. The roller supports represent the elastomeric pads at both sides of the deck panels. The load was applied in very small increments using the explicit dynamic option in ABAQUS. The edge of the loading plate was parallel to the precast–UHPC interface (Fig. 5).

Fig. 4
figure 4

Displacement time history (8H)

Full size image
Fig. 5
figure 5

a Concrete mesh configuration, b reinforcement details (straight bars), c reinforcement details (headed bars)

Full size image

Sensitivity analysis

In this section, sensitivity analysis of the numerical models was conducted based on the constitutive models of concrete and steel, concrete input properties such as dilatancy angle and mesh size of the elements. Numerical models for both headed and straight bars were named SB-XYZ-Pφ and HB-XYZ-Pφ. Where SB and HB stand for straight bar and headed bars, respectively, X represents the initial letter of the concrete constitutive model being used (H, S, and P), Y is the mesh size (5, 10, and 20 mm), Z represents the contact model type used (T for Tie contact and F for friction model), P stands for steel model (E for elastic—perfectly plastic and B for bilinear model), and φ is the angle of dilatancy. All these variables are shown in Table 5.

Table 5 Variables used for sensitivity analysis
Full size table

Effect of concrete model

Three different constitutive models of concrete were considered to investigate the overall behavior the UHPC hybrid connections. The ultimate load carrying capacity for the models HB-S20T-E35°, HB-P20T-E35°, and HB-H20T-E35° was found 480.21, 486.07, and 469.811 kN, respectively. For SB-S20T-E35°, SB-P20T-E35°, and SB-H20T-E35°, the ultimate load carrying capacity was found 486.98, 473.76, and 482.62 kN. Though all the models predicted the ultimate load quite satisfactorily, but these models showed stiffer behavior compared to the experimental results and that was expected due to the initial cracking developed in the real specimens due to casting and shrinkage. It is observed from Fig. 6 that the model proposed by Saenz (1964) indicates a decrease in initial stiffness which is 2 and 45% less than the models proposed by Hsu and Hsu (1994) and Park and Paulay (1975), respectively, for headed bar. Concrete damage plasticity (CDP) model is used for modeling both normal strength concrete and UHPC which incorporates both tensile cracking and compressive crushing of concrete. Defining tension stiffening in CDP model is necessary as it allows to model strain-softening behavior for cracked concrete. Due to unavailability of post-peak behavior of UHPC, the ratio of the strength in the biaxial state to the strength in the uniaxial state, the eccentricity is assumed as input to the CDP model.

Fig. 6
figure 6

Effect of concrete models; a 8G and b 8H

Full size image

Effect of dilation angle

In this section, the angle of dilatancy of concrete was varied from 20° to 40° for the precast concrete. Figure 7 shows that the results are not varying drastically as the dilation angle changes. Numerical results from both panels 8G and 8H also showed that higher dilation angle results in slightly higher ultimate load without effect in initial stiffness. For panel 8G, changing the dilation angle from 20° to 40° results in an increase of 7.81% in ultimate load, whereas for panel 8H, the increase in ultimate load was found 8.56%. The amount of dilation depends strongly on the density of the material (ABAQUS). For this reason, increasing confinement results in an increase in the angle of friction. In both 8G and 8H panels, higher dilation angle produced slightly higher initial stiffness which was expected. In case of headed bar specimens, the stiffness of the composite panel for a dilation angle of 40° was found 9.69% greater than the stiffness found for dilation angle 20°, whereas for the 8G panel, 5.47% higher value of initial stiffness was found for 40° dilation angle.

Fig. 7
figure 7

Effect of dilation angle; a 8G and b 8H

Full size image

Effect of steel properties

Both elastic–plastic and bilinear models of the reinforcement steel were implemented to investigate their effect on the overall performance of the panels. It is evident from Fig. 8 that the bilinear model of the steel showed lesser stiffness than the elastic-perfectly model and both models showed low stiffness compared to the experimental load–displacement response. The initial stiffness decreased 8 and 20% for 8G and 8H panels, respectively, which justifies that the bilinear model could predict the experimental results quite satisfactorily in both panels.

Fig. 8
figure 8

Effect of steel properties; a 8G and b 8H

Full size image

The highest strain in steel bars was observed at mid span in the connection between UHPC and normal strength precast concrete. The stress–strain history of the steel bar for both elastic-perfectly plastic and bilinear cases is shown in Fig. 9. In both cases, the steel bar reached the yield stress which was provided as 414 MPa. It also verifies that the finite-element model is in good agreement with the input data provided for steel properties.

Fig. 9
figure 9

Axial stress vs axial strain response for the reinforcement steel at the UHPC connection

Full size image

Convergence study

A sensitivity test was carried out to investigate an optimum mesh size for the simulation to capture the load–displacement response accurately. The numerical simulation was performed for 5, 10, and 20 mm mesh size. Figure 10 shows that there is no significant change observed between 20 and 5 mm mesh size. The ultimate load is found 486.98 and 490.31 kN for 20 and 5 mm mesh, respectively, which are very close. In consequence, all the simulations were conducted for 20 mm mesh.

Fig. 10
figure 10

Convergence study for 8G

Full size image

Contact modeling

The contact between the normal strength precast concrete deck panels and UHPC is the most crucial part to model in ABAQUS, because no numerical data available about the behavior of this kind of hybrid connection. Two different kinds of contact properties were in ABAQUS to predict this behavior. First, a perfect bond between the UHPC and the conventional concrete was assumed and later, a friction model considering a friction coefficient of 1.09 (Hussein et al. 2016) was implemented in which little slip between the interfaces (normal concrete and UHPC) was allowed. Figure 11 shows that both models were quite capable of predicting the response of experimental program satisfactorily. It seems that the friction model has less stiffness than the perfect bond model which was anticipated, though the predicted ultimate load was less than the experimental one

Fig. 11
figure 11

Effect of contact model

Full size image

Validation of the finite-element model

The proposed finite-element model has been validated with two full-scale experimentally tested deck panels as described in all the previous sections, which includes both headed and straight reinforcement bars under monotonic loading. The failure mode of deck panels was due to the large deformemin associated with a reduction in ultimate load. A comparison of full-scale experimentally tested and the finite-element model is presented in Figs. 12 and 13 to validate the competency of FEM to foresee the failure load, mode of failure, and overall behavior of UHPC connection in precast deck panels.

Fig. 12
figure 12

Load vs displacement response at mid span

Full size image
Fig. 13
figure 13

Damage a in compression, b in tension (FEM) and c in tension (Graybeal 2010)

Full size image

Figure 12 shows that inelastic cracking response continued to increase until the load reaches to approximately 370–390 kN, and up to this level, the numerical models showed higher initial stiffness than the experimental ones. Above that load level, the displacement has been changed significantly without noticeable increase in the failure loads. The same behavior is also observed in the experimental results. Figure 13 shows the damage in concrete panels both in compression and tension. As UHPC could endure higher compressive strength than normal strength concrete so less damage was found in the UHPC connection. It is also apparent from the figure that there is no indication of slip or de-bonding along either of the two connection interfaces which is in good agreement with the experiments. The crack pattern found in the tension side of the deck panels is in good agreement with the cracks observed from the experiment. Figure 14 shows the damage pattern found around the reinforcement bars in tension. It is evident from Fig. 14a, b that less damage is found around headed bar.

Fig. 14
figure 14

Damage in tension around; a headed bar, b straight bar

Full size image

The axial stain history of normal precast concrete and the UHPC both in panel 8H for compression and tension is shown in Fig. 15. The ultimate axial compressive strain was found 0.01 and 0.0065 mm/mm for normal concrete and UHPC, respectively. As UHPC can withstand more tensile strain, it was observed that the tensile strain is found higher in UHPC which is 0.08 mm/mm.

Fig. 15
figure 15

Strain response of NSC and UHPC in compression and tension (8H)

Full size image

The overall comparison between the FEM and experimental results is summarized in Table 6. The energy absorption was calculated for each case (AFEM) and compared with the respective experimental results (Aexp). The ratio between the energy absorption in the experiments to the energy absorption in the FEM ranges from 0.91 to 1.01. It was also shown in Table 6 that the FEM considering the bilinear steel properties accompanied by friction model predicts more close results than other parameters.

Table 6 Comparison between FEM and experimental results
Full size table

Conclusions

This paper presents a sensitivity analysis based on numerical simulations of the behavior of UHPC bridge deck connections under monotonic loading. The software package ABAQUS was used to perform all the simulations. Various key parameters were investigated such as the concrete constitutive models for the normal concrete, steel stress strain behavior, mesh size, contact properties, and concrete dilation angles with the following conclusions were drawn:

  • The damage in concrete under monotonic loading is found higher in normal concrete than UHPC with no signs of de-bonding between the two materials.

  • The FE model captured the damage pattern of the composite slab deck quite satisfactorily.

  • The numerical model is well capable of predicting the load displacement response, though it experiences higher stiffness initially.

  • Changing the dilation angle from 20° to 40° results in an increase of 7.81% in ultimate load for the panel with straight reinforcing bars, whereas for panel with headed bars, the increase in ultimate load was found 8.56%.

  • It was fund that for the panel with straight reinforcement bars, higher dilation angle produced slightly higher initial stiffness. In case of headed bar specimens, the stiffness of the composite panel for a dilation angle of 40° was found 9.69% greater than the stiffness found for dilation angle 20°, whereas for the straight bar panel, 5.47% higher value of initial stiffness was found for 40° dilation angle.

  • The initial stiffness decreased 8 and 20% for panel with straight bars and panels with headed bars, respectively, which justifies that the bilinear model could predict the overall panel performance closely to the experimental results.

  • The energy absorption ratios of all the experimental results compared to the developed FEM models were in the range of 89–110%, which justifies that the FEM models are in good agreement with the experimental results.