Abstract
The aim of the study is to investigate the distortional buckling behaviour of intermediate cold-formed lipped channel section under pinned end condition subjected to axial compression. An extensive test and numerical investigation of cold-formed lipped channel column with various types of intermediate web stiffeners is presented. In this study, three types of intermediate web stiffeners are chosen such as V, U and Σ. The entire cross-sectional dimensions meet with the pre-qualified column dimension given in Direct Strength Method for cold-formed steel structures. Totally, 12 columns are tested and results are compared with the numerical analysis. Numerical analysis is carried out using software ABAQUS. Material and geometric imperfections are incorporated in the FE model. Selected section dimensions met with the distortional buckling mode. Good correlation is achieved between experiment and finite element analysis. All the results are compared with the Direct Strength Method specifications for cold-formed steel structures. Based on the comparison of results, a suitable design modification is proposed. Furthermore, results are verified with the existing results which are available from the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The primary advantages of the cold-formed steel section are high strength to weight ratio, low self weight, easy lifting and fabrications, etc. Open sections are normally used in the industry. The basic failure modes are local buckling, distortional buckling, flexural buckling, torsional buckling or interaction between them. The buckling characteristics depend on the shape and the slenderness ratio of the cross-sectional profile.
Hancock (1985) studied the distortion mode of buckling. Kwon and Hancock (1992) described a design curve for sections undergoing distortional buckling. Schafer and Pekoz (1998a, b) adopted a new procedure for calculating the effective width of stiffened elements with multiple longitudinal intermediate stiffeners. Yan and Young (2002) discussed the behaviour of cold-formed steel channels with complex stiffeners subjected to pure axial compression. Yang and Hancock (2004) described a series of compression tests on lipped channel section columns fabricated from cold-reduced high-strength steel of thickness 0.42 mm with nominal yield stress 550 MPa. The test results show that distortional buckling and the interaction of local and distortional buckling may have a significant effect on the strength of the section. Zhang et al. (2007) were presented an investigation on cold-formed channels with inclined simple edge stiffeners under compression. Liu (2008) presented a crashworthiness design of regular multi-corner thin-walled columns with different types of cross sections and different profiles, including straight octagonal columns and curved hexagonal columns.
Kwon et al. (2009) described a series of compression tests on cold-formed simple lipped channels and lipped channels with intermediate stiffeners in the flanges and web. Nguyen and Kim (2009) studied the buckling of thin-walled composite columns in hat sections and lipped channel sections reinforced with web stiffener under axial compression. Chen et al. (2010) conducted a series of stub column tests on complex sections with intermediate stiffeners. It was shown that the intermediate stiffeners could effectively enhance the local buckling stress sections. Yap and Hancock (2011) described the design and testing of web-stiffened high-strength steel cold-formed lipped channel sections with web stiffener. If a section failing in the distortional mode and subjected to the interaction of local and distortional buckling modes, the test results showed that the sections failed prematurely and the DSM distortional strength curve was inadequate to account for such interactions.
He et al. (2014) examined the design and load-carrying capacity of fixed-ended web-stiffened lipped channel columns eroded by mode interaction behaviour combined with distortional and local deformations. Anil Kumar and Kalyanaraman (2014) presented about distortional buckling of CFS stiffened lipped channel compression members. Zhang and Young (2015) investigate the behaviour of cold-formed steel built-up open section columns with edge and web stiffeners. Zhou et al. (2015) offered explicit analytical formulae to provide distortional critical stress estimates for cold-formed steel C-section columns. Aruna et al. (2015) described a series of experiments conducted in cold-formed built-up square sections with intermediate flange and web stiffeners under axial compression with hinged end conditions. Wang et al. (2016) conducted a series of pin-ended compression tests and numerical analysis of channels with complex edge stiffeners and two different types of web stiffeners.
From the literature, it is observed that edge stiffeners and intermediate web stiffeners are improving the distortional and local buckling strength, respectively. Though many of the literatures pertaining strength and behaviour of simple cold-formed steel channel column with edge and intermediate web stiffeners. However, the results are scattered. Hence, in this study, lipped cold-formed steel channel column with various types of intermediate web stiffeners are selected.
In this study, cold-formed steel lipped channel sections with various types of intermediate web stiffeners are analysed. The dimensions of the cross sections are arrived based on the North American Specifications (NAS) for the cold-formed steel structures. The cross-sectional dimensions also satisfy the pre-qualified section profile Direct Strength Method (DSM) for the cold-formed steel structures. In this study, a series of 12 specimens are fabricated from the locally available cold-rolled sheets with a press-braking operations. The strength of the sections is calculated from the DSM and NAS for cold-formed steel structures. The strength obtained from the experiments is being compared with the strength of the section calculated from the DSM and NAS for cold-formed steel structures. From the comparability of the results, modifications of the design specifications are being suggested. The main aim of this study is to investigate the strength and buckling behaviour of cold-formed steel lipped channel column with various types of intermediate web stiffeners.
Experimental programme
Details of the specimen and material properties
Details of the specimens and material properties of the sections are discussed in this chapter. All the specimens are fabricated from 1.6-mm-thick cold-rolled sheets. The selected cross-sectional profiles and dimensions are shown in Fig. 1.
Specimen labelling
In this study, four cross-sectional geometries are chosen. From the specimen label, the cross-sectional geometry and length of the section are easily identified. For an example, “LC-V-500”, first letter defines the type of cross section (LC-lipped channel), the second letters defines the type of intermediate stiffener, second is lipped channel with V-shaped intermediate stiffener (LC-V), third is lipped channel with U-shaped intermediate stiffener (LC-U) and fourth is lipped channel with Σ-shaped intermediate stiffener (LC-Σ), and a third letter defines the length of the column in mm.
Design of specimen
Selected cross-sectional profile with defined nomenclature and the corresponding dimensions are presented in Figs. 1, 2 and Table 1, respectively. All the specimens having equal cross-sectional area. To avoid local buckling and minimize the fabrication problem and industrial requirements, the size of lip and (W) and size of intermediate stiffeners (H2 and H3) is 20 mm. The nominal width of flange (B) is 50 mm and total depth of the section (H) is 150 mm. The entire cross-sectional dimensions meet with the pre-qualified column dimension given in Direct Strength Method (DSM). Before a test, section dimensions of each specimen are measured by vernier caliper. The actual measured sizes of the specimens are shown in Table 1.
Material properties
The material properties of the test specimens are determined by tensile coupon tests, as shown in Fig. 3. Tensile coupons are prepared to test according to IS 1608-5 to determine the yield stress, ultimate stress, Young’s modulus and percentage of elongation (Table 2).
Experimental setup
Totally, 12 specimens are fabricated with four different section geometry as shown in Fig. 1. Locally available 1.6 mm thick cold-rolled sheets are used to fabricate the specimens with three different heights such as 500, 700 and 1000 mm. Specimens are fabricated from the latest locally available press-braking operations as shown in Fig. 4. The specimen is manufactured by press-braking operation to the required shape from the locally available cold-rolled steel sheets. All the specimens are tested under pinned end condition subjected to axial-loading condition. A total of twelve intermediate columns are tested to failure. To achieve the axial-loading condition and even distribution of load over the entire cross section of the column, 8-mm-thick end plates are milled flat and welded on both ends of the specimens. The end plate is welded in such a manner that the centre of gravity of the plate coincides with the point of loading of the specimen. A 200 kN capacity loading frame is used for testing the specimens and 100 kN capacity hydraulic ram is used for applying compressive load. Simply supported end condition is achieved by rubber gas (Sukumar et al. 2006; Manikandan and Arun 2016) cut insert at both ends of the specimens. The entire loading process is recorded using the data acquisition system. Applied load and deformation of the specimens are found by load cell and LVDT, respectively. A detailed experimental setup and entire tested specimens are shown in Figs. 5 and 7, respectively.
Finite element modelling
The numerical modelling is thorough in the commercial finite element software ABAQUS. The finite element program ABAQUS is used to simulate the experimental behaviour of the four types of members. An Eigenvalue elastic buckling analysis is first conducted to establish probable buckling modes (Eigen modes) of the specimens. A nonlinear buckling analysis is then performed to predict the ultimate loads, deformations and failure modes of the specimens.
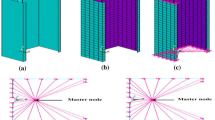
S4R four node shell element with a size of 10 mm mesh are used for meshing shell. Residual stress and cold forming process significantly does not affect the strength and behaviour of the specimens (Yan and Young 2002). Hence, the cold forming process and residual stress are not incorporated in the FE model, whereas the material non linearity and geometric non linearity are considered in the FE model. Material behaviour is described by multi-linear stress–strain curve. The material properties are extracted in a straight line from through tests. The entire column is analysed under pinned end condition subjected to axial load. For analysing the axial loading condition, the load is applied through the centre of gravity of the section. For applying loads and boundary conditions at the ends of the column, a reference point (RP) is created as shown in Fig. 6.
In this study, geometric non linearity is not measured. However, the scaled imperfection value is considered in the FE model (Schafer and Pekoz 1998a, b). The Eigen mode 1 scaled by a factor is used to obtain the geometric imperfection for the nonlinear buckling analysis. According to the buckling type of Eigen mode 1, the magnitude of the geometric imperfection of local, distortional and overall which from Schafer and Pekoz (1998a, b) is 0.34 t, 0.9 t and L/1000, respectively, used to specify the factor.
Results and discussion
The aim of the study is to investigate the distortional buckling strength and behaviour of cold-formed steel lipped channel column with different types of intermediate stiffeners (Fig. 1). Totally, 12 columns are tested and tested specimens are shown in Fig. 7. Most of the specimens fail by distortional buckling (Fig. 7). During the experimental investigation local buckling, distortional buckling and interaction between local and distortional buckling are observed. Results obtained from the experiments are compared with the results predicted from the FE analysis. Load deformation behaviour and failure modes obtained from experiments and FE analysis are compared as shown in Figs. 7, 8, and 9, respectively.
For an example, load deformation curve for some of the specimens as shown in Fig. 8. Similar results are obtained for all other specimens and results are presented in Table 3. From Fig. 9, it is clearly observed that the strength and stiffness of the member increase with modifying the cross-sectional geometries. Three types of intermediate stiffener are used. They are V, U and Σ types. Among the entire intermediate stiffener, Σ-type stiffener provides higher strength and stiffness of the section.
There are four series of section are chosen. The first series is lipped channel column without intermediate stiffener; the second series is lipped channel column with V-shaped intermediate stiffener; third series is lipped channel column with U-shaped intermediate stiffener and fourth series is lipped channel column with Σ-shaped intermediate stiffener. All the series, three different lengths are chosen such as 500, 700, 1000 mm. In this study, all the specimens are having equal cross-sectional area. All the specimens having 500 mm length fail by local buckling, whereas specimen LC-Σ-500 fails by distortional buckling. Likewise the specimens having 700 mm length, except specimen LC-700, fail by pure distortional buckling, whereas specimen LC-700 fails by interaction of local and distortional buckling. Similarly, the specimens having 1000 mm length, such as specimen LC-1000 and LC-V-1000, fail by interaction of local and distortional buckling, whereas all other remaining specimens fail by pure distortional buckling.
Load-carrying capacities of LC-500, LC-V-500, LC-U-500 and LC-Σ-500 are 41.33, 69.78, 70.11, and 80.11 kN, respectively. Similar improvement of load-carrying capacity is observed for all other length variations, and the corresponding results are presented in Table 3. From this study, it is observed that an intermediate stiffener significantly affects the strength and behaviour of the specimens. And also noted that, a specimen with Σ-type intermediate stiffeners provides better performance compared to all other types of intermediate stiffeners.
The results obtained from experiments (PEXP) and FE analysis (PFEM) are discussed in Table 3. Similarly, comparison of failure modes observed from the experiment and FE analysis is shown in Figs. 10, 11, and 12. From Table 3, it is observed that ratio between PEXP and PFEM for most of the cases lies between 0.90 and 1.00. The average and standard deviation of PEXP/PFEM are 0.92 and 0.08, respectively. The results from Table 3 and Figs. 10, 11 indicate that the proposed FE model predicts the strength and behaviour of the column with a high degree of accuracy and consistency. From the results it is accomplished that the developed FE model is more appropriate for the parametric analysis.
Theoretical investigations
Based on the specification of direct strength method (DSM) for cold-formed steel design, the capacity of members in axial compression (Pn, DSM) shall be minimum of local buckling (Pnl), distortional buckling (Pnd) and flexural torsional buckling (Pne),
where
λc = \( \sqrt {P_{\text{y}} /P_{\text{cre}} } \)and Py = Afy.Py is the squash load.
The nominal axial strength (Pnl) for local buckling is
where
λ1 = \( \sqrt {P_{\text{ne}} /P_{\text{crl}} } \).
The nominal axial strength (Pnd) for distortional buckling is
where
λd = \( \sqrt {P_{\text{y}} /P_{\text{crd}} } \).
The elastic local load Pcrl and distortional buckling load Pcrd are obtained from the linear elastic finite strip buckling analysis. The comparison of results between the experiment, FE analysis and DSM specifications is discussed in Table 3. The mean values of PEXP and PDSM and PFEM and PDSM are 0.88 and 0.95, respectively. Similarly, standard deviation of PEXP and PDSM and PFEM and PDSM is 0.09 and 0.04, respectively. From this comparison, it is observed that DSM specification predicts the strength almost equal to the experiment and finite element analysis. However, all the values are below to the one. Therefore, for obtaining exact values, a regression analysis is conducted between PEXP and PDSM as shown in Fig. 6. From the regression analysis, in this study, a new design expression is proposed,
The proposed new design equation is verified by the results available from the literature (13) and the results are displayed in Table 4. The mean and standard deviation of PEXP/PProp are 1.04 and 0.03, respectively. From the results, it is concluded that the proposed design equation reasonably predicts the strength of the lipped channel column with and without intermediate stiffener.
Summary and conclusions
The objective of the study is to investigate the strength and behaviour of intermediate cold-formed steel column with different intermediate stiffeners under pinned end condition subjected to axial loading. Experimental results are also verified with the numerical investigation. Numerical investigation also carried out using the software ABAQUS. Totally, twelve columns are tested. The results obtained from experiment, numerical investigation is compared with the direct strength method specification for cold formed steel structures. Finally, a new design expression is proposed for the cold formed steel column with various intermediate stiffener. Based on the experimental investigation, the following conclusions are drawn:
-
Results obtained from the numerical investigation agreed well with the experimental investigation.
-
Local buckling, distortional buckling and interaction between local and distortional buckling are observed experimentally and compared well numerically.
-
Strength and stiffness of the member increase with modifying the cross-sectional geometries. A specimen with Σ-type intermediate stiffeners provides better performance compared to all other types of intermediate stiffeners.
-
Intermediate stiffener significantly affects the strength and behaviour of the sections.
-
The average and standard deviation of PEXP/PFEM are 0.92 and 0.08, respectively.
-
The mean values of PEXP and PDSM and PFEM and PDSM are 0.88 and 0.95, respectively. Similarly, standard deviations of PEXP and PDSM and PFEM and PDSM are 0.09 and 0.04, respectively.
-
From this comparison, it is observed that DSM specification predicts the strength almost equal to the experiment and finite element analysis. However, all the values are below to the one.
-
Hence, a new design expression is proposed and also verified with the results available from the literature.
-
The mean and standard deviation of PEXP/PProp are 1.04 and 0.03, respectively. From the results, it is concluded that the proposed design equation reasonably predicts the strength of the lipped channel column with and without intermediate stiffener.
References
Anil Kumar MV, Kalyanaraman V (2014) Distortional buckling of CFS stiffened lipped channel compression members. J Struct Eng. https://doi.org/10.1061/(asce)st.1943-541x.0001027
Aruna G, Sukumar S, Karthika V (2015) Study on cold-formed steel built-up square sections with intermediate flange and web stiffeners. Asian J Civ Eng (bhrc) 16:919–931. https://doi.org/10.1061/(ASCE)0733-9445(2008)134:5(727)
Chen J, He Y, Jin WL (2010) Stub column tests of thin-walled complex section with intermediate stiffeners. Thin-Walled Structures 48:423–429. https://doi.org/10.1016/j.tws.2010.01.008
Hancock GJ (1985) Distortional buckling of steel storage rack columns. J Struct Eng 111:2770–2783. https://doi.org/10.1680/stbu.12.00055
He Z, Zhou X, Liu Z, Chen M (2014) Post-buckling behaviour and DSM design of web-stiffened lipped channel columns with distortional and local mode Interaction. Thin-Walled Struct 84:189–203. https://doi.org/10.1016/j.tws.2014.07.001
Kwon YB, Hancock GJ (1992) Tests of cold-formed channels with local and distortional buckling. J Struct Eng 117(7):438–448
Kwon YB, Kim BS, Hancock GJ (2009) Compression tests of high strength cold-formed steel channels with buckling interaction. J Constr Steel Res 65:278–289. https://doi.org/10.1016/j.jcsr.2008.07.005
Liu Y (2008) Crashworthiness design of multi-corner thin-walled columns. Thin-Walled Structures 46:1329–1337. https://doi.org/10.1016/j.tws.2008.04.003
Manikandan P, Arun N (2016) Behaviour of partially closed stiffened cold-formed steel compression member. Arab J Sci Eng. https://doi.org/10.1007/s13369-015-2015-0
Nguyen HT, Kim SE (2009) “Buckling of composite columns of lipped-channel and hat sections with web stiffener. Thin-Walled Struct 47(2009):1149–1160
Schafer BW, Pekoz T (1998a) Cold-formed steel members with multiple longitudinal intermediate stiffeners. J Struct Eng 124:17060. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:10(1175)
Schafer B, Pekoz T (1998b) Computational modelling of cold-formed steel: characterizing geometrical imperfections and residual stresses. J Constr Steel Res. https://doi.org/10.1016/s0143-974x(98)00007-8
Sukumar S, Parameswaran P, Jayagopal LS (2006) Local distortional and Euler-buckling of thin walled built-up open sections under compression. J Struct Eng SERC India 32:447–454
Wang C, Zhang Z, Zhao D, Liu Q (2016) Compression tests and numerical analysis of web-stiffened channels with complex edge stiffeners. J Constr Steel Res 116:29–39. https://doi.org/10.1016/j.jcsr.2015.08.013/
Yan J, Young B (2002) Column tests of cold-formed steel channels with complex stiffeners. J Struct Eng 128:737–745. https://doi.org/10.1061/(asce)0733-9445(2002)128:6(737)
Yang D, Hancock GJ (2004) Compression tests of high strength steel channel columns with interaction between local and distortional buckling. J Struct Eng 130(12):1298–1305. https://doi.org/10.1061/(ASCE)0733-9445(2004)130:12(1954)
Yap DCY, Hancock GJ (2011) Experimental study of high-strength cold-formed stiffened-web C-sections in compressions. J Struct Eng 137:162–172. https://doi.org/10.1061/ASCEST.1943-541X.0000271
Zhang JH, Young B (2015) Numerical investigation and design of cold-formed steel built-up open section columns with longitudinal stiffeners. Thin-Walled Struct 89(2015):178–191
Zhang Y, Wang C, Zhang Z (2007) Tests and finite element analysis of pin-ended channel columns with inclined simple edge stiffeners. J Constr Steel Res 63:383–395. https://doi.org/10.1016/j.jcsr.2006.04.008
Zhou X, Liu Z, He Z (2015) General distortional buckling formulae for both fixed-ended and pinned-ended C-section columns. Thin Walled Struct 94:603–611. https://doi.org/10.1016/j.tws.2015.04.032
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Manikandan, P., Sukumar, S. & Kannan, K. Distortional buckling behaviour of intermediate cold-formed steel lipped channel section with various web stiffeners under compression. Int J Adv Struct Eng 10, 189–198 (2018). https://doi.org/10.1007/s40091-018-0191-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-018-0191-3