Abstract
SRCFT columns are formed by inserting a steel section into a concrete-filled steel tube. These types of columns are named steel-reinforced concrete-filled steel tubular (SRCFT) columns. The current study aims at investigating the various types of reinforcing steel section to improve the strength and hysteresis behavior of SRCFT columns under axial and lateral cyclic loading. To attain this objective, a numerical study has been conducted on a series of composite columns. First, FEM procedure has been verified by the use of available experimental studies. Next, eight composite columns having different types of cross sections were analyzed. For comparison purpose, the base model was a CFT column used as a benchmark specimen. Nevertheless, the other specimens were SRCFT types. The results indicate that reinforcement of a CFT column through this method leads to enhancement in load-carrying capacity, enhancement in lateral drift ratio, ductility, preventing of local buckling in steel shell, and enhancement in energy absorption capacity. Under cyclic displacement history, it was observed that the use of cross-shaped reinforcing steel section causes a higher level of energy dissipation and the moment of inertia of the reinforcing steel sections was found to be the most significant parameter affecting the hysteresis behavior of SRCFT columns.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Composite columns have higher strength and ductility efficiency due to composite action between steel and concrete core. In this type of composite column, the concrete can be plain such as (CFT) or reinforced concrete with steel bar (RCFT). Current studies (Xiamuxi and Hasegawa 2012; Endo et al. 2000; Hua et al. 2005; Xiamuxi and Hasegawa 2011) show that RCFT columns have better performance regarding moderate and severe earthquake excitations, higher toughness, and ductility in comparison with CFT columns.
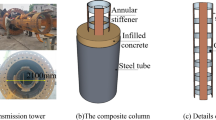
A new form of concrete-filled steel tube (CFT) column, namely steel-reinforced concrete-filled steel tubular (SRCFT) column, has been proposed recently (Ellobody and Young 2006; Elchalakani and Zhao 2008). The new composite column consists of a steel tube outside and a reinforcing steel section inside to reinforce concrete, as shown in Fig. 1.
Hamidian et al. (2016) have investigated the axial compressive behaviors of concrete-filled steel tube columns reinforced with different spiral pitch spacing. They found that the rate of pitch spacing has an important role on the post-yield behavior of the reinforced concrete-filled steel tube. The results show that as the rate of pitch spacing decreases, the post-yield behavior of SRCFTs improves. In addition, the effectiveness of the pitch spacing rate on the post-yield behavior of a SRCFT column is more than the thickness rate of the steel tube. Wang et al. (2004) investigated the strength and ductility of cross-shaped steel-reinforced concrete-filled tube (SRCFT) columns subjected to axial compressive loads. The results showed that composite columns had higher strength, energy absorption capacity, and ductility performance due to the composite action between steel tube, reinforcing steel section, and concrete. Chang et al. (2012) present a numerical study of cyclically loaded cross-shaped steel-reinforced concrete-filled tube (SRCFT) and the mechanical performance of SRCFT columns under cyclic loading. They found that the presence of the section steel could carry the lateral load and reduce the tensile zone of the concrete section. The structural steel section could provide a confinement effect on the concrete core and increase the load-carrying capacity and post-peak strength of SRCFT columns. Lai and Ho (2016) mentioned that the composite action could not be fully developed because of various dilatation attributes of concrete and steel tube in the elastic stage. In addition, due to the inelastic outward buckling of steel tube, CFT columns might suffer serious degradation. Qin and Xiao (2013) have been conducted a research on concrete-filled steel tube columns subjected to cyclic lateral force. They found that the ratio of diameter to thickness and the material properties strongly affect the seismic behavior of CFT columns. Better performance could be observed for CFT columns with smaller tube diameter to thickness ratio and higher material strengths.
The reinforcing steel section has a significant role in improving the strength of SRCFT columns and due to the lack of previous researches, this paper presents the mechanical and hysteretic behavior of different types of SRCFT columns under compressive axial and lateral cyclic loading.
Finite-element modeling of SRCFT columns
Understanding the structural behavior of SRCFT columns and caring out a comparative investigation, geometric, and material nonlinear finite-element analyses based on the commercial FE package ANSYS® User’s Manual (2005) have been undertaken under axial and lateral cyclic loading. In this paper, the effect of various types of reinforcing steel sections and interaction between steel and concrete surface has been investigated.
Characteristics of finite-element modeling
For modeling of various components of SRCFT column, ANSYS® User’s Manual (2005) elements and capabilities are as follows.
The concrete was modeled using a special concrete element SOLID 65. This element is an eight-node solid brick element that has crushing (compressive) and cracking (tensile) capabilities. For modeling of steel tube and reinforcing steel profile, a 3D solid element SOLID 45 was used. The element has plasticity, creep, swelling, stress stiffening, large deflection, and large strain capabilities. CONTAC52 (for the modeling of gap between steel and concrete) represents two surfaces that might maintain or break physical contact or might slide relative to each other. SHELL43 (for the modeling of the rigid plate for load applying) is well suited to model linear, warped, and moderately thick shell structures. The element has plasticity, stress stiffening, creep, large strain, and large deflection capabilities.
Material characteristics
For multi-linear isotropic properties, stress–strain relation of concrete was defined based on modified Popovic model (1973) for un-confined concrete and Belarbi and Hsu’s model (1994) was used for modeling the concrete tensile behavior. The model presented by Mander et al. (1988) for confined concrete is a simplified version of the Karsan and Jirsa (1969) model that also models the capability of concrete to carry some tensile stresses. The envelope curve is assumed to be given by the Popovic equation, which also accounts for the effect of confinement.
The stress–strain behavior of un-confined concrete and the steel wall, used for material and geometric static analyses, is given in Figs. 2 and 3, respectively.
For the un-confined concrete element, the elastic modules (Ex = 3E4 MPa), the Poisson’s ratio (ν xy = 0.2), the values for the ultimate tensile strength (f r = 3.72), and ultimate compressive strength (fc = 40 MPa) are the properties of isotropic material, as shown in Fig. 2. Considering Fig. 3, the behavior of steel is characterized with an initial linear elastic portion of stress–strain relationship with a modulus of elasticity, 2E5 MPa and up to the yield stress fy (ST 37 with F u = 370 N/mm2), is equal to 240 MPa, followed by a strain plateau of varying length (strain = 0.015) and a following region of strain hardening.
Verification of finite-element modeling under axial loading
To verify the accuracy and validity of the finite-element modeling of SRCFT columns under axial loading, the numerical results obtained from material and geometric nonlinear static analysis have been compared with the experimental test result of Wang et al. (2004). Table 1 shows material and geometric property of test specimen (NS-A1) for the verification purpose, where H is the height of column, D is diameter of circular cross section, t is thickness of steel tube, fy is yield stress of steel, Es is elastic modulus of steel, fc′ is specified stress of concrete, and Ec is elastic modulus of concrete. The monotonic axial compression was applied for all specimens. All nodes in the base of column were restraint, whereas the only degree of freedom for top nodes of column was along the column height (z direction).
Figure 4 illustrates that theoretical behavior was simulated using ANSYS 10.0 finite-element static analysis, followed closely the actual behavior exhibited by the experimental model. Consequently, it was found that the finite-element model is reliable enough to be simulated for nonlinear analyses of steel-reinforced concrete-filled steel tubular (SRCFT) columns. Figure 5a–c shows meshing, deformation form and concrete crack of NS-A1 specimen after finite-element analysis, respectively. It is noticeable to say that for buckling analysis according to ANSYS user’s manual, a perturbation load was applied to specimen.

After Wang et al. (2004)
Experimental and numerical responses of a SRCFT column under axial loading, NS-A1 specimen.
Verification of finite-element modeling under lateral cyclic loading
To verify the accuracy and validity of the finite-element modeling under lateral cyclic loading, the experimental test results of a previously published test specimen by Chang et al. (2012) were used and compared with the numerical results obtained from material and geometric nonlinear static analysis for calibration of analyses. The geometrical and material parameters for the test specimen are summarized in Table 2. In this table, fy1 and fy2 are yield strengths for the steel tube and the section steel, respectively. fcu is the strength of tested cube for the concrete.
As illustrated in Fig. 6, a comparison between hysteresis loops of test result and FE modeling lateral load–displacement curve indicated that the maximum lateral load and displacement, and degradation of shear strength towards the enclosed area of loops of FEM technique were fairly close to experimental data and they were in reasonable agreement. Contour plots of Von-Mises stress distribution, yielding area, hinge equivalent plastic, and lateral deformation of column are illustrated in Fig. 7. The higher stress at the column base caused flexural cracking started at the early stages of loading and the number of flexural cracks increased and propagated with increasing in drift ratios. Therefore, the numerical result of SRCFT column subjected to lateral cyclic loading was in good agreement with experimental data to estimate the maximum lateral load capacity of columns. This confirms that the present numerical model can be used with confidence to simulate the behavior of SRCFT columns under lateral cyclic loading.

After Chang et al. (2012)
Comparison of lateral force–displacement curves between numerical and test results of HC12-1 specimen.
Numerical results of SRCFT specimens under axial loading
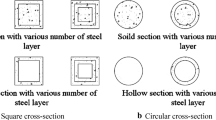
To investigate the behavior of SRCFT columns and compare them with the CFTs, 12 CFT and SRCFT specimens in two groups have been considered for the analyses, as shown in Figs. 8 and 9, respectively.
To carry out the analyses, some assumptions were considered with the following details:
-
The column is not slender and all nodes are restrained at the columns’ base and top.
-
The internal steel reinforcement was selected from among DIN standard profiles and dimension. In addition, geometric parameters of CFT specimens controlled by the help of BS 5400-1 (1990) and EC4 (1994) codes.
-
The units of length and force are in millimeter and Newton units, respectively.
-
The columns are considered as fixed-end columns.
-
Modulus of elasticity of steel is in the form of Es = 2E5 MPa.
-
The yield strength of steel is in the form of fy = 240 MPa.
-
The compressive strength of concrete is in the form of fc′ = 40 MPa.
-
The concrete modulus of elasticity of concrete is in the form Ec = 3E4 MPa.
-
Length of specimens, L = 6000 mm.
-
Area percentage of steel reinforcement ratio to the total cross-sectional area = ρs.
-
Circular SRCFT column reinforced with IPB (120, 160, 200) steel section, 2 IPE steel section, and cross-shaped steel section, respectively = CB (120, 160, 200), C 2 IPE, C-Cross.
-
Square SRCFT column reinforced with IPB (120, 160, 200) steel section, 2 IPE steel section, and cross-shaped steel section, respectively = SB (120, 160, 200), S 2 IPE, S-Cross.
-
Circular CFT column and square CFT column, respectively = C-CFT, S-CFT.
The specifications of the first and second groups of SRCFT columns are given in Table 3.
Effect of ratio of reinforcing steel section
To investigate the ratio of steel section area total area, first two common circular and square CFT columns (C-CFT and S-CFT) have been analyzed. Then, to investigate the effect of the reinforcing steel section, three types of circular and square CFT sections, each reinforced by IPB120, IPB160, and IPB200 have been analyzed. Figure 10a, b shows the comparison curves of load–lateral deflection of circular and square columns, respectively. As expected, by the increase of ρs, load-carrying capacity of sections increases.
Therefore, variation of reinforcing steel ratio had a significant effect on the performance of SRCFT columns under axial loading in such a way that load reduction in SRCFT columns with lower ρ is more than the states which had higher reinforcing ratio due to larger cross-sectional area of the reinforcing steel profiles.
However, in Fig. 11, to accurately investigate the effect of ρs on the increase of load-carrying capacity of SRCFT columns, strength increments in SRCFT specimens in comparison with CFT section have been indicated. Figure 11 indicates that with the increase of axial deformation, axial load increases. In a way that for the specimen CB200 at axial deformation about 10 mm, this increment is about 50%, and at axial deformation about 60 mm, this increment is about 100%.
It shows that increase in load-carrying capacity of column after post-buckling level is more obvious and more tangible. In addition, it is absorbed that increase in load-carrying capacity of circular SRCFT columns is superior to that of Square sections. The significant point is that, at square CFT columns, load buckling occurs on the steel shell at axial deformation about 28 mm. On the other hand, by reinforcing CFT section with the reinforcing steel section, load-carrying capacity of column increases and local buckling of the steel shell does not occur. In addition, the column is able to bear more deflections.
Figure 12a, b presents the deformed shape of square CFT column before and after reinforcing by a steel section, respectively. As demonstrated in Fig. 12a, at common square CFT columns, buckling and separation of steel shell from concrete core occur at middle point of length of column. However, this section after being reinforced by a steel section (Fig. 12b) does not show any local buckling and loss of strength is just because of overall buckling of the column.
Effect of types of reinforcing steel section
To investigate the effect of steel section shape on the increment of column strength, first, circular and square CFT specimen (C-CFT and S-CFT) of each group has been analyzed. Then, three types of circular SRCFT columns (C-Cross, CB 200, and C 2 IPE) and square SRCFT (S-Cross, SB 200, and S 2 IPE) columns of each groups with the same cross-sectional area of reinforcing steel sections (IPB200, 2 IPE, and cross section) have been analyzed. Figure 13a, b shows the axial load–axial deformation curves of the specimens in the first and second groups, respectively. Figure 13a shows that the yield load and stiffness of C-Cross specimen are higher than that of the CB 200 and C 2 IPE specimens. These findings clearly show the considerable effects of reinforcing steel section on the behavior of SRCFT columns. Therefore, C-Cross specimen had the best load–deflection behavior than to CB 200 and C 2 IPE specimens towards more stable post buckling behavior with admissible descending branch of strength degradation. The influence of higher moment inertia of C-Cross-reinforcing steel profiles and the confinement effect of concrete were the main reasons of better behavior and helped to delay the formation of internal splitting cracks along the steel profiles length. It is worth noting that the SRCFT specimen shows appropriate behavior in comparison with the CFT specimen due to the use of reinforcing steel section.
Figure 13 demonstrates that under axial loading, at small deflections, reinforcing steel section shape does not have any impact on the strength of SRCFT columns. However, at large deflections, the effect of reinforcing steel section appears gradually. In addition, it is observed that S-Cross, SB 200, and S 2 IPE sections have the highest impacts on the increment of SRCFT columns’ strength, respectively.
Effect of interaction between steel and concrete
To get a better realization of the interaction mechanism, three types of circular SRCFT columns (C-Cross, CB 200, and C 2 IPE) and square SRCFT columns (S-Cross, SB 200, and S 2 IPE) from each group have been analyzed. The specimens were loaded under axial compression. The geometric and material specifications of the specimens are illustrated in Table 3. For this purpose, first, reinforcing steel section (St.steel) and CFT section have been separately analyzed. Then, the superposed curves, achieved from the addition of the St.steel section and CFT section, have been compared with the curves achieved from the analyses of SRCFT specimens.
Figure 14a, b shows the axial load–axial displacement responses of circular and square SRCFT specimens reinforced with 2 IPE steel sections, respectively.
Considering the curves of SRCFT and St.Steel + CFT achieved from the analysis of C 2 IPE specimen, it is obvious that at the linear section of the curves, the interaction between steel and concrete has not exhibited a higher impact on the load-carrying capacity of columns. After this point, this mechanism is very efficient, because the concrete prevents the local buckling of reinforcing steel section and interface friction between the reinforcing steel section and the concrete surface will cause more transition of contact stress between two surfaces, and therefore, the axial load carrying of specimen will be increased.
Considering Fig. 14, it is obvious that the degradation of axial strength at SRCFT column was initiated at a deformation equal to 20 mm, whereas this quantity for St.Steel + CFT specimen is approximately 12 mm; thus, the important role of contact stress in increment of axial strength can be perceived.
Figure 15 shows the strength increment percentage of circular and square SRCFT specimens in comparison with the superposed strength of reinforcing steel section and CFT specimen (St.Steel + CFT) of corresponding SRCFT specimens. For comparison purpose, CFT specimens of each group have been selected as a benchmark. Considering the envelopes in Fig. 15, it is observed that the interaction between steel and concrete in circular section is considerably higher than that of square sections. In addition, the strength and performance of 2 IPE specimens from the viewpoint of interaction between steel and concrete are higher than B 200 section. Furthermore, strength and performance of B 200 is higher than cruciform section. In SRCFT column reinforced with 2 IPE section, the increment in SRCFT columns’ strength at the point of deflection about 60 mm is around 75%, compared with the superposed strength of reinforcing steel section and CFT column.
Numerical results of SRCFT specimens under lateral cyclic loading
To investigate the effect of steel section shapes on the hysteretic behavior of SRCFT columns, first, a monotonic axial load equal to 0.3 · fc′ · A g was applied on the top nodes of the column. Then, displacement history according to Hajjar and Goerley (1997) was applied to model the condition of cyclic loading, as shown in Fig. 16.
To illustrate the impact of steel reinforcement on the hysteretic behavior of SRCFT columns, four specimens were selected with the following details and geometric properties, as given in Table 4.
-
The columns are considered as fixed-end columns.
-
Es = 2E5 MPa, fy = 240 MPa, fc′ = 40 MPa, Ec = 3E4 MPa, L = 3000 mm.
The total cross-sectional area of the outer steel tube is 23,047 mm2 and the cross-sectional area of concrete is 204,282 mm2. In addition, the area of steel reinforcement is 7810 mm2. It is noticeable that the area of cross-shaped section for the reinforcing steel section is equal to IPB 200 standard steel profile.
Hysteretic behavior of SRCFT columns
Comparative investigation into the behavior of different types of reinforcing steel section on the hysteretic loops, ductility, elastic stiffness, and energy dissipation capacity of specimens was investigated here based on analyses results. Shear strength–drift ratio hysteretic loops for CFT and SRCFT specimens are shown in Fig. 17.
It is observed that the maximum shear force in cycle No. 8 in CFT specimen is 1180 kN where as this quantity for any of SRCFT specimens is more than 1298 kN. Figure 19 clearly shows that SRCFT specimens have the lower degradation of load at the further cycles. However, in SRCFT columns, the reinforcing steel section will not be buckled before reaching the steel wall to the yield stress. Thus, the confinement effect of concrete has been increased.
Considering Fig. 17, the degradation of strength in CFT column was began suddenly at 4% of lateral displacement, whereas the degradation of shear strength has inclined slope at SRCFT column. At the end of loading, crushing of concrete and local buckling of steel tube was observed for CFT column, while those were prevented at SRCFT column because of good effect of reinforcing steel section.
Comparison of the hysteresis loops of SRCFT columns
To compare the hysteresis loops of SRCFT columns, the envelope curves of hysteresis loops regarding the four specimens are illustrated in Fig. 18. This envelope clearly indicates the lesser degradation of load and higher shear strength of SRCFT columns than CFT columns.
By considering the specimens, it is observed that C-Cross, CB 200, and C 2 IPE sections (which both have the same cross-sectional area) have the higher moment of inertia, respectively. Figure 18 shows that C-Cross, CB 200, and C 2 IPE sections have the higher amount of shear strength, respectively. Therefore, it is concluded that shear strength capacity of SRCFT columns has a positive correlation with the moment of inertia of reinforcing steel section under cyclic loading.
In the envelope curves of hysteresis loops, it is observed that CFT column loses its strength in upper cycles due to the concrete crushing of steel shell. However, this phenomenon is not occurs in SRCFT columns because of the effect of reinforcing steel section in the concrete core confinement and the prevention of quick crushing of concrete.
Comparison of energy dissipation
Energy dissipation is a very important parameter to describe the hysteretic performance of columns. The area enclosed by each cycle of displacement has been considered as the energy dissipated from the column at the same cycle.
More quantity of energy dissipated of a column is an indicator of the convenient cyclic behavior. Furthermore, the column will be able to withstand more cycles of displacement. Figure 19 illustrates the comparative column chart of energy dissipation in each cycle of loading. It shows that the implementation of reinforcing steel section resulted in higher dissipated energy and a more stable hysteretic behavior for SRCFT specimens. In addition, C-Cross, C 2 IPE, and CB 200 specimens showed the best performance regarding stiffness, ductility, and energy absorption capacity, respectively.
The quantitative comparison made between some of the parameters involved including the maximum shear strength, the energy dissipated, and the plastic stiffness in cycle No. 10, for CFT and SRCFT column is given in Table 5. For comparison, CFT specimen (C-CFT) has been selected as a benchmark specimen.
Considering the maximum shear strength parameter, C-Cross specimen showed differences about 24% higher than that of the CFT specimen. Considering the energy dissipation parameter, SRCFT specimen reinforced with cross-shaped steel section had almost 159% improvement in comparison with the circular CFT column. For plastic stiffness, C-Cross specimen exhibited a minimum value of 15% increase against the circular CFT specimen. It is obvious from the findings provided in Table 5 that SRCFT columns have higher shear strength, absorbing energy capacity, and more appropriate ductility characteristics compared to CFT columns. Furthermore, columns C-Cross, C 2 IPE, and CB 200 showed the best performance with regard to stiffness, the maximum shear strength, and energy absorption capacity, respectively.
Summery and conclusions
In the present study, through finite-element modeling, the mechanical and hysteretic behavior of steel-reinforced CFT column (SRCFT) was investigated and compared with common CFT columns. The contact stress between steel and concrete causes more axial load strength and larger region of permanent axial strength and the degradation of strength at larger axial displacement. Use of cross steel reinforcement for CFT column caused more energy absorption under cyclic displacement history in comparison with CFT columns. Shear strength of SRCFT column was increased and the degradation of shear strength of specimen occurred at larger lateral drift ratio than CFT column. This performance is related to an increment in total area of steel component, increment of concrete confinement supplied by steel reinforcement, and obtained interruption at cracking of concrete. Thus, SRCFT column can be adopted for many structural engineering applications especially in moment-resistant frames.
-
1.
Variation of reinforcing steel ratio had a significant effect on the performance of SRCFT columns under axial loading in such a way that load reduction in SRCFT columns with lower ρ is more than the states which had higher reinforcing ratio. By the increase of ρs parameter, load-carrying capacity of section increases. This increment at CFT circular section is considerably higher than that of CFT square section.
-
2.
The effect of types of reinforcing steel section from the viewpoint of load-carrying capacity and stiffness, and it is resulted that C-Cross specimen has a better performance compared to that of CB 200 and C 2 IPE. The influence of higher moment inertia of C-Cross-reinforcing steel profiles, the confinement effect of concrete was the main reasons of better behavior and helped to delay the formation of internal splitting cracks along the steel profiles length.
-
3.
Load-bearing capacity of SRCFT columns compared to the superposed load bearing of reinforcing steel section and CFT columns increases because of the positive effects of interaction between steel and concrete in SRCFT columns. The effects of composite action in C 2 IPE specimens are considerably higher than that of CB 200 and C-Cross specimens.
-
4.
It is found that the presence of the section steel can carry the lateral load and reduce the tensile zone of the concrete section. As a result, SRCFT columns have higher stiffness and peak lateral load than common CFT columns even with the same geometrical and material parameters. The section steel can also enhance the deformation ability of a SRCFT column. The flanges and webs of the reinforcing steel section can also give some confining effect on the core concrete.
-
5.
By the investigation of envelope curves of hysteresis loops of SRCFT columns, it is observed that reinforcing CFT column by a steel section causes less degradation of load at large deflections, increase of energy absorption capacity, and shows the appropriate behavior of them under lateral cyclic loading.
-
6.
Considering the results, C-Cross, C 2 IPE, and CB 200 sections have the higher amount of moment of inertia, higher shear strength, and energy absorption capacity, respectively. Therefore, the moment of inertia in the reinforcing steel section was found to be the most significant parameter on the hysteresis behavior of SRCFT columns.
Design recommendation
-
The reinforcing steel cross section is offered for the design of SRCFT columns under axial loading. For the design of SRCFT columns under cyclic loading, reinforcing steel section with the maximum moment of inertia is proposed. In general, considering the symmetry property of cross-shaped steel section, this section has a better performance compared to the other sections for axial and seismic loading. Therefore, cross-shaped steel section is proposed for the reinforcement of CFT columns.
References
ANSYS® User’s Manual (2005) Structural Analysis Guide. Release 10.0 Documentation
Belarbi A, Hsu TTC (1994) Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete. Struct J 91(4):465–474
BS 5400-1 (1990) Steel, concrete and composite bridges, code of practice for design of concrete bridges
Chang X, Wei YY, Yun YC (2012) Analysis of steel-reinforced concrete-filled steel tubular (SRCFST) columns under cyclic loading. Constr Build Mater 28:88–95
Elchalakani M, Zhao XL (2008) Concrete-filled cold-formed circular steel tubes subjected to variable amplitude cyclic pure bending. Eng Struct 30:287–299
Ellobody E, Young B (2006) Design and behavior of concrete-filled cold formed stainless steel tube columns. Eng Struct 28:716–728
Endo T, Shioi Y, Hasegawa A, Wang HJ (2000) Experimental study on reinforced concrete filled steel tubular structures. In: 25th conference on our world in concrete & structures, Singapore, 23–24 Aug 2000
Euro code 4 (1994) Design of composite steel and concrete structures. Commission of the European Communities, British Steel Institute, London
Hajjar JF, Goerley BC (1997) A cyclic nonlinear model for concrete filled tubes, formulation. J Struct Eng 123(6):736–744
Hamidian MR, Jumaat MZ, Alengaram UJ, Ramli SNH, Shafigh P (2016) Pitch spacing effect on the axial compressive behavior of spirally reinforced concrete-filled steel tube. Thin Walled Struct 100:213–223
Hua W, Wang HJ, Hasegawa A, Shioi Y, Iwasaki S, Miyamoto Y (2005) Study on strength of reinforced concrete filled circular steel tubular columns. Struct Eng 19:653–677
Karsan ID, Jirsa JO (1969) Behavior of concrete under compressive loadings. ASCE J Struct Div 95(12):2543–2563
Lai MH, Ho JCM (2016) A theoretical axial stress-strain model for circular concrete-filled-steel-tube columns. Eng Struct 125:124–143
Mander JB, Priestley MJN, Park R (1988) Theoretical stress–strain model for confined concrete. J Struct Eng 114(8):1804–1826
Popovic S (1973) A numerical approach to the complete stress–strain curve of concrete. Cem Concr Res 3(5):583–599
Qin P, Xiao Y (2013) Research on concrete-filled steel tube columns subjected to cyclic lateral force. In: The 2013 world congress on advances in structural engineering and mechanics. ASEM13, Jeju, Korea
Wang Q, Zhao D, Guan P (2004) Experimental study on the strength and ductility of steel tubular columns filled with steel-reinforced concrete. Eng Struct 26:907–915
Xiamuxi A, Hasegawa A (2011) Compression test of RCFT columns with thin-walled steel tube and high strength concrete. Steel Compos Struct 11:391–402
Xiamuxi A, Hasegawa A (2012) A study on axial compressive behaviors of reinforced concrete filled tubular steel columns. J Constr Steel Res 76:144–154
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to urisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Farajpourbonab, E., Kute, S.Y. & Inamdar, V.M. Steel-reinforced concrete-filled steel tubular columns under axial and lateral cyclic loading. Int J Adv Struct Eng 10, 61–72 (2018). https://doi.org/10.1007/s40091-018-0186-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-018-0186-0