Abstract
Rehabilitation of weak and damaged structures has been considered widely during recent years. A relatively modern way of strengthening concrete components is to confine parts under tension and shear by means of carbon fiber reinforce polymer (CFRP). This way of strengthening due to the conditions of composite materials such as light weight, linear elastic behavior until failure point, high tensile strength, high elastic modulus, resistance against corrosion, and high fatigue resistance has become so common. During structural strengthening by means of not pre-stressed FRP materials, usually, it is not possible to benefit from the maximum capacity of FRP materials. In addition, sometimes, the expensive cost of such materials will not make a suitable balance between rates of strengthening and consuming spending. Thus, pre-stressing CFRP materials has an undeniable role in the effective use of materials. In the current research, general procedure of simulation using finite-element method (FEM) by means of the numerical package ABAQUS has been presented. In this article, 12 reinforced concrete (RC) models in two states (strengthened with simple and pre-stressed CFRP) under cycling loading have been considered. A parametric study has been carried out in this research on the effects of parameters such as CFRP surface area, percentage of tensile steel rebar and pre-stressing stress on ultimate load carrying capacity (ULCC), stiffness, and the ability of depreciation energy for the samples. In the current article also, for design parameters, percentages of tensile steel rebars, surface area of CFPR sheets, and the effective pre-stressing stress in RC beams retrofitted with pre-stressed CFPR sheets have investigated. In this paper, it was investigated that using different amount of parameters such as steel rebar percentage, CFRP surface area percentage, and CFRP pre-stressing, the resulted ULCC and energy depreciation of the specimens was observed to be increasing and decreasing. Results from examined specimens with optimum steel rebar percentage, CFRP surface area percentage, and CFRP pre-stressing which had the most enhancement on ULCC and energy depreciation are reported in the current article.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
FRP materials to the form of outer coverage have been used for enhancing the resistance and improvement of the existing concrete structures from 1980s so far. The related FPR strengthening projects have been dramatically increased all over the world. This growth rate has started from a couple of projects to thousands during last decade. The EMPA Switzerland Institute can be mentioned as the primary researchers in the field of FPR strengthening. The researches were performed on CFRP strengthened RC beams in 1984. The most important advantages of using FRP sheets are the high ratio of resistance to weight and also high ratio of resistance to corrosion (Jankowiak 2012). The first quality would cause the ease of application in place and reduction of the wage cost. The second characteristic would cause the durability of execution. Different parts of strengthened structures with FRP systems with the forms of outer coverage are: beams, columns, walls, joints, chimneys, circular arches, tunnels, bins, pipes, and trusses. FRP coverage as an alternative for other strengthening strategies such as using steel sheets and ducts around concrete columns has been invented. The FRP coverage has been developed for the first time in 1980s in Japan and Europe for improvement of concrete structures. Nowadays, FRP systems have been used as steel sheet alternatives. FRP sheets are 2–10 times stronger than steel sheets, while they weigh 20% of steel sheets (Ahmad and van Gernert 1999). The limitations to use this sort of materials in civil engineering applications are just because of high cost. FRP composites are so resistant against the corrosion, salty, and alkali environment. Nowadays, FRP composites have been topic of wide spread studies as alternatives of steel bars and pre-stressed cables. The connection of steel sheets to tensile part of concrete pieces by epoxy resins to enhance bending strength of such pieces is a normal and durable method. This method has been used for strengthening of many bridges and buildings around the world. Since steel sheets would corrode and cause destruction of steel sheet connections with concrete, and also they are hard to establish and should be installed using extremely heavy machines, researchers have tried to replace FRP materials instead of steel (Darby 1999; Holloway 1999).
FRP composite materials are consisted of fibers and adhesive. In most of applied FRP composites, the behavior of fibers is unidirectional. Fibers perform capacity of FRP and adhesive distribute stress between fibers while keeping fibers unified. Among performed studies, many researchers have on the FRP strengthening of flexural members and also modes of failure specially the debonding failure mode (Zhang and Toshiyuki 2016; Pesic 2005). In addition, some researches have focused on manuals and design guide lines considering FRP applications in concrete structures (Pilakoutas et al. 2011).
In the current research, behavior of RC beams retrofitted with pre-stressed CFRP has been studied. It can be mentioned that the main difference between RC beams with pre-stressed steel cables and RC beams retrofitted with pre-stressed CFRP sheets is at the range of yielding. This is because FRP has linear behavior till to fracture unlike RC beams with pre-stressed steel cables in the failure behavior is due to yielding. Failure of RC beams with pre-stressed CFRP occurs with concrete crushing or FRP failure with no alert. Carbon fibers have the best behavior in pre-stressing application rather than other types of fibers; however, the expense is considerable (El-Hacha et al. 2001; Jonsson 2011).
Strengthening beams
Depending on the level of beams destructions, several solutions can be chosen for rehabilitation and strengthening of such structures. For instance, injecting resin, attaching steel sheets or FRP, concrete replacing, and using concrete jackets, could be mentioned of such rehabilitation and strengthening methods (Ahmad and van Gernert 1999).
FEM analyses
ABAQUS software, which is a perfect mean for simulating and analyzing based on FEM, has been applied for the numerical examination of models in the current research. Materials specifications and the numerical analyses approach are discussed as the following.
Plastic failure of concrete
This method of plastic failure is a capable mean to simulate the behavior of nonlinear concrete and semi brittle materials constructing elements. This model is suitable for plain concrete and reinforced concrete. The general idea of this method is applicable for monotonic, cyclic, and dynamical loading, and is also capable to carry out stiffness recovery under cyclic loading.
With this method of simulation, it is assumed that the concrete failure with two forms of cracking in tension and crushing under pressure would be assessed. The growth of yielding would be controlled by two factors of hardening. Plastic equivalent strain in tension and pressure \(\tilde{\varepsilon }_{\text{t}}^{\text{pl}}\) and \(\tilde{\varepsilon }_{\text{c}}^{\text{pl}}\) would control the concrete failure under tension and pressure.
Details of numerical simulations (Teng 2002; Meier et al. 1992)
Material characteristics were allocated to all the model components. For models which contact between components existed, mechanical specifications specified and connections and interactions specified as the following:
-
Connections and interactions between bars and concrete by the technique of embedded elements.
-
For the contact surfaces, properties of perpendicular to plane (hard contact) and tangential by method of penalty have been applied.
Suitable meshing for the model and assigning suitable structural elements for the components were applied as the following: For beams sections by the form of C3D8R elements (3D continual element with 8 nodes for integration) and for placing bars, axial elements of B31 and also for polymer sheets S8R (surface element with 8 nodes of integration) have been used. All examined model data informations regarding materials specifications, geometry and dimensions, steel rebar percentages, CFRP surface area percentages, and CFRP pre-stressing, are depicted in Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
Validation
Monotonic examination
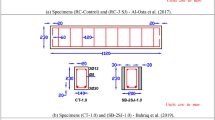
For validation of FE simulation, experiments done by Xue et al. (2010) have been referenced. With this series of examinations, researchers assessed the effects of CFRP sheets on the resistance of reinforced concrete beams with different proportions of steel rebars. From the tested samples, PC-1 model has been chosen for FE simulation in ABAQUS. Figures 1 and 2 illustrate tested sample (Xue et al. 2010).
Experimental sample of PC-1 reinforced concrete beam retrofitted with CFRP (Xue et al. 2010)
Selected beam BC-1 for finite-element analysis (dimensions are in mm) (Xue et al. 2010)
Geometric and mechanical characteristics of CFRP, steel rebars and concrete assigned to ABAQUS, are presented in the following tables.
Pre-stressing rate of CFRP sheets was 1052 MPa which was about 42.1% of ULCC. At the first step of loading, stress in the CFRP achieved the pre-stressing stress rate as shown in Fig. 3.
Figure 4 presents experimental load–displacement curve of the sample beam BC-1 in comparison with FE.
Cyclic examination
To control validation of FE analysis of cyclic behavior of RC member, the study bellow is presented. In this study, a reinforced concrete beam-column specimen under the influence of axial and shear force was modeled in the ABAQUS software. Experimental test setup of the tested beam-column is shown below. To validate the modeling, laboratory model of the concrete beam-column was investigated. This beam-column was located first against axial load and then lateral load as illustrated (Bae 2005). In Fig. 5 schematic illustration and dimensions of the tested RC beam-column is presented.
Image of the investigated reinforced concrete beam-column (Bae 2005)
The laboratory test setup and the FE modeled sample in the software are shown in Figs. 6 and 7. RC specimen has been modeled in ABAQUS software.
Test setup of the RC sample in laboratory devices (Bae 2005)
As mentioned previously, after the application of the axial load, the specimen was subjected to progressively increasing lateral displacement cycles following the displacement protocol, shown in the figure below. As such, three fully reversed cycles were applied for each displacement step as required by FEMA 356 (2000).
Figure 8 shows that the lateral force–displacement response diagram of the cyclic loading of the tested specimen resulted from the FE analysis (drawn with dots), which is very close to the experimental result obtained from (Bae 2005). Therefore, the study validation has been achieved.
FEM simulation process for parametric studies
In this section, procedure of FE simulation and total results originated from loading are presented. Totally, 12 RC models were strengthened with simple and pre-stressed CFRP and subjected to cyclic loading based on code Applied Technology Council (1992). ULCC, stiffness, and the ability of energy depreciation of these samples effected by parameters such as percentage of tensile steel, CFRP surface area, and the effect of pre-stressing stress. In Table 6, models specifications are represented.
In Table 6, samples 1–4 with the beam surface area of 250 × 150 mm and CFRP surface area of 50 × 1.4 mm and constant pre-stressing stress of 1052 MPa are presented.
For these samples with stable surface area of CFRP and pre-stressing stress, effects of variation in tensile steel rebar have been assessed. For samples 5–8 with stable percentage of tensile steel rebar and the rate of pre-stressing, the effect of CFRP surface area on ULCC and ability of depreciation were studied. Finally, for samples 9–12 effects of pre-stressing level was studied.
Effects of tensile steel percentage (A s)
In this section, four beams with tensile steel percentages of 0.45, 1.25, 1.36 and 1.61% in two states of strengthening with not pre-stressed and pre-stressed CFRP sheets were modeled and subjected to cyclic loading with displacement control of 5Δy. The rate of increasing of the resistance and the capability of energy depreciation were assessed in 4 percentages of tensile bars. In Table 7, characteristics of steel bars and strengthening CFRP are illustrated.
Following notes should be considered about Fig. 9:
-
Maximum load of beam number 1 with tensile steel rebar percentage of 0.45% strengthened with CFRP in two states without pre-stressing \(\sigma_{\text{eff}} = 0\,{\text{MPa}}\) and with pre-stressing stress of \(\sigma_{\text{eff}} = 1052\,{\text{MPa}}\), are 77.78 and 86.36 kN, respectively. It can be observed that the CFRP pre-stressing state resulted in 11% increase in ULCC.
-
Surface areas inside both diagrams which are equal to depreciated energy during cyclic loading for the both strengthening states with CFRP, were 1.59E+07 and 1.57E+07 N mm, respectively which caused increasing of 1.3% of this factor.
Considering Fig. 10, the following notes are obtained:
-
The ULCC of the beam strengthened with not pre-stressed CFRP was 92.19 kN at the ultimate displacement of 20.86 mm.
-
The ULCC of the beam strengthened with pre-stressed CFRP was 101.99 kN at the ultimate displacement of 21.89 mm. In this sample, the pre-stressing of CFRP sheets enhanced capacity of about 10.46%.
-
Surface areas inside both diagrams, which are equal to depreciated energy during cyclic loading for the two strengthening states, were 1.84E+07 and 1.93E+07 N mm, respectively, which enhanced this factor of about 4.89%.
The following notes can be considered about Fig. 11:
-
Beam capacity rate in two states of strengthening with pre-stressed and not pre-stressed CFRP was equal to: 104.88 and 97.13 kN, respectively. Pre-stressing with effective tensile stress of 1052 MPa for CFRP sheets caused 7.8% enhancement for ULCC.
-
On the other hand, energy depreciation ability resulted from pre-stressed CFRP sheets has increased from 2.06E+07 to 2.12E+07 N mm which enhanced this factor about 2.92%.
Considering results depicted in Fig. 12, the following descriptions are derived:
-
Maximum load capacity for this beam for the state of strengthened with not pre-stressed CFRP was calculated as 103.23 kN at the displacement of about 20.29 mm.
-
For the state of strengthening with pre-stressed CFRP, the rate of maximum load capacity of the beam reached to 110.93 kN when the displacement changed 21.79 mm. In this situation, increasing of 7.46% for ULCC has happened.
-
The surface area inside load–displacement diagram has changed from 2.17E+07 to 2.23E+07 N mm which showed the growth of 2.76%.
Effects of CFRP surface area
In this section, effect of geometric specifications of CFRP sheets on ULCC and ability of energy depreciation for RC beams strengthened with pre-stressed CFRP sheets would be presented. Samples for studying in this section are considered in Table 8. Parameters such as CFRP pre-stressing effect and percentage of tensile steel rebar are taken as constant parameters, and dimensions of CFRP sheets are variables.
In Figs. 13, 14, 15, 16, and 17, cyclic load–displacement curves of beam number 2–8 have been represented for the two states of strengthening with not pre-stressed and pre-stressed CFRP (with the effective pre-stressing stress of 1052 MPa). The results prepared from these samples would be criteria for the effects of geometric characteristics of CFRP sheets in ULCC and the energy depreciation ability of beams. The following notes are considered in this section:
-
The final load rate for the beam number 2 with tensile steel percentage of 1.25% and CFRP surface area percentage of 1.9% CFRP for two states of strengthening with not pre-stressed and with pre-stressed CFRP, were 92.33 and 101.99 kN, respectively. For this beam, the CFRP pre-stressing stress of 1052 MPa caused the enhancement of 10.46% in ULCC.
-
The surface area of both load–displacement curves which is equivalent to depreciated energy during cyclic loading was 1.84E+07 and 1.93E+07 N mm, respectively, which shows the enhancement of 4.89% for this factor.
Figure 13 represents cyclic load–displacement of beam number 5 with tensile steel percentage of 1.25% and CFRP percentage of 0.95% for two states of strengthening with not pre-stressed and with pre-stressed CFRP. Considering Fig. 10, the following notes can be driven:
-
With the pre-stressing of CFRP sheets with mentioned tension rate, ULCC changed from 84.94 to 93.83 kN in which this means almost 10.46% enhancement.
-
Surface area also has increased from 1.62E+07 to 1.67E+07 N mm which means about 3.08% enhancement.
Figure 15 illustrates diagram of load–displacement for beam number 6 with tensile steel percentage of 1.25% and CFRP surface area percentage of 2.85% (surface area 75 × 1.4 mm). The beam in this case which was strengthened with not pre-stressed CFRP sheets could bear maximum load of 100.12 kN. In the next step, the beam was strengthened with the same CFRP surface area with the pre-stressing stress of 1052 MPa, and the ULCC raised to 117.28 kN which has increased 17.14% in comparison with the previous step. In addition, enhancement of energy depreciation ability was about 5.19%.
Figure 16 depicts that using pre-stressed CFRP sheets with surface area percentage of about 3.80% of beam surface area, the ULCC increased from 114.67 to 126.67 kN which was about 10.46% increase. Moreover, energy depreciation in the beam increased from 1.96E+07 to 2.06E+07 N mm, which shows the enhancement of about 5.1%.
In Fig. 17, beam number 8 like number 2 had tensile steel percentage equal to 1.25% and CFRP surface area percentage of 1.90%. In the mentioned two samples, CFRP sheets were used with same surface area percentage; however, dimensions of the assembled sheets were different (1.4 × 50 mm for number 2 and 2.8 × 25 mm for number 8).
The following notes can be concluded:
-
The rate of final load caused by CFRP pre-stressing has increased from 95.1 to 105.15 kN which represented 10.5% enhancement. This growth of the ULCC was inconsiderable in comparison with the beam number 2.
-
Energy depreciation growth, with the value of 4.88%, also was negligible in comparison with the beam number 2.
Effects of pre-stressing stress
In the final stage, effects of value of pre-stressing stress on ULCC and depreciation ability have been studied. To realize that such parameter how and to what extend would affect the RC ULCC, it is necessary to compare the beams strengthened with not pre-stresses and pre-stressed. In this section, beams number 2 and 9–12 were explained with an initial CFRP pre-stressing stress of 1052, 250, 750, 1250, and 1750 MPa, respectively.
Table 9 represents characteristics of tensile steel rebars and strengthening CFRP sheets and pre-stressing levels for the samples 9–12.
In the next stage, beams were subjected to cyclic loading and the load–displacement curves were obtained. Considering diagrams illustrated in Fig. 18, the following notes are presented:
Load–displacement curves of reinforced concrete beams with tensile steel percentage of 1.61% and retrofitted with a without pre-stressing, b pre-stressed CFRP with the stress of 250 MPa, c pre-stressed CFRP with the stress of 750 MPa, d pre-stressed CFRP with the stress of 1052 MPa, e pre-stressed CFRP with the stress of 1250 MPa, and d pre-stressed CFRP with the stress of 1750 MPa
-
Considering pre-stressing stresses with the rates of 0, 250, 750, 1052, 1250, and 1750 MPa in concrete beam with tensile steel percentage of 1.25% and CFRP surface area percentage of 1.90%, ULCC reached to 81.13, 83.99, 87.91, 101.99, 91.45, and 95.61 kN.
-
Surface area which is equivalent to depreciated energy of selected 6 sample beams subjected to cyclic loading calculated as 1.84E+07, 1.86E+07, 1.92E+07, 2.03E0+7, 1.91E+07, and 2.96E+07 N mm.
Conclusion
-
In the section of FEM analysis, effects of tensile steel rebar percent for strengthened RC beams with pre-stressed CFRP on two parameters of ULCC and energy depreciation ability have been studied. Four sample beams with steel rebar percentage of 0.45, 1.25, 1.36, and 1.61% have been simulated which are available in Fig. 16; among these beams, the one with steel rebar percentage of 1.25% had the most enhancement. These final results are presented in Figs. 19, 20.
Fig. 19 -
In Sect. 5.2, effects of CFRP surface area percentage with the values of 0.95, 1.90, 2.85, 3.80, and 1.90% have been studied, which is between all of these five samples, the one with CFRP percentage of 2.85% experienced the highest percentage of ULCC and depreciated energy.
Finally, In Sect. 5.3, effects of CFRP pre-stressing of strengthened reinforced concrete beams on two parameters of ULCC and energy depreciation ability studied. In the current Sect. 5, beams with the initial pre-stressing stress values of 1052, 250, 750, 1250, and 1750 MPa have been simulated for which comparison with the results of mentioned parameters is presented in Table 10. Among all sample beams, the one with pre-stressing percentage of 42.1% and failure stress of 1052 MPa had the highest amount of enhancement percentage in ULCC and energy depreciation ability. Consequently, in this article, the pre-stressing percentage of 42.1% suggested and breaking stress is 1052 MPa.
References
Applied Technology Concil (1992) Guidelines for cyclic seismic testing of components of steel structures. ATC 24, Redwood City, CA
Ahmad O, van Gernert D (1999) Effect of longitudinal carbon fiber reinforced plastic laminates on shear capacity of reinforced concrete beams. American Concrete Institute, Farmington Hills, pp 933–943
Bae S (2005) Siesmic performance of full-scale reinforced concrete columns. Ph.D. dissertation, The University of Texas at Austin, p 312
Darby J (1999) Role of bonded fibre-reinforced composites in strengthening of structures. In: Hollaway LC, Leeming MB (eds) Strengthening of reinforced concrete structures using externally-bonded FRP composites in structural and civil engineering. Woodhead Publishing, Cambridge
El-Hacha R, Wight R, Green M (2001) Prestressed fibre-reinforced polymer laminates for strengthening. Prog Struct Mater Eng 3(2):111–121
Federal Emergency Management Agency (2000) Prestandard and commentary for the seismic rehabilitation of buildings. FEMA 356, Washington, DC
Holloway LC (1999). In: Hollaway LC, Leeming MB (eds) Strengthening of reinforced concrete structures: using externally-bonded FRP composites in structural and civil engineering. Angle Terre: CRC Press, Boca Raton
Jankowiak I (2012) Analysis of RC beams strengthened by CFRP strips—experimental and FEA study. Arch Civ Mech Eng 12(3):376–388
Jonsson B (2011) Prestressed FRP tendons in concrete beams. Master thesis in civil engineering with specialization in structural design submitted to the School of Science and Engineering at Reykjavik University
Meier U, Deuring M, Meier H, Schwegler G (1992) Strengthening of structures with CFRP laminates: research and applications in Switzerland
Pesic N (2005) Flexural analysis and design of reinforced concrete beams with externally bonded FRP reinforcement. Mater Struct 38(276):183–192
Pilakoutas K, Guadagnini M, Neocleous K, Matthys S (2011) Design guidelines for FRP reinforced concrete structures. Proc Inst Civ Eng Struct Build 164(SB4):255–263
Teng JG (2002) FRP-strengthened RC structures, 1st edn. Wiley, West Sussex
Xue W, Tan Y, Zeng L (2010) Flexural response predictions of reinforced concrete beams strengthened with prestressed CFRP plates. Compos Struct 92(3):612–622
Zhang W, Toshiyuki K (2016) Flexural strengthening of RC beams with externally bonded CFRP plate: experimental study on shear-peeling debonding. Mag Concr Res 68(14):724–738
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to urisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hojatkashani, A., Zanjani, S. Assessment of the behavior of reinforced concrete beams retrofitted with pre-stressed CFPR subjected to cyclic loading. Int J Adv Struct Eng 10, 17–28 (2018). https://doi.org/10.1007/s40091-018-0182-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-018-0182-4