Advertisement

Study of wind-induced vibrations in tall buildings with tuned mass dampers taking into account vortices effects

  • Ali Ajilian Momtaz
  • Mohamadreza Akhavan Abdollahian
  • Anooshiravan Farshidianfar
Open Access
Original Research
First Online:

Abstract

In recent years, construction of tall buildings has been of great interest. Use of lightweight materials in such structures reduces stiffness and damping, making the building more influenced by wind loads. Moreover, tall buildings of more than 30 to 40 stories, depending on the geographical location, the wind effects are more influential than earthquakes. In addition, the complexity of the effects of wind flow on the structure due to the interaction of the fluid flow and solid body results in serious damages to the structure by eliminating them. Considering the importance of the issue, the present study investigates the phenomenon of wind-induced vibration on high-rise buildings, taking into account the effects of vortices created by the fluid flow and the control of this phenomenon. To this end, the governing equations of the structure, the fluid flow and the tuned mass damper (TMD) are first introduced, and their coefficient values are extracted according to the characteristics of ACT skyscraper in Japan. Then, these three coupled equations are solved using a program coded in MATLAB. After validation of the results, the effects of wind loads are analyzed and considered with regard to the effects of vortices and the use of TMD, and are compared with the results of the state where no vortices are considered. Generally, the results of this study point out the significance of vibrations caused by vortices in construction of engineering structures as well as the appropriate performance of a TMD in reducing oscillations in tall buildings.

Keywords

Vibration Vortices Tall building Tuned mass damper 

Introduction

Today, the construction of tall buildings, especially in big cities, which are facing the problem of lack of space for housing, is highly regarded. The materials used in such buildings are usually lightweight with very high flexibility. In the construction of high-rise structures, it should be noted that elevation is often accompanied by an increase in the softness and weakness of damping, which increases the sensitivity of the structure to dynamic forces such as wind, sea waves and earthquakes (Poulos 2016). Moreover, due to their high energy absorption, these structures are prone to high-amplitude vibrations even at low wind speeds. Vortex-induced vibrations are nonlinear, self-propagation and multi-degree-of-freedom phenomena, caused by the vortices formed behind bluff bodies as a result of interactions between the fluid flow and the structure (Fig. 1). A bluff body can be defined as a body that, as a result of its shape, has separate flow over a substantial part of its surface, leading to formation of vortices behind the body. These vortices impose oscillatory forces on the structure, which are composed of a normal component to and a tangential force along the streamline, namely the drag and the lift forces, respectively.
Fig. 1

Formation of vortices behind a bluff body (Ul-Islam and Zhou 2009)

Assuming the body is secured by an elastic support of relatively low mass and damping, it starts vibrating due to the oscillatory forces, which, if not controlled, may lead to damages to the structure or even its destruction. This is of great concern especially in high-rise buildings housing a significant number of people or in oil extraction pipes that are installed deep into the ocean at high cost for extraction of petroleum products. The destruction of the cooling towers of Ferrybridge power plant in England in 1960 and the Tacoma Bridge in USA, in 1940, are practical examples where neglecting vortex effects resulted in disasters (Sarpkaya 2004). The Tacoma Bridge was designed to withstand winds at a speed of 100 mph; however, due to neglecting the vibrations caused by the vortex effects, the wind loads caused torsional instability at a traveling speed of 42 mph and destroyed the bridge.

Tuned mass dampers (TMDs) have been widely used in practice, among other devices and configurations for supplemental damping, for vibration mitigation in wind-excited tall buildings to meet occupants’ comfort performance criteria prescribed by building codes and guidelines (Giaralis and Petrini 2017). In its simplest form, the linear passive TMD comprises a mass attached toward the top of the building (primary structure), via linear stiffeners, or hangers in case of pendulum-like TMD implementations, and supplemental damping devices (dampers). The effectiveness of the TMD relies on “tuning” its stiffness and damping properties for a given primary structure and attached mass, such that significant kinetic energy is transferred from the vibrating primary structure to the TMD mass and eventually dissipated through the dampers. Focusing on the suppression of lateral wind-induced vibrations in (tall) buildings, the TMD is tuned to the first natural frequency of the primary structure aiming to control the fundamental (translational) lateral mode shape. As an example, TMD was used in Taipei 101, formerly known as Taipei World Financial Center, a skyscraper built in 2004 with 101 stories located in Taipei, Taiwan (Alex and Tuan Shang 2014). The major part of this TMD system is a 6-m-diameter sphere that is made of steel and weighs 600 tons. It is the largest of its kind in the world. It is installed at the center of the 87th floor and suspended from the 91st floor by cables. There are eight dampers around the mass, to prevent it from moving excessively. This TMD is essentially a pendulum that spans five floors (88–92th), whose primary function is to suppress wind-induced vibration in this building and reduces the vibrations in the building up to 40%.

The governing differential equations

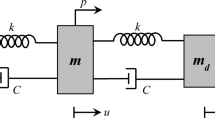
Vortex-induced vibrations cause in-line and cross-flow oscillations on the structure; however, in-line oscillations are significantly larger. Hence, only vortex-induced vibrations along the streamlines are considered in the present study. In Fig. 2, the diagram of a structure with a hydraulic diameter D and a regulated TMD is shown. The structure is maintained with an elastic support and exposed to a fluid flow. (In Fig. 2, parameter w denotes the width of the solution domain. Since the effect of the walls around the domain on the wind flow and structure is neglected, this parameter was considered sufficiently large so that it has no effects on the results.)
Fig. 2

Simplified diagram of the structure and the TMD

According to Fig. 2, the dimensionless equations of motion for the structure and the TMD can be derived as follows:
$$\ddot{x} + 2\xi \omega \dot{x} + \omega^{2} x - 2({\text{mabr}})\xi_{\text{d}} \omega_{\text{d}} \dot{x}_{\text{d}} - ({\text{mabr}})\omega_{\text{d}}^{2} x_{\text{d}} = \frac{p}{{m_{s} }}$$
(1)
$$\ddot{x} + \ddot{x}_{\text{d}} + 2\xi_{\text{d}} \omega_{\text{d}} \dot{x}_{\text{d}} + \omega_{\text{d}}^{2} x_{\text{d}} = 0$$
(2)
where \({\text{mbar}} = \frac{{m_{\text{d}} }}{{m_{\text{s}} }}\) (m s and m d are the masses of structure and TMD), \(\xi_{\text{d}}\) and \(\omega_{\text{d}}\) are the TMD damping ratio and frequency. As suggested by the figure, the planar motion along the body streamlines, X, is described using the linear oscillatory Eq. 4:
$$\left( {m_{\text{s}} + m_{\text{f}} } \right)\ddot{X} + \left( {c_{\text{s}} + c_{\text{f}} } \right)\dot{X} + kX = E$$
(3)
where \(c_{\text{s}}\) and k are damping coefficient and the stiffness of the body, respectively, when the fluid is not present. The hydrodynamic effects of the fluid on the structure are identified as the main effects of the fluid added in the form of added fluid mass and damper according to the equations \(m_{\text{f}} = \frac{1}{4}\pi C_{\text{m}} \rho D^{2}\) and \(c_{\text{f}} = \varOmega \gamma \rho D^{2}\), respectively. Additionally, the vortex effects are modeled as the external force E defined as \(E = \frac{1}{2}\rho U^{2} DC_{\text{D}}\). In these equations, ρ is the fluid density, C m is the added mass coefficient (usually considered 1), C D is the drag coefficient, U is the wind velocity and \(\gamma\) is the damping coefficient of the added fluid flow (Facchinetti et al. 2004). Moreover, \(\varOmega\) is the vortex formation frequency defined as \(\varOmega = \varOmega_{\text{f}} = \frac{2\pi StU}{D}\), where St is the Strouhal number. By defining the natural frequency of the oscillations as \(\varOmega_{\text{s}} = \left( {\frac{k}{{m_{\text{s}} }}} \right)^{0.5}\), the reduced-damping coefficient of the structure as \(\xi = \frac{{c_{\text{s}} }}{{2m_{\text{s}} \varOmega }}\), the total mass as m = m s  + m f and the dimensionless mass ratio as \(\mu = \frac{{m_{\text{s}} + m_{\text{f}} }}{{\rho D^{2} }}\), we may rewrite Eq. 3 to obtain Eq. 4:
$$\ddot{X} + \left( {2\xi \varOmega_{\text{s}} + \frac{\varUpsilon }{\mu }\varOmega_{\text{f}} } \right)\dot{X} + \varOmega_{\text{s}}^{2} X = \frac{E}{m}$$
(4)
Moreover, the vortex effects are modeled using the Van der Pol equation due to its good agreement with the experimental results (Facchinetti et al. 2004):
$$\ddot{q} + \varepsilon \varOmega_{\text{f}} (q^{2} - 1)\dot{q} + \varOmega_{\text{f}}^{2} q = F$$
(5)
The main dimensionless vortex variable, q, which associated with the drag coefficient on the structure, is defined as \(q\left( t \right) = \frac{{2C_{\text{D}} (T)}}{{C_{{{\text{D}}_{0} }} }}\), where C D(T) is the drag coefficient and C D0 is the reference drag coefficient related to a stationary body exposed to vortices. The amplification factor \(\frac{q}{2} = \frac{{C_{\text{D}} }}{{C_{{{\text{D}}0}} }}\) is multiplied by the drag coefficient of the stationary body to give the amplified drag coefficient of the oscillatory body. The parameter F indicates the effect of cylinder motion in the vortex formation region. Hence, the coupled dimensionless equations of the fluid–structure system are obtained as follows:
$$\ddot{x} + \left( {2\xi \delta + \frac{\gamma }{\mu }} \right)\dot{x} + \delta^{2} x = e$$
(6)
$$\ddot{q} + \varepsilon \left( {q^{2} - 1} \right)\dot{q} + q = f$$
(7)
where \(\delta = \frac{{\varOmega_{\text{s}} }}{{\varOmega_{\text{f}} }}\) is the ratio of the vortex formation to the ratio of body oscillations and is defined as \(\delta = \frac{{\varOmega_{\text{s}} }}{{2\pi {\text{St}}(\frac{U}{D})}} = \frac{1}{{{\text{StU}}_{\text{r}} }}\), where U r is the reduced flow velocity defined as \(U_{\text{r}} = \frac{2\pi U}{{\varOmega_{\text{s}} D}}\). Moreover, the coupling parameters are defined as \(e = \frac{E}{{D\varOmega_{f}^{2} m}} = E\frac{D}{{4\pi^{2} {\text{St}}^{2} U^{2} m}}\) and \(f = \frac{F}{{D\varOmega_{f}^{2} }} = F\frac{D}{{4\pi^{2} {\text{St}}^{2} U^{2} }}\). Using these parameters and by substituting them in the above equations, the coefficient e is defined as \(e = \frac{{C_{D} }}{{8\pi^{2} {\text{St}}^{2} \mu }}\), and by definition of the coefficient M as the relation \(M = \frac{1}{2}\frac{{C_{{{\text{D}}_{0} }} }}{{8\pi^{2} {\text{St}}^{2} \mu }}\), we may rewrite e as e = Mq.
Different parameters of the model are required to solve the presented equations. The Strouhal number and the drag coefficient can be considered 0.12 and \(C_{{{\text{D}}0}}\) = 0.2, respectively, for a wide range of Reynolds numbers. Hence, the coefficient M is obtained from Eq. 8 as follows:
$$M = \frac{1}{2}\frac{0.2}{{8\pi^{2} \left( {0.12} \right)^{2} \mu }} \approx \frac{0.08}{\mu }.$$
(8)

The added damping coefficient \(\gamma = \frac{{C_{\text{D}} }}{4\pi \text{St}}\) is the last parameter to be determined, which is proportional to the drag coefficient. In case of an oscillating body, the drag coefficient can be approximated to 2, so that the value of \(\gamma\) is obtained as 1.32. Different studies show that the applied force on the body can be a function of the displacement, velocity or acceleration of the body. However, a review of other similar studies suggests that the coupled acceleration model can produce better results. Moreover, following (Srinil et al. 2013), the values A = 12 and ε = 0.3 are assumed for the coupling model.

Using the above equations and considering the vortex effects, the equations of motion for the system with a TMD can be rewritten in the form of Eqs. 9–11 as follows:
$$\begin{aligned} & \ddot{x} + \left( {2\zeta \varOmega_{\text{s}} + \frac{\gamma }{\mu }\varOmega_{\text{f}} } \right)\dot{x} + \varOmega_{\text{s}}^{ 2} x - \frac{{c_{\text{d}} }}{{\left( {m_{\text{s}} + m_{\text{f}} } \right)}}\dot{x}_{\text{d}} - \frac{{k_{\text{d}} }}{{\left( {m_{\text{s}} + m_{\text{f}} } \right)}}x_{\text{d}} \\ &\;= \frac{P}{{\left( {m_{\text{s}} + m_{\text{f}} } \right)}} + \frac{E}{{\left( {m_{\text{s}} + m_{\text{f}} } \right)}} \end{aligned}$$
(9)
$$m_{\text{d}} \left( {\ddot{x} + \ddot{x}_{\text{d}} } \right) + c_{\text{d}} \dot{x}_{\text{d}} + k_{\text{d}} x_{\text{d}} = 0$$
(10)
$$\ddot{q} + \varepsilon \varOmega_{\text{f}} \left( {4C_{{{\text{D}}o}}^{2} q^{2} - 1} \right)\dot{q} + \varOmega_{\text{f}}^{2} q = \frac{{A\ddot{x}}}{{C_{{{\text{D}}o}} }}$$
(11)
Analysis of high-rise structures is normally very difficult. However, by considering a shear-wall building for the structure, a point mass can be attributed to the building. Under this assumption, each story of the building is considered as one degree of freedom, the mass for each of which equals the mass of the respective story (Chopra 1995). Moreover, the building was considered symmetric in the conducted dynamic analysis, and the effect of torsional forces was neglected. In addition, the building was individually analyzed and the effect of the neighboring buildings was neglected. In order to solve the above equations, the time step Δt is defined, and the values of acceleration, velocity and displacement are calculated in each step using the rectangle (midpoint) method and solved by MATLAB code. Unconditional stability is the main advantage of this method. According to (Julien 2012), the one DOF system’s stiffness is given by \(k = \frac{\kappa }{n}\). The typical floor value according to the equivalent formula for fixed columns is:
$$\kappa = \beta \frac{12EI}{{h^{3} }}$$
(12)
where β is a factor relating to the number of columns and their contribution and equal to 19/6, h is the height of a floor (typical value is 4 m), EI is the stiffness of one column (typical value is \(15 \times 10^{6} \;{\text{Nm}}^{ - 1} )\) and \(n = \frac{{H_{\text{total}} }}{h}\), where H total has been picked as the ACT Tower height. Using these values, yields to k = 168,000 Nm−1. The other specifications of ACT Tower are given in Table 1. Moreover, the optimum values for the TMD are adapted from (Chopra 1995). According to (Kawai 1992), at height to width ratios of higher than eight for the structure, the vortices formed in the flow have a great influence on the oscillations of the structure. Hence, this ratio was considered ten for the structure considered in this study. Moreover, the wind flow velocity was considered 25 m/s.
Table 1

Properties of the considered structure (Julien 2012; Ahsan et al. 2012)

Mass of the ACT tower

m = 110,000,000 kg

Stiffness of the ACT tower

k = 168,000 Nm−1

Values in civil engineering range from 0 to 5%, in rare case to 10%

\(\xi = 2\%\)

Damping

\(c = 2\xi \omega = 2m\xi \sqrt {\frac{k}{{m_{\text{s}} }}}\)

Results and discussion

Validation of results

In order to validate the results, the acceleration values of the structure at the presence of TMD are demonstrated in Fig. 3 and are compared with those of Ahmad (2008). In Ahmad (2008), the governing differential equations for vibrations of a high-rise building with a height of 274 m subjected to wind flow were derived using the Lagrange equations and solved through the fourth-order Runge–Kutta method. The TMD was installed at the top of the building. The system was initially modeled as a single-DOF system, and by considering the installed TMD, the system has a total of two DOFs (similar to the present research). In order to better compare the results, the mass and damping ratios were considered 0.01 and 0.1 in both researches. In addition, the wind force was modeled as a harmonic function with an amplitude and excitation frequency similar to those of (Ahmad 2008). The governing equations were then solved, and the accelerations at the top of the building in both researches are compared in Fig. 3. As shown, the trend of the diagram is in good agreement, which indicates the appropriate accuracy of the computer code used in this study.
Fig. 3

Comparison of structure acceleration with the results given in Ahmad (2008), when a TMD is used

In what follows, the structure responses to various wind power profiles like (Julien 2012), in the presence of a TMD, are addressed for the cases where the vortex effects are once considered and once neglected.

Free vibrations

In the free vibration problem, the load matrix is constantly equal to 0, and initial values are given for displacements and velocity. Results only vary with a factor when adding initial displacement or giving initial displacement without initial velocity. In Figs. 4 and 5, the results with assuming no external force and taking into account the effects of the vortices are shown. In this case, it was assumed that the structure had an initial velocity of 0.01 m/s with no initial displacements. As demonstrated by the figure, in case the TMD is used, the steady state of the structure is achieved after 2500 s. However, in the absence of the TMD, the time increases up to 4000 s. Moreover, the structure including a TMD damper stops moving after 1000 s and then starts to oscillate after a short period of time. In order to further investigate the results, maximum oscillation amplitudes are compared in Table 2, in two vibration modes, taking into account the effects of vortices and without. The comparison results indicate a slight reduction in the oscillation amplitudes in the case of the effects of vortices is considered. In other words, in this case, the vortices created behind the object are similar to the frictional force and in the opposite direction of the movement of the structure and reduce the amplitude of the oscillations.
Fig. 4

Free vibrations in the 1-DOF system, assuming an initial velocity of 0.01 in the system and taking into account the effects of vortices

Fig. 5

Displacement of the structure and its attached TMD, assuming an initial velocity of 0.01 in the system and taking into account the effects of vortices

Table 2

Comparison of the maximum vibration amplitudes during free vibrations, once considering the vortex effects and once neglecting them

 

Maximum vibration amplitudes neglecting the vortex effects (m)

Maximum vibration amplitudes taking into account the vortex effects (m)

The structure with a TMD

0.2361

0.2367

The structure without a TMD

0.2360

0.2365

Harmonic loading taking into the vortex effects

In this section, the amplitude of the force applied to the structure is selected a small (10 N) in the form of \(p = 10{ \cos }(\alpha \times \omega t)\). The effect of parameter α is shown in Fig. 6 (Connor 2002). It has different effects on the optimal TMD that can be estimated by comparing the two continuous lines, which represent the amplification factor for the optimally tuned case and the case without a TMD. The detailed effect of this parameter is discussed in “Without any effects” to “Optimum effects” Sects.
Fig. 6

Response curve for amplitude of system with optimally tuned TMD (Connor 2002)

Without any effects

According to (Connor 2002), when \(\alpha < 0.8\) or \(\alpha > 0.15\), it is expected that the TMD does not affect the amplitude of the structure oscillations. The amplitude of vibrations at \(\alpha = 0.2\) for both cases where a TMD is considered or neglected is demonstrated in Fig. 7. As expected, the presence of the TMD damper did not reduce the amplitude of oscillations. The response of the systems, as well as the TMD at \(\alpha = 0.2\), is depicted in Fig. 8. As shown, the vibration amplitude of the TMD is much larger than that of the structure. Moreover, the results in Table 3 indicate that the vortices formed behind the body increase the forces applied to the structure and, as a result, the maximum amplitude of the oscillations in this case is greater than the maximum range of vibrations, regardless of the effects of vortices.
Fig. 7

Effects of the TMD at an external harmonic forces at \(\alpha = 0.2\) and taking into account the effects of vortices

Fig. 8

Responses of the structure and the TMD in the presence of external harmonic forces at \(\alpha = 0.2\) when vortex effects are considered

Table 3

Comparison of maximum vibration amplitudes at \(\alpha = 0.2\) in two cases where vortex effects are once considered and once neglected

 

Maximum vibration amplitudes neglecting the vortex effects (m)

Maximum vibration amplitudes taking into account the vortex effects (m)

The structure with a TMD

1.08 × 10−4

3.24 × 10−4 

The structure without a TMD

1.09 × 10−4 

3.46 × 10−4 

Inverse effects

In accordance with the (Connor 2002), it is expected that the addition of TMD to the system increase the amplitude of the oscillations in 0.96 < α < 0.8 or 1.15 < α < 1.03. For example, by considering the vortex effects, the amplitude of the system response at \(\alpha = 0.92\) is demonstrated Fig. 9 in the case of using and not using the TMD. As shown by the figure, the TMD causes an increase in the amplitude of vibrations. Moreover, according to Fig. 10, the amplitude of the TMD is much larger than that of the structure. As depicted in Table 4, the vortices amplified that amplitude of oscillations as well as the forces applied to the structure. Therefore, the maximum amplitude of oscillations in the structure increased both in the presence and absence of a TMD.
Fig. 9

Effect of using the TMD on the structure response at \(\alpha = 0.92\) when vortex effects are taken into consideration

Fig. 10

Responses of the structure as well as the TMD at \(\alpha = 0.92\) in the presence of external harmonic forces when vortex effects are taken into consideration

Table 4

Comparison of the maximum amplitudes of vibrations at \(\alpha = 0.92\) with and without considering vortex effects

 

Maximum vibration amplitudes neglecting the vortex effects (m)

Maximum vibration amplitudes taking into account the vortex effects (m)

The structure with a TMD

4.75 × 10−4 

7.21 × 10−4 

The structure without a TMD

5.56 × 10−4 

8.13 × 10−4 

Optimum effects

According to (Connor 2002), assuming 1.03 < α < 0.96, it is expected that the TMD reduces the amplitude of vibrations. As demonstrated in Fig. 11, for \(\alpha = 0.997\), the amplitude of the structure oscillation is highly reduced when the TMD is used. Moreover, as Fig. 12 suggests, in this case, the amplitude of TMD oscillations is much larger than that of the structure. According to Table 5 and similar to the previous section, the formed vortices behind the body cause an increase in the maximum amplitude of the vibrations. However, in this case, the increase in the amplitude of oscillations, particularly for the TMD, is smaller as compared with the other two values of \(\alpha\).
Fig. 11

Optimum effect of using TMD at \(\alpha = 0.997\) when external harmonic forces are applied and vortex effects are taken into consideration

Fig. 12

Responses of the structure as well as the TMD at \(\alpha = 0.997\) when external harmonic force are applied and vortex effects are taken into consideration

Table 5

Comparison of the maximum amplitudes of vibrations at α = 0.92 with and without considering vortex effects

 

Maximum vibration amplitudes neglecting the vortex effects (m)

Maximum vibration amplitudes taking into account the vortex effects (m)

The structure with a TMD

1.50 × 10−3 

1.70 × 10−3 

The structure without a TMD

5.57 × 10−4 

8.73 × 10−4 

External random sawtooth wave by taking vortex effects into consideration

The wind load applied on a structure is not usually in a harmonic form and may also contain random components. Hence, a random function to be applied to the structure was considered in MATLAB as follows:
$$10\left[ {\frac{2}{\pi }{\text{rand}}cos^{ - 1} (\cos \left( {\left( {50 + 0.5{\text{rand}}} \right)\omega t} \right) + 0.3{\text{rand}} - 1} \right].$$
(12)
The diagram of this load with an amplitude of 10 N is demonstrated in Fig. 13. The rand function used in Eq. 12 indicates a random value ranging from zero to one. This load is very similar to real-world wind loads, which consequently results in structure responses close to the reality.
Fig. 13

Random sawtooth function

As shown in Fig. 14, initially, the TMD significantly reduces the amplitude of vibrations in the structure, i.e., for the first 150 s. After that, however, motion prediction becomes very complex due to the rapid frequency changes, as well as large amplitude changes in the structure, so that the TMD sometimes reduces and sometimes increases the amplitude of vibrations. In other words, the importance and effectiveness of the TMD is at the start of vibrations.
Fig. 14

Structure response to the sawtooth loads when the vortex effects are taken into consideration (the overall response is enlarged)

Figure 15 demonstrates the responses of the structure and the TMD when external sawtooth loads are combined with random components. It is worth pointing out the significantly large displacement as well as vibrations amplitude of the TMD compared to the main structure.
Fig. 15

Responses of the structure and the TMD to random wind loads when vortex effects are taken into consideration

The vortex effects on the maximum amplitude of the oscillations are demonstrated in Table 6 when wind effects are modeled as sawtooth loads with random components. As shown, the formed vortices behind the body again increase the vibration amplitude of the structure.
Table 6

Comparison of the maximum amplitudes of vibrations with and without considering vortex effects when random external loads are applied

 

Maximum vibration amplitudes neglecting the vortex effects (m)

Maximum vibration amplitudes taking into account the vortex effects (m)

The structure with a TMD

2.59 × 10−4 

3 × 10−4 

The structure without a TMD

2.11 × 10−4 

3.16 × 10−4 

Conclusions

The present paper investigated the vibrations induced by vortices formed around high-rise buildings due to wind flow, with and without considering the TMD. Different profiles and excitation frequencies were used to simulate the wind forces on the structure. To this end, three coupled governing differential equations were used to simulate the phenomenon and solved using a MATLAB program. The most important results of this study can be drawn as follows:
  1. 1.

    The wind forces exerted on the high-rise structures can induce large vibrations to the buildings. The results suggest that in addition to earthquake forces, which are among the most important design parameters, the effect of wind forces should also be accurately taken into consideration in such buildings.

     
  2. 2.

    The TMD performs optimally when the wind blows at frequencies close to that of the natural frequency of the structure. This optimal performance can considerably reduce the amplitude of oscillations (up to 70%) and hence prevents extreme structural vibrations. In other frequencies, the effect of the TMD is reduced and, even in some cases, it has reverse effects and the amplitude of structural oscillations is increased.

     
  3. 3.

    The vortices formed around the structure increase the amplitude of building oscillations. Comparison of the amplitude of vibrations indicates that structural oscillations increase up to 40% by taking into account the effects of vortices. Therefore, neglecting the effects of vortices in high-rise buildings can lead to serious damages to the structure.

     
  4. 4.

    TMD performs favorably against both harmonic and non-harmonic excitations. In other words, use of TMD is one of the effective methods to reduce the amplitude of oscillations in high-rise buildings subject to wind flow, especially at frequencies close to the natural frequency of the structure.

     

Notes

References

  1. Ahmad Sh (2008) Suppression of wind induced vibrations using tuned mass damper. J Wind Eng 5:29–38Google Scholar
  2. Ahsan K, Kijewski T, Tamura Y (2012) Mitigation of motion of tall buildings with specific examples of recent applications. Wind Eng 2(3):201–251Google Scholar
  3. Alex Y, Tuan Shang GQ (2014) Vibration control in a 101-storey building using a tuned mass damper. J App Sci Eng 17:141–156Google Scholar
  4. Chopra AK (1995) Dynamics of structures: theory and application to earthquake engineering, 4th edn. Prentice Hall Inc, New JerseyzbMATHGoogle Scholar
  5. Connor J (2002) Introduction to motion based design, 1st edn. Prentice Hall Inc, New JerseyGoogle Scholar
  6. Facchinetti ML, de Langre E, Biolley F (2004) Vortex-induced travelling waves along a cable. Eur J Mech B Fluids 23:199–208CrossRefzbMATHGoogle Scholar
  7. Giaralis A, Petrini F (2017) Wind-induced vibration mitigation in tall buildings using the tuned mass-damper-inerter (TMDI). J Struct Eng 143:256–285CrossRefGoogle Scholar
  8. Julien C (2012) Effects of tuned mass damper on wind-induced motions in tall buildings. Department of Civil and Environmental Eng, Massachusetts Inst. of TechGoogle Scholar
  9. Kawai H (1992) Vortex induced vibration of tall buildings. J Wind Eng and Indust Aero 41:117–128CrossRefGoogle Scholar
  10. Poulos HG (2016) Tall building foundations: design methods and applications. Innov Infrastruct Solut 10:1–10Google Scholar
  11. Sarpkaya T (2004) A critical review of the intrinsic nature of vortex-induced vibrations. J Fluid Struct 19:389–447CrossRefGoogle Scholar
  12. Srinil N, Zanganeh H, Day A (2013) Two-degree-of-freedom on circular cylinder with variable natural frequency ratio: experimental and numerical investigations. J. Ocean Eng 73:179–194CrossRefGoogle Scholar
  13. Ul-Islam S, Zhou CY (2009) Characteristics of flow past a square cylinder using the lattice boltzmann method. Inform Technol J 8:1094–1114CrossRefGoogle Scholar

Copyright information

© The Author(s) 2017

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  • Ali Ajilian Momtaz
    • 1
  • Mohamadreza Akhavan Abdollahian
    • 2
  • Anooshiravan Farshidianfar
    • 1
  1. 1.Department of Mechanical EngineeringFerdowsi University of MashhadMashhadIran
  2. 2.Department of Urban PlanningUniversity of IsfahanIsfahanIran

Personalised recommendations