Introduction

Earthquakes are among the most destructive phenomena observed in the nature. Studies have shown that building collapses caused 75% of earthquake fatalities during the last century (Elnashai and Di Sarno 2008). The probability of failure of the RC structures is higher in developing countries due to the quality of the construction which is often not adequate. Albania is an earthquake prone country located on the Alpine-Mediterranean seismic belt and its most active zones are situated in the Southern Balkans and around the Aegean Sea. According to the catalogue of Albanian earthquakes by Sulstarova et al. (2005), from 58 BC until 2000, Albania has been struck by 89 strong earthquakes with intensities over VIII (MSK-64) of which 57 of them have happened from the 19th century onwards. It is estimated that during the 20th century as much as 7% of shallow earthquake energy was generated by seismic sources in the Albanian territory (UNDP 2003). Despite the high risk, the seismic codes adopted in Albania up-to-date have not used probabilistic hazard maps but relayed on seismic zonation maps in terms of seismic intensities which may not be adequate in the light of recent modern seismic code practices. As the Albanian seismic code was updated for the last time in 1989, it is of great interest to understand the seismic response of newly constructed structures based on relatively old codes such as KTP-N.2-89 (1989). For this reason, it is important to evaluate buildings designed according to these provisions to assess their expected performance and take necessary measures for future planning.

The majority of existing building stock in Albania, like in many developing countries, has been designed considering the older code requirements when loads were not required or the design was to lesser level of what is currently specified (Inel et al. 2008; Ozmen et al. 2014; Morales-González and Vidot-Vega 2017). Public buildings that are mostly built of RC with template designs constitute an important part of vulnerable building stock in this region. This type of structures is expected to provide aid and shelter and be in operational mode to ensure life safety during earthquakes (Isik and Kutanis 2015; Bilgin 2015). Structures such as healthcare facilities are expected to be prepared to deal with emergency situations presented as in the case of earthquakes. However, recent destructive earthquakes have shown that many times these structures fail to provide their services and have inadequate seismic performance (Çırak et al. 2015). Worldwide, the seismic safety of public buildings such as healthcare facilities and schools has been questioned after earthquakes in Turkey (Bilgin 2015), Nepal (Gautam et al. 2016), Italy (Kaplan et al. 2010), Algeria (Remki and Benouar 2014) and the 2012 Emilia Romagna in Italy.

This study aims to assess the expected seismic performance of an existing reinforced concrete health clinic constructed in Albania. This building is a representative of healthcare facilities designed in that area according to the mid-1980s seismic code provisions. Nonlinear static and dynamic analyses were used to predict the seismic response of the prototype RC hospital building. For the assessment, ZEUS-NL (Elnashai et al. 2003), which uses a fiber model approach, was used. Global and local response parameters were derived. The Prestandart and Commentary for the Seismic Rehabilitation of Buildings (FEMA 356 2000) performance criteria were used to evaluate the seismic performance of the case study building using the ZEUS-NL response analysis.

Performance criteria

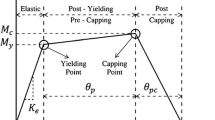
There exist several nonlinear static analysis procedures to determine the seismic performance levels of the structures such as ATC-40 (1996), FEMA 356 and N2 method from EC 8 (CEN 2004). FEMA 356 guidelines provides analytical techniques and principles for the performance-based evaluation of current existing buildings and for designing seismic rehabilitation options. Performance level is a limit stage on the capacity curve that is used to quantify the damage, while performance objective defines the target performance level to be attained for a specific intensity of ground motion. Immediate occupancy (IO), life safety (LS), and collapse prevention (CP) levels area defined as structural performance levels (Fig. 1) in FEMA 356.

Fig. 1
figure 1

Force deformation relationships for concrete elements

Full size image

Buildings at IO should have only slight damage. Buildings at LS may have sustained noteworthy damage, but still provide a considerable margin against collapse while the buildings at the CP are likely to remain standing, but with little margin against collapse. Basic safety objective is described as LS performance for the Basic Safety Earthquake-1 earthquake hazard level and CP performance for the Basic Safety Earthquake-2 earthquake hazard level in FEMA 356 guidelines. Basic Safety Earthquake-1 is defined as the smaller of an event corresponding to 10% probability of exceedance in 50 years (10% in 50 years) and 2/3 of Basic Safety Earthquake-2, which is the 2% probability of exceedance in 50 years (2% in 50 years) event.

Description of the case study building

The investigated five-story building was conceived as a representative of older construction intended for neurological rehabilitation health clinic in Albania. The structure was designed in 2002 complying the latest version of the Albanian seismic code KTP-N.2-89 as a moment frame system. The structure has a relatively regular composition in plan and elevation and a common height for the building stock of the city. The overall height of the structure is 16.0 m, with regular story heights of 3.2 m each. The footprint of the building has dimensions of 15.0 m by 19.0 m. In the shorter direction, it has three bays of 4.0 m, 2 m × 5.5 m each, while in the longer direction it has a symmetrical configuration with five bays of 2 m × 3.0 m, 2 m × 4.0 m, 5.0 m, with the longer bays at the internal spans. The structure is sited on category II soils as defined in the Albanian seismic code KTP-N2-89. The infill walls are composed of lightweight ceramic blocks with no bearing capacity. A floor plan is shown in Fig. 2.

Fig. 2
figure 2

Plan view of case study building (units in cm)

Full size image

The size of the columns changes between different floors. The columns of first two floors have cross sections of 35 cm × 50 cm, while the columns of floors 3, 4 and 5 have smaller cross sections of 30 cm × 50 cm. The size of the beams is same for whole the structure with cross sectional dimensions of 30 cm × 45 cm. The dimensions of the beams and columns are summarized in Table 1.

Table 1 Structural member dimensions
Full size table

The beams and columns differ in their reinforcement as well. Outer and inner columns have different configurations of their longitudinal and transverse reinforcement. The reinforcement also varies in height, with the upper stories columns having lower reinforcement ratios. The outer columns have a 3 × 4 configuration of the longitudinal reinforcement while the inner columns have a 4 × 5 configuration of the longitudinal reinforcement. Transverse reinforcement is placed at 15 cm spacing near joints and at 20 cm spacing on midspan. Table 2 summarizes the reinforcement of the columns.

Table 2 Column reinforcements
Full size table

The column reinforcements are shown below (Figs. 3, 4, 5, 6) for each type of column.

Fig. 3
figure 3

General layout of the columns

Full size image
Fig. 4
figure 4

Columns type 1 reinforcement for floor 1 (left) and floor 2 (right)

Full size image
Fig. 5
figure 5

Columns type 1 reinforcement for floor 3 (left) and floors 4–5 (right)

Full size image
Fig. 6
figure 6

Columns type 2 reinforcement for floors 1-2 (left) and floors 3–5 (right)

Full size image

Beams have different configurations of their longitudinal reinforcement depending on their locations on the structure. There are five types of beams for this structure. All the beams have a longitudinal reinforcement configuration with four bars at the bottom and 4, 5 or 6 bars at their top face. Transverse reinforcement is placed at 10 cm spacing near joints and at 20 cm spacing on midspans. Table 3 summarizes the reinforcement of the beams.

Table 3 Beam reinforcements
Full size table

The beam reinforcements are shown below (Figs. 7, 8) for each type of beam.

Fig. 7
figure 7

General layout of the beams

Full size image
Fig. 8
figure 8

Beam reinforcements

Full size image

The blueprints also define the class of the concrete and steel used in the structural components of the building as class M250 concrete (f c = 25 MPa) and steel class 500 s (f y = 500 MPa). While consulting the construction archives for other RC public buildings built in the period after the adoption of KTP-89, these classes of concrete and steel seemed an exception rather than the case. It has been observed in many studies using experimental field investigations that often the actual class of the materials does not reflect the one defined in the design or the codes due to poor construction quality, aging, poor workmanship, etc. This is observed for developing countries such as Albania (Frangu 2013).

In this study, the same analysis was performed for the building with two different sets of material properties. One with concrete a concrete compressive strength of 25 MPa and steel reinforcement yield strength of 500 MPa named STR.1 as was taken for the original building, and one with concrete compressive strength of 16 MPa and steel of 220 MPa named as STR.2 representing the material classes used till 2000 in the region (Frangu 2013).

Analytical models

ZEUS-NL software was developed for 2D/3D finite element modeling by Elnashai et al. (2003) at the Mid-America Earthquake Center, University of Illinois at Urbana-Champaign. The program is capable of various static and dynamic analyzes and uses the fiber approach to model the inelasticity along the structural member length and section depth while accounting for material and geometric nonlinearities. Each fiber is defined with the corresponding material stress–strain relationship. For the calculation of the element forces it is performed a numerical integration at two Gauss points. Figure 9 shows the decomposition of a RC section.

Fig. 9
figure 9

Decomposition of a rectangular RC section (Elnashai et al. 2003)

Full size image

The case study structure was modeled in 2D with the corresponding frames in each direction. The structure has a regular configuration and it is symmetrical in its longer direction while one of the spans in the other direction is shorter. For this reason, the whole structure was modeled for the longer direction (x direction). The model takes the advantage of the symmetry of the building such that only half of the structure is analyzed in y direction. In the longer direction were modeled all the four frames which were linked with each other by rigid truss elements which allow only the lateral force and displacement transfers between the frames. In the shorter direction were modeled only one external frame and two internal ones linked with the same method by rigid elements. Only lateral forces and displacements are transmitted between frames. The views of the modeled frames for each direction are shown in the Figs. 10 and 11.

Fig. 10
figure 10

Frame model in x-direction

Full size image
Fig. 11
figure 11

Frame model in y-direction

Full size image

The seismic dead weight was included in the model by specifying lumped masses at each node along the horizontal members. Rigid zones were used to define the joint regions such that nonlinear response is monitored outside the joint. For the case study, the horizontal dimension of the rigid zone within each joint was taken to be equal to the column width. The height of the rigid zone was set equal to the spandrel beam depth for connections around the perimeter of the building and equal to the slab thickness, excluding the additional thickness due to the shear capital, for interior slab column joints. Members were divided such that a Gauss point would monitor the section of members just outside the joint region. Additional nodes were used along the horizontal members to allow the self-weight to be included as equivalent point loads (Fig. 12).

Fig. 12
figure 12

Model of case study building used in ZEUS-NL analysis (units in mm)

Full size image

To model the beam, column, slab and rigid connections, a cubic elasto-plastic type 3D element (cubic) was used. The joint element with uncoupled axial, shear and moment actions was used to model the rigid joints. The cross-sections of the column elements were described using the RC rectangular section (rcrs), while the cross-sections of the beam and slab members were defined using the RC T-section (rcts). The bilinear elasto-plastic material model with kinematic strain hardening (stl1) was used for the steel reinforcement and rigid links modeling, and the uniaxial constant confinement concrete material model (conc2) was used for the concrete. For the confined and unconfined concrete was used the nonlinear concrete model with active confinement as developed by Mander et al. (1988). This model (con2), considers the transverse pressure from confining reinforcement steel. This is defined in the model parameters in ZEUS-NL through the constant confinement factor k. The values of the k factor were determined to be 1.2 for confined concrete and 1.02 for the unconfined concrete as the default recommended values. This model requires to input the parameters for compressive strength f’ c, tensile strength f t, maximum strain ε co, and confinement factor k. For the steel reinforcement and rigid links modeling, was used the bilinear elasto-plastic material model with kinematic strain hardening (stl1). This model requires to input the parameters for the Young’s modulus E, yield strength σ y, and strain hardening parameter μ. The yield strength considered were 500 and 220 MPa for the reinforcement and a very high value was used for the rigid links to avoid their yielding.

The material properties for each material used in the model are defined in Table 4.

Table 4 Values of the material properties used for modeling
Full size table

Ground motion records

Using acceleration records with different characteristics is important for dynamic analyses (Özdemir and Bayhan 2015). Therefore, the non-linear dynamic analysis was performed using seven real earthquake ground motions. The ground motions were chosen from earthquakes that have happened around the Mediterranean region in countries neighboring Albania. The records were obtained from the Pacific Earthquake Engineering Research Center (PEER) database and from the European Strong-Motion Database (ESD). The characteristics of the ground motions are presented in Table 5 below.

Table 5 Ground motion characteristics
Full size table

Discussion of analytical results

Pushover analysis

Pushover analysis was used to evaluate the capacity of each frame model. The frame models were analyzed in ZEUS-NL for both orthogonal directions. The analysis as mentioned previously was performed on two sets of frames for different material properties and lateral load patterns. The material properties used to model the structural elements in ZEUS-NL are uncracked ones as the program updates the section properties under loading conditions based on the material properties relationships defined. Both an inverted triangular and rectangular load pattern was used for comparison. The pushover curves were developed. In the pushover graphs, the horizontal axis corresponds to the building drift which is defined as the displacement of the top story divided by the total height of the building. On the other hand, the vertical axis represents the base shear in terms of total base shear divided by the total seismic weight of the building, given as the ratio V/W. Structure type 1 (STR.1) refers to the structure modeled with higher material strengths (C25/S500), while structure type 2 (STR.2) refers to the structure modeled with lower material strengths (C16/S220). The pushover curves developed with a rectangular load pattern (REC.) and with an inverted triangular load pattern (TRI.) are shown below (Figs. 13, 14, 15, 16).

Fig. 13
figure 13

Comparison of pushover results for the x direction. REC pattern (left) and TRI pattern (right)

Full size image
Fig. 14
figure 14

Comparison of pushover results for the x direction. STR.1 (left) and STR.2 (right)

Full size image
Fig. 15
figure 15

Comparison of pushover results for the y direction. REC pattern (left) and TRI pattern (right)

Full size image
Fig. 16
figure 16

Comparison of pushover results for the y direction. STR.1 (left) and STR.2 (right)

Full size image

When pushover is run with a rectangular load pattern the strength capacity is higher for all the frames compared to inverted triangular load pattern analysis. This is a result that has been observed in past studies as well (Saleemuddin and Sangle 2016; Ni 2014). The models defined with higher material properties showed a higher strength capacity as well, which is an expected outcome. These are true for the frames in both directions. In the x direction the building shows a higher strength capacity when compared with the other direction. In the x direction the frames exhibited slightly more ductility, as well. The negative slope after the yielding point signifies a soft story mechanism, which may be a result of the change in column sizes and reinforcement after the second story.

Performance evaluation

There exist various nonlinear static analysis procedures to determine the performance levels of the structures such as the Capacity Spectrum Method-CSM (ATC-40 1996), the Displacement Coefficients Method-DCM (FEMA 356 2000), the N2 Method, etc. The Capacity Spectrum Method was used in this study. This method uses the intersection of the capacity curve with a reduced response spectrum to estimate maximum displacements. The application of this method requires that both the capacity curve and the demand response spectra to be plotted in the Acceleration-Displacement Response Spectra format (ADRS format). To convert the capacity curve and the demand spectra, the procedures outlined in ATC-40 are followed. The capacity curves were determined from the pushover analysis as shown in the previous section, and the corresponding curves were converted to the ADRS format. For the demand curves were used the response spectra defined both in EC8 and KTP-N.2-89 to compare the effect of the different response spectra on the evaluation of the performance point of the building. The main parameters in determining the response spectra for both codes are presented in the Table 6.

Table 6 Parameters used to define the spectra for each code
Full size table

The importance factor in KTP-N.2-89 for hospital structures is defined as 1.5 while in EC8 as 1.4. The structural type coefficient is basically the same in both code as in EC8 the equation that defines the spectra is divided by the q-factor while in KTP-N.2-89 it is directly multiplied by this factor. The soil types considered are types II and C, respectively, corresponding to stiff soils. The acceleration coefficient in KTP-89 is defined based on the soil type and the expected seismic intensities for the site which in our case is intensity VII. The seismic intensities defined the code seismicity map are based on return periods of around 100 years. In EC-8 the ground accelerations are defined by probabilistic methods for return periods of 475 years. The value of 0.25 g was defined based on the findings of recent studies on the ground acceleration values for the city of Tirana where the structure is located (Aliaj et al. 2010). The type 1 spectra were used for the EC-8 case. In EC-8 the improved performance for important structures such as health care facilities is not achieved as in US codes by upgrading the performance level for a given earthquake, but by increasing the hazard level through the structure importance factor (Fardis 2004).

ATC-40 presents three procedures for determining the performance of the structure. Both procedure A and procedure B were checked to determine the performance point for each case (ATC-40 1996). They were developed in Excel spreadsheets which facilitate the calculations and iterations involved in each of them. Examples of the application of the two procedures are shown below (Fig. 17). In these representative figures, blue lines represent the spectrum for demand and red lines defines the capacity diagram for performance point calculation.

Fig. 17
figure 17

Determination of performance point by CSM procedure A (left) and procedure B (right), e.g.: x dir. str.2, EC8 spectrum

Full size image

The displacement of δ vs V coordinates are converted to Sd (spectral displacements) and S a (spectral accelerations), respectively, by the use of PFϕroof (modal participation factors) and α (effective modal weight) ratios as obtained from dynamic characteristics of the fundamental mode of the building. The results from the capacity spectrum method for all the cases are presented in the tables below. δ max and V T are the, respectively, the displacement and the shear force at the calculated performance point.

From the results presented in the above (Tables 7, 8), in can be noticed the differences when the structure is evaluated based on EC8 and KTP-89 demand spectra. Clearly when using the KTP-89 spectra, the demands are significantly lower. This is consistent with the findings of other studies on this matter (Baballeku and Pojani 2008). The maximum displacements calculated at the performance point are higher for the y- direction in all cases. The values of maximum roof displacement are nearly twice as much when considering EC-8 demands compared to KTP-89 demands. Considering that the KTP-89 in an older code and has not been updated to reflect modern design concepts for more than two decades, as well as the fact that new codes which will be implemented soon in Albania will be a version of the Eurocodes.

Table 7 Performance points obtained by CSM with EC8 demands
Full size table
Table 8 Performance points obtained by CSM with KTP-89 demands
Full size table

Generally, structures are required to meet certain structural performance criteria which are defined as a series of target performance levels for various earthquake hazard levels, according to the concepts of Performance Based Seismic Design (PBSD). These criteria range from global level to member level evaluation of structures. The main performance levels defined are usually three, such as immediate occupancy (IO), life safety (LS) and collapse prevention (CP) levels as defined in FEMA 356 regulations, and follow the same logic in other codes as well although they may have different denominations. FEMA regulations require that the structure must meet the basic safety objective (BSO) by performing within the LS and CP limits for the corresponding earthquake levels.

FEMA 356 provides suggestions on the inter-story drift values for evaluating the performance of a structure. The typical suggested values of inter-story drifts are 1% for IO performance level, 2% for LS performance level and 4% for CP performance level for concrete frame structures. But these values of drifts are determined for structures designed properly for seismic loadings and with sufficient member detailing defined as special moment frames (SMF) and not intermediate moment frames (IMF). Some of the member detailing provisions are: the spacing of the hoops near plastic hinge zones must be less than ¼ of the distance between tension reinforcement and compression face of the RC section, the column width must be greater than 20 times the largest longitudinal rebar diameter, etc. According to these rules the case study building would not qualify as a SMF, because as an example the section widths of columns and beams are 30–35 cm while rebars with diameters of 20–22 mm have been used not fulfilling the criteria, while the spacing of the hoops in the plastic hinge zones just equals the ¼ of the section effective depth with a value of 10 mm. For intermediate moment frames it has been proposed that inter-story drift limits should be reduced to 0.5, 1 and 2% for IO, LS and CP levels, respectively (Ramamoorthy et al. 2006).

The maximum inter-story drifts from the pushover analysis for both types of structures and load patterns are shown below (Figs. 18, 19) below together with the drift limit for the LS performance level.

Fig. 18
figure 18

Maximum interstory drifts in x direction. STR1 (left) and STR2 (right)

Full size image
Fig. 19
figure 19

Maximum interstory drifts in y direction. STR1 (left) and STR2 (right)

Full size image

It can be observed that for all cases the interstory drift limit is exceeded at story 3 level and doesn’t meet the performance requirement. At these level the drifts vary between 1 and 1.3%. It can be noted that for the structure type STR.2 (lower material properties), the maximum interstory drift values observed are higher when compared to structure type STR.1. The interstory drifts from a pushover analysis with an inverted triangular load pattern are higher for the upper three stories and lower for the bottom two when compared to the results from pushover with rectangular load pattern. The interstory drifts seem critical at the story 3 level where there is a higher concentration of drift demands. It should be noted that at this story level there is a decrease in the width of the columns by 5 cm as well as a decrease in reinforcement ratio for most of the columns. The concentration of the drift demands at this level may indicate that this reduction in column sections has adverse effects in interstory drift values.

The interstory drifts are higher in the y direction compared to those in x direction. It can be observed that for all cases the interstory drift limit is exceeded at story 2 and story 3 levels and does not meet the performance requirement. For structure type STR.2 the interstory drift limit is exceeded at story 4 as well from the results of triangular pushover. At level 3 the drifts vary between 1.2 and 2.5%, while at level 2 the drifts vary between 1 and 1.5% It can be noted that for the structure type STR.2 (lower material properties), the maximum interstory drift values observed are higher when compared to structure type STR.1. The interstory drifts from the pushover analysis with inverted triangular load pattern are higher for the upper three stories and lower for the bottom two when compared to the results from pushover with rectangular load pattern. The interstory drifts seem critical at the story 2 and story 3 levels where there is a higher concentration of drift demands.

Time history analysis

The non-linear dynamic time history analysis was performed using seven real earthquake ground motions (Table 5). Tables 9 and 10 gives the maximum dynamic response for each case study structure for the set of the ground motions and the median response as well. The table defines the maximum base shear ratio V/W and the maximum building drift.

Table 9 Maximum base shear and building drift ratios in the x direction
Full size table
Table 10 Maximum base shear and building drift ratios in the y direction
Full size table

The results for the median responses in the x direction for the given set of ground motions show that structure type STR.1 had grater shear demands when compared to STR.2. This trend is observed also for individual earthquake responses. The median drift value for STR.2 is lower, although for three of the ground motions drifts are grater.

The median responses in the y direction for the given set of ground motions also show greater shear demands for structure type STR.1. The median drift value for STR.2 is lower, although for three of the ground motions drifts are grater.

Comparison of pushover and dynamic time history analyses

Results from the subsequent dynamic analyses are plotted versus pushover response curves to indicate the maximum base shear and building drift from each analysis (Figs. 20, 21).

Fig. 20
figure 20

Comparison of Pushover and dynamic results a STR.1, x direction; b STR.2, x direction

Full size image
Fig. 21
figure 21

Comparison of Pushover and dynamic results a STR.1, y direction; b STR.2, y direction

Full size image

From Figs. 20 and 21 it can be observed that the results from the dynamic analysis generally follow those from the pushover analysis and they fall mostly between the pushover curves developed with rectangular and triangular load patterns. For most of the cases the rectangular pushover has higher values of shear demands. The results from dynamic analysis are closer to those from triangular pushover analysis.

In the x direction, the dynamic response of STR.1 fell slightly below the pushover curves indicating that the structure has a lower lateral resistance when subjected to earthquake ground motions than that predicted by pushover analysis, but nevertheless still the greatest form all the cases. The dynamic analysis results for STR.2 in x direction are closer to the pushover results. The dynamic results do not show the strength reduction observed in the pushover curves for STR.2 in x direction.

The results of the dynamic analysis for the y direction are more consistent with the pushover curves. The results for STR.1 fall generally between the rectangular and triangular pushover curves. While for STR.2 dynamic results show some higher values of base shears at higher drift demands.

Inter-story drifts from dynamic time history analyses

The maximum inter-story drifts from the dynamic analysis with the set of ground motions is presented in Figs. 22 and 23 below. The figures also show the inter-story drift limit for the LS performance level which was considered the same as in the pushover results evaluation section. The median maximum inter-story drift is shown in the red line with triangular markers.

Fig. 22
figure 22

Inter-story drifts; a STR.1, x direction; b STR.2, x direction

Full size image
Fig. 23
figure 23

Inter-story drifts; a STR.1, y-direction; b STR.2, y direction

Full size image

In the x direction, the median maximum inter-story drifts for structure STR.1 exceeded the 1% limit for all the stories, with peak values in stories 3 and 4. The inter-story drift limit in the case of STR.2 was exceeded for stories 1 and 4 only. Three of the ground motions gave higher inter-story drifts for the first three stories with values going up to 4–5%.

In the y- direction, the median maximum inter-story drifts for structure STR.1 followed the trend of the x direction. The inter-story drift limit was exceeded in al stories except story 5, while the maximum value of inter-story drift was observed in story 3. In this case the results are more consistent with those from pushover analysis. Structure STR.2 in the y direction showed higher inter-story drifts for the first two stories. Some of the ground motions gave higher inter-story drifts for the first three stories in y direction as well. Based on these results, none of the structures satisfies the LS inter-story drift limit.

Conclusions

The aim of this study was to evaluate the performance of an existing reinforced concrete public building designed for mid-1980s code requirements in Albania. The seismic demands considered were both those defined in KTP-N.2-89 and EC8. In the study were considered two types of structures, STR.1 and STR.2, even though the original structure corresponds to the former per the blueprints. The lower material qualities were taken into consideration because of the uncertainty of the actual material strength from the lack of experimental test on the structure and to create an idea about structures which have been constructed with lower strength material, a common case for older structures.

For the performance evaluation two types of non-linear analyses were used: a static pushover and a dynamic time-history analysis. For the static pushover analysis were followed the procedures of the capacity spectrum method, and design spectra of both KTP-N.2-89 and EC8 were considered. The demands from KTP-N.2-89 were determined to be in the range of 50% of those from EC8. Considering KTP-N.2-89 seismic demands the structure satisfies the performance requirements, while this is not the case for EC8. The inter-story drifts were checked and they exceeded the limits for some of the floors.

The dynamic time-history analysis was conducted with a set of seven ground motions from natural earthquakes that occurred around the Mediterranean region. The results were generally consistent with those from the pushover analysis. The median responses showed higher values of inter-story drifts, especially in the first floor, when compared to pushover results. The inter-story drifts exceeded the limit in most of the cases. The conclusions of the study are summarized as follows:

  • The comparison of two structural types with different material strengths showed their influence in the overall seismic performance of the structure. The original building corresponds to structure type STR.1 according to the blueprints having high material strengths, but this may not be the case for many other structures constructed in that period, thus results for STR.2 may give indications for this kind of structures.

  • When comparing, the seismic demands defined by the response spectra of KTP-N.2-89 and EC8 codes it is evident that demands from KTP-N.2-89 are much lower than those from EC8, and the structure would satisfy the performance requirements if KTP-N.2-89 response spectra are considered. Again, this underscores the importance of adopting EC8 norms in Albania as it has been already recognized in various studies.

  • The maximum inter-story drifts for each structure type in both directions were compared. The results showed that the values of inter-story drifts exceeded the limit in most of the cases and the structure did not meet the performance requirements. From the static pushover analysis, the highest values of inter-story drifts were observed in the middle stories, while the dynamic time-history analysis showed that higher values of drifts are observed in the first story as well.

  • The higher inter-story drift values in the third story correspond to the sudden reduction in column size and reinforcement at this level. This reduction may attract drift demands at this level of the structure, thus a more uniform reduction would benefit the structure.

  • When evaluating the global performance of the structure in terms of inter-story drifts, the limit values defined in FEMA 356 are affected by the type of structure taken into consideration. The detailing requirements for special moment frames designed for seismic effects such as the width of the RC elements in relation to the rebar sizes, or the width of the RC elements in comparison to the stirrup spacing, were not fulfilled by the case study structure. Thus, the inter-story drift limits considered were lower.

It must be noted that this evaluation is specific to the characteristics of this structure. Additional studies are needed to characterize the expected seismic performance of vulnerable structures and to develop effective seismic rehabilitation techniques that meet the selected performance objectives.