Introduction

Conventional seismic resisting systems that comply with current codes are typically designed for collapse prevention performance level, in which significant structural damage because of large residual drifts and yielded elements is expected. Accordingly, after a design level earthquake, the structure should be demolished or may need major repairs in the main structural elements, which is neither feasible nor economical. In the last decade, a high level of interest in proposing and design of low-damage structural systems have been observed among the researchers and the professional engineers.

One idea is based on directing the damage to some pre-decided parts of the system to be damaged, while the overall system remains in the safe margin. Considering such approach in the buildings will minimize the residual damage on the main structural elements, implementing dissipative connections introduced as structural fuses, which can be replaced after a strong ground motion. The main concept of these systems is to provide life safety during a severe seismic event, whilst the structural system does not experience any major plastic deformation and remain stable and operational after the earthquake by only replacing the damaged elements (Vargas and Bruneau 2006; Clifton et al. 2007; Eatherton et al. 2008; Christopoulos et al. 2008; Eatherton et al. 2010; Hosseini and Noroozinejad Farsangi 2012; Loo et al. 2015; Hashemi et al. 2017).

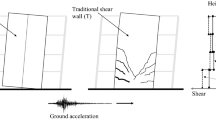
Reinforced concrete moment resisting frame equipped with shear walls is one of the most common structural systems in the region of high seismicity. In the recent earthquakes with large magnitudes, it was observed that these systems experience high level of damage especially in the shear wall elements. To overcome this problem, self-centering systems with rocking motions have been proposed by the researchers in different parts of the world. The idea of rocking or seesaw motion in the structural system was first studied by Housner (1963), in which the behavior of such systems subjected to earthquake following the May 1960 Chile earthquake was monitored, during which several buildings unintentionally rocked on their bases without collapsing (Fig. 1).

Fig. 1
figure 1

General behavior of a rocking block under lateral loadings (Housner 1963)

Full size image

The main characteristics of these systems is, that they can stabilize themselves easily after a major seismic event and the probable damage will be reduced in the main load carrying elements. However, implementing such systems have some complexities in the real construction and may be uneconomical as well. To this end, the researchers in the recent years have tried to improve such shortages by introducing some energy dissipating elements to be connected to the main structural systems. By doing this, most of the damage will be concentrated at these structural fuses, and they can be repaired/replaced after the seismic event very easily, and the main structure will remain safe and undamaged (Eatherton and Hajjar 2011; Ozaki et al. 2012; Nicknam and Filiatrault 2015; Hashemi et al. 2016; Nouri et al. 2016; Lu et al. 2016).

This article addresses rocking shear walls (RSWs) with replaceable devices implemented as connectors to introduce an economical low-damage structure for the seismic prone areas. Several configurations of the proposed system have been constructed and tested in experimental and numerical environments. Experiments on several RSWs with replaceable connectors are discussed and results are presented. Schematic illustration of the proposed connection is depicted in Fig. 2. The detailed test set-up and system configuration will be explained in detail in the next section.

Fig. 2
figure 2

Components of the proposed repairbale connection

Full size image

Test set-up and specimens fabrication

The main purpose of the experimental test program conducted in this study is to evaluate the structural performance and behavior of an innovative self-centering rocking RC shear wall (SC-RRCSW). The experimental program was implemented at the structural engineering laboratory of IIEES and displacement control quasi-static cyclic tests were conducted on the models with a scale factor of 1/3 to facilitate testing of the constructed specimens. The test set-up used an existing modular system for experimental testing of scaled specimens.

The dimension of specimens has been chosen in a way to produce various probable damages for a better comparison. To this end, a conventional RC-SW is designed and constructed as the reference model, while four different specimens with the new connection and having the rocking capability have been fabricated to evaluate the feasibility and applicability of the proposed system. It’s worth mentioning that during the concreting and construction stage, several concrete cube specimens have been sampled and used for the normal compressive test (Fig. 3).

Fig. 3
figure 3

Specimens’ fabrication, concreting and compressive strength test

Full size image

The physical dimensions of the shear walls and test set-up were identical for all the specimens; however, the proposed connection details and loading parameters were different for different SC-RRCSWs. The design details and configurations of tested SC-RRCSWs and the reference model are given in Table 1. The reference model is fully fixed in the foundation to behave as a conventional shear wall, while the proposed models are not fixed to the base to provide the desired rocking mechanism in SC-RRCSWs. The proposed connections are designed and connected to the wall corners using several high strength steel bolts. To provide the possibility of the rocking motion in the wall, bean-shaped holes (short slotted in vertical direction) are used on the connections’ external plates (Fig. 2). Using such the configuration will minimize the damage level on the wall corners and the connection can be repaired/replaced after major damage. An important stage in this study is the preliminary design of the proposed system, which can be beneficial for practical engineers as well. The external steel plate which is the main component of the proposed system is designed based on the tension and compression forces (T and C) acting on the wall corners as shown in Fig. 4. On the other hand, the proposed stiffeners on the last specimen should be designed in a way to tolerate the shear force applied at the SW base. Welding length and dimension should also be calculated based on the stiffeners’ capacity.

Table 1 Specimens details
Full size table
Fig. 4
figure 4

Equilibrium condition of the SW and the design forces for connectors

Full size image

As depicted in Fig. 2, three high strength bolts have been used on each side to connect the external plates to the SW. Based on table J3.3M given in AISC 360 (2010), vertical short-slotted holes with 30 mm width and 37 mm length are fabricated on the external steel plates. Material properties for SW and used materials in the proposed connection are given in Table 2.

Table 2 Material properties, size and dimensions of components in the new system
Full size table

The shear walls are designed using ACI-318 (2011) and the loading protocol for quasi-static tests was adopted from ATC-24 (Krawinkler H 1992) which is shown in Fig. 5. The graphical representation of test set-up and the hydraulic actuator with the capacity of 1000 kN to apply force on the top wall corner is as well presented in Fig. 6. To prevent stress concentration and local damage to the SW top corners, the force was transferred through a 35 × 35 × 5 cm3 steel plate on the wall at loading location. During all the experiments, the transfer plate was monitored continuously for possible slip; however, because of the rigidity of the connections, no slip was observed under the loading regime. The proposed structural fuses were as well connected to the wall bottom corners using three high strength bolts at each side. The proposed connections at the other end were carefully secured by welding to the foundation steel plate.

Fig. 5
figure 5

Displacement-control loading protocol for the quasi-static analyses

Full size image
Fig. 6
figure 6

Perspective view of the test set-up

Full size image

To compare the stress levels in different specimens, several strain gauges have been implemented inside the experimental models and on the proposed connections. To measure the deformation of the shear walls at the connections’ location, six linear variable displacement transducers (LVDTs) at the elevation of 20, 30 and 40 cm from the base are utilized to record horizontal displacement, while 2 LVDTs are used to measure the vertical uplift on the wall face, and the data were recorded using UPM-100 acquisition device which can capture up to 100 signals simultaneously. The location of strain gauges and horizontal LVDTs are shown in Fig. 7. For the proposed models and to measure the rocking motion, a pair of symmetrically placed LVDTs was used on the shear wall face as well. On the other hand, and to determine the strain history of the specimens, eight strain gauges have been installed on the vertical longitudinal bars at 25 and 35 cm from the base beam inside the SWs at the wall corners, while 4 strain gauges were installed on the external plates at 10 cm from the base beam to monitor the behavior of proposed connections under cyclic loadings. The locations are shown in Figs. 6 and 7.

Fig. 7
figure 7

Position of instrumentations in the specimens a Strain Gauges b LVDTs

Full size image

Results and discussion

Hysteretic behaviour of shear walls

Figures 8 and 9 show the hysteresis response of the reference and the proposed models. From the hysteresis loops, it can be easily observed that the proposed models have dissipated much more energy compared to the conventional system. The first proposed specimen has similar loops to conventional model, while the other three specimens have much better hysteresis behavior compared to reference model.

Fig. 8
figure 8

Hysteretic behavior of the reference model (Conventional SW)

Full size image
Fig. 9
figure 9

Horizontal load–displacement behavior of the proposed models

Full size image

The other point which should be noted is that the reference model which is the representative of the classical code-based SW can only tolerate forces up to 500 kN and severe damage has occurred at the wall base, in which the system cannot be even repaired and is fully out of service after the cyclic test. On the other hand, the proposed models have tolerated around 560–750 kN of lateral loading and based on the observation, no specific damage was monitored in the SW; however, the external steel plates which were connected to the base steel chassis were yielded that can be easily replaced after the experiment. In case of more severe loadings, the steel bolts at connection interface may fail as well, which can be replaced with the new ones as well, but such the case is not observed in the current investigation. Based on the observation and the hysteresis response, the last configuration (Specimen 4) is considered as the best model and will be studied and investigated in the next sections and in the future studies (representative of SC-RRCSWs in general).

For a better comparison of the various specimens, the backbone curves of all tested SWs are plotted in Fig. 10. Based on the depicted results, conventional SW (Ref. Model) has the least ductility and strength compared to proposed system with various configurations. On the other hand, all the proposed models (specimens 1–4) have much better ductility, seismic performance and strength capacities, in which specimens 3 and 4 are behaving relatively better than the other cases. In terms of initial stiffness, significant differences are not observed, and all the tested models are behaving very much similar.

Fig. 10
figure 10

Comparison of Backbone curves for experimentally tested specimens

Full size image

To compare the dissipated hysteresis energy during the quasi static test, a comparison is made between the reference and the proposed models and the outcome is illustrated in Fig. 11. Based on the experimental results, the last configuration of the proposed system (Case 4) have had the best performance among all the specimens, hence the result of this model has been considered for the comparison. From Fig. 9, it can be observed that in the shear wall with the proposed connection, the stiffness and strength degradations have been lower compared to the conventional SW; hence, the energy dissipation capacity is nearly doubled in the proposed system, which is mainly concentrated at the connections’ locations. It should be emphasized that for the new system with reparable connections, a higher rate of damping is provided with the least damage in the core SW system, which is the key characteristic of a low-damage structural system.

Fig. 11
figure 11

Comparison of the dissipated energy for the proposed and the reference models

Full size image

Based on the observation, the conventional SW specimen was severely damaged after applying the loading protocol; however, the final proposed model (Case 4) did not affect significantly. Some minor cracks were observed at the wall face, but the overall behavior has been in the elastic range and no repairing/retrofitting was needed. In the proposed model, most of the damage have been concentrated on the connection’s location, in which the stiffeners were yielded and welded connections to the base beam were cracked and failed, which can be repaired easily (Fig. 12).

Fig. 12
figure 12

Experimental models after the quasi-static test a Reference b Proposed

Full size image

For a better comparison, the strain time history of the models was investigated as well. As can be seen in Fig. 13, the conventional SW system has experienced relatively much higher level of strain (Data are extracted from strain gauge # S57 located at 35 cm from the wall base) and undergone large deformations in the plastic region. On the other hand, the trend for the proposed system is uniform and steady in elastic range, and no plastic deformation is monitored by the strain gauges inside the SW. On the other hand, the structural fuses were activated as expected and the damages were concentrated to the connections’ locations. The strain gauge installed on the proposed connection has successfully captured the plastic deformation of the plates because of the high-energy concentration (Fig. 14).

Fig. 13
figure 13

Comparison of strain time history in the most critical strain gauge inside the SWs

Full size image
Fig. 14
figure 14

Strain time history of the proposed connection under cyclic loading

Full size image

To make sure that the rocking motion is achieved in the proposed system, the vertical uplift time history captured by the installed LVDT at the bottom corner is plotted in Fig. 15. As can be seen, a maximum value of 24 mm uplift is measured by the LVDT. Horizontal displacement is also plotted versus the vertical displacement. It can be observed that, the wall repeatedly returns to foundation level and the desired rocking mechanism is successfully achieved.

Fig. 15
figure 15

Horizontal and vertical time history of the fuses to monitor SW rocking motion

Full size image

Finite element models validation against test data

Numerical and analytical models attempt to simulate and predict the actual mechanisms. As it is not often practical to test every aspect, people need to rely on suitable analytical models. For establishing the accuracy and applicability of the analytical model, experimental and analytical load–deflection plots for SC-RRCSW specimens should be compared and calibrated.

In this study ABAQUS finite element program, which is one of the most powerful platforms in the field has been used for numerical investigation of structural specimens (ABAQUS 2014). Material and section properties and the transverse and longitudinal bars were defined. After determining the elements, nodes, modeling elements and the analysis type, support boundary conditions; lateral loadings based on the experimental test program were applied to the simulated FE models. To improve the accuracy of the simulated models, 8-node C3D8R solid elements, which is a linear 3D hex-dominated shape element was adopted to model the SW. An important stage in the FE modeling of the proposed system is to model the contact and interaction between the proposed connection and SW. To this end, surface to surface contact elements considering the appropriate friction coefficient were utilized. For simulating the real behavior of the bolts used in the proposed connection, embedded region constraint was used in ABAQUS platform.

To accurately simulate the constitutive behavior of concrete in ABAQUS platform, concrete damage plasticity (CDP) model proposed by Jason et al. (2004) is used in this study, in which compressive crushing and tensile cracking of concrete are considered as the main failure modes. Based on CDP model, the compressive and tensile behaviors of concrete material are different and the stress–strain curves are plotted in Fig. 16. Steel materials for steel components and bolts are as well defined based on the data given in Table 2 using bilinear material models with 15% strain hardening. The modeling details of the proposed connection are as well presented in Fig. 17. The friction coefficient between the external and embed wall plates is considered as 0.4 by defining finite sliding for surface to surface interaction.

Fig. 16
figure 16

Stress–strain curves for concrete material used in ABAQUS

Full size image
Fig. 17
figure 17

Details of proposed connection in ABAQUS

Full size image

The modified Newton–Raphson method was used for nonlinear analysis (Ben-Israel 1966). The schematic assembly of the FE model and stress distribution of the final SC-RRCSW are illustrated in Figs. 18 and 19 accordingly. As can be seen, the stress distribution very well agrees with the failure pattern in the experimental test and most of the damage was concentrated at the proposed connection, while the SW was maintained at an elastic state.

Fig. 18
figure 18

Simulated FE model of the proposed system in ABAQUS

Full size image
Fig. 19
figure 19

Von-Mises stress distribution of the final model a global view, b local view

Full size image

An important stage in the FE modeling of structures is to make sure that the simulated models are reliable and have enough accuracy. To this end, calibration and verification stages should be done in accordance with the experimental test results. At the later stage, the FE models can be used for further analysis and investigations. For the sake of brevity, the calibrated and verified hysteretic result of the 5th experimental specimen (Case 4) is given in Fig. 20. As can be seen from this figure, the numerical results match very well with the experimental outcome with less than 10% differences in the peak values and the numerical models are successfully verified. Further study including sensitivity analyses and seismic performance factor quantification of the proposed system are being investigated in a separate manuscript utilizing the verified FE models.

Fig. 20
figure 20

Comparison of the verified FE model of the proposed model with experimental results

Full size image

Conclusions and future work

As an alternative to current capacity design, low-damage systems can significantly reduce the induced damage in structural elements and improve the functionality of structures in the post-earthquake condition, by transferring the members’ plastic hinges to replaceable structural fuses. In this study, the application of an innovative SW system with repairable connections is introduced. The proposed SC-RRCSW model combines the advantages of high initial stiffness and substantial energy dissipation provided by the rocking mechanism at the base. The main characteristic of the new system is its applicability in real construction, which can be repaired and recovered to its pre-earthquake condition after moderate to strong seismic events. The proposed system has the potential to survive DBE and even MCE ground excitations with the least structural damage.

The key highlights of the proposed system can be summarized as:

  • The residual stress and deformations will be minimized or even eliminated. Based on the strain time-history results, the main SW in the proposed system is maintained in the elastic region during and after the cyclic loading.

  • The connections will undergo the nonlinear state, whereas the main structural system will remain in the elastic region.

  • The cumulative dissipated energy is notably higher compared to conventional SW system. This significance difference can be attributed to stiffness and strength deterioration rates in the conventional SW system.

  • The structural system will not significantly damage by even large magnitude and long duration seismic events, and can be quickly reoccupied and business disruption will be minimized.

  • Overall, the proposed concept in this study has excellent promise as a means of damage minimization in any type of structures designed to uplift or rock.

These are initial steps towards practical implementation; however, much remains to be done. Future research will involve implementing the proposed system in a multi-storey RC framed structure to be used for quasi-static and shake-table testing. Determination of the seismic performance factors of the proposed SC-RRCSW using (FEMA P-695 2009) guideline for possible consideration by future edition of (ASCE-7 2010) is another topic to be covered in the upcoming studies.