Introduction

If a structure is operated beyond the elastic limit, inevitably present variable portions of the load, even when of low intensity, that is to say even in “predominantly static loading,” can cause progressive deformations so that strains and displacements continue to grow with each load cycle. This process is also called ratcheting. Its computation is usually associated with a very high numerical effort, because possibly thousands of load cycles must be calculated incrementally with an elastic–plastic material model—at least if no suitable simplified analysis methods are available.

Ratcheting can trigger different failure mechanisms. Examples which may be mentioned are that the elongations become so great that, after a certain number of load cycles, the ductility of the material is exceeded, or that the mean elongation in a cycle can reach a level for which the material or component fatigue curves no longer apply and premature fatigue fracture occurs. Further effects may be that the deformations become so great after a series of load changes that the serviceability of the structure is no longer ensured, or the application of first-order theory is no longer tolerable but instead application of second- or third-order theory is required.

Ratcheting can have different causes. A distinction has already been made between material and structural ratcheting by Hübel (1996). Material ratcheting can be identified on the level of homogeneously stressed material test bodies. Its consideration in the framework of a structural analysis requires a material model which describes this phenomenon correctly. Structural ratcheting, on the other hand, can be attributed to inhomogeneous stress conditions and can also occur in materials that do not have material ratcheting. In the simplest case, structural ratcheting can be explained by the development of several plastic hinges, which are only alternately active in the different states of a variable load (Hübel 2016).

The best known examples of this are a load configuration consisting of two fixed loads, one of which is constant with time and the other cyclically variable (“Structural ratcheting at stationary load position and varying load level”). The present paper is intended to illustrate the fact that there is also a second, less known type of structural ratcheting, in which the progressive deformation can be caused by a single load, provided that it is moved in space. This behavior is illustrated by a continuous beam under a single moving lateral force (“Continuous beam subjected to a moving lateral force”), a three-bar model with consecutive temperatures in the individual bars (“Three-bar model”), a thick-walled cylinder subjected to a fluctuating thermal load (“Thermal fluctuation in a pipe”), and a thin-walled cylindrical shell under a traveling axial temperature gradient (“Cylindrical shell under moving axial temperature gradient”). The effects of material hardening are discussed (“Hardening”), of elastic foundation (“Elastic foundation”), of second-order geometric effects (formulation of equilibrium condition at the displaced configuration, “Second-order geometric effects”), and of true geometry of the displacement (“Third-order geometric effects”).

Structural ratcheting at stationary load position and varying load level

Many configurations are known to produce progressive deformation. Simple examples, including the following ones, require not more than two different loads at fixed locations of the structure, one of constant level (and often interpreted to be the driving force of ratcheting) while the other is cyclically varying.

The two-bar model (Fig. 1) is useful for a lucid explanation of structural ratcheting and can, at least in the case of a linear elastic–perfectly plastic material model, easily be analyzed by hand (Hübel 2016). Two bars are interconnected by a rigid plate so that only vertical displacements are possible. A constant force F is applied along with a cyclical change in temperature T in the left bar.

Fig. 1
figure 1

Two-bar model (Hübel 2016)

Full size image

A continuous beam (Fig. 2) is subjected to a constant force F 1 in the first span and a cyclically varying force F 2 in the second span (Hübel 2016; Burth and Brocks 1992).

Fig. 2
figure 2

Continuous beam (Hübel 2016)

Full size image

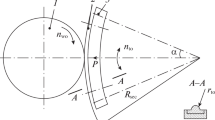
The so-called Bree tube (Fig. 3) is defined by a thin-walled pipe subjected to constant internal pressure p and a cyclic through-wall radial temperature gradient ΔT (Bree 1967). This example forms the basis for rules guarding against ratcheting in numerous international design codes, in particular related to nuclear technology.

Fig. 3
figure 3

Bree tube (Hübel 2016)

Full size image

In all these examples, a constant primary load is always required (forces in Figs. 1, 2, internal pressure in Fig. 3) in order to establish a ratcheting mechanism together with a second, variable load. This has led to numerous misunderstandings in practice, because not only in technical literature, but even in design rules, the presence of a constant primary load is suggested to be an inevitable prerequisite for structural ratcheting to occur. However, “Structural ratcheting at spatially moving load and constant load level” shows that this is not necessarily the case.

Structural ratcheting at spatially moving load and constant load level

In the following, it will be shown by way of example that load configurations other than those described in “Structural ratcheting at stationary load position and varying load level” can lead to ratcheting, thus constituting a further type of structural ratcheting, which is systematically different from that shown in “Structural ratcheting at stationary load position and varying load level.” It requires neither a combination of constant primary load with other, variable loads, nor a variable load level. Rather, a single load of constant load level is sufficient, if it just moves in space.

We will assume additivity of the elastic, plastic, and, if applicable, thermal strains, and that the strains remain “small.”

Continuous beam subjected to a moving lateral force

Starting from the continuous beam shown in Fig. 2, the load F 1 in the left-hand span is dispensed with and the force F is applied at constant load level only in the right-hand span. It moves repeatedly over the second span (Fig. 4). Dynamic effects are neglected. Therefore, the specification of “time” only serves to describe the sequence of successive events and has no physical meaning. Only bending stresses are considered (no deformation due to transverse forces). The rotations remain “small” (first-order theory).

Fig. 4
figure 4

Continuous beam subjected to moving lateral force

Full size image

In the following, the theory of plastic hinges is used. The interaction between the bending moment and the transverse force is neglected, so that only the plastic moment M pl of the section is effective.

Plastic limit load

The plastic limit load F T of the structure evaluates to

$$F_{\text{T}} = \frac{1}{{(\sqrt 2 - 1)^{2} }}\frac{{M_{\text{pl}} }}{L} \approx 5.828\frac{{M_{\text{pl}} }}{L},$$
(1)

and is associated with the position of the force at

$$x_{\text{T}} = (2 - \sqrt 2 )L \approx 0.586\,L.$$
(2)

The underlying mechanism is a kinematic chain due to two plastic hinges (in the right span and on the inner support), which are both active at the same time.

Force moving to the right

For our study of a variable load, we select a load level just below the plastic limit load:

$$F = 5.75\frac{{M_{\text{pl}} }}{L}.$$
(3)

First, a movement of the load from the inner support to the right is examined. In the first load cycle, the first plastic hinge is formed in the second span, when the load reaches the position x 1. The corresponding bending moment diagram is shown in Fig. 5.

Fig. 5
figure 5

Continuous beam: bending moment diagram at the formation of the first plastic hinge

Full size image

If, from this load position, the force F is shifted further to the right, the previously created plastic hinge is relieved, since the most highly stressed point is now located at the new load position, where a new plastic hinge is formed and the moment M pl cannot be exceeded. Only the most recently formed plastic hinge is active, whereas all previously formed plastic hinges experience elastic relief, and the plastic kinks present there act as constraining load (Fig. 6).

Fig. 6
figure 6

Continuous beam: previously formed plastic hinge (bending moment diagram dashed at point in time of its formation) is relieved upon the formation of the next plastic hinge

Full size image

Any movement of the force to the right makes this process continue. An infinite number of plastic hinges are emerging, of which however only one is active at a time. This process comes to a standstill at a certain load position. If the force moves even further to the right, no new plastic hinges are created. The system then behaves elastically, whereas, in addition to the traveling force F, the displacement-controlled loads due to the plastic kinks also act in all previously created but now passive plastic hinges.

During a second load cycle, in which the force F travels again from x = 0 to the right over the second span, the residual moments created in the first cycle act as a pretension. As a consequence, a plastic hinge is formed at the mid-support when the force reaches a certain position, remaining active (i.e. opening continuously), while the force travels further to the right. At some travel distance, the plastic hinge at the mid-support becomes passive. If the load is shifted further to the right, the plastic hinges in the second span become active again, as in the first cycle.

From the second cycle, the force quantities and the plasticizing portions of the beam behave strictly periodically. However, this does not apply to the displacements! Since at most only one of the infinite number of plastic hinges is active at each point in time, the alternating activation of the plastic hinges has resulted in a ratcheting mechanism which causes the deformations to increase in each load cycle, with the same increment in each cycle. However, the location of maximum deflection changes in the first cycles.

Figure 7 shows the deformations of the first 50 cycles, each at the time of the load positioned at x F = 0.5 L. The histogram of the deflections in the center of the right span is shown in Fig. 8. Accordingly, the deflection in each cycle increases at a constant rate.

Fig. 7
figure 7

Continuous beam: displacements of the first 50 load cycles (enlarged scale) at loading times corresponding to a load position at the middle of the right span in the case of a force moving to the right in the second span

Full size image
Fig. 8
figure 8

Continuous beam: histogram of the deflection (m) in the center of the right span in the case of a force moving to the right in the second span; numbers apply to a steel profile HEB 300 made from S355

Full size image

The analysis was carried out using the FE program ANSYS (element type BEAM188). Adopting the theory of plastic hinges, the result is not particularly sensitive to the number of discrete load positions, so that a few hundred load positions per cycle are sufficient. In view of the necessary number of equilibrium iterations in an incremental analysis, the computational equivalent of about 10,000–20,000 elastic analyses is to be spent for 50 cycles.

Since the range of the section moments does not reach twice the plastic moment M pl at any point in the structure, reversed plasticizing, i.e. the opening of a plastic hinge in the opposite direction, is excluded. Therefore, a pronounced low-cycle fatigue problem is not to be expected.

Force moving to the left

In contrast to the direction of movement to the right, a plastic hinge is formed not only in the span, but also at the inner support in the first cycle, if the force is moved to the left, starting at the right support until the inner support is reached. The corresponding displacements of the first 5 load cycles are shown in Fig. 9.

Fig. 9
figure 9

Continuous beam: displacements of the first 5 load cycles (enlarged scale) at loading times corresponding to a load position at the middle of the right span in the case of a force moving to the left in the second span

Full size image

Force moving alternatingly to the right and left

If the movement of the traveling force is first directed to the right, starting at the inner support, and then back to the left, we obtain the displacements shown in Fig. 10 for the first 5 cycles.

Fig. 10
figure 10

Continuous beam: displacements of the first 5 load cycles (enlarged scale) at loading times corresponding to a load position at the middle of the right span in the case of a force alternatingly moving to the right and left in the second span

Full size image

Thus, we can conclude that the progressive deformation depends on the direction of the movement of the load in space.

Theory of plastic zones

When adopting the theory of plastic zones instead of the theory of plastic hinges, partially plastic cross-sections can also be considered. The incremental analysis required for this is performed with the 3-node element type BEAM189 from ANSYS, with 14 integration points across the thickness of the beam. It is found that the analysis result is quite sensitive to the selected number of discrete load positions, unlike when using the theory of plastic hinges (“Force moving to the right,” “Force moving to the left,” “Force moving alternatingly to the right and left”). In addition, the plastic zone and the axial distribution of strains within the plastic zone develop only gradually with the number of cycles, so that, in contrast to the theory of plastic hinges, the deformation increment per cycle is not constant. Instead, a phase with transient ratcheting is observed. In this, the deformation increments decrease and the residual moments change from cycle to cycle until a quasi-stationary state with approximately constant deformation increments and periodic moments is reached. This transient behavior is all the more pronounced the less discrete load positions are analyzed.

Figure 11 shows the histogram of the deflection according to the theory of plastic zones for a number of discrete load positions compared with the theory of plastic hinges. For this purpose, a rectangular cross-section with the same bending stiffness and the same plastic moment M pl as the HEB profile in Fig. 9 was used. In the case of the theory of plastic zones, the computational equivalent of several hundred thousand elastic analyses must be used for 50 cycles in order to achieve a good approximation to the solution for continuous load positioning.

Fig. 11
figure 11

Continuous beam (analysis with theory of plastic zones): histogram of the deflection (m) in the center of the right span in the case of a force moving to the right in the second span

Full size image

Three-bar model

Not only forces can change their position, but temperatures can also migrate and thus allow for spatially variable thermal loading.

In Wolters and Majumdar (1994), a three-bar model was developed for the study of the ratcheting behavior of the first wall of a fusion reactor. A modification of this model will be considered in the following. Three bars are arranged parallel to one another and are connected to one another in such a way that they are always of the same length (Fig. 12). They are subjected to a temperature T in succession.

Fig. 12
figure 12

Three-bar model

Full size image

If we apply a negative thermal strain in bar 1 (time 2), causing a fictitious elastic tensile stress (i.e. according to an analysis assuming purely elastic behavior) of, say, 1.3 times the yield stress f y, we have

$$\sigma_{ 1}^{\text{fel}} = 1.3f_{\text{y}} .$$
(4)

Assuming linear elastic–perfectly plastic material, an axial plastic hinge develops in this bar, while the other two bars remain elastic. The stresses in the three bars are

$$\sigma_{1} = f_{\text{y}} ;\quad \sigma_{2} = \sigma_{3} = - 0.5f_{\text{y}} ,$$
(5)

and the mechanical (elastic plus plastic) strains (Young’s modulus E)

$$\varepsilon_{1} = + 1.45f_{\text{y}} /E;\quad \varepsilon_{2} = \varepsilon_{3} = - 0.5f_{\text{y}} /E.$$
(6)

Unloading (time 3) is associated with purely elastic action, resulting in the stresses and strains:

$$\sigma_{1} = - 0.3f_{\text{y}} ;\quad \sigma_{2} = \sigma_{3} = + 0.15f_{\text{y}} ,$$
(7)
$$\varepsilon_{1} = \varepsilon_{2} = \varepsilon_{3} = + 0.15f_{\text{y}} /E.$$
(8)

At time 4, the thermal load is applied to bar 2. This bar becomes plastic, while the two other bars behave elastically, so that only the newly formed axial plastic hinge in bar 2 is active. We obtain the stresses and strains

$$\sigma_{1} = - 0.725f_{\text{y}} ;\quad \sigma_{2} = f_{\text{y}} ;\quad \sigma_{3} = - 0.275f_{\text{y}} ,$$
(9)
$$\varepsilon_{1} = - 0.275f_{\text{y}} /E;\quad \varepsilon_{2} = 1.675f_{\text{y}} /E;\quad \varepsilon_{3} = - 0.275f_{\text{y}} /E.$$
(10)

Upon unloading (time 5), we obtain

$$\sigma_{1} = - 0.075f_{\text{y}} ;\quad \sigma_{2} = - 0.3f_{\text{y}} ;\quad \sigma_{3} = 0.375f_{\text{y}} ,$$
(11)
$$\varepsilon_{1} = \varepsilon_{2} = \varepsilon_{3} = + 0.375f_{\text{y}} /E.$$
(12)

After applying the temperature in bar 3 (time 6), an axial plastic hinge is created there, while the other two bars experience elastic relief:

$$\sigma_{1} = - 0.3875f_{\text{y}} ;\quad \sigma_{2} = - 0.6125f_{\text{y}} ;\quad \sigma_{3} = f_{\text{y}} ,$$
(13)
$$\varepsilon_{1} = 0.0625f_{\text{y}} /E;\quad \varepsilon_{2} = 0.0625f_{\text{y}} /E;\quad \varepsilon_{3} = 2.0125f_{\text{y}} /E.$$
(14)

After unloading (time 7), we have

$$\sigma_{1} = 0.2625f_{\text{y}} ;\quad \sigma_{2} = 0.0375f_{\text{y}} ;\quad \sigma_{3} = - 0.3f_{\text{y}} ,$$
(15)
$$\varepsilon_{1} = \varepsilon_{2} = \varepsilon_{3} = 0.7125f_{\text{y}} /E,$$
(16)

and the first loading cycle is completed. The stresses at time 7 represent residual stresses, so that the second cycle, which begins with renewed thermal load in bar 1, leads to stresses and strains in bars 2 and 3 that are different from time 2. This process continues from cycle to cycle. Only after an infinite number of cycles, a periodic state is achieved, in which the same residual stresses occur in each cycle and the same strain increment δε per cycle. At the end of each cycle, we then have

$$\sigma_{1} = 0.3f_{\text{y}} ;\quad \sigma_{2} = 0;\quad \sigma_{3} = - 0.3f_{\text{y}} ,$$
(17)
$$\delta \varepsilon = 0.9f_{\text{y}} /E.$$
(18)

However, this state is very well approximated very quickly. Thus, after eight cycles, the periodic state at the respective cycle end is known within an eight-digit accuracy.

Figure 13 shows the histogram of the stresses and mechanical strains in all three bars in the first five cycles so that the progressive deformation is evident, as also in the stress–strain diagram shown in Fig. 14. It can be seen that reversed plasticizing does never occur so that no pronounced fatigue problem is present at the load level given by Eq. (4) (and not for all load levels \(\sigma_{ 1}^{\text{fel}} = 1 \ldots \frac{5}{3}f_{\text{y}}\)).

Fig. 13
figure 13

Three-bar model: stress and strain histograms of the first 5 cycles

Full size image
Fig. 14
figure 14

Three-bar model: stress–strain diagram of the first 5 cycles

Full size image

Thermal fluctuation in a pipe

As a more practical example for illustrating the fact that a sequence of temperature profiles leads to migrating locations of maximum stress, a pipe is considered. The inner surface is subjected to temperature changes so that an unsteady temperature profile develops over the wall thickness.

If such temperature fluctuations are of high frequency, the penetration depth of the temperature front into the pipe wall is low, so that zones close to the inner surface are strongly stressed, which is also referred to as “thermal striping.” This can lead to a fatigue problem but not to a ratcheting problem. We therefore consider, in the following, slower processes in which a pronounced temperature profile can develop over the wall thickness.

A pipe with internal radius r i (=95 mm) and external radius r a (=135 mm) is passed through by a fluid which changes its temperature T F within 10 s from 350 to 50 °C, maintains this temperature for 10 s, then within 10 s returns to 350 °C, and maintains this temperature for 30 s, after which the same temperature cycle is repeated (Fig. 15). The heat transfer coefficient is infinitely large, so that the fluid temperature strikes the inner surface of the pipe undamped. The outer surface is perfectly insulated. The tube is infinitely long, so that end effects need not be taken into account. The thermal and mechanical material data are temperature-independent and are indicated in Fig. 15.

Fig. 15
figure 15

Pipe subjected to thermal transient

Full size image

Thermal analysis

With a thermal analysis (FE program ANSYS, axisymmetric element type PLANE55, 200 elements across the wall thickness), the temperature profiles are calculated over the wall thickness at many points in time of the fluid temperature transient. After 20 cycles, periodic temperature curves are obtained in a good approximation. Figure 16 shows the temperature profiles at four points of time in the 20th cycle.

Fig. 16
figure 16

Temperature profiles (°C) after 10, 20, 30, and 60 s in the 20th cycle

Full size image

Elastic–plastic analysis

As a result of the temperature load, a three-dimensional stress state is produced. The most highly stressed point is the inner surface. A linear elastic–perfectly plastic material model with Mises yield surface is used. The FE calculation is performed with the axisymmetric PLANE182 elements of ANSYS.

The plastic zone extends over the entire wall thickness. However, at any time, only parts thereof are actively plastic, while other parts experience a temporary elastic relief and only become actively plastic again at a later point in time. The active part of the plastic zone thus travels through the pipe wall with time. Figure 17 shows the development of the expansion of the inner surface during the first 10 cycles based on the thermal behavior in the 20th cycle. There is also a length change in the axial direction, but this is much smaller.

Fig. 17
figure 17

Development of the radial displacement on the inner surface of the pipe during the first 10 cycles, after a periodic unsteady temperature field is established

Full size image

The elementary difference to the Bree tube (Fig. 3) is that the Bree tube is subjected to maximum stress at the same locations (i.e., inside and outside surfaces) at any time of the load cycle, and there is also a location (the wall center), where no thermal stresses occur. Therefore, due to the temperature gradient alone, the pipe wall cannot be completely plasticized, so that ratcheting is only possible with the simultaneous effect of other additional loads, such as, for example, internal pressure.

Cylindrical shell under moving axial temperature gradient

In liquid-filled containers with vertical axis, axial temperature gradients can occur at the level of a free liquid surface. If the liquid changes its temperature, its change in density results in a change of the position of this surface.

The ratcheting behavior of thin-walled cylindrical shells was investigated as a result of stationary or moving axial temperature gradients with and without additional axial force by many researchers (Abdel-Karim 2005; Angiolini et al. 2016; Igari et al. 1993, 2000, 2002; Karadeniz and Ponter 1984; Karadeniz et al. 1987; Kobayashi and Ohno 1996; Kobayashi et al. 1998; Koo and Lee 2002, 2004; Lee et al. 2003, 2004; Ohno et al. 1998; Okajima (2016); Ponter and Carter 1989; Wada et al. 1993, 1995; Watanabe et al. 2008). In the case of a moving axial temperature gradient, the travel distance plays an important role. Most of the research work is related to a practical design problem encountered in Fast Reactors, where the temperature gradient is moving only in one direction (i.e. not alternately up and down). Due to the thermal inertia of the structure, the axial temperature gradient is caused by a rapid change in liquid temperature and is not inverted when the liquid slowly returns to its previous temperature.

In the following, a thin-walled, practically infinitely long axisymmetric shell (length L, Fig. 18) is subjected to a temperature distribution in the longitudinal direction. It consists of two regions of constant temperature (difference ΔT) with a step-like transition between the two. This transition region shifts cyclically in the positive x direction along a distance Δx, which is a multiple of the elastic decay length L cr of the shell, so that the two extreme load positions do not interfere with each other:

$$\Delta x = 100\;{\text{mm}} \approx 5.8 L_{\text{cr}} ,\quad L_{\text{cr}} = \pi \frac{{\sqrt {{{\left( {r_{a}^{2} - r_{i}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {r_{a}^{2} - r_{i}^{2} } \right)} 2}} \right. \kern-0pt} 2}} }}{{\sqrt[4]{{3(1 - \nu^{2} )}}}} \approx 17.3\;{\text{mm}} .$$
(19)
Fig. 18
figure 18

Cylindrical shell with axially moving temperature step

Full size image

The temperature is constant over the wall thickness. An incremental analysis is performed for linear elastic–perfectly plastic material with Mises yield surface and temperature-independent material data (Fig. 18) using axisymmetric shell elements (4000 elements of type SHELL109 from ANSYS). The shift of the temperature step must be discretized in time and be carried out in each cycle in at least 800 load steps. If a load step is subdivided into several substeps with several equilibrium iterations, a computational equivalent of several hundred thousand elastic analyses is to be expended for 50 cycles. The sudden temperature change between two adjacent elements is realized in the FE calculation in that the two elements do not share a common node (otherwise the temperature change would be distributed in a ramp-shaped manner over both elements), but the degrees of freedom of both nodes at the same geometric location are coupled.

At the location of the temperature step, compressive stresses occur in the circumferential direction at one element, and tensile stresses at the other element, which lead to different changes in the wall thickness due to Poisson’s ratio effects. Constraints caused by this can be disregarded using shell elements.

Figure 19 shows the displacement as well as the circumferential and axial stress components in the vicinity of the temperature step due to a fictitiously elastic analysis.

Fig. 19
figure 19

Cylindrical shell subjected to axial temperature step: fictitious elastic analysis results (limited to the vicinity of the temperature step)

Full size image

For the loading time at the end of the cycle (after the temperature step in the load position +Δx/2 is removed and before it is applied again at the load position −Δx/2), the residual displacements as a result of the incremental elastic–plastic analysis are shown in Fig. 20 for the first load cycles. In addition to the plateau-like radial displacement growing in each cycle, a progressive longitudinal contraction can also be observed. This is due to transverse effects as a result of the progressive circumferential tensile membrane strain. The asymmetry of the radial displacement is due to the fact that the region of the upper bending stress (see Fig. 19) is relieved because of the progressive radial displacement, while the lower region is additionally stressed.

Fig. 20
figure 20

Cylindrical shell with axially moving temperature step: residual displacements (enlarged scale) of the first load cycles in the vicinity of the travel distance

Full size image

Figure 21 shows the development of the radial displacement at x = 0. The displacement increment is approximately 0.1 mm per cycle, hence consistent with the data given in Kobayashi and Ohno (1996) and in Igari et al. (2000) for a “long” travel distance of the temperature step:

$$u = r_{\text{m}} \left( {\alpha_{\text{T}} \Delta T - 2\frac{{f_{\text{y}} }}{E}} \right) = 0.1 \;{\text{mm}} .$$
(20)
Fig. 21
figure 21

Cylindrical shell with axially moving temperature step: histogram of the radial displacement at x = 0 and the axial displacement at the upper shell end in the first load cycles

Full size image

According to the histogram of the load position in Fig. 18, the temperature step moves from the top to bottom in each load cycle. Thus, the cold front always shifts into the hot region. If the temperature step moves in the opposite direction (from hot to cold), the stresses and strains are reversed so that the progressive deformation takes place inwards, associated with an extension of the shell. If the temperature step is not always moving in the same direction but alternately up and down, the displacement changes cancel each other out in each half cycle so that no ratcheting occurs.

Finite ratcheting

Up to now, examples have been dealt with in which ratcheting is expressed in such a way that, in each load cycle, strains and displacements continuously increase with the same increment per cycle (possibly after a phase of transient ratcheting, “Theory of plastic zones”). Thus, theoretically infinitely large strains and displacements are achieved after infinity many cycles. This, however, does not always have to be the case. Instead the increments of strains and displacements can also increase or decrease from cycle to cycle and possibly disappear completely, so that the monotonous strain accumulation is limited. Such a state is then characterized either by the fact that, in the course of further load cycles, only elastic deformation changes occur (elastic shakedown), or the stress–strain hysteresis is closed in each cycle, so that the plastic strains mutually cancel each other during a cycle (plastic shakedown). An initial accumulation of the deformation, which however comes to a standstill after a finite or infinite number of load cycles, is called “finite ratcheting.”

In the following, four effects are presented which lead to a gradual reduction in the increments of progressive deformation from cycle to cycle:

  • material hardening, which is very pronounced in the case of cyclic plastic material behavior, since a yield plateau, which can be observed with some steels at monotonic behavior, no longer exists;

  • elastic foundation;

  • geometric effects due to the second-order theory, when a stabilizing axial tensile force is present; and

  • consideration of the true deformation geometry (third-order theory).

Hardening

Under cyclic loading, almost all steel materials have pronounced hardening properties, including those which can well be described as linear elastic–perfectly plastic at monotonic loading.

If we analyze the continuous beam from “Theory of plastic zones” by adopting the theory of plastic zones, but now taking into account linear kinematic hardening (tangent modulus E t) and choose

$$\frac{{E_{\text{t}} }}{E} = 0.0002,$$
(21)

we get the displacements for all load cycles until shakedown is achieved (38 cycles) and the histogram of the deflection in the middle of the right span as shown in Fig. 22.

Fig. 22
figure 22

Continuous beam: displacements (enlarged scale) at loading times corresponding to a load position at the middle of the right span, and histogram of the deflection (m) in the center of the right span in the case of a force moving to the right in the second span; analysis according to theory of plastic zones with material hardening

Full size image

Elastic foundation

The continuous beam from “Force moving to the right” is continuously elastically supported. The spring model used is the Winkler foundation, in which the sole pressure p and the deflection u are linearly related by the parameter k:

$$p = k\,u.$$
(22)

Figure 23 shows, based on an incremental analysis adopting the theory of plastic hinges, that the effect of the elastic foundation is comparable to the effect of material hardening (“Hardening”). For the selected value

$$k = 20\frac{kN}{{m^{2} }},$$
(23)

at least 200 load cycles are to be analyzed to obtain a good approximation to the state of shakedown.

Fig. 23
figure 23

Continuous beam on elastic foundation: displacements (enlarged scale) at loading times corresponding to a load position at the middle of the right span, and histogram of the deflection (m) in the center of the right span in the case of a force moving to the right in the second span

Full size image

Second-order geometric effects

The analyses presented so far are all based on the theory of “small” deflections and “small” rotations (equilibrium conditions are set up based on the undeformed system; rotations are linearized, i.e. first-order theory). As a result of the ratcheting process, however, the deflections can rapidly become so great that the equilibrium conditions have to be formulated on the deformed system (second-order theory).

If, for example, the continuous beam treated in “Force moving to the right” adopting the theory of plastic hinges is subjected to an additional axial compression force of 1608 kN, the displacement increments increase continuously from one cycle to the next when applying the second-order theory (Fig. 24) until the system becomes unstable after a series of load cycles. On the other hand, the displacement increments decrease from cycle to cycle when an axial tensile force is applied (Fig. 25). The change of length due to the axial force as well as the plastic interaction between bending moment and normal force is disregarded here.

Fig. 24
figure 24

Continuous beam with superimposed compressive axial force: displacements (enlarged scale) at loading times corresponding to a load position at the middle of the right span, and histogram of the deflection [m] in the center of the right span in the case of a force moving to the right in the second span according to the theory of plastic hinges including second-order geometric effects

Full size image
Fig. 25
figure 25

Continuous beam with superimposed tensile axial force: displacements (enlarged scale) at loading times corresponding to a load position at the middle of the right span, and histogram of the deflection (m) in the center of the right span in the case of a force moving to the right in the second span according to the theory of plastic hinges including second-order geometric effects

Full size image

Third-order geometric effects

So far only the theory of “small” rotations has been considered (first- and second-order theory). If finite rotations are accounted for (third-order theory), shakedown is achieved solely by the lateral force, since the arc length of the deformed beam cannot exceed the length of the undeformed beam, Fig. 26. A change of length due to the axial force arising in the deformed structure at large rotations as well as the plastic interaction between bending moment and normal force are disregarded here. Note that the support at the right is sliding.

Fig. 26
figure 26

Continuous beam: displacements (enlarged scale) at loading times corresponding to a load position at the middle of the right span, and histogram of displacements (m) in the case of a force moving to the right in the second span according to the theory of plastic hinges including third-order geometric effects

Full size image

Conclusion

In the case of variable loads, progressive deformation (ratcheting) can occur as soon as the elastic limit is exceeded in the structure. Then, in the case of cyclic loading, strains and displacements increase in each load cycle. This process limits the service life of a structure, but is to be regarded independently of any possibly occurring fatigue damage.

Known as triggers for ratcheting and already being addressed in structural design codes (in particular in nuclear industry) are configurations in which a load-bearing structure is subjected to at least two different types of load, namely a constant force-controlled load (the primary load) and cyclic thermal loads.

In this paper, another mechanism that generates ratcheting was introduced, which can be attributed solely to the change in the location of a single load variable. In the simplest case, this can be explained by the successive activation of (possibly infinitely many existing) plastic hinges. A primary load as a driving force for ratcheting is not required, but can increase the accumulation of strain and displacement. In this case, small portions of additional variable loadings can be sufficient to initiate progressive deformation.

It has been shown that the direction of movement of the spatially variable load can play a role. It has also been shown that the increments of strains and displacements can increase or decrease from cycle to cycle, whereby in the latter case the progressive deformation is then limited. Possible reasons for this are hardening of the material, elastic foundation, the formulation of the equilibrium on the deformed system (theory of second order), and the consideration of finite rotations (theory of third order).