Introduction

Tremendous increase in demand for resources and acute shortage of the same is like a double-edged sword. Codes and construction practices are emphasizing durability to cope with the situation. The fact embedded steel corrodes faster than exposed has made researchers revisit the area to refine and redefine analysis and design.

Corrosion is defined as the destruction or deterioration of a material because of its reaction with environment (Fontana 2005). Chloride ingress into the concrete is a major cause of steel corrosion. Presence of chloride ions at the rebar level leads to the breakdown of passive firm thin film layer and consequently initiates the corrosion (Pradhan and Bhattacharjee 2009). Rust produced as a result of corrosion increases its volume 2–6 times than that of original steel; it causes increase in volume of tensile stresses in concrete (Bhaskar et al. 2010).

Corrosion of reinforcement is a prime concern as stability, strength, safety, serviceability, durability and economy of RC structures are severely affected. One of the most important prerequisites of reinforced concrete construction is adequate bond between the reinforcement and the concrete.

Significance of bond strength

Reinforced steel bar can receive its external loads only from the surrounding concrete, because external loads are very rarely applied directly on it. ‘Slip’ is the differential displacement between steel and concrete. Composite action between concrete and reinforcing steel cannot occur without bond (Amleh 2000).

Bond resistance of reinforcing bars embedded in concrete depends primarily on frictional resistance and mechanical interlock. Chemical adhesion provides withholding property between steel and concrete. Frictional bond provides initial resistance against loading and further loading mobilizes the mechanical interlock between the concrete and bar ribs. Mechanical interlocks lead to inclined bearing forces which in turn lead to transverse tensile stresses and internal inclined splitting (bond) cracks along reinforcing bars. These cracks are commonly referred as Goto cracks (Goto 1971).

This work is an attempt to understand affect of corrosion on bond characteristic. The study envisaged to quantify loss in bond strength due to corrosion.

Experimental investigation

Details of experiments, mix design and of test setup used for the study are explained below.

Mix design details

According to the recommendation of IS 456-2000 code, minimum concrete grade to be adopted in coastal environment is M30 and maximum water cement ratio is 0.45. Hence, target strength of 30 N/mm2 and slump range of 50–60 mm are selected for the present study. Mix design calculations are made as per IS 10262-2009. Test results of materials are used in the calculation of determination of mix proportions. After several trials, the mix proportion of 1:1.77:2.87 is achieved. An addition of 2 ml/kg of commercially available chemical admixture is used to get the desired level of slump. Compressive strength of control cube is obtained as 34.44 N/mm2.

Preparation of test specimens

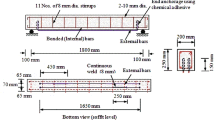
For the present study, National Bureau of Standard (NBS) beam specimens of size 2.44 m × 0.457 m × 0.203 m [Fig. 1 (Paul 1978)] are used. After curing of beam specimens for 28 days, to accelerate the corrosion process in beam specimens impressed current technique is used. Specimens are partially immersed in a 5 % NaCl solution for an duration of 8 days. Current required to achieve different corrosion levels can be obtained using Faraday’s law (Eq. 1) (Ahmad 2009). Based on the calculation amount of 2.5–10 A current at the variation of 2.5 A are applied to obtain the required corrosion level, i.e., 2.5–10 % at the variation of 2.5 %, respectively. Monitoring of corrosion process is done by applied corrosion monitoring (ACM) instrument.

$$ i_{\text{app}} = \frac{{(\rho \times w_{i} \times F)}}{100 \times \pi \times D \times L \times W \times T}, $$
(1)

where \( \rho \) is the degree of corrosion, T is the time in seconds, W i is the initial weight of steel (=20,000 g present study), F is equal to 96487 A-s, W is the equivalent weight of steel (=27.925 g), i app is the applied current (A).

Fig. 1
figure 1

Reinforcement details of NBS beam specimen

Full size image

Test setup used for flexural bond study

Test setup used for the present study is shown in Fig. 2. Beam specimens are tested under two-point loading condition. The load is applied at 15 kN increments. Proving ring of 50 ton capacity is used to note the applied load.

Fig. 2
figure 2

Test setup of NBS beam specimen

Full size image

Strain value recordings have been done using demec gauges at every load interval. Positions of demec targets have been shown in Fig. 3.

Fig. 3
figure 3

Demec buttons were at 100 mmc/c

Full size image

Determination of bond stress

Average bond stress values are obtained from Eq. (2).

$$ \tau_{\text{bd}} = \frac{{\phi_{1} \times f_{s} }}{{4 \times l_{d} }}, $$
(2)

where the diameter of bar is

$$ \phi_{1} = \phi \sqrt {\left( {1 - \frac{p}{100}} \right)}; $$
(3)

\( \tau_{\text{bd}} \) is the average bond stress (N/mm2); \( \phi \) is the initial diameter (25 mm); \( \phi_{1} \) are the reduced diameter (mm) values presented in Tables 1 and 2; \( p \) is the weight loss in percentage; \( l_{\text{d}} \) is the embedment length of the bar (747 mm) from the test setup; \( f_{\text{s}}^{{}} \) are the steel stress values obtained for initiation and end strain values at slip region for different corrosion levels from stress corresponding to strains at that load level (Fig. 4).

Fig. 4
figure 4

Stress–strain curve for 25 mm diameter TMT Fe-415 reinforcing steel bar

Full size image
Table 1 Bar force, reduced diameter and bond stress performance for different levels of corrosion in experimental beam specimens
Full size table
Table 2 Bar force, reduced diameter and bond stress performance for different levels of corrosion in numerical model beam specimens
Full size table

To overcome the problems of material cost and long time duration in real-time study, FEM (Numerical modeling) analysis is carried out on NBS beams based on the experimental study.

Numerical investigation

To model NBS beam specimen of size 2.44 m × 0.203 m × 0.457 m by FEM, a commercial ANSYS software package is used. Graphical user interface in ANSYS provides different element types, which suits the problem on hand. Hence this software is preferred for the present study.

Element types

To model concrete, Solid 65 element is used. The element has eight nodes with three degrees of freedom at each node translation in the nodal x, y and z direction. To model steel reinforcement, Link 8 element is used. Link 8 element has two nodes with three degrees of freedom at each node translation in the nodal x, y and z direction.

Real constants

Real constant Set 1 is defined for the Solid 65 element. In the present study, the beam is modeled using discrete reinforcement. Therefore, a value of zero is entered for all real constants, which turn the smeared reinforcement capability of the Solid 65 element off. Real constant Sets 2, 3 and 4 are defined for the Link 8 element. Real constant values of Link 8 (cross-sectional area and initial strain) are entered as follows,

  • Set 2: cross-sectional area of 25 mm bar: 490.87 mm2

  • Set 3: cross-sectional area of 12 mm bar: 113.10 mm2

  • Set 4: cross-sectional area of 8 mm two-legged stirrups: 50.27 mm2

A value of zero is entered for the initial strain because it is assumed that there is no initial stress in the reinforcement.

For different levels of corrosion (2.5, 5, 7.5 and 10 %), reduced bar diameter can be obtained from the Eq. (3).

Real constant Set 4 is defined for the Combin39 element; to simulate the bonding behavior, nonlinear spring element is adopted at the bar concrete interface for simulating its bond–slip relationship. Combin39 elements’ nonlinearity can be defined by giving load displacement relationship as input.

The relationship between local bond stress and slip at the bar concrete interface along the longitudinal direction is given below (Xiaoming and Hongqiang 2012):

$$ \tau (s) = (61.5s - 693s^{2} + 3.14 \times 10^{3} \times s^{3} - 0.478 \times 10^{4} \times s^{4} ) \times f_{\text{t,s}} \times \sqrt {{\raise0.7ex\hbox{$c$} \!\mathord{\left/ {\vphantom {c d}}\right.\kern-0pt} \!\lower0.7ex\hbox{$d$}}} , $$
(4)

in which ‘s’ is the slip value (mm), ‘c’ the thickness of cover layer (mm), ‘d’ the diameter of reinforcement (mm), f t,s the concrete’s splitting tensile strength (N/mm2), where

$$ f_{\text{t,s}} = 0.19 \times f_{\text{ck}}^{0.75} . $$
(5)

In the FE model of the RC beam, the relationship between the bond force ‘L’ and slip value ‘s’ can be calculated as follows:

$$ L(s) = \,\tau (s)\,\pi dl\,\,, $$
(6)

where d is the diameter of a bar (mm) and l the distance between two adjacent spring elements (mm). From Eqs. (4) and (6), the load displacement relationship (L–D) of the spring element longitudinal direction can be obtained.

When the corrosion rate is \( \eta \), the reduction factor \( \beta \) of the bond strength at the corroded bar–concrete interface can be calculated as follows (Xu 2003):

$$ \begin{aligned} \beta = \left\{ {1 + 0.5625\eta - 0.3357\eta^{2} + } \right.0.055625\eta^{3} - 0.003\eta^{4} \,\eta \le \left. {7\;\% } \right\} \hfill \\ \beta \, = \left\{ {2.0786\eta^{ - 1.0369} \,\eta > 7\;\% } \right\}. \hfill \\ \end{aligned} $$
(7)

Substituting Eqs. (7) into (6), the relationship between the bond force ‘L’ and slip value ‘s’ after corrosion can be obtained as:

$$ L(s) = \,\beta \times \tau (s) \times \pi dl $$
(8)

Thus, the L–D curves of the spring element along the longitudinal direction under different corrosion rates are presented in Fig. 5.

Fig. 5
figure 5

Load–displacement relationship of the spring element (Combin39) along the longitudinal direction

Full size image

Modeling

Input values for numerical model of beam are given as per the experimental study. In the present study, elastic modulus of concrete (Solid 65) element is 29,342.8 N/mm2 and Poisson ratio is 0.2. Simplified compressive uniaxial stress strain curve for concrete is shown in Fig. 6. Uniaxial tensile strength is 4.1 N/mm2, crack opening shear transfer coefficient is 0.3 and crack closing shear transfer coefficient is 0.95. To obtain good results, hexahedric mesh is used for the modeling (ANSYS 2012). Full beam was modeled using 56 nodes in the x direction (i.e., longitudinal direction) placed with a spacing of 39.6 mm between successive nodes in the loading places, 18 mm at the support point and 75 mm at the center. In Y direction (i.e., transverse direction), 9 nodes were placed at 50 mm between two successive nodes. In Z direction, the nodes were placed at 32 mm distance. Concrete element model of beam is shown in Fig. 7.

Fig. 6
figure 6

Simplified compressive uniaxial stress–strain curve for concrete

Full size image
Fig. 7
figure 7

Concrete element of NBS beam model

Full size image

Elastic modulus of Link 8 element is 2 × 105 N/mm2 and its Poisson ratio is 0.3. The yield strength of the main bar is 485 N/mm2. The bar model is shown in Fig. 8.

Fig. 8
figure 8

Reinforcement element model of NBS beam

Full size image

In case of main reinforcement bar modeling (25 mm diameter), separate nodes at same location (Link 8 elements and Solid 65 elements) are connected with Combin39 element to simulate the bond slip behavior. A view of reinforcements inside concrete volume is shown in Fig. 9. Other reinforcement is modeled through discrete reinforcement modeling method (concrete and steel nodes merged into single entities).

Fig. 9
figure 9

View of Reinforcements inside concrete

Full size image

Loads and boundary conditions

To get the unique solution constraining the models using displacement boundary conditions, same ways as that of experimental beam boundary conditions are very much necessary.

Supports are modeled such a way that a roller is created. A single line of nodes on the beam are given constraint in the UY and UZ (translation in Y and Z) directions, applied as constant values of 0. By doing this, the beam will be allowed to rotate at the support. Loading and support conditions are shown in Fig. 10a, b.

Fig. 10
figure 10

a Loading condition for NBS beam specimen. b Support and loading conditions of NBS beam specimen

Full size image

Analysis process for the finite element model

The FE analysis of the model is considered to examine the results of different corrosion levels. Static analysis type is utilized in the present investigation since the finite element model for this analysis is a NBS beam under transverse loading.

The Newton–Raphson method of analysis is used to compute the nonlinear response. The loads are applied at 15 kN increment up to failure. After each load increment, the restart option is used to go to the next step after convergence.

Strain values are noted from the numerical results at the load points and bond stress values can be obtained from Eq. (2).

Results and discussion

Ultimate load-carrying capacity and bond stress of NBS beams

Effect of corrosion on ultimate load-carrying capacity is shown in Fig. 11. As the degree of corrosion level increases, load-carrying capacity decreases (Fig. 11). It is also observed that for every percentage increase in corrosion level there is about 1.6 and 1.8 % decrease in load-carrying capacity for experimental and numerical results, respectively. Numerical beam behaves stiffer compared to the experimental beam specimens. It is mainly because the numerical model beams are completely unhandled compared to experimental beam specimens.

Fig. 11
figure 11

Effect of corrosion on ultimate load-carrying capacity of beam specimen

Full size image

Load strain behavior for experimental beam and numerical model beam specimens is shown in Figs. 12 and 13, respectively. It is observed that experimental beam shows higher strain values compared to the numerical model beam specimen. From Figs. 12 and 13, it is seen that as the load level increases strain value increases linearly in the initial stage. Then at higher corrosion levels, rate of increase of strain is higher for the same increment of load level compared to lower levels of corrosion. Control beam specimen performs better at increased corrosion levels. It is also observed that there is a sudden increase in strain values observed for the applied load interval, in all beam specimens. This indicates that there is a slip between reinforcement and surrounding concrete, since the corresponding strain value for yield strength of 25 mm diameter bar is much higher than the value of sudden increase in strain value. Slip at initiation indicates the point where flat portion begins and slip at end point where flat portion ends and strain values start continuing again. A view of strain contour is shown in Fig. 14.

Fig. 12
figure 12

Effect of different levels of corrosion on load strain behavior of beam specimen (0, 2.5 and 5 %)

Full size image
Fig. 13
figure 13

Effect of different levels of corrosion on load strain behavior of beam specimen (0, 7.5 and 10 %)

Full size image
Fig. 14
figure 14

A view of strain contour at control beam specimen

Full size image

Bar stress and bond stress performance of NBS beam

Bond stress results for different levels of corrosions are obtained from Eq. (2). From Tables 1 and 2, it is observed that as the corrosion level increases bond stress value decreases. Poisson’s effect is not considered in reduction of bar diameter. Percentage reduction in bond stress for different levels of corrosion, i.e., 2.5, 5, 7.5 and 10 % with respect to control beam specimen is 6.6, 13.2, 21.6 and 29.4 %, respectively, for experimental concrete beam specimens and for numerical model it varies as 7.6, 15.8, 24.1 and 30.4 %, respectively.

From Figs. 15 and 16, it is exhibited that bond stress approximately drops for about 2.6 % and 3 % (at initiation of slip point) and also 2.1 and 2.4 % (at end of slip point) for experimental and numerical model concrete beam specimens, respectively, for every percentage increase in corrosion level.

Fig. 15
figure 15

Effect of corrosion levels on bond stress at initiation of slip values

Full size image
Fig. 16
figure 16

Effect of corrosion levels on bond stress at end of slip values

Full size image

Bond stress values for different degree of corrosion can be calculated from following equations obtained from Figs. 15 and 16, where x is the corrosion level (%) and y the bond stress (N/mm2).

At initiation of slip point

$$ \left( {\text{experimental}} \right)\;y = \, - 0.049x + 1.678\,\,R^{2} = 0.996 $$
(9)
$$ \left( {\text{numerical}} \right)\;y = \, - 0.049x + 1.577\,\,R^{2} = 0.999 $$
(10)

At end of slip point

$$ \left( {\text{experimental}} \right)\;y = \, - 0.076x + 3.099\,\,R^{2} = 0.992 $$
(11)
$$ \left( {\text{numerical}} \right)\;y = \, - 0.078x + 3.019\,\,R^{2} = 0.996 $$
(12)

From the results, it is observed that numerical results show a variation less than 10 % in load-carrying capacity and bond stress behavior compared to experimental results. Hence, proposed regression equation can be used for the determination of reduction in load-carrying capacity and bond stress behavior in the real-life structures subjected to different levels of corrosion.

Conclusions

Based on the comparison of experimental results to those obtained from analytical results, following remarks are drawn:

  1. 1.

    Experimental and numerical results show an variation less than 10 % in load-carrying capacity, load deflection and bond stress behavior.

  2. 2.

    Reinforcement corrosion leads to the decline of load-carrying capacity of NBS RC beam specimens. For every percentage increase in corrosion level, there is about 1.6 and 1.8 % decrease in load-carrying capacity for experimental and numerical model beam specimen, respectively.

  3. 3.

    For increasing corrosion level, strain values increase in the initial stages. Then at higher corrosion levels, rate of increase of strain is higher for the same increment of load level, compared to the lower levels of corrosion.

  4. 4.

    Reinforcement corrosion causes degradation of the bond behavior. The strain value becomes large due to corrosion and the larger the corrosion lesser the bond stress value.

  5. 5.

    Percentage reduction in bond stress for different levels of corrosion, i.e., 2.5, 5, 7.5 and 10 % with respect to control beam specimen was 6.59, 13.17, 21.56 and 29.34 %, respectively, for experimental concrete beam specimens and for numerical analysis it varies as 7.6, 15.82, 24 and 30.4 %, respectively.

  6. 6.

    Bond stress approximately drops for about 2.6 and 3 % (at initiation of slip point) and also 2.1 and 2.4 % (at end of slip point) for experimental and numerical model concrete beam specimens, respectively, for every percentage increase in corrosion level.

  7. 7.

    Proposed regression equation is very much useful for quick assessment to predict the bond strength values for different corrosion levels in structures. Structures can be monitored for different corrosion levels using the applied corrosion monitoring instrument. Based on measured corrosion current density values, corrosion percentage can be determined. With the help of empirical prediction equation for different corrosion percentage, drop in load-carrying capacity as well as bond strength values can be determined.