Abstract
Behaviour of beam depends on its depth. A beam is considered as deep, if the depth span ratio is 0.5 or more. In the available beam theories, we have to apply correction in case of deep beams. In the present work, method of initial functions (MIF) is used to study the effect of depth on the behaviour of concrete beam. The MIF is an analytical method of elasticity theory. It gives exact solutions of different types of problems without the use of assumptions about the character of stress and strain. In this method, no correction factor is required for beams having larger depth. Results are obtained for three different cases of depth span ratios and compared with available theory and finite element method-based software ANSYS. It is observed that deep beam action starts at depth span ratio equal to 0.25.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A beam is considered as a deep beam when the ratio of effective span to overall depth is <2.0 for simply supported members. The beam theories which are based on assumptions are useful in case of those problems, where thickness of beams is moderate. Available beam theories which are based on assumptions produces two types of errors. The first is the error in the stress and the second error is in the strains, i.e. in deflections. So we need a theory to analyse the beams having higher depth span ratio. In this paper, we have used method of initial functions (MIF) for the analysis of concrete beams of different depth span ratios. It gives exact solutions of different types of problems without the use of assumptions about the character of stress and strain. In comparison to Timoshenko beam theory which is used for analysis of deep beam, this method requires no assumption regarding position of neutral axis of beams and no shear correction factor is required.
A method was suggested for solving problems of theory of elasticity for the analysis of thick plates as well as shells and was known as the MIF. In this method, unknowns of the problem were expanded in Maclaurin’s series in the thickness coordinate and hence the solutions were obtained in terms of unknown initial functions on the reference plane (Vlasov 1957). Two-dimensional elasticity equations were used in this method (Timoshenko and Goodier 1951).
Method of initial functions was used for the analysis of beams under symmetric central loading and uniform loading for different end conditions (Iyengar et al. 1974). It was used for the analysis of free vibration of rectangular beams of arbitrary depth. The frequency values were calculated for different values of Poisson’s ratio (Iyengar and Raman 1979). MIF had been applied for deriving theories for laminated composite thick rectangular plates. The governing equations had been obtained for perfectly and imperfectly bonded plates subjected to normal loads (Iyengar and Pandya 1986). Governing equations were developed for composite laminated deep beams by using MIF and results were compared with the available theory (Dubey 2000).
Method of initial functions has been applied for the composite beams having two layers of orthotropic material (Patel et al. 2012). MIF is successfully applied for the analysis of brick-filled reinforced concrete beams (Patel et al. 2013).
In deep beams, the bending stress distribution across any transverse section deviates appreciably from straight line distribution as assumed in the elementary theory of beam. Consequently, a transverse section which is plane before bending does not remain approximately plane after bending and the neutral axis does not usually lie at the mid-depth (Krishna Raju 2005).
There are so many other theories which are used in the place of prevailing theories for the analysis of beams. hyperbolic shear deformation theory was developed for transverse shear deformation effects. It was used for the static flexure analysis of thick isotropic beams. The results of the present theory are compared with those of other refined shear deformation theories of beams (Ghugal and Sharma 2011). A layer-wise trigonometric shear deformation theory was used for the analysis of two-layered cross-ply laminated simply supported and fixed beams subjected to sinusoidal load. Virtual work principle was employed to obtain governing equations and boundary conditions (Ghugal and Shinde 2013). Keeping in view the limitations of theories in practice and advantages of MIF, it is clear that we can use this theory effectively for beams of any depth span ratio. Significance of the research is that the available theory like bending theory is not useful for the beam sections having more depth.
MIF formulation
The equations of equilibrium for solids ignoring the body forces for two-dimensional case are:
The stress–strain relations for isotropic material are:
The values of the coefficients C′11–C′33 for isotropic materials are given in the “Appendix”.
The strain displacement relations for small displacements are:
Eliminating σ x between Eqs. (1) and (2) the following equations are obtained, which can be written in matrix form as
where
Equation (9) can be expressed as:
The solution of Eq. (10) is
where {S0} is the vector of initial functions, being the value of the state vector {S} on the initial plane.
If u0, v0, Y0 and X0 are values of u, v, Y and X, respectively, on the initial plane, then
Expanding Eq. (13) in the form of a series
Consider a simply supported beam of isotropic material having length l, depth, d and loaded with uniformly distributed load P in the y direction.
The bottom plane of the beam is taken as the initial plane. Due to loading at the top plane of the beam one has X0 = Y0 = 0.
On the plane, y = d, the conditions are X = 0, Y = −P.
Y = −P on y = d, after simplification yields the governing partial differential equation:
Initial functions are obtained by substituting the value of Φ:
From the value of initial functions the value of displacements and stresses are obtained.
Analysis of concrete beams
The following values of concrete beam dimensions are chosen for the particular problem,
d = 400, 750 and 1,500 mm, l = 3,000 mm
The following material properties are taken, E = 22,360 N/mm2, G = 10,164 N/mm2, µ = 0.10 (Fig. 1).
The boundary conditions of the simply supported edges are:
The boundary conditions are exactly satisfied by the auxiliary function Φ = A1sin (πx/l). A uniformly distributed load P = 20.0 N/mm is applied, on the top surface of the beam. The value of auxiliary function Φ is obtained from Eq. 15. Using this value of auxiliary function, the values of initial functions u0 and v0 are obtained from Eq. 16. These are substituted in Eq. 11 for obtaining the values of displacements and stresses.
Results and discussion
Numerical results have been given in Tables 1, 2 and 3 for uniformly distributed load. The values of displacements and stresses are obtained using MIF for different depth span ratios. The results obtained by MIF are compared with bending theory and FEM-based software ANSYS. Two-dimensional analyses are performed taking PLANE 183 element. Material properties E and µ are required for concrete. Mapped meshing is used for the modelling. The displacements and stresses across the thickness in the particular problem of concrete beams are presented in Figs. 2, 3, 4, 5, 6, 7, 8 and 9.
Variation of “Displacement u” for different depth span ratios. The displacement (u) is more at the top surface of the beam as compared to the bottom surface. Its value decreases with the increase in depth and neutral layer of the beam is shifted from its original position and reaches the depth lower than the middle layer
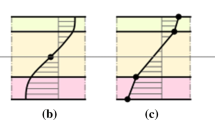
Variation of “Bending stress σ x ” for different depth span ratios. It is observed that the distribution of bending stress across the depth of beam section is linear in case of d/l = 0.133. Stress distribution across the depth becomes nonlinear when d/l = 0.25 and d/l = 0.5. It is because of the warping of the section near neutral axis which is due to deep beam action
Comparison of “Bending stress σ x ” for d/l = 0.25 by bending theory, FEM and MIF. This figure shows that distribution of bending stress across the depth of beam is nearly linear in case of bending theory and FEM. In case of MIF the distribution reflects warping of the section. It shows that deep beam action starts earlier than d/l = 0.5
Comparison of “Bending stress σ x ” for d/l = 0.50 by bending theory, FEM and MIF. It is seen that the value of bending stress calculated at any depth of beam is more in case of MIF in comparison to bending theory and FEM. Shifting of neutral axis from the mid-depth is seen; it is because of the deep beam effect (d/l = 0.50). Also the warping of section takes place in MIF and FEM analysis. But the theory based on assumptions (bending theory) still shows the nearly linear variation of bending stress
Conclusions
It is observed that the deep beam action is seen at d/l = 0.25 which is less than the specified value d/l = 0.5. It is necessary to apply an appropriate method of analysis for beams having large depth span ratio. Deep beam effect is not seen in bending theory based on assumptions that transverse sections which are plane before bending remain plane after bending. MIF gives correct result for both shallow and deep beams. In this method we need not apply corrections. Also in this method it is not necessary to assume the position of neutral axis; it incorporates the position of neutral axis by itself. So we can conclude that analysis done by MIF provides more realistic behaviour of beam sections of any depth.
Abbreviations
- L :
-
Effective span of beam
- d :
-
Total thickness of beam
- E :
-
Young’s modulus of elasticity
- G :
-
Shear modulus of elasticity
- µ :
-
Poisson’s ratio
- ε :
-
Strain
- σ x :
-
Bending stress
- σ y :
-
Normal stress
- τ xy :
-
Shear stress
- u :
-
Displacements in x direction
- v :
-
Displacements in y direction
- α :
-
References
Dubey SK (2000) Analysis of composite laminated deep beams. In: Proceedings of the third International Conference on Advances in Composites, Bangalore, pp 30–39
Ghugal YM, Sharma R (2011) A refined shear deformation theory for flexure of thick beams. Lat Am J Solids Struct 8:183–195
Ghugal YM, Shinde SB (2013) Flexural analysis of cross-ply laminated beams using layer wise trigonometric shear deformation theory. Lat Am J Solids Struct 10:675–705
Iyengar KTS, Pandya SK (1986) Application of the method of initial functions for the analysis of composite laminated plates. Arch Appl Mech 56(6):407–416. doi:10.1007/BF00533827
Iyengar KTS, Raman PV (1979) Free vibration of rectangular beams of arbitrary depth. Acta Mech 32(1):249–259
Iyengar KTS, Chandrashekhara K, Sebastian VK (1974) Thick rectangular beams. J Eng Mech Div ASCE 100(6):1277–1282
Krishna Raju N (2005) Advanced reinforced concrete design, chapter 18, 2nd edn. CBS Publishers Book, New Delhi
Patel R, Dubey SK, Pathak KK (2012) Method of initial functions for composite laminated beams. In: ICBEST-12 Proceedings published by International Journal of Computer applications, USA, October, pp 4–7
Patel R, Dubey SK, Pathak KK (2013) Analysis of RC brick filled composite beams using MIF. Procedia Eng J (Elsevier) 51:30–34. doi:10.1016/j.proeng.2013.01.008
Timoshenko SP, Goodier JN (1951) Theory of elasticity, 2nd edn. McGraw-Hill Book, New York
Vlasov VZ (1957) Method of initial functions in problems of theory of thick plates and shells. In: Proceedings of 9th International conference of Applied Mechanics, University of Brussels, Belgium, 6, pp 321–33
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Patel, R., Dubey, S.K. & Pathak, K.K. Effect of depth span ratio on the behaviour of beams. Int J Adv Struct Eng 6, 3 (2014). https://doi.org/10.1007/s40091-014-0056-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40091-014-0056-3