Introduction

In several studies regarding the alcoholic fermentation oscillations in batch fermenters resulting from ethanol inhibition and the lag response to yeast cells to this inhibition has been observed and reported. It is often conventional during the modeling of ethanol fermentation to predefine an inhibition pattern but the success of this practice is based on probabilities, since such patterns vary based on the type and strength of the fermentation wort. Sorghum, a cereal which belongs to the family Graminae was first used as a brewing adjunct during the Second World War and is now used in most breweries as locally available alternative to imported barley malt. In recent years, the search for cheaper locally available substitutes to imported barley malt rekindled the involvement of most firms in expensive experiments regarding beer production from various materials and today, most of the more successful firms use maize and sorghum in their beer production process. In a generalized view of processing sorghum and maize for beer production, though involves several unit operations, the fermentation step is regarded as the heart of the entire production where a near optimal environment is desired for microorganisms to grow, multiply and produce the desired product, Alford [1]. However, the fermentation of sorghum and maize extracts at large scale is usually hampered by sub optimal conditions including instability, in the form of oscillations resulting from ethanol inhibition and the lag response of yeast cells to this inhibition, Chen and McDonald [2, 3], Beuse et al. [4], Fengwu [5]. These inhibitions observed results in an increase in residual sugar at the end of the fermentation, which decreases raw material consumption and correspondingly, decreases the ethanol yield if no economically acceptable attenuation strategies are developed, Fengwu [5]. In a typical procedure for modeling ethanol fermentation, if inhibition is considered, it is often conventional to predefine the inhibition pattern and this practice increases uncertainties in the model since ethanol inhibition pattern varies depending on the type of microorganism, and on the type and strength of fermentation wort, Russell [6]. This increase the unreliability of process controllers and simulators since these automatic tools are usually based on a mathematical representation of the considered system, Alford [1]. Dynamic models were developed, incorporating three effects of product inhibition into the kinetic model and simulation resulted in interesting findings.

Model development

The fermentation process kinetics was described with a Monod type cell growth model that accounts for substrate and product inhibition.

Modeling kinetics of growth and product formation

Starting from the Monod Equation for cell growth and product formation, Eq. (1), three inhibition patterns were considered in modeling product inhibition; linear, Sudden growth stop and exponential as shown in Table 1 below.

Table 1 Mathematical expressions for the product inhibition factors
Full size table
$$\varvec{\mu}\left( \varvec{S} \right) = \frac{{\varvec{\mu}_{{\varvec{max}}} \varvec{S}}}{{\varvec{K}_{{\varvec{sx}}} + \varvec{S}}}\varvec{ }$$
(1)
$$\varvec{q}_{\varvec{p}} \left( \varvec{S} \right) = \frac{{\varvec{q}_{{\varvec{pmax}}} \varvec{S}}}{{\varvec{K}_{{\varvec{sp}}} + \varvec{S}}}\varvec{ }$$
(2)

Introducing the effect of product inhibition on the Monod equation, using the respective inhibition factors, the following kinetic models were obtained:

Kinetics with Linear Product Inhibition, -Hinshelwood–Dagley model [7]

$$\varvec{\mu}\left( {\varvec{S},\varvec{P}} \right) = \left( {1 - \varvec{K}_{{\varvec{ix}}} \varvec{P}} \right)\frac{{\varvec{\mu}_{{\varvec{max}}} \varvec{S}}}{{\varvec{K}_{{\varvec{sx}}} + \varvec{S}}}\varvec{ }$$
(3)
$$\varvec{q}\left( {\varvec{S},\varvec{P}} \right) = \left( {1 - \varvec{K}_{{\varvec{ip}}} \varvec{P}} \right)\frac{{\varvec{q}_{{\varvec{max}}} \varvec{S}}}{{\varvec{K}_{{\varvec{sx}}} + \varvec{S}}}\varvec{ }$$
(4)

Kinetics Sudden Growth Stop Product Inhibition, -Ghose and Tyagi [8]

$$\varvec{\mu}\left( {\varvec{S},\varvec{P}} \right) = \left( {1 - \frac{\varvec{P}}{{\varvec{P}_{{\varvec{max}}} }}} \right)\frac{{\varvec{\mu}_{{\varvec{max}}} \varvec{S}}}{{\varvec{K}_{{\varvec{sx}}} + \varvec{S}}}\varvec{ }$$
(5)
$$\varvec{q}\left( {\varvec{S},\varvec{P}} \right) = \left( {1 - \frac{\varvec{P}}{{\varvec{P}_{{\varvec{pmax}}} }}} \right)\frac{{\varvec{q}_{{\varvec{max}}} \varvec{S}}}{{\varvec{K}_{{\varvec{sx}}} + \varvec{S}}}\varvec{ }$$
(6)

Kinetics with Exponential Product Inhibition,- Aiba and Shoda model [9]

$$\mu \left( {\varvec{S},\varvec{P}} \right) = \varvec{exp}\left( { - \varvec{K}_{{\varvec{ix}}} \varvec{P}} \right)\frac{{\varvec{\mu}_{{\varvec{max}}} \varvec{S}}}{{\varvec{K}_{{\varvec{sx}}} + \varvec{S}}}\varvec{ }$$
(7)
$$q\left( {\varvec{S},\varvec{P}} \right) = \varvec{exp}\left( { - \varvec{K}_{{\varvec{ip}}} \varvec{P}} \right)\frac{{\varvec{q}_{{\varvec{max}}} \varvec{S}}}{{\varvec{K}_{{\varvec{sx}}} + \varvec{S}}}$$
(8)

Material Balance and development of Differential Equations

The dynamic equations describing the cell growth, product formation and substrate utilization can be developed by applying the principle of conservation of mass. The following system of first order ordinary differential equations that present cell growth, product formation and substrate utilization are in Eqs. (9)–(11)

$$\frac{{{\text{d}}X}}{{{\text{d}}t}} = \mu X$$
(9)
$$\frac{{{\text{d}}P}}{{{\text{d}}t}} = qX$$
(10)
$$\frac{{{\text{d}}S}}{{{\text{d}}t}} = - \frac{1}{{Y_{x} }}\frac{{{\text{d}}X}}{{{\text{d}}t}} - \frac{1}{{Y_{p} }}\frac{{{\text{d}}P}}{{{\text{d}}t}} - G_{s} X - M_{s} X$$
(11)

Using the batch kinetic models developed above and substituting µ and q in Eq. (5) with each of their product inhibition expressions, the approximate representation of the fermentation process in each inhibition scenario could be described by the following equations;

Dynamics with linear product inhibition:

$$\frac{{{\text{d}}X}}{{{\text{d}}t}} = \left( {1 - K_{ix} P} \right)\frac{{\mu_{\hbox{max} } S}}{{K_{sx} + S}}X$$
(12)
$$\frac{{{\text{d}}P}}{{{\text{d}}t}} = \left( {1 - K_{ip} P} \right)\frac{{q_{\hbox{max} } S}}{{K_{sp} + S}}X$$
(13)
$$\frac{{{\text{d}}S}}{{{\text{d}}t}} = - \frac{1}{{Y_{x} }}\frac{{{\text{d}}X}}{{{\text{d}}t}} - \frac{1}{{Y_{p} }}\frac{{{\text{d}}P}}{{{\text{d}}t}} - G_{s} X - M_{s} X$$
(14)

Dynamics with sudden growth stop product inhibition:

$$\frac{{{\text{d}}X}}{{{\text{d}}t}} = \left( {1 - \frac{P}{{P_{\hbox{max} } }}} \right)\frac{{\mu_{\hbox{max} } S}}{{K_{sx} + S}}X$$
(15)
$$\frac{{{\text{d}}P}}{{{\text{d}}t}} = \left( {1 - \frac{P}{{P_{p\hbox{max} } }}} \right)\frac{{q_{\hbox{max} } S}}{{K_{sp} + S}}X$$
(16)
$$\frac{{{\text{d}}S}}{{{\text{d}}t}} = - \frac{1}{{Y_{x} }}\frac{{{\text{d}}X}}{{{\text{d}}t}} - \frac{1}{{Y_{p} }}\frac{{{\text{d}}P}}{{{\text{d}}t}} - G_{s} X - M_{s} X$$
(17)

Dynamics with exponential product inhibition:

$$\frac{{{\text{d}}X}}{{{\text{d}}t}} =_{ } \exp \left( { - K_{ix} P} \right)\frac{{\mu_{\hbox{max} } S}}{{K_{sx} + S}}X$$
(18)
$$\frac{{{\text{d}}P}}{{{\text{d}}t}} =_{ } \exp \left( { - K_{ip} P} \right)\frac{{q_{\hbox{max} } S}}{{K_{sp} + S}}X$$
(19)
$$\frac{{{\text{d}}S}}{{{\text{d}}t}} = - \frac{1}{{Y_{x} }}\frac{{{\text{d}}X}}{{{\text{d}}t}} - \frac{1}{{Y_{p} }}\frac{{{\text{d}}P}}{{{\text{d}}t}} - G_{s} X - M_{s} X$$
(20)

Parameter Estimation and Model Statistical Validity

The identification of model parameters for each of the three systems of equations was made with Matlab and the ode45 solver used to simulate the differential equations. This was done by minimizing the overall sum of squared error, Eq. (11) between the model simulation and experimental data points of the process variables (Biomass, Substrate and Product).

$$\begin{aligned} \varepsilon = \hbox{min} \mathop \sum \nolimits \left( {X\left( {k_{1} ,k_{2} , \ldots ,k_{n} } \right) - X^{e} } \right)^{2} + \left( {S\left( {k_{1} ,k_{2} , \ldots ,k_{n} } \right) - S^{e} } \right)^{2} \hfill \\ + \left( {P(k_{1} ,k_{2} , \ldots ,k_{n} } \right) - P^{e} )^{2} \hfill \\ \end{aligned}$$

For that purpose the Matlab routine “fmincon” was applied. Here \(k_{i} , i = 1 \div n\) was vector of model parameters to be determined as output of minimization procedure. Once the model parameters were estimated, the capability of the mathematical model to describe the ethanol fermentation process was tested statistically using the F- tests and this was done using STATA at a confidence interval of 99%, to find out the confidence level for the developed mathematical model.

Results and discussion of sorghum extract

Table 2 presents the parameters for the four different models used to describe the dynamics of fermentation, while Figs. 1, 2, 3 and 4 presents the fitting of the models with respect to the experimental data. The results led to the following interesting conclusions; alcoholic fermentation of sorghum extracts using Saccharomyces cerevisiae shows the existence of product inhibition, and the patterns of inhibition could be described as linear or exponential models which showed lowest error. It is shown in this work that the errors for the models showing product inhibition were all lower than that of the Monod which was used as a control. The results confirmed previous observations by Chen and McDonald, 1990a,b; Beuse et al., 1998, 1999; Ingledew, 1999 and Fengwu, 2007 that results ethanol, whether produced by yeast cells during fermentation or externally added into a fermentation system, can trigger inhibitions once its concentration approaches inhibitory levels. Also important in fermentation kinetics is the product yield, growth and maintenance coefficients.

Table 2 Model Parameters for fermentation using Sorghum Extracts
Full size table
Fig. 1
figure 1

Experimental results and model fitting, case of no inhibition (Monod-model)

Full size image
Fig. 2
figure 2

Experimental results and model fitting, case of linear inhibition model

Full size image
Fig. 3
figure 3

Experimental results and model fitting, case of Exponential inhibition model

Full size image
Fig. 4
figure 4

Experimental results and model fitting, case of Sudden Growth Stop inhibition model

Full size image

The linear model showed a relatively high product yield coefficient with a relatively low growth and maintenance coefficient compared to the exponential model. This suggest that even though both models showed similar accuracy in describing the fermentation dynamics, designing a control policy with the Linear model will result in more substrate being converted into extracellular product and lesser amount for cell growth and maintenance hence higher productivity and yield. Tables 3 and 4 presents the model statistical validity using two sample F-test for variance and the results show that at a 99% confidence interval, the states prediction of the linear and exponential models showed no significant difference with the experimental data.

Table 3 Model Statistical Validity with kinetics of linear inhibition, two sample F-test for variance (Biomass)
Full size table
Table 4 Model Statistical Validity with kinetics of Exponential inhibition, two sample F-test for variance
Full size table

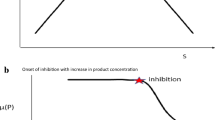
Also important in a fermentation process is how the substrate and product vary in the fermenter as the cells grow. The linear and exponential inhibition models were both used to simulate this variation and both showed a decrease in substrate concentration and an increase in product concentration with cell growth. However, with the linear model the process arrives at steady state within the time used for the simulation as shown in Fig. 5 by the curve at the edges of the plots. This behavior was not observed in the exponential inhibition model as shown in Fig. 6, confirming our earlier assertions with the yield coefficients that using the linear model in a control policy will result in high productivity. 3D profiles using the proximal interpolant method implemented using the Matlab curve fitting tool also revealed interesting findings regarding the fermentation process. This was to observe the formation of product as cells grow and consume substrate. Figure 7 presents product variation with cell growth and substrate consumption using the linear model and Fig. 8 using the exponential model. It can be found that with the linear model, as ethanol accumulated in the fermenter up to a certain concentration, nonlinearities, described as instabilities were observed in the product profile. This can be attributed to the higher product yield coefficient of the linear model compared to the exponential model which resulted in ethanol accumulating faster in the fermenter and rapidly reaching inhibitory levels, resulting in transient instabilities in the fermenter showed by the nonlinearity, Ingledew [10], Fengwu [5]. This high ethanol concentration is inhibitory to the yeast cell by disrupting the integrity of the cell membrane, Russell [6], Sutton [11]. Figures 9, 10, 11 and 12 show comparisons between models developed for linear, sudden growth stop and exponential inhibitions during the fermentation process.

Fig. 5
figure 5

Simulation of substrate and Product variation as a function of biomass during fermentation using linear inhibition kinetics

Full size image
Fig. 6
figure 6

Simulation of substrate and Product as a function of biomass during fermentation using exponential inhibition kinetics

Full size image
Fig. 7
figure 7

3D Proximal Interpolant Simulation of Product variation as a function of substrate and biomass using Linear inhibition kinetic Model

Full size image
Fig. 8
figure 8

3D Proximal Interpolant Simulation of Product variation as a function of substrate and biomass using Exponential inhibition kinetic Model

Full size image
Fig. 9
figure 9

Experimental results and model fitting, case of no inhibition (Monod-model)

Full size image
Fig. 10
figure 10

Experimental results and model fitting, case of linear inhibition model

Full size image
Fig. 11
figure 11

Experimental results and model fitting, case of Sudden Growth Stop inhibition model

Full size image
Fig. 12
figure 12

Experimental results and model fitting, case of Exponential inhibition model

Full size image

Results and discussion maize extract

Table 5 presents the parameters for the four different models used to describe the dynamics of fermentation while Figs. 1, 2, 3 and 4 presents the fitting of the models with respect to the experimental data. The results led to the following interesting conclusions; there exist ethanol inhibition in the alcoholic fermentation of maize extracts, and the patterns of inhibition could be described as linear decrease on the inhibitory ethanol concentration or sudden growth seizure at inhibitory concentration (models which showed lowest error). It is shown in this work that the errors for the models showing product inhibition were all lower than that of the Monod which was used as the control. The results confirmed previous observations by Chen and McDonald [2, 3], Beuse et al. [4], Ingledew [10], Fengwu [5], that ethanol either produced by yeast cells during fermentation or externally added into a fermentation system, can trigger inhibitions once its concentration approaches inhibitory levels. Also important in fermentation kinetics is the rate of ethanol accumulation in the fermentation broth, which depicts the maximum achievable rate of product. Even though the linear and sudden growth stop models described the dynamics of ethanol inhibition, the sudden growth stop model showed a very high maximal rate of ethanol accumulation compared to the exponential model. This suggests that designing a control policy with this model will result in high process productivity.

Table 5 Model Parameters for beer fermentation using maize extracts
Full size table

Tables 6 and 7 presents the model statistical validity using two sample F-test for variance and the results show that at a 99% confidence interval, the states prediction of the linear and exponential models showed no significant difference with the experimental data.

Table 6 Model Statistical Validity with kinetics of linear inhibition, two sample F-test for variance
Full size table
Table 7 Model Statistical Validity with kinetics of Sudden Growth Stop inhibition, two sample F-test for variance
Full size table

The linear and sudden growth stop models inhibition models were both used to simulate this variation and both showed a decrease in substrate concentration and an increase in product concentration with cell growth. What was intriguing is the curve-like behavior that was observed at the end of the profiles, as shown in Figs. 13 and 14. There are two theories to the explanation of this behavior: Ethanol inhibition and stationary/decline phases in batch growth kinetics. In the case of ethanol inhibition, accumulation of ethanol to inhibitory levels leads to disruption of the cell membrane and correspondingly nonlinearity in the substrate consumption and product formation profiles, Chen and McDonald [2, 3], Beuse et al. [4], Fengwu [5], Sutton [11]. The more intense curvature observed with the sudden growth model is due to its relatively high maximal rate of product formation, hence rapidly accumulates ethanol to inhibitory concentration. Regarding the stationary and decline phase theory in batch growth kinetics, the curve-like behavior observed in the linear model can be attributed to the fact the cells grow and get to the stationary and decline phases resulting and hence no longer consume substrate and produce ethanol as in the exponential phase, resulting in the observed nonlinearity. These theories are further confirmed by the Figs. 15 and 16 which, respectively, simulates cell growth and product formation throughout the duration of fermentation. It can be observed that cells in the fermenter start declining after a certain time of fermentation buttressing the attainment of ethanol inhibition and disruption of cell membrane leading to cell death. The nonlinear patterns observed at the start of the fermentation can be attributed to high sugar concentrations encountered immediately after hydrolysis which exert osmotic stress on yeast leading to nonlinearity in their pattern of growth and product formation Russell [6], Sutton [11].

Fig. 13
figure 13

Simulation of substrate and Product variation as a function of biomass during fermentation of maize extracts using Linear Inhibition kinetic model

Full size image
Fig. 14
figure 14

Simulation of substrate and Product as a function biomass during fermentation, using Sudden Growth Stop Inhibition kinetic

Full size image
Fig. 15
figure 15

3D Proximal Interpolant Simulation of product dynamics during fermentation using linear inhibition kinetic Model. Nearest neighbor interpolant

Full size image
Fig. 16
figure 16

3D Proximal Interpolant Simulation of Biomass Variation during fermentation using Sudden Growth Stop inhibition kinetic Model

Full size image

Conclusions and recommendations-sorghum

A mathematical approach to study the product inhibitor on the kinetics of alcoholic fermentation of sorghum and maize has been presented. The results of sorghum extract fermentation showed that there exist both ethanol inhibition in the alcoholic fermentation of sorghum extracts and can be described at a 99% confidence interval as being a linear and or an exponential. The results of maize extract fermentation showed that there exist ethanol inhibition which can be described with a 99% confidence interval as being either a linear or sudden growth at the inhibitory ethanol concentration. The sudden growth stop model resulted in a relatively high maximal rate of ethanol accumulation hence rapidly approaching inhibitory levels. The paper, therefore, recommends for further research to study optimal control problems that can be formulated using the models suggested in this work to understand controls variables that can minimize the effect of such inhibitions in batch fermentations.