Introduction

The study of corrosion of mild steel and iron is a matter of tremendous theoretical and practical concern and as such has received a considerable amount of interest. Acid solutions, widely used in industrial acid cleaning, acid descaling, acid pickling and oil well acidizing, require the use of corrosion inhibitors in order to restrain their corrosion attack on metallic materials [1–4].

Over the years, considerable efforts have been deployed to find suitable corrosion inhibitors of organic origin in various corrosive media [5–8]. Most of these studies reveal that almost all organic molecules containing heteroatoms such as nitrogen, sulfur, phosphorous and oxygen show significant inhibition efficiency [9, 10]. The polar function is usually regarded as the reaction center for the establishment of the adsorption process [11]. However, due to increasing ecological awareness and strict environmental regulations, as well as the inevitable drive toward sustainable and environmentally friendly processes, attention has now focused toward the development of nontoxic alternatives to inorganic and organic inhibitors applied so far.

Current research in corrosion is oriented to the development of compounds with good inhibition efficiency but low risk of environmental pollution. Plants represent a class of interesting source of compounds currently being explored for use in metal corrosion protection in most systems, as possible replacement of toxic synthetic inhibitors. Plant extracts are biodegradable and constitute remarkable rich sources of natural chemical compounds that can be extracted by simple procedures at low cost. The basic components of extracts are sugars, gallic acid, ellagic acid and flavanoids [12, 13]. The presence of tannins, cellulose and polycyclic compounds normally enhances the film formation over the metal surface, thus decreasing corrosion [14, 15]. The use of these natural products such as extracted compounds from leaves or seeds as corrosion inhibitors have been widely reported by several authors [16–26].

Chrysophyllum albidum (CA) from the family sapotaceae is a dominant canopy tree of lowland/mixed rain forest, sometimes riverine. It is widely distributed from West Africa to the Sudan with an eastern limit in Kakamega forest, Kenya. It grows up to a height of 25–37 m with a major girth varying from 1.5 to 2 m [27, 28]. The root, bark and leaves of CA have been employed in folklore medicine for the treatment of diseases. Cotyledons from the seed of CA have been used in ointments in the treatment of vaginal and dermatological infections in western Nigeria [29]. Carbohydrates, proteins, flavonoids, glycosides and terpinoides are the major phytochemical constituents that have been reported in the leaves and seeds of CA [30].

The present work evaluates the corrosion inhibiting properties of CA extract by gravimetric and electrochemical techniques. The necessary GC-mass spectra of the crude extract were obtained to enable identification of the components responsible for corrosion inhibition. In addition, quantum chemical modeling will be employed to model the structures of the major constituents of CA extract and calculate the molecular properties most relevant to their action as corrosion inhibitors.

Experimental

Weight loss measurements

The steel coupons of 3.0 cm × 3.0 cm × 0.2 cm was used for the weight loss measurement studies. The coupons were first polished with different grades of emery paper, dried and weighed and then suspended in a beaker containing 200 ml of the test solutions at different inhibitor concentration. The coupons were totally immersed and retrieved after 24 h exposure, rinsed with distilled water, dried in acetone and then weighed again. Measurements were taken in triplicate, and the loss in weight was calculated by taking an average of these values. The surface coverage (θ) and inhibition efficiency (IE %) was determined by using following equation:

$$\theta \, = \,\frac{{w_{\text{o}} \, - \,w_{\text{i}} }}{{w_{\text{o}} }}$$
(1)
$${\text{IE}}\,\% \, = \,\left( {1\, - \,\frac{w}{{w_{\text{o}} }}} \right)\, \times \,100$$
(2)

where w o and w i are the weight loss in the absence and presence of extract molecules, respectively.

Electrochemical procedure

The electrochemical experiments were carried out using a conventional three-electrode cylindrical glass cell at a temperature of 30 ± 2 °C. Metal samples for electrochemical experiments were machined into test electrodes of dimension 2 × 2 cm2 and sealed with epoxy resin in such a way that only one square surface area (1 cm2) was left uncovered. The exposed surface was abraded with different grades of emery papers, washed with water and degreased with acetone. A saturated calomel electrode (SCE) and a graphite rod were used as the reference and auxiliary electrodes, respectively. All electrochemical measurements were taken using a Potentiostat/Galvanostat (VERSASTAT 400), K0047 model corrosion system with V3 studio software. Before each experiment, the electrode was allowed to corrode freely, and its open circuit potential (OCP) was recorded as a function of time up to 30 min. Electrochemical impedance measurements were taken using AC signals of 10 mV amplitude peak-to-peak in the frequency range of 100 kHz–10 MHz. The impedance diagrams are given in the Nyquist representation. The charge transfer resistance values were obtained from the diameter of the semicircles of the Nyquist plots. The inhibition efficiency of the inhibitor was calculated from the charge transfer resistance values using the following relationship:

$${\text{IE}}_{R} \,\% \, = \,\,\left( {\frac{{R_{{{\text{ct}}({\text{inh}})}} \, - \,\,R_{\text{ct}} }}{{R_{{{\text{ct}}({\text{inh}})}} }}} \right)\, \times \,100$$
(3)

where (R ct, inh) and (R ct, bl) are the values of the charge transfer resistance at the mild steel with and without the CA extract, respectively. Tafel curves were obtained by changing the electrode potential from −250 to +250 mV versus OCP at a scan rate of 0.333 mV s−1. The linear Tafel segments of anodic and cathodic curves were extrapolated to corrosion potential to obtain corrosion current densities (I corr). The inhibition efficiency (IEp %) was calculated as follows:

$${\text{IE}}_{\text{p}} \,\% \, = \,\frac{{I_{\text{o}} \, - \,I_{\text{i}} }}{{I_{\text{o}} }}\, \times \,100$$
(4)

where \(I_{\text{o}}\) and \(I_{\text{i}}\) are the corrosion current in the absence and in the presence of inhibitor, respectively.

Gas chromatography–mass spectrometry (GC–MC)

About 10 µl of CA extract sonicated with n-hexane was analyzed by GC–MS using Shimazu model GCMS-QP2010 PLUS equipped with column (25 m, 0.25 mm i.d., 0.22 µm film thickness). The oven temperature was held at 50 °C for 2 min, then programmed 10 °C/min to 250 °C and held for 2 min. Other operating conditions were as follows: carrier gas, He (99.99 %), inlet pressure 76 kPa. With a linear velocity of 20 cm/s, injector temperature, 250 °C; detector temperature, 310 °C; and split ratio, 1:25.

Results and discussions

Effect of extract concentration

Gravimetric measurements of mild steel subjected to the effects of 1 M HCl acid solution in the absence and in the presence of various concentrations of CA extract were taken at 303 K for 24-h immersion period. Values of inhibition efficiency IE (%) and corrosion rates (mg/cm2h) obtained from the measurements are summarized in Table 1. The extract showed maximum inhibition efficiency of 96 % at the optimum concentration of 1000 mg/L. The corrosion rate decreases gradually as the inhibitor is added to the system to reach a value of 0.0075 mg/cm2 h at the optimum concentration. The gradual increase in inhibition efficiency at higher concentrations can be explained by the fact that the more sites of the exposed metal surface become covered with inhibitor components causing the reduction in corrosion rate. Further increase in extract concentration did not cause any significant change in the performance of the extract.

Table 1 Corrosion parameters from weight loss technique for mild steel corrosion in 1 M HCl solution free and containing different concentrations of CA extract at 303 K for 24 h
Full size table

Effect of immersion time

In order to assess the stability of the inhibitive behavior of the leaf extract on a timescale, weight loss measurements were taken in the presence of optimum concentration from 1- to 5-day immersion period at 303 K. The variation in inhibition efficiency and surface coverage with immersion time is shown in Table 2. It is found that inhibition efficiency remained fairly constant within the test period. This suggests strong adsorption of the constituents present in the extract on the mild steel surface.

Table 2 Effect of time on inhibition efficiency of CA extract at 1000 mg/L concentration during mild steel corrosion in 1 M HCl for 5 days at 303 K
Full size table

Effect of temperature

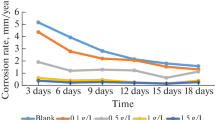
The effect of temperature on the corrosion of mild steel in 1 M HCl solution in the absence and presence of 50 and 1000 mg/L of the aqueous extracts of CA was studied using weight loss measurements in the range of 303–333 K for 3 h of immersions. The trend of the corrosion rate of the mild steel and the inhibition efficiency of the extract is shown in Figs. 1 and 2, respectively. It is evident from Fig. 1 that the corrosion rates of the mild steel in both free and inhibited acid media increased as the temperature was increased. However, the extent of the rate increment in the inhibitor-free acid solution is higher than in the presence of the extracts. Therefore, the inhibition efficiency of the extract decreases with increasing temperature (Fig. 2), which may be attributed to a possible shift of the adsorption–desorption equilibrium toward desorption of the already adsorbed inhibitor. This behavior, as well as the roughening of the metal surface as a result of enhanced corrosion, may also reduce the ability of the inhibitor to be adsorbed on the metal surface [31]. This result supports the idea that the adsorption of the extract components on the steel surface may be physical in nature. An alternative approach to restoring the efficiency obtained at 303 K would be to increase the concentration of the extracts at higher temperatures.

Fig. 1
figure 1

Effect of temperature on the corrosion rate of mild steel in 1 M HCl solution free and containing 50 and 1000 mg/L CA extract

Full size image
Fig. 2
figure 2

Effect of temperature on inhibition efficiency of CA extract in 1 M HCl solution during corrosion of mild steel for 3-h immersions

Full size image

Figure 3 represents the Arrhenius plots of the natural logarithm of the corrosion rates versus 1/T for CA extract in 1 M HCl solution. The apparent activation energy (E a) for mild steel corrosion in 1 M HCl solution in the absence and presence of Ca extract was evaluated from the modified form of Arrhenius equation as follows:

$$\ln \left( {\frac{{k_{2} }}{{k_{1} }}} \right){\mkern 1mu} = {\mkern 1mu} \frac{{ + E_{{\text{a}}} }}{R}\left( {\frac{1}{{T_{1} }}{\mkern 1mu} - {\mkern 1mu} \frac{1}{{T_{2} }}} \right)$$
(5)

where k 1 and k 2 are the corrosion rates (mg/cm2 h) at temperatures T 1 and T 2 (K) and R is the universal gas constant. The values of activation energy E a obtained are given in Table 3. The data show that the activation energy (E a) of the corrosion of mild steel in 1 M HCl solution in the presence of extract is higher than that in the free acid solution. The increase in the apparent activation energy for mild steel dissolution in inhibited solution may be interpreted as physical adsorption that occurs in the first stage [32]. Szauer and Brand explained [33] that the increase in activation energy can be attributed to an appreciable decrease in the adsorption of the inhibitor on the mild steel surface with increase in temperature.

Fig. 3
figure 3

Arrhenius plot for mild steel corrosion in 1 M HCl solution free and containing 50 and 1000 mg/L CA extract

Full size image
Table 3 Value of activation energy, E a (kJ/mol) and heat of adsorption for corrosion of mild steel in 1 M HCl solution free and containing 50 and 1000 mg/L CA extract
Full size table

An estimate of the heat of adsorption (Q ads) was obtained from the trend of surface coverage with temperature as follows [34–36]:

$$Q_{{{\text{ads}}}} {\mkern 1mu} = {\mkern 1mu} 2.303{\mkern 1mu} \log \left\{ {\left( {\frac{{\theta 2}}{{1{\mkern 1mu} - {\mkern 1mu} \theta 1}}} \right)} \right.{\mkern 1mu} - {\mkern 1mu} \left. {\left( {\frac{{\theta 1}}{{1{\mkern 1mu} - {\mkern 1mu} \theta 2}}} \right)} \right\}{\mkern 1mu} \times {\mkern 1mu} \frac{{T_{1} T_{2} }}{{T_{2} {\mkern 1mu} - {\mkern 1mu} T_{1} }}$$
(6)

where θ 1 and θ 2 are the degree of surface coverage at temperatures T 1 and T 2, respectively. The calculated values of both parameters are given in Table 3. The negative values of heats of adsorption (Q ads) indicate that the degree of surface coverage decreased with rise in temperature, again, suggesting physical adsorption mechanism [34–36].

Electrochemical measurements

Polarization measurement

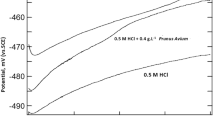
The polarization curves of mild steel in 1.0 M HCl solution in the absence and presence of 50 and 1000 mg/L concentrations of CA extract are shown in Fig. 4. Various parameters such as corrosion potential (E corr), corrosion current density (I corr), anodic Tafel slope (β a), cathodic Tafel slope (β c) and inhibition efficiency (IEp %) are summarized in Table 4. The inhibition efficiency is calculated from the value of corrosion current density, which can be evaluated from extrapolation method, using Eq. (4) [37, 38]. As shown in Fig. 4, both the anodic and cathodic corrosion current densities decrease considerably when the extract was added into the corrosive media, while the E corr remained fairly constant. The result suggests that CA extract components act as a mixed-type inhibitor.

Fig. 4
figure 4

Tafel plot of mild steel corrosion in 1 M HCl solution free and containing 50 and 1000 mg/L CA extract

Full size image
Table 4 PDP kinetic parameters, inhibition efficiency for CA extract in 1.0 M HCl solution free and containing 50 and 1000 mg/L CA extract at 303 K
Full size table

It should be noted that the cathodic polarization curves give rise to almost parallel Tafel lines, which indicates that the addition of CA extract did not modify the mechanism of the hydrogen evolution reaction process. That is to say, the presence of CA extract can inhibit the corrosion reaction only by blocking the reaction sites without affecting the actual reaction mechanism [39–41]. However, the increase of the anodic Tafel slopes in the presence of the additive suggests that CA extract can affect the kinetics of the anodic process. This may be an implication of the formation of a complex compound through the adsorption of the extract components. Thus, it can change the dissolution mechanism of the mild steel. In addition, as shown in Table 4, the inhibition efficiency increased on increasing the extract concentration, showing that extract is concentration dependent and thus corroborating the weight loss result.

Electrochemical impedance spectroscopy measurement

The impedance response in Nyquist modulus of mild steel in 1 M HCl solution free and containing 50 and 1000 mg/L CA extract at 30 min immersion is shown in Fig. 5. For both uninhibited and inhibited immersions, only a single capacitive loop exists in the spectra. This capacitive loop should be related to the electrical double layer at the boundary between the mild steel and the corrosive solution. The equivalent circuit with only one time constant was used for EIS data analyzing (Fig. 6). In this model, R s and R ct characterize the solution resistance and charge transfer resistances, respectively. The constant phase element (CPEdl) is used instead of ideal capacitance (C dl) to account for nonideal behavior of double layer due to surface inhomogeneity, roughness and adsorption effects [42]. The CPE impedance is given by:

$$Z_{\text{cpe}} \, = \,\frac{1}{Q}\mathop {\left( {j\omega } \right)}\nolimits^{ - n}$$
(7)

where Q is the CPE constant, ω is the angular frequency (in rad s−1), J = (1)−1/2 is the imaginary number and n is a CPE exponent which can be used as a gauge of the heterogeneity or roughness of the surface. Depending on the value of n, CPE can represent resistance (n = 0, Q = R), capacitance (n = 1, Q = C), inductance (n = −1, Q = L) or Warburg impedance (n = 0.5, Q = W). The capacitance values of electrical double layer were calculated according to the following equation [43]:

$$C_{\text{dl}} \, = \,\mathop {\left( {QR_{\text{ct}} } \right)}\nolimits^{1/n}$$
(8)
Fig. 5
figure 5

Nyquist plots for mild steel in 1 M HCl solution free and containing 50 and 1000 mg/L of CA extract

Full size image
Fig. 6
figure 6

Electrochemical equivalent circuit used to fit the impedance spectra

Full size image

The EIS data were fitted by ZSimpWin software using previously described electrical model. The impedance parameters such as solution resistance (R s), charge transfer resistance (R ct), derived double layer capacitance (C dl) and inhibition efficiency (IE %) are listed in Table 5. It is clear from Table 5 that by increasing the inhibitor concentration, the C dl values tend to decrease and the inhibition efficiency increases. The decrease in C dl values can be attributed to a decrease in local dielectric constant and/or an increase in the thickness of the electrical double layer, suggesting that CA extract components act by adsorption at the mild steel/solution interface [3, 20, 44]. This situation was the result of an increase in the surface coverage by this inhibitor, which led to an increase in the inhibition efficiency. The thickness of the protective layer, δ org, was related to C dl by the following equation:

$$\delta_{\text{org}} \, = \,\frac{{\varepsilon_{\text{o}} \varepsilon_{\text{r}} }}{{C_{\text{dl}} }}$$
(9)

where \(\varepsilon_{\text{o}}\) is the dielectric constant and \(\varepsilon_{\text{r}}\) is the relative dielectric constant. Since adsorption of an organic inhibitor on a metal surface involves the replacement of water molecules and other ions originally adsorbed on the surface, the smaller dielectric constant of organic compounds compared to water as well as the increased thickness of the double layer due to inhibitor adsorption acts simultaneously to reduce the interfacial capacitance [45–47]. This provides experimental evidence of adsorption of the extract organic matter on the corroding mild steel surface.

Table 5 EIS parameters for mild steel in 1.0 M HCl solution free and containing 50 and 1000 mg/L CA extract
Full size table

Adsorption considerations

The establishment of adsorption isotherms that describe the adsorptive behavior of a corrosion inhibitor is an important part of the stability as they can provide important clues as to the nature of the metal–inhibitor interaction [48–50]. Adsorption of the organic molecule occurs as the interaction energy between the molecule and metal surface is higher than that between the water molecule and the metal surface [51, 52]. In order to obtain the isotherm, the degree of surface coverage θ was calculated from the weight loss measurements using Eq. 1. The values of θ were tested graphically for fitting to a suitable adsorption isotherm, and the best fit was obtained with the Langmuir adsorption isotherm described by the equation [53–55]:

$$\frac{C}{\theta }\, = \,\frac{1}{{K_{\text{ads}} }}\, + \,C$$
(10)

where C is the inhibitor concentration and K ads is the adsorption equilibrium constant.

The plot of C/θ versus C yields a straight line (Fig. 7) with a slope of 1.05, proving that the adsorption of the CA extract from 1 M HCl solutions obeys the Langmuir adsorption isotherm. The strong correlation (R 2 = 0.999) for the Langmuir adsorption isotherm confirms the validity of this approach. The first stage in the action mechanism of inhibitor in acid media is adsorption on the metal surface [33]. In most inhibition studies, the formation of donor–acceptor surface complexes between π-electrons of inhibitor and the vacant d-orbital of metal were postulated [3].

Fig. 7
figure 7

Langmuir isotherm of CA extracts adsorption on mild steel surface in 1 M HCl solution at 303 K for 24 h

Full size image

Characterization of CA extract

It is now known that CA extract provides inhibition to mild steel corrosion in HCl media; however, the characteristic of the constituents that provide the inhibition is still unclear. To identify the probable constituents responsible for the inhibition, the chemical composition of the extract was studied by use of gas chromatography (GC) and mass spectrometry (MS).

GC–MS chromatogram of the ethanolic extract of CA showed 12 peaks indicating the presence of 12 chemical constituents (Fig. 8). The 12 active constituents with their retention time (RT), molecular formula, molecular weight (MW) and peak area (%) in the ethanolic extract of CA are presented in Table 6. In comparison of the mass spectra of the constituents with the NIST library, the eight predominant constituents were identified and the structures are presented in Fig. 9.

Fig. 8
figure 8

GC–MS of CA extract

Full size image
Table 6 The GC–MS results of CA extract
Full size table
Fig. 9
figure 9

The structures of the predominant compounds of CA extract

Full size image

Theoretical study

As with other organic inhibitors, which act through the adsorption to the metal surface, the rationalization of plant extract inhibitory action demands knowledge not only of the various electrochemical, kinetic and thermodynamic parameters of the corrosion system but also the knowledge of the extract composition and molecular properties. Some quantum chemical studies have successfully linked the corrosion inhibition efficiency with molecular properties for different kinds of organic inhibitors/compounds [50, 56–58].

Table 7 provides some quantum chemical parameters related to the molecular electronic structures of four predominant components of CA extract obtained from Fig. 9. These are namely the total energy, the highest energy occupied molecular orbital (E HOMO) and lowest unoccupied molecular orbital energies (E LUMO), the LUMO–HOMO energy gap (ΔE), the dipole moment, µ, and the molecular surface area (MSA). Parameters that gave valuable information about the reactivity behavior, electronegativity of molecules, their hardness and electron-donating ability were also calculated.

Table 7 Quantum chemical parameters calculated at DFT level for NMA, DMP, BZL and GTS
Full size table

The molecular modeling calculations were performed in vacuum phase by means of VAMP module available in Material Studio 4.0 package. Complete geometry of each structure was optimized at the restricted Hartre Fork (UHF) level using neglect of diatomic differential overlap (NDDO) [15] approach with PM3 parameterization.

There is an electron transfer taking place during the adsorption of neutral organic molecules at the metal surface. According to the frontier molecular orbital theory, this transition process includes removing electrons from HOMO or adding electrons to LUMO [59–61]. Localization of HOMO and LUMO for the CA components is given in Fig. 10, which shows that the most susceptible site for electrophilic attack is centered on aromatic rings, pi-electrons of double bonds and the heteroatoms.

Fig. 10
figure 10

Optimized structures as well as the density of HOMO and LUMO of the four major constituents of CA extract

Full size image

The energy levels of the frontier molecular orbital are significant for this transfer. E HOMO is often related with the molecule’s electron-donating ability. High values of E HOMO indicate a tendency of the molecule to donate electrons to appropriate acceptor molecules with low energy or empty electron orbital. The energy of the LUMO is directly related to the electron affinity and characterizes the susceptibility of the molecule toward attack by nucleophiles. The lower the values of E LUMO are, the stronger the electron-accepting abilities of the molecules. As a result, it can be assumed that when there is an increasing value of E HOMO, there is an increased level of inhibition efficiency and it is so also for a decreasing value of E LUMO.

The energy difference (ΔE) between LUMO and HOMO is described as the minimum energy required to excite an electron from the last occupied orbital in the molecule [62]. ΔE values are correlated to inhibition efficiency; the lower the value of the energy difference, the higher the value of the inhibition efficiency.

From the results for E HOMO, E LUMO and ΔE yield (Table 7), it is possible to get better performance with DMD as corrosion inhibitor and hence greater contribution to the observed inhibition efficiency. Therefore, the reactivity order for these components is DMP > BZL > NMA > DGS.

In a corrosion system containing inhibitor, the inhibitor and the metal act as a Lewis base and a Lewis acid, respectively; therefore, the frontier orbital theory may be used to determine possible modes of interaction between the inhibitor and metal. The frontier orbital energies E HOMO and E LUMO shown in Table 7, according to the Koopman’s theorem [63], can be related to the ionization potential, I, and the electron affinity, A, of iron and the inhibitor molecule by the following relations:

$$I\, = \, - E_{\text{HOMO}}$$
$$A\, = \, - \,E_{\text{LUMO}}$$

Absolute electronegativity, \(\chi\), and the absolute hardness, η, of the inhibitor molecule are given by [63]:

$$\chi \, = \,\frac{{(I\, + \,{\rm A})}}{2}$$
$$\eta \, = \,\frac{(I\, - \,A)}{2}.$$

The softness is the inverse of the hardness:

$$\sigma \, = \,\frac{1}{\eta }.$$

The fraction of the electrons transferred from the inhibitor to the mild steel atom is given by [15]:

$$\Delta N\, = \,\frac{{\chi_{\text{Fe}} \, - \,\chi_{\text{inh}} }}{{2\left( {\eta_{\text{Fe}} \, + \,\eta_{\text{inh}} } \right)}}$$

where a theoretical electronegativity value of χ Fe = 7.0 eV is taken for iron and absolute hardness of η Fe = 0 is assumed, since I = A for bulk metals. The values of A, I, X inh and ∆N for the modeled molecules are included in Table 7.

According to Lukovits, if ΔN < 3.6, the inhibition efficiency increased with increasing electron-donating ability at the metal surface [64]. It can be inferred from the calculation results that inhibitors investigated in this study were donors of electrons, and the iron surface was the acceptor. Order of ΔN is as follows: DMP > BZL > NMA > DGS, which is in accordance with the trends of E HOMO and E LUMO established earlier.

Frontier molecular orbital (HOMO and LUMO) may be used to predict the adsorption centers of the inhibitor molecule. For the simplest transfer of electrons, adsorption should occur at the part of the molecule where the softness, σ, which is a local property, has the highest value. Local softness σ* for the inhibitor molecule that acts as the nucleophile is given by Klopman [65]:

$$\sigma^{*} \, = \,\sigma \rho_{{_{\text{HOMO}} }}$$

where ρ HOMO is a normalized electron density of the frontier orbital. The isosurfaces for the same value of the HOMO density of all the modeled molecules are shown in Fig. 10. Evidently, adsorption of these molecules could proceed via sharing of the oxygen or nitrogen or aromatic ring π-electrons, between the inhibitor molecule and the partly filled d-orbital of iron, as long as the region of high HOMO density was oriented toward the electrode surface.

The higher mass fractions such as the plant acids and their esters with even more complicated geometries have not been considered in the present analysis. However, a synergistic or antagonistic effect of these molecules may play an important role on the observed inhibition efficiency of CA extract.

Mechanism of inhibition

As follows from weight loss, potentiodynamic polarization and EIS measurements and theoretical studies, corrosion of mild steel in 1 M HCl is retarded in the presence of different concentrations of the CA extract. The results clearly showed that the inhibition mechanism involves blocking of the mild steel surface by the inhibitor molecules via adsorption. In general, the phenomenon of adsorption is influenced by the nature of the metal and chemical structure of inhibitor [55]. Most of the CA extract constituents are hydroxyl aromatic compounds, the predominant components of which are shown in Table 7. Therefore, the possible reaction centers are unshared electron pair of O-atoms and π-electrons of aromatic ring. Aromatic compounds whose structures include a cyclic delocalized π-electron system are susceptible to electron delocalization in acidic media [3]. Thus, the inhibitors may adsorb on the metal/acid solution interface by one and/or more of the following ways: (i) donor–acceptor interactions between the π-electrons of aromatic ring and vacant d-orbital of surface iron atoms, (ii) interaction between unshared electron pairs of heteroatoms and vacant d-orbital of iron surface atoms. Therefore, the adsorption of main constituents of CA extract on the mild steel surface can be attributed to the presence of O-atoms, π-electrons and aromatic rings.

Conclusion

  1. 1.

    GC–MS analysis of CA extract shows that this plant extract contains 12 major components including plant acids and aromatic polyols.

  2. 2.

    CA extract acts as a mixed-type corrosion inhibitor for mild steel corrosion in 1.0 M solution. Inhibition efficiency increased with increase in extract concentration, and IE % values from different methods employed are in good agreement.

  3. 3.

    The inhibition efficiency remained stable with respect to time but decreases with increase in temperature.

  4. 4.

    CA extract remained effective in all studied temperature. The thermodynamic parameters reveal a physical adsorption between CA extract and the metal surface.

  5. 5.

    The adsorption of CA extract onto the mild steel surface in 1 M HCl solution obeys Langmuir adsorption isotherm with high correlation coefficient.

  6. 6.

    The inhibitory action CA components were elucidated by means of frontier orbital theory applied to the results of the molecular modeling and the EIS results.

Material preparation

Tests were performed on carbon steel specimens with weight percentage composition as follows: C, 0.05; Mn, 0.6; P, 0.36; Si, 0.3; and the balance Fe. The blank corrodent was 1.0 M HCl solution. Stock solutions of the plant extract were prepared by boiling weighed amounts of the dried and ground leaves of CA under reflux for 3 h in 1.0 M HCl solutions. The resulting solutions were cooled and then filtered twice. The amount of plant material extracted into solution was obtained by comparing the weight of the dried residue with the initial weight of the dried plant material before extraction. From the respective stock solutions, inhibitor test solutions were prepared in the concentration range 50–1200 mg/L in the given corrodent.