Introduction

Suspension of solid nanoparticles (< 100 nm diameter) of very low concentrations (1–5% volume) in conventional heat transfer fluid is called nanofluid [7]. This increases the heat transfer significantly because the thermal conductivity of nanoparticles is higher than that of the liquid, which increases the thermal conductivity of nanofluid [1, 10, 20, 22, 25, 31]. The dispersion of particles of mini- or micro-size into liquids significantly increases heat transfer compared to nanofluid. But some major deficiencies, such as erosion of surface, clogging the flow which is not suitable for small channels, sedimentation of particles, and more pumping power, limit their industrial applications when compared to nanofluid. Many researchers found that the increased value of thermal conductivity of nanofluid is not the sole reason for heat transfer boost but some other factors such as Reynolds number, particle diameter, and volume fraction also affect the heat transfer rate [20, 29, 30]. It was concluded that the convective heat transfer coefficient increased by increasing volume fraction of nanoparticles and flow rate, and decreased by increasing particle diameter. Nanofluid suffers from all the problems of mini- or micro-sized suspended fluid when the volume fraction and particle diameter increased from its maximum value suggested by [7]. Nanofluids are insignificant for low flow rate applications, whereas its performance increases with the Reynolds number. Static mixing equipment or strip twisted tape is usually used to increase the heat transfer performance in comparatively low Reynolds number flows. These devices promote radial mixing. Sharma et al. [24] examined the effect of inclusion of strip twisted tape on heat transfer through transition flow of nanofluid and found a better heat transfer than the flow without twisted tapes.

Nanofluid has a great potential to carry heat in wide area of applications, which is not limited to heat exchanger, engine cooling, etc., but also in magneto-hydrodynamic application, which are mainly used in bioengineering, paint technology and medical sciences. Many researches have used nanofluid of Newtonian as well as non-Newtonian types to investigate the effect of solid particle concentration on magneto-hydrodynamic flow over stretching sheet [5, 21, 28]. It was concluded that nanofluid with metallic nanoparticle shows better performance than that of base fluid.

It has been proven by many researchers that the induced vibration on the flow system increases heat transfer rate by producing chaotic motion, which leads to mixing of fluid [6, 16, 18]. Sufficient radial mixing of fluid can be achieved either by turbulent flow, which requires higher pumping power or by use of static mixture, but these types of devices have manufacturing complexity and the problem of cleaning as well.

Lee and Chang [18] applied transverse vibration of 0–70 Hz frequency and 0.1–1.0 mm amplitude on the 8-mm-diameter pipe to investigate the effects on critical heat flux. Noteworthy increment in critical heat flux was reported, that was the function of both amplitude and frequency. Chen et al. [6] had selected a copper heat pipe with internal groove and imposed vibration in longitudinal direction. Their study found that heat transfer increment of heat pipe was directionally proportional to vibration energy applied to this mode of vibration. Easa and Barigou [13] numerically evaluated the performance of transverse vibration on heat pipe. It has been shown by contour plot of temperature and vorticity plot that vibration produces strong spiraling motion due to the secondary component of velocity, which enhances the radial mixing of fluid and great addition in heat transfer comparatively in short length pipe. Such methods are capable of reducing the length of the pipe because it reduces the hydrodynamic entrance length and the thermal entrance length considerably. It also performs cleaning action on the walls as its strong chaotic motion reduces fouling of the pipe.

Compared with longitudinal and rotational direction, the transverse vibration produces more chaotic motion when applied in the transverse direction. It was also proved that radial mixing is much better than the recognized Kenics helical static-mixer, which has the disadvantage of unhygienic fluid processing and more pressure drop, if transverse vibration is applied with the change in the orientation of pipe with step rotation [27].

Zhang et al. [32] conducted an experiment to investigate the effect of vibration in a circular straight pipe in transient flow condition. Comparisons were made among the flow of base fluid and SiO2–water nanofluid under steady state and unsteady (vibration) state. Sharp increment in heat transfer was achieved when the base fluid flows under vibration condition than the steady-state flow. The Reynolds number and vibration frequencies have greater influence on the enhancement effect. The maximum increase of 182% was found when the vibrational flow of nanofluid was compared to the steady-state flow of base fluid and it augmented further with the vibration amplitude.

A large number of studies has been done by researchers for the improvement of heat transfer by dispersing nanoparticles into conventional liquids used for heat transfer process with/or use of static mixture devices, or use of superimposed vibration at pipe wall. Nanofluids have its limitation of particle diameter and volume fraction as discussed earlier. Heat transfer through nanofluids can be increased by increasing Reynolds number but requires higher pumping power. Vibrating the flow of nanofluid through a pipe can solve all the problems described. The studies reviewed above publicized that no methodical study has been conceded out to appraise the effect of vibration on nanofluid flow with varying rheological properties and flow parameters. The work described in this paper is a CFD investigation of effects of vibration on laminar forced convection thermal flow of pure water and of Al2O3–water nanofluid through pipe. Simulations were carried out for different Reynolds numbers. Constant heat flux boundary condition was applied at pipe wall. The viscosity of nanofluid has been calculated using Corcione [9] correlation which is the function of temperature, solid particle diameter and volume fraction of nanoparticle; while the thermal conductivity of nanofluid was calculated from Chou et al. [8] correlation. Three average particle sizes of 25 nm, 50 nm, and 100 nm and four volume concentration of 0% (base liquid), 1.0, 1.5, and 2.0% were used. The effects of vibration parameters on pure liquid and nanofluid have also been investigated for different frequencies and amplitudes, and results have been presented through the ratio of heat transfer coefficient of vibrational flow to steady-state flow.

Theory

Thermophysical properties of nanofluid

Dispersion of nanoparticles of very low concentration in the carrier fluid behaves like a single-phase fluid of uniform properties. To achieve accurate results with this model, it is very necessary to use the most suitable correlations for nanofluid properties. The following equations are used to represent mathematical formulation of nanofluid as a single-phase model.

  • Density [26]

$$\rho_{\text{nf}} = \left( {1 - \emptyset } \right)\rho_{\text{f}} + \emptyset \rho_{\text{s}} .$$
(1)

Teng and Hung, [26] have experimentally verified the equation of effective density (Eq. 1) of Al2O3–water nanofluid with 0.06–1.50% density deviation, which shows good agreement.

  • Specific heat

$$\left( {C_{\text{p}} } \right)_{\text{nf}} = \frac{{\left( {1 - \emptyset } \right)\left( {\rho C_{\text{p}} } \right)_{\text{f}} + \emptyset \left( {\rho C_{\text{p}} } \right)_{\text{s}} }}{{\rho_{\text{nf}} }},$$
(2)

  • Viscosity [9]

Corcione [9] has developed an empirical relation with the experimental data taken from literature with 1.84% deviation.

$$\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} = \frac{1}{{1 - 34.87\left( {d_{\text{s}} /d_{\text{f}} } \right)^{ - 0.3} \emptyset^{1.03} }},$$
(3)

where \(d_{\text{f}}\) is the equivalent diameter of the base fluid molecule and can be represented in terms of molecular weight of base fluid \(\left( M \right)\), given by

$$d_{\text{f}} = 0.1\left( {\frac{6M}{{N\pi \rho_{\text{fo}} }}} \right)^{1/3} ,$$
(4)

where \(\rho_{\text{fo}}\) is the mass density of the base fluid calculated at temperature \(T_{\text{o}} = 293 \;\;K\).

  • Thermal conductivity [8]

Chou et al. [8] has developed correlation of thermal conductivity of nanofluid. All possible factors to represent nanofluid as a single-phase fluid such as solid particle diameter, volume fraction, and Brownian motion were considered. With a linear regression for experimental results, Buckingham-pi theorem was used to develop empirical correlation with a 95% confidence level.

$$\frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = 1 + 64.7\ \emptyset^{0.7460} \left( {\frac{{d_{\text{f}} }}{{d_{\text{s}} }}} \right)^{0.3690} \left( {\frac{{k_{\text{s}} }}{{k_{\text{f}} }}} \right)^{0.7476} Pr^{0.9955} Re_{\text{b}}^{1.2321} ,$$
(5)

in which \(Pr\) is the Prandtl number of the base fluid and nanoparticle Reynolds number (Brownian-motion Reynolds number) \(Re_{\text{b}}\) defined as

$$Re_{\text{b}} = \frac{{\rho_{\text{f}} K_{\text{b}} T}}{{3\pi \mu_{\text{f}}^{2} \lambda_{\text{f}} }},$$
(6)

where \(K_{\text{b}} \left( { = 1.38066\; \times \;10^{ - 23} {\text{J K}}^{ - 1} } \right)\) is the Boltzmann constant and \(\lambda_{\text{f}}\) is the molecular free path and dynamic viscosity of the base fluid is given by [14]

$$\mu_{\text{f}} = D.10^{{\frac{B}{{\left( {T - C} \right)}}}} ,$$
(7)

where \(D = 2.414 \times 10^{ - 5} , \;\;B = 278.8\; {\text{and }}\;C = 140\) in case of water.

CFD modelling

Consider the case of incompressible thermal laminar flow through the pipe, all the properties of the base fluid are assumed to be constant except the temperature-dependent viscosity. While for nanofluid, the viscosity and thermal conductivity are considered to be the function of temperature. The governing equations [15] are the equation of continuity:

$$\nabla \cdot \left( {\rho_{\text{nf}} U} \right) = 0$$
(8)

where \(U\) is the velocity vector and the equation of motion:

$$\rho_{\text{nf}} \frac{{{\text{D}}U}}{{{\text{D}}t}} = - \nabla p + \nabla \cdot \eta \dot{\gamma } + \rho_{\text{nf}} g,$$
(9)

where \(p\) is fluid pressure, \(t\) time, \(\dot{\gamma }\) shear rate, \(\eta\) apparent viscosity function, and \(g\) is gravitational acceleration; the gravitational effect can be neglected here for horizontal flow and the thermal energy equation:

$$\rho_{\text{nf}} \left( {C_{\text{p}} } \right)_{\text{nf}} \frac{{{\text{D}}T}}{{{\text{D}}t}}\; = \; \nabla \cdot \left( {\lambda \nabla T} \right)\; + \;\frac{1}{2}\eta \left( {\dot{\gamma }:\dot{\gamma }} \right).$$
(10)

Viscous dissipation (last term on the right side) can be neglected for low velocities. Therefore, it was neglected in this study. These equations can be combined with viscosity function and thermal conductivity function of nanofluid (Eqs. 3 and 5) to fully describe flow and heat transfer problem.

In CFX, different terms of generic transport equations have been discretized separately according to the physics involved in the problem via finite volume method and converted it into system of linear algebraic equation for individual subdomain which was then solved by numerical technique.

Discretization of advection term: the integration of field variable \(\varphi\) is approximated by its neighboring values then its value (\(\varphi )\) can be cast in the form (called advection scheme):

$$\varphi_{\text{ip}} = \varphi_{\text{up}} + \beta \nabla \varphi \cdot \overrightarrow {\Delta r} ,$$
(11)

where \(\varphi_{\text{ip}}\) is the value of \(\varphi\) at the integration point, which is the geometrical center of subdomain, \(\varphi_{\text{up}}\) the value at the upwind node, \(\beta\) the blend function, and \(\overrightarrow {\Delta r}\) is the vector from upwind node to integration point. Advection term was discretized using high-resolution advection scheme. In this scheme, the blend function varies from 0 to 1 for small variable gradient (i.e. at the center) to large variable gradient (i.e. near the wall), respectively, and this makes it both first- and second-order accurate (for more details refer [2]. It prevents the nonphysical values and avoids local oscillations of physical variable by varying blend factor 0–1[4].

Discretization of transient term: The second-order backward Euler scheme was used to discretize unsteady term. In this scheme, current time step and last two time steps were used to calculate the transport variable at the start and at the end of time step. This scheme is of second-order accurate, robust, implicit, and conservative in time, and has no time step limitation.

For unsteady-state (vibration) flow, displacement of wall boundary in transverse direction (\(x\) direction, considered) is given by

$$x = A{ \sin }\left( {2\pi ft} \right),$$
(12)

and then velocity function is defined as

$$\dot{x} = A2\pi f{ \cos }\left( {2\pi ft} \right) .$$
(13)

The considered flow condition is laminar, incompressible and fully developed. For such type of flow, Reynolds number can be expressed as:

$$Re = \frac{{\rho_{\text{nf}} \bar{w}D}}{{\mu_{\text{nf}} }}.$$
(14)

As vibration yields flow in transverse direction that plays a significant role in overall flow behavior and this can be defined by vibrational Reynolds number as

$$Re_{\text{v}} = \frac{{\rho_{\text{nf}} A2\pi fD}}{{\mu_{\text{nf}} }} .$$
(15)

Flow velocities in both the direction were selected such that the flow remained laminar for all the cases considered.

CFD simulation

Commercially available CFD software package ANSYS CFX 16.2 was used to simulate the steady-state and unsteady-state (vibrational) flow of nanofluid and compared it with the base fluid flow. The effective viscosity and thermal conductivity of nanofluid were described by Eqs. (3) and (5), respectively. The flow geometry was created and meshed using ICEM CFD 16.2. software.

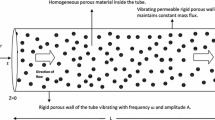
Straight pipe of 6 mm diameter is considered for the analysis. For evaluating nanofluid flow behavior through the horizontal pipe, this much diameter of the pipe is adequate as reported by many researchers [1, 10]. Sufficient 1000 mm length of pipe for comparatively low Reynolds number with three surface boundaries: wall, inlet and outlet were considered to capture the effect of heat transfer.

Structured grid with hexahedral cells was generated using map technique by ICEM-CFD 16.2 [3]. The study of grid independence was done by performing several simulations of various mesh shapes and sizes in the axial as well as in radial direction. Simulations were performed to validate the variation of local Nusselt number along the length by keeping other direction grid size fixed and vice versa. Simulations were started with coarse grid and refined it more till simulation results were not dependent or negligible improvement to grid size. Appropriate grid size was obtained thus contained 4000 cells per centimeter length and about 1100 cells across the tube section. To better capture the different variables nearer to where high velocity and temperature gradient exist, 0.05 mm thickness and 1.1 factor of increment were applied as indicated in Fig. 1.

Fig. 1
figure 1

Section of meshed geometry of pipe

Full size image

Flow specification was given using CFX-Pre [2]. CFD simulation has been done by following steps for clear demonstration of vibration effects in shorter pipe. Isothermal steady-state simulation was done so that velocity gets fully developed and can be used as inlet for next two simulations; (a) steady-state thermal flow, and (b) unsteady (vibration)-state flow with initial and/or boundary conditions stated in Table 1. Computational domain is in motion due to vibration and the mesh deformation option was checked in CFX for its care. This option takes care the deformation of mesh and their relative motion allowing by the stiffness of elements. For all the flow conditions, zero gauge pressure was set at outlet of pipe. For internment of the effect of radial mixing of fluid on temperature and heat transfer, simulations were executed for various Reynolds numbers (range given in Tables 2, 3).

Table 1 Initial and/or boundary conditions for different flow conditions
Full size table
Table 2 The thermophysical properties of the base fluid, nanoparticles, and nanofluid
Full size table
Table 3 Range of parameters used for simulation of flow
Full size table

Unsteady-state simulations were run for the residence time which is the time taken by fluid to come out from the pipe. Residence time was calculated by dividing the length of pipe with velocity. Depending upon the frequency, one oscillation time was divided into 12 equal numbers to get the value of time step. For example, \(0.2 \;{\text{s}}\) required to complete one cycle for the frequency of 50 Hz and then the time step would be \(0.2/12 = 1.6667 \times 10^{ - 3} \;{\text{s}}\). Time step chosen was such that the pipe attended two minimum and two maximum positions in a cycle. Simulations were executed for different values of time steps and found that by reducing time step size, simulation time increases with negligible increment in solution accuracy. 12 iterations/time was set by performing a number of simulations with the residual accuracy of \(10^{ - 4}\) and \(10^{ - 5}\). For such complex flow, when the residuals of continuity, momentum, and energy reached to the value of \(10^{ - 4}\) of root mean square, then it assumes that solution is converged for each time step. Solution was continued for next time step until simulation time reached its value to residence time.

Validation of CFD model

Validation of convective heat transfer coefficient for steady-state flow

Variation of local Nusselt number along the length obtained from Eq. (16) was compared with results obtained from CFD for distilled water at \(Re = 483.24 \;{\text{and}}\; 1000\) and for constant wall heat flux of \(q_{\text{w}} = 10,500 \;\;{\text{W/m}}^{2}\). Figure 2 shows excellent agreement between CFD results and those predicted by Shah’s equation of variation of local Nusselt number of thermally developing internal flow [23].

Fig. 2
figure 2

CFD results compared with equation of thermally developing Hagen–Poiseuille flow (Shah et al. 1987) for water subjected to different Reynolds numbers: \(D = 7\; {\text{mm}}; \;L = 1\; {\text{m}};\; q_{\text{w}} = 10,500\; {\text{W m}}^{ - 2} ;\;T_{\text{in}} = 25\;^{ \circ } {\text{C}}.\)

Full size image
$$Nu_{x} = \left\{ {\begin{array}{*{20}l} {~~~3.303x^{{* - \frac{1}{3}}} - 1.0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x^{*} \le 0.00005} \\ {1.302x^{{* - \frac{1}{3}}} - 0.50~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~0.00005x^{*} \le 0.0015} \\ {4.364 + 8.68\left( {~x^{*} 10^{3} } \right)^{{ - 0.506}} e^{{ - 41~x^{*} }} ~~~~~~~~~~~~~~~~~~x^{*} \ge 0.001} \\ \end{array} } \right.,$$
(16)

where \(x^{*} = \frac{x}{dRePr}\).

The flow and heat parameters selected for validation were such that the dimensionless length is always greater than \(x^{*} \ge 0.001\). It is because of this reason that the range of Reynolds number was taken such that \(x^{*}\) always lies in the third condition of Shah equation.

Unsteady-state isothermal flow validation

Deshpande and Barigou [11] were the first to experimentally prove that the flow of Newtonian fluid was unaffected by vibration in longitudinal direction. Whereas, there was a significant increase in the flow rate for non-Newtonian fluid accessible in terms of enhancement ratio, \(E_{\text{R}}\), which is the ratio of time-averaged flow rate of vibrational flow to steady-state flow. It has also been numerically confirmed by Easa and Barigou (2008) that \(E_{\text{R}}\) of Newtonian fluid flow is unaffected by any mode of vibration (i.e. longitudinal, transverse, and rotational direction) and CFD results also agree with this argument. To validate isothermal vibrational flow, CFD results were compared with the experimental results obtained by Deshpande and Barigou [11] for power-law-type fluid flowing through pipe subjected to longitudinal vibration shown in Fig. 3. Deshpande and Barigou [11] have also compared their experimental results with the CFX 4.3 simulations results. It was concluded that both results show a good level of accuracy for low frequency (\(10 \;\;{\text{Hz}}\)) while a slight nonconformity in the results was obtained as it was increased. They had argued that some lateral oscillations were unavoidable under the circumstances of experimental set-up used at high frequency. Due to this reason, CFD-predicted results were in good agreement with results obtained with CFX 4.3 results and it was higher than experimental results.

Fig. 3
figure 3

Validation of CFD Simulation results with the experimental data for power-law-type fluid under the longitudinal vibrational flow: \(K = 1.47\; {\text{Pa s}}^{\text{n}} ;\;n = 0.57;\,\,\varvec{ }\rho = 1000\varvec{ }\;\,\,{\text{kg m}}^{ - 3} ;\,\,\varvec{ }A = 1.60\varvec{ }{\text{mm}};\varvec{ }\Delta p/L = 9.81\varvec{ }\;{\text{kPa m}}^{ - 1}\)

Full size image

Thermal steady-state internal flow validation

Simulation model is validated for non-isothermal steady-state flow through pipe in the following two sections: in the first section, validation of radial temperature profile has been done because it gives the assurance of correct radial profile with the same setting used for unsteady-state flow and second validation is done for non-isoviscous flow because temperature-dependent viscosity of nanofluid is considered here.

  1. 1.

    Numerical results of Lyche and Bird [19] for Newtonian fluid at a Graetz number of 5.24 are used to validate simulation results of temperature distribution in radial direction of laminar isoviscous flow. Figure 4 shows very good agreement between the results obtained.

    Fig. 4
    figure 4

    CFD simulation result comparison with theoretical temperature profiles [19] for isoviscous Newtonian \(\left( {{\text{power}} - {\text{law index}}\ n = 1} \right)\) in steady-state flow:\(\mu = 1.0 {\text{Pa s }};\,\,T_{\text{in}} = 27\; ^\circ {\text{C}}; \,\,\)\(T_{\text{w}} = 127 \;^\circ {\text{C}};{\text{Gr}} = 5.24\); \(\bar{w} = 0.01 \;\,\,{\text{m s}}^{ - 1} ;\,\, \rho = 1000 \;{\text{kg m}}^{ - 3} ;\,\,C_{\text{p}} = 4180 \;\,\,{\text{J kg}}^{ - 1} {\text{K}}^{ - 1} ;\;\,\,k = 0.668 {\text{W m}}^{ - 1 } {\text{K}}^{ - 1}\)

    Full size image
  2. 2.

    Temperature-dependent viscosity is considered for base fluid and nanofluid, and so it is necessary to validate CFD model for non-isoviscous fluid. Kwant et al.’s [17] experimental results have been used to validate the CFD-predicted results shown in Fig. 5. Radial profile of isoviscous fluid shows the usual feature, whereas velocity profile of non-isoviscous fluid becomes flattened compared to that of isothermal condition.

    Fig. 5
    figure 5

    Experimental velocity profile for a temperature-dependent viscosity [17] used to validate CFD result:\(T_{\text{in}} = 27\; ^\circ {\text{C}}; \;\;T_{\text{w}} = 127\; ^\circ {\text{C}}; L = 1900\;\;\; {\text{mm}}; \overline{w} = 0.09 \;{\text{m s}}^{ - 1} ; \;\;C_{\text{p}} = 4180\; {\text{J kg}}^{ - 1} {\text{K}}^{ - 1} ; \;\;\)\(\mu = 1.3{ \exp }\left[ {1.49\left( {T - 25\; ^\circ C} \right)/(T_{\text{w}} - T_{\text{in}} )} \right] \;{\text{Pa s}}; \;\;\rho = 1000 \;\;{\text{kg m}}^{ - 3} ;\;\; k = 0.668\; {\text{W m}}^{ - 1 } {\text{K}}^{ - 1}\)

    Full size image

Deshpande and Barigou [11] have confirmed that CFD-predicted results for isothermal Newtonian and non-Newtonian fluid flow under forced vibration are consistent with experimental data. It has also proved that CFD codes are good enough to predict the flow behavior of such complex fluid flow within approximately \(\pm \;\;10\%\), for a variety of rheological behaviors and under a wide range of vibration conditions [13, 27]. CFD codes are also capable for internment of the flow (isoviscous and non-isoviscous) behavior in view of radial profile and heat transfer, etc., as discussed in aforementioned sections. The statement could be made based on the validation that CFD codes are robust, reliable, and upright for the purpose of studying the effect of vibration on heat transfer characteristics of the flow considered here, as there are no experimental data and numerical data available in the literature to validate the codes for non-isothermal unsteady flow.

Results and discussion

CFD simulations have been carried out for different Reynolds numbers to evaluate the effects of vibration frequency and vibration magnitude on the thermal developing laminar flow through pipe. In pipe flow, the effect of rheology (i.e. solid particle concentration and its size) of nanofluid has also been compared with the base fluid under vibration condition. Local and average heat transfer coefficients were calculated using the following equations:

$$h_{x} = \frac{{q_{\text{w}} }}{{\left( {T_{\text{w}} } \right)_{x} - \left( {T_{\text{nf}} } \right)_{x} }},$$
(17)
$$h = \mathop \int \limits_{0}^{l} \frac{{q_{\text{w}} }}{{T_{\text{w}} - T_{\text{nf}} }},$$
(18)

where \(q_{\text{w}} ,\left( {T_{\text{w}} } \right)_{x} ,\left( {T_{\text{nf}} } \right)_{x} , T_{\text{w}} ,T_{\text{nf}}\) are constant wall heat flux, wall temperature, fluid temperature across the tube at an axial position, mean wall temperature and mean bulk fluid temperature, respectively.

For different concentrations of nanoparticles (\(\emptyset \ 0,\; 1.0, \;{\text{and}}\; 1.5\%\)), Fig. 6 is plotted between the Reynolds number and the ratio of average heat transfer coefficient (unsteady-state to steady-state flow). As shown in figure, the heat transfer coefficient ratio for \(Re = 400\) enhanced about 51% by rising \(\emptyset \;{\text{from}} \;0 \;{\text{to}}\; 1.5\%\). Whereas, for \(\emptyset = 1.0\%\), with an increase in Reynolds number from 400 to 600, the heat transfer coefficient ratio decreases and about five times the enhancement of heat transfer obtained from the steady-state flow, and this further decreases with the Reynolds number. Similar trends were observed for all the volume fraction of nanoparticles. However, the value of heat transfer coefficient obtained for unsteady-state flow of nanofluid for all considered volume fractions are increased with an increase of Reynolds number while the ratio of heat transfer coefficient is decreased so it is clearly stated from the figure that vibration effects are dominated by Reynolds number. It is because of the reason that under the vibration conditions nanoparticles are influenced more by the inertia force as it has densities markedly different from the base fluid that leads to slippage between the base fluid and solid particles. This produces collision of nanoparticle surrounded by base fluid with the pipe wall that destructs the boundary layer and because of vorticity in \(xy\) plane created by transverse vibration the radial mixing is enhanced [32].

Fig. 6
figure 6

Ratio of average heat transfer coefficient of vibrational flow \(\left( {h_{\text{VF}} } \right)\) to steady flow \(\left( {h_{\text{SF}} } \right)\) with varying Reynolds numbers along the pipe: \(A = 2 {\text{mm}}; \;\;d_{\text{s}} = 25\; {\text{nm}}; \;\;\rho_{\text{nf}} = 1027.72\; \;\;{\text{kg m}}^{ - 3} ;\)\(\left( {C_{\text{p}} } \right)_{\text{nf}} = 4048 \;\;{\text{J kg}}^{ - 1} {\text{K}}^{ - 1} ,\)\(D = 6 \;{\text{mm}};\;\;L = 1000\; \;\;{\text{mm}}; \;\;q_{\text{w}} = 10500\;\;\; {\text{W m}}^{ - 2} ;\;\;T_{\text{in}} = 20\; ^{ \circ } {\text{C}};\;\;\mu_{\text{nf}} = {\text{Eq }}\left( 3 \right);\;\;k_{\text{nf}} = {\text{Eq}}\left( 5 \right);\;\;f = 50 {\text{Hz}}\)

Full size image

Figure 7 shows temperature contour of Al2O3-based nanofluid flow for different Reynolds numbers (solid particle of 25 nm diameter and \(\emptyset = 1.0\%\)) in steady-state, unsteady-state, and fluid trajectories at the end of pipe. It can be concluded from the figure that vorticity in the \(xy\) plane increases through transverse vibration which enhances the radial mixing of fluid. Vibration creates swirling or spiraling motion in the fluid that enhances heat transfer by promoting micro-convection and hence the result of uniform temperature profile. Swirling effects were subjugated by increasing flow velocity, as shown in Fig. 7b. It shows a decrease in radial mixing in the direction perpendicular to the induced vibration as the vibration effects are dominated by inertia effect of flow leading to non-uniform temperature distribution. This also increases the thermal entrance length. However, these effects can be overcome by increasing the vibrational parameters discussed in the next section.

Fig. 7
figure 7

Temperature distribution contour a steady flow, b vibrated flow, and c fluid trajectories, at outlet of the pipe

Full size image

Effect of nanoparticle concentration and its size, on the enhancement of heat transfer coefficient, are presented in Fig. 8 for \(Re = 600, \;\;A = 2 \;\;{\text{mm}}, \;\;{\text{and}} \;\;f = 50\;\; {\text{Hz}}\). Significant enhancement in heat transfer has been achieved with increasing particle diameter \(\left( {d_{\text{s}} = 25 - 50\;\; {\text{nm}}} \right)\) and volume fraction. This is due to the fact that fluid nearer to the core region of pipe gets exposed frequently to the wall due to cyclic motion and receives high heat from the wall which is not possible in steady-state flow. Heat transfer in steady-state flows is done only through conduction from the wall and through the convection within the fluid. Chaotic motion forms because of the cyclic process as shown in Fig. 7c leading to higher increment in heat transfer. This decreased further by increasing the particle diameter from 50 to 100 nm. This is because of the reason that for small diameter of nanoparticle, it is better exposed to the wall surface and this exposure becomes saturated with further increment in diameter. However, for further increment of volume fraction, heat transfer ratio becomes linearly increasing in nature but more increment of concentration causes a rapid settlement of nanoparticles, results that can cause interruption of flow and create local heating at the bottom of the wall.

Fig. 8
figure 8

Effect of nanoparticle diameter \(d_{\text{s}}\) and volume fraction of nanoparticle on the enhancement of heat transfer coefficient \(h_{\text{vf}} /h_{\text{sf}}: D = 6;\,\, {\text{mm}};\,\,L = 1000;\,\, {\text{mm}};\,\, q_{\text{w}} = 10,500;\,\, {\text{W m}}^{ - 2} ;\,\,T_{\text{in}} = 20\;^{ \circ } {\text{C}};\,\,\mu_{\text{nf}} \;\,\,{ = }\;{\text{Eq}} \left( 3 \right);\,\,k_{\text{nf}} = {\text{Eq}}\left( 5 \right);\,\,f = 50 {\text{Hz}};\,\, A = 2 {\text{mm}};\,\, Re = 600 ;\,\,\rho_{\text{nf}} \;\,\,{ = }\;\,\,1027.72 {\text{kg m}}^{ - 3};\,\, \left( {C_{\text{p}} } \right)_{\text{nf}} = 4048\;\,\, {\text{J kg}}^{ - 1} {\text{K}}^{ - 1}\)

Full size image

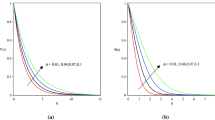
Effect of vibration frequency and amplitude on the heat transfer of both the fluid flows is presented in Fig. 9. For typical value of frequency \(\left( {f = 50\;\; {\text{Hz}}} \right)\), amplitude has been varied from \(1.0 - 2.0\; {\text{mm}}\) and for amplitude \(\left( {A = 2\; {\text{mm}}} \right)\) frequency ranges \(50 - 100\; {\text{Hz}}\). From Fig. 9, it is examined that there is increase in heat transfer coefficient ratio with increase in vibration parameters for both liquids. But the rate of increase for nanofluid is significantly higher than the base fluid and the heat transfer coefficient is more prone to amplitude than that of frequency. This is due to the fact that the movement of nanoparticles for typical value of Reynolds number increases within the pipes with an increasing frequency of 50–75 Hz and these effects become saturated for further increment of the frequency. The above trend of heat transfer augmentation has been reported in the form of more secondary flow (in transverse direction) with the increase in amplitude, which leads to more uniform radial mixture. On the increase of heat transfer, the same effect of vibration frequency and amplitude was obtained by Easa and Barigou [12], but the ratio of the increase is much higher than that of pure liquid. It is probable that different nanoparticles were exposed to the pipe surface very frequently because of vibration and as the heat capacity of nanoparticle is very high compared to the base fluid which acts as a good source of heat conduction through wall and hence much enhancement of heat transfer.

Fig. 9
figure 9

Effect of frequency and amplitude on the ratio of heat transfer coefficient \(\left( {\frac{{h_{{v{\text{f}}}} }}{{h_{\text{sf}} }}} \right)\) of base fluid and nanofluid flow: \(D = 6\;\,\, {\text{mm}};L = 1000\;\,\, {\text{mm}};\,\, q_{\text{w}} = 10,500\; {\text{W m}}^{ - 2} ;T_{\text{in}} = 20\;^{ \circ } {\rm C};\,\,\mu_{\text{nf}} = {\text{Eq}} \left( 3 \right);\,\,k_{\text{nf}} = {\text{Eq}}\left( 5 \right);\,\,d_{\text{s}} = 25 {\text{nm}}; \,\,Re = 600 ; \,\,\rho_{\text{nf}} = 1027.72\;\,\, {\text{kg m}}^{ - 3} ;\,\, \left( {C_{\text{p}} } \right)_{\text{nf}} = 4048\; \,\,{\text{J kg}}^{ - 1} {\text{K}}^{ - 1}\)

Full size image

Conclusion

In this paper, the comparison has been made among the convective heat transfer coefficient of steady-state and unsteady-state (vibration) laminar flow of Al2O3–water-based nanofluid and of pure water. A well-validated CFD model used to simulate the flow of water and nanofluid through a horizontal pipe subjected to uniform constant heat flux. Numerical simulation has been conducted for a different range of Reynolds number and for different nanofluid parameters. Considerable enhancement of convective heat transfer coefficient has been reported for pure water at low Reynolds number and further, the ratio of heat transfer coefficient decreased with Reynolds number. In comparison with the base fluid, by adding nanoparticles with different concentration about 51% maximum enhancement was obtained for \({\varnothing} = 2.0 \%\) and this continued with a slight fall of values with the Reynolds number.

For a typical value of Reynolds number, ratio of heat transfer coefficient can be maximized with increment in volume fraction of nanoparticles and the use of solid particles with a moderate diameter. But a considerable increment of volume fraction causes the sedimentation of particles. In addition, heat transfer rate can be optimized between volume fraction and solid particle diameter for comparatively low Reynolds number that would lead to low power consumption.

Mechanical vibration with different frequencies produced substantial enhancements in heat transfer than that of amplitude. Heat transfer rate for nanofluid flow greatly influenced by amplitude and frequency compared with the base fluid and much enhancement than that of base fluid were achieved under vibration. Further, this study can be extended for two-phase flow CFD model so that the influence of solid particles concentration and its behavior under vibration flow condition can be evaluated and can be extended to verify the effect of higher concentration of volume fraction on friction factor and distribution of nanoparticles.