Introduction

QCA is a new nano-technology for the implementation of logic circuits first introduced by Lent and Tougaw [1]. Low power consumption, low area, high processing speed, fast data transmission as well as higher operating frequency are the benefits of this technology [2]. In the future, there is a chance that QCA will be named as a new competitor to CMOS technology due to its good features. Circuits made under CMOS technology have a very significant difference in area and power consumption compared to circuits under QCA technology [3]. This means they occupy a lot of area than QCA circuits and have much higher power consumption. This is how the QCA with these unique features represents a major evolution in the field of computer science and logic circuits. QCA is much smaller than CMOS, even the dimensions of a QCA cell can be implemented at the molecular or atomic level [4].

Today, signals in digital electronic systems have only two distinct values. Digital computers operate on discrete components of information and are displayed in binary form. Therefore, for calculations on this type of equipment, the information must first be converted into acceptable code for them and then processed. This is why it is important to design and build different code converters, so that they can be understood and processed by a digital system. To convert different codes such as Decimal, Octal, Hexadecimal, Binary, etc., most of the circuits are designed and manufactured under CMOS technology but have high area occupancy (low integration capability), low switching speed compared to QCA technology and high power consumption are some of the factors that have led scientists to adopt the emerging QCA technology [5]. QCA consumes very low power compared to CMOS because not only there is no current in the circuit but also no output capacitor is in it [6].

Few papers have dealt the design of digital code converters in the QCA domain. In [7], an XOR gate is introduced and based on that, a digital code converter circuit is designed. In this paper, a gray code to binary converter and vice versa have been proposed. Since the proposed XOR structure does not have optimal cell numbers and space, the proposed design also does not have the desired performance conditions. In [8], also designs for gray code to binary converters and vice versa have been proposed. Structures for the parity circuit have also been proposed which all the presented structures suffer from a high cell numbers and occupied space. Also, the XOR gate proposed in this paper, which is the basis for designing other circuits, also has poor performance and delay conditions. In [9] for parity, designs are also presented that all of them have weaknesses in the latency, cell number, and occupancy. Also, the complexity of the presented circuits in these papers and their higher power consumption can be due to other weaknesses of them.

In this research, QCA technology was used to improve the structure of digital codes converter in terms of occupied area, number of cells, and latency. Converter of different codes, such as binary to BCD and BCD to Decimal code converter, … have been a major component of digital electronic equipment, especially digital computers, which have many applications. For this reason, making stable and fast code converters, with smaller dimensions and less power consumption than in the past, can greatly improve the performance of digital circuits and computers. In this paper, a new design method for the creation of XOR gates using QCA cells will be introduced that will increase the read and write speed in QCA circuit cells. Then, some designs will be presented for digital code converters with a focus on improving latency and lower cell numbers than previous designs.

The paper is organized as follows. Next section describes QCA functional principles. Section “Proposed parity generator and digital code converter circuits” shows the XOR structures. Also, proposed code converters and parity check circuit are described in this section. Simulation and results are explained in Sect. “Simulation and results”. Finally, Sect. “Conclusions” concludes the paper.

QCA functional principles

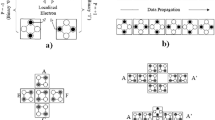
QCA is a new technology that will allow quantum dots to be used for digital computing. Quantum cells can dramatically reduce occupied area and power consumption. The polarization of QCA cells that represent logical 0 and 1 is shown in Fig. 1. Four quantum dots are arranged in a square, and two moving electrons are in this single cell that can move easily between these quantum dots [12].

Fig. 1
figure 1

The polarization of QCA cell [10]

Full size image

The movement of electrons in these cells is based on the phenomenon of tunneling. It is assumed that these tunnels are fully controllable by potential barriers. If we consider quantum dots as quasi-zero-dimensional potential wells and consider the cell as a square, each of these wells can have 2 electrons [12].

The two positions where these electrons can occupy are the main and secondary diagonals of this square structure and, as shown in the Fig. 1, the positioning of the electrons on the main and secondary diagonal represents 1 binary and diameter 0 binary, respectively [13]. In the arrangement of adjacent cells, no external potential energy will be applied to the structure, and what arranges the cells is the Coulomb force. It is clear that due to the Coulomb repulsion in each cell, electrons are placed at the poles.

The simplest circuit in QCA technology is the binary wire shown in Fig. 2. With the polarization of the cell at the left end of the wire, the cells are polarized from left to right, and each cell takes the polarization of the left cell before itself. So according to Coulomb interaction between the cells, logical 1 will be transmitted in the wire. Other data are similarly propagated along a binary wire.

Fig. 2
figure 2

Binary wire [11]

Full size image

Another basic and important gate in QCA technology is the NOT gate shown in Fig. 3. This gate can also be made in other ways. One of these methods is shifting the output QCA cell up or down within a previous QCA cell. Obviously, with this technique, the output will be the opposite of the input.

Fig. 3
figure 3

QCA Not gate [10]

Full size image

Maybe the most important gate in QCA circuits is the majority gate which is shown in Fig. 4. The performance of a 3-input majority gate is considered as below:

$$F\, = \,{\text{MAJ }}\left( {A,B,C} \right)\, = \,AB\, + \,AC\, + \,BC.$$
(1)
Fig. 4
figure 4

QCA majority gate (C, B, A are inputs and F is output.)

Full size image

This gate can be called as a basic logic gate because if one input is fixed at 1, the output of the gate will be the OR of the other two inputs. Similarly, if one of the inputs is fixed at 0, the output of the gate will be the AND of the other two inputs.

Proposed parity generator and digital code converter circuits

In this section, the proposed design is divided into different sections including: XOR gates, parity generator, binary to gray code converter, gray to binary code converter and BCD to gray code converter. Each of these sections will be designed by QCA technology.

XOR gates

One of the most important parts of digital gate converter circuits is XOR gate [13]. To implement the proposed circuits, the block diagram of Fig. 5a is used for the XOR gate. According to this structure, the proposed XOR gate in QCA technology is shown in Fig. 5b. In the proposed structure, 20 QCA cells are used to implement the XOR gate and the input-to-output delay is 0.75 clock cycles.

Fig. 5
figure 5

a XOR block diagram, b proposed structure for the XOR gate in QCA technology

Full size image

There is also another structure in the Fig. 6 for the XOR gate. This structure is proposed for using in circuits that require multiple XOR circuits. The number of used cells is greater than the first structure, but it can be integrated and bridge can be used for internal input. For more complex structures, both structures can be combined. This can utilize advantage of both structures simultaneously.

Fig. 6
figure 6

Second presented structure for the XOR gate in QCA technology

Full size image

Proposed circuit of parity generation

Parity is the simplest method of coding [14]. In this way, the encoded information contains N bits of the original data along with a bit that holds parity. There are two types of parity:

  • In the Even Parity method, parity is set such that the total number of logical one bits (original data and Parity) is even.

  • The Odd Parity method works the opposite. This means that in the method, the parity bit is set such that the total number of logical one bits (original data and Parity) is odd.

The Parity bit is controlled every time the information of byte is used or moved. The result of this control may not be complete, but the probability of a problem that eliminates two “1”s from a single byte simultaneously is very low. If all the bytes are completely destroyed, this bug can still be detected.

Finally, the total number of bits is equal to N + 1, in which one bit is added to the original N bits data. Parity code has Hamming Distance 2. As a result, it can detect any single bit error but cannot make any correction. Parity code cannot detect a two-bit error, but it can detect a three-bit error. In general, the parity code is capable of detecting any odd number of errors.

Figure 7 shows the proposed structure to generate Even Parity in QCA technology, consisting of the three proposed XOR gates in this paper. The proposed structure has 86 QCA cells with a delay of 1.5 cycles. In the proposed structure, it is tried to reduce the number of used cell and delay by optimizing the results of previous investigations.

Fig. 7
figure 7

The proposed structure to generate even parity in QCA technology

Full size image

Proposed circuit for converting binary numbers to gray code

The logical structure of converting binary numbers to gray numbers is shown in Fig. 8a. As can be seen, the components of this structure are the XOR gates. Based on this structure, the presented circuit for converting binary numbers to gray code in QCA technology is shown in Fig. 8b. The structure utilizes 99 QCA cells and the delay of the circuit is 0.75 cycles.

Fig. 8
figure 8

a The logical structure of converting binary numbers to gray numbers, b the presented circuit for converting binary numbers to gray code in QCA technology

Full size image

Proposed circuit to convert gray code to binary code

The logical structure of converting gray code to binary numbers is shown in Fig. 9a. It consists of three XOR gates. The delay of this circuit is equal to the delay of three XOR gates. Based on this structure, the presented circuit for converting the gray code to binary numbers in QCA technology is shown in Fig. 9b. The circuit has 76 QCA cells and the delay of this circuit is 2.25 cycles.

Fig. 9
figure 9

a The logical structure of converting gray code to binary numbers, b the proposed circuit for converting gray code to binary numbers in QCA technology

Full size image

Proposed circuit for converting BCD code to Gray code

The logical structure of converting BCD code to Gray code is shown in Fig. 10a. It consists of two XOR gates and an OR gate. Based on this structure, the presented circuit for this structure in QCA technology is shown in Fig. 10b. The structure utilizes 99 QCA cells and the delay of this circuit is a cycle.

Fig. 10
figure 10

a The logical structure of converting BCD code to Gray code, b the Proposed circuit for converting BCD code to Gray code in QCA technology

Full size image

Simulation and results

In this section, the simulation results of the proposed designs to confirm their performance and structural evaluation such as cell number, area and delay from input to output will be presented. The simulations are done by QCADesigner software. It is a popular tool for QCA structure and has been developed at the University of Calgary [15].

Figure 11 shows the results of the simulation of the first and second XOR gates. The results show that the output is correct and the circuit is correctly implemented.

Fig. 11
figure 11

a The obtained results for the first proposed XOR gate in QCA technology, b the obtained results for the second proposed XOR gate in QCA technology

Full size image

In Table 1, the XOR gate structures are compared with the proposed structures in terms of delay and number of QCA cells. As can be seen, the first proposed circuit has a 37% improvement in cell number.

Table 1 Comparison of XOR gate structures
Full size table

Also, the result of the simulation of the proposed circuit for the parity bit is shown in Fig. 12 which indicates the proper operation of this structure. The delay is also 1.5 QCA cycles.

Fig. 12
figure 12

The obtained results from the generator of the parity bit

Full size image

Table 2 presents the results of the generator of the parity bit. This table shows the number of QCA cells and the delay. According to the Table 2, the proposed circuit is better than the other circuits in terms of both the number of cells and the delay. The proposed structure has the ability to integrate better than other structures.

Table 2 Comparison of the generator of the parity bit in QCA technology
Full size table

In Fig. 13, the simulated output for the binary number to Gray code converter circuit is given. This circuit is implemented using the proposed structures for the XOR gate. As the simulation results show, the delay of this circuit is 0.75 cycles. This circuit is also implemented using three XOR gates with 4 inputs and 4 outputs.

Fig. 13
figure 13

Simulation results of binary number to Gray code converter circuit in QCA technology

Full size image

Figure 14 also presents the simulation result of the proposed circuit to convert gray code to binary. The output signals are complete and noise free and the accuracy of the converter can be checked according to the Figure.

Fig. 14
figure 14

Obtained outputs from the proposed circuit to convert Gray code to binary

Full size image

The result of the proposed circuit simulation for converting BCD code to gray code is shown in Fig. 15. The output indicates that the circuit is implemented properly and it operates correctly.

Fig. 15
figure 15

The results of the proposed circuit simulation for converting BCD code to gray code in QCA technology

Full size image

Finally, the power of the structures is fully investigated and the results are presented in Table 3. According to this table, the second proposed circuit for the XOR gate has less power consumption despite having more cells. The binary to Gray code converter circuit also has lower power consumption, though its cell numbers are higher than all the proposed circuits.

Table 3 Obtained results for the proposed circuits
Full size table

Conclusions

This paper presents two XOR gates in QCA technology. The proposed structures were used in digital code converter circuits. In the same direction, circuits of parity generation, binary to gray, vice versa and BCD to gray converter circuit were proposed. The proposed circuits are evaluated and the final structures are suitable in terms of cell number, occupied area, delay and power.