Introduction

Surface morphology at nanoscale is a key factor in technological applications as well as fundamental science [1,2,3]. In the past decade, atomic force microscope (AFM) images were considered as the best source of information about surface topography obtained through a very small probe which forms the profile of the surface morphology quantitatively [4]. There exist various types of methods which give information about surface texture, i.e. surface regulations including skewness, power spectral density (PSD), autocorrelation function, RMS roughness, and fractal dimension (Df) [5]. Statistical descriptions of RMS roughness represent the average square of the difference between the heights of peaks and valleys and they do not describe lateral distribution. One of the significant differences between investigating surface topography by RMS roughness and PSD methods is that the first method does not describe surfaces with complex morphology and behavior in the appropriate way since it may show the same value of RMS roughness. In addition, the first method depends just on the length scale. Thus, PSD is a more accurate method due to its ability in performing fast Fourier transform (FFT) of the squared height profile versus wavelength. PSD method helps to compare roughness in different spatial frequency regions [6, 7].

Among various types of surfaces whose morphology can be estimated, human tooth attracts a lot of attention nowadays [8]. Enamel, dentin, and cementum are three hard tissues which form human tooth. Amongst, enamel which covers the crown is the most rigid and mineralized tissue whose main content is 96 wt% inorganic materials mainly composed of hydroxyapatite (HAP) crystals [9] composed of phosphorous and calcium. Formation of enamel, called amelogenesis, occurs by cytodifferentiation, matrix secretion, and maturation process [10]. Dentin is the second tissue which contains dental pulps and it is composed of mineral components and complex protein [11]. Dentin is formed by odontoblasts where 30% and 50% of its compositions are collagen and HAP minerals [12]. Finally, Cementum, whose composition is similar to bone, is mainly composed of HAP (65 wt%), along with organic matrix including collagen and noncollagenous proteins and also water [13]. These tissues with their complex structure are highly organized. In order to investigate surface morphology of enamel, dentin, and cementum, atomic force microscopy (AFM) was applied as the best technique to specify surface morphology along x, y, and z axes. The aim of the present work was to analyze AFM images of hard tissue of canine teeth by PSD plots which provide information about height distribution. Afterward, fractal geometry was extracted through FFT algorithm as a tool which can describe dental complex nature. The calculated parameters can affect physical properties of each tissue as the hallmark of fractals.

Experimental details

In a dental clinic, three extracted human canine teeth were placed in saline and transferred to the laboratory. After when they reached the laboratory, they were all cleaned ultrasonically and finally air-dried. Each tooth was sectioned with diamond discs (Discoflex, KG Sorensen, Brazil) to access inter enamel. Enamel, inter enamel, dentin, and cementum tissue of each tooth were imaged with an AFM (Veeco, Santa Barbara, CA, USA) in non-contact mode at room temperature with scan rates of 10–20 μm/s over square areas of 1 μm × 1 μm. Quantitative information including PSD and fractal dimension was obtained from the AFM images.

Results and discussion

Morphological analysis

As mentioned before, Rrms evaluation does not give essential information about height scale and makes scientists replace it with another statistical parameter called PSD which describes roughness changes with length scale.

PSD is defined as the square of surface roughness amplitude versus wavelength which is applied to compare surface quality quantitatively [14]. AFM images are for PSD analysis as presented in Fig. 2 for all tissue. Figure 3 represents the PSD plots of dental hard tissue, i.e. enamel out, inter enamel, dentin, and cementum calculated through FFT algorithm. Moreover, frequency distribution versus frequency are calculated by FFT and finally PSD functions as |F(x, y)|2 in which F(x, y) are FFT coefficients. On the other hand, normalizing PSD reaches units of (length)4 [15].

Microstructure fractal information is obtained by PSD versus spatial frequency [16] via AFM data. The following equation describes PSD function [17]:

$$ S_{2} (f_{x} ,f_{y} ) = \left[ {\frac{1}{{L^{2} }}\left[ {\sum\limits_{m = 1}^{N} {\sum\limits_{n = 1}^{N} {Z_{mn} } } {\text{e}}^{{ - {\text{e}}\pi i\Delta L(f_{x} m + f_{y} n)}} (\Delta L)^{2} } \right.} \right]\frac{1}{{L^{2} }}, $$
(1)

where S2 denotes 2D PSD and N and L2 are data points and surface area. N = 181 in the present study. fx and fy are the spatial frequency and ΔL = L/N [18]. Also, PSD in polar coordinates and frequency space is obtained through

$$ S_{2} (f) = \frac{1}{2\pi }\int_{1}^{2\pi } {S_{2} } (f,\varphi ){\text{d}}\varphi . $$
(2)

We have

$$ {\text{PSD}}(f) = \frac{K}{{f^{ - \gamma } }}. $$
(3)

In addition, the power \( \gamma \) is the inverse slope of log–log plot of PSD-K. Here, sample rate is 30.12 μm−1 while L is set as 3.0 μm [19]. On the other hand, the relationship between S(k) which is defined as PSD and K is illustrated in Eq. (5) while the slope of a log S(k)–log k plot ends at Df [20]:

$$ S(k) \propto k^{ - \beta } . $$
(4)

Moreover, the relation between Df and the slope of log–log plot is given by β in Eq. (6), which is presented by as follows:

$$ D = 4 + \beta /2. $$
(5)

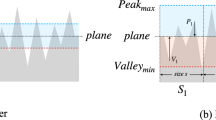
At different scales, D determines surface irregularities (Fig. 1).

Fig. 1
figure 1

AFM images (1 × 1 µm2, 512 × 512 pts) of each dental tissue: a enamel, b dentin, c cementum

Full size image

From another aspect, PSDABC plots can be described by k-correlation function which gives information about plot features [20] and hence, by considering f as the spatial frequency, it is defined as follow:

$$ {\text{PSD}}_{ABC} = \frac{A}{{(1 + B^{2} f^{2} )^{{\frac{(C + 1)}{2}}} }}. $$
(6)

Here, “A” is the magnitude of low spatial frequency, “B” is the ‘knee,’ i.e. the slope of connective line between two points of the surface of enamel, dentin, and camentum, and “C” with its constant value refers to the nature of roughness.

In Fig. 2, high spatial frequency region is characterized. While the shapes of curves were similar in both low- and mid-frequency region where the most energy exists, some differences were observed in the specified region. As mentioned before, tooth structures in all tissue are fine and highly organized and they increase by increasing fractal dimension (D). The results of Fig. 1 are summarized in Table 1 and it was observed that decreasing slope ends increase of fractal dimension at high-frequency region which occurs by moving from enamel to dentin and cementum.

Fig. 2
figure 2

The spectral log PSD–log K plots for each dental tissue and their comparison

Full size image
Table 1 The values of Df for each tissue extracted from Eq. (6)
Full size table

In Fig. 3, the slope variation (D) of log PSD–log K diagram was estimated for enamel and confirms the dependency of D to frequency and spectrum region. In addition, the results of Fig. 3 are presented in Table 2. As can be seen, the best fitted line in Fig. 3 is line III since slope changes depend directly on spectral range, frequency, and data size [20]. Moreover, Tables 3 and 4 describe the dependency of slope and fractal dimension on dentin and cementum. Hence, in enamel, increase of fractal dimension takes place by decreasing slope.

Fig. 3
figure 3

The diagram of log PSD–log frequency which confirms the effect of frequency region on the values of slopes in enamel

Full size image
Table 2 The values of Df and slopes in specified frequency region of enamel
Full size table
Table 3 The values of Df and slopes in specified frequency region of dentin
Full size table
Table 4 The values of Df and slopes in specified frequency region of cementum
Full size table

Moreover, Table 3 shows that by decreasing slope from low to mid frequency region in dentin, fractal dimension was increased while by moving to high-frequency region, increasing slope reduces the fractal dimension. In Table 4, as can be seen for cementum, increasing frequency from low to mid decreases fractal dimension while moving from mid to high-frequency region decreases the slope which finally ends in increase of fractal dimension.

According to Raman spectra of enamel and cementum in Fig. 4, a large variety of lines are due to mechanical stress whose width confirms their solid nature with a complex structure. Moreover, strong peak at 960 cm−1 represents HAP structure (PO4 functional group) which is similar in both tissue but with more intensity in enamel. As can be seen, the mentioned peak is surrounded by weak peaks around it. Wide bands are also observed in cementum in the range of 900 cm−1 to 1100 cm−1. There are some similarities in phosphate bands of enamel and cementum. On the other hand, the groups of amides and organic materials are revealed at 1450, and 1245 cm−1 while double C–O bond is illustrated in the range 1600–1700 cm−1.

Fig. 4
figure 4

Raman spectra of cementum (top) and enamel (bottom)

Full size image

Conclusion

The present work focused on the surface morphology of hard tissue of canine tooth including enamel, dentin, and cementum. The obtained results confirm that PSD method and fractal dimension are the best candidates for measuring surface morphology and performing functional characteristics of surface. According to the statistical parameters obtained from 3D AFM images, surface roughness parameters were measured precisely so that surface characterization was strongly affected by external factors. In addition, the dependency of surface roughness on the slope of log PSD–log K diagram along with fractal dimensions was investigated for different dental tissue. As can be seen, increasing slope ends in increase of fractal dimension and surface complexity. Moreover, by moving from enamel to cementum, fractal dimension has been increased. Finally, fine but complex structure of dental tissues was observed through Raman spectra in which functional groups of HAP were clear.