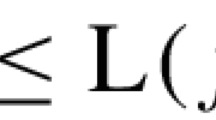Bismut-Stroock Hessian formulas and local Hessian estimates for heat semigroups and harmonic functions on Riemannian manifolds

Abstract

In this article, we develop a martingale approach to localized Bismut-type Hessian formulas for heat semigroups on Riemannian manifolds. Our approach extends the Hessian formulas established by Stroock (An estimate on the Hessian of the heat kernel: 355–371, 1996) and removes in particular the compact manifold restriction. To demonstrate the potential of these formulas, we give as application explicit quantitative local estimates for the Hessian of the heat semigroup, as well as for harmonic functions on regular domains in Riemannian manifolds.

1 Introduction

Let M be a complete Riemannian manifold of dimension n with Levi-Civita connection $\nabla$. We consider the operator $L=\frac{1}{2}\Delta$ where $\Delta :={{\text {tr}}}\,\nabla \mathbf{d}$ is the Laplace-Beltrami operator on M and $\mathbf{d}$ the exterior differential (note that we use a bold letter for the exterior differential to distinguish it from the Itô differential d appearing later). Denote by X.(x) a Brownian motion on M starting at $x\in M$ with generator L and explosion time $\zeta (x)$. The explosion time is the random time at which the process leaves all compact subsets of M. Furthermore, let $B_t$ be the stochastic anti-development of X.(x) which is a Brownian motion on $T_xM$, stopped at the lifetime $\zeta (x)$ of X.(x), and denote by $P_tf$ the associated minimal heat semigroup, acting on bounded measurable functions f, which is represented in probabilistic terms by the formula

$$\begin{aligned} (P_tf)(x)={\mathbb {E}}\big [f(X_t(x))\mathbf {1}_{\{t< \zeta (x)\}}\big ]. \end{aligned}$$

Recall that for any $T>0$ fixed, $(t,x)\mapsto (P_tf)(x)$ is smooth and bounded on ${(0,T]}\times M$ with $P_0f=f$.

Let $Q_t:T_xM\rightarrow T_{X_t}M$ be defined by

$$\begin{aligned} DQ_t=-\frac{1}{2}{{\text {Ric}}}^{\sharp }(Q_t)\,dt, \quad Q_0={\mathrm {id}}, \end{aligned}$$

where $D:=/\!/_t\,d \,/\!/_t^{-1}$ and $/\!/_t:=/\!/_{0,t}: T_{x}M \rightarrow T_{X_{t}(x)}M$ denotes parallel transport along X(x). The following formula is taken from [16] and gives a typical probabilistic derivative formula for the semigroup $P_tf$; it extends earlier formulas of Elworthy-Li [8]. Results in this direction are centered around Bismut’s integration by parts formula [3]. To be precise, let D be a fixed regular domain in M and $\tau _D$ be the first exit time of X.(x) from D when started at $x\in D$. A regular domain is by definition an open, relatively compact connected domain in M with non-empty boundary. Then for $v\in T_xM$,

$$\begin{aligned} \nabla P_tf(x)={\mathbb {E}}\left[ f(X_t(x)) \mathbf {1}_{\{t<\zeta (x)\}} \int _0^{\tau _D \wedge t} \langle Q_t({\dot{k}}(s)v), /\!/_s \,d B_s \rangle \right] , \end{aligned}$$

where the function $k\in L^{1,2}({\mathbb {R}}^+, [0,1])$ satisfies the property that $k(0)=0$ and $k(s)=1$ for all $s\ge \tau _D\wedge t$. An explicit choice of the random function k in the above Bismut formula can be used to derive sharp gradient estimates in various situations, e.g. for heat semigroups, as well as for harmonic functions on regular domains in Riemannian manifolds, see [17, 20] for explicit results. Recently, such formulas have also been applied to quantitative estimates for the derivative of a $C^2$ function u in terms of local bounds on u and $\Delta u$ [6].

A similar approach has been used by Arnaudon, Driver and Thalmaier [1] to approach Cheng-Yau type inequalities for the harmonic functions. Actually, the effect of curvature on the behavior of harmonic functions on a Riemannian manifold M is a classical problem (see e.g. [13, 21]), see also [7] for characterizations of gradient estimates in the context of metric measure spaces. In this paper, we aim to clarify in particular the effect of curvature on the Hessian of harmonic functions on regular domains in Riemannian manifolds. To this end, we establish a local version of a Bismut type formula for ${{\text {Hess}}}P_tf$ which is consistent with Stroock’s formula in [14] while here we follow a martingale approach and allow the manifold to be non-compact.

We start by giving some background on Bismut type formulas for second order derivatives of heat semigroups. A first such formula appeared in Elworthy and Li [8, 9] for a non-compact manifold, however under strong curvature restrictions. An intrinsic formula for ${{\text {Hess}}}P_tf$ was given by Stroock [14] for a compact Riemannian manifold, while a localized intrinsic formula was obtained by Arnaudon, Planck and Thalmaier [2] adopting a martingale approach. A localized version of the Hessian formula (still with doubly stochastic damped parallel translations) for the Feynman-Kac semigroup was derived by Thompson [19]. The study of the Hessian of a Feynman-Kac semigroup generated by a Schrödinger operator of the type $\Delta +V$ where V is a potential, has been pushed forward by Li [10, 11]. Very recently, Bismut-type Hessian formulas have been used for new applications, see for instance Cao-Cheng-Thalmaier [4] where $L^p$ Calderón-Zygmund inequalities on Riemannian manifolds have been established under natural geometric assumptions for indices $p>1$.

The following formula is taken from [2] and gives a localized intrinsic Bismut type formula for the Hessian of the heat semigroup. Define an operator-valued process $W_t:T_xM\otimes T_xM\rightarrow T_{X_t}M$ as solution to the covariant Itô equation

$$\begin{aligned} D W_t(v, w)=&R\big (/\!/_td B_t, Q_t(v)\big )Q_t(w)\\&-\frac{1}{2}(\mathbf{d}^*R+\nabla {{\text {Ric}}})^{\sharp }(Q_t(v), Q_t(w))\,d t-\frac{1}{2}{{\text {Ric}}}^{\sharp }(W_t(v, w))\,dt \end{aligned}$$

with initial condition $W_0(v,w)=0$. Here R denotes the Riemann curvature tensor. It is easy to check that

$$\begin{aligned} W_t(v,w)= & {} Q_t\int _0^t Q_r^{-1}\Bigg (R\big (/\!/_r d B_r, Q_r(v)\big )Q_r(w)-\frac{1}{2}(\mathbf{d}^*R+\nabla {{\text {Ric}}})^{\sharp }\\&\quad (Q_r(v), Q_r(w))\,d r\Bigg ). \end{aligned}$$

The operator $\mathbf{d}^*R$ is defined by $\mathbf{d}^*R(v_1)v_2:=-{{\text {tr}}}\nabla {.}R(\cdot , v_1)v_2$ and satisfies

$$\begin{aligned} \langle \mathbf{d}^*R(v_1)v_2,v_3\rangle =\langle (\nabla _{v_3}{{\text {Ric}}}^{\sharp })(v_1),v_2 \rangle -\langle (\nabla _{v_2}{{\text {Ric}}}^{\sharp })(v_3),v_1 \rangle \end{aligned}$$

for all $v_1,v_2,v_3\in T_xM$ and $x\in M$. Let $v,w\in T_xM$ with $x\in D$, $f\in {\mathcal {B}}_b(M)$ and fix $0<S<T$. Suppose that $D_1$ and $D_2$ are regular domains such that $x\in D_1$ and ${\bar{D}}_1\subset D_2\subset D$. Let $\sigma$ and $\tau$ be two stopping times satisfying $0<\sigma \le \tau _{D_1}<\tau \le \tau _{D_2}$. Assume $k,\ell$ are bounded adapted processes with paths in the Cameron-Martin space $L^{1,2}([0,T]; [0,1])$ such that

• $k(0)=1$ and $k(s)=0$ for $s\ge \sigma \wedge S$;

• $\ell (s)=1$ for $s\le \sigma \wedge S$ and $\ell (s)=0$ for $s\ge \tau \wedge T$.

Let ${{\text {Hess}}}=\nabla \mathbf{d}$. Then for $f\in {\mathcal {B}}_b(M)$, we have

$$\begin{aligned}&({{\text {Hess}}}_x P_{T}f)(v,v)=-{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T< \zeta (x)\}}\int _0^{T\wedge \tau }\langle W_s({\dot{k}}(s)v, v), /\!/_s d B_s\rangle \right] \nonumber \\&\quad +\mathbb {E}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _S^{T}\langle Q_s({\dot{\ell }}(s)v), /\!/_s d B_s\rangle \int _0^{S}\langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \right] .\quad \end{aligned}$$

(1.1)

This formula has the advantage to be concise with only two terms on the right-hand side to characterize the Hessian of semigroup; the martingale approach to this formula is direct and does not need advanced path perturbation theory on Riemannian manifold. However, it depends on the choice of two random test functions k and $\ell$. For local estimates the construction of two different random times $\tau$ and $\sigma$ is required, which complicates the calculation of the coefficients in the estimates, see [2].

Let us compare formula (1.1) with the Hessian formula from [14] where the manifold is supposed to be compact. Stroock proved that in this case one deterministic function test function $k\in C^{1}([0,T], [0,1])$ satisfying $k(0)=1$ and $k(t)=0$ is sufficient in a Bismut-type formula for the Hessian of the semigroup (see [15, Eq. (1.6)] and formula (2.17) below). In what follows, we call it the Bismut-Stroock Hessian formula. Although its proof relies on perturbation theory of Brownian paths and more terms are involved in the formula, the fact that only one test function k enters makes it attractive for applications to the short-time behavior of the heat kernel, see [15]. Recently, Chen, Li and Wu [5] adopted a perturbation of the driving force $B_t$ with a second order term for a new approach to this formula. The formula is derived with localized vector fields and extends to a general (non-compact) complete Riemannian manifold by introducing a family of cut-off processes.

The described works motivate the following two questions:

• (i) Can one extend the Stroock-Bismut Hessian formula [14] to a local Bismut-type formula for the Hessian heat semigroup by a direct construction of suitable martingales, and achieve from it explicit local estimates of ${{\text {Hess}}}P_tf$ by a proper choice of k?

• (ii) Can the localized Bismut-Stroock Hessian formula be transformed into a formula for the Hessian of harmonic functions on regular domains in Riemannian manifolds from where quantitative estimates can be derived?

In the sequel we answer both questions positively. Note that for the first question, it has been explained in [5, Section  4] that it seems difficult to adopt the perturbation theory of M-valued Brownian motions in order to replace the non-random vector field on path space by a random one; the time reversed field will not be adapted anymore and the Itô integral no longer be well defined. This reason motivates our search for a different stochastic approach to the problem in the form of a direct martingale argument. Actually, establishing localized Bismut-Stroock Hessian formula of semigroup relies on the proper construction of martingales which turns out to be the main difficulty for the first question. As an application of our formula, we can give explicit local Hessian estimates for the heat semigroup: for any regular domain $D\subset M$ and $x\in D$,

$$\begin{aligned} |{{\text {Hess}}}P_tf|(x) \le&\inf _{\delta >0}\left\{ \left( \frac{t}{2}\sqrt{ K_1^2+\frac{K_2^2}{\delta }}+\frac{2}{ t}\right) \right. \nonumber \\&\left. \exp \left( t\,\Biggl (K_0^-+ \frac{\delta }{2}+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+3)}{4\delta _x^2}\Biggl )\right) \right\} \Vert f\Vert _{D}, \end{aligned}$$

(1.2)

where $\delta _x=\rho (x,\partial D)$ is the Riemannian distance of x to the boundary of D and constants $K_0$, $K_1$ and $K_2$ are defined as in (2.10)–(2.12) below. Compared with known estimates, e.g. [2], the constants in (1.2) are explicit and concise. The estimate is not essentially more complicated, compared to the local gradient estimate [17].

The second problem is then to extract Hessian estimates for harmonic functions from the Bismut-Stroock Hessian formula which requires a careful estimate of the terms involving W.(v, w) and Q.(v), along with a proper choice of the process k. Let $D\subset M$ be a regular domain. In Section 3, we obtain that for a bounded positive harmonic function u on D,

$$\begin{aligned} |{{\text {Hess}}}\, u|(x)&\le \inf _{\begin{array}{c} 0<\delta _1<1/2\\ \delta _2>0 \end{array}}\Bigg \{\sqrt{(1+2\mathbf {1}_{\{K_0^-\ne 0\}})\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) }\nonumber \\&\quad +\sqrt{6}\,\Bigg (\frac{1}{2\delta _2}+3K_0^-+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+3+\delta _1^{-1})}{4\delta _x^2}\Bigg )\Bigg \}\sqrt{\Vert u\Vert _D\,u(x)}, \end{aligned}$$

see also Theorem 3.5.

The paper is organized as follows. In Section 2 we construct several local martingales to achieve local Hessian formulas for the heat semigroup which are consistent with Stroock’s construction [15] on compact manifolds with a deterministic function k. In Section 3 we give explicit local Hessian estimates for harmonic functions. For reader’s convenience, Section 3.1 provides the method to construct k which follows [17]. Finally, in Section 4, we apply our method to estimate the second derivative of heat semigroups and heat kernels.

2 Bismut-type formulas for the Hessian of $P_tf$

We start by constructing our fundamental martingale which will be the basis for our approach. To this end, for $v,w\in T_xM$ and $k\in L^{1,2}({\mathbb {R}}^+,\mathbb {R})$ let

$$\begin{aligned} W_{t}^k(v,w)&=Q_t\int _0^tQ_{r}^{-1}R\big (/\!/_{r} d B_r, Q_{r}(k(r)v)\big )Q_{r}(w)\\&\quad -\frac{1}{2} Q_t\int _0^t Q_{r}^{-1}(\mathbf{d}^* R+\nabla {{\text {Ric}}})^{\sharp }\big (Q_{r}(k(r)v), Q_{r}(w)\big )\, d r. \end{aligned}$$

It is easy to see that $W_{t}^k$ solves the following equation:

$$\begin{aligned}&DW^k_{t}(v, w)=R\big (/\!/_{t}\, d B_t, Q_{t}(k(t)v)\big )Q_{t}(w)\\&\quad -\frac{1}{2}(\mathbf{d}^* R+\nabla {{\text {Ric}}})^{\sharp }\big (Q_{t}(k(t)v), Q_{t}(w)\big )\,d t-\frac{1}{2}{{\text {Ric}}}^{\sharp }(W^k_{t}(v, w))\,d t, \end{aligned}$$

and $W_{0}^k(v,w)=0$.

Theorem 2.1

Let $x\in M$ and D be a relatively compact open domain in M such that $x\in D$. Let $\tau$ be a stopping time such that $0<\tau \le \tau _D$ where $\tau _D$ denotes the first exit time of X(x) with starting point $x\in D$. Fix $T>0$ and suppose that k is a bounded, non-negative and adapted process with paths in the Cameron-Martin space $L^{1,2}([0,T];{\mathbb {R}})$ such that $k(s)=0$ for $s\ge T\wedge \tau$, $k(0)=1$. Then for $f\in {\mathcal {B}}_b(M)$ and $v,w\in T_xM$,

$$\begin{aligned}&({{\text {Hess}}}P_{T-t}f)\big (Q_t(k(t)v), Q_t(k(t) v)\big )+(\mathbf{d}P_{T-t}f) (W_t^k(v,k(t) v)) \nonumber \\&\quad -2\mathbf{d}P_{T-t}f(Q_t(k(t) v))\int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \nonumber \\&\quad -P_{T-t}f(X_t)\int _0^t\langle W_s^k(v,{\dot{k}}(s) v),/\!/_sd B_s \rangle \nonumber \\&\quad +P_{T-t}f(X_t)\left( \left( \int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \right) ^2-\int _0^t |Q_s({\dot{k}}(s)v)|^2 \,ds\right) \end{aligned}$$

is a local martingale on $[0, \tau \wedge T)$.

Proof

First of all, by an approximation argument we may assume that $f\in C^{\infty }(M)$ and is constant outside a compact set so that $|\mathbf{d}f|$ and $\Delta f$ are bounded.

Let

$$\begin{aligned} N_t(v,v)={{\text {Hess}}}P_{T-t}f(Q_t(v), Q_t(v))+(\mathbf{d}P_{T-t}f)(W_t(v,v)). \end{aligned}$$

Then $N_t(v,v)$ is a local martingale, see for instance the proof of [19, Lemma 2.7] with potential $V\equiv 0$. Furthermore, define

$$\begin{aligned} N^k_t(v,v)={{\text {Hess}}}P_{T-t}f(Q_t(k(t)v), Q_t(v))+(\mathbf{d}P_{T-t}f)(W^k_t(v,v)). \end{aligned}$$

According to the definition of $W^k_t(v,v)$, resp. $W_t(v,v)$, and in view of the fact that $N_t(v,v)$ is a local martingale, it is easy to see that

$$\begin{aligned} N_t^k(v,v)&-\int _0^t({{\text {Hess}}}P_{T-s}f)(Q_s({\dot{k}}(s) v), Q_s(v))\,ds \end{aligned}$$

(2.1)

is a local martingale as well. Replacing in $N_t^k(v,v)$ the second argument v by k(t)v, we further see that also

$$\begin{aligned} N_t^k(v,k(t)v)&-\int _0^t({{\text {Hess}}}P_{T-s}f)(Q_s({\dot{k}}(s) v), Q_s(k(t)v))\,ds\nonumber \\&-\int _0^t{{\text {Hess}}}P_{T-s}f(Q_s(k(s)v), Q_s({\dot{k}}(s)v))\,ds\nonumber \\&-\int _0^t(\mathbf{d}P_{T-s}f)(W^k_s(v,{\dot{k}}(s)v))\,ds \nonumber \\&+ \int _0^t\int _0^s({{\text {Hess}}}P_{T-r}f)(Q_r({\dot{k}}(r) v), Q_r({\dot{k}}(s)v))\,dr\ ds \end{aligned}$$

(2.2)

is a local martingale. Note that $N_t^k(v,k(t)v)=N_t^k(v,v)\,k(t)$. Exchanging the order of integration in the last term shows that

$$\begin{aligned}&N_t^k(v,k(t)v)-\int _0^t({{\text {Hess}}}P_{T-s}f)(Q_s({\dot{k}}(s) v), Q_s(k(t)v))\,ds\nonumber \\&\qquad -\int _0^t{{\text {Hess}}}P_{T-s}f(Q_s(k(s)v), Q_s({\dot{k}}(s)v))\,ds\nonumber \\&\qquad -\int _0^t(\mathbf{d}P_{T-s}f)(W^k_s(v,{\dot{k}}(s)v))\,ds \nonumber \\&\qquad + \int _0^t({{\text {Hess}}}P_{T-r}f)(Q_r({\dot{k}}(r) v), Q_r((k(t)-k(r))v))\,dr\nonumber \\&\quad =N_t^k(v,k(t)v) -\int _0^t(\mathbf{d}P_{T-s}f)(W^k_s(v,{\dot{k}}(s)v))\,ds\nonumber \\&\qquad -2\int _0^t{{\text {Hess}}}P_{T-s}f(Q_s(k(s)v), Q_s({\dot{k}}(s)v))\,ds \end{aligned}$$

(2.3)

is a local martingale. Moreover, by the formula

$$\begin{aligned} P_{T-t}f(X_t)=P_Tf(x)+\int _0^t\mathbf{d}P_{T-s}f(/\!/_sd B_s) \end{aligned}$$

(2.4)

and integration by parts,

$$\begin{aligned} \int _0^t(\mathbf{d}P_{T-s}f)(W_s^k(v,{\dot{k}}(s)v))\,ds-P_{T-t}f(X_t) \int _0^t\langle W_s^k(v,{\dot{k}}(s)v), /\!/_s\,d B_s \rangle \end{aligned}$$

(2.5)

is a local martingale. Similarly, from the formula

$$\begin{aligned} \mathbf{d}P_{T-t}f(Q_t(k(t)v))= & {} \mathbf{d}P_{T}f(v)+\int _0^t({{\text {Hess}}}P_{T-s}f) (/\!/_sd B_s, Q_s(k(s) v))\\&+\int _0^t\mathbf{d}P_{T-s}f(Q_s({\dot{k}}(s)v))\,ds \end{aligned}$$

it follows that

$$\begin{aligned}&\int _0^t({{\text {Hess}}}P_{T-s}f)(Q_s({\dot{k}}(s)v), Q_s(k(s) v)) \,ds\nonumber \\&\quad -\mathbf{d}P_{T-t}f(Q_t(k(t) v))\int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s\rangle \nonumber \\&\quad +\int _0^t\mathbf{d}P_{T-s}f(Q_s({\dot{k}}(s)v))\,ds \,\int _0^t\langle Q_s({\dot{k}}(s)v) /\!/_sd B_s\rangle \end{aligned}$$

(2.6)

is also a local martingale. Concerning the last term in (2.6), we note that

$$\begin{aligned}&\int _0^t\mathbf{d}P_{T-s}f(Q_s({\dot{k}}(s)v))\,ds \,\int _0^t\langle Q_s({\dot{k}}(s)v),/\!/_sd B_s\rangle \\&\quad - \int _0^t \mathbf{d}P_{T-s}f(Q_s({\dot{k}}(s)v))\int _0^s\langle Q_r({\dot{k}}(r)v),/\!/_rd B_r\rangle \,ds \end{aligned}$$

is a local martingale. Combining this with (2.6) we conclude that

$$\begin{aligned}&\int _0^t({{\text {Hess}}}P_{T-s}f)(Q_s({\dot{k}}(s)v), Q_s(k(s) v)) \,ds\nonumber \\&\quad -\mathbf{d}P_{T-t}f(Q_t(k(t) v))\int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s\rangle \nonumber \\&\quad +\int _0^t \mathbf{d}P_{T-s}f(Q_s({\dot{k}}(s)v))\int _0^s\langle Q_r({\dot{k}}(r)v),/\!/_rd B_r\rangle \,ds \end{aligned}$$

(2.7)

is a local martingale. Using the local martingales (2.5) and (2.7) to replace the last two terms in (2.3), we conclude that

$$\begin{aligned}&({{\text {Hess}}}P_{T-t}f)(Q_t(k(t)v), Q_t(k(t) v))+(\mathbf{d}P_{T-t}f) (W_t^k(v,k(t) v)) \nonumber \\&\quad -P_{T-t}f(X_t)\int _0^t\langle W_s^k(v,{\dot{k}}(s) v),/\!/_sd B_s \rangle \nonumber \\&\quad -2\mathbf{d}P_{T-t}f(Q_t(k(t) v))\int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \nonumber \\&\quad +2\int _0^t\mathbf{d}P_{T-s}f(Q_s({\dot{k}}(s)v)) \int _0^s\langle Q_r({\dot{k}}(r)v),/\!/_rd B_r\rangle \,ds \end{aligned}$$

(2.8)

is a local martingale as well. On the other hand, by the product rule for martingales, we have

$$\begin{aligned}&\left( \int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \right) ^2-\int _0^t |Q_s({\dot{k}}(s)v)|^2\,ds \nonumber \\&\quad = 2\int _0^t \left( \int _0^s\langle Q_r({\dot{k}}(r)v), /\!/_rd B_r \rangle \right) \langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \end{aligned}$$

(2.9)

which along with (2.4) implies that

$$\begin{aligned}&P_{T-t}f(X_t)\left( \left( \int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \right) ^2-\int _0^t |Q_s({\dot{k}}(s)v)|^2\,ds\right) \\&\quad -2\int _0^t\mathbf{d}P_{T-s}f(Q_s({\dot{k}}(s)v)) \int _0^s\langle Q_s({\dot{k}}(s)v),/\!/_sd B_s\rangle \,ds \end{aligned}$$

is a local martingale. Applying this observation to Eq. (2.8), we finally see that

$$\begin{aligned}&({{\text {Hess}}}P_{T-t}f)\big (Q_t(k(t)v), Q_t(k(t) v)\big ) +(\mathbf{d}P_{T-t}f) (W_t^k(v,k(t) v)) \nonumber \\&\quad -2\mathbf{d}P_{T-t}f(Q_t(k(t) v))\int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \nonumber \\&\quad -P_{T-t}f(X_t)\int _0^t\langle W_s^k(v,{\dot{k}}(s) v),/\!/_sd B_s \rangle \nonumber \\&\quad +P_{T-t}f(X_t)\left( \left( \int _0^t\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \right) ^2-\int _0^t |Q_s({\dot{k}}(s)v)|^2\,ds\right) \end{aligned}$$

is a local martingale. This completes the proof. $\square$

In order to formulate explicit Hessian estimates we need to introduce some geometric bounds. Let $D\subset M$ be a regular domain and $\tau _D$ be the first exit time of X(x) from D. We consider the following constants:

$$\begin{aligned}&K_0:=\inf \left\{ \mathrm{Ric}(v,v):y\in D,\ v\in T_yM,\ |v|=1\right\} ; \end{aligned}$$

(2.10)

$$\begin{aligned}&K_1:=\sup \left\{ |R|(y):y\in D \right\} ;\end{aligned}$$

(2.11)

$$\begin{aligned}&K_2:=\sup \left\{ |(\mathbf{d}^*R+\nabla {{\text {Ric}}})^{\sharp }(v,v)|(y):y\in D,\ v\in T_yM, |v|=1\right\} . \end{aligned}$$

(2.12)

For $x\in M$ and $v,w\in T_xM$, we remark that

$$\begin{aligned} |R^{\sharp , \sharp }(v,v)|_{\tiny \text {HS}}(x)\le |R|(x)|v|^2 \end{aligned}$$

where

$$\begin{aligned} |R^{\sharp , \sharp }(v,v)|_{\tiny \text {HS}}:=\sqrt{\sum _{i,j=1}^nR(e_i, v,v,e_j)^2} \end{aligned}$$

and $\{e_i\}_{i=1}^n$ denotes an orthonormal base of $T_xM$.

We shall need the following lemma.

Lemma 2.2

Keep the assumptions and the definition of k as in Theorem 2.1, and assume that k is bounded by 1. If $\int _0^T|{\dot{k}}(t)|^{2q}\,dt\in L^1$ for some $q\in (1,+\infty ]$ and $v\in T_xM$, then

$$\begin{aligned} {\mathbb {E}}\left[ \int _0^T|W_t^k(v,{\dot{k}}(t)v)|^2\,dt\right]\le & {} \left( \frac{(2p-1) ^{p}K_1^{2p}}{2^2\delta ^{p-1}}+\frac{K_2^{2p}}{2^2\delta ^{2p-1} }\right) ^{1/p}\\&{\text {e}}^{(2K_0^-+\delta )T}T^{1/p}\, \left( {\mathbb {E}}\left[ \int _0^T|{\dot{k}}(t)|^{2q}\,dt\right] \right) ^{1/q}<\infty \end{aligned}$$

for $\delta >0$ and $1/p+1/q=1$. In particular, if $K_2\equiv 0$ and $k\in C^1([0,T],[0,1])$ a deterministic function, then

$$\begin{aligned} {\mathbb {E}}\left[ \int _0^T|W^k_t(v,{\dot{k}}(t)v)|^2\,dt\right] \le K_1^2T{\text {e}}^{2K_0^-T}\,\int _0^T|{\dot{k}}(t)|^2\,dt<\infty . \end{aligned}$$

Proof

From the definition of the operator $Q_s$ and the constant $K_0$, we know that $|Q_s|\le {\text {e}}^{-K_0s/2}$. According to Itô’s formula and the definitions of $K_1,K_2$, we have for $v\in T_xD$ and $s<\tau \le \tau _D$,

$$\begin{aligned} d |W_s^k(v, v)|^{2p}&= p\,(|W^k_s(v,v)|^2)^{p-1}\left[ 2 \left\langle R\big (/\!/_sd B_s, Q_s(k(s)v)\big )Q_s(v), W^k_s(v,v)\right\rangle \right. \nonumber \\&\quad \left. + |R^{\sharp ,\sharp }\big (Q_s(k(s)v),Q_s(v)\big )|_{{\tiny {\text {HS}}}}^2\,ds\right. \nonumber \\&\quad - \left. \left\langle (\mathbf{d}^* R+\nabla {{\text {Ric}}}^{\sharp })(Q_s(k(s)v), Q_s(v)), W^k_s(v,v) \right\rangle \,ds\right. \nonumber \\&\quad \left. - {{\text {Ric}}}(W^k_s(v,v),W^k_s(v,v))\,ds\right] \nonumber \\&\quad +2p(p-1)\,(|W^k_s(v,v)|^2)^{p-1} |R^{\sharp ,\sharp }\big (Q_s(k(s)v),Q_s(v)\big )|_{{\tiny {\text {HS}}}}^2\,ds\nonumber \\&\le p\, (|W^k_s(v,v)|^2)^{p-1}\left[ 2\left\langle R\big (/\!/_sd B_s, Q_s(k(s)v)\big )Q_s(v), W^k_s(v,v)\right\rangle \right. \nonumber \\&\quad + \left. K_2 {\text {e}}^{-K_0s} |v|^2\, |W^k_s(v,v)|\,ds-K_0 \,|W^k_s(v,v)|^2\,ds\right] \nonumber \\&\quad +p(2p-1)\,K_1^2{\text {e}}^{-2K_0s}|v|^4\,(|W^k_s(v,v)|^2)^{p-1}\,ds\nonumber \\&\le 2p\,(|W^k_s(v,v)|^2)^{p-1}\left\langle R\big (/\!/_sd B_s, Q_s(k(s)v)\big )Q_s(v), W^k_s(v,v)\right\rangle \nonumber \\&\quad +p(2p-1)\, K_1^2{\text {e}}^{-2K_0s}(|W^k_s(v,v)|^2)^{p-1}|v|^4\,ds\nonumber \\&\quad + K_2 p\,{\text {e}}^{-2K_0s}|v|^2(|W^k_s(v,v)|)^{2p-1}\,ds-K_0p\, |W^k_s(v,v)|^{2p}\,ds. \end{aligned}$$

(2.13)

Taking into account that for $\delta >0$,

$$\begin{aligned}&p(2p-1) K_1^2{\text {e}}^{-2K_0s}(|W^k_s(v,v)|^2)^{p-1}|v|^4\\&\quad \le \frac{\delta p}{2} |W^k_t(v,v)|^{2p} +\frac{(2p-1)^p}{2\delta ^{p-1}}{\text {e}}^{-2pK_0s}K_1^{2p}|v|^{4p};\\&K_2 p{\text {e}}^{-2K_0s}|v|^2(|W^k_s(v,v)|)^{2p-1}\\&\quad \le \frac{\delta p}{2} |W^k_t(v,v)|^{2p}+\frac{1}{2\delta ^{2p-1}}{\text {e}}^{-2pK_0s}K_2^{2p}|v|^{4p}, \end{aligned}$$

we thus have

$$\begin{aligned}&d {\text {e}}^{(K_0p-\delta p )s} |W^k_s(v, v)|^{2p}\\&\quad =2p{\text {e}}^{(K_0p-\delta p)s} |W^k_s(v, v)|^{2(p-1)} \left\langle R\big (/\!/_sd B_s, Q_s(k(s)v)\big )Q_s(v), W^k_s(v,v)\right\rangle \\&\qquad +{\text {e}}^{-(K_0p+\delta p)s}\left( \frac{(2p-1)^pK_1^{2p}}{2\delta ^{p-1}}+\frac{K_2^{2p}}{2\delta ^{2p-1} }\right) |v|^{4p}\,ds. \end{aligned}$$

Integrating this inequality from 0 to $t\wedge \tau$ and taking expectation yields

$$\begin{aligned}&{\mathbb {E}}\left[ {\text {e}}^{(K_0-\delta )p(t\wedge \tau )}|W^k_{t\wedge \tau }(v,v)|^{2p}\right] \\&\quad \le \left( \frac{(2p-1)^pK_1^{2p}}{2\delta ^{p-1}}+\frac{K_2^{2p}}{2\delta ^{2p-1} }\right) {\mathbb {E}}\left[ \int _0^{t\wedge \tau }{\text {e}}^{-(K_0+\delta )ps}|v|^{4p}\,ds\right] . \end{aligned}$$

If $|v|=1$, we then arrive at

$$\begin{aligned}&{\mathbb {E}}\left[ {\text {e}}^{(K_0-\delta )p(t\wedge \tau )}|W^k_{t\wedge \tau }(v,v)|^{2p}\right] \\&\quad \le \left( \frac{(2p-1)^pK_1^{2p}}{2\delta ^{p-1}}+\frac{K_2^{2p}}{2\delta ^{2p-1} }\right) {\mathbb {E}}\left[ \int _0^{t\wedge \tau }{\text {e}}^{-(K_0+\delta )ps}\,ds\right] , \end{aligned}$$

from where we conclude that

$$\begin{aligned} {\mathbb {E}}\left[ |W^k_{t}(v,v)|^{2p}\right]&\le \left( \frac{(2p-1)^pK_1^{2p}}{2\delta ^{p-1}}+\frac{K_2^{2p}}{2\delta ^{2p-1} }\right) {\text {e}}^{(K_0^-+\delta )pt}\left[ \int _0^{t}{\text {e}}^{-(K_0+\delta )ps}\,ds\right] \nonumber \\&\le \left( \frac{(2p-1)^pK_1^{2p}}{2\delta ^{p-1}}+\frac{K_2^{2p}}{2\delta ^{2p-1} }\right) {\text {e}}^{\delta pt} {\text {e}}^{K_0^-pt}\int _0^t{\text {e}}^{K_0^- ps}\,ds. \end{aligned}$$

(2.14)

Thus we have

$$\begin{aligned}&{\mathbb {E}}\left[ \int _0^T|W^k_t(v,{\dot{k}}(t)v)|^2\,dt\right] \\&\quad ={\mathbb {E}}\left[ \int _0^T{\dot{k}}(t)^2|W^k_t(v,v)|^2\,dt\right] \\&\quad \le {\mathbb {E}}\left[ \left( \int _0^T{\dot{k}}(t)^{2q}\,dt\right) ^{1/q} \left( \int _0^T|W^k_t(v,v)|^{2p}\,dt\right) ^{1/p} \right] \\&\quad \le \left( {\mathbb {E}}\left[ \int _0^T{\dot{k}}(t)^{2q}\,dt\right] \right) ^{1/q} \left( {\mathbb {E}}\left[ \int _0^T|W^k_t(v,v)|^{2p}\,dt\right] \right) ^{1/p}\\&\quad \le \left( {\mathbb {E}}\left[ \int _0^T{\dot{k}}(t)^{2q}\,dt\right] \right) ^{1/q} \left( \frac{(2p-1)^pK_1^{2p}}{2\delta ^{p-1}}+\frac{K_2^{2p}}{2\delta ^{2p-1} }\right) ^{1/p}{\text {e}}^{\delta T} \\&\qquad \times \left( \int _0^T{\text {e}}^{K_0^-pt}\int _0^t{\text {e}}^{K_0^- ps}\,ds dt\right) ^{1/p}\\&\quad \le \left( {\mathbb {E}}\left[ \int _0^T{\dot{k}}(t)^{2q}\,dt\right] \right) ^{1/q} \left( \frac{(2p-1)^pK_1^{2p}}{2^2\delta ^{p-1}}+\frac{K_2^{2p}}{2^2\delta ^{2p-1} }\right) ^{1/p}{\text {e}}^{\delta T+2K_0^-T} T^{1/p} \end{aligned}$$

which completes the proof of first inequality.

In particular, if $k\in C^1([0,T])$, then

$$\begin{aligned} {\mathbb {E}}\left[ \int _0^T|W^k_t(v,{\dot{k}}(t)v)|^2\,dt\right]&=\left[ \int _0^T{\dot{k}}(t)^2\,{\mathbb {E}}(|W^k_t(v,v)|^2)\,dt\right] . \end{aligned}$$

(2.15)

Moreover, from the calculation in (2.13) with $K_2\equiv 0$ we see that

$$\begin{aligned} d |W_s^k(v, v)|^{2}&= 2\left\langle R\big (/\!/_sd B_s, Q_s(k(s)v)\big )Q_s(v), W^k_s(v,v)\right\rangle \nonumber \\&\quad + K_1^2{\text {e}}^{-2K_0s}|v|^4\,ds -K_0 |W^k_s(v,v)|^{2}\,ds \end{aligned}$$

which implies

$$\begin{aligned} {\mathbb {E}}|W_{t}^k(v,v)|^{2} \le K^2_1{\text {e}}^{2K_0^-T}T. \end{aligned}$$

(2.16)

Combining (2.15) and (2.16) we obtain

$$\begin{aligned} {\mathbb {E}}\left[ \int _0^T|W^k_t(v,{\dot{k}}(t)v)|^2\,dt\right]&\le K^2_1{\text {e}}^{2K_0^-T}T\left[ \int _0^T{\dot{k}}(t)^2\,dt\right] \end{aligned}$$

which gives the additional claim. $\square$

By means of Theorem 2.1 and Lemma 2.2 we are now in position to formulate the localized Bismut-Stroock Hessian formula as follows.

Theorem 2.3

Let D be a relatively compact open domain such that $x\in D$. Let $\tau$ be a stopping time such that $0<\tau \le \tau _D$. Suppose that k is a bounded, non-negative and adapted process with paths in the Cameron-Martin space $L^{1, 2q}([0,T]; {\mathbb {R}})$ such that $k(t)=0$ for $t\ge T\wedge \tau$, $k(0)=1$ and $\int _0^{T\wedge \tau }|{\dot{k}}(t)|^{2q}\,dt\in L^1$ for some constant $q>1$. Then for $f\in {\mathcal {B}}_b(M)$ and $v\in T_xM$, we have

$$\begin{aligned}&({{\text {Hess}}}P_{T}f)(v,v)\nonumber \\&\quad =-{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _0^{T\wedge \tau }\Bigg \langle Q_s\int _0^sQ_{r}^{-1}R(/\!/_{r} d B_r, Q_{r}(k(r)v))Q_{r}({\dot{k}}(s)v), /\!/_s d B_s\Bigg \rangle \right] \nonumber \\&\quad -{\mathbb {E}}^x\Bigg [f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _0^{T\wedge \tau }\Bigg \langle Q_s\int _0^sQ_{r}^{-1}(\mathbf{d}^* R+\nabla {{\text {Ric}}})^{\sharp }(Q_{r}(k(r)v),\nonumber \\&\quad \times Q_{r}({\dot{k}}(s)v))\, d r, /\!/_s d B_s\Bigg \rangle \Bigg ] \nonumber \\&\quad +{\mathbb {E}}\left[ f(X_T)\mathbf {1}_{\{T< \zeta (x)\}}\left( \left( \int _0^{T\wedge \tau }\langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \right) ^2-\int _0^{T\wedge \tau } | Q_s({\dot{k}}(s)v)|^2 \,ds\right) \right] . \end{aligned}$$

(2.17)

Proof

For $\varepsilon >0$ small, let $k^{\varepsilon }(t)$ be a bounded, non-negative and adapted process with path in the Cameron-Martin space $L^{1, 2q}([0,T]; {\mathbb {R}})$ such that $k^{\varepsilon }(t)=0$ for $t\ge (T-\varepsilon )\wedge \tau$, $k^{\varepsilon }(0)=1$. We know that

$$\begin{aligned} |Q_{t\wedge \tau }|\le {\text {e}}^{-\frac{1}{2}K_0(t\wedge \tau )}\quad \text {and}\quad {\mathbb {E}}\left[ \int _0^T|W_t^{k^{\varepsilon }}(v,{\dot{k}}^{\varepsilon }(t)v)|^2\,dt\right] <\infty . \end{aligned}$$

By the boundedness of $P_tf$ on $[0,T]\times D$ and the boundedness of $|\mathbf{d}P_tf|$ and $|{{\text {Hess}}}P_tf|$ on $[\varepsilon ,T]\times D$ since P.f is smooth on $(0,T]\times M$, it follows first that the local martingale in Theorem 2.1 is a true martingale for the chosen $k^{\varepsilon }$. By taking expectations, along with the strong Markov property, we get the formula

$$\begin{aligned}&({{\text {Hess}}}P_{T}f)(v,v)= -{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _0^{T\wedge \tau }\langle W^{k^{\varepsilon }}_s(v,{\dot{k}}^{\varepsilon }(s)v), /\!/_s d B_s\rangle \right] \\&\quad +{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\left( \left( \int _0^{T\wedge \tau }\langle Q_s({\dot{k}}^{\varepsilon }(s)v), /\!/_s d B_s\rangle \right) ^2-\int _0^{T\wedge \tau }| Q_s({\dot{k}}^{\varepsilon }(s)v)|^2 \,ds\right) \right] . \end{aligned}$$

Finally, through approximating the given k by an appropriate sequence of $k^{\varepsilon }$ as above and letting $\varepsilon \downarrow 0$, we finish the proof. $\square$

Remark 2.4

• (i) In view of Eq. (2.9), formula (2.17) also can be written as

  $$\begin{aligned}&({{\text {Hess}}}P_{T}f)(v,v)= -{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _0^{T\wedge \tau }\langle W^k_s(v,{\dot{k}}(s)v), /\!/_s d B_s\rangle \right] \nonumber \\&\quad +2{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _0^{T\wedge \tau }\left( \int _0^{s}\langle Q_r({\dot{k}}(r)v), /\!/_r d B_r\rangle \right) \langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \right] . \end{aligned}$$

  (2.18)

• (ii) Since $({{\text {Hess}}}P_{T}f)$ is a symmetric form, it is straightforward from Theorem 2.3 that

  $$\begin{aligned}&({{\text {Hess}}}P_{T}f)(v,w)= -\frac{1}{2}{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _0^{T\wedge \tau }\langle W^k_s(v,{\dot{k}}(s)w), /\!/_s d B_s\rangle \right] \nonumber \\&\quad -\frac{1}{2}{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _0^{T\wedge \tau }\langle W^k_s(w,{\dot{k}}(s)v), /\!/_s d B_s\rangle \right] \nonumber \\&\quad +{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\left( \int _0^{T\wedge \tau }\langle Q_s({\dot{k}}(s)v), /\!/_sd B_s \rangle \right) \left( \int _0^{T\wedge \tau }\langle Q_s({\dot{k}}(s)w), /\!/_sd B_s \rangle \right) \right] \nonumber \\&\quad -{\mathbb {E}}^x\left[ f(X_T)\mathbf {1}_{\{T<\zeta (x)\}}\int _0^{T\wedge \tau } \langle Q_s({\dot{k}}(s)v), Q_s({\dot{k}}(s)w) \rangle \,ds\right] \end{aligned}$$

  (2.19)

  for $v,w\in T_xM$ and $x\in D$.

Denoting by $p_t(x,y)$ the transition density of the diffusion with generator L, using Theorem 2.3, we obtain the following Bismut-type Hessian formula for the logarithmic density.

Corollary 2.5

We keep the assumptions of Theorem 2.3. Then

$$\begin{aligned}&\left( {{\text {Hess}}}_x \log p_T(x,y)\right) (v,v) \\&\quad = -{\mathbb {E}}^x\left[ \int _0^{T\wedge \zeta (x)}\langle W^k_s(v,{\dot{k}}(s)v), /\!/_s d B_s\rangle \,\Big |\,X_T=y\right] \\&\qquad +{\mathbb {E}}^x\left[ \left( \int _0^{T\wedge \zeta (x)}\langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \right) ^2\,\Big |\,X_T=y\right] \\&\qquad -{\mathbb {E}}^x\left[ \int _0^{T\wedge \zeta (x)}| Q_s({\dot{k}}(s)v)|^2 \,ds\,\Big |\,X_T=y\right] \\&\qquad -\left( {\mathbb {E}}^x\left[ \int _0^{T\wedge \zeta (x)}\langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \,\Big |\,X_T=y\right] \right) ^2. \end{aligned}$$

Remark 2.6

Corollary 2.5 is well adapted to determine the short-time behavior of the Hessian of the heat kernel on a non-compact manifold (see the procedure in [5, Section 5]).

3 Hessian estimates for Harmonic functions

We now adjust Theorem 2.3 to the case of harmonic functions on regular domains. Recall that by a regular domain we mean a connected relatively compact open subset of M with non-empty boundary. For $D\subset M$ a regular domain and $f\in C^2({\bar{D}})$, let

$$\begin{aligned} |{{\text {Hess}}}f|(x)=\sup \big \{ |({{\text {Hess}}}f)(v,w)|:|v|\le 1, |w|\le 1, \ v,w \in T_xM\big \},\quad x\in D. \end{aligned}$$

Since ${{\text {Hess}}}f$ is symmetric, it is easy to see that

$$\begin{aligned} |{{\text {Hess}}}f|(x)=\sup \big \{ |({{\text {Hess}}}f)(v,v)|:|v|\le 1, \ v \in T_xM\big \},\quad x\in D. \end{aligned}$$

Theorem 3.1

Let $D\subset M$ be a regular domain, $u\in C^2({\bar{D}})$ be harmonic on D, further $x\in D$ and $v\in T_xM$. Then for any bounded adapted process k with sample paths in $L^{1,2q}({\mathbb {R}}^+;{\mathbb {R}})$ for some $q>1$ such that

$$\begin{aligned} \int _0^{\tau _D}|{\dot{k}}(s)|^{2q}\,ds\in L^{1}, \end{aligned}$$

and the property that $k(0)=0$ and $k(s)=1$ for all $s\ge \tau _D$, the following formula holds:

$$\begin{aligned}&({{\text {Hess}}}\,u)_x (v,v)\\&\quad =-{\mathbb {E}}^x\left[ u(X_{\tau _D}(x))\int _0^{\tau _D}\langle W^k_s(v,{\dot{k}}(s)v), /\!/_s d B_s\rangle \right] \\&\qquad +{\mathbb {E}}^x\left[ u(X_{\tau _D}(x))\left\{ \left( \int _0^{\tau _D}\langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \right) ^2-\int _0^{\tau _D} |Q_s({\dot{k}}(s)v)|^2\,ds\right\} \right] . \end{aligned}$$

Proof

Let $(P_t^Du)(x):={\mathbb {E}}[u(X_{t\wedge \tau _D}(x))]$. Since u is harmonic, we have $P^D_tu=u$ for $t\ge 0$, and then analogously to Theorem  2.3,

$$\begin{aligned} ({{\text {Hess}}}&\,u)_x (v,v)=({{\text {Hess}}}\,P^D_t u)_x (v,v)\\ =&-{\mathbb {E}}^x\left[ u(X_{t\wedge \tau _D}(x))\int _0^{t\wedge \tau _D}\langle W^k_s(v,{\dot{k}}(s)v), /\!/_s d B_s\rangle \right] \\&+{\mathbb {E}}^x\left[ u(X_{t\wedge \tau _D}(x))\left( \int _0^{t\wedge \tau _D}\langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \right) ^2\right] \\&-{\mathbb {E}}^x\left[ u(X_{t\wedge \tau _D}(x))\int _0^{t\wedge \tau _D}|Q_s({\dot{k}}(s)v)|^2 \,ds\right] . \end{aligned}$$

By letting t tend to infinity, we obtain the claim. $\square$

Remark 3.2

Taking Eq. (2.9) into account, the above formula can be rewritten as follows:

$$\begin{aligned}&({{\text {Hess}}}\,u)_x (v,v) =-{\mathbb {E}}^x\left[ u(X_{\tau _D}(x))\int _0^{\tau _D}\langle W^k_s(v,{\dot{k}}(s)v), /\!/_s d B_s\rangle \right] \nonumber \\&\quad +2{\mathbb {E}}^x\left[ u(X_{\tau _D}(x))\int _0^{\tau _D} \left( \int _0^{s}\langle Q_r({\dot{k}}(r)v), /\!/_r d B_r\rangle \right) \langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \right] . \end{aligned}$$

(3.1)

3.1 Construction of the random function k

We are now going to briefly sketch the method from [17, 18] to construct the function k. We restrict ourselves to Brownian motion on D with lifetime $\tau _D$ (exit time from D). Let f be a continuous function defined on $\bar{D}$ which is strictly positive on D. For $x\in D$, we consider the strictly increasing process

$$\begin{aligned} T(t)=\int _0^tf^{-2}(X_s(x))\,ds,\quad t\le \tau _D, \end{aligned}$$

(3.2)

and let

$$\begin{aligned} \tau (t)=\inf \{s\ge 0: T(s)\ge t\}. \end{aligned}$$

(3.3)

Obviously $T(\tau (t))=t$ since $\tau _D<\infty$, and $\tau (T(t))=t$ for $t\le \tau _D$. Note that since X is a diffusion with generator $\frac{1}{2}\Delta$, the time-changed diffusion $X_t':=X_{\tau (t)}$ has generator $L'=\frac{1}{2}f^2\Delta$. In particular, the lifetime $T(\tau _D)$ of $X'$ is infinite, see [17].

Fix $t>0$ and let

$$\begin{aligned} h_0(s)=\int _0^sf^{-2}(X_r(x)){1}_{\{r<\tau (t)\}}\,dr,\quad s\ge 0. \end{aligned}$$

Then for $s\ge \tau (t)$,

$$\begin{aligned} h_0(s)=h_0(\tau (t))=\int _0^{\tau (t)}f^{-2}(X_r(x))\,dr=t. \end{aligned}$$

Next, let $h_1\in C^1([0,t],{\mathbb {R}})$ with $h_1(0)=0$ and $h_1(t)=1$. We consider $k(s)=1-(h_1\circ h_0)(s)$. Then k is an adapted bounded process with $k(0)=1$ and $k(s)=0$ for $s\ge \tau (t)$.

Lemma 3.3

Suppose with $0<f\le 1$ on D, $f(x)=1$ and $f\vert _{\partial D} = 0$. For $\delta _1, \delta _2>0$ and $q>1$ set

$$\begin{aligned} c_1(f)&:=\sup _D\left\{ \left( (2\delta _2)^{-1}+K_0^-\right) f^2+(3+\delta _1^{-1})|\nabla f|^2-f\Delta f\right\} ; \end{aligned}$$

(3.4)

$$\begin{aligned} c_2(f)&:=\sup _D\left\{ K_0^-f^2+5|\nabla f|^2-f\Delta f\right\} ; \end{aligned}$$

(3.5)

$$\begin{aligned} c_3(f)&:=\sup _D\left\{ K_0^-f^2+3|\nabla f|^2-f\Delta f\right\} ;\end{aligned}$$

(3.6)

$$\begin{aligned} {\tilde{c}}_q(f)&:= \sup _D \Big \lbrace (2q+1)|\nabla f|^2 - f \Delta f \Big \rbrace \end{aligned}$$

(3.7)

where $K_0$ is defined as in (2.10). Then there exists f satisfying conditions with,

$$\begin{aligned} c_1(f)&\le \frac{1}{2\delta _2}+K_0^-+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+3+\delta _1^{-1})}{4\delta _x^2}:=c_1,\\ c_2(f)&\le K_0^-+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+5)}{4\delta _x^2}:=c_2,\\ c_3(f)&\le K_0^-+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+3)}{4\delta _x^2}:=c_3,\\ {\tilde{c}}_q(f)&\le \frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+2q+1)}{4\delta _x^2}:={\tilde{c}}_q, \end{aligned}$$

where $\delta _x:=\rho (x,\partial D)$ denotes the Riemannian distance of x to the boundary $\partial D$.

Proof

Take

$$\begin{aligned} f(y)=\sin {\left( \frac{\pi \rho (y,\partial D)}{2}\right) },\quad y\in B(x,\delta _x). \end{aligned}$$

This choice of f clearly satisfies the conditions and furthermore,

$$\begin{aligned} |\nabla f|\le \frac{\pi }{2\delta _x}. \end{aligned}$$

(3.8)

By the Laplacian comparison theorem, we have

$$\begin{aligned} -\Delta f\le \frac{\pi }{2\delta _x}\sqrt{(n-1)K_0^-}+\frac{\pi ^2 n}{4\delta _x^2} \end{aligned}$$

which together with (3.8) gives the claimed estimates on ${\tilde{c}}_q(f),c_1(f), c_2(f)$ and $c_3(f)$. $\square$

The following lemma is taken from [6, Lemma 2.2] or [17] with a trivial modification.

Lemma 3.4

Suppose with $f >0$ and $f \le 1$ on D, $f(x)=1$, $f\vert _{\partial D} = 0$ and set ${\tilde{c}}_q(f)$ as in (3.7) for $q\ge 1$. Then there exists a bounded adapted process k with paths in the Cameron-Martin space $L^{1,2q}([0,t];{\mathbb {R}})$ for some $q\in [1,\infty )$ such that $k(0)=1$, $k(s)=0$ for $s\ge t\wedge \tau _D$ and

$$\begin{aligned} {\mathbb {E}}\left[ \int _0^{t\wedge \tau _D}|{\dot{k}}(s)|^{2q}\,ds\right] \le \frac{{\tilde{c}}_q(f)}{1-{\text {e}}^{-{\tilde{c}}_q(f)t}}, \end{aligned}$$

where ${\tilde{c}}_q$ is defined in Lemma 3.3.

3.2 Estimate for the Hessian of a harmonic function

In this subsection we focus on explicit Hessian estimates for harmonic functions defined on regular domains in Riemannian manifolds.

Theorem 3.5

Let $D\subset M$ be a regular domain. For $x\in D$, let $\delta _x=\rho (x,\partial D)$ be the Riemannian distance of x to the boundary of D. For a bounded positive harmonic function u on D, one has

(3.9)

(3.10)

where $K_0$, $K_1$ and $K_2$ are defined as in (2.10)–(2.12).

Proof of Theorem 3.5 (Part I)

We fix $x\in D$ and denote by $B=B(x,\delta _x)$ the open ball about x of radius $\delta _x$. Then Theorem 3.1 applies with B now playing the role of D. First, by formula (3.1) and the Cauchy inequality, we get

$$\begin{aligned}&\big |({{\text {Hess}}}\,u)_x(v,v)\big |=\lim _{t\rightarrow \infty }\big |({{\text {Hess}}}\, P^D_tu)_x (v,v)\big |\nonumber \\&\quad \le \left| {\mathbb {E}}^x\left[ u(X_{\tau _D}(x))\int _0^{\tau _D}\langle W^k_s(v,{\dot{k}}(s)v), /\!/_s d B_s\rangle \right] \,\right| \nonumber \\&\quad +2\left| {\mathbb {E}}^x\left[ u(X_{\tau _D}(x))\int _0^{\tau _D}\left( \int _0^{s}\langle Q_r({\dot{k}}(r)v), /\!/_r d B_r\rangle \right) \langle Q_s({\dot{k}}(s)v), /\!/_s d B_s\rangle \right] \,\right| \nonumber \\&\quad \le \sqrt{\Vert u\Vert _D\,u(x)}\sqrt{\lim _{t\rightarrow \infty }{\mathbb {E}}^x\left[ \int _0^{\tau (t)}|W^k_s(v,v)|^2{\dot{k}}(s)^2\,ds\right] }\nonumber \\&\quad +2\sqrt{\Vert u\Vert _D\,u(x)}\sqrt{\lim _{t\rightarrow \infty }{\mathbb {E}}^x\left[ \int _0^{\tau (t)} \left( \int _0^{s}\langle Q_r({\dot{k}}(r)v), /\!/_r d B_r\rangle \right) ^2 | Q_s({\dot{k}}(s)v)|^2 \,ds\right] } :=\text {I}+\text {II}, \end{aligned}$$

(3.11)

where the stopping time $\tau (t)$ is defined by (3.3). For the first term I, according to the relation between $\tau (t)$ and f, we can estimate as

$$\begin{aligned} {\mathbb {E}}^x&\left[ \int _0^{\tau (t)}|W^k_s(v,v)|^2{\dot{k}}(s)^2\,ds\right] \le {\mathbb {E}}^x\left[ \int _0^{\tau (t)}|W^k_s(v,v)|^2{\dot{k}}(s)^2\,ds\right] \nonumber \\&\le {\mathbb {E}}^x\left[ \int _0^{\tau (t)}|W^k_s(v,v)|^2{\dot{h}}_1(h_0(s))^2 f^{-4}(X_{s})\,ds\right] \nonumber \\&={\mathbb {E}}^x\left[ \int _0^{t}|W^k_{\tau (s)}(v,v)|^2{\dot{h}}_1(s)^2 f^{-4}(X_{\tau (s)})\,d\tau (s)\right] \nonumber \\&=\int _0^{t}{\dot{h}}_1(s)^2{\mathbb {E}}^x\big [|W^k_{\tau (s)}(v,v)|^2 f^{-2}(X_{\tau (s)})\big ]\,ds. \end{aligned}$$

(3.12)

For the second term II, we find

$$\begin{aligned}&{\mathbb {E}}^x\left[ \int _0^{\tau (t)} \left( \int _0^{s}\langle Q_r({\dot{k}}(r)v), /\!/_r d B_r\rangle \right) ^2 | Q_s({\dot{k}}(s)v)|^2 \,ds\right] \\&\quad \le {\mathbb {E}}^x\left[ \int _0^{t}{\dot{h}}_1(s)^2f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{\tau (s)}\langle Q_r({\dot{k}}(r)v), /\!/_r d B_r\rangle \right) ^2 ds\right] . \end{aligned}$$

Substituting these estimates back into (3.11) yields

$$\begin{aligned}&\big |({{\text {Hess}}}\,u)_x(v,v)\big | \le \sqrt{\Vert u\Vert _D\,u(x)}\sqrt{\lim _{t\rightarrow \infty }\int _0^{t}{\dot{h}}_1(s)^2\,{\mathbb {E}}^x\big [|W^k_{\tau (s)}(v,v)|^2f^{-2}(X_{\tau (s)})\big ]\,ds}\nonumber \\&\quad +2\sqrt{\Vert u\Vert _D\,u(x)}\sqrt{\lim _{t\rightarrow \infty }\int _0^{t}{\dot{h}}_1(s)^2\,{\mathbb {E}}^x\left[ f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{\tau (s)}\langle Q_r({\dot{k}}(r)v), /\!/_r d B_r\rangle \right) ^2\right] \,ds}. \end{aligned}$$

(3.13)

Let

$$\begin{aligned}&\Phi _1(s):={\mathbb {E}}^x\big [|W^k_{\tau (s)}(v,v)|^2f^{-2}(X_{\tau (s)})\big ]; \\&\Phi _2(s):={\mathbb {E}}^x\left[ f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{\tau (s)}\langle Q_r({\dot{k}}(r)v), /\!/_r d B_r\rangle \right) ^2\right] . \end{aligned}$$

Itô’s formula gives

$$\begin{aligned} d&\left( f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\right) \\&=-2f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\langle \nabla f(X_{\tau (s)}), /\!/_{\tau (s)}\,dB_s \rangle \\&\quad +(3|\nabla f|^2-f\Delta f)f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\,ds\\&\quad +f^{-2}(X_{\tau (s)})\,d|W^k_{\tau (s)}(v,v)|^2\\&\quad + 2f^{-1}(X_{\tau (s)})\,\langle R(\nabla f, Q_{\tau (s)}(k(\tau (s))v))Q_{\tau (s)}(v),W^k_{\tau (s)}(v,v)\rangle \,ds. \end{aligned}$$

According to the definition of $W^k_s$, we thus obtain

$$\begin{aligned} d&\left( f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\right) \\&=-2f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\langle \nabla f(X_{\tau (s)}), /\!/_{\tau (s)} dB_s \rangle \\&\quad +2f^{-1}(X_{\tau (s)})\langle R(/\!/_{\tau (s)}\,dB_s,Q_{\tau (s)}(k(\tau (s))v))Q_{\tau (s)}(v), W^k_{\tau (s)}(v,v) \rangle \\&\quad +(3|\nabla f|^2-f\Delta f)(X_{\tau (s)})f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\,ds\\&\quad + 2f^{-1}(X_{\tau (s)})\langle R(\nabla f, Q_{\tau (s)}(k(\tau (s))v))Q_{\tau (s)}(v),W^k_{\tau (s)}(v,v)\rangle \,ds\\&\quad +|R^{\sharp , \sharp }(Q_{\tau (s)}(k(\tau (s))v),Q_{\tau (s)}v)|_{\tiny {\text {HS}}}^2\,ds\\&\quad -\langle (\mathbf{d}^*R+\nabla \mathrm{Ric}^\sharp )(Q_{\tau (s)}(k(\tau (s))v), Q_{\tau (s)}(v)), W^k_{\tau (s)}(v,v) \rangle \,ds\\&\quad -\mathrm{Ric}(W^k_{\tau (s)}(v,v),W^k_{\tau (s)}(v,v))\,ds. \end{aligned}$$

Since all geometric quantities are bounded on D and $|Q_{\tau (s)}|\le \exp \big (-\frac{1}{2}K_0\tau (s)\big )$, we have

$$\begin{aligned} d&\left( f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\right) \\&\overset{\tiny {\text {m}}}{\le } \big (3|\nabla f|^2-f\Delta f\big )(X_{\tau (s)})f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\,ds\\&\quad +2|R|(X_{\tau (s)}) {\text {e}}^{-K_0\tau (s)}|W^k_{\tau (s)}(v,v)|\, |\nabla f|(X_{\tau (s)})f^{-1}(X_{\tau (s)})\,ds\\&\quad +|R|^2(X_{\tau (s)}){\text {e}}^{-2K_0\tau (s)}\,ds\\&\quad +K_2{\text {e}}^{-K_0\tau (s)}|W^k_{\tau (s)}(v,v)|\,ds-K_0|W^k_{\tau (s)}(v,v)|^2\,ds. \end{aligned}$$

For any $\delta _1>0$ and $\delta _2>0$, it thus follows that

$$\begin{aligned} d&\left( f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\right) \\&\quad \overset{\tiny {\text {m}}}{\le } \left( 3|\nabla f|^2-f\Delta f\right) (X_{\tau (s)})f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\,ds\\&\qquad +(\delta _1+1)K_1^2 {\text {e}}^{-2K_0\tau (s)}\,ds+\frac{1}{\delta _1}|W^k_{\tau (s)}(v,v)|^2\, |\nabla f|^2(X_{\tau (s)})f^{-2}(X_{\tau (s)})\,ds\\&\qquad +\frac{\delta _2}{2}K_2^2{\text {e}}^{-2K_0\tau (s)}\,ds+\left( \frac{1}{2\delta _2}-K_0\right) |W^k_{\tau (s)}(v,v)|^2\,ds\\&\quad =\left[ \left( \frac{1}{2\delta _2}-K_0\right) f^2+\left( 3+\frac{1}{\delta _1}\right) |\nabla f|^2-f\Delta f\right] f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\,ds\\&\qquad +\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) {\text {e}}^{-2K_0\tau (s)}\,ds\\&\quad \le c_1(f)f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\,ds+\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) {\text {e}}^{-2K_0\tau (s)}\,ds, \end{aligned}$$

where

$$\begin{aligned} c_1(f):=\sup _D\left\{ \left( \frac{1}{2\delta _2}+K_0^-\right) f^2+\left( 3+\frac{1}{\delta _1}\right) |\nabla f|^2-(f\Delta f)\right\} . \end{aligned}$$

This implies

$$\begin{aligned}&d\left( {\text {e}}^{-c_1(f) s}f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2 \right) \\&\quad \overset{\tiny {\text {m}}}{\le } \left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) {\text {e}}^{-c_1(f) s}{\text {e}}^{-2K_0\tau (s)}\,ds\\&\quad \le \left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) {\text {e}}^{(2K_0^--c_1(f)) s}\,ds. \end{aligned}$$

By integrating from 0 to s and taking expectations, we then arrive at

$$\begin{aligned} \Phi _1(s)= & {} {\mathbb {E}}^x\left[ f^{-2}(X_{\tau (s)})|W^k_{\tau (s)}(v,v)|^2\right] \nonumber \\\le & {} \left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) {\text {e}}^{c_1(f)s} \int _0^s{\text {e}}^{(2K_0^--c_1(f)) r}\,dr. \end{aligned}$$

(3.14)

On the other hand, concerning $\Phi _2$, we first observe

$$\begin{aligned}&d \left( f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{\tau (s)}\langle Q_u({\dot{k}}(u)v),/\!/_ud B_u \rangle \right) ^2\right) \\&\quad =d \bigg [f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)}(v),/\!/_{\tau (u)}d B_u \rangle \right) ^2\bigg ]\\&\qquad \overset{\mathrm{m}}{=}{\text {e}}^{-K_0 \tau (s)} \dot{h}_{1} (s)^{2} f^{{ - 4}} (X_{{\tau (s)}} ){} \langle Q_{{\tau (s)}} (v),Q_{{\tau (s)}} (v)\rangle {} ds\\&\qquad -K_0{\text {e}}^{-K_0\tau (s)}\left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)} (v), /\!/_{\tau (u)}dB_{u} \rangle \right) ^2\,ds\\&\qquad -4{\text {e}}^{-K_0\tau (s)}f^{-3}(X_{\tau (s)})\int _0^s{\dot{h}}_1(u)f^{-1}(X_{\tau (u)}) \langle Q_{\tau (u)}(v), /\!/_{\tau (u)}dB_u\rangle \,{\dot{h}}_1(s)\,\\&\qquad \times \langle \nabla f(X_{\tau (s)}), Q_{\tau (s)}(v) \rangle ds+(3|\nabla f|^2-f\Delta f)(X_{\tau (s)})f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\\&\qquad \times \left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)} (v), /\!/_{\tau (u)}dB_{u} \rangle \right) ^2 ds\\&\quad \le {\text {e}}^{-2K_0 \tau (s)}{\dot{h}}_1(s)^2 f^{-4}(X_{\tau (s)}) \,ds\\&\qquad -K_0{\text {e}}^{-K_0\tau (s)}\left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)} (v), /\!/_{\tau (u)}dB_{u} \rangle \right) ^2\,ds\\&\qquad +2 f^{-2}(X_{\tau (s)})|\nabla f|^2(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^s{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)}(v), /\!/_{\tau (u)}dB_u\rangle \right) ^2 ds\\&\qquad +2 {\text {e}}^{-2K_0\tau (s)}{\dot{h}}_1(s)^2 f^{-4}(X_{\tau (s)}) ds +(3|\nabla f|^2-f\Delta f)(X_{\tau (s)})f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\\&\qquad \times \left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)} (v), /\!/_{\tau (u)}dB_{u} \rangle \right) ^2 ds \end{aligned}$$

and conclude

$$\begin{aligned}&d \left( f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)}(v),/\!/_{\tau (u)}d B_u \rangle \right) ^2\right) \\&\quad \overset{\tiny {\text {m}}}{\le } 3{\text {e}}^{-2K_0 \tau (s)}{\dot{h}}_1(s)^2 f^{-4}(X_{\tau (s)}) \,ds\\&\quad +\left( -K_0f^2+5|\nabla f|^2-f\Delta f\right) (X_{\tau (s)})f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\\&\qquad \bigg (\int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)} (v), /\!/_{\tau (u)}dB_{u} \rangle \bigg )^2 ds\\&\quad \le 3{\text {e}}^{-2K_0 \tau (s)}{\dot{h}}_1(s)^2 f^{-4}(X_{\tau (s)}) \,ds\\&\quad +c_2(f)f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)} \bigg (\int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)} (v), /\!/_{\tau (u)}dB_{u} \rangle \bigg )^2 ds, \end{aligned}$$

where $c_2(f)$ is defined in (3.5). Integrating the above inequality from 0 to s then yields

$$\begin{aligned}&{\mathbb {E}}^x\left[ f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)}(v),/\!/_{\tau (u)}d B_u \rangle \right) ^2\right] \nonumber \\&\quad \le 3{\text {e}}^{c_2(f)s}\int _0^s{\text {e}}^{-c_2(f)u}{\dot{h}}_1(u)^2{\mathbb {E}}^x\left[ {\text {e}}^{-2K_0\tau (u)} f^{-4}(X_{\tau (u)})\right] \,du. \end{aligned}$$

(3.15)

Hence it remains to estimate the term ${\mathbb {E}}^x\left[ {\text {e}}^{-2K_0\tau (u)} f^{-4}(X_{\tau (u)})\right]$. By Itô’s formula, we have

$$\begin{aligned} d&\left( {\text {e}}^{-2K_0\tau (u)}f^{-4}(X_{\tau (u)})\right) \\&\overset{m}{=} -2K_0{\text {e}}^{-2K_0\tau (u)}f^{-2}(X_{\tau (u)})\,du +(-2f\Delta f+10|\nabla f|^2)(X_{\tau (u)}) {\text {e}}^{-2K_0 \tau (u)}f^{-4}(X_{\tau (u)})\,du\\&\le 2 c_2(f){\text {e}}^{-2K_0\tau (u)}f^{-4}(X_{\tau (u)})\,du \end{aligned}$$

which implies

$$\begin{aligned} {\mathbb {E}}^x\left[ {\text {e}}^{-2K_0\tau (u)}f^{-4}(X_{\tau (u)})\right] \le f^{-4}(x){\text {e}}^{2c_2(f)u}. \end{aligned}$$

Substituting this estimate into (3.15) leads to

$$\begin{aligned} \Phi _2(s)&={\mathbb {E}}^x\left[ f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)}(v),/\!/_{\tau (u)}d B_u \rangle \right) ^2\right] \\&\le 3f^{-4}(x){\text {e}}^{c_2(f)s}\int _0^s{\dot{h}}_1(u)^2{\text {e}}^{-c_2(f)u}{\text {e}}^{2c_2(f)u}\,du\\&\le 3f^{-4}(x){\text {e}}^{c_2(f)s}\int _0^s{\dot{h}}_1(u)^2 {\text {e}}^{c_2(f)u}\,du. \end{aligned}$$

By means of this inequality we can estimate the second integral on the right-hand side of (3.13) to obtain

$$\begin{aligned}&\int _0^t {\dot{h}}_1(s)^2 {\mathbb {E}}^x\bigg [f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\left( \int _0^{s}{\dot{h}}_1(u)f^{-1}(X_{\tau (u)})\langle Q_{\tau (u)}(v),/\!/_{\tau (u)}d B_u \rangle \right) ^2\bigg ]\,ds\\&\quad \le 3f^{-4}(x)\int _0^t{\dot{h}}_1(s)^2{\text {e}}^{c_2(f)s}\int _0^s{\dot{h}}_1(u)^2 {\text {e}}^{c_2(f)u}\,du ds\\&\quad =\frac{3}{2}f^{-4}(x) \left( \int _0^t{\dot{h}}_1(s)^2{\text {e}}^{c_2(f)s}\,ds\right) ^2. \end{aligned}$$

Combining this estimate and inequality (3.14) with inequality (3.13) yields

$$\begin{aligned}&\big |({{\text {Hess}}}\,u)_x(v,v)\big |\\&\quad \le \sqrt{\Vert u\Vert _D\,u(x)}\sqrt{\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) \,\lim _{t\rightarrow \infty }\int _0^{t}{\dot{h}}_1(s)^2 {\text {e}}^{c_1(f)s}\int _0^s{\text {e}}^{(2K_0^--c_1(f)) r}\,dr\,ds}\\&\qquad +2f^{-2}(x)\sqrt{\Vert u\Vert _D\,u(x)}\sqrt{3\lim _{t\rightarrow \infty }\int _0^{t}{\dot{h}}_1(s)^2{\text {e}}^{c_2(f)s}\int _0^s{\dot{h}}_1(u)^2 {\text {e}}^{c_2(f)u}\,du\,ds}\\&\quad \le \sqrt{\Vert u\Vert _D\,u(x)}\sqrt{\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) \,\lim _{t\rightarrow \infty }\int _0^{t}{\dot{h}}_1(s)^2 {\text {e}}^{c_1(f)s}\int _0^s{\text {e}}^{(2K_0^--c_1(f)) r}\,dr\,ds}\\&\qquad +\sqrt{6}f^{-2}(x)\sqrt{\Vert u\Vert _D\,u(x)}\,\lim _{t\rightarrow \infty }\bigg (\int _0^{t}{\dot{h}}_1(s)^2{\text {e}}^{c_2(f)s}\,ds\bigg ). \end{aligned}$$

It now suffices to choose a suitable function $h_1$. By Lemma 3.3, we have

$$\begin{aligned}&{\text {e}}^{c_1(f)s}\int _0^s{\text {e}}^{(2K_0^--c_1(f)) r}\,dr\le {\text {e}}^{c_1s}\int _0^s{\text {e}}^{(2K_0^--c_1) r}\,dr\le {\text {e}}^{(c_1+2K_0^-)s}\int _0^s{\text {e}}^{-c_1 r}\,dr \\&\quad \le \frac{{\text {e}}^{(c_1+2K_0^-)s}}{c_1}. \end{aligned}$$

We define

$$\begin{aligned} h_1(s)=\frac{\int _0^s{\text {e}}^{-(c_1+2K^-_0)r}\,dr}{\int _0^t{\text {e}}^{-(c_1+2K^-_0)r}\,dr}. \end{aligned}$$

If $\delta _1\le \frac{1}{2}$, then it is easy to see that $c_2(f)\le c_2\le c_1$ and $c_1\ge K_0^-$,

$$\begin{aligned}&|({{\text {Hess}}}\,u)_x(v,v)| \le \sqrt{\Vert u\Vert _D\,u(x)}\sqrt{\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) \frac{c_1+2K_0^-}{c_1}}\\&\quad +f^{-2}(x)\sqrt{6\Vert u\Vert _D\,u(x)}(c_1+2K_0^-)\\&\quad \le \sqrt{\Vert u\Vert _D\,u(x)}\sqrt{(1+2{1}_{K_0\ne 0})\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) }\\&\quad +\sqrt{6\Vert u\Vert _D\,u(x)}\,\left( (2\delta _2)^{-1}+3K_0^-+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+3+\delta _1^{-1})}{4\delta _x^2}\right) \end{aligned}$$

for $0<\delta _1\le \frac{1}{2}$ and $\delta _2>0$. We complete the proof of inequality (3.9) by taking the infimum with respect to $\delta _1$ and $\delta _2$. $\square$

Proof of Theorem 3.5 (Part II)

Theorem 3.1 allows to control $|{{\text {Hess}}}\,u(v,v)|$ directly in terms of $\Vert u\Vert _D$ as follows:

$$\begin{aligned} |({{\text {Hess}}}\,u)_x(v,v)|&=\lim _{t\rightarrow \infty }|({{\text {Hess}}}\,P^D_tu)_x(v,v)|\nonumber \\&\le \Vert u\Vert _D\sqrt{{\mathbb {E}}^x\left[ \lim _{t\rightarrow \infty }\int _0^{\tau (t)}|W_s^k(v,v)|^2\,{\dot{k}}(s)^2\,ds\right] }\nonumber \\&\quad +2\Vert u\Vert _D\,{\mathbb {E}}^x\left[ \lim _{t\rightarrow \infty }\int _0^{\tau (t)}\Vert Q_s\Vert ^2\,{\dot{k}}(s)^2\,ds\right] \nonumber \\&\le \Vert u\Vert _D\sqrt{{\mathbb {E}}^x\left[ \lim _{t\rightarrow \infty }\int _0^{\tau (t)}|W_s^k(v,v)|^2\,{\dot{k}}(s)^2\,ds\right] }\nonumber \\&\quad +2\Vert u\Vert _D\,{\mathbb {E}}^x\left[ \lim _{t\rightarrow \infty }\int _0^{\tau (t)}{\text {e}}^{-K_0s}{\dot{k}}(s)^2\,ds\right] =\mathrm{I}+\mathrm{II}. \end{aligned}$$

(3.16)

For the second term $\mathrm{II}$ we observe

$$\begin{aligned} {\mathbb {E}}^x\left[ \int _0^{\tau (t)}{\text {e}}^{-K_0s}{\dot{k}}(s)^2\,ds\right] =\int _0^{t}{\dot{h}}_1(s)^2{\mathbb {E}}^x\big [{\text {e}}^{-K_0\tau (s)}f^{-2}(X_{\tau (s)})\big ]\,ds; \end{aligned}$$

the first term has been dealt with in (3.12) above. We conclude from (3.16) that

$$\begin{aligned} \big |({{\text {Hess}}}\,u)_x(v,v)\big |&\le \Vert u\Vert _D\sqrt{\lim _{t\rightarrow \infty }\int _0^{t}{\dot{h}}_1(s)^2\,{\mathbb {E}}^x\left[ |W^k_{\tau (s)}(v,v)|^2f^{-2}(X_{\tau (s)})\right] \,ds}\\&\quad +2\Vert u\Vert _D\,\lim _{t\rightarrow \infty }\int _0^{t}{\dot{h}}_1(s)^2\,{\mathbb {E}}^x\big [{\text {e}}^{-K_0\tau (s)}f^{-2}(X_{\tau (s)})\big ]\,ds. \end{aligned}$$

Recall that by Lemma 3.3,

$$\begin{aligned} c_3(f)&=\sup _D\left\{ K_0^-f^2+3|\nabla f|^2-(f\Delta f)\right\} \\&\le K_0^-+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+3)}{4\delta _x^2}=:c_3<c_1. \end{aligned}$$

Thus

$$\begin{aligned} {\mathbb {E}}^x\big [f^{-2}(X_{\tau (s)}){\text {e}}^{-K_0\tau (s)}\big ]\le f^{-2}(x){\text {e}}^{c_3(f)s}\le {\text {e}}^{c_3s}, \end{aligned}$$

and hence

$$\begin{aligned} \big |({{\text {Hess}}}\,u)_x(v,v)\big |&\le \sqrt{\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) \left( \int _0^{t}{\dot{h}}_1(s)^2 {\text {e}}^{c_1s}\int _0^s{\text {e}}^{(2K_0^--c_1) r}\,dr\,ds\right) }\,\Vert u\Vert _D\nonumber \\&\qquad +2\left( \int _0^{t}{\dot{h}}_1(s)^2 {\text {e}}^{c_3s}\,ds\right) \Vert u\Vert _D. \end{aligned}$$

(3.17)

Define

$$\begin{aligned} h_1(s)=\frac{\int _0^s{\text {e}}^{-(c_1+2K_0^-)r}\,dr}{\int _0^t{\text {e}}^{-(c_1+ 2K_0^-)r}\,dr}, \end{aligned}$$

so that

$$\begin{aligned} {\dot{h}}_1(s)=\frac{{\text {e}}^{-(c_1+2K_0^-)s}}{\int _0^t{\text {e}}^{-(c_1+ 2K_0^-)r}dr}. \end{aligned}$$

The estimate

$$\begin{aligned} {\text {e}}^{c_1s}\int _0^s{\text {e}}^{(2K_0^--c_1) r}\,dr\le {\text {e}}^{(c_1+2K_0^-)s}\int _0^s{\text {e}}^{-c_1 r}\,dr \le \frac{{\text {e}}^{(c_1+2K_0^-)s}}{c_1} \end{aligned}$$

is immediate. Since $c_3(f)\le c_3\le c_1$, we have

$$\begin{aligned} \int _0^t \frac{{\text {e}}^{-2(c_1+2K_0^-)s}{\text {e}}^{c_3s}}{\left( \int _0^t{\text {e}}^{-(c_1+ 2K_0^-)r}dr\right) ^2} \,ds&\le \int _0^t \frac{{\text {e}}^{-(c_1+2K_0^-)s}}{\left( \int _0^t{\text {e}}^{-(c_1+ 2K_0^-)r}dr\right) ^2} \,ds\\&\le \frac{1}{\int _0^t{\text {e}}^{-(c_1+ 2K_0^-)r}dr}= \frac{c_1+ 2K_0^-}{1-{\text {e}}^{-(c_1+ 2K_0^-)t}}. \end{aligned}$$

Using these estimates to bound (3.17) from above and letting t tend to $\infty$, we deduce

$$\begin{aligned} |({{\text {Hess}}}\,u)_x(v,v)|&\le \sqrt{\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) \left( \frac{c_1+2K_0^-}{c_1}\right) }\,\Vert u\Vert _D+2\left( c_1+2K_0^-\right) \Vert u\Vert _D\\&\le \sqrt{(1+2\mathbf {1}_{\{K_0^-\ne 0\}})\left( (\delta _1+1)K_1^2+\frac{\delta _2}{2}K_2^2\right) }\,\Vert u\Vert _D\\&\quad +2\left( (2\delta _2)^{-1}+3K_0^-+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+3+\delta _1^{-1})}{4\delta _x^2}\right) {\Vert u\Vert _D} \end{aligned}$$

for $\delta _1>0$ and $\delta _2>0$. This completes the proof of inequality (3.10). $\square$

4 Estimate of the Hessian of the semigroup

We are now going to apply our results to give explicit local Hessian estimates for the heat semigroup on a Riemannian manifold.

Remark 4.1

Local Hessian estimates for the semigroup have been derived in [12, Section 4.2] by using the Hessian formula in [2]. We can improve these results significantly by clarifying the coefficients.

Theorem 4.2

Let $x\in M$ and D be a relatively compact open domain such that $x\in D$. Then for $f\in {\mathcal {B}}_b(M)$,

$$\begin{aligned} |{{\text {Hess}}}P_Tf|(x)&\le \inf _{\delta >0}\left\{ \left( \frac{T}{2}\sqrt{ K_1^2+\frac{K_2^2}{\delta }}+\frac{2}{ T}\right) \right. \\&\quad \left. \exp \left( T\left( K_0^-+ \frac{\delta }{2}+\frac{\pi \sqrt{(n-1)K^-_0}}{2 \delta _x} + \frac{\pi ^2 (n+3)}{4\delta _x^2}\right) \right) \right\} \Vert f\Vert _{D}. \end{aligned}$$

Proof

By Theorem 2.3 and Cauchy’s inequality, we have

$$\begin{aligned} \big |({{\text {Hess}}}{P_Tf})_x(v,v)\big |&\le \Vert f\Vert _{D}\left( {\mathbb {E}}^x\left[ \int _0^T|W^k_s(v,{\dot{k}}(s)v)|^2\,ds\right] \right) ^{1/2}\nonumber \\&\quad +2\Vert f\Vert _{D}\left( {\mathbb {E}}^x\int _0^T|Q_s({\dot{k}}(s)v)|^2\, ds\right) \nonumber \\&\le \Vert f\Vert _D\sqrt{{\mathbb {E}}^x\left[ \int _0^{\tau (T)}|W^k_s(v,v)|^2\,{\dot{k}}(s)^2\,ds\right] }\nonumber \\&\quad +2\Vert f\Vert _D\,{\mathbb {E}}^x\left[ \int _0^{\tau (T)}|Q_s|^2\,{\dot{k}}(s)^2\, ds\right] =\mathrm{I}+\mathrm{II}. \end{aligned}$$

(4.1)

Using a similar argument as in the proof of Theorem 3.5 (Part II) and Lemma 2.2, we obtain

$$\begin{aligned} \big |(&{{\text {Hess}}}{P_Tf})_x(v,v)\big |\\&\le \Vert f\Vert _{D} \left( \frac{(2p-1) ^{p}K_1^{2p}}{2\delta ^{p-1}}+\frac{K_2^{2p}}{2\delta ^{2p-1} }\right) ^{1/(2p)}{\text {e}}^{(K_0^-+\frac{1}{2}\delta )T}T^{1/p}\,\left[ {\mathbb {E}}^x\int _0^T|{\dot{k}}(t)|^{2q}\,dt\right] ^{1/(2q)}\\&\quad +2\Vert f\Vert _{D}\,{\mathbb {E}}^x\left[ \int _0^T{\text {e}}^{-K_0s}{\dot{k}}(s)^2\, ds\right] \\&\le \Vert f\Vert _{D} \left( \frac{(2p-1) ^{p}K_1^{2p}}{2^2\delta ^{p-1}}+\frac{K_2^{2p}}{2^2\delta ^{2p-1} }\right) ^{1/(2p)}{\text {e}}^{\big (K_0^-+\frac{1}{2}\delta +\frac{{\tilde{c}}_q}{2q}\big )T}T^{3/(2p)-1/2}\\&\quad +\Vert f\Vert _{D}{\text {e}}^{(K_0^-+{\tilde{c}}_1)T}\frac{2}{T}\\&\le \Vert f\Vert _{D} \left( \frac{(2p-1) ^{p}K_1^{2p}}{2^2\delta ^{p-1}}+\frac{K_2^{2p}}{2^2\delta ^{2p-1} }\right) ^{1/(2p)}{\text {e}}^{\big (K_0^-+\frac{1}{2}\delta +\frac{{\tilde{c}}_1}{2}\big )T}T^{(3-p)/2p}\\&\quad +\Vert f\Vert _{D}{\text {e}}^{(K_0^-+{\tilde{c}}_1)T}\frac{2}{T} \end{aligned}$$

for any $\delta >0$. We complete the proof by substituting ${\tilde{c}}_1$ defined in Lemma 2.2 into the above inequality and letting $p \rightarrow 1$. $\square$

For global results (i.e. the case $D=M$), if M is compact, Theorem 2.3 holds with $\tau \equiv \infty$ and the Cameron-Martin valued process k can be chosen deterministic and linear, which leads immediately to straightforward estimates. If the manifold is non-compact, ${{\text {Ric}}}\ge K_0$, $\Vert R\Vert _{\infty }:=\sup _{x\in M}|R|(x)<\infty$ and

$$\begin{aligned}&K_2:=\sup \left\{ |(\mathbf{d}^* R+\nabla {{\text {Ric}}})^{\sharp }(v,v)|:\in T_xM,\ x\in M,\ |v|=1\right\} <\infty , \end{aligned}$$

then Theorem 4.2 still holds when replacing D by M and letting $\delta _x\rightarrow \infty$. In the following, we use a different argument by choosing $k\in C^1([0,T])$ such that $k(0)=0$ and $k(T)=1$ and estimating ${\mathbb {E}}^x|W^k_s(v,v)|^2$.

Corollary 4.3

Let M be a complete Riemannian manifold. Assume ${{\text {Ric}}}\ge K_0$ and $K_1:=\Vert R\Vert _{\infty }<\infty$,

$$\begin{aligned}&K_2=\sup \left\{ |(\mathbf{d}^* R+\nabla {{\text {Ric}}})^{\sharp }(v,v)|:\in T_xM,\ |v|=1\right\} <\infty . \end{aligned}$$

Then,

$$\begin{aligned} |{{\text {Hess}}}P_Tf| \le \left( \left( \frac{K_1^2}{2}+\frac{K_2^2}{2\delta }\right) ^{1/2}+\frac{2}{T}\right) \exp \left( \left( K_0^-+ \frac{1}{2}\delta \right) T\right) \Vert f\Vert _{\infty } \end{aligned}$$

(4.2)

for $\delta >0$. Moreover, if the manifold M is Ricci parallel, i.e. $\nabla {{\text {Ric}}}=0$, then

$$\begin{aligned} |{{\text {Hess}}}P_Tf| \le \left( \frac{K_1}{\sqrt{2}}+\frac{2}{T}\right) {\text {e}}^{K_0^-T}\Vert f\Vert _{\infty }. \end{aligned}$$

(4.3)

Proof

From (4.1), we know that for $k\in C^1([0,T])$ such that $k(0)=0$ and $k(T)=1$,

$$\begin{aligned} \big |({{\text {Hess}}}{P_Tf})_x(v,v)\big |&\le \Vert f\Vert _{\infty }\left( \int _0^{T}{\mathbb {E}}^x|W^k_s(v,v)|^2\,{\dot{k}}(s)^2\,ds\right) ^{1/2}\\&\quad +2\Vert f\Vert _{\infty }\,{\mathbb {E}}^x\left[ \int _0^{T}|Q_s|^2\,{\dot{k}}(s)^2\, ds\right] . \end{aligned}$$

If we choose $k(s)=(T-s)/T$, then it follows from (2.14) that

$$\begin{aligned} \big |({{\text {Hess}}}{P_Tf})_x(v,v)\big |&\le \left( \frac{K_1^2}{2}+\frac{K_2^2}{2\delta }\right) ^{1/2}{\text {e}}^{(K_0^-+\frac{\delta }{2})T}\Vert f\Vert _{\infty }+\frac{2}{T^2}\,{\mathbb {E}}^x\left[ \int _0^{T}|Q_s|^2\, ds\right] \Vert f\Vert _{\infty }\\&\le \left( \left( \frac{K_1^2}{2}+\frac{K_2^2}{2\delta }\right) ^{1/2}+\frac{2}{T}\right) \exp \left( \left( K_0^-+ \frac{1}{2}\delta \right) T\right) \Vert f\Vert _{\infty }. \end{aligned}$$

If the manifold is Ricci parallel, then $\mathbf{d}^* R+\nabla {{\text {Ric}}}=0$ and $\delta$ is not needed in the estimate of ${\mathbb {E}}^x|W_t(v,v)|^2$, see inequality (2.13). Thus, in this case, estimate (4.2) reduces to (4.3). $\square$