Abstract
In this paper, our discussion mainly focuses on equations with energy supercritical nonlinearities. We establish probabilistic global well-posedness (GWP) results for the cubic Schrödinger equation with any fractional power of the Laplacian in all dimensions. We consider both low and high regularities in the radial setting, in dimension \(\ge 2\). In the high regularity result, an Inviscid - Infinite dimensional (IID) limit is employed while in the low regularity global well-posedness result, we make use of the Skorokhod representation theorem. The IID limit is presented in details as an independent approach that applies to a wide range of Hamiltonian PDEs. Moreover we discuss the adaptation to the periodic settings, in any dimension, for smooth regularities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this work, we consider the initial value problem of the cubic fractional nonlinear Schrödinger equation (FNLS)
on both the \(d-\)dimensional torus \({\mathbb {T}}^d\), \(d\ge 1\), and the unit ball \(B^d\), \(d\ge 2\), supplemented with a radial assumption and a Dirichlet boundary condition
Here \(\sigma \in (0,1]\). When \(\sigma =1\) we have the standard Schrödinger equation. The FNLS equation satisfies the following conservation laws referred as the mass and the energy
It also enjoys the scaling invariance given by
Consequently, its critical regularity is given by the Sobolev space \(H^{s_c}\) where
Data of regularity weaker than \(s_c\) (resp. stronger than \(s_c\)) are called supercritical (resp. subcritical). The equation is called energy-supercritical (resp. energy-criticical, energy-subcritical) if \(s_c>\sigma \) (resp. \(s_c=\sigma \), \(s_c<\sigma \)); that is, \(\sigma <\frac{d}{4}\) (resp. \(\sigma =\frac{d}{4}\), \(\sigma >\frac{d}{4}\)). Since \(\sigma \in (0,1)\), the cubic FNLS equations have energy-supercritical ranges in all dimensions \(d\le 3\), and is fully energy-supercritical in dimensions \(d\ge 4.\) In this paper we address all the scenarios listed above. We construct global solutions by mean of an invariant measure argument and establish long-time dynamics properties.
1.1 Motivation
In recent decades, there has been of great interest in using fractional Laplacians to model physical phenomena. The fractional quantum mechanics was introduced by Laskin [42] as a generalization of the standard quantum mechanics. This generalization operates on the Feynman path integral formulation by replacing the Brownian motion with a general Levy flight. As a consequence, one obtains fractional versions of the fundamental Schrödinger equation. That means the Laplace operator \((-\Delta )\) arising from the Gaussian kernel used in the standard theory is replaced by its fractional powers \((-\Delta )^\sigma \), where \(0<\sigma <1\), as such operators naturally generate Levy flights. Also, it turns out that the equation (1.1) and its discrete versions are relevant in molecular biology as they have been proposed to describe the charge transport between base pairs in the DNA molecule where typical long range interactions occur [46]. The continuum limit for discrete FNLS was studied rigorously first in [36]. See also [27, 28, 33] for recent works on the continuum limits.
The FNLS equation does not enjoy the strong dispersion estimates as the classical NLS does. The bounded domain setting naturally highlights this lack of dispersion. This makes both the well-posedness and the long-time behavior more difficult than the Euclidean setting on one hand, an the classical NLS on the other hand.
The problem of understanding long-time behavior of dispersive equations on bounded domains is widely open. While on Euclidean spaces scattering turns out to apply to most of the defocusing contexts, on bounded domains one does not expect such scattering and there is no well-established general asymptotic theory. It is however expected that solutions would generically exhibit weak turbulenceFootnote 1. See for example [7, 12, 16, 29, 31, 32, 41, 49] and references therein for results in the direction of weak turbulence. A way to detect a weak turbulent behavior is to analyze the higher order Sobolev norms of the solutions and determine whether or not the quantity
is infinite for some s.
In this paper, we prove probabilistic global well-posedness for (1.1) by mean of invariant measures and discuss the long-time behavior by employing ergodic theorems. In particular, we show that a slightly different version of (1.2) remains bounded almost surely with respect to non-trivial invariant measures of FNLS.
1.2 History and related works
Let us briefly present some works related to (1.1). The authors of [21] employed a high-low method, originally due to Bourgain [8], to prove global well-posedness for (1.1) posed on the circle with \(\sigma \in (\frac{1}{2},1)\) below the energy space. Local well-posedness on subcritical and critical regularities and global existence for small data was proved in [23], the authors of [23] established also global well-posedness in the energy space for some powers \(\sigma \) depending on the dimension, see also [30] where a convergence from the fractional Ginzburg-Landau to the FNLS was obtained. FNLS with Hartree type nonlinearity was studied in [13]. On the circle, Gibbs measures were constructed in [50] and the dynamics on full measure sets with respect to these measures was studied. The authors of the present paper proved the deterministic global well-posedness below the energy space for FNLS posed on the unit disc by extending the I-method (introduced by Colliander, Keel, Staffilani, Takaoka and Tao [15]) to the fractional context [55].
1.3 Invariant measure as a tool of globalization
Bourgain [5] performed an ingenious argument based on the invariance of the Gibbs measure of the nonlinear one-dimensional NLS to prove global existence on a rich set of rough data. The Gibbs measure of the one-dimensional NLS is supported on the space \(H^{\frac{1}{2}-}\) and was constructed by Lebowitz, Rose and Speer [44]. The non existence of a conservation law at this level of regularity was a serious issue for the globalization. The method introduced by Bourgain to solve this issue was to derive individual bounds from the the statistical control given by the Fernique theorem. A crucial fact is that these bounds do not depend on the dimension of the Galerkin projections of the equation which are used in the construction of the Gibbs measure. With such estimates, the local solutions of the equation are globalized by an iteration argument based on comparison with the global solutions of the finite-dimensional projections. This is how an invariant measure can play the role of a conservation law. More precisely, we should say how the role played by a conservation law survive through the invariant measure; indeed such quantity are essentially constructed by the use of a conservation laws and can be seen as their statistical duals. This approach is widely exploited in different contexts. For instance, we refer the reader to the papers [6, 9, 11, 22, 56, 57] and references therein.
A second approach based on a fluctuation-dissipation method was introduced by Kuksin [38] in the context of the two-dimensional Euler equation, and developed in the context of the cubic NLS by Kuksin and Shirikyan [39]. This method uses a compactness argument and relies on stochastic analysis with an inviscid limit. The Hamiltonian equation is viewed as a limit as viscosity goes to 0 of an appropriately scaled fluctuation-dissipation equation that enjoys a stationary measure for any given vicosity. By compactness, this family of stationary measures admit at least one accumulation point as the viscosity vanishes, this turns out to be an invariant measure for the limiting equation. The scaling of the fluctuations with respect to the dissipation is such that one obtains estimates not depending on the viscosity. These estimates allow to perform a globalization argument. See [25, 40, 51, 53] for works related to this method.
The two approaches discussed above were developed on various setting. However for energy supercritical equations, both approaches come across serious obstructions. The first author initiated a new approach that combines the two methods and applied it to the energy-supercritical NLS [52], this approach was developed further by the authors in [54]. This approach utilizes a fluctuation-dissipation argument on the Galerkin approximations of the equation, we then have a double approximation: a finite-dimensional one and a viscous one. Two limits are considered in the following order: (i) an inviscid limit to recover the Galerkin projection of the Hamiltonian equation, (ii) then an infinite-dimensional limit to recover the equation itself. In the infinite-dimensional limit, a Bourgain type iteration is used. Overall, different difficulties arise in adapting the Bourgain strategy to a non Gaussian situation. That is why new ingredients were involved. This method is what we refer to Inviscid-Infinite-dimensional limit, or simply the “IID” limit. See also the work [43] for a similar procedure. We perform in Sect. 3 a general and independent version of the IID limit.
1.4 Main results
We set the regularity index for local well-posedness
Once we fix the dimension and the fractional powere in the FNLS equaation, that is \(d\ge 1\) and \(\sigma \in (0,1]\), we define the following interval \(I_g (d,\sigma )\), which is the range of globalization in Theorem 1.1.
where \(I_g^i:=I_g^i(d,\sigma )\), \(i=1,2,3\) are defined as follows
See Remark 1.5 below for a comment on the intervals \(I_g\); it is a result of constraints imposed by the local well-posedness index above and statistical estimations on the dissipation of the energy in Sect. 4.
Theorem 1.1
Let \(\sigma \in (0,1]\) and \(d\ge 2\). Let \(s\in I_g\), and \(\xi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a one-to-one concave function. Then there is a probability measure \(\mu =\mu _{\sigma ,s,\xi ,d}\) and a set \(\Sigma =\Sigma _{\sigma ,s,\xi ,d}\subset H^s_{rad}(B^d)\) such that
-
(1)
\(\mu (\Sigma )=1\);
-
(2)
The cubic FNLS is globally well-posed on \(\Sigma \);
-
(3)
The induced flow \(\phi _t\) leaves the measure \(\mu \) invariant;
-
(4)
We have that
$$\begin{aligned} \int _{L^2}\Vert u\Vert _{H^s}^2\mu (du)<\infty ; \end{aligned}$$(1.5) -
(5)
We have the bound
$$\begin{aligned} \Vert \phi _tu_0\Vert _{H^{s-}}\le C(u_0)\xi (1+\ln (1+|t|))\quad t\in {\mathbb {R}}; \end{aligned}$$(1.6) -
(6)
The set \(\Sigma \) contains data of large size, namely for all \(K>0\), \(\mu (\{\Vert u\Vert _{H^s}>K\})>0\).
Remark 1.2
Notice the strong bound obtained in (1.6). This is to be compared with the bounds obtained in the Gibbs measures context which are of type \(\sqrt{\ln (1+t)}\) (see for instance [5, 56, 56, 57]).
Theorem 1.1 is based on a deterministic local well-posedness. However, for \(\sigma \le \frac{1}{2}\) or \(s\le \frac{d-1}{2}\), we do not have such local well-posedness. We have a different result in this case. Set the probabilistic GWP interval for Theorem 1.3 below:
where
Theorem 1.3
Consider \(\sigma \in (0,1]\) and \(s\in J_g\), let \(d\ge 2\). There is a measure \(\mu =\mu _{\sigma ,s,d}\) and a set \(\Sigma =\Sigma _{\sigma ,s,d}\subset H_{rad}^s(B^d)\) such that
-
(1)
\(\mu (\Sigma )=1\);
-
(2)
The cubic FNLS is globally well-posed on \(\Sigma \);
-
(3)
The induced flow \(\phi _t\) leaves the measure \(\mu \) invariant;
-
(4)
We have that
$$\begin{aligned} \int _{L^2}\Vert u\Vert _{H^s}^2\mu (du)<\infty ; \end{aligned}$$(1.7) -
(5)
The set \(\Sigma \) contains data of large size, namely for all \(K>0\), \(\mu (\{\Vert u\Vert _{H^s}>K\})>0\).
A common corollary to Theorems 1.1 and 1.3 is as follows
Corollary 1.4
For any \(u_0\in \Sigma \), where \(\Sigma \) is any of the sets constructed in Theorems 1.1 and 1.3, there is a sequence of times \(t_k\uparrow \infty \) such that
The corollary above is a direct application of the Poincaré recurrence theorem and describes a valuable asymptotic property of the flow. Another corollary of interest is a consequence of the Birkhof ergodic theorem [37]Footnote 2. From (1.5) and (1.7), we have that for the data \(u_0\) constructed in Theorems 1.1 and 1.3,
The quantity above is slightly weaker than that given in (1.2). Even though (1.8) does not rule out weak turbulence for the concerned solutions, it gives to a certain extent an ‘upper bound’ on the eventual energy cascade mechanism. The estimate (1.8) is especially important in the context of the data constructed in Theorem 1.1 where the regularity \(H^s\) can be taken arbitrarily high.
Remark 1.5
The intervals given in (1.4) can be explained as follows: the result of Theorem 1.1 requires a deterministic local well-posedness and a strong statistical estimate. This statistical estimate is obtained by using the dissipation operator \({\mathscr {L}}(u)\) defined in (4.4). The operator \({\mathscr {L}}(u)\) is defined differently on low and high regularities. In fact the estimates in low regularities \(\max (\sigma ,\frac{1}{2})\le s\le 1+\sigma \) rely on a use of a Córdoba-Córdoba inequality (see Corollary 2.5) while the high regularity estimates \(s>\frac{d}{2}\) use an algebra property. It is clear that the FNLS has a good local well-posedness on \(H^s\) for \(s>d/2\) for all \(\sigma \in (0,1]\). This explains the globalization interval given in the first scenario in (1.4). However, in low regularities the local well-posedness (LWP) is only valid for some indexes: (i) for \(\sigma =1\), LWP holds for \(s> \frac{d-2}{2}\), then we can globalize for \(\max (\sigma ,\frac{1}{2},\frac{d-2}{2})=\max (1,\frac{d-2}{2})<s\le 1+\sigma \) which necessitates \(d\le 5\); hence the third scenario in (1.4). (ii) For \(\sigma \in [\frac{1}{2},1)\), LWP holds for \(s>\frac{d-1}{2}\), which leads to the second scenario in (1.4).
Let us also remark that for the classical cubic NLS (\(\sigma =1\)), an invariant measure was constructed in dimension \(d\le 4\) on the Sobolev space \(H^2\) in [39]. See also [52] for higher dimensions and higher regularities invariant measures for the periodic classical NLS (\(\sigma =1\)).
The complete description of the supports of fluctuation-dissipation measures is a very difficult open question. Only few results are known on substantially simple cases compared to nonlinear PDEs (see e.g. [3, 45]). In the context of nonlinear PDEs, it is traditional to ask about qualitative properties to exclude some trivial scenarios. Without giving details of computation we refer to [48] and Theorem 9.2 and Corollary 9.3 in [52] as a justification of the following statement which is valid for the different settings presented in Theorems 1.1 and 1.3.
Theorem 1.6
The distributions via \(\mu \) of the functionals M(u) and E(u) have densities with respect to the Lebesgue measure on \({\mathbb {R}}.\)
Remark 1.7
The equation (1.1) admits planar waves as solutions, we cannot exclude the scenario that the measures constructed here are concentrated on the set of these trivial solutions. However, this property is very unlikely because of the scaling between the dissipation and the fluctuations which leaves a balance in the stochastic equation (4.5): If the inviscid measures were concentrated on planar waves, the latter should be very close to the “complicated” solutions of (4.5) (these are not trivial at all because of the noise and the scaling); for small \(\alpha \) and large N, this would result in a non-trivial and highly surprising attractivity of the planar waves in the dynamics of (1.1).
1.5 Adaptation to the periodic case
Theorem 1.8
-
(1)
Let \(d\ge 1\), \(\sigma \in (0,1]\) and \(s>\frac{d}{2}\), the result of Theorem 1.1 are valid on \({\mathbb {T}}^d\).
-
(2)
The result of Theorem 1.3 are valid on \({\mathbb {T}}^d\) for:
-
(a)
\(d=1,2\) and \(s\in [\max (1/2,\sigma ),1]\) for all \(\sigma \in (0,1]\);
-
(b)
\(d=3\) and \(s\in [\max (1/2,\sigma ),1]\) for all \(\sigma \in (1/2,1]\);
-
(a)
Remark 1.9
-
(1)
For the periodic extension of Theorem 1.1 given in item (1.8), we just notice that the smoothness of the regularities (\(s>d/2\)) allows a naive fixed point argument (without using Strichartz estimates) for a local well-posedness result and the calculation in Sect. 4 can be used to obtain the exponential bounded needed in the Bourgain argument.
-
(2)
The argument behind the extensions in item (1.8) above is essentially the fact that the uniqueness argument in Theorem 1.3 is based on the radial Sobolev inequality which requires an \(H^{\frac{1}{2}+}\) regularity. This regularity however is not enough for the periodic case if \(d\ge 2.\) Nevertheless, for \(d=1,2\) and \(\frac{d}{2}<s\le 1+\sigma \), we have uniqueness in \(H^s({\mathbb {T}}^d)\), thanks to the embedding \(H^s\subset L^\infty \), and the same procedure gives the claim for \(d=3.\) However, once \(d\ge 4\), Theorem 1.3 fails on \({\mathbb {T}}^d\) because \(\frac{d}{2}\ge 1+\sigma \) for all \(\sigma \in (0,1]\).
1.6 Comparison with [52, 54]
The probabilistic technique employed in this paper is closed to [52, 54]. It is worth mentioning the novelty in the present work beside the fact that fractional NLS equations are much less understood than the standard NLS which motivated our interest to the problem considered here, and the presentation of the IID limit in a general form that is independent of characteristics of (1.1). A main difference from [52, 54] is the fact that the result of Theorem 1.3 goes below the energy space, and s can go all the way toward 0. The major issue in achieving this is the uniqueness in low regularity. Our strategy is to control the gradient of the nonlinearity, that is the term \(|u|^2\), and then to combine it with the radial Sobolev embedding and an approximation argument. This control is anticipated in the preparation of the dissipation operator.
Let us present the dissipation operator (see (4.4)) on which the low regularity result (see e.g. Sect. 6) is based, in particular:
The dissipation rate \({\mathscr {E}}(u)\) of the energy will be of regularity s which, for \(s<\sigma \), is weaker than the energy. Since \({\mathscr {E}}(u)\) is the highest regular quantity controlled, we are then in new ranges of regularity compared to [52, 54]. To deal with these ranges we need new inputs at different levels of the proof. For instance, the large data argument relies on the identity (4.17) whose proof cannot be achieved by using the approach of [52] and [54] (where the dissipation was of positive order and then the dissipation rate of the energy was smoother than the energy itself which made it useful in the derivation of the identity concerning the dissipation rate of the mass). We, instead, introduce a modified approach which use a careful cutoff on the frequencies.
It is worth mentioning the central quantity that we manage to control at the finite-dimensional level (the control is however uniform in the dimension) by the use of a fluctuation-dissipation strategy:
Below is the role of each term in the quantity above:
-
The term \(\Vert u\Vert _{H^s}\) determines the minimal regularity of the measure
-
The term \(\Vert |u|^2\Vert ^2_{{\dot{H}}^\sigma }+\Vert |u|^2\Vert ^2_{{\dot{H}}^{s-\sigma }}\) combined with the radial Sobolev inequality and an approximation argument allows to obtain uniqueness of solutions in Theorem 1.3 (see Sect. 6.1). To this end we need either \(\sigma >\frac{1}{2}\) or \(s-\sigma >\frac{1}{2}\), this results in a control of gradient of the nonlinearity \(|u|^2u\) far from the origin of the ball, and then an approximation argument introduce in our previous work [54] is employed.
-
The term \(\Vert \Pi ^N|u|^2u\Vert _{L^2}^2\) combined with the Skorokhod representation theorem and a compactness argument allows to pass to the limit \(N\rightarrow \infty \) and prove the existence of solutions.
-
The term \(e^{\xi ^{-1}(\Vert u\Vert _{H^{s-}})}\) is employed in the Bourgain argument to obtain, in particular, the concave bounds on the solutions claimed in Theorem 1.1.
1.7 Organization of the paper
We present the inviscid - infinite dimensional (IID) limit in details in Sect. 3. We consider a general Hamiltonian PDE and present the general framework of the IID limit, formulate assumptions and, based on them, prove the essential steps of the method. Section 4 is devoted to fulfill the assumptions made in Sect. 3. Section 5 ends the fulfillment of the assumptions by establishing the local well-posedness one, hence the proof of Theorem 1.1 is complete. Section 6 is devoted to the proof of Theorem 1.3.
2 Preliminaries
In this section we present some notations, functions spaces, properties the radial Laplacian and useful inequalities.
2.1 Notation
We define

where I is a time interval and D is either the ball \(B^d\) or the torus \({\mathbb {T}}^d\).
For \(x\in {\mathbb {R}}\), we set  . We adopt the usual notation that \(A \lesssim B\) or \(B \gtrsim A\) to denote an estimate of the form \(A \le C B\) , for some constant \(0< C < \infty \) depending only on the a priori fixed constants of the problem. We write \(A \sim B\) when both \(A \lesssim B \) and \(B \lesssim A\).
. We adopt the usual notation that \(A \lesssim B\) or \(B \gtrsim A\) to denote an estimate of the form \(A \le C B\) , for some constant \(0< C < \infty \) depending only on the a priori fixed constants of the problem. We write \(A \sim B\) when both \(A \lesssim B \) and \(B \lesssim A\).
For a real number a, we set \(a-\) (resp. \(a+\)) to represent to numbers \(a-\epsilon \) (resp. \(a+\epsilon \)) with \(\epsilon \) small enough.
For a metric space X, we denote by \({\mathfrak {p}}(X)\) the set of probability measures on X and \(C_b(X)\) is the space of bounded continuous functions \(f:X\rightarrow {\mathbb {R}}.\) If X is a normed space, \(B_R(X)\) represents the ball \(\{u\in X\ |\ \Vert u\Vert _{X}\le R\}\).
2.2 Eigenfunctions and eigenvalues of the radial Dirichlet Laplacian on the ball
From Sect. 2 in [2], one has the following bound for the eigenfunctions of the radial Laplacian

We have also the asymptotics for the eigenvalues
2.3 \(H_{rad}^s\) spaces
Recall that \((e_n)_{n=1}^{\infty }\) form an orthonormal bases of the Hilbert space of \(L^2\) radial functions on \(B^d\). That is,
where dL is the normalized Lebesgue measure on \(B^d\). Therefore, we have the expansion formula for a function \(u \in L^2 (B^d)\),

For \(s \in {\mathbb {R}}\), we define the Sobolev space \(H_{rad}^{s} (B^d)\) on the closed unit ball \(B^d\) as

We can equip \(H_{rad}^{s} (B^d)\) with the natural complex Hilbert space structure. In particular, if \(s =0\), we denote \(H_{rad}^{0} (B^d)\) by \(L_{rad}^2 (B^d)\). For \(\gamma \in {\mathbb {R}}\), we define the map \(\sqrt{-\Delta }^{\gamma }\) acting as isometry from \(H_{rad}^{s} (B^d)\) and \(H_{rad}^{s - \gamma } (B^d)\) by
We denote \(S_{\sigma }(t) = e^{- {\mathbf{i }}t (-\Delta )^{\sigma }}\) the flow of the linear Schrödinger equation with Dirichlet boundary conditions on the unit ball \(B^d\), and it can be written as
2.4 \(X_{\sigma , rad}^{s,b}\) spaces
Using again the \(L^2\) orthonormal basis of eigenfunctions \(\{ e_n\}_{n=1}^{\infty }\) with their eigenvalues \(z_n^2\) on \(B^d\), we define the \(X^{s,b}\) spaces of functions on \({\mathbb {R}}\times B^d\) which are radial with respect to the second argument.
Definition 2.1
(\(X_{\sigma , rad}^{s,b}\) spaces) For \(s \ge 0\) and \(b \in {\mathbb {R}}\),

where

and
Moreover, for \(u \in X_{\sigma , rad}^{0, \infty } ({\mathbb {R}}\times B^d) = \cap _{b \in {\mathbb {R}}} X_{\sigma , rad}^{0,b} ({\mathbb {R}}\times B^d)\) we define, for \(s \le 0\) and \(b \in {\mathbb {R}}\), the norm  by (2.3).
by (2.3).
Equivalently, we can write the norm (2.3) in the definition above into

For \(T > 0\), we define the restriction spaces \(X_{\sigma , T}^{s,b} (B^d)\) equipped with the natural norm

Lemma 2.2
(Basic properties of \(X_{\sigma , rad}^{s,b}\) spaces)
-
(1)
We have the trivial nesting
$$\begin{aligned} X_{\sigma , rad}^{s,b} \subset X_{\sigma , rad}^{s' , b' } \end{aligned}$$whenever \(s' \le s\) and \(b' \le b\), and
$$\begin{aligned} X_{\sigma , T}^{s,b} \subset X_{\sigma , T'}^{s,b} \end{aligned}$$whenever \(T' \le T\) .
-
(2)
The \(X_{\sigma , rad}^{s,b}\) spaces interpolate nicely in the s, b indices.
-
(3)
For \(b > \frac{1}{2}\), we have the following embedding
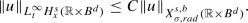
-
(4)
An embedding that will be used frequently in this paper
$$\begin{aligned} X_{\sigma , rad}^{0, \frac{1}{4}} \hookrightarrow L_t^4 L_x^2 . \end{aligned}$$
Note that

Lemma 2.3
Let \(b,s >0\) and \(u_0 \in H_{rad}^s (B^d)\). Then there exists \(c >0\) such that for \(0 < T \le 1\),

The proofs of Lemma 2.2 and Lemma 2.3 can be found in [1].
We also recall the following lemma in [4, 26]
Lemma 2.4
Let \(0< b' < \frac{1}{2}\) and \(0< b < 1-b'\). Then for all \(f \in X_{\sigma , \delta }^{s, -b'} (B^d)\), we have the Duhamel term \(w(t) = \int _0^t S_{\sigma }(t-s) f(\tau ) \, ds \in X_{\sigma , \delta }^{s,b} (B^d)\) and moreover

From now on, for simplicity of notation, we write \(H^s\) and \(X_{\sigma }^{s,b}\) for the spaces \(H_{rad}^s\) and \(X_{\sigma , rad}^{s,b}\) defined in this subsection.
2.5 Useful inequalities
Lemma 2.5
(Córdoba-Córdoba inequality [17, 18]) Let \(D\subset {\mathbb {R}}^n\) be a bounded domain with smooth boundary (resp. the n-dimensional torus). Let \(\Delta \) be the Laplace operator on D with Dirichlet boundary condition (rep. periodic condition). Let \(\Phi \) be a convex \(C^2({\mathbb {R}},{\mathbb {R}})\) satisfying \(\Phi (0)=0\), and \(\gamma \in [0,1]\). For any \(f\in C^\infty (D,{\mathbb {R}})\), the inequality
holds pointwise almost everywhere in D.
Lemma 2.6
(Complex Córdoba-Córdoba inequality) Let D and \(\Delta \) be as in Lemma 2.5. For any \(f\in C^\infty (D,{\mathbb {C}})\), the inequality
holds pointwise almost everywhere in D.
Proof of Lemma 2.6
Let us write \(f=a+{\mathbf{i }}b\) with real valued functions a and b. We have
Now we use Lemma 2.5 with \(\Phi (x)=\frac{x^2}{2}\), we arrive at
This finishes the proof of Lemma 2.6. \(\square \)
Corollary 2.7
Let \(\gamma \in [0,1]\), we have, for \(f\in C^\infty (D,{\mathbb {C}})\), that
Lemma 2.8
(Radial Sobolev lemma on the unit ball) Let \(\frac{1}{2}<s<\frac{d}{2}\). Then for any \(f\in H^s:=H_0^s(B^d)\)Footnote 3, we have
Proof of Lemma 2.8
Let \(\frac{1}{2}<s<\frac{d}{2}\). We have for any \(f\in H^s({\mathbb {R}}^d)\) (see [14]), that
On the other hand, since \(B^d\) is a regular domain, we have the extension theorem (see for instance [34] and reference therein): there is a bounded operator \({\mathfrak {E}}:H^s_0(B^d)\rightarrow H^s({\mathbb {R}}^d)\) satisfying the following
-
(1)
\({\mathfrak {E}}f(r)=f(r)\ \forall r\in [0,1]\), for any \(f\in H^s_0(B^d)\);
-
(2)
(continuity)
$$\begin{aligned} \Vert {\mathfrak {E}}f\Vert _{H^s({\mathbb {R}}^d)}\le C\Vert f\Vert _{H^s_0(B^d)}. \end{aligned}$$(2.5)
Therefore using (2.5), we notice that
Then for \(r\in (0,1]\), we use the item (2.5) above to arrive at
Hence we finish the proof of Lemma 2.8. \(\square \)
3 Description of the Inviscid-Infinite dimensional (IID) limit
The IID limit combines a fluctuation-dissipation argument and an abstract version of the Bourgain’s invariant measure globalization [5].
We consider a Hamiltonian equation
where J is a skew-adjoint operator on suitable spaces, H(u) is the hamiltonian function, \(H'\) is the derivative with respect to u (or a function of u, for instance to its complex conjugate). We can, for simplicity, assume the following form for the Hamiltonian
where \(E_K\) and \(E_p\) refer to the kinetic energy of the system (having a quadratic power) and the potential energy, respectively. In the sequel we construct a general framework allowing to apply the Bourgain’s invariant measure argument to the context of a general probability measure (not necessarily Gaussian based). We then present the strategy of the construction of the required measures.
3.1 Abstract version of Bourgain’s invariant measure argument
Let \(\Pi ^N\) be the projection on the N-dimensional space \(E^N\) spanned by the first N eigenfunctions \(\{e_1, \cdots , e_N\}\). Consider the Galerkin projections of (3.1)
The equation (3.1) will be seen as (3.2) with \(N=\infty \).
Assumption 1
(Uniform local well-posedness) The equation (3.2) is uniformly (in N) locally wellposed in the Cauchy-Hadamard sense on some Sobolev space \(H^s\). And there is a function f independent of N, such that for any given data \(u_0\in \Pi ^NH^s\), the time existence \(T(u_0)\) of the corresponding solution u is at least \(f(\Vert u_0\Vert _{H^s})\). Also, the following estimate holds
We denote by \(\phi ^N_t\) the local flow of (3.2), for \(N=\infty \) we set \(\phi _t=\phi ^\infty _t\).
For \(N<\infty \), we assume that \(\phi ^N_t\) is defined globally in time.
Remark 3.1
For the power-like nonlinear Schrödinger equation, f(x) is of the form \(x^r\) where r is related to the power of the nonlinearity.
Assumption 2
(Convergence) For any \(u_0\in H^s\), any sequence \((u_0^N)_N\) such that
-
(1)
for any N, \(u_0^N\in \Pi ^NH^s\);
-
(2)
\((u_0^N)\) converges to \(u_0\) in \(H^s\);
then \(\phi ^N_tu^N\) converges \(\phi _tu\) in \(C_tH^{s-}.\)
Assumption 3
(Invariant measure) For any N, there is a measure \(\mu _N\) invariant under the projection equations (3.2) and satisfying
-
(1)
There is an increasing one-to-one function \(g:{\mathbb {R}}\rightarrow {\mathbb {R}}_+\) and a function \(h:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) such that we have the uniform bound
$$\begin{aligned} \int _{E^N}g(\Vert u\Vert _{H^{s}})h(\Vert u\Vert _{H^{s_0}})\mu ^N(du)\le C, \end{aligned}$$where \(C>0\) is independent of N and \(s_0\) is some fixed number. We then have
$$\begin{aligned} \int _{E^N}e^{\ln (1+ g(\Vert u\Vert _{H^{s}}))}h(\Vert u\Vert _{H^{s_0}})\mu ^N(du)\le 1+C. \end{aligned}$$(3.3)We set \({\tilde{g}}(\Vert u\Vert _{H^{s}})=\ln (1+ g(\Vert u\Vert _{H^{s}}));\)Footnote 4
-
(2)
The following limit holds
$$\begin{aligned} \lim _{i\rightarrow \infty }e^{-2i}\sum _{j\ge 0}\frac{e^{-j}}{f\circ {\tilde{g}}^{-1}(2(i+j))}=0. \end{aligned}$$We set the number
$$\begin{aligned} \kappa (i):=e^{-2i}\sum _{j\ge 0}\frac{e^{-j}}{f\circ {\tilde{g}}^{-1}(2(i+j))}. \end{aligned}$$
Remark 3.2
For the case of Gibbs measures for NLS like equations, g(x) is of the form \(e^{ax^2}, \ a>0\) and h(x) is a constant.
The Prokhorov theorem (Theorem A.4) combined with the estimate (3.3) implies the existence of a probability measure \(\mu \in {\mathfrak {p}}(H^s)\) as an accumulation point when \(N\rightarrow \infty \) for the measures \(\{\mu ^N\}\).
Theorem 3.3
Under the Assumptions 1, 2, and 3, there is a set \(\Sigma \subset H^s\) such that
-
(1)
\(\mu (\Sigma ) =1\)
-
(2)
The equation (3.1) is GWP on \(\Sigma \)
-
(3)
The measure \(\mu \) is invariant under the flow \(\phi _t\) induced by the GWP;
-
(4)
For every \(u_0\in \Sigma \), we have that
$$\begin{aligned} \Vert \phi _t u_0\Vert _{H^{s}}\le C(u_0){\tilde{g}}^{-1}(1+\ln (1+|t|)). \end{aligned}$$
The following is devoted to the proof of Theorem 3.3.
3.1.1 Individual bounds
Fix an arbitrary (small) number \(a>0\), define the set
Proposition 3.4
Let \(r\le s,\ N\ge 1,\ i\ge 1\), there exists a set \(\Sigma ^N_{r,i}\subset E^N_a\) such that
and for any \(u_0\in \Sigma ^N_{r,i}\), we have
Moreover, we have the properties
Proof of Proposition 3.4
It suffices to consider \(t>0\). We define the sets
Let \(T_0\) be the local time existence on \(B^N_{r,i,j}\). From the local well-posedness, we have for \(t\le T_0=f({\tilde{g}}^{-1}(2(i+j)))\) (see Assumption 1), that
Now, let us define the set
We use (3.3) and the Chebyshev inequality to obtain the following
Let us finally define
We then obtain
We claim that for \(u_0\in \Sigma ^N_{r,i,j}\), the following estimate holds
Indeed we write \(t=kT_0+\tau \) where k is an integer in \([0,\frac{e^j}{T_0}]\) and \(\tau \in [0,T_0]\). We have
Now, recall that \(u_0\in \phi ^N_{-kT_0}(B^N_{r,i,j})\), then \(u_0\in \phi ^N_{-kT_0}w\) where \(w\in B^N_{r,i,j}\). Then \(\phi ^N_tu_0=\phi ^N_\tau w\).
For \(t>0\), there \(j\ge 0\) such that
Then
We arrive at
The properties (3.7) follow easily from the definition of the sets \(\Sigma ^N_{r,i}\). Remark that the definition of \(\Sigma ^N_{r,i}\) does not depend on the measure \(\mu ^N\) but just on the functions h and g, as can be noticed in (3.4), (3.8), (3.9) and (3.10). If \(N_1\le N_2\), then we see trivially that \(B^{N_1}_{r,i,j}\subset B^{N_2}_{r,i,j}\), it then follows from (3.9) and (3.10) that \(\Sigma ^{N_1}_{r,i}\subset \Sigma ^{N_2}_{r,i}\). Using the fact that \(g^{-1}\) is increasing, we obtain \(\Sigma ^N_{s,i_1}\subset \Sigma ^N_{s,i_2}\) for \(i_1\le i_2\). Similarly, the inequality \(\Vert u\Vert _{H^{s_2}}\le \Vert u\Vert _{H^{s_1}}\) for \(s_1\ge s_2\) leads to remaining inclusion. The proof of Proposition 3.4 is finished. \(\square \)
3.1.2 Statistical ensemble
We want to pass to the limit \(N\rightarrow \infty \) in the sets \(\Sigma ^N_{r,i}\). We introduce the following limiting set:
We then define the following set
Let \((l_k)\) be a sequence such that \(\lim _{k\rightarrow \infty }l_k=s\), the statistical ensemble is given by
Proposition 3.5
The set \(\Sigma \) constructed above is of full \(\mu \)-measure:
Proof of Proposition 3.5
Let us first observe that
because for any \(u \in \Sigma _{r,i}^N \) the constant sequence \(u_N = u\) converges to u, and then \(u \in \Sigma _{r,i}\).
Now by the Portmanteau theorem (see Theorem A.3) and the use of the bound (3.5) we have that
On the other hand, from the properties (3.7), we have that \((\overline{\Sigma _{r,i}})_{i \ge 1}\) is non-decreasing. In particular,
Therefore
Since \(\mu \) is a probability measure, we obtain
This finishes the proof of Proposition 3.5. \(\square \)
3.1.3 Globalization
Proposition 3.6
Let \(r\le s\). For any \(u_0\in \Sigma _r\), there is a unique global solution \(u\in C_tH^s\) such that
Proof of Proposition 3.6
For \(u_0\in \Sigma _r\cap \text {supp}(\mu )\) (recall that \(\mu (\Sigma _r)=1\)), we have that
-
(1)
\(u_0\in H^s\) since \(\text {supp}(\mu )\subset H^s\);
-
(2)
there is \(i\ge 1\) such that \(u_0\in \overline{\Sigma _{r,i}}\).
We will consider that \(u_0\in \Sigma _{r,i}\), the case \(u_0\in \partial \Sigma _{r,i}\) can be obtained by a limiting argument (see [54]). By construction of \(\Sigma _{r,i}\), there is \(N_k\rightarrow \infty \) such that
Now using (3.6), we have
this gives in particular that, at \(t=0\),
A passage to the limit \(N_k\rightarrow \infty \) shows that
Now for any fixed \(T>0\), set \(b=2{\tilde{g}}^{-1}(1+i+\ln (1+|T|))\) and \(R=b+1\), so that \(u^{N_k},\ u_0\in B_R(H^r)\). Let \(T_R\) be the local existence time of \(B_R\). We have that \(\phi _t\) and \(\phi ^{N_k}_tu^{N_k}\) exist for \(|t|\le T_R\). Using Assumption 2, we have for \(r<s\),
This bound tells us that after the time \(T_R\) the solution stays in the same ball as the initial data. We can then iterate on intervals \([nT_R,(n+1)T_R]\) still consuming the fixed time T. Since this time is arbitrary, we conclude to the global existence. The estimate (3.11) follows easily a passage to the limit from (3.6). Now the proof of Proposition 3.6 is finished. \(\square \)
Remark 3.7
It follows from the proof above that, if \(u_0\in \Sigma _r\) we have that
where \(u^{N_k}\in \Sigma ^{N_k}_{r,i}\) and \(\lim _{k\rightarrow \infty }\Vert u_0-u^{N_k}\Vert _{H^r}=0.\)
3.1.4 Invariance results
Theorem 3.8
The measure \(\mu \) is invariant under \(\phi _t\).
Proof of Theorem 3.8
It follows from the Skorokhod representation theorem (Theorem A.5) the existence of \(u^N_0\) a random variable distributed by \(\mu ^N\) and \(u_0\) a one distributed by \(\mu \) such that
Combining this with the Assumption 2, we then have the almost sure convergence
For any fixed t, we know that the distribution \({\mathscr {D}}(\phi ^N_tu_0^N)\) is \(\mu ^N\), by the invariance of \(\mu ^N\) under (3.2). Let us look at \(\phi ^N_tu_0^N\) and \(\phi _t u_0\) as \(H^{s-}-\)valued random variables. We then have the following two results:
-
(1)
The pointwise convergence in (3.13) implies that \(\mu ^N\) weakly converges to \({\mathscr {D}}(\phi _tu_0)\) for any fixed t, hence the invariance of \({\mathscr {D}}(\phi _tu_0)\) because \(\mu ^N\) does not depend on t;
-
(2)
We already know that \(\mu ^N\) converges weakly to \(\mu \).
The proof of Theorem 3.8 is complete. \(\square \)
Assumption 4
(Second conservation law) The equation (3.1) admits a conservation law of the form
where \(\gamma <s.\)
Theorem 3.9
Under the Assumption 4 we have the following
The proof of Theorem 3.9 relies on the lemma 3.10 below. This lemma roughly states that the evolution under \(\phi ^N_t\) of a set \(\Sigma ^N_{r,i}\) is a set of the same kind, giving then the essential mechanism needed for the invariance. The remaining part relies on the definition of the set \(\Sigma \) and on a limiting argument.
Lemma 3.10
Let \(r\le s\), for any \(\gamma<r_1<r\) and any t, there exists \(i_1:=i_1(t)\) such that for any i, if \(u_0\in \Sigma ^N_{s,i}\) then \(\phi ^N_tu_0\in \Sigma ^N_{r_1,i+i_1}\).
Proof of Lemma 3.10
We can assume without loss of generality that \(t\ge 0\). For \(u_0\in \Sigma ^N_{r,i}\), we have, by definition, that
Let us pick a function \(i_1:=i_1(t)\) satisfying \(e^{j}+t\le e^{i_1+j}\) for any \(j\ge 0.\) Then
But for \(t+t_1\le e^{j+i_1}\), one readily has \(t_1\le e^{j+i_1}-t\). On the other hand we have, from the definition of \(i_1\), that \(e^{j+i_1}-t\ge e^{j}\). From these two facts, we obtain
Since \(u_0\in \Sigma ^N_{i,s}\), using the estimate (3.6), we have
Hence, using Assumption 4, we have
Using the conservation of the \(H^\gamma -\)norm (Assumption 4), we obtain
For \(\gamma<r_1<r\), by interpolation there is \(0<\theta <1\) such that
As \({\tilde{g}}^{-1}\) is increasing, we take \(i_1\) large enough to obtain the bound
Thus \(\phi ^N_{t+t_1}u_0\in B^N_{r_1,i+i_1,j}\) for all \(t_1\le e^{j}\), for all \(j\ge 0.\) We then have \(\phi ^N_{t}u_0\in \Sigma ^N_{r_1,i+i_1}.\) Then the proof of Lemma 3.10 is finished. \(\square \)
Remark 3.11
In some situation, Assumption 4 is not necessary. If the control on the \(H^s\)-norm provides a control on the energy, we can proof Lemma 3.10 without any supplementary conservation law.
Now let us finish the proof of Theorem 3.9. Since any \(\Sigma _r\) is of full \(\mu -\)measure and the intersection is countable, we obtain the first statement.
Let us take \(u_0\in \Sigma \), then \(u_0\) belong to each \(\Sigma _r\), \(r\in l.\) First, consider \(u_0\in \Sigma _{i_r}\). There is \(i\ge 1\) such that \(u_0\in \Sigma _{i_r}\), therefore \(u_0\) is the limit of a sequence \((u_{0}^N)\) such that \(u_{0}^N\in \Sigma _{i,r}^N\) for every N. Now thanks to Lemma 3.10, there is \(i_1:=i_1(t)\) such that \(\phi ^N_t(u_{0}^N)\in \Sigma _{i+i_1,r_1}^{N}\). Using the convergence (3.12), we see that \(\phi ^t(u_0)\in \Sigma _{i+i_1,r_1}\). Now if \(u_0\in \partial \Sigma _{i,r}\), there is \((u_0^k)_k\subset \Sigma _{i,r}\) that converges to \(u_0\) in \(H^r\). Since we showed that \(\phi _t\Sigma _{i,r}\subset \Sigma _{i+i_1,r_1}\) and \(\phi _t(\cdot ) \) is continuous, we see that \(\phi _t(u_0)=\lim _{k}\phi _t(u_0^k)\in \overline{\Sigma _{i+i_1,r_1}}\). One arrives at \(\phi _t\overline{\Sigma _{i,r}}\subset \overline{\Sigma _{i+i_1,r_1}}\subset \Sigma _{r_1}\). Hence \(\phi _t\Sigma \subset \Sigma .\)
Now, let u be in \(\Sigma \). Since \(\phi _t\) is well-defined on \(\Sigma \) we can set \(u_0=\phi _{-t}u\), we then have \(u=\phi _tu_0\), hence \(\Sigma \subset \phi _{t}\Sigma .\)
3.2 Construction of the required invariant measures
Here we present a strategy to achieve the fulfillment of Assumption 3. It is based on a fluctuation-dissipation method.
Let us introduce a probabilistic setting and some notations that are going to be used from this section on. First, \((\Omega , {\mathscr {F}}, {\mathbb {P}})\) is a complete probability space. If E is a Banach space, we can define random variables \(X:\Omega \rightarrow E\) as Bochner measurable functions with respect to \({\mathscr {F}}\) and \({\mathscr {B}}(E)\), where \({\mathscr {B}}(E)\) is the Borel \(\sigma -\)algebra of E.
For every positive integer N, we denote by \(W^N\) an \(N-\)dimensional Brownian motion with respect to the filtration \(({\mathscr {F}}_t)_{t\ge 0}\).
Throughout the sequel, we use \(\langle \cdot ,\cdot \rangle \) as the real dot product in \(L^2\):
Ocassionally this notation is used to write a duality bracket when the context is not confusing.
We set the fluctuation-dissipation equation
where \({\mathscr {L}}(u)\) is a dissipation operator.
Assumption 5
(Exponential moment) We assume that \({\mathscr {L}}(u)\) satisfies the dissipation inequality
where \(\xi ^{-1}(x)\ge x\) is a one-to-one convex function from \({\mathbb {R}}_+\) to \({\mathbb {R}}_+\).
We assume also that the (local existence) function f defined in Assumption 1 is of the form \(Cx^{-r}\) for some \(r>0\).
Assumption 6
The equation (3.14) is stochastically globally well-posed on \(E^N,\) that is:
For every \({\mathscr {F}}_0\)-measurable random variable \(u_0\) in \(E_N\), we have
-
(1)
for \({\mathbb {P}}\)-almost all \(\omega \in \Omega \), (3.14) with initial condition \(u(0) = \Pi ^N u_0^{\omega }\) has a unique global solution \(u_{\alpha }^N (t; u_0^{\omega })\);
-
(2)
if \(u_{0,n}^{\omega } \rightarrow u_0^{\omega }\) then \(u_{\alpha }^N (\cdot ; u_{0,n}^{\omega }) \rightarrow u_{\alpha }^N(\cdot ; u_0^{\omega })\) in \(C_t E^N\);
-
(3)
the solution \(u^N_\alpha \) is adapted to \(({\mathscr {F}}_t)\).
Under Assumption (6), we can introduce the transition probability
We then define the Markov operators
Let us remark that
Using the continuity of the solution \(u^N_\alpha (t,\cdot )\) in the second variable (the initial data), we observe the Feller property:
Here \(C_b(L^2,{\mathbb {R}})\) is the space of continuous bounded functions\(f:L^2\rightarrow {\mathbb {R}}\).
Let us also define the Markov groups associated to (3.2), recall that in Assumption (1) we assume that \(\phi ^N_t\) exists globally in t. The associated Markov groups are the following
Combining the Itô formula, the Krylov-Bogoliubov argument (Lemma A.9), the Prokhorov theorem (Theorem A.4) and Lemma A.10 we obtain the following:
Theorem 3.12
Under Assumptions 5 and 6, let \(N\ge 1\), there is an stationary measure \(\mu ^N_\alpha \) for (3.14) such that
where C does not depend on \((N,\alpha )\).
There is a subsequence \(\{\alpha _k\}\) such that
Assumption 7
(Inviscid limit) The following convergence holds
Theorem 3.13
Under Assumptions 5 and 7, the measures \(\mu ^N\) are invariant under (3.2) respectively. They satisfy
where C is independent of N.
Moreover, we have that
Proof of Theorem 3.13
For simplicity we write the measure \(\mu ^N_{\alpha _k}\) constructed above as \(\mu ^N_k\). The invariance of \(\mu ^N\) under (3.2) follows from the following diagram

The step (I) is the stationarity of \(\mu ^N_k\) under (3.14), the step (II) describes the weak convergence of \((\mu ^N_k)\) to \(\mu ^N\). Therefore, with the help of the weak convergence in (III) (Assumption 7), we obtain the desired invariance in (IV).
As for the proof of (3.17), we first remark that the weak convergence \(\mu ^N_k\rightarrow \mu ^N\) combined with the lower semi-continuity of \({\mathscr {E}}(u)\) yields
with C is the same constant in (3.16), in particular C does not depend on N.
Now using the form of f, we have that
Now recall that \(\xi ^{-1}\ge x\), then \(\xi \le x^{-1}\). So, we obtain \(f\circ \xi (2(i+j)){\ \gtrsim \ \ }(i+j)^{-r}\), which leads readily to (3.18). Then the proof of Theorem 3.13 is finished. \(\square \)
From now, Assumption 3 is disintegrated into Assumptions 5 to 7.
4 Proof of Theorem 1.1: Probabilistic part
In this section, we present the probabilistic part of the proof of Theorem 1.1, that is, the fulfillment of Assumptions 4 to 7. First, we remark that Assumption 3 was decomposed in the strategy given in Sect. 3.2 into Assumptions 5 to 7. Assumptions 1 and 2 are of deterministic type and will be given in Sect. 5. We also prepare, simultaneously, the setting for the proof of Theorem 1.3. Assumption 4 is given by the existence of a second conservation law (the \(L^2\)-norm).
Let N be a positive integer, consider the Galerkin approximation

We define a Brownian motion following the case we set the equation on the unit ball \(B^d\):
where \((e_n)_n\) is the sequence of eigenfunctions of radial Dirichlet Laplacian \(-\Delta \) on \(B^d\). Here \((\beta _n (t))\) is a fixed sequence of independent one dimensional Brownian motions with filtration \(({\mathscr {F}}_t)_{t\ge 0}\). The numbers \((a_m)_{m\ge 1}\) are complex numbers such that \(|a_m|\) decreases sufficiently fast to 0. More precisely we assume that
where \((z_n^2)\) are the eigenvalues of \(-\Delta \) associated to \((e_n)\). Set
Let us introduce the following fluctuation-dissipation model of (4.1). For \(\sigma \in (0,1]\), we define a dissipation operator as follows
where \(\xi :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) is any one-to-one increasing concave function. We assume that \(\xi ^{-1}(x)\ge x.\) We then write the stochastic equation

where \(\alpha \in (0,1)\).
Remark 4.1
The setting of Theorem 1.3 is contained in the case \(0<s\le 1+\sigma :\)
Therefore the estimates obtained using that form of \({\mathscr {L}}(u)\) will also serve in the proof of Theorem 1.3 (see Sect. 6).
4.1 Fulfillment of Assumption 5 (The dissipation inequality and time of local existence)
For the polynomial nature of the time of local existence we refer to Theorem 5.1.
For the dissipation inequality, we set \({\mathscr {E}}(u):=E'(u,{\mathscr {L}}(u))\). We have the following.
-
(1)
For \(s>\frac{d}{2}\),
$$\begin{aligned} {\mathscr {E}}(u)&= \Vert u\Vert _{H^s}^2+\langle (-\Delta )^{s-\sigma }u,\Pi ^N|u|^2u\rangle +e^{\xi ^{-1}(\Vert u\Vert _{H^{s -}})}\left( \Vert u\Vert _{L^4}^4 +\Vert u\Vert _{H^\sigma }^2\right) . \end{aligned}$$Using Cauchy-Schwarz and Agmon’s inequalities and the algebra property of \(H^{s-}\) for \(s>\frac{d}{2}\), we obtain
$$\begin{aligned} |\langle (-\Delta )^{s-\sigma }u,\Pi ^N|u|^{2}u\rangle |&\le \Vert u\Vert _{H^{s-\sigma }}\Vert |u|^2u\Vert _{H^{s-\sigma }}\le C\Vert u\Vert _{L^\infty }\Vert |u|^2u\Vert _{H^{s-\sigma }}\\&\le C\Vert u\Vert _{L^2}^{1-\frac{d}{2s}}\Vert u\Vert _{H^s}^{\frac{d}{2s}}\Vert |u|^2u\Vert _{H^{s-\sigma }}\le C\Vert u\Vert _{H^s}\Vert u\Vert _{H^{s-}}^3 \\&\le {\tilde{C}}+\frac{1}{2}\Vert u\Vert _{H^s}^2\Vert u\Vert _{H^{s-}}^{6} \le {\tilde{C}}+\frac{1}{2}e^{\xi ^{-1}(\Vert u\Vert _{H^{s -}})}\Vert u\Vert _{H^s}^2. \end{aligned}$$Remark that the \({\tilde{C}}\) is an absolute constant. Overall,
$$\begin{aligned} {\mathscr {E}}(u)\ge \Vert u\Vert _{H^{s}}^2+\frac{1}{2}e^{\xi ^{-1}(\Vert u\Vert _{H^{s -}})}\left( \Vert u\Vert _{L^4}^4 +\Vert u\Vert _{H^s}^2\right) -{\tilde{C}}. \end{aligned}$$(4.6) -
(2)
For \(0< s\le 1+\sigma \),
$$\begin{aligned} {\mathscr {E}}(u)&=e^{\xi ^{-1}(\Vert u\Vert _{H^{s -}})}\big (\Vert u\Vert _{H^s}^2 +\langle (-\Delta )^{s-\sigma }u,\Pi ^N|u|^{2}u\rangle \\&+\langle \Pi ^N|u|^2u,(-\Delta )^\sigma u\rangle +\Vert \Pi ^N|u|^2u\Vert _{L^2}^2\big ). \end{aligned}$$We are able to give a useful estimate of \({\mathscr {E}}(u)\) in the following two cases:
-
(a)
For \(\max (\frac{1}{2},\sigma )\le s\le 1+\sigma :\)
In order the treat the term \(\langle (-\Delta )^{s-\sigma }u,\Pi ^N|u|^{2}u\rangle \) and \(\langle \Pi ^N|u|^2u,(-\Delta )^\sigma u\rangle \), we use the Córdoba-Córdoba inequality ( see Corollary 2.7) since \(s-\sigma \in [0,1]\), s being in \([\max (\frac{1}{2},\sigma ),1+\sigma ]\). We have the following
$$\begin{aligned} \langle (-\Delta )^{s-\sigma }u,|u|^{2}u\rangle&\ge \frac{1}{2}\Vert (-\Delta )^\frac{s-\sigma }{2}|u|^2\Vert _{L^2}^2,\\ \langle (-\Delta )^{\sigma }u,|u|^{2}u\rangle&\ge \frac{1}{2}\Vert (-\Delta )^\frac{\sigma }{2}|u|^2\Vert _{L^2}^2. \end{aligned}$$We finally obtain that
$$\begin{aligned} {\mathscr {E}}(u)&\ge \frac{1}{2}e^{\xi ^{-1}(\Vert u\Vert _{H^{s -}})}\left( \Vert |u|^2\Vert _{{\dot{H}}^\sigma }^2+\Vert \Pi ^N|u|^2u\Vert _{L^2}^2+\Vert u\Vert _{H^s}^2+\Vert |u|^2\Vert _{{\dot{H}}^{s-\sigma }}^2\right) . \end{aligned}$$(4.7) -
(b)
For \(0<s\le \sigma :\) Since \(\sigma \) still lies in (0, 1], we can use the Córdoba-Córdoba inequality to obtain
$$\begin{aligned} \langle (-\Delta )^{\sigma }u,|u|^{2}u\rangle&\ge \frac{1}{2}\Vert (-\Delta )^\frac{\sigma }{2}|u|^2\Vert _{L^2}^2. \end{aligned}$$However, we cannot use the Córdoba-Córdoba inequality for \((-\Delta )^{s-\sigma }\) in the term \(\langle (-\Delta )^{s-\sigma }u,|u|^{2}u\rangle \) since \(s\le \sigma \). We instead employ a direct estimation (using in particular the Sobolev embedding \(L^4=W^{0,4}\subset W^{s-\sigma ,4}\)):
$$\begin{aligned} \langle (-\Delta )^{s-\sigma }u,|u|^{2}u\rangle&\ge -\Vert (-\Delta )^{s-\sigma }u\Vert _{L^4}\Vert u\Vert _{L^4}^3\ge -C\Vert u\Vert _{L^4}^4. \end{aligned}$$We arrive at
$$\begin{aligned} {\mathscr {E}}(u)&\ge \frac{1}{2}e^{\xi ^{-1}(\Vert u\Vert _{H^{s -}})}\left( \Vert |u|^2\Vert _{{\dot{H}}^\sigma }^2+\Vert \Pi ^N|u|^2u\Vert _{L^2}^2+\Vert u\Vert _{H^s}^2-C\Vert u\Vert _{L^4}^4\right) . \end{aligned}$$Now, let us set
$$\begin{aligned} {\mathscr {M}}(u):=M'(u,{\mathscr {L}}(u)), \end{aligned}$$where \(M(u)=\frac{1}{2}\Vert u\Vert _{L^2}^2.\) We obtain that
$$\begin{aligned} {\mathscr {M}}(u)=e^{\xi ^{-1}(\Vert u\Vert _{H^{s-}})}\left( \Vert u\Vert _{L^4}^4+\Vert u\Vert _{H^{s-\sigma }}^2\right) . \end{aligned}$$This gives us that
$$\begin{aligned} {\mathscr {E}}(u)&\ge \frac{1}{2}e^{\xi ^{-1}(\Vert u\Vert _{H^{s -}})}\left( \Vert |u|^2\Vert _{{\dot{H}}^\sigma }^2+\Vert \Pi ^N|u|^2u\Vert _{L^2}^2+\Vert u\Vert _{H^s}^2\right) -\frac{C}{2}{\mathscr {M}}(u). \end{aligned}$$(4.8)
-
(a)
Remark 4.2
Notice that for \(\sigma <\frac{1}{2}\), we do not have an estimate of \({\mathscr {E}}(u)\) for \(s\in (\sigma ,d/2)\). So we construct global solutions in that case using the arguments in Sect. 6. Surprisingly enough, we construct solutions, for such \(\sigma \), in lower regularities \(s\in (0,\sigma )\) since in that cases the need estimates are obtained through the control of \({\mathscr {E}}(u)\) established above (see Sect. 6).
For any \(\sigma \in (0,1]\), Assumption 5 is now fulfilled for \(s\in (d/2,\infty )\cup [\max (1/2,\sigma ),1+\sigma ]\cup [0,\sigma ]\). Notice that the term \(-\frac{C}{2}{\mathscr {M}}(u)\) in (4.8) does not have any obstruction because it is controlled under expectation (see (4.18) for details of the Itô estimate on M(u)). It’s expectation is just added the to right hand side of (3.16) and similarly for absolute \({\tilde{C}}\) in (4.6).
In particular, we notice that
where \(C=C(s,\sigma )\) does not depend on \((u,N,\alpha )\).
4.2 Fulfillment of Assumption 6 (The stochastic GWP)
For simplicity we present the proof of stochastic GWP in the case \(0\le s\le 1+\sigma \), we then consider the corresponding dissipation \({\mathscr {L}}(u)\). The other case involves a simpler dissipation operator and can be treated similarily.
We follow the well-known Da Prato-Debussche decomposition [19] (also known as Bourgain decomposition [6]). Let us consider the following linear stochastic equation
This equation admits a unique solution known as stochastic convolution:
It follows the Itô theory that z(t) is an \({\mathscr {F}}_t-\)martingale. The Doob maximal inequality combined with the Itô isometry shows that, for any \(T>0\)
We notice that z exists globally in t for almost all \(\omega \in \Omega \). Let \(u_0\) be \(E^N-\)valued \({\mathscr {F}}_0-\)independent random variable. Fix \(\omega \) such \(z^\omega \) exists globally in time, and consider the nonlinear deterministic equation
where \(F(v,z)=-{\mathbf{i }}((-\Delta )^\sigma v+|v+z|^2(v+z))-\alpha e^{\xi ^{-1}(\Vert v+z\Vert _{H^{s-}})}[\Pi ^N|v+z|^2(v+z)+(-\Delta )^{s-\sigma }(v+z)]\).
We remark that for a global solution v to (4.12), we have that \(u=v+z\) is a global solution to (4.5) supplemented with the initial condition \(u(t=0)=u_0^\omega \).
The local existence for (4.12) follows from the classical Cauchy-Lipschitz theorem since F(v, z) is smooth. Let us show that this local solution is in fact global. By an standard iteration argument, it suffices to show that the \(L^2\)-norm does not blow up in finite time. We have that
By adding \(z-z\) and using Cauchy-Schwarz, we obtain
We then have two complementary cases for a \(t\in [0,T]\):
-
(1)
either \(\Vert v\Vert _{H^{s-\sigma }}^2\le {\tilde{C}}_N(\Vert z\Vert _{L^2}^2+\Vert z\Vert _{L^4}^4)\); in this case
$$\begin{aligned} {\partial _t}\Vert v\Vert _{L^2}^2 \le C^0_\alpha (\omega ,T), \end{aligned}$$(4.13) -
(2)
or \(\Vert v\Vert _{H^{s-\sigma }}^2> {\tilde{C}}_N(\Vert z\Vert _{L^2}^2+\Vert z\Vert _{L^4}^4)\); in this case
$$\begin{aligned} e^{\xi ^{-1}(\Vert v+z\Vert _{H^{s-}})}\left( -\Vert v\Vert _{H^{s-\sigma }}^2+{\tilde{C}}_N\Vert z\Vert _{L^2}^2\right) \le 0, \end{aligned}$$and
$$\begin{aligned} {\partial _t}\Vert v\Vert _{L^2}^2 \le C^1_\alpha (\omega ,T). \end{aligned}$$Taking \(C_\alpha =\max (C^0_\alpha ,C^1_\alpha )\), we obtain the wished finiteness of \(\Vert v\Vert _{L^2}\).
Now, using the mean value theorem and the Gronwall lemma, we find for u and v two solutions to (4.5) that
where \(f(u)=F(u,0).\)
Standard arguments show that the constructed solution u is adapted to \(\sigma (u_0,{\mathscr {F}}_t).\)
4.3 Fulfillment of Assumption 7 (Zero viscosity limit, \(\alpha \rightarrow 0\))
The difficulty in the convergence of Assumption 7 is the fact that both \(P^{N*}_{t,\alpha _k}\) and \(\mu ^N_{\alpha _k}\) depend on \(\alpha _k\), we then need some uniformity in the convergence \(u^N_{\alpha _k}(t,\cdot )\rightarrow \phi ^N_t(\cdot )\) as \(\alpha _k\rightarrow 0\). The following lemma gives the needed uniform convergence. To simplify the notation, we use the abuse of notation: \(P^{N*}_{t,\alpha _k}=:P^{N*}_{t,k}\), \(\mu ^N_{\alpha _k}=:\mu ^N_{k}\) and \(u_{\alpha _k}=:u_k\).
Lemma 4.3
Let \(T>0\). For any \(R>0\), any \(r>0\),
where
We postpone the proof of Lemma 4.3. We remark that, using the Ito isometry and the Chebyshev inequality we have
where C does not depend on (r, k, t).
Let \(f:L^2\rightarrow {\mathbb {R}}\) be a bounded Lipschitz function. Without any loss of generality we can assume that f is bounded by 1 and its Lipschitz constant is also 1. We have
We see that \(B\rightarrow 0\) as \(k\rightarrow \infty \) according to the weak convergence \(\mu ^N_k\rightarrow \mu ^N.\)
Using the boundedness of f we obtain
Now from (3.16),
where C does not depend on \((N,\alpha ).\) Combining this with the Chebyshev inequality we obtain that
Using the boundedness and Lipschitz properties of f, we obtain
where
Using the (4.14) we obtain that
We finally obtain
We pass to the limit on k first, by applying apply Lemma 4.3, we obtain \(A_{1,1}\rightarrow 0\). Then we take the limits \(r\rightarrow \infty \) and \(R\rightarrow \infty \), we arrive at the conclusion of Assumption 7.
Now let us prove Lemma (4.3):
Proof of Lemma 4.3
Let \(u_0\in B_R(L^2)\) and \(u_k\) and u be the solutions of (4.5) (with viscosity \(\alpha _k\)) and (4.1) starting at \(u_0\), respectively. Recall that \(u_k\) can be decomposed as \(u_k=v_k+z_k\) where \(v_k\) is the solution of (4.12) with initial datum \(u_0\) and \(z_k\) is given by (4.10) with \(\alpha _k\). In order to prove Lemma 4.3, it suffice to show that
Indeed, we already have by (4.11) that \({\mathbb {E}}\sup _{t\in [0,T]}\Vert z_k(t)\Vert _{L^2}\rightarrow 0\) as \(k\rightarrow \infty \). Set \(w_k=v_k-u\). We will treat the case \(s\le 1+\sigma \) which is more delicate. We then consider the equation satisfied by \(w_k\):
where f and g is a homogeneous of degree 2 complex polynomial. We claim that \(\lim _{k\rightarrow \infty }\Vert w_k\Vert _{L^2}=0\) almost surely. Indeed, by taking the dot product with \(w_k\), we obtain after the use of the Gronwall inequality,
We pass to the limit \(k\rightarrow \infty \) with the use of (4.11) to obtain the claim.
Now, writing the Itô formula for \(\Vert u_k\Vert _{L^2}^2\), we have
where
Since \(\alpha _k\le 1,\) we have that, on the set \(S_{r,k}(t),\)
where C(r, N) does not depend on k. Hence we see that, on \(S_{r,k}(t)\),
In particular, we have the following two estimates:
Hence coming back to (4.15) and using the (deterministic) conservation \(\Vert u(t)\Vert _{L^2}=\Vert P_N u_0\Vert _{L^2}\) and the estimate (4.16), we obtain
Therefore, using again the bound (4.11), we obtain the almost sure convergence \(\Vert z_k\Vert _{L^2}\rightarrow 0\) (as \(k\rightarrow \infty \), up to a subsequence), we obtain then the almost sure convergence
Now, we use (4.16) and the Lebesgue dominated convergence theorem to obtain
The proof of Lemma 4.3 is finished. \(\square \)
4.4 Estimates
Let us recall that
Proposition 4.4
We have that
Proof of Proposition 4.4
We present the more difficult case in which the dissipation is given by
In this case we have
The other case can be proved using a similar procedure. We split the proof in different steps:
-
(1)
Step 1: Identity for the \((\mu ^N_\alpha \)).
Applying the Itô formula to M(u), where u is the solution to (4.5), we obtain
$$\begin{aligned} dM(u)=\left[ -\alpha {\mathscr {M}}(u)dt+\frac{\alpha }{2}A_0^N\right] dt+\sqrt{\alpha }\sum _{m=0}^Na_m\langle u,e_m\rangle d\beta _m. \end{aligned}$$Integrating in t and in ensemble with repect to \(\mu ^N_\alpha \), we obtain
$$\begin{aligned} \int _{L^2}{\mathscr {M}}(u)\mu ^N_\alpha (du)=\frac{A_0^N}{2}, \end{aligned}$$(4.18)this identity used the invariance \(\mu ^N_\alpha .\)
Let us now establish an auxiliary bound. Apply the Itô formula to \(M^2(u)\)
$$\begin{aligned} dM^2(u)=&\left[ \alpha M(u)\left( -{\mathscr {M}}(u)+\frac{A_0^N}{2}\right) +\frac{\alpha }{2}\sum _{m\le N}\langle u,e_m\rangle ^2\right] dt\\&+2\sqrt{\alpha }M(u)\sum _{m\le N}\langle u,e_m\rangle d\beta _m. \end{aligned}$$Integrating in t and with respect respect to \(\mu ^N_\alpha \) we arrive at
$$\begin{aligned} \int _{L^2}M(u){\mathscr {M}}(u)\mu ^N_\alpha (du) \le C, \end{aligned}$$(4.19)where C does not depend in \((N,\alpha )\). The estimate above is obtained after the following remark
$$\begin{aligned} \int _{L^2}M(u)\mu ^N_\alpha (du)\le \int _{L^2}{\mathscr {E}}(u)\mu ^N_\alpha (du)\le C_1 \end{aligned}$$where \(C_1\) is independent of \((N,\alpha )\).
-
(2)
Step 2: Identity for the \((\mu ^N\)). By usual arguments, we obtain the following estimates for \((\mu ^N)\):
$$\begin{aligned} \int _{L^2}{\mathscr {M}}(u)\mu ^N(du)&=\frac{A_0^N}{2}; \end{aligned}$$(4.20)$$\begin{aligned} \int _{L^2}M(u){\mathscr {M}}(u)\mu ^N(du)&\le C. \end{aligned}$$(4.21)We do not give details of proof of the identities. In the next step we will prove more delicate estimates whose proof is highly more difficult as the passage to the limit cannot use any finite-dimensional advantage.
-
(3)
Step 3: Identity for the \(\mu \). In this part of the proof we perform the passage to the limit \(N\rightarrow \infty \) in (4.20) in order to obtain the identity (4.17).
The inequality
$$\begin{aligned} \int _{L^2}{\mathscr {M}}(u)\mu (du)\le \frac{A_0}{2} \end{aligned}$$can be obtained by invoking lower semi-continuity of \({\mathscr {M}}\). The other way around, the analysis is more challenging. In [54] a similar identity was established with the use of an auxiliary estimate on a quantity of type \(E(u){\mathscr {E}}(u)\). But in our context, such an estimate is not available. Indeed, in order to obtain it, we shall apply the Itô formula on \(E^2\), the dissipation will be \(E(u){\mathscr {E}}(u)\); but other terms including \(A_\sigma ^NE(u)\) have to be controlled in expectation. However, we do not have an \(N-\)independent control on \(\int _{L^2}E(u)\mu ^N(du)\) because this term is smoother than \({\mathscr {E}}(u)\) for \(s<\sigma \). Therefore the latter cannot be exploited. We remark, on the other hand, that this is why the measure \(\mu \) is expected to be concentrated on regularities lower than the energy space \(H^\sigma \). Now, without a control on \(E(u){\mathscr {E}}(u)\), we can only handle the weaker quantity \(M(u){\mathscr {M}}(u)\) from (4.19). So our proof here will be more tricky than that in [54].
Coming back to the proof of the remaining inequality, we write for some fixed frequency F, the frequency decomposition (setting \(\Pi ^{>F}=1-\Pi ^F\))
$$\begin{aligned} \frac{A_0^N}{2}&\le {\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}\left( \Vert \Pi ^F|u^N|^2\Vert _{L^2}^2+\Vert \Pi ^{F}u^N\Vert _{H^{s-\sigma }}^2\right) \\&\quad +{\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}\left( \Vert \Pi ^{> F}|u^N|^2\Vert _{L^2}^2+\Vert \Pi ^{> F}u^N\Vert _{H^{s-\sigma }}^2\right) \\&=:i+ii, \end{aligned}$$where \(u^N\) is distributed by \(\mu ^N\). Let us follow the following sub-steps:
-
(a)
First, ii can be estimated by using the control on \({\mathscr {E}}\) (4.7) as follows
$$\begin{aligned} ii&{\ \lesssim \ \ }F^{-\sigma }\left( {\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}(\Vert \Pi ^{> F}|u^N|^2\Vert _{H^\sigma }^2+ \Vert u^N\Vert _{{\dot{H}}^s}^2)\right) \\&{\ \lesssim \ \ }F^{-\sigma }{\mathbb {E}}{\mathscr {E}}(u^N){\ \lesssim \ \ }F^{-\sigma }C. \end{aligned}$$ -
(b)
As for i, we can split it by using localization in \(H^{s-}\) (notice that by using the Skorokhod theorem \((u^N)\) converges almost surely on \(H^{s-}\) to some \(H^{s-}-\)valued random variable u). For any fixed \(R>0\) we set \(\chi _R=1_{\{\Vert u^N\Vert _{H^{s-}}\ge R\}}\). We have
$$\begin{aligned}&{\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}(\Vert \Pi ^{F}|u^N|^2\Vert _{L^2}^2 + \Vert \Pi ^Fu^N\Vert _{H^{s-\sigma }}^2)\chi _R\\&\quad {\ \lesssim \ \ }{\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}(\Vert \Pi ^{F}|u^N|^2\Vert _{H^{\frac{d}{2}+}}^2 + \Vert \Pi ^Fu^N\Vert _{H^{s-\sigma }}^2)\chi _R\\&\quad {\ \lesssim \ \ }{\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}(\Vert u^N\Vert _{H^{\frac{d}{2}+}}^4 + \Vert \Pi ^Fu^N\Vert _{H^{s-\sigma }}^2)\chi _R\\&\quad {\ \lesssim \ \ }F^{\frac{d}{2}+}{\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}(\Vert u^N\Vert _{L^2}^4+ \Vert u^N\Vert _{H^{s-\sigma }}^2)\chi _R\\&\quad {\ \lesssim \ \ }F^{\max (\frac{d}{2}+, s-\sigma )}R^{-2}{\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}\Vert u^N\Vert _{H^{s-}}^2\left( \Vert u^N\Vert _{L^2}^4+ \Vert u^N\Vert _{H^{s-\sigma }}^2\right) \\&\quad {\ \lesssim \ \ }F^{\max (\frac{d}{2}+, s-\sigma )+s}R^{-2}{\mathbb {E}}\Vert u^N\Vert _{L^2}^2e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}\left[ \Vert u^N\Vert _{L^4}^4+ \Vert u^N\Vert _{H^{s-\sigma }}^2\right] . \end{aligned}$$Let us use the estimate (4.20) and (4.21) to arrive at
$$\begin{aligned}&{\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}\left( \Vert \Pi ^F|u^N|^2\Vert _{L^2}^2+\Vert \Pi ^Fu^N\Vert _{H^{s-\sigma }}^2\right) \chi _R\\&\quad {\ \lesssim \ \ }F^{\max (\frac{d}{2}+, s-\sigma )+s}R^{-2}{\mathbb {E}}M(u^N){\mathscr {M}}(u^N)\\&\quad {\ \lesssim \ \ }F^{\max (\frac{d}{2}+, s-\sigma )+s}R^{-2}C, \end{aligned}$$where C does not depend on N.
-
(c)
On the other hand, we have the following convergence, thanks to the Lebesgue dominated convergence theorem,
$$\begin{aligned}&\lim _{N\rightarrow \infty } {\mathbb {E}}e^{\xi ^{-1}(\Vert u^N\Vert _{H^{s-}})}\left( \Vert \Pi ^F|u^N|^2\Vert _{L^2}^2+ \Vert \Pi ^Fu^N\Vert _{H^{s-\sigma }}^2\right) (1-\chi _R)\\&={\mathbb {E}}e^{\xi ^{-1}(\Vert u\Vert _{H^{s-}})}\left( \Vert \Pi ^F|u|^2\Vert _{L^2}^2+ \Vert \Pi ^Fu\Vert _{H^{s-\sigma }}^2\right) (1-\chi _R). \end{aligned}$$
Gathering all this, we obtain, after the limit \(N\rightarrow \infty \), that
$$\begin{aligned} \frac{A_0}{2}\le&{\mathbb {E}}e^{\xi ^{-1}(\Vert u\Vert _{H^{s-}})}\left( \Vert \Pi ^F|u|^2\Vert _{L^2}^2+ \Vert \Pi ^Fu\Vert _{H^{s-\sigma }}^2\right) (1-\chi _R)+ F^{-\sigma } C_1\\&+F^{\max (\frac{d}{2}+, s-\sigma )+s}R^{-2}C_2. \end{aligned}$$We let \(R\rightarrow \infty \), then \(F\rightarrow \infty \) and obtain
$$\begin{aligned} \frac{A_0}{2}\le e^{\xi ^{-1}(\Vert u\Vert _{H^{s-}})}{\mathbb {E}}\left( \Vert u\Vert _{L^4}^4+ \Vert u\Vert _{H^{s-\sigma }}^2\right) . \end{aligned}$$ -
(a)
The proof of Proposition 4.4 is finished. \(\square \)
Remark 4.5
The identity (4.17) is crucial for establishing the non-degeneracy properties of the measure \(\mu .\) It trivially rule out the Dirac measure at 0, notice that the Dirac at 0 is a trivial invariant measure for FNLS.
Also, by considering a noise \(\kappa dW\), (4.17) becomes
Such scaled noises provide invariant measures \(\mu _\kappa \) for FNLS, all satisfying (4.22). Define a cumulative measure \(\mu ^*\) by a convex combination
where \(\kappa _j\uparrow \infty \) and \(\sum _0^\infty \rho _j=1\). The measure \(\mu ^*\) is invariant for FNLS. Moreover, for any \(K>0\), we can find a positive \(\mu ^*\)-measure set of data whose \(H^s\)-norms are larger than K.
In order to finish the proof of Theorem 1.1, we present in the section below the fulfillment of Assumptions 1 and 2.
5 End of the proof of Theorem 1.1: Local well-posedness
In this section, we present a deterministic local well-posedness result for \(\sigma \in [\frac{1}{2} ,1]\) in (1.1), which heavily replies on a bilinear Strichartz estimate obtained in Sect. 5.1. See also Sect. 3 in [55]. We also show a convergence from Galerkin approximations of FNLS to FNLS.
Theorem 5.1
(Deterministic local well-posedness on the unit ball) The fractional NLS (1.1) with \(\sigma \in [\frac{1}{2} ,1]\) is locally well-posed for radial data \(u_0 \in H_{rad}^s (B^d)\), \(s> s_l (\sigma )\), where \(s_l(\sigma )\) is defined as in (1.3). More precisely, let us first fix \(s > s_l (\sigma )\) (defined as in (1.3)), and for every \(R> 0\), we set \(\delta = \delta (R) = c R^{-2s}\) for some \(c \in (0,1]\). Then there exists \(b> \frac{1}{2}\) and \(C , {\widetilde{C}} >0\) such that every \(u_0 \in H_{rad}^s (B^d)\) satisfying  , there exists a unique solution of (1.1) in \(X_{\sigma , rad}^{s,b} ([-\delta , \delta ] \times B^d)\) with initial condition \(u(0) = u_0\). Moreover,
, there exists a unique solution of (1.1) in \(X_{\sigma , rad}^{s,b} ([-\delta , \delta ] \times B^d)\) with initial condition \(u(0) = u_0\). Moreover,

Remark 5.2
The function f in Assumption 1 is found to be equal to \(\delta (x)=cx^{-2s}\).
5.1 Bilinear Strichartz estimates
In this subsection, we prove the bilinear estimates that will be used in the rest of this section. The proof is adapted from [1] with two dimensional modification and a different counting lemma.
Lemma 5.3
(Bilinear estimates for fractional NLS) For \(\sigma \in [\frac{1}{2} ,1]\), \(j =1,2\), \(N_j >0\) and \(u_j \in L_{rad}^2 (B^d)\) satisfying
we have the following bilinear estimates.
-
(1)
The bilinear estimate without derivatives.
Without loss of generality, we assume \(N_1 \ge N_2 \), then for any \(\varepsilon >0 \)
 (5.1)
(5.1) -
(2)
The bilinear estimate with derivatives.
Moreover, if \(u_j \in H_0^1 (B^d)\), then for any \(\varepsilon >0 \)
 (5.2)
(5.2)
Remark 5.4
Notice that in (5.1) and (5.2), the upper bounds are independent on the fractional power \(\sigma \). This is because a counting estimate in Claim 5.7 does not see difference on \(\sigma \). Hence the local well-posedness index is uniform for \(\sigma \in [\frac{1}{2},1)\).
Lemma 5.5
(Bilinear estimates for classical NLS) Under the same setup as in Lemma 5.3, the bilinear estimate analogue is given by

Notice that the proof of Lemma 5.5 in fact can be extended from [1], hence we will only focus on the proof of Lemma 5.3 and the proof of the local theory for fractional NLS in the rest of this section.
Proposition 5.6
(Lemma 2.3 in [10]: Transfer principle) For any \(b > \frac{1}{2}\) and for \(j =1,2\), \(N_j >0\) and \(f_j \in X_{\sigma }^{0,b} ({\mathbb {R}}\times B^d)\) satisfying
one has the following bilinear estimates.
-
(1)
The bilinear estimate without derivatives.
Without loss of generality, we assume \(N_1 \ge N_2\), then for any \(\varepsilon >0 \)
 (5.3)
(5.3) -
(2)
The bilinear estimate with derivatives.
Moreover, if \(f_j \in H_0^1 (B^d)\), then for any \(\varepsilon >0 \)
 (5.4)
(5.4)
Proof of Lemma 5.3
First we write
where \(c_{n_1} = (u_1 , e_{n_1})_{L^2}\) and \(d_{n_2} = (u_2 , e_{n_2})_{L^2}\). Then
Therefore, the bilinear objects that one needs to estimate are the \(L_{t,x}^2\) norms of
Let us focus on (5.1) first.

Here we employ a similar argument used in the proof of Lemma 2.6 in [50]. We fix \(\eta \in C_0^{\infty } ((0,1))\), such that \(\eta \big |_{I} \equiv 1\) where I is a slight enlargement of (0, 1). Thus we continue from (5.5)

where

By expanding the square above and using Plancherel, we have

Then by Schur’s test, we arrive at

We claim that
Claim 5.7
-
(1)
\(\# \Lambda _{N_1, N_2, \tau } = {\mathscr {O}}(N_2)\) ;
-
(2)
 .
.
Assuming Claim 5.7, we see that

Therefore, (5.1) follows.
Now we are left to prove Claim 5.7.
Proof of Claim 5.7
In fact, (2) is due to Hölder inequality and the logarithmic bound on the \(L^p\) norm of \(e_n\) in (2.1)

For (1), we have that for fixed \(\tau \in {\mathbb {N}}\) and fixed \(n_2 \sim N_2\)

There are at most 1 integer \(z_{n_1}\) in this interval, since by convexity
Then

We finish the proof of Claim 5.7. \(\square \)
The estimation of (5.2) is similar, hence omitted.
The proof of Lemma 5.3 is complete now. \(\square \)
5.2 Nonlinear estimates
In the local theory, we need a nonlinear estimate of the following form

where \(u_j \in \{ u, {\bar{u}} \}\) for \(j = 1 , 2, 3\).
To this end, we first study the nonlinear behavior of all frequency localized \(u_j\)’s based on the bilinear estimates that we obtained, then sum over all frequencies.
For \(j \in \{ 0, 1,2, 3\}\), let \(N_j = 2^k, k \in {\mathbb {N}}\). We denote

Also we denote by \({\underline{N}} = (N_0, N_1 , N_2, N_3)\) the quadruple of \(2^k\) numbers, \(k \in {\mathbb {N}}\), and
Lemma 5.8
(Localized nonlinear estimates) Assume that \(N_1 \ge N_2 \ge N_3 \). Then there exists \(0< b' < \frac{1}{2}\) such that one has


Remark 5.9
Lemma 5.8 will play an important role in the local theory. Moreover, the first estimate (5.9) will be used in the case \( N_0 \le c N_1\) while the second one will be used in the case \(N_0 \ge c N_1 \). The proof of Lemma 5.8 is adapted from Lemma 2.5 in [1]. We briefly present the proof, since a treatment in this proof will be used in the next section.
Proof of Lemma 5.8
We start with (5.9).
On one hand, by Hölder inequality, Bernstein inequality and Lemma 2.2, we write

On the other hand, we can estimate  using Proposition 5.6. That is,
using Proposition 5.6. That is,

where \(b_0 > \frac{1}{2}\).
Interpolation between the two estimates above implies

where \(b' \in (0, \frac{1}{2})\) and \(\varepsilon ' \) is a small positive power after interpolation. This finishes the computation of (5.9).
For (5.10), we will use a trick to introduce a Laplacian operator into the integral. This is the treatment that we mentioned earlier that will be used in the next section.
First recall Green’s theorem,

Note that
where \( z_k^2\)’s are the eigenvalues defined in (2.2). Then we write
Define
It is easy to see that for all s

Using this notation, we write
and
By the product rule and the assumption that \(N_1 \ge N_2 \ge N_3\), we only need to consider the two largest cases of \(\Delta ( u_1 u_{2} u_{3}) \). They are
-
(1)
\((\Delta u_{1}) u_{2} u_{3}\)
-
(2)
\((\nabla u_{1}) \cdot (\nabla u_{2}) u_{3} \) .
We denote
Using \(\Delta u_i = -N_i^2 V u_i\), we obtain

Now for  , we estimate it in a similar fashion that we did in (5.9). On one hand, by Hölder inequality, Bernstein inequality and Lemma 2.2, we have
, we estimate it in a similar fashion that we did in (5.9). On one hand, by Hölder inequality, Bernstein inequality and Lemma 2.2, we have

On the other hand, using Proposition 5.6, we get

Interpolation between the two estimates above implies

Similarly \(\varepsilon '\) is a small positive power after interpolation. The proof of Lemma 5.8 is complete. \(\square \)
Proposition 5.10
(Nonlinear estimates) For \(\sigma \in [\frac{1}{2} ,1]\), \(s > s_{l}(\sigma )\) as in (1.3), there exist \(b, b' \in {\mathbb {R}}\) satisfying
such that for every triple \((u_1, u_2 , u_3)\) in \(X_{\sigma }^{s,b} ({\mathbb {R}}\times B^d)\),

Proof of Proposition 5.10
Based on Lemma 5.8, we only need to consider \(L= \sum _{{\underline{N}}} L({\underline{N}})\). By symmetry, we can reduce the sum into the following two cases:
-
(1)
\( N_0 \le c N_1\)
-
(2)
\( N_0 \ge c N_1\).
Case 1: \( N_0 \le c N_1\).
Using Lemma 5.8 and Cauchy–Schwarz inequality, we obtain

where \(s > s_l(\sigma ) \). For the last inequality, we sum from the smallest index \(N_{3}\) to the largest one using Cauchy–Schwarz inequality. Then by the embedding \(X_{\sigma }^{s,b} \subset X_{\sigma }^{s , b' } \) and duality, we have the estimate in Case 1.
Case 2: \( N_0 \ge c N_1\).
Similarly, by Lemma 5.8 and Cauchy–Schwarz inequality again, we have

where \(s > s_l(\sigma )\). Then by the embedding \(X_{\sigma }^{s,b} \subset X_{\sigma }^{s , b' } \) and duality, we have the estimate in Case 2. The proof of Proposition 5.10 is complete. \(\square \)
5.3 Local well-posedness
We now turn to the proof of the main result in this section: local well-posedness.
Proof of Theorem 5.1
Let \(u_0 \in H^{s}\). We first define a map

We prove this locally well-posedness theory using a standard fixed point argument. Let \(R_0>0\) and \(u_0 \in H^s (B^d)\) with  . We show that there exists \(R>0 \) and \(0< \delta = \delta (R_0) <1 \) such that F is a contraction mapping from \(B(0, R) \subset X_{\sigma , \delta }^{s,b} (B^d)\) onto itself.
. We show that there exists \(R>0 \) and \(0< \delta = \delta (R_0) <1 \) such that F is a contraction mapping from \(B(0, R) \subset X_{\sigma , \delta }^{s,b} (B^d)\) onto itself.
Define \(R = 2 c_0 R_0\).
-
(1)
F is a self map from \(B(0, R) \subset X_{\sigma ,\delta }^{s,b} (B^d)\) onto itself.
For \(\delta < 1\), by Lemma 2.4, Proposition 5.10 and Sobolev embedding

Taking \(\delta _1 = (\frac{c_0}{c_2 R^{2}})^{\frac{1}{1 +2 b - 4b'}} <1\) such that \( c_2 \delta _1^{1 +2 b - 4b'} R^{3} = c_0 R\), we see that F is a self map.
-
(2)
F is a contraction mapping.
Similarly, by Lemma 2.4 and Proposition 5.10
 (5.11)
(5.11)Taking \(\delta _2 = (\frac{1}{2c_4 R^{2}})^{\frac{1}{1 +2 b - 4b'}}\) such that \(c_4 \delta _2^{1 +2 b - 4b'} R^{2} = \frac{1}{2}\), we can make F a contraction mapping.
Now we choose
$$\begin{aligned} \delta _R = \min \{\delta _1, \delta _2 \}. \end{aligned}$$(5.12)As a consequence of the fixed point argument, we have

-
(3)
Stability.
If u and v are two solutions to (1.1) with initial data \(u(0) =u_0\) and \(v(0) = v_0\) respectively. Then by (5.11) and the choice of \(\delta _R\) (5.12)

which implies

Now the proof of Theorem 5.1 is finished. \(\square \)
Remark 5.11
For finite N let us denote \(\Pi ^N L^2\) by \(E_N\) and the local flow on \(E_N = \Pi ^N L^2\) by \(\phi _t^N\). We verify easily that the local existence time obtained in Theorem 5.1 is valid for the Galerkin approximations for the same radius R of the balls. We set \(\phi _t\) to be the local flow constructed in Theorem 5.1 in \(X_{\sigma }^{s,b}\).
Proposition 5.12
(Convergence of Galerkin projections to FNLS) Let \(s>s_l(\sigma )\) as in (1.3), \(u_0 \in H^{s}\) and \((u_0^N) \) be a sequence that converges to \(u_0 \) in \(H^{s}\), where \(u_0^N \in E_N\). Then for any \(r\in (s_l(\sigma ),s)\)

Proof of Proposition 5.12
Since \(u_0^N \rightarrow u_0\), there exists an R such that \(u_0^N \in B_R(H^{\gamma })\). Take the same \(T_R\) as in (5.12). Set \(w_0^N = u_0^N - u_0\) and \(w^N = \phi _t^N u_0^N - \phi _t u_0\), then we write

Using Hölder inequality, Lemma 2.4, Proposition 5.10 and the choice of \(T_R\) as in (5.12), we have

Therefore,

Recall that \(z_N^2 \sim N^2\), then

Hence the proof of Proposition 5.12 is finished. \(\square \)
Remark 5.13
In Sect. 4, we fulfilled Assumptions 4 to 7 for any \(\sigma \in (0,1]\). However, Theorem 5.1 covers only the range \(\sigma \in [\frac{1}{2},1]\) and the given regularities. The case \(\sigma \in (0,\frac{1}{2})\) was not treated in Theorem 5.1 because of the convexity needed in the proof of Claim 5.7. Nevertheless, in smooth regularities \(s>\frac{d}{2}\) a same local well-posedness as in Theorem 5.1 for \(\sigma \in (0,\frac{1}{2})\) holds true. We will not present the details of such easy argument. We also readily have the convergence established in Proposition (5.12) for such values of \(\sigma \). This ends the proof of Theorem 1.1.
6 Proof of Theorem 1.3
In this section we present the proof of Theorem 1.3. We consider then \(\sigma \in (0,1]\) and \(\max (\sigma ,\frac{1}{2})\le s\le 1+\sigma \), or \(\sigma \in (\frac{1}{2},1]\) and \(s\in (0,\sigma ]\), with \(d\ge 2\). Recall that from (4.7)
where C does not depend on N.
6.1 Existence of global solutions and invariance of the measure
For an arbitrary positive integer k, let us consider the spaces
Combining standard embedding results we obtain the compact embedding \(X_k\subset \subset Y_k\).
Denote by \(\nu ^N_k\) the laws of the processes \((u^N(t))_{t\in [0,k)}\) that are seen as random variables valued in \(C([0,k],H^{(s-2\sigma )-})\). We see, using the invariance, the relation between \(\mu ^N\) and \(\nu ^N_k\):
Proposition 6.1
We have the estimate
where C does not depend on N.
Proof of Proposition 6.1
Let us write the fractional NLS (4.1) in the integral form
Now using (6.1) we have that
We recall that,
Combining the above estimates we obtain Proposition 6.1. \(\square \)
Proposition 6.2
\(u^N\) is compact in \(Y_k\) \({\mathbb {P}}-\)almost surely.
Proof of Proposition 6.2
Combining Proposition (6.1) and the Prokhorov theorem (Theorem A.4) we obtain a weak compactness of \((\nu ^N_k)\). Thanks to the Skorokhod representation theorem (see Theorem A.5), there are random variables \({\tilde{u}}_k^N\) and \({\tilde{u}}_k\), defined on a same probability space that is denoted by \((\Omega ,{\mathbb {P}})\), such that
-
(1)
\({\tilde{u}}_k^N\rightarrow \tilde{u_k}\) weakly on \(X_k\),
-
(2)
\({\tilde{u}}_k^N\) and \({\tilde{u}}_k\) are distributed by \(\nu _k^N\) and \(\nu _k\) respectively.
The proof of Proposition 6.2 is finished. \(\square \)
Proposition 6.3
\(\Pi ^N|u^N|^2u^N\) converges to \(|u|^2u\) in \(L^1_{t}H^{-\frac{d}{2}-1}\) as \(N\rightarrow \infty \).
-
(1)
\(u^N\) converges to u almost surely in \(L^2_tH^{s-}\subset L^2_{t,x}\)
-
(2)
\(|u^N|^2\) converges almost surely in \(L^2_tH^{\sigma -}\subset L^2_{t,x}\). In particular \(|u^N|^2\) is bounded in \(L^2_{t,x}\) almost surely, i.e \(\Vert u^N\Vert _{L^4_{t,x}}\) is bounded \({\mathbb {P}}-\)almost surely.
Now let us write, by using \(\Pi ^N|u^N|^2u^N=|u^N|^2u^N-\Pi ^{> N}|u^N|^2u^N\), a Bernstein inequality and convergence and boundedness established above,
Combining Propositions 6.2 and 6.3 with a diagonal argument we obtain the almost sure existence of global solutions for FNLS with \(\sigma \in (0,1)\), \(0< s\le 1+\sigma \) and \(d\ge 2\).
For the invariance of the law of the constructed solution u(t), let us denote by \(\nu \) the law of the process \(u=(u(t))_{t\in {\mathbb {R}}}\). From the subsequence in the N-parameter that produced the limiting measure \(\nu \), we can extract a subsequence, using the Prokhorov theorem and (6.1), that produces a measure \(\mu \) as a weak limit point of \((\mu ^N={\nu ^N}{\Big |_{t=t_0}})\). Passing to the limit along this subsequence in the relation (6.2), we see that \(\mu =\nu \Big |_{t=t_0}\) for any \(t_0\in {\mathbb {R}}\). This implies that \(\mu \) is an invariant law for u.
6.2 Uniqueness and Continuity
The uniqueness argument is formulated in the following observation.
Proposition 6.4
The space \(\Lambda = C_tL^2_x \cap L^2_tH^{\frac{1+}{2}}(B^d)\) is a uniqueness class for the fractional NLS (1.1).
Proof of Proposition 6.4
Let \(u,\ v\in \Lambda \) be two solutions to (1.1), both starting at \(u_0\). Let us write the Duhamel formulation
and the same for v.
Set \(w=u-v\) and \(\chi _\epsilon =1_{\{r\ge \epsilon \}}\).
Now using the radial Sobolev inequality (2.4), we obtain
Hence
It follows from the Gronwall that \(\Vert w\chi _\epsilon \Vert _{L^2}=0\). Now, write
First, since \(u,v\in \Lambda _s\), we have that \(w^2\in L^2\) almost surely in the t variable (hence \(w\in L^4\) almost surely in t). Second, the Lebesgue dominated convergence theorem shows that \(\Vert 1-\chi _\epsilon \Vert _{L^4}\rightarrow 0\) as \(\epsilon \rightarrow 0\). We obtain \(\Vert w\Vert _{L^2}=0\) almost surely in t. Now by continuity in t, we have that \(\Vert w\Vert _{L^2}=0\) for all t.Then the proof of Proposition 6.4 is finished. \(\square \)
As for the continuity, let us present the following result:
Proposition 6.5
For \(u_0,\ v_0\in \text {supp}(\mu )\), let \(u, \ v\) be the corresponding solutions to (1.1). Let us set \(w=u-v\) and \(w_0=u_0-v_0\), we have
where \(\epsilon (\Vert w_0\Vert _{L^2})\rightarrow 0\) as \(\Vert w_0\Vert _{L^2}\rightarrow 0\).
Proof of Proposition 6.5
Let us take \(\theta =\frac{1}{2}+\) and set
Since \(\theta <\frac{d}{2}\), we see that \(\gamma \rightarrow 0\) as \(\Vert w_0\Vert _{L^2}\rightarrow 0\). So we can consider \(\gamma<<1\) and take, as above, the function \(\chi _\gamma =1_{\{r\ge \gamma \}}\). Using the radial Sobolev inequality (2.4), we have
By the Gronwall inequality we obtain
Therefore
Since \(\Vert 1-\chi _\gamma \Vert _{L^4}^2\rightarrow 0\) as \(\Vert w_0\Vert _{L^2}\rightarrow 0\) we arrive at the result of Proposition 6.5. \(\square \)
Notice that Remark 4.5 applies also in the present situation. This completes the proof of Theorem 1.3.
Notes
Here weak turbulence refers to an energy cascade from low to high frequencies as time evolves. The norms higher than the energy tend to blow up at infinity.
Notice that we use here the version of the Birkhof ergodic theorem (Theorem 2.3 in [37]) that doesn’t require ergodicity of the dynamics under the considered measure. Therefore, we then loose in the characterisation of the limits of the orbital averages. However the claim does not need such characterisation, it requires only the finiteness of the limits which holds true with the invariance property of the measure.
\(H^s_0(B^d)\) is the Sobolev space of order s of functions \(f:B^d\rightarrow {\mathbb {C}}\) vanishing on the boundary of \(B^d.\)
Remark that \({\tilde{g}}\) is increasing and one-to-one from \({\mathbb {R}}\) to \({\mathbb {R}}\).
References
Anton, R.: Cubic nonlinear Schrödinger equation on three dimensional balls with radial data. Comm. Partial Differ. Equ. 33(10–12), 1862–1889 (2008)
Ayache, A., Tzvetkov, N.: \(L^p\) properties for Gaussian random series. Trans. Amer. Math. Soc. 360(8), 4425–4439 (2008)
Bedrossian, J., Zelati, M.C., Glatt-Holtz, N.: Invariant measures for passive scalars in the small noise inviscid limit. Commun. Math. Phys. 348(1), 101–127 (2016)
Bourgain, J.: Exponential sums and nonlinear Schrödinger equations. Geom. Funct. Anal. 3(2), 157–178 (1993)
Bourgain, J.: Periodic nonlinear Schrödinger equation and invariant measures. Comm. Math. Phys. 166(1), 1–26 (1994)
Bourgain, J.: Invariant measures for the \(2\)D-defocusing nonlinear Schrödinger equation. Comm. Math. Phys. 176(2), 421–445 (1996)
Bourgain, J.: On the growth in time of higher Sobolev norms of smooth solutions of Hamiltonian PDE. Int. Math. Res. Notices 1996(6), 277–304 (1996)
Bourgain, J.: Refinements of Strichartz’ inequality and applications to \(2\)D-NLS with critical nonlinearity. Int. Math. Res, Notices (1998)
Bourgain, J., Bulut, A.: Almost sure global well-posedness for the radial nonlinear Schrödinger equation on the unit ball II: the 3d case. J. Eur. Math. Soc. JEMS 16(6), 1289–1325 (2014)
Burq, N., Gérard, P., Tzvetkov, N.: Bilinear eigenfunction estimates and the nonlinear Schrödinger equation on surfaces. Invent. Math. 159(1), 187–223 (2005)
Burq, N., Thomann, L., Tzvetkov, N.: Remarks on the Gibbs measures for nonlinear dispersive equations. Ann. Fac. Sci. Toulouse Math. 27(3), 527–597 (2018)
Carles, R., Faou, E.: Energy cascades for NLS on the torus. Discrete and Continuous Dynamical Systems - A, 32 (2012)
Cho, Y., Hajaiej, H., Hwang, G., Ozawa, T.: On the Cauchy problem of fractional Schrödinger equation with Hartree type nonlinearity. Funkcialaj Ekvacioj 56(2), 193–224 (2013)
Cho, Y., Ozawa, T.: Sobolev inequalities with symmetry. Commun. Contemp. Math. 11(03), 355–365 (2009)
Colliander, J., Keel, M., Staffilani, G., Takaoka, H., Tao, T.: Almost conservation laws and global rough solutions to a nonlinear Schrödinger equation. Math. Res. Lett. 9(5–6), 659–682 (2002)
Colliander, J., Keel, M., Staffilani, G., Takaoka, H., Tao, T.: Transfer of energy to high frequencies in the cubic defocusing nonlinear Schrödinger equation. Invent. Math. 181(1), 39–113 (2010)
Constantin, P., Ignatova, M.: Remarks on the fractional laplacian with dirichlet boundary conditions and applications. Int. Math. Res. Notices 2017(6), 1653–1673 (2017)
Córdoba, A., Córdoba, D.: A pointwise estimate for fractionary derivatives with applications to partial differential equations. Proc. National Acad. Sci. 100(26), 15316–15317 (2003)
Da Prato, G., Debussche, A.: Two-dimensional navier-stokes equations driven by a space-time white noise. J. Funct. Anal. 196(1), 180–210 (2002)
Da Prato, G., Zabczyk, J.: Stochastic Equations in Infinite Dimensions. Cambridge University Press (2014)
Demirbas, S., Erdogan, M., Tzirakis, N.: In: Lect. Math. (ALM), (ed.) Existence and uniqueness theory for the fractional Schrödinger equation on the torus, volume 34 of Adv, pp. 145–162. Int. Press, Somerville, MA (2016)
Deng, Y., Nahmod, A., Yue, H.: Invariant Gibbs measures and global strong solutions for nonlinear Schröodinger equations in dimension two. arXiv preprint arXiv:1910.08492, (2019)
Dinh, V.D.: Well-posedness of nonlinear fractional Schrödinger and wave equations in Sobolev spaces. arXiv preprint arXiv:1609.06181, (2016)
Dudley, R.M.: Real Analysis and Probability. Cambridge University Press (2002)
Foldes, J., Sy, M.: Invariant measures and global well posedness for SQG equation. arXiv preprint arXiv:2002.09555 (2020)
Ginibre, J.: Le problème de Cauchy pour des EDP semi-linéaires périodiques en variables d’espace (d’après Bourgain). Number 237, pages Exp. No. 796, 4, 163–187. (1996). Séminaire Bourbaki, Vol. 1994/95
Grande, R.: Continuum limit for discrete NLS with memory effect. arXiv preprint arXiv:1910.05681 (2019)
Grande, R.: Space-time fractional nonlinear Schrödinger equation. SIAM J. Math. Anal. 51(5), 4172–4212 (2019)
Guardia, M.: Growth of sobolev norms in the cubic nonlinear Schrödinger equation with a convolution potential. Commun. Math. Phys. 329(1), 405–434 (2014)
Guo, B., Huo, Z.: Global well-posedness for the fractional nonlinear Schrödinger equation. Commun. Partial Differ. Equ. 36(2), 247–255 (2010)
Hani, Z.: Long-time instability and unbounded sobolev orbits for some periodic nonlinear Schrödinger equations. Arch. Ration. Mech. Anal. 211(3), 929–964 (2014)
Hani, Z., Pausader, B., Tzvetkov, N., Visciglia, N.: Modified scattering for the cubic Schrödinger equation on product spaces and applications. In: Forum of mathematics, Pi, volume 3. Cambridge University Press (2015)
Hong, Y., Yang, C.: Strong convergence for discrete nonlinear Schrödinger equations in the continuum limit. SIAM J. Math. Anal. 51(2), 1297–1320 (2019)
Jonsson, A., Wallin, H.: A Whitney extension theorem in \(L_p\) and Besov spaces. Annales de l’institut Fourier 28, 139–192 (1978)
Karatzas, I., Shreve, S.E.: Brownian Motion and Stochastic Calculus. Springer (1998)
Kirkpatrick, K., Lenzmann, E., Staffilani, G.: On the continuum limit for discrete NLS with long-range lattice interactions. Commun. Math. Phys. 317(3), 563–591 (2013)
Krengel, U.: Ergodic Theorems, vol. 6. Walter de Gruyter (2011)
Kuksin, S.: The Eulerian limit for 2D statistical hydrodynamics. J. Statist. Phys. 115(1–2), 469–492 (2004)
Kuksin, S., Shirikyan, A.: Randomly forced CGL equation: stationary measures and the inviscid limit. J. Phys. 37, 3805–3822 (2004)
Kuksin, S., Shirikyan, A.: Mathematics of Two-Dimensional Turbulence. Cambridge University Press, Cambridge (2012)
Kuksin, S.B.: Oscillations in space-periodic nonlinear Schrödinger equations. Geom. Funct. Anal. GAFA 7(2), 338–363 (1997)
Laskin, N.: Fractional quantum mechanics. Phys. Rev. E 62(3), 3135 (2000)
Latocca, M.: Construction of high regularity invariant measures for the 2D and 3D Euler equations and remarks on the growth of the solutions. arXiv preprint arXiv:2002.11086 (2020)
Lebowitz, J.L., Rose, H.A., Speer, E.R.: Statistical mechanics of the nonlinear Schrödinger equation. J. Statist. Phys. 50(3–4), 657–687 (1988)
Mattingly, J.C., Pardoux, E.: Invariant measure selection by noise: an example. Discrete and Continuous Dynamical Systems. (2014)
Mingaleev, S.F., Christiansen, P.L., Gaididei, Y.B., Johansson, M., Rasmussen, K.: Models for energy and charge transport and storage in biomolecules. J. Biol. Phys. 25(1), 41–63 (1999)
Øksendal, B.: Stochastic Differential Equations. Springer (2003)
Shirikyan, A.: Local times for solutions of the complex Ginzburg-Landau equation and the inviscid limit. J. Math. Anal. Appl. 384(1), 130–137 (2011)
Staffilani, G.: On the growth of high Sobolev norms of solutions for KdV and Schrödinger equations. Duke Math. J. 86(1), 109–142 (1997)
Sun, C., Tzvetkov, N.: Gibbs measure dynamics for the fractional nls. SIAM J. Math. Anal. 52(5), 4638–4704 (2020)
Sy, M.: Invariant measure and long time behavior of regular solutions of the Benjamin-Ono equation. Anal. PDE 11(8), 1841–1879 (2018)
Sy, M.: Almost sure global well-posedness for the energy supercritical Schrödinger equations. arXiv preprint arXiv:1905.03866 (2019)
Sy, M.: Invariant measure and large time dynamics of the cubic Klein-Gordon equation in 3D. Stochast. Partial Differ. Equ. Anal. Comput. 7(3), 379–416 (2019)
Sy, M., Yu, X.: Almost sure global well-posedness for the energy supercritical NLS on the unit ball of \({\mathbb{R}}^3 \). arXiv preprint arXiv:2007.00766 (2020)
Sy, M., Yu, X.: Global well-posedness for the cubic fractional NLS on the unit disk. arXiv preprint arXiv:2011.05517, (2020)
Tzvetkov, N.: Invariant measures for the nonlinear Schrödinger equation on the disc. Dyn. Partial Differ. Equ. 3(2), 111–160 (2006)
Tzvetkov, N.: Invariant measures for the defocusing nonlinear Schrödinger equation. Ann. Inst. Fourier (Grenoble) 58(7), 2543–2604 (2008)
Acknowledgements
X.Y. was funded in part by the Jarve Seed Fund and an AMS-Simons travel grant. Both authors are very grateful to the anonymous referees for valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author’s (M.S.) current address is Department of Mathematics, Imperial College London, United Kingdom. This work was written at Department of Mathematics, University of Virginia, Charlottesville, VA
The second author’s (X.Y.) current address is Department of Mathematics, University of Washington, Seattle, WA. This work was written at Department of Mathematics, MIT, Cambridge, MA.
Appendices
APPENDIX A. Results on probability measures and stochastic processes
In this section \((E,\Vert .\Vert )\) is a Banach space, \(C_b(E)\) denotes the space of bounded continuous functions \(f:E\rightarrow {\mathbb {R}}.\) We present some useful standard results from measure theory.
1.1 A.1. Convergence of measures
Definition A.1
Let \((\mu _n)_n\) be a sequence of Borel probability measures and \(\mu \) a Borel probability measure on E. We say that \((\mu _n)_n\) converges weakly to \(\mu \) if for all \(f\in C_b(E)\)
We write \(\mu _n\rightharpoonup \mu .\)
Definition A.2
A family \(\Lambda \) of Borel probability measures on E is said to be tight if for all \(\epsilon >0\) there is a compact set \(K_\epsilon \subset E\) such that for all \(\mu \in \Lambda \)
Theorem A.3
(Portmanteau theorem, see Theorem 11.1.1 in [24]) Let \((\mu _n)_n\) be a sequence of probability measures and \(\mu \) a probability measure on E, the following are equivalent:
-
(1)
\(\mu _n\rightharpoonup \mu \),
-
(2)
for all open sets U, \(\liminf _{n\rightarrow \infty }\mu _n(U)\ge \mu (U)\),
-
(3)
for all closed sets F, \(\limsup _{n\rightarrow \infty }\mu _n(F)\le \mu (F)\).
Theorem A.4
(Prokhorov theorem, see Theorem 2.3 in [20]) A set \(\Lambda \) of Borel probability measures is relatively compact in E if and only if it is tight.
Theorem A.5
(Skorokhod representation theorem, see Theorem 2.4 in [20]) For any sequence \((\mu _n)_n\) of Borel probability measures on E converging weakly to \(\mu \), there is a probability space \((\Omega _0,{\mathscr {F}}^0,{\mathbb {P}}_0)\), and random variables \(X,\ X_1,\cdots \) on \((\Omega _0,{\mathscr {F}}^0,{\mathbb {P}}_0)\) such that
-
(1)
\({\mathscr {L}}(X_n)=\mu _n\) and \({\mathscr {L}}(X)=\mu \),
-
(2)
\(\lim _{n\rightarrow \infty }X_n=X\), \({\mathbb {P}}_0-\)almost surely.
Here \({\mathscr {L}}(Y)\) stands for the law of the random variable Y.
1.2 A.2. Stochastic processes
Recall that if \((X_t)_t\) is an \(E-\)valued martingale, then since \(\Vert .\Vert \) is a convex function, we have that \((\Vert X_t\Vert )_t\) is a submartingale (by Jensen inequality). Here is a version of the Doob maximal inequality (see Theorem 3.8 in [35]):
Theorem A.6
(Doob maximal inequality) We have that for \(p>1.\)
The following can be found in Chapters 3 and 4 in [47].
Definition A.7
An N-dimensional Itô process is a proces \(X=(X_t)_{t}\) of the form
where \(B=(B_i)_{1\le i\le N}\) is an N-dimension Brownian motion, \(u=(u_i)_{1\le i\le N}\) is an N-dimensional stochastic process and \(v=(v_{ij})_{1\le i,j\le N}\) is a \(N\times N\) matrix that both are adapted with respect to \((B_t)_t\) and satisfy the following
A short notation for (6.3) is given by
Theorem A.8
(N-dimensional Itô formula) Let X be a N-dimensional Itô process as in (6.3). Let \(f:{\mathbb {R}}^N\rightarrow {\mathbb {R}}\) be a \(C^2\) function, then f(X) is a 1-dimensional Itô process and satisfy
with the properties \(dB_i \, dB_j=\delta _{ij} \, dt\), \(dt \, dB_i=0\).
Using the properties above, we can remark that in the particular case where v is diagonal (as in this paper), we have
APPENDIX B. Some important lemmas
In this section \((P_t)_{t \ge 0}\) be a Feller semi-group (a Markov semi-group satisfying the Feller property) on a Banach space X, \(P_t^*\) is the adjoint operator of \(P_t\).
Lemma A.9
(Krylov-Bogoliubov argument) If there exists \(t_n \rightarrow \infty \) and \(\mu \in {\mathfrak {P}} (X)\) such that \(\frac{1}{t_n} \int _0^{t_n} P_{t}^* \delta _0 \, dt \rightharpoonup \mu \) in X, then \(P_t^* \mu = \mu \) for all \(t \ge 0\). \(\delta _0\) is the Dirac measure at 0.
Proof of Lemma B
Note that \(P_r f \in C_b\). We have
where \( \lim _{t_n \rightarrow \infty } \langle f , \frac{1}{t_n} \int _{t_n}^{t_n +r} P_{t}^* \delta _0 \, dt\rangle =0\) and \(\lim _{t_n \rightarrow \infty } \langle f , \frac{1}{t_n} \int _0^{r} P_{t}^* \delta _0 \, dt\rangle =0\), since \(\int _{t_n}^{t_n +r} P_{t}^* \delta _0 \, dt \) and \(\int _0^{r} P_{t}^* \delta _0 \, dt \) are bounded. Therefore, \(P_r^* \mu = \mu \). Now the proof of Lemma B is finished. \(\square \)
Lemma A.10
Set
Assume that X is compactly embedded into a Banach space \(X_0\) and
for some function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that \(\lim _{x\rightarrow \infty }f(x)=\infty \), and C does not depend on n. Then there exists \(\mu \in {\mathfrak {P}} (X)\) such that \(\nu _n \rightharpoonup \mu \) weakly on \(X_0\).
Proof of Lemma A.10
Consider \(B_R(X)\), by Markov inequality

then \((\nu _n)\) is tight in \(X_0\). Now, the Prokhorov theorem (see Theorem A.4) implies the existence of \(\mu \) in \({\mathfrak {P}}(X_0)\).
Now, let us show that \(\mu (X) =1\). It suffices to show that

since, with such property, we obtain

Now, let \(\chi _R\) be a \(C^{\infty }\) function on \([0, \infty )\) such that \(\chi _R =1 \) on [0, R] and \(\chi _R =0\) on \([R+1 , \infty )\).

Since  is bounded continuous on \(X_0\), by Fatou’s lemma, we have
is bounded continuous on \(X_0\), by Fatou’s lemma, we have

The proof of Lemma A.10 is finished. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sy, M., Yu, X. Global well-posedness and long-time behavior of the fractional NLS. Stoch PDE: Anal Comp 10, 1261–1317 (2022). https://doi.org/10.1007/s40072-021-00210-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40072-021-00210-0



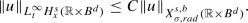




 .
.



