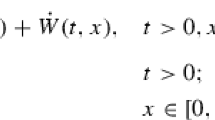Abstract
We investigate the growth of the tallest peaks of random field solutions to the parabolic Anderson models over concentric balls as the radii approach infinity. The noise is white in time and correlated in space. The spatial correlation function is either bounded or non-negative satisfying Dalang’s condition. The initial data are Borel measures with compact supports, in particular, include Dirac masses. The results obtained are related to those of Conus et al. (Ann Probab 41(3B):2225–2260, 2013) and Chen (Ann Probab 44(2):1535–1598, 2016) where constant initial data are considered.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the stochastic heat equation in \(\mathbb {R}^\ell \)
where \(t\ge 0\), \(x\in \mathbb {R}^\ell \)\((\ell \ge 1)\) and \(u_0\) is a Borel measure. Herein, W is a centered Gaussian field, which is white in time and it has a correlated spatial covariance. More precisely, we assume that the noise W is described by a centered Gaussian family \(W=\{ W(\phi ), \phi \in C_c^\infty (\mathbb {R}_+\times \mathbb {R}^\ell )\}\), with covariance
where \(\mu \) is non-negative measurable function and \({\mathcal {F}}\) denotes the Fourier transform in the spatial variables. To avoid trivial situations, we assume that \(\mu \) is not identical to zero. The inverse Fourier transform of \(\mu \) is in general a distribution defined formally by the expression
If \(\gamma \) is a locally integrable function, then it is non-negative definite and (1.2) can be written in Cartesian coordinates
The following two distinct hypotheses on the spatial covariance of W are considered throughout the paper.
-
(H.1)
\(\mu \) is integrable, that is \(\int _{\mathbb {R}^\ell }\mu (\xi )d \xi <\infty \). In this case, the inverse Fourier transform of \(\mu (\xi )\) exists and is a bounded continuous function \(\gamma \). Assume in addition that \(\gamma \) is \(\kappa \)-Hölder continuous function at 0.
-
(H.2)
\(\mu \) satisfies the following conditions:
-
(H.2a)
The inverse Fourier transform of \(\mu (\xi )\) is either the Dirac delta mass at 0 or a nonnegative locally integrable function \(\gamma \).
-
(H.2b)
$$\begin{aligned} \int _{ \mathbb {R}^\ell }\frac{\mu (\xi ) }{1+ |\xi |^2}d \xi <\infty \,. \end{aligned}$$(1.5)
-
(H.2c)
(Scaling) There exists \(\alpha \in (0,2)\) such that \(\mu (c \xi )=c^{\alpha -\ell }\mu (\xi )\) for all positive numbers c.
-
(H.2a)
Hereafter, we denote by \(|\cdot |\) the Euclidean norm in \(\mathbb {R}^\ell \) and by \(x\cdot y\) the usual inner product between two vectors x, y in \(\mathbb {R}^\ell \). Condition (H.2b) is known as Dalang’s condition and is sufficient for existence and uniqueness of a random field solution. If \(\gamma \) exists as a function, condition (H.2c) induces the scaling relation \(\gamma (c x)=c^{-\alpha }\gamma (x)\) for all \(c>0\).
Equation (1.1) with noise satisfying condition (H.2) was introduced by Dalang in [9]. In [16], for a large class of initial data, we show that Eq. (1.1) has a unique random field solution under the hypothesis (H.2). Under hypothesis (H.1), we note that \(\gamma \) may be negative, but proceeding as in [18], a simple Picard iteration argument gives the existence and uniqueness of the solution. In addition, in both cases, the solution has finite moments of all positive orders. We give a few examples of covariance structures which are usually considered in literatures.
Example 1.1
Covariance functions satisfying (H.2) includes the Riesz kernel \(\gamma (x)=|x|^{-\eta }\), with \(0<\eta <2\wedge \ell \), the space-time white noise in dimension one, where \(\gamma =\delta _0\), the Dirac delta mass at 0, and the multidimensional fractional Brownian motion, where \(\gamma (x)= \prod _{i=1}^\ell H_i (2H_i-1) |x^i|^{2H_i-2}\), assuming \(\sum _{i=1}^\ell H_i >\ell -1\) and \(H_i >\frac{1}{2}\) for \(i=1,\dots , \ell \). Covariance functions satisfying (H.1) includes \(e^{-|x|^2}\) and the inverse Fourier transform of \(|\xi |^2 e^{-|\xi |^2}\).
Suppose for the moment that \(\dot{W}\) is a space-time white noise and \(u_0\) is a function satisfying
It is first noted in [7] that there exist positive constants \(c_1,c_2\) such that almost surely
Later Chen shows in [3] that indeed the precise almost sure limit can be computed, namely,
One of the key ingredients in showing (1.8) is the following moment asymptotic result
Thanks to the scaling property of the space-time white noise, Chen has managed to derive (1.9) from the following long term asymptotic result
where the constant \({\mathcal {E}}_m\) grows as \(\frac{1}{24}m^3\) when \(m\rightarrow \infty \).
Under condition (1.6), analogous results for other kinds of noises are also obtained in [3]. More precisely, for noises satisfying (H.1)
and for noises satisfying (H.2),
where the variational quantity \({\mathcal {E}}_H(\gamma )\) is introduced in (3.3).
On the other hand, it is known that Eq. (1.1) has a unique random field solution under either (H.1) or (H.2) provided that \(u_0\) satisfies
In the above and throughout the remaining of the article, \(*\) denotes the convolution in spatial variables. Hence, condition (1.6) excludes other initial data of interests such as compactly supported measures. It is our purpose in the current paper to investigate the almost sure spatial asymptotic of the solutions corresponding to these initial data.
Upon reviewing the method in obtaining (1.8) described previously, one first seeks for an analogous result to (1.10) for general initial data. In fact, it is noted in [16] that for every \(u_0\) satisfying (1.13), one has
where \({\mathcal {E}}_m\) is a constant whose asymptotic as \(m\rightarrow \infty \) is known. It is suggestive from (1.14) that with a general initial datum, one should normalized u(t, x) in (1.8) (and (1.9)) by the factor \(p_t*u_0(x)\). Therefore, we anticipate the following almost sure spatial asymptotic result.
Conjecture 1.2
Assume that \(u_0\) satisfies (1.13). Under (H.1) we have
Under (H.2), we have
In the particular case of space-time white noise, we conjecture that
In the case of space-time white noise, note that if \(u_0\) satisfies the condition (1.6), (1.17) is no different than (1.8). On the other hand, if \(u_0\) is a Dirac delta mass at \(x_0\), (1.17) precisely describes the spatial asymptotic of \(\log u(t,x)\): at large spatial sites, \(\log u(t,x)\) is concentrated near a logarithmic perturbation of the parabola \(-\frac{1}{2t} (x-x_0)^2\). More precisely, (1.17) with this specific initial datum reduces to
While a complete answer for Conjecture 1.2 (including (1.18)) is still undetermined, the current paper offers partial results, focusing on initial data with compact supports, especially Dirac masses. To unify the notation, we denote
where the variational quantity \({\mathcal {E}}_H(\gamma )\) is introduced below in (3.3). For bounded covariance functions, we obtain the following result.
Theorem 1.3
Assume that (H.1) holds and \(u_0=\delta (\cdot - x_0)\) for some \(x_0\in \mathbb {R}^\ell \). Then (1.15) holds.
For noises satisfying (H.2), or for initial data with compact supports, the picture is less complete.
Theorem 1.4
Assume that \(u_0\) is a non-negative measure with compact support and either (H.1) or (H.2) holds. Then we have
For initial data satisfying (1.6), the lower bound of (1.16) is proved in [3] using a localization argument initiated from [7]. In our situation, a technical difficulty arises in applying this localization procedure, which leads to the missing lower bound in Theorem 1.4. A detailed explanation is given at the beginning of Sect. 6.2. As an attempt to obtain the exact spatial asymptotics, we propose an alternative result which is described below. We need to introduce a few more notation. For each \(\varepsilon >0\), we denote
which is a bounded non-negative definite function. Let \(W_ \varepsilon \) be a centered Gaussian field defined by
for all \(\phi \in C_{c}^{\infty }(\mathbb {R}_+\times \mathbb {R}^\ell )\). In the above, \(p_ \varepsilon =(2 \pi \varepsilon )^{-\ell /2}e^{-|x|^2/(2 \varepsilon )}\). The covariance structure of \(W_ \varepsilon \) is given by
for all \(\phi ,\psi \in C_c^{\infty }(\mathbb {R}_+\times \mathbb {R}^\ell )\). In other words, \(W_ \varepsilon \) is white in time and correlated in space with spatial covariance function \(\gamma _ \varepsilon \), which satisfies (H.1). Under condition (H.2c), \(\gamma _ \varepsilon \) satisfies the scaling relation
Let \(u_ \varepsilon \) be the solution to Eq. (1.1) with \(\dot{W}\) replaced by \(\dot{W}_ \varepsilon \). It is expected that as \(\varepsilon \downarrow 0\), \(u_ \varepsilon (t,x)\) converges to u(t, x) in \(L^2(\Omega )\) for each (t, x), see [1] for a proof when the initial data is a bounded function. The following result describes spatial asymptotic of the family of random fields \(\{u_\varepsilon \}_{\varepsilon \in (0,1)}\).
Theorem 1.5
Assume that \(u_0\) is a non-negative measure with compact support and either (H.1) or (H.2) holds. Then
If, in particular, \(u_0=\delta (\cdot -x_0)\) for some \(x_0 \in \mathbb {R}^{\ell }\), then
Neither one of (1.16) and (1.26) is stronger than the other. While the result of Theorem 1.5 relates to the solution of (1.1) indirectly, it is certainly interesting. In Hairer’s theory of regularity structures (cf. [14]), one first regularizes the noise to obtain a sequence of approximated solutions. The solution of the corresponding stochastic partial differential equation is then constructed as the limiting object of this sequence. From this point of view, (1.26) provides a unified characteristic of the sequence of approximating solutions \(\{u_ \varepsilon \}_{\varepsilon \in (0,1)}\), which approaches the solution u as \(\varepsilon \downarrow 0\). The proof of (1.26) does not rely on localization, rather, on the Gaussian nature of the noise. This leads to a possibility of extending (1.26) to temporal colored noises, which will be a topic for future research.
The remainder of the article is structured as follows: In Sect. 2 we briefly summarize the theory of stochastic integrations and well-posedness results for (1.1). In Sect. 3 we introduce some variational quantities which are related to the spatial asymptotics. In Sect. 4 we derive some Feynman–Kac formulas of the solution and its moments, these formulas play a crucial role in our consideration. In Sect. 5 we investigate the high moment asymptotics and Hölder regularity of the solutions of (1.1) with respect to various parameters. The results in Sect. 5 are used to obtain upper bounds in (1.15) and (1.16). This is presented in Sect. 6, where we also give a proof of the lower bounds in Theorems 1.3, 1.4 and 1.5.
2 Preliminaries
We introduce some notation and concepts which are used throughout the article. The space of Schwartz functions is denoted by \({\mathcal {S}}(\mathbb {R}^\ell )\). The Fourier transform of a function \(g\in {\mathcal {S}}(\mathbb {R}^\ell )\) is defined with the normalization
so that the inverse Fourier transform is given by \({\mathcal {F}}^{-1}g(\xi )=(2 \pi )^{-\ell }{\mathcal {F}}g(- \xi )\). The Plancherel identity with this normalization reads
Let us now describe stochastic integrations with respect to W. We can interpret W as a Brownian motion with values in an infinite dimensional Hilbert space. In this context, the stochastic integration theory with respect to W can be handled by classical theories (see for example, [11]). We briefly recall the main features of this theory.
We denote by \(\mathfrak {H}_0\) the Hilbert space defined as the closure of \(\mathcal {S}(\mathbb {R}^\ell )\) under the inner product
which can also be written as
If \(\gamma \) satisfies (H.1), then \(\mathfrak {H}_0\) contains distributions such as Dirac delta masses. The Gaussian family W can be extended to an isonormal Gaussian process \(\{W(\phi ), \phi \in L^2(\mathbb {R}_+, \mathfrak {H}_0)\}\) parametrized by the Hilbert space \(\mathfrak {H}:=L^2(\mathbb {R}_+, \mathfrak {H}_0)\). For any \(t\ge 0\), let \(\mathcal {F}_{t}\) be the \(\sigma \)-algebra generated by W up to time t. Let \(\Lambda \) be the space of \(\mathfrak {H}_0\)-valued predictable processes g such that \(\mathbb {E}\Vert g\Vert _{\mathfrak {H}}^{2}<\infty \). Then, one can construct (cf. [16]) the stochastic integral \(\int _0^\infty \int _{\mathbb {R}^\ell }g(s,x) \, W(ds,dx)\) such that
To emphasize the variables, we sometimes write \(\Vert g(s,y)\Vert _{\mathfrak {H}_{s,y}}\) for \(\Vert g\Vert _\mathfrak {H}\). Stochastic integration over finite time interval can be defined easily
Finally, the Burkholder’s inequality in this context reads
which holds for all \(p\ge 2\) and \(g\in \Lambda \). A useful application of (2.4) is the following result
Lemma 2.1
Let \(m\ge 2\) be an integer, f be a deterministic function on \([0,\infty )\times \mathbb {R}^\ell \) and \(u=\{u(s,x): s\ge 0,x\in \mathbb {R}^\ell \}\) be a predictable random field such that
Under hypothesis (H.2), we have
and under hypothesis (H.1), we have
Proof
We consider only the hypothesis (H.2), the other case is obtained similarly. In view of Burkholder inequality (2.4) and Minkowski inequality, it suffices to show
In fact, using (2.2) and Minkowski inequality, the left-hand side in the above is at most
Note in addition that by Cauchy–Schwarz inequality,
From here, (2.5) is transparent and the proof is complete. \(\square \)
We now state the definition of the solution to Eq. (1.1) using the stochastic integral introduced previously.
Definition 2.2
Let \(u=\{u(t,x), t\ge 0, x \in \mathbb {R}^\ell \}\) be a real-valued predictable stochastic process such that for all \(t \ge 0\) and \(x\in \mathbb {R}^\ell \) the process \(\{p_{t-s}(x-y)u(s,y) \mathbf {1}_{[0,t]}(s), 0 \le s \le t, y \in \mathbb {R}^\ell \}\) is an element of \(\Lambda \).
We say that u is a mild solution of (1.1) if for all \(t \in [0,T]\) and \(x\in \mathbb {R}^\ell \) we have
The following existence and uniqueness result has been proved in [16] under hypothesis (H.2). Under hypothesis (H.1), one can proceed as in [18], using a simple Picard iteration argument to obtain the existence and uniqueness of the solution.
Theorem 2.3
Suppose that \(u_0\) satisfies (1.13) and the spectral measure \(\mu \) satisfies hypotheses (H.1) or (H.2). Then there exists a unique solution to Eq. (1.1).
When \(u_0=\delta (\cdot -z)\), we denote the corresponding unique solution by \(\mathcal {Z}(z; t, x)\). In particular \(\mathcal {Z}(z;\cdot ,\cdot ) \) is predictable and satisfies
for all \(t\ge 0\) and \(x\in \mathbb {R}^\ell \).
Next, we record a Gronwall-type lemma which will be useful later.
Lemma 2.4
Suppose \(\alpha \in [0,2)\) and f is a locally bounded function on \([0,\infty )\) such that
where A, B are positive constants and g is non-decreasing function. Then there exists a constant \(C_ \alpha \) such that
Proof
Fix \(T>0\). For each \(\rho >0\), denote \(D_ \rho =\sup _{t\in [0,T]}f_t e^{-\rho t}\). It follows that
It is easy to see
for some suitable constant C depending only on \(\alpha \). We then choose \(\rho =(2AC)^{\frac{2}{2- \alpha }} \) so that \(AC\rho ^{-\frac{2- \alpha }{2}}=\frac{1}{2}\). This leads to \(D_ \rho \le 2Bg_T\), which implies the result. \(\square \)
Let us conclude this section by introducing a few key notation which we will use throughout the article. Let \(B=(B(t),t\ge 0)\) denote a standard Brownian motion in \(\mathbb {R}^\ell \) starting at the origin. For each \(t>0\), we denote
The process \(B_{0,t}=(B_{0,t}(s),0\le s\le t)\) is independent from B(t) and is a Brownian bridge which starts and ends at the origin. An important connection between B and \(B_{0,t}\) is the following identity. For every \(\lambda \in (0,1)\) and every bounded measurable function F on \(C([0,\lambda t];\mathbb {R}^d) \) we have
This is in fact an application of Girsanov’s theorem, see [16, Eq. (2.8)] for more details.
Let \(B^1,B^2,\dots \) be independent copies of B and \(B^{1}_{0,t},B^2_{0,t},\dots \) be the corresponding Brownian bridges. An important quantity which appears frequently in our consideration is
From the proof of Proposition 4.2 in [16], it is easy to see that under one of the hypotheses (H.1) and (H.2), \(\Theta _t(m) < \infty \) for any \(t>0\). Finally, \(A\lesssim E\) means \(A\le CE\) for some positive constant C, independent from all the terms appearing in E.
3 Variations
We introduce two variational quantities and give their basic properties and relations. The high moment asymptotic is governed by a variational quantity which is known as the Hartree energy (cf. [8]). If there exists a locally integrable function \(\gamma \) whose Fourier transform is \(\mu \), then the Hartree energy can be expressed as
where \({\mathcal {G}}\) is the set
The subscript H stands for “Hartree”. We can also write this variation in Fourier mode. Indeed, the presentation (1.3) leads to
Setting \(h=(2 \pi )^{-\frac{\ell }{2}}{\mathcal {F}}g\) so that \(\Vert h\Vert _{L^2}=1\), we arrive at
where
Under (H.1), from (3.1), we bound \(\gamma (x-y)\) from above by \(\gamma (0)\), it follows that \({\mathcal {E}}_H(\gamma )\le \gamma (0)\), which is finite. The fact that this variation (either in the form (3.1) or (3.3)) is finite under the condition (H.2) is not immediate. In some special cases, this is verified in [6] and [5].
Proposition 3.1
Suppose (1.5) holds. Then \({\mathcal {E}}_H(\gamma )\) is finite.
Proof
Our proof is based on the argument in [5, Proposition 3.1]. Here, however, we work on the frequency space and use the presentation (3.3). Let h be in \({\mathcal {A}}\). Applying Cauchy–Schwarz inequality yields
On the other hand, using the elementary inequality
and Cauchy–Schwarz inequality, we also get
Then, for every \(R>0\) we have
We now choose R sufficiently large so that \({ 4}(2 \pi )^{-\ell } \int _{|\xi |>R}\frac{ \mu (\xi )}{|\xi |^2} d \xi <1\). This implies
for all h in \({\mathcal {A}}\), which finishes the proof. \(\square \)
In establishing the lower bound of spatial asymptotic, another variation arises, which is given by
or alternatively in frequency mode
Lemma 3.2
\(\lim _{\varepsilon \rightarrow 0}{\mathcal {E}}_H(\gamma _\varepsilon )={\mathcal {E}}_H(\gamma ) \) and \(\lim _{\varepsilon \rightarrow 0}{\mathcal {M}}(\gamma _\varepsilon )={\mathcal {M}}(\gamma ) \), where we recall that \(\gamma _\varepsilon \) is defined in (1.21).
Proof
We only prove the first limit, the second limit is proved analogously. Let g be in \({\mathcal {G}}\). Note that
by Fatou’s lemma. Since \({\mathcal {E}}_H(\gamma _\varepsilon )\) is finite, we have
Sending \(\varepsilon \) to 0 yields
Since the above inequality holds for every g in \({\mathcal {G}}\), we obtain \({\mathcal {E}}_H(\gamma )\le \liminf _{\varepsilon \downarrow 0}{\mathcal {E}}_H(\gamma _\varepsilon )\). On the other hand, it is evident (from (3.3)) that \({\mathcal {E}}_H(\gamma _\varepsilon )\le {\mathcal {E}}_H(\gamma )\). This concludes the proof.\(\square \)
Under the scaling condition (H.2c), \({\mathcal {E}}_H\) and \({\mathcal {M}}\) are linked together by the following result.
Proposition 3.3
Assuming condition (H.2c), \({\mathcal {E}}_H(\gamma )\) is finite if and only if \({\mathcal {M}}(\gamma )\) is finite. In addition,
Before giving the proof, let us see how (3.1) and (3.4) are connected to a certain interpolation inequality. Under scaling condition (H.2c), it is a routine procedure in analysis to connect the finiteness of \({\mathcal {E}}_H(\gamma )\) with a certain interpolation inequality. For instance, when \(\gamma = \delta \) and \(\ell =1\), the fact that
is equivalent to the following Gagliardo–Nirenberg inequality
for all g in \(W^{1,2}(\mathbb {R})\). For readers’ convenience, we provide a brief explanation below.
Proposition 3.4
Assume that the scaling relation (H.2c) holds.
(i) If \({\mathcal {E}}_H(\gamma )\) is finite then there exists \(\kappa >0\) such that for all g in \(W^{1,2}(\mathbb {R}^\ell )\)
In addition the constant \(\kappa \) can be chosen to be \(\kappa (\gamma )\) where
(ii) If (3.6) holds for some finite constant \(\kappa >0\), then \({\mathcal {E}}_H(\gamma )\) is finite and the best constant in (3.6) is \(\kappa (\gamma )\).
Proof
Recall that \({\mathcal {G}}\) is defined in (3.2).
(i) Let g be in \({\mathcal {G}}\). For each \(\theta >0\), the function \(x\mapsto g_ \theta (x):=\theta ^{\frac{\ell }{2}}{g(\theta x)}\) also belongs to \({\mathcal {G}}\). Hence,
Writing these integrals back to g and using (H.2c) yields
for all \(\theta >0\). Optimizing the left-hand side (with respect to \(\theta \)) leads to
Removing the normalization \(\Vert g\Vert _{L^2}=1\) and some algebraic manipulation yields the result.
(ii) Let \(\kappa _0\) be the best constant in (3.6). Then for every \(g\in {\mathcal {G}}\),
This shows \({\mathcal {E}}_H(\gamma )\) is finite and at most \(\frac{2- \alpha }{\alpha }( \frac{\alpha }{2} \kappa _0)^{\frac{2}{2- \alpha }}\), which also means \(\kappa (\gamma )\le \kappa _0\). On the other hand, (i) already implies \(\kappa _0\le \kappa (\gamma )\), hence completes the proof. \(\square \)
Proof of Proposition 3.3
Reasoning as in Proposition 3.4, we see that \({\mathcal {M}}(\gamma )\) is finite if and only if (3.6) holds for some constant \(\kappa >0\). In addition, the best constant \(\kappa (\gamma )\) in (3.6) satisfies the relation
Together with (3.7), this yields the result. \(\square \)
The following result preludes the connection between \({\mathcal {E}}_H,{\mathcal {M}}\) with exponential functional of Brownian motions.
Lemma 3.5
Let \(\{B(s),s\ge 0\}\) be a Brownian motion in \(\mathbb {R}^n\) and D be a bounded open domain in \(\mathbb {R}^n\) containing 0. Let h(s, x) be a bounded function defined on \([0,1]\times \mathbb {R}^n\) which is continuous in x and equicontinuous (over \(x\in \mathbb {R}^n\)) in s. Then
where \({\mathcal {G}}_D\) is the class of functions g in \(W^{1,2}(\mathbb {R}^n)\) such that \(\int _{D}|g(x)|^2dx=1\) and \(\tau _D\) is the exit time \(\tau _D := \inf \{t\ge 0: B_t \notin D\}\).
Proof
Observe that the process \(\{B_{0,t}(s)=B(s)-\frac{s}{t} B(t)\}_{s\in [0,t]}\) is a Brownian bridge. An analogous result with Brownian bridge replaced by Brownian motion has been obtained in [6]. Our main idea here is to apply a change of measure to transfer the known result for Brownian motion to the result for Brownian bridge (i.e. the limit (3.8)). Since the probability density of Brownian bridge \(B_{0,t}\) with respect to a standard Brownian motion is singular near t, a truncation is needed. We fix \(\theta \in (0,1)\) and consider first the limit
Let M be such that \(|x|\le M\) for all \(x\in D\). Using Girsanov theorem (see [16, Eq. (2.38)]), we can write
The result of [6, Proposition 3.1] asserts that
This leads to
In obtaining the above limit, we have used the trivial facts
Note that the singularity when \(\theta \uparrow 1\) has disappeared at this stage. On the other hand, the estimate
implies that
Hence, we can send \(\theta \uparrow 1\) in (3.11) to obtain the lower bound for (3.8). The upper bound for (3.8) is proved analogously. Indeed, from (3.9), we have
which when combined with (3.10) yields
Since the singularity when \(\theta \uparrow 1\) has been eliminated in the regime \(t\rightarrow \infty \), we can send \(\theta \uparrow 1\) as previously to obtain the upper bound for (3.8). \(\square \)
We conclude this section with an observation: (H.2c) induces the following scaling relation on \({\mathcal {E}}_H(\gamma )\)
4 Feynman–Kac formulas and functionals of Brownian Bridges
We derive Feynman–Kac formulas for the moments \(\mathbb {E}u^m(t,x)\) for integers \(m\ge 2\). These formulas play important roles in proving upper and lower bounds of (1.15) and (1.26).
To discuss our contributions in the current section, let us assume for the moment that \(\dot{W}\) is a space-time white noise and \(\ell =1\). The most well-known Feynman–Kac formula for second moment is
where \(B^1,B^2\) are two independent Brownian motions starting at 0. If \(u_0\) is merely a measure, some efforts are needed to make sense of \(u_0(B(t)+x)\), which appears on the right-hand side above. An attempt is carried out in [4] using Meyer-Watanabe’s theory of Wiener distributions.
The Feynman–Kac formulas presented here (see (4.10) below) have appeared in [16]. However, there seems to have a minor gap in that article. Namely, Eq. (4.52) there has not been proven if \(u_0\) is a measure. In the current article, we take the chance to fill this gap. Our approach is in the same spirit as [16] and is different from [4]. In particular, we do not make use of Wiener distributions.
Proposition 4.1
Let \(u_0\) be a measure satisfying (1.13). Then
In addition, if (H.1) holds, then
Proof
Let v(t, x) be the integral on the right-hand side of (4.1). From (2.7), integrating z with respect to \(u_0(dz)\) and applying the stochastic Fubini theorem (cf. [10, Theorem 4.33]), we have
Hence, v is a solution of (1.1) with initial datum \(u_0\). By unicity, Theorem 2.3, we see that \(u=v\) and (4.1) follows.
Next, we show (4.2) assuming (H.1). Fix \(t>0\) and \(x\in \mathbb {R}^\ell \). For every \(u_0\in C_c^\infty (\mathbb {R}^\ell )\), the following Feynman–Kac formula (see [17, Prop. 5.2] for a general case) holds
Using the decomposition (2.8) and the fact that \(B_{0,t}\) and B(t) are independent, we see that
where
Together with (4.1) we obtain
for all \(u_0\in C^\infty _c(\mathbb {R}^\ell )\).
Next we show that \(z\mapsto Y(z;t,x)\) is continuous. Fix \(p>2\). From the elementary relation \(|e^x-e^y| \le (e^x + e^y)|x-y|\) and the Cauchy–Schwarz inequality, it follows
Since \(\gamma \) is bounded, conditioned on \(B_{0,t}\), \(V_{t,x}(z)\) is a normal random variable with uniformly (in x, z) bounded variance. It follows that \(V_{t,x}(z)\) has uniformly bounded exponential moments. That is,
for some constant \(C_{p,t}\). We now resort to Minkowski inequality, our exponential bound for \(V_{t,x}(z)\) and the relation between \(L^p\) and \(L^2\) moments for Gaussian random variables in order to obtain
In addition, under (H.1), \(\gamma \) is Hölder continuous with order \(\kappa >0\) at 0, it follows that
We have shown
Thus, the process \(z\rightarrow Y(z;t,x)\) has a continuous version. On the other hand, \(z\mapsto \mathcal {Z}(z;t,x)\) is also continuous (see Proposition 5.5 below). It follows that \(\mathcal {Z}(z;t,x)=Y(z-x;t,x) p_t(z-x)\), which is exactly (4.2). \(\square \)
Proposition 4.2
Assuming (H.1), we have
and
Proof
We observe that conditioned on B,
is a normal random variable with mean zero. In addition, for every \(x,x',z,z'\in \mathbb {R}^\ell \), applying (1.23), we have
For every \((x_1,\dots ,x_m)\in (\mathbb {R}^\ell )^m\), using (4.2) and (4.6), we have
Note that in the exponent above, the diagonal terms (with \(j=k\)) are removed because there are cancellations with the normalization factor \(-\frac{t}{2} \gamma (0)\) in (4.2), which occur after taking expectation with respect to W. Finally, apply [16, Lemma 4.1], we obtain (4.5) from (4.7). \(\square \)
To extend the previous result to noises satisfying (H.2), we need the following result.
Proposition 4.3
Assuming (H.2). There exists a constant c depending only on \(\alpha \) such that for any \(\beta \in (0, 4\wedge (\ell -\alpha ))\),
where \(\mathcal {Z}_\varepsilon \) is the solution to (2.7) with W replaced by \(W_\varepsilon \) and \(\Theta _t(m)\) is defined in (2.10)
Proof
Let us put
From (2.7), we have
Then we obtain
To estimate \(I_1\), we use Lemma 2.1 and (H.2c) to obtain
To estimate \(I_2\), we first note that the noise \(W-W_ \varepsilon \) has spectral density \((1- e^{-\varepsilon |\xi |^2})^2\mu (\xi )\). Applying Lemma 2.1, we obtain
Let us fix \(\beta \in (0,4\wedge (\ell - \alpha ))\). Applying the elementary inequality \(1-e^{-\varepsilon |\xi |^2}\le \varepsilon ^{\beta /4}|\xi |^{\beta /2}\) together with the estimate
we get
Reasoning as in [16, Lemma 4.1], we see that
Two key observations here are \(\gamma _ \varepsilon ,\gamma \) have spectral measures \(\mu (\xi ),e^{-\varepsilon |\xi |^2}\mu (\xi )\) respectively and \(e^{-\varepsilon |\xi |^2}\mu (\xi )\le \mu (\xi )\). Hence, it follows from (4.5) and the previous estimate that
In summary, we have shown
Applying Lemma 2.4, this yields
for some constant c depending only on \(\alpha \). \(\square \)
We are now ready to derive Feynman–Kac formulas for positive moments.
Proposition 4.4
Let \(u_0\) be a measure satisfying (1.13). Under (H.1) or (H.2), for every \(x_1,\dots ,x_m\in \mathbb {R}^\ell \), we have
and
Proof
We prove the result under the hypothesis (H.2). The proof under hypothesis (H.1) is easier and omitted.
Step 1: we first consider (4.10) and (4.11) when the initial data are Dirac masses. More precisely, we will show that
and
Fix \(\varepsilon >0\), identity (4.12) with \(\mathcal {Z},\gamma \) replaced by \(\mathcal {Z}_\varepsilon ,\gamma _\varepsilon \) has been obtained in (4.4). Namely, we have
Using analogous arguments to [16, Proposition 4.2], we can show that for every \(\kappa \in \mathbb {R}\), as \(\varepsilon \downarrow 0\), the functions
converge uniformly on \(\mathbb {R}^{2m\ell }\) to the function
In addition, in view of Proposition 4.3,
Sending \(\varepsilon \downarrow 0\) in (4.14), we obtain (4.12). The estimate (4.13) is obtained analogously using (4.5). We omit the details.
Step 2: For general initial data satisfying (1.13), we note that from (4.1),
From here, it is evident that (4.10), (4.11) are consequences of (4.12), (4.13) and Fubini’s theorem. \(\square \)
We conclude this section with the following observation.
Remark 4.5
Under (H.1), it is evident from (4.2) that \(\mathcal {Z}(z;t,x) \) is non-negative for every z, t, x. Under (H.2), thanks to Proposition 4.3, \(\mathcal {Z}(z;t,x)\) is the limit of non-negative random variables, hence \(\mathcal {Z}(z;t,x) \) is also non-negative for every z, t, x. Furthermore, in view of (4.1), if \(u_0\) is non-negative then u(t, x) is non-negative for every t, x.
5 Moment asymptotic and regularity
5.1 Moment asymptotic
We begin with a study on high moments. Under hypothesis (H.1), the high moment asymptotic is governed by the value of \(\gamma \) at the origin.
Proposition 5.1
Under (H.1), for every \(T>0\), we have
Proof
Since \(\gamma \) is positive definite, \(\gamma (x)\le \gamma (0)\) for all \(x \in \mathbb {R}^{\ell }\). It follows from (4.11) that
This immediately yields (5.1). \(\square \)
The following intermediate result will be applied to the measure \(e^{-2 \varepsilon |\xi |^2} \mu (d \xi )\) to obtain moment asymptotic under (H.2).
Lemma 5.2
Suppose that \(\mu (\mathbb {R}^\ell )<\infty \). For each t, T, m, we put \(t_m = m^{\frac{2}{2-\alpha }}t\) and \(T_m = m^{\frac{2}{2-\alpha }}T\). Then
Proof
The condition \(\mu (\mathbb {R}^\ell )<\infty \) implies that the inverse Fourier transform of \(\mu (\xi )\) exists and is a bounded continuous function \(\gamma \). Furthermore, \(\max _{x\in \mathbb {R}^\ell }\gamma (x)=\gamma (0)\). For each \(\lambda \in (0,1)\), we note that
Using (2.9), we see that the expectation above is at most
In addition, reasoning as in [16, Lemma 4.1], we see that
It follows that
where we have used the fact that \(\lim _{m\rightarrow \infty }\frac{1}{mT_m}\log (1- \lambda )^{-\frac{m\ell }{2}}=0\). Applying [8, Theorem 1.1], we get
Thus we have shown
Finally, we send \(\lambda \rightarrow 1^-\) to finish the proof. \(\square \)
Proposition 5.3
Assuming (H.2), for every fixed \(T>0\),
where \({\mathcal {E}}_H(\gamma )\) is the Hartree energy defined in (3.1).
Proof
Applying inequality (4.11), we have
In addition, by the change of variable \(s \rightarrow s m^{-\frac{2}{2- \alpha }}\) and the scaling property of Brownian bridge, \(\{B_{0,\lambda t}(\lambda s),s\in [0, t]\} {\mathop {=}\limits ^{\text{ law }}} \{\sqrt{\lambda } B_{0,t}(s),s\in [0,t]\}\), the right hand side in the above expression is the same as
Hence, denoting \(t_m=m^{\frac{2}{2- \alpha }}t\) and \(T_m=m^{\frac{2}{2- \alpha }}T\), we see that (5.3) is equivalent to the statement
Let \(p,q>1\) such that \(p^{-1}+q^{-1}=1\). By Hölder inequality
where
From Lemma 5.2 and the fact that \({\mathcal {E}}_H(\gamma _\varepsilon ) \le {\mathcal {E}}_H(\gamma )\) (see (3.3)), we have
Hence, it suffices to show for every fixed \(q>1\),
By Cauchy–Schwarz inequality and the fact that \(B_{0,t} {{\mathop {=}\limits ^{\text {law}}}} B_{0,t}(t-\cdot )\), we have
Together with (2.9), we arrive at
Note that the right hand side of the above inequality is the m-th moment of the solution to the Eq. (1.1) driven by the noise with spatial covariance \(\frac{2q}{m}\left( \gamma - \gamma _{\varepsilon }\right) \), i.e., \(\mathbb {E}u(\frac{t_m}{2}, x)^m\), the initial condition is \(u_0(x) \equiv 2^{\ell }\). Using the hyper-contractivity as in [16, 19], we have
where in the last line we have used the estimate (3.7) in [15], \([0,\frac{t_m}{2}]^k_<=\{(s_1,\dots ,s_k)\in [0,\frac{t_m}{2}]^k:s_1<\cdots <s_k \}\) and \(\mu (\eta )d \eta ds\) is abbreviation for \(\prod _{j=1}^k \mu (\eta _j)d\eta _j ds_j\). Since \(\alpha < 2\), we can find a \(\beta >0\) such that \(\beta < 1-\frac{\alpha }{2}\). Then using the elementary inequality
and asymptotic behavior of Mittag-Leffler function ([12, p. 208]), we obtain
Hence, we have shown
from which (5.5) follows. The proof for (5.3) is complete. \(\square \)
5.2 Hölder continuity
We investigate the regularity of the process \(\frac{\mathcal {Z}(x;t,y)}{p_t(y-x)}\) in the variables x and y. These properties will be used in the proof of upper bound. For each integer \(m\ge 2\) and \(t>0\), we recall that \(\Theta _t(m)\) is defined in (2.10).
Note that from Proposition 4.4, we have
Lemma 5.4
For every \(r>0\) and \(y_1,y_2\in \mathbb {R}^\ell \)
under (H.2); and
under (H.1). In the above, the constant C does not depend on \(y_1,y_2\) nor r.
Proof
We denote \(f(\cdot )=|p_r(\cdot -y_1)-p_r(\cdot -y_2)|\). Assuming first (H.2), we observe the following simple estimate
Noting that
and
the result easily follows. Under (H.1), we used the following inequality
together with (5.7) to obtain the result. \(\square \)
Proposition 5.5
Assuming (H.1) or (H.2). There exists a constant \(\eta \in (0,1)\) such that for every compact set K and every integer \(m\ge 2\),
and
where B(w, 1) is the closed unit ball in \(\mathbb {R}^\ell \) centered at w. In the above, the constant c depends only on \(\bar{\alpha }\) and \(\eta \) and \(c_K(t)\) depends only on \(K,t, \eta \).
Proof
We present the proof under hypothesis (H.2) in detail. The proof for the other case is similar and is omitted. We first show that for every \(\eta \in (0,2- \alpha )\),
In the above, we have added a subscript t to \(\lesssim \) to emphasize that the implied constant depends on t. Fix \(t>0\) and \(x_1,x_2,x\in \mathbb {R}^\ell \). From (2.7), we have
where
Obviously f also depends on \(t,x_1,x_2\) and x, however these parameters will be omitted. For each integer \(m\ge 2\), applying Lemma 2.1 we see that
Applying Lemma 5.4, for every \(\eta \in (0,2- \alpha )\), there exists \(c_{\eta }>0\) such that
Hence,
For each \(s>0\), we set
It follows from Lemma 2.1 that
where c is some constant. Applying these estimates in (5.11) yields
We now apply Lemma 2.4 to get
which is exactly (5.10).
To complete the proof of the estimate (5.8). Fix \(t>0\) and \(x_1,x_2,y_1,y_2\in \mathbb {R}^\ell \). Observe that
where
Similar to (5.12), we have
\(I_2\) can be estimated using Lemma 2.1 and (5.10)
Hence, we have shown
At this point, the estimate (5.8) follows from the Garsia-Rodemich-Rumsey inequality (cf. [13]).
The proof of (5.9) is simpler. Actually, by writing
we get an estimate for \(\Vert \frac{\mathcal {Z}(x;t,y_1)}{p_t(y_1-x)}-\frac{\mathcal {Z}(x;t,y_2)}{p_t(y_2-x)}\Vert _{L^m(\Omega )}\) as in (5.13). The estimate (5.9) again follows from the Garsia-Rodemich-Rumsey inequality (cf. [13]). We omit the details. \(\square \)
In proving (1.26), we need to handle the asymptotic of \(\sup _{\varepsilon <1}\sup _ {x\in K,|y|\le R} \frac{\mathcal {Z}_{\varepsilon }(x;t,y)}{p_t(y-x)}\), thus we write down the Hölder continuity result for \(\frac{\mathcal {Z}_{\varepsilon }(x;t,y)}{p_t(y-x)}\) with respect to \(\varepsilon ,x,y\). The proof is similar to Proposition 5.5 and is left to the reader.
Proposition 5.6
Assuming (H.1) or (H.2). There exists a constant \(\eta \in (0,1)\) such that for every compact set K and every integer \(m\ge 2\),
and
In the above, the constant c depends only on \(\bar{\alpha }\) and \(\eta \) and \(c_K(t)\) depends only on \(K,t, \eta \).
6 Spatial asymptotic
In this section we study the asymptotic of
as described in Theorems 1.3, 1.4 and 1.5. In what follows, we denote
where we recall that \(\bar{\alpha }\) is defined in (1.19). Since \(0\le \bar{\alpha }<2\), a ranges inside the interval [1 / 2, 1). Because \(R\mapsto \sup _{|y|\le R}\frac{u(t,y)}{p_t*u_0(y)}\) is monotone, it suffices to show these results along lattice sequence \(R\in \{e^n\}_{n\ge 1}\).
6.1 The upper bound
This subsection is devoted to the proof of upper bounds in Theorems 1.3 and 1.4 by combining the moment asymptotic bounds and the regularity estimates obtained in Sect. 5. We also recall that \(\Theta _t(m)\) is defined in (2.10). Propositions 5.1, 5.3 together with (5.6) imply
where \({\mathcal {E}}\) is defined in (1.19). The following result gives an upper bound for spatial asymptotic of \(\mathcal {Z}(x;\cdot ,\cdot )\).
Theorem 6.1
For every compact set K, we have
Proof
We begin by noting that according to Remark 4.5, \(\mathcal {Z}(x;t,y)\) is non negative a.s. for each x, y, t. Let t be fixed and put
where we have omitted the dependence on t. For every \(n>1\) and every \(\lambda >0\), we consider the probability
Let b be a fixed number such that \(a< b <1\). We can find the points \(x_i\), \(i = 1, \dots , M_{n}\), such that \(K \subset \cup _{i=1}^{M_n}B(x_i, e^{-n^b})\) and \(M_n\lesssim e^{\ell n^b}\). In addition, by partitioning the ball \(B(0,e^n)\) into unit balls, we see that \(P_n\) is at most
Applying Chebychev inequality, we see that
The above m-th moment is estimated by triangle inequality
Using Proposition 5.5 and (5.6), we see that
Altogether, we have
For each \(\beta >0\), we choose \(m= \lfloor \beta n^{1-a} \rfloor \). In addition, for every fixed \(\varepsilon >0\), (6.2) yields
for all n sufficiently large. It follows from (6.4) and (6.5) that
where
Since \(1-a+b>1\), the term \(e^{-\eta \beta n^{1-a+b}}\) is dominant, and hence, \(S_1\) is finite for every \(\lambda ,\beta >0\). To ensure the convergence of \(S_2\), we choose \(\lambda \) such that
It follows that the series on the right hand side of (6.6) is finite. By Borel-Cantelli lemma, we have almost surely
Evidently, the best choice for \(\lambda \) is
which yields (6.3). \(\square \)
Remark 6.2
Using Proposition 5.6 and analogous arguments in Theorem 6.1, we can show that
We omit the details.
6.2 The lower bound
We now focus on the lower bound of (1.15) and (1.26). To start, we explain an issue of using the localization procedure as in [3, 7]. In these papers, a localized version of the Eq. (1.1) is introduced, i.e.
for some \(\beta >0\). For fixed t and \(\beta \) sufficiently large, \(\sup _{|x|\le R} U^\beta (t,x)\) gives a good approximation for \(\sup _{|x|\le R}u(t,x)\) as \(R\rightarrow \infty \). In our situation, suppose for instance that \(u_0=\delta (\cdot -x_0)\), the random field \(\frac{\mathcal {Z}(x_0; t,x)}{p_t(x-x_0)}\) satisfies the equation
Since the kernel \(p_{\frac{s(t-s)}{t}}\left( y-x_0-\frac{s}{t}(x-x_0)\right) \) now involves s and t with s moving from 0 to t, the mass concentration of the stochastic integration on the right-hand side of (6.11) varies and depends on s. We are not able to find a fixed localized integration domain similar as \(\{y:|y-x|\le \beta \sqrt{t}\}\). To get around this difficulty, we propose an alternative result (Theorem 1.5) which is about the regularized version of \(\mathcal {Z}\), i.e., \(\mathcal {Z}_{\varepsilon }\). To handle the spatial asymptotic of \(\mathcal {Z}_ {\varepsilon }\), we rely on the Feynman–Kac representation (4.2) and adopt an argument developed by Xia Chen in [3] with an additional scaling procedure.
Hereafter, t and \(\varepsilon \) are fixed positive constants, n is the driving parameter which tends to infinity,
Let \(y_1,\dots ,y_N\) be N points in \(B(0,e^n)\) and d be a positive number such that
Under (H.1), d is chosen to be sufficiently large, depending on the shape of \(\gamma \), while under (H.2), we can simply choose \(d=1\). See Lemma 6.4 below for more details.
Theorem 6.3
For every \(x_0\in \mathbb {R}^\ell \)
Proof
Step 1: Let \(m=m_n\) be a natural number such that
Under hypothesis (H.1), for each j, we define the stopping time
where \(r_0>0\) is chosen so that
Such a constant always exists since \(\gamma \) is continuous and \(\gamma (0)>0\). Under hypothesis (H.2), the stopping time depends on n and an arbitrary domain. More precisely, let D be an open bounded ball in \(\mathbb {R}^\ell \) which contains 0. For each j, \(\tau ^j=\tau ^j_n(D)\) denotes the stopping time
As previously, we denote
omitting the dependence on t. We note that from (4.2)
where
Conditioning on B, the variance of \(\xi _m(x_0,y)\) is given by
For every \(\lambda >0\), it is evident that
where we have put
and
Combining all previous estimates, we arrive at an important inequality
It follows that
We put
Applying the estimate
we obtain
Noting that \(N^{-\frac{1}{m}} \lesssim e^{\ell \frac{n}{m}} \) and by (1.24), \(\gamma _{\varepsilon _n}(0)=\varepsilon _n^{-\frac{\alpha }{2}}\gamma _1(0)\lesssim n^{\frac{\alpha }{2}a}\), we see that
In other words, the factor \(N^{-\frac{1}{m}}e^{-\frac{t}{2} \gamma _{\varepsilon _n(0)}}\) in (6.24) is negligible. In addition, we claim that for every \(\lambda \in (0,\sqrt{2\ell })\) and every \(x\in \mathbb {R}^\ell \)
We postpone the proof of this claim till Lemma 6.4 below. It follows that
Step 2: We will show that
We consider first the hypothesis (H.1). Since \(\gamma \) is continuous, for any \(\varepsilon >0\), there is \(\delta \) such that whenever \(|z|\le \delta \wedge r_0\), \(\gamma (z) \ge \gamma (0)-\varepsilon \). Hence,
Since as \(n \rightarrow \infty \), \(m \rightarrow \infty \) too, we have
which proves (6.28) under (H.1).
Assume now that (H.2) holds. We put \(t_n=t^{1-a}n^a\) so that \(\varepsilon _n=\varepsilon \frac{t}{t_n}\). The Brownian motion scaling and the relation (1.24) yield
It follows that
where
Let \(K_ \varepsilon \) be the function defined by
so that
Hence, we can write
Let \(\mathcal D\) be the set of compactly supported continuous functions on \(\mathbb {R}^\ell \) with unit \(L^2(\mathbb {R}^{\ell })\)-norm. For every \(f\in \mathcal D\), applying Cauchy–Schwarz inequality, we see that the right-hand side in the equation above is at least
where we have set
Using independence of Brownian motions, we obtain
where \(\tau _D := \inf \{s \ge 0: B(s) \notin D\}\). Applying Lemma 3.5 we obtain
We now let \(D\uparrow \mathbb {R}^\ell \) to get
We now link the variation on the right-hand side with \({\mathcal {M}}(\gamma )\) (cf. (3.4)) by observing that
Indeed, for each fixed \(g\in {\mathcal {G}}\), applying Fubini’s theorem, Hahn-Banach theorem and (6.29), we have
This leads us the identity (6.30). We can send \(\varepsilon \downarrow 0\), applying Lemma 3.2 and Proposition 3.3, to obtain (6.28) under hypothesis (H.2).
Step 3: Combining the inequalities (6.27) and (6.28) together, we have for every \(\lambda \in (0,\sqrt{2\ell })\)
Finally we let \(\lambda \rightarrow \sqrt{2\ell }^-\) to conclude the proof. \(\square \)
We now provide the proof of (6.26).
Lemma 6.4
For every \(\lambda \in (0,\sqrt{2\ell })\), we have
where we recall \(\eta _n^c\) is defined in (6.23).
Proof
Assuming first that (H.1) holds. We recall that \(\varepsilon _n=0\) in this case so that \(\gamma _{\varepsilon _n}=\gamma \). Let \(\mathcal {B}\) be the \(\sigma \)-field generated by the Brownian motions \(\{B^j\}_{1\le j \le m}\). First we will show that for any \(0< \rho < \frac{1}{2}\), we can find \(d>0\) sufficiently large so that on the event \(\{\min _{1\le j\le m}\tau ^j\ge t\}\), for every \(z,z'\in B(0,e^n)\) with \(|z -z'|\ge d\).
We recall that d and \(\tau ^j\) are defined in (6.13) and (6.16) respectively. We choose and fix \(\varkappa \in (0,1)\) such that
Note that on the event \(\{\min _{1\le j\le m}\tau ^j\ge t\}\), we have \(\sup _{s\le t,j\le m}|B^j_{0,t}(s)|\le r_0\). Then for every \(j,k\le m\),
In addition, from (1.3) and Riemann–Lebesgue lemma, \(\lim _{x\rightarrow \infty } \gamma (x)=0\). Hence, when \(s\in [\varkappa t , t]\), we can choose d large enough such that whenever \(|y|\le 2r_0\) and \(|z-z'|\ge d\)
In particular, for every \(|z-z'|\ge d\) we have
It follows that
which verifies (6.32).
Since \(\lambda < \sqrt{2\ell }\), we can choose \(\kappa , \rho \in (0,\frac{1}{2})\) sufficiently small so
Let us now recall Lemma 4.2 in [2]. For a mean zero n-dimensional Gaussian vector \((\xi _1, \cdots , \xi _n)\) with identically distributed components,
and for any \(A,B >0\), we have
where U is a standard normal random variable. Applying this inequality conditionally with \(A=\lambda S_m(t) \sqrt{n}\) and \(B= \kappa S_m \sqrt{n}\), we have for sufficiently large n,
where \(v>0\) is independent of n. Now for any \(\theta >0\), this yields
An application of Borel-Cantelli lemma yields (6.31) under hypothesis (H.1).
We now consider the hypothesis (H.2). The argument is similar to the previous case. There is, however, an additional scaling procedure. Recall that \(\mathcal {B}\) is the \(\sigma \)-field generated by the Brownian motions \(\{B^j\}_{1\le j \le m}\). We choose \(d=1\). It suffices to prove (6.32) on the event \(\{ \min _{0\le j\le m} \tau ^j\ge t \}\), for any \(|z-z'|\ge 1\). Indeed, we have
For every \(j,k\le m\), using the scaling relation (1.24), we can write
We now choose and fix \(\theta >0\) such that
this is always possible since \(\gamma _1=p_{2}*\gamma \) is a strictly positive function. It follows that
In addition, on the event \(\{\min _{0\le j\le m} \tau ^j\ge t \}\), \(\varepsilon _n^{-\frac{1}{2}}(B_{0,t}^j(t-s)-B_{0,t}^k(t-s))\) belongs to \(2\varepsilon ^{-\frac{1}{2}}D\) for all \(s\in [0,t]\). Hence, for every \(s\in [\theta t,t]\) and \(|z-z'|\ge 1\), we have
We note that from Riemann–Lebesgue lemma, \(\lim _{x\rightarrow \infty } \gamma _1(x)=0\). Hence, whenever n is sufficiently large,
for all \(|y|\ge \theta \varepsilon _n^{-\frac{1}{2}}- 2 \varepsilon ^{-\frac{1}{2}} \mathrm {diag}(D)\). It follows that for every \(z,z'\) with \(|z-z'|\ge 1\),
Upon combining these estimates, we arrive at (6.32), which in turn, implies (6.31). \(\square \)
6.3 Proofs
Theorems 1.3, 1.4 and 1.5 follow from the asymptotic results from the previous two subsections. Indeed, Theorem 1.3 follows by combining the upper bound in Theorem 6.1 and the lower bound in Theorem 6.3. To obtain Theorem 1.4, we first observe that from (4.1),
Then, an application of Theorem 6.1 yields the result. For Theorem 1.5, the upper bound of (1.25) follows from Remark 6.2 and the bound (6.39) with \(u,\mathcal {Z}\) replaced respectively by \(u_{\varepsilon }, \mathcal {Z}_ \varepsilon \), together with the obvious fact that \(\mathcal {E}_H(\gamma _{\varepsilon })\le \mathcal {E}_H(\gamma )\), see (3.3). The lower bound of (1.26) is immediate from Theorem 6.3.
References
Chen, L., Huang, J.: Comparison principle for stochastic heat equation on \(\mathbb{R}^{d}\). Ann. Probab. (to appear)
Chen, X.: Quenched asymptotics for Brownian motion in generalized Gaussian potential. Ann. Probab. 42(2), 576–622 (2014)
Chen, X.: Spatial asymptotics for the parabolic Anderson models with generalized time-space Gaussian noise. Ann. Probab. 44(2), 1535–1598 (2016)
Chen, L., Hu, Y., Nualart, D.: Two-point correlation function and Feynman–Kac formula for the stochastic heat equation. Potential Anal. 46(4), 779–797 (2017)
Chen, X., Hu, Y., Nualart, D., Tindel, S.: Spatial asymptotics for the parabolic Anderson model driven by a Gaussian rough noise. Electron. J. Probab. 22, Paper No. 65, 38 (2017)
Chen, X., Hu, Y., Song, J., Xing, F.: Exponential asymptotics for time-space Hamiltonians. Ann. Inst. Henri Poincar’e Probab. Stat. 51(4), 1529–1561 (2015)
Conus, D., Joseph, M., Khoshnevisan, D.: On the chaotic character of the stochastic heat equation, before the onset of intermitttency. Ann. Probab. 41(3B), 2225–2260 (2013)
Chen, X., V Phan, T.: Free energy in a mean field of Brownian particles (preprint)
Dalang, R.C.: Extending the martingale measure stochastic integral with applications to spatially homogeneous s.p.d.e.’s. Electron. J. Probab. 4(6), 29 (1999). (electronic)
Da Prato, G., Zabczyk, J.: Stochastic Equations in Infinite Dimensions. Encyclopedia of Mathematics and its Applications, vol. 44. Cambridge University Press, Cambridge (1992)
Dalang, R.C., Quer-Sardanyons, L.: Stochastic integrals for spde’s: a comparison. Expos. Math. 29(1), 67–109 (2011)
Erd’elyi, A., Magnus, W., Oberhettinger, F., Tricomi, F.G.: Higher Transcendental Functions, vol. III. Robert E. Krieger Publishing Co. Inc, Fla., Melbourne (1981). Based on notes left by Harry Bateman, Reprint of the 1955 original
Garsia, A.M., Rodemich, E., Rumsey Jr., H.: A real variable lemma and the continuity of paths of some Gaussian processes. Indiana Univ. Math. J. 20, 565–578 (1970/1971)
Hairer, M.: A theory of regularity structures. Invent. Math. 198(2), 269–504 (2014)
Hu, Y., Huang, J., Nualart, D., Tindel, S.: Stochastic heat equations with general multiplicative Gaussian noises: Hölder continuity and intermittency. Electron. J. Probab. 20(55), 50 (2015)
Huang, J., Lê, K., Nualart, D.: Large time asymptotics for the parabolic Anderson model driven by spatially correlated noise. Ann. Inst. Henri Poincar’e Probab. Stat. 53(3), 1305–1340 (2017)
Hu, Y., Nualart, D.: Stochastic heat equation driven by fractional noise and local time. Probab. Theory Relat. Fields 143(1–2), 285–328 (2009)
Huang, J.: On stochastic heat equation with measure initial data. Electron. Commun. Probab. 22, Paper No. 40, 6 (2017)
Lê, K.: A remark on a result of Xia Chen. Statist. Probab. Lett. 118, 124–126 (2016)
Acknowledgements
The project was initiated while both authors were visiting the Mathematical Sciences Research Institute in Berkeley, California, during the Fall 2015 semester. The first named author thanks Professor Davar Khoshnevisan for stimulating discussions and encouragement. The second named author thanks PIMS for its support through the Postdoctoral Training Centre in Stochastics. Both authors thank Professor Yaozhong Hu and Professor David Nualart for support and encouragement. We also thank the referee for a thorough report and numerous comments which improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is partially supported by NSF Grant No. 0932078000.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Huang, J., Lê, K. Spatial asymptotic of the stochastic heat equation with compactly supported initial data. Stoch PDE: Anal Comp 7, 495–539 (2019). https://doi.org/10.1007/s40072-019-00133-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40072-019-00133-x