Abstract
Recently, a solution theory for one-dimensional stochastic PDEs of Burgers type driven by space-time white noise was developed. In particular, it was shown that natural numerical approximations of these equations converge and that their convergence rate in the uniform topology is arbitrarily close to \(\frac{1}{6}\). In the present article we improve this result in the case of additive noise by proving that the optimal rate of convergence is arbitrarily close to \(\frac{1}{2}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The goal of this article is to study numerical approximations of stochastic PDEs of Burgers type on the circle \(\mathbb {T} = {\mathbb {R}}/ (2\pi {\mathbb {Z}})\) given by
Here, \(u : {\mathbb {R}}_+ \times \mathbb {T} \times \Omega \rightarrow {\mathbb {R}}^n\), where \(\left( \Omega , \mathcal {F}, \mathbb {P} \right) \) is a probability space, \(\Delta =\partial ^2_x\) is the Laplace operator on the circle \(\mathbb {T}\), the derivative \(\partial _x\) is understood in the sense of distributions, the function \(F:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) is of class \(\mathcal {C}^1\), the function \(G:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^{n \times n}\) is of class \(\mathcal {C}^{\infty }\), and \(\nu , \sigma \in {\mathbb {R}}_+\) are positive constants. Finally, W is an \(L^2\)-cylindrical Wiener process [6], i.e. Eq. (1.1) is driven by space-time white noise. The product appearing in the term \(G(u) \partial _{x} u\) is matrix-vector multiplication.
The difficulty in dealing with (1.1) comes from the nonlinearity \(G(u) \partial _{x} u\) and is caused by the low space-time regularity of the driving noise. Indeed, it is well-known that the pairing
is well defined if and only if \(\alpha + \beta > 1\) (see Appendix 1; [2]). On the other hand, one expects solutions to (1.1) to have the spatial regularity of the solution of the linearised equation
For any fixed time \(t > 0\), the solution to the stochastic heat equation (1.2) has Hölder regularity \(\alpha < \frac{1}{2}\), but is not \(\frac{1}{2}\)-Hölder continuous (see [6, 17, 29]). This implies in particular that the product \(G(X) \partial _x X\) is not well-defined in this case, and it is not a priori clear how to define a solution to the Eq. (1.1).
In the case \(G \equiv 0\) this problem does of course not occur. Equations of this type and their numerical approximations were well studied and the results can be found in [15, 16]. Moreover, it was shown in [5] that the optimal rate of uniform convergence in this case is \(\frac{1}{2} - \kappa \), for every \(\kappa > 0\), as the spatial discretisation tends to zero.
For non-zero G, the difficulty can easily be overcome in the gradient case, i.e. when \(G = \nabla \mathcal {G}\) for some smooth function \(\mathcal {G} : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\). In this case, postulating the chain rule, the nonlinear term can be rewritten as
which is a well-defined distribution as soon as u is continuous. The existence and uniqueness results in the gradient case can be found in [7, 14]. In the article [1], the finite difference scheme was studied for the case \(G(u)=u\), and \(L^2\)-convergence was shown with rate \(\gamma \), for every \(\gamma < \frac{1}{2}\). The same rate of convergence was obtained in [3] in the \(L^\infty \) topology for Galerkin approximations.
For a general sufficiently smooth function G, a notion of solution was given in [18]. The key idea of the approach was to test the nonlinearity with a smooth test function \(\varphi \) and to formally rewrite it as
As it was stated above, we expect u to behave locally like the solution to the linearised equation (1.2). It was shown in [18] that the latter can be viewed in a canonical way as a process with values in a space of rough paths. This correctly suggests that the theory of controlled rough paths [11, 12] could be used to deal with the integral (1.4) in the pathwise sense. The quantity (1.4) is uniquely defined up to a choice of the iterated integral which represents the integral of u with respect to itself. This implies that for different choices of the iterated integral we obtain different solutions, which is similar to the choice between Itô and Stratonovich stochastic integrals in the theory of SDEs. In the present situation however, there is a unique choice for the iterated integral which respects the symmetry of the linearised equation under the substitution \(x \mapsto -x\), and this corresponds to the “Stratonovich solution”. This natural choice is also the one for which the chain rule (1.3) holds in the particular case when G is a gradient.
Using the rough path approach, numerical approximations to (1.1) in the gradient case without using the chain rule were studied in [19]. It was shown that the corresponding approximate solutions converge in suitable Sobolev spaces to a limit which solves (1.1) with an additional correction term, which can be computed explicitly. This term is an analogue to the Itô-Stratonovich correction term in the classical theory of SDEs.
In [20], the solution theory was extended to Burgers-type equations with multiplicative noise (i.e. when the multiplier of the noise term is a nonlinear local function \(\theta (u)\) of the solution). Analysis of numerical schemes approximating the equation in the multiplicative case was performed in [21], where the appearance of a correction term was observed and the rate of convergence in the uniform topology was shown to be of order \(\frac{1}{6}-\kappa \), for every \(\kappa > 0\).
In this article, we prove that in the case of additive noise the rate of convergence in the supremum norm is \(\frac{1}{2}-\kappa \), for every \(\kappa > 0\). Actually, it turns out to be technically advantageous to consider convergence in Hölder spaces with Hölder exponent very close to zero. The main difference to [21] is that we cannot use the classical theory of controlled rough paths which applies only in the Hölder spaces of regularity from \(\left( \frac{1}{3}, \frac{1}{2}\right] \), to approximate the rough integral (1.4). To show the convergence in the Hölder spaces of lower regularity, we use the results from [12], which generalize the theory of controlled rough paths for functions of any positive regularity.
1.1 Assumptions and statement of the main result
As before we assume that \(F \in \mathcal {C}^1\) and \(G \in \mathcal {C}^{\infty }\) in (1.1). For \(\varepsilon > 0\) we consider the approximate stochastic PDEs on the circle \(\mathbb {T}\) given by
Here, the operators \(\Delta _{\varepsilon }\), \(D_{\varepsilon }\) and \(H_{\varepsilon }\) are defined as Fourier multipliers providing approximations of \(\Delta \), \(\partial _{x}\) and the identity operator respectively, and are given by
Below we provide the assumptions on the functions f, g and h. We start with the assumptions on f.
Assumption 1
The function \(f: {\mathbb {R}}\rightarrow (0,\infty ]\) is even, satisfies \(f(0)=1\), is continuously differentiable on the interval \([-\delta , \delta ]\) for some \(\delta > 0\), and there exists \(c_{f} \in (0,1)\) such that \(f \ge c_{f}\).
Furthermore, the functions \(b_t\) given by \(b_{t}(x) := \exp \left( -x^{2}f(x)t \right) \) are uniformly bounded in \(t > 0\) in the bounded variation norm, i.e. \(\sup _{t > 0} |b_{t}|_{\mathrm {BV}} < \infty \).
Our next assumption concerns g, which defines the approximation to the spatial derivative.
Assumption 2
There exists a signed Borel measure \(\mu \) on \({\mathbb {R}}\) such that \(\int _{{\mathbb {R}}} e^{ikx} \mu (dx) = ik g(k)\), and such that
Moreover, the measure \(\mu \) has all finite moments, i.e. \(\int _{{\mathbb {R}}} |x|^{k} |\mu |(dx) < \infty \), for any integer \(k \ge 1\).
In particular, the approximate derivative can be expressed as
where we identify \(u: \mathbb {T} \rightarrow {\mathbb {R}}\) with its periodic extension to all \({\mathbb {R}}\). Our last assumption is on the function h, which defines the approximation of noise.
Assumption 3
The function h is even, bounded, and such that \(h^{2}/f\) and \(h/(f + 1)\) are of bounded variation. Furthermore, h is twice differentiable at the origin with \(h(0)=1\) and \(h'(0)=0\).
The difference with the assumptions in [21] is that we require in Assumption 2 all the moments of the measure \(\mu \) to be finite and in Assumption 3 the function \(h/(f + 1)\) to be of bounded variation. We use the latter assumption in Lemma 4.1 in order to use the bounds on lifted rough paths obtained in [10]. All the examples of approximations provided in [19] (including finite difference schemes) still satisfy our assumptions.
Let \(\bar{u}\) be the solution to the modified equation (1.1),
where, for \(i = 1, \ldots , n\), the modified reaction term is given by
Here, we denote by \(G_i\) the ith row of the matrix-valued function G, and the correction constant is defined by
It follows from the assumptions that \(\Lambda \) is well-defined. In fact, the Assumption 3 says that \(|h^2 / f|\) is bounded, and by the Assumption 2 the measure \(\mu \) has a finite second moment, what yields the existence of \(\Lambda \).
As we do not assume boundedness of the functions F and G, and their derivatives, the solution can blow up in finite time. To overcome this difficulty we consider solutions only up to some stopping times. More precisely, for any \(K > 0\) we define the stopping times
where \(\Vert \cdot \Vert _{\mathcal {C}^{0}}\) is the supremum norm. The blow-up time of \(\bar{u}\) is then defined as \(\tau ^* := \lim _{K \uparrow \infty } \tau ^*_K\) in probability.
Our main theorem gives the convergence rate of the solutions of the approximate equations (1.5) to the solution of the modified equation (1.6).
Theorem 1.1
Let for every \(0 < \eta < \frac{1}{2}\) the initial values satisfy
Moreover, we assume that for every \(\alpha > 0\) small enough the following estimate holds
where the proportionality constant can depend on \(\alpha \). Then, for every such \(\alpha > 0\), there exists a sequence of stopping times \(\tau _{\varepsilon }\) satisfying \(\lim _{\varepsilon \downarrow 0} \tau _{\varepsilon } = \tau ^*\) in probability, such that the following convergence holds
Remark 1.2
The rate of convergence obtained in [21] was “almost” \(\frac{1}{6}\), in the sense that it is \(\frac{1}{6} - \kappa \) for any \(\kappa > 0\). To improve this result we consider convergence of the solutions in the Hölder spaces of the regularities close to zero. This approach creates difficulties when working with the rough integrals (1.4). In fact, the bounds on the rough integrals, in particular in [21, Lemma 5.3], hold only in the Hölder spaces \(\mathcal {C}^\alpha \) with \(\alpha \in \left( \frac{1}{3}, \frac{1}{2}\right) \) and the norms explode as \(\alpha \) approaches \(\frac{1}{3}\). To have reasonable bounds in the Hölder spaces of lower regularity, we have to include into the definition of the rough integrals the iterated integrals of the controlling process X of higher order. In [21] it was enough to consider only the iterated integrals of order two. In particular, the smaller \(\alpha \) is in Theorem 1.1, the more iterated integrals we have to consider to define the rough integral (1.4) (see Sect. 2 for more details).
If the function G is only of class \(\mathcal {C}^p\) for some \(p \ge 3\), we can consider the iterated integrals of X only up to the order \(p-1\) (see Sect. 4.1). As a consequence, the argument in the proof of Theorem 1.1 gives the rate of convergence only “almost” \(\frac{1}{2} - \frac{1}{p}\). This is precisely the rate of convergence obtained in [21], where p was taken to be 3.
Remark 1.3
By changing the time variable and the functions in (1.1) by a constant multiplier, we can obtain an equivalent equation with \(\nu = 1\). Moreover, we can assume \(\sigma = 1\). In what follows we only consider these values of the constants.
1.2 Structure of the article
In Sect. 2 we review the theories of rough paths and controlled rough paths. Section 3 is devoted to the results obtained in [18]. In particular, here we provide a notion of solution and the existence and uniqueness results for the Burgers type equations with additive noise. In Sect. 4 we define the rough integrals and formulate the mild solution to the approximate equation (1.5) in a way appropriate for working in the Hölder spaces of low regularity. The proof of Theorem 1.1 is provided in Sect. 5. The following sections give bounds on the corresponding terms in the equations (1.6) and (1.5): in Sects. 6 and 7 we consider the reaction terms and Sect. 8 is devoted to the terms involving the rough integrals. In Appendix 1 we prove a Kolmogorov-like criterion for distribution-valued processes. Appendix 2 provides regularity properties of the heat semigroup and its approximate counterpart on the Hölder spaces.
1.3 Spaces, norms and notation
Throughout this article, we denote by \(\mathcal {C}^0\) the space of continuous functions on the circle \(\mathbb {T}\) endowed with the supremum norm.
For functions \(X: {\mathbb {R}}\rightarrow {\mathbb {R}}^n\) (or \({\mathbb {R}}^{n \times n}\)) and \(R: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^n\) (or \({\mathbb {R}}^{n \times n}\)), such that R vanishes on the diagonal, we define respectively Hölder seminorms with a given parameter \(\alpha \in (0,1)\):
By \(\mathcal {C}^\alpha \) and \(\mathcal {B}^\alpha \) respectively we denote the spaces of functions for which these seminorms are finite. Then \(\mathcal {C}^\alpha \) endowed with the norm \(\Vert \cdot \Vert _{\mathcal {C}^\alpha } = \Vert \cdot \Vert _{\mathcal {C}^0} + \Vert \cdot \Vert _{\alpha }\) is a Banach space. \(\mathcal {B}^\alpha \) is a Banach space endowed with \(\Vert \cdot \Vert _{\mathcal {B}^\alpha } = \Vert \cdot \Vert _{\alpha }\).
The Hölder space \(\mathcal {C}^\alpha \) of regularity \(\alpha \ge 1\) consists of \(\lfloor \alpha \rfloor \) times continuously differentiable functions whose \(\lfloor \alpha \rfloor \)-th derivative is \((\alpha - \lfloor \alpha \rfloor )\)-Hölder continuous. For \(\alpha < 0\) we denote by \(\mathcal {C}^\alpha \) the Besov space \(\mathcal {B}^\alpha _{\infty , \infty }\) (see Appendix 1 for the definition).
We also define space-time Hölder norms, i.e. for some \(T > 0\) and functions \(X:[0,T] \times \mathbb {T} \rightarrow {\mathbb {R}}^n\) (or \({\mathbb {R}}^{n \times n}\)) and \(R:[0,T] \times \mathbb {T}^2 \rightarrow {\mathbb {R}}^n\) (or \({\mathbb {R}}^{n \times n}\)), any \(\alpha \in {\mathbb {R}}\) and any \(\beta > 0\) we define
We denote by \(\mathcal {C}^{\alpha }_{T}\) and \(\mathcal {B}^{\alpha }_{T}\) respectively the spaces of functions/distributions for which the norms (1.7) are finite. Furthermore, in order to deal with functions X exhibiting a blow-up with rate \(\eta >0\) near \(t=0\), we define the norm
Similarly to above, we denote by \(\mathcal {C}^{\alpha }_{\eta , T}\) the space of functions/distributions for which this norm is finite.
By \(\Vert \cdot \Vert _{\mathcal {C}^\alpha \rightarrow \mathcal {C}^\beta }\) we denote the operator norm of a linear map acting from the space \(\mathcal {C}^\alpha \) to \(\mathcal {C}^\beta \). When we write \(x \lesssim y\), we mean that there is a constant C, independent of the relevant quantities, such that \(x \le Cy\).
2 Elements of rough path theory
In this section we provide an overview of rough path theory and controlled rough paths. For more information on rough paths theory we refer to the original article [23] and to the monographs [8, 9, 24, 25].
One of the aims of rough paths theory is to provide a consistent and robust way of defining the integral
for processes \(Y, X \in \mathcal {C}^\alpha \) with any Hölder exponent \(\alpha \in \left( 0,\frac{1}{2}\right] \). If \(\alpha > \frac{1}{2}\), then the integral can be defined in Young’s sense [30] as the limit of Riemann sums. If \(\alpha \le \frac{1}{2}\), however, the Riemann sums may diverge (or fail to converge to a limit independent of the partition) and the integral cannot be defined in this way. Given \(X \in \mathcal {C}^\alpha \) with \(\alpha \in \left( 0, \frac{1}{2}\right] \), the theory of (controlled) rough paths allows to define (2.1) in a consistent way for a certain class of integrands Y. To this end however, one has to consider not only the processes X and Y, but suitable additional “higher order” information.
We fix \(0 < \alpha \le \frac{1}{2}\) and \(p = \lfloor 1 / \alpha \rfloor \) to be the largest integer such that \(p \alpha \le 1\). We then define the p-step truncated tensor algebra
whose basis elements can be labelled by words of length not exceeding p (including the empty word), based on the alphabet \(\mathcal {A} = \{1, \ldots , n\}\). We denote this set of words by \(\mathcal {A}_p\). Then the correspondence \(\mathcal {A}_p \rightarrow T^{(p)}({\mathbb {R}}^n)\) is given by \(w \mapsto e_w\) with \(e_w = e_{w_1} \otimes \ldots \otimes e_{w_k}\), for \(w = w_1 \ldots w_k\) and \(e_{\emptyset } = 1 \in \big ({\mathbb {R}}^n\big )^{\otimes 0}\approx {\mathbb {R}}\), where \(\{e_{i}\}_{i \in \mathcal {A}}\) is the canonical basis of \({\mathbb {R}}^n\).
There is an operation \(,\) called shuffle product [27], defined on the free algebra generated by \(\mathcal {A}\). For any two words the shuffle product gives all the possible ways of interleaving them in the ways that preserve the original order of the letters. For example, if a, b and c are letters from \(\mathcal {A}\), then one has the identity

We also define both the shuffle and the concatenation product of two elements from \(T^{(p)}\big ({\mathbb {R}}^n\big )\), i.e. for any two words \(w, \bar{w} \in \mathcal {A}_p\) we define

if the sums of the lengths of the two words do not exceed p and  otherwise. This is extended to all of \(T^{(p)}\big ({\mathbb {R}}^n\big )\) by linearity. With these notations at hand, we give the following definition:
otherwise. This is extended to all of \(T^{(p)}\big ({\mathbb {R}}^n\big )\) by linearity. With these notations at hand, we give the following definition:
Definition 2.1
A geometric rough path of regularity \(\alpha \in \left( 0, \frac{1}{2}\right] \) is a map \(\mathbf {X} : {\mathbb {R}}^2 \rightarrow T^{(p)}\big ({\mathbb {R}}^n\big )\), where as above \(p = \lfloor 1 / \alpha \rfloor \), such that
-
1.
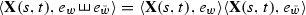 , for any \(w, \bar{w} \in \mathcal {A}_p\) with \(|w| + |\bar{w}| \le p\),
, for any \(w, \bar{w} \in \mathcal {A}_p\) with \(|w| + |\bar{w}| \le p\), -
2.
\(\mathbf {X}(s,t) = \mathbf {X}(s,u) \otimes \mathbf {X}(u,t)\), for any \(s, u, t \in {\mathbb {R}}\),
-
3.
\(\Vert \langle \mathbf {X}, e_w \rangle \Vert _{\mathcal {B}^{\alpha |w|}} < \infty \), for any word \(w \in \mathcal {A}_p\) of length |w|.
If we define \(X^i(t) := \langle \mathbf {X}(0,t), e_i \rangle \) for any \(i \in \mathcal {A}\), then the components of \(\mathbf {X}(s,t)\) of higher order should be thought of as defining the iterated integrals
for \(w=w_1 \ldots w_k \in \mathcal {A}_p\). Of course, the integrals on the right hand side of (2.2) are not defined, as mentioned at the start of this section. Hence, for a given rough path \(\mathbf {X}\), then the left hand side of (2.2) is the definition of the right hand side.
The conditions in Definition 2.1 ensure that the quantities (2.2) behave like iterated integrals. In particular, if X is a smooth function and we define \(\mathbf {X}\) by (2.2) in Young’s sense, then \(\mathbf {X}\) satisfies the conditions of Definition 2.1, as was shown in [4]. In particular, if \(x = e_i\) and \(y = e_j\), for any two letters \(i, j \in \mathcal {A}\), then the first property gives
where we write \(X^i(s,t) := X^i(t) - X^i(s)\). This is the usual integration by parts formula. The second condition of Definition 2.1 provides the additivity property of the integral over consecutive intervals.
Given an \(\alpha \)-regular rough path \(\mathbf {X}\), we define the following quantity
2.1 Controlled rough paths
The theory of controlled rough paths was introduced in [11] for geometric rough paths of Hölder regularity from \(\big (\frac{1}{3}, \frac{1}{2} \big ]\). In [12], the theory was generalised to rough paths of arbitrary positive regularity.
Definition 2.2
Given \(\alpha \in \left( 0, \frac{1}{2}\right] \), \(p = \lfloor 1/\alpha \rfloor \), a geometric rough path \(\mathbf {X}\) of regularity \(\alpha \), and a function \(Y: {\mathbb {R}}\rightarrow \big (T^{(p-1)}\big ({\mathbb {R}}^n\big )\big )^*\) (the dual of the truncated tensor algebra), we say that Y is controlled by \(\mathbf {X}\) if, for every word \(w \in \mathcal {A}_{p-1}\), one has the bound
for some constant \(C > 0\).
An alternative statement of Definition 2.2 is that for every word \(w \in \mathcal {A}_{p-1}\) there exists a function \(R_Y^w \in \mathcal {B}^{(p-|w|)\alpha }\) such that
Given an \(\alpha \)-regular geometric rough path \(\mathbf {X}\), we then endow the space of all controlled paths Y with the semi-norm
Given a rough path Y controlled by \(\mathbf {X}\), one can define the integral (2.1) by

where we denoted \(X^i(t) := \langle \mathbf {X}(0,t), e_i \rangle \) for \(i \in \mathcal {A}\), and
Here, the limit is taken over a sequence of partitions \(\mathcal {P}\) of the interval [s, t], whose diameters \(|\mathcal {P}|\) tend to 0. It was proved in [12, Theorem 8.5] that the rough integral (2.5) is well defined, i.e. the limit in (2.5) exists and is independent of the choice of partitions \(\mathcal {P}\).
If every coordinate \(Y^j\) of the process Y is controlled by \(\mathbf {X}\), then we denote the rough integral of Y with respect to X by

We use the symbol  for the rough integral in (2.5), in order to remind the abuse of notation, since the integral depends not only on \(X^i\) and \(Y^j\), but on much more information contained in \(\mathbf {X}\) and Y. In the following proposition we provide several bounds on the rough integrals.
for the rough integral in (2.5), in order to remind the abuse of notation, since the integral depends not only on \(X^i\) and \(Y^j\), but on much more information contained in \(\mathbf {X}\) and Y. In the following proposition we provide several bounds on the rough integrals.
Proposition 2.3
Let Y be controlled by a geometric rough path \(\mathbf {X}\) of regularity \(\alpha \in \left( 0, \frac{1}{2}\right] \). Then there is a constant C, independent of Y and \(\mathbf {X}\), such that


Moreover, if \(\bar{Y}\) is controlled by another rough path \(\bar{\mathbf{X}}\) of regularity \(\alpha \), then there is a constant C, independent of \(\mathbf {X}\), \(\bar{\mathbf{X}}\), Y and \(\bar{Y}\), such that

where we have used the quantity
Proof
The bounds follow from [12, Theorem 8.5, Proposition 6.1]. \(\square \)
Remark 2.4
The notation \(\vert \vert \vert \mathbf {X} - \bar{\mathbf{X}} \vert \vert \vert _{\alpha }\) is a slight abuse of notation since \(\mathbf {X} - \bar{\mathbf{X}}\) is not a rough path in general. The definition (2.3) does however make perfect sense for the difference.
In fact, the article [12] gives more precise bounds on the rough integrals than those provided in Proposition 2.3, but we prefer to have them in this form for the sake of conciseness.
3 Definition and well-posedness of the solution
Let us now give a short discussion of what we mean by “solutions” to (1.1), as introduced in [18]. The idea is to find a process X such that \(v = u - X\) is of class \(\mathcal {C}^1\) (in space), so that the definition of the integral (1.4) boils down to defining the integral
If we have a canonical way of lifting X to a rough path \(\mathbf {X}\), this integral can be interpreted in the sense of rough paths.
A natural choice for X is the solution to the linear stochastic heat equation. In order to get nice properties for this process, we build it in a slightly different way from [18]. First, we define the stationary solution to the modified SPDE on the circle \(\mathbb {T}\),
where \(\Pi \) denotes the orthogonal projection in \(L^{2}\) onto the space of functions with zero mean. Second, we define the process
where \(w^0\) if the zeroth Fourier mode of W.
Remark 3.1
We need to use \(\Pi \) in (3.1) in order to obtain a stationary solution. In [18], the author used instead the stationary solution to \(d X = \Delta X dt - X dt + dW\) as a reference path. Our choice of X was used in [21] and does not change the results of [18].
The following lemma shows that there is a natural way to extend X to a rough path.
Lemma 3.2
For every \(\frac{1}{3} < \alpha < \frac{1}{2}\), the stochastic process X can be canonically lifted to a process \(\mathbf {X}: {\mathbb {R}}\times \mathbb {T}^2 \rightarrow T^{(2)}\big ({\mathbb {R}}^n\big )\), such that for every fixed \(t \in {\mathbb {R}}\), the process \(\mathbf {X}(t)\) is a geometric \(\alpha \)-rough path.
The term “canonically” means that for a large class of natural approximations of the process X by smooth Gaussian processes \(X_\varepsilon \), the iterated integrals of \(X_\varepsilon \), defined by (2.2), converge in \(L^2\) to the corresponding elements of \(\mathbf {X}\) (see [9] for a precise definition and the proof). Denote by \(S_t = e^{t\Delta }\) the heat semigroup, which is given by convolution on the circle with the heat kernel
Assuming that the rough path-valued process \(\mathbf {X}\) is given, we then define solutions to (1.1) as follows:
Definition 3.3
Setting \(U(t) := S_t \left( u(0) - X(0) \right) \), a stochastic process u is a mild solution to the Eq. (1.1) if the process \(v(t) := u(t) - X(t) - U(t)\) belongs to \(\mathcal {C}^{1}_T\) and the identity
holds almost surely. Here, we write for brevity \(u(t) = v(t) + X(t) + U(t)\), and the process Z(s, x) is a rough integral

whose derivative we consider in the sense of distributions.
Remark 3.4
In [18], the last integral in (3.4) was defined by

but as noticed in [21], the notion of solution in Definition 3.3 is more convenient, as it simplifies treatment of the rough integral. This change does not affect the existence and uniqueness results of [18], and the resulting solutions are the same.
For our convenience we rewrite the mild formulation of (1.6) as
where we have set
and as before \(\bar{u} = \bar{v} + X + U\), \(U(t) = S_t(u^0 - X(0))\) and

Although the two terms \(\Phi ^{\bar{v}}\) and \(\Upsilon ^{\bar{v}}\) are of the same type, we give them different names since they will arise in completely different ways from the approximation.
3.1 Existence and uniqueness results
The next theorem provides the well-posedness result for a mild solution to the Eq. (1.1).
Theorem 3.5
Let us assume that \(u^0 \in \mathcal {C}^\beta \) for some \(\frac{1}{3} < \beta < \frac{1}{2}\). Furthermore, let \(F \in \mathcal {C}^1\) and \(G \in \mathcal {C}^{3}\). Then for almost every realisation of the driving noise, there is \(T > 0\) such that there exists a unique mild solution to (1.1) on the interval [0, T] taking values in \(\mathcal {C}\big ([0,T], \mathcal {C}^\beta (\mathbb {T})\big )\). If moreover, F, G and all their derivatives are bounded, then the solution is global (i.e. \(T = \infty \)).
Proof
The proof can be done by performing a classical Picard iteration for v given by (3.4) on the space \(\mathcal {C}^{1}_{T}\) for some \(T \le 1\), see [18]. \(\square \)
Remark 3.6
The argument of [18, Theorem 3.7] also works in the space \(\mathcal {C}^{1+\alpha }_{\alpha /2, T}\), for any \(\alpha \in \left[ 0, \frac{1}{2}\right) \). Hence, the real regularity of v(t) is \(1 + \alpha \) rather than 1. This fact will be used in Sect. 6 to estimate how close the approximate derivative of v is to \(\partial _x v\).
4 Solutions of the approximate equations
In this section we rewrite the mild solution to the approximate equation (1.5) in a way convenient for working in Hölder spaces of low regularity. In particular, we define the iterated integrals of higher order of the controlling process.
Similarly to (3.1) and (3.2) we define the stationary process \(Y_{\varepsilon }\) and \(X_\varepsilon \) by
where \(w^0\) is the zeroth Fourier mode of W. Moreover, we define the approximate semigroup \(S^{(\varepsilon )}_t = e^{t\Delta _{\varepsilon }}\) generated by the approximate Laplacian and given by convolution on the circle \(\mathbb {T}\) with the approximate heat kernel
Furthermore, we define \(U_\varepsilon (t) := S^{(\varepsilon )}_t \left( u_\varepsilon (0) - X_\varepsilon (0) \right) \) and \(v_\varepsilon := u_\varepsilon - X_\varepsilon - U_\varepsilon \). Then the mild version of the approximate equation (1.5) can be rewritten as
where we write for brevity \(u_\varepsilon = v_\varepsilon + X_\varepsilon + U_\varepsilon \), and set
As already mentioned in Sect. 2, the rough integrals are approximated by Riemann-like sums, but these include additional higher-order correction terms. Hence, we cannot expect in general that Z(s, x), defined in (3.5), is approximated by
as \(\varepsilon \downarrow 0\). In order to approximate Z(s, x), we have to add some extra terms to (4.5). These extra terms give raise to the correction term in the limiting equation, mentioned in the introduction. In the rest of this section we build these missing extra terms.
4.1 Iterated integrals
In order to use the theory of rough paths with regularities close to zero, we need to build the iterated integrals of arbitrarily high orders of X and \(X_\varepsilon \) with respect to themselves.
The expansion of \(X_{\varepsilon }\) defined in (4.1) in the Fourier basis is given by
Here, \(w_{k}\) are \({\mathbb {C}}^{n}\)-valued standard Brownian motions (i.e. real and imaginary parts of every component are independent real-valued Brownian motions so that \(\mathbb {E}|w^{i}_{k}(t)|^{2}=t\)), which are independent up to the constraint \(w_{k}=\bar{w}_{-k}\) ensuring that \(X_{\varepsilon }\) is real-valued. Furthermore, for every fixed \(t \ge 0\), \(\eta ^{(\varepsilon )}_{k}(t)\) are independent \({\mathbb {R}}^{n}\)-valued standard Gaussian random vectors such that
and the coefficients \(q^{(\varepsilon )}_{k}\) are defined by
Similarly, the Fourier expansion of the process X is
where \(\eta _{k}(t)\) are independent \({\mathbb {R}}^{n}\)-valued standard Gaussian random vectors such that
Furthermore, the random vectors \(\{(\eta ^{(\varepsilon )}_{k}(t), \eta _{k}(t)) : k \in {\mathbb {Z}}\setminus \{0\}\}\) are independent and satisfy
The following lemma provides bounds on the canonical lifts of X(t) and \(X_\varepsilon (t)\) to Gaussian rough paths.
Lemma 4.1
For \(\alpha \in \left( 0,\frac{1}{2}\right) \), \(t \ge 0\) and \(p = \lfloor 1/\alpha \rfloor \), consider the canonical lifts \(\mathbf {X}(t), \mathbf {X}_\varepsilon (t): \mathbb {T}^2 \rightarrow T^{(p)}\big ({\mathbb {R}}^n\big )\) of the processes X(t) and \(X_\varepsilon (t)\) to Gaussian rough paths of regularity \(\alpha \) given by Lemma 3.2.
Furthermore, for any \(\lambda < \frac{1}{2}-\alpha \) and any \(T > 0\) the following bounds hold
Moreover, for any word \(w \in \mathcal {A}_p\) with \(|w| \ge 2\) we have
where we use the notation \(\mathbf {X}^w = \langle \mathbf {X}, e_w \rangle \).
Proof
The proof of (4.9) is provided in [21, Lemma 3.3]. We only have to show that there exist the claimed lifts which satisfy the estimates (4.10). To this end, we define, for some \(\kappa >0\), the following sequences
where \(k \ge 1\). First, for the increments of \(\beta _k^{(\varepsilon , \kappa )}\) we have
for some constant \(C > 0\), where \(q^{(\varepsilon )}_{k}\) is defined in (4.7). To get the last inequality we have used the bounds on the functions f and h, provided in Assumptions 1 and 3, and the estimate
which follows from the bound on the total variation of the function \(h^2/f\), provided by Assumption 3. Second, the convergence \(\beta _k^{(\varepsilon , \kappa )} \log k \rightarrow 0\) holds as \(k \rightarrow \infty \).
Using these properties of \(\beta _k^{(\varepsilon , \kappa )}\), we obtain from [28, Theorem 4] that the series \(\sum _{k=1}^N \beta _k^{(\varepsilon , \kappa )} \cos kx\) converge in \(L^1\) as \(N \rightarrow \infty \), and the \(L^1\)-norm of the limit is independent of \(\varepsilon \), which proves that for any \(\kappa > 0\) the parametrized sequence \(\beta _k^{(\varepsilon , \kappa )}\) is uniformly negligible in \(\varepsilon \in (0,1)\) in the sense of [10, Definition 3.6].
Similarly, using the bound on the total variation of \(h/(f+1)\), which is stated in Assumption 3, we can obtain that for any \(\kappa > 0\) the sequence \(\rho _k^{(\varepsilon , \kappa )}\) is uniformly negligible in \(\varepsilon \in (0,1)\) as well.
Noticing that the coefficients of the Fourier expansions (4.6) and (4.8) satisfy
we can apply [10, Theorem 3.14] and obtain that for every t and \(\alpha < \frac{1}{2}\) the processes X(t) and \(X_\varepsilon (t)\) can indeed be lifted to \(\alpha \)-regular rough paths \(\mathbf {X}(t)\) and \(\mathbf {X}_\varepsilon (t)\) respectively, such that for any word \(w \in \mathcal {A}_p\) with \(|w| \ge 2\) the bounds
hold uniformly in \(t \in [0,T]\). Furthermore, by [10, Theorem 3.15] we obtain that for all \(\gamma < \frac{1}{2} - \alpha \) and \(\kappa > 0\) small enough,
uniformly in \(t \in [0,T]\). The last bound can be shown almost identically to [21, (3.16d)], but taking \(\theta \equiv 1\) and the time interval from \(-\infty \).
Now we will investigate the temporal regularity of \(\varvec{X}_\varepsilon \). Our aim is to apply [10, Theorem 3.15] to the processes \(\varvec{X}_\varepsilon (s)\) and \(\varvec{X}_\varepsilon (t)\), with \(s, t \in [0,T]\). To this end, let us define \(\tau = |t-s|\) and the parametrized sequence \(\mu ^{(\tau , \varepsilon )}_k = e^{-k^2 f(\varepsilon k) \tau }\). Then, in the same way as in the beginning of the proof and using Assumptions 1 and 3, we obtain that for any \(\kappa > 0\) the sequence \(\beta _k^{(\kappa , \varepsilon )} \mu ^{(\tau , \varepsilon )}_k\) is uniformly negligible in \(\tau > 0\) and \(\varepsilon \in (0,1)\) and by [10, Theorem 3.15] we obtain, for any word \(w \in \mathcal {A}_p\) with \(|w| \ge 2\),
for all \(\gamma < \frac{1}{2} - \alpha \). Here, the last bound can be derived similarly to [21, (3.16a)], but with \(\theta \equiv 1\) and the time interval from \(-\infty \). In the same way, we get
Applying the Kolmogorov criterion [22] together with the bounds (4.11) and (4.14), we get the first estimate in (4.10).
Now, let us take any word \(w \in \mathcal {A}_p\) with \(|w| \ge 2\). Then, on the one hand, the estimate (4.12) gives
On the other hand, from (4.14) and (4.13) the following estimate follows
Combining these two bunds we obtain
for any \(\delta > 0\) small enough and uniformly in \(s, t \in [0,T]\). From this bound, estimate (4.12) and the Kolmogorov criterion [22] we obtain the second bound in (4.10). \(\square \)
4.2 Approximation of the rough integral
Now, having defined the iterated integrals of \(X_\varepsilon \), we can build an approximation of the process Z defined in (3.5).
The idea comes from the fact that if u(t) is controlled by \(\mathbf {X}(t)\), then the process G(u(t)) is controlled by \(\mathbf {X}(t)\) as well. The Taylor expansion gives an approximation for \(G_{ij}(u(t))\),
Here, \(\tilde{C}_w\) are combinatorial factors which can be calculated explicitly. Furthermore, we use the following notation: for \(w = w_1 \cdots w_k \in \mathcal {A}_{p-1}\) and \(k \ge 1\) we denote \(D^w = D^{w_1} \cdots D^{w_k}\) and \(u(t,x)_w = u_{w_1}(t,x) \cdots u_{w_k}(t,x)\).
Recalling that we will look for solutions such that \(u(t) - X(t) \in \mathcal {C}^1\), we obtain an approximation of \(G_{ij}(u(t))\) via \(\mathbf {X}(t)\),
Symmetrising this expression and using Definition 2.1, this can be rewritten as
for some slightly different constants \(C_w\). This expansion motivates our choice of the terms in the approximation of the rough integral.
In view of Assumption 2, it is natural to define the process \(D_\varepsilon \mathbf {X}_{\varepsilon } : {\mathbb {R}}_+ \times \mathbb {T} \rightarrow T^{(p)}\big ({\mathbb {R}}^n\big )\) in the following way: for any word \(w \in \mathcal {A}_p\) we set
Combining the expansion (4.15) with the definition (2.6), it appears plausible that a good approximation of Z is given by
Here, to simplify the notation we have omitted the sum over j.
Now we can rewrite the mild solution (4.3) as
where the functions \(\Phi _{\varepsilon }^{v_{\varepsilon }}\) and \(\Psi _{\varepsilon }^{v_\varepsilon }\) are defined in (4.4). The term involving the rough integral is denoted by
The additional terms in (4.18) which we used to approximate the rough integral we denote by
In the next sections we will show that the term \(\bar{\Upsilon }_{\varepsilon }^{v_{\varepsilon }}\) tends to 0 and the other terms in (4.18) converge to the corresponding terms in (3.6) in the space \(\mathcal {C}^1_T\).
5 Convergence of the solutions of the approximate equations
In this section we provide a proof of Theorem 1.1. In what follows we use the constant \(\alpha _{\star } = \frac{1}{2} - \alpha \), for some fixed small \(\alpha > 0\). This constant represents the real spatial regularity of the process X defined in (3.2). To obtain better bounds we will work in the spaces of regularity \(\alpha \), which is close to 0. The constants \(\alpha \) and \(\alpha _\star \) are used throughout the article as fixed values.
To shorten notations we define the norm
See (2.3) for the definition of the norm of a rough path. For any \(K > 0\) we define the stopping time
Note that in view of Remark 3.6, the condition on the norm \(\Vert \bar{v} \Vert _{\mathcal {C}^{1+\alpha _\star }_{\alpha _\star /2, t}}\) is reasonable. For any two letters \(i, j \in \mathcal {A}\) we define the process
where \(\delta \) is the Kronecker delta. To have a priori bounds on the corresponding \(\varepsilon \)-quantities we introduce the stopping time
The blow-up of the norm \(\Vert \bar{v}(t) - v_\varepsilon (t) \Vert _{\mathcal {C}^{1}}\) comes from the regularization property of the heat semigroup and the fact that we work in the \(\alpha \)-regular spaces, i.e. we use the bound
See Appendix 2 for the properties of the heat semigroup. Finally, we define the stopping time \(\varrho _{K,\varepsilon } := \sigma _{K} \wedge \sigma _{K, \varepsilon }\) and write in what follows
Remark 5.1
In the article we always consider time intervals up to the stopping time \(\varrho _{K, \varepsilon }\). Therefore, all the quantities involved in the definition of \(\varrho _{K, \varepsilon }\) are bounded by \(K + 1\) and all the proportionality constants can depend on K.
Proof of Theorem 1.1
For \(\alpha > 0\) as in the beginning of this section we define \(p = \lfloor 1/\alpha \rfloor \). From the derivation of the bounds below we will see how small the value of \(\alpha \) must be. To make the notation shorter, we introduce the following norm
For \(t \le \varrho _{K, \varepsilon }\), we obtain from (3.6) and (4.18) the bound
We consider only time periods \(t < 1\), for larger times the claim can easily be obtained by iteration. To find a bound on the first term in (5.3) we use the results of Sect. 6. Applying Proposition 6.1 with a small constant \(\kappa = \alpha \) we get
In order to bound the second term in (5.3), we use Proposition 6.2 with \(\kappa = \alpha \),
Applying Proposition 7.2 with the parameter \(\kappa = \alpha \), we bound the expectation of the third term in (5.3) by
A bound on the fourth term in (5.3) is a straightforward application of Proposition 6.4,
Using Proposition 8.2 with the small parameter \(\kappa = \alpha / 2\) we can bound the last term in (5.3) by
where \(\mathcal {D}_\varepsilon \) is defined in (8.1).
Combining the bounds (5.3)–(5.8) together we obtain
where we have used \(\alpha _\star = \frac{1}{2} - \alpha \). By Lemma 4.1 we can bound the norms of the controlling processes,
Furthermore, by choosing \(t = t_*\) small enough we can absorb the first term on the right-hand side of (5.9) into the left-hand side and obtain
From the definition of \(\bar{u}\) via \(\bar{v}\) and (5.10) we conclude
Here, we have also used Lemma 4.1 and the bound
which can be derived similarly to (6.7). The rest of the proof is almost identical to the proof of [21, Theorem 1.5]. \(\square \)
6 Estimates on the reaction term
In this section we prove convergence of the reaction terms of the approximate equation (4.18) to the corresponding terms of (3.6). Let us recall the notation (5.2) and Remark 5.1, which says that all the quantities involved in the definition of the stopping time \(\varrho _{K,\varepsilon }\) are bounded on the interval \((0, t_\varepsilon ]\) by the constant \(K + 1\) and all the proportionality constants below can depend on K.
The next proposition gives a bound on the terms \(\Psi ^{\bar{v}}\) and \(\Psi ^{v_\varepsilon }_{\varepsilon }\) defined in (3.7) and (4.4) respectively.
Proposition 6.1
For any \(\gamma \in (0, 1]\), \(t > 0\) and \(\kappa > 0\) small enough the following bound holds
Proof
For any \(t > 0\), using the notation (5.2), we can rewrite
To bound the term \(J_1\), we first investigate how good the operator \(D_\varepsilon \) approximates \(\partial _x\). Let us take a function \(\varphi \in \mathcal {C}^{1+\alpha _\star }(\mathbb {T})\). Then by the Assumption 2, we can rewrite
Using the fact, that the Hölder regularity of \(\varphi \) is \(1 + \alpha _\star \), we obtain
This yields the estimate
where we have used the boundedness of the \((1+\alpha _\star )\)th moment of \(\mu \).
Using this estimate we derive
where we have used boundedness of \(\Vert \bar{u} \Vert _{\mathcal {C}^{0}_{t_\varepsilon }}\) and \(\Vert \bar{v} \Vert _{\mathcal {C}^{1+\alpha _\star }_{\alpha _\star /2, t_\varepsilon }}\).
To derive a bound on \(J_2\), we notice that
which follows from Lemma 8.7. Hence, using the estimate (6.2) for U, we obtain
Note, that for any function \(\varphi \in \mathcal {C}^1(\mathbb {T})\) we have by Assumption 2,
Using this bound we obtain
where we have used boundedness of \(\Vert \bar{u} \Vert _{\mathcal {C}^{0}_{t_\varepsilon }}\).
To bound \(J_4\) we note that
for any \(\kappa > 0\) sufficiently small. Here, in the last estimate we used Lemma 8.8 with \(\lambda = \alpha _\star - \kappa \). Using this estimate and (6.5) we obtain
Exploiting continuous differentiability of the function G we get
where in the second line we have used a bound, similar to (6.7),
Moreover, in the estimate (6.9) we have used the bound
which is obtained in a way similar to (6.7).
Using Lemma 8.8, the integral \(J_6\) can be bounded by
where we have used the bound (6.10).
Combining the bounds (6.3)–(6.12) we obtain the claimed estimate (6.1). \(\square \)
In the following proposition we provide a bound on the terms \(\Phi ^{\bar{v}}\) and \(\Phi ^{v_\varepsilon }_{\varepsilon }\) defined in (3.7) and (4.4) respectively.
Proposition 6.2
For any \(\gamma \in (0,1]\) and \(\kappa > 0\) small enough the following bound holds
Proof
Using continuous differentiability of the function F, Lemma 8.8 and recalling that \(\bar{u} = \bar{v} + X + U\) we get
Here, we have used boundedness of \(\Vert u_\varepsilon \Vert _{\mathcal {C}^0_{t_\varepsilon }}\) and the estimate (6.11). \(\square \)
The following lemma shows how the processes (4.16) behave in the supremum norm. In particular, it shows that they converge to 0 as soon as \(|w| > 2\).
Lemma 6.3
For any word \(w \in \mathcal {A}_p\), the bound
holds uniformly in \(\varepsilon \) and t.
Proof
Since \(\mathbf {X}_{\varepsilon }(s)\) is a rough path of regularity \(\alpha _\star \), we can use the third property in Definition 2.1 to get
Here, we have used the assumption on the moments of \(|\mu |\). \(\square \)
In the following proposition we obtain a bound on the term \(\bar{\Upsilon }^{v_\varepsilon }_{\varepsilon }\) defined in (4.20).
Proposition 6.4
For any \(\gamma \in (0,1]\) we have the estimate \(\Vert \bar{\Upsilon }^{v_\varepsilon }_{\varepsilon } \Vert _{\mathcal {C}_{t_\varepsilon }^{\gamma }} \lesssim \varepsilon ^{3\alpha _{\star }-1}\).
Proof
We use Lemma 8.9 to estimate the approximate heat semigroup, and Lemma 6.3:
for \(\kappa > 0\) small enough. This is the claimed bound. \(\square \)
7 Convergence of the correction term
In this section we show that the term \(\Upsilon _{\varepsilon }^{v_{\varepsilon }}\), defined in (4.20), converges to the correction term \(\Upsilon ^{\bar{v}}\) from (3.7). In view of Remark 5.1, we only consider time intervals up to the stopping time \(\varrho _{K,\varepsilon }\), by using the notation (5.2).
To shorten the notation we define \(\mathbb {X}_\varepsilon (t)\) to be the projection of the rough path \(\mathbf {X}_\varepsilon (t)\) to the second level of the tensor algebra. The following lemma is similar to [21, Proposition 4.1], but the bound is in a Hölder norm rather than a Sobolev norm.
Lemma 7.1
For any \(\gamma \in \left( 0, \frac{1}{2}\right) \), any \(t > 0\) and any \(\kappa > 0\) small enough we have
Proof
The proof is almost identical to that of [21, Proposition 4.1], but we use Lemma 8.5 to reduce oneself to moment bounds on the Paley–Littlewood blocks of \(D_\varepsilon \mathbb {X}_{\varepsilon }\), instead of using pointwise bounds. \(\square \)
A bound on \(\Upsilon ^{\bar{v}}\) and \(\Upsilon ^{v_\varepsilon }_\varepsilon \), defined in (3.7) and (4.20) respectively, is given in the next proposition.
Proposition 7.2
For any \(\gamma \in (0, 1]\) and any \(\kappa > 0\) sufficiently small we have
Proof
Let us define the functions \(\mathcal {F}(u)_i = \Lambda ~\mathrm {div} G_i(u)\) and
where as usual the sum over j is omitted. Then we can write
To bound \(J_1\) we note that we can rewrite
Therefore, applying Lemma 8.7 with \(\eta \in (0, \alpha _\star )\) and Lemma 8.6, we obtain
That gives us, using the boundedness of \(\Vert u_\varepsilon \Vert _{\mathcal {C}_{t_\varepsilon }^{\alpha _\star }}\) and Lemma 7.1,
A bound on \(J_2\) follows from Lemma 8.7 and regularity of G,
Here, we have used the representation of \(\bar{u}\) via \(\bar{v}\) and the bound (6.11).
For the third term we use Lemma 8.8 with \(\lambda = \frac{1}{2} - \kappa \),
where we have used boundedness of the second-order iterated integral \(\mathbb {X}_\varepsilon \) and \(\Vert u_\varepsilon \Vert _{\mathcal {C}_{t_\varepsilon }^\alpha }\). Combining the estimates (7.1), (7.2) and (7.3) we obtain the claimed bound. \(\square \)
8 Estimates on rough terms
In this section we obtain bounds on the terms involving rough integrals. As usual, we will use the notation (5.2), which in view of Remark 5.1 means that all the quantities involved in the definition of \(\varrho _{K,\varepsilon }\) are bounded. Furthermore, let us define the quantity
where the norm \(\vert \vert \vert \cdot \vert \vert \vert _{\alpha , t_\varepsilon }\) was introduced in (5.1).
The next lemma provides bounds on the rough integrals Z and \(Z_\varepsilon \) defined in (3.5) and (4.17) respectively.
Lemma 8.1
For \(t>0\) we have the following results
where, for \(\kappa > 0\) small enough, the bounds
hold with \(\mathcal {D}_{\varepsilon }\) defined in (8.1).
Proof
Since \(\bar{u}(s) - X(s) \in \mathcal {C}^1\), for \(s \le t_\varepsilon \), the process \(Y_{ij}(s) = G_{ij}(\bar{u}(s))\) is controlled by the \(\alpha _\star \)-regular rough path \(\mathbf {X}(s)\) with the rough path derivative \(Y'_{ij}(s) = DG_{ij}(\bar{u}(s))\) and the remainder
where we use the notation \(\bar{v}(s; x, y) = \bar{v}(s, y) - \bar{v}(s, y)\) and respectively for U and \(\bar{u}\). Here, by the rough path derivative we mean the projection of the controlled rough path on \(({\mathbb {R}}^n)^*\) in Definition 2.2, and the remainder is a collection of all the processes \(R_Y^w\) from (2.4).
From the regularity assumptions for the function G and the processes \(\bar{u}\) and \(\bar{v}\), we obtain the bounds
The power of s in the last estimate comes from the bound \(\Vert U(s) \Vert _{2\alpha _\star } \lesssim s^{-\frac{\alpha _{\star }}{2}}\), which is a consequence of Lemma 8.7. The estimate (8.2) follows from (2.8) and (8.4).
Similarly, for \(s \le t_\varepsilon \), the process \(Y_{\varepsilon , ij}(s) = G_{ij}(u_\varepsilon (s))\) is controlled by the \(\alpha _\star \)-regular rough path \(\mathbf {X}_\varepsilon (s)\) with the rough path derivative \(Y'_{\varepsilon , ij}(s) = DG_{ij}(u_\varepsilon (s))\) and the remainder \(R_{Y_{\varepsilon ,ij}}(s)\), such that the following bounds hold
To prove the bound (8.3), we consider the processes \(\bar{u}(s)\) and \(u_\varepsilon (s)\) to be of Hölder regularity \(\alpha \). Then they are controlled by the \(\alpha \)-regular rough paths \(\mathbf {X}(s)\) and \(\mathbf {X}_\varepsilon (s)\) respectively. Hence, we can extend \(G_{ij}(\bar{u}(s))\) to the process \(\mathcal {G}_{ij}(s): \mathbb {T} \rightarrow \big (T^{(p-1)}\big ({\mathbb {R}}^n\big )\big )^*\) which is controlled by \(\mathbf {X}(s)\) as well and such that
for \(w \in \mathcal {A}_{p-1}\). Then, as it was noticed in Sect. 4.2, for every \(w \in \mathcal {A}_{p-1}\) the following expansion holds
For any word \(w \in \mathcal {A}_{p-1}\), the assumptions on G and \(\bar{u}\) imply \(\Vert \langle \mathcal {G}_{ij}(s), e_w \rangle \Vert _{\mathcal {C}^{\alpha }} \lesssim 1\). Furthermore, from the argument of Sect. 4.2, it is not difficult to obtain the estimate on the remainder: \(\Vert R^w_{\mathcal {G}_{ij}}(s) \Vert _{\mathcal {B}^{(p - |w|) \alpha }} \lesssim s^{\frac{\alpha _{\star } - 1}{2}}\). The latter bound follows from \(|\bar{u}(s; x,y)_{\bar{w}}| \lesssim |y-x|^{(p-|w|) \alpha }\), for any word \(\bar{w}\) such that \(|\bar{w}| = p-|w|\), and
for any word \(\bar{w} \in \mathcal {A}_{p-|w|-1} \setminus \{\emptyset \}\). Here, in the last line we have used the bound
which follows from Lemma 8.7.
In the same way the process \(G_{ij}(u_\varepsilon (s))\) can be extended to \(\mathcal {G}^\varepsilon _{ij}(s): \mathbb {T} \rightarrow \big (T^{(p-1)}\big ({\mathbb {R}}^n\big )\big )^*\) which is controlled by \(\mathbf {X}_\varepsilon (s)\). We denote the remainders by \(R_{\mathcal {G}^\varepsilon _{ij}}^w\). Furthermore, the corresponding bounds hold
for any word \(w \in \mathcal {A}_{p-1}\).
The following estimate follows from the regularity of the function G,
where \(w \in \mathcal {A}_{p-1}\). Furthermore, the following bound holds
for a word \(\bar{w}\) such that \(|\bar{w}| = p-|w|\), and for any word \(\bar{w} \in \mathcal {A}_{p-|w|-1} \setminus \{\emptyset \}\) one has
Here, in the last line we have used the bound
for any \(\kappa > 0\) sufficiently small, which follows from Lemmas 8.7 and 8.8. From these bounds and Sect. 4.2 we obtain
In order to prove (8.3), we define

where we have omitted as usual the sum over j. From (2.7), (8.5) and Definition 2.1 we obtain
Next, we can rewrite \(Z^i - Z^i_{\varepsilon }\) in the following way

Here, we have used the Fubini-type result proved in [20, Lemma 2.10].
To bound \(I_1\) we apply (2.9) and use the bounds (8.6), (8.7),
where \(\mathcal {D}_{\varepsilon }\) is defined in (8.1). It follows from (8.8) that
In the same way from the second bound in (8.8) we derive
To bound the integral \(I_3\) let us define the process \(u_{x,z,\varepsilon }(t_\varepsilon ,y) := u_\varepsilon (t_\varepsilon , \varepsilon y - \varepsilon z - x)\) and the rough path \(\mathbf {X}_{x,z,\varepsilon }(t_\varepsilon ;y, \bar{y}) := \mathbf {X}_{\varepsilon }(t_\varepsilon ; \varepsilon y - \varepsilon z - x, \varepsilon \bar{y} - \varepsilon z - x)\). Then we can perform the change of variables \(\bar{y} = (y - \varepsilon z - x)/\varepsilon \) in the integral \(I_3\) and obtain

where \(X_{x,z,\varepsilon }(t_\varepsilon , \bar{y}) - X_{x,z,\varepsilon }(t_\varepsilon , y)\) is the projection of \(\mathbf {X}_{x,z,\varepsilon }(t_\varepsilon ;y, \bar{y})\) onto \({\mathbb {R}}^n\) and
Taking into account the a priori bounds on \(u_\varepsilon \), we obtain from [18, Lemma 2.2] that \(Y_{x,z,\varepsilon }(t_\varepsilon )\) is controlled by \(\mathbf {X}_{x,z,\varepsilon }(t_\varepsilon )\) with the rough path derivative
and the remainder \(R_{Y_{x,z,\varepsilon }}(t_\varepsilon )\) such that
Hence, the following bound follows from Proposition 2.3 and the simple estimate \(\vert \vert \vert \mathbf {X}_{x,z,\varepsilon }(t_\varepsilon ) \vert \vert \vert _{\alpha _\star } \le \varepsilon ^{\alpha _\star } \vert \vert \vert \mathbf {X}_{\varepsilon }(t_\varepsilon ) \vert \vert \vert _{\alpha _\star }\):

Here we have also used the bound on the \(\alpha _\star \)th moment of the measure \(\mu \). Similarly, we can obtain the bound \(\Vert I_2(t_\varepsilon ) \Vert _{\mathcal {C}^{\alpha _\star }} \lesssim \varepsilon ^{\alpha _\star } t_\varepsilon ^{-\frac{\alpha _\star }{2}}\).
Now we set \(T_1=I_1\) and \(T_2=I_2 + I_3 + I_4 + I_5\) and obtain the claim. \(\square \)
In the following proposition we prove a bound on \(\Xi ^{\bar{v}}\) and \(\Xi ^{v_\varepsilon }_{\varepsilon }\) defined in (3.7) and (4.19) respectively.
Proposition 8.2
For \(\gamma \in (0,1]\) and \(\kappa > 0\) small enough we have the estimate
where \(\mathcal {D}_{\varepsilon }\) is defined in (8.1).
Proof
We can rewrite \(\Xi ^{\bar{v}} - \Xi ^{v_\varepsilon }_{\varepsilon }\) in the following way
By (8.2) and Lemma 8.8 with \(\lambda = \alpha _\star - \alpha - \kappa \) we obtain for any \(\kappa > 0\) small enough
The second term can be estimated using Lemma 8.9 and (8.3) by
Combining (8.9) and (8.10) we obtain the claimed bound. \(\square \)
References
Alabert, A., Gyöngy, I.: On numerical approximation of stochastic Burgers’ equation. In: Kabanov, Yu., Liptser, R., Stoyanov, J. (eds.), From Stochastic Calculus to Mathematical Finance, pp. 1–15. Springer, Berlin, (2006)
Bahouri, H., Chemin, J.-Y., Danchin, R.: Fourier analysis and nonlinear partial differential equations. Grundlehren der Mathematischen Wissenschaften, vol. 343. Springer, Heidelberg (2011). doi:10.1007/978-3-642-16830-7
Blömker, D., Jentzen, A.: Galerkin approximations for the stochastic Burgers equation. SIAM J. Numer. Anal. 51(1), 694–715 (2013)
Chen, K.-T.: Iterated integrals and exponential homomorphisms. Proc. Lond. Math. Soc. (3) 4, 502–512 (1954)
Davie, A.M., Gaines, J.G.: Convergence of numerical schemes for the solution of parabolic stochastic partial differential equations. Math. Comput. 70(233), 121–134 (2001)
Da Prato, G., Zabczyk, J.: Second Order Partial Differential Equations in Hilbert Spaces. London Mathematical Society Lecture Note Series, vol. 293. Cambridge University Press, Cambridge (2002). doi:10.1017/CBO9780511543210
Da Prato, G., Debussche, A., Temam, R.: Stochastic Burgers’ equation. NoDEA Nonlinear Differ. Equ. Appl. 1(4), 389–402 (1994)
Friz, P.K., Hairer, M.: A Course on Rough Paths. Universitext. Springer, Cham (2014). With an introduction to regularity structures. doi:10.1007/978-3-319-08332-2
Friz, P., Victoir, N.: Multidimensional Stochastic Processes as Rough Paths. Theory and Applications, Cambridge Studies in Advanced Mathematics, vol. 120. Cambridge University Press, Cambridge (2010)
Friz, P.K., Gess, B., Gulisashvili, A., Riedel, S.: Jain-Monrad criterion for rough paths and applications (2013). arXiv:1307.3460v2
Gubinelli, M.: Controlling rough paths. J. Funct. Anal. 216(1), 86–140 (2004)
Gubinelli, M.: Ramification of rough paths. J. Differ. Equ. 248(4), 693–721 (2010)
Gubinelli, M., Imkeller, P., Perkowski, N.: Paracontrolled distributions and singular PDEs (2012). arXiv:1210.2684
Gyöngy, I.: Existence and uniqueness results for semilinear stochastic partial differential equations. Stoch. Process. Appl. 73(2), 271–299 (1998)
Gyöngy, I.: Lattice approximations for stochastic quasi-linear parabolic partial differential equations driven by space-time white noise. I. Potential Anal. 9(1), 1–25 (1998)
Gyöngy, I.: Lattice approximations for stochastic quasi-linear parabolic partial differential equations driven by space-time white noise. II. Potential Anal. 11(1), 1–37 (1999)
Hairer, M.: An introduction to stochastic PDEs (2009). arXiv:0907.4178
Hairer, M.: Rough stochastic PDEs. Commun. Pure Appl. Math. 64(11), 1547–1585 (2011)
Hairer, M., Maas, J.: A spatial version of the Itô-Stratonovich correction. Ann. Probab. 40(4), 1675–1714 (2012)
Hairer, M., Weber, H.: Rough Burgers-like equations with multiplicative noise. Probab. Theory Relat. Fields 155(1–2), 71–126 (2013)
Hairer, M., Maas, J., Weber, H.: Approximating rough stochastic PDEs. Commun. Pure Appl. Math. 67(5), 776–870 (2014)
Kallenberg, O.: Foundations of Modern Probability. Probability and Its Applications (New York), 2nd edn. Springer, New York (2002)
Lyons, T.J.: Differential equations driven by rough signals. Rev. Mat. Iberoam. 14(2), 215–310 (1998)
Lyons, T., Qian, Z.: System Control and Rough Paths. Oxford Mathematical Monographs. Oxford University Press, Oxford (2002). doi:10.1093/acprof:oso/9780198506485.001.0001
Lyons, T., Caruana, M., Lévy, T.: Differential equations driven by rough paths. Lecture Notes in Mathematics, vol. 1908. Springer, Berlin (2007)
Nelson, E.: The free Markoff field. J. Funct. Anal. 12, 211–227 (1973)
Reutenauer, C.: Free Lie Algebras. London Mathematical Society Monographs. New Series, vol. 7. The Clarendon Press, Oxford University Press, New York (1993). Oxford Science Publications
Teljakovskiĭ, S.A.: A certain sufficient condition of Sidon for the integrability of trigonometric series. Mat. Zametki 14, 317–328 (1973)
Walsh, J.B.: An introduction to stochastic partial differential equations. In: École d’été de probabilités de Saint-Flour, XIV—1984. Lecture Notes in Mathematics, vol. 1180, pp. 265–439. Springer, Berlin (1986)
Young, L.C.: An inequality of the Hölder type, connected with Stieltjes integration. Acta Math. 67(1), 251–282 (1936)
Acknowledgments
We would like to thank H. Weber for numerous discussions of this and related problems. MH’s research was funded by the Philip Leverhulme trust through a leadership award, by the Royal Society through a research merit award, and by the ERC through a consolidator award.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Regularity of distribution-valued processes
In this section we introduce the Besov spaces and give a Kolmogorov-like criterion for distribution-valued processes to belong to these spaces.
Any distribution \(\psi \) defined on the circle \(\mathbb {T}\) can be written as the Fourier series
For \(m \ge 1\) we define the mth Paley–Littlewood block of \(\psi \) as
and by definition \(\delta _0 \psi \equiv \hat{\psi }(0) / \sqrt{2\pi }\).
Definition 8.3
For any \(\alpha \in {\mathbb {R}}\), the Besov space \(\mathcal {B}^{\alpha }_{\infty , \infty }(\mathbb {T})\) consists of those distributions on \(\mathbb {T}\), for which the norm
is finite. We denote \(\mathcal {C}^\alpha (\mathbb {T}) = \mathcal {B}^{\alpha }_{\infty , \infty }(\mathbb {T})\) for \(\alpha < 0\).
For \(\alpha \in (0,1)\) the Besov space \(\mathcal {B}^{\alpha }_{\infty , \infty }(\mathbb {T})\) coincides with the Hölder space \(\mathcal {C}^{\alpha }(\mathbb {T})\). The proof of this fact and more information on the Besov spaces can be found in [2].
For \(m \ge 1\) we define the Dirichlet kernel
and \(D_0 \equiv 1\).
The following Lemma provides a bound on the Dirichlet kernel \(D_m\) in \(L^p\) spaces.
Lemma 8.4
For every \(1 < p \le \infty \) there is a constant \(C = C(p)\) such that
holds for every \(m \ge 0\), where \(p'\) is the conjugate exponent of p.
Proof
In the case \(p = \infty \), the function can be bounded by its value at 0, which gives \(|D_m(x)| \le 2^{m+1}\). If \(1 < p < \infty \), then we can rewrite
The latter integral is bounded by a constant C(p), since the integrand can be estimated up to a constant multiplier by \(1 \wedge |x|^{-p}\). That gives the claimed estimate. \(\square \)
Now, we provide a Kolmogorov-like criterion for distribution-valued processes.
Lemma 8.5
Let \(\psi \) be a random field on \([0,T] \times \mathbb {T}\), such that for every \(t \in [0,T]\), \(\psi (t)\) is a distribution taking values in a fixed Wiener chaos. Furthermore, let us assume that for every \(m \ge 0\) the mth Paley–Littlewood block satisfies
for every \(x \in \mathbb {T}\), and \(t,s \in [0,T]\), and some constants \(A, B >0\), \(\delta > 0\) and \(\alpha < 1\), \(\alpha \ne 0\). Then, for any \(\gamma < \alpha \), \(\gamma \ne 0\), there is a constant \(C = C(\alpha , \gamma )\) such that
Proof
We can notice that \(\delta _m \psi (t,x) = D_m * \delta _m \psi (t,x)\), where the convolution is taken over the variable \(x \in \mathbb {T}\). Therefore, the Hölder inequality yields
for any \(p \ge 1\), where as usual \(p'\) is the exponent conjugate of p. Since \(\psi (t)\) belongs to a fixed Wiener chaos, the same is true for the Paley–Littlewood block \(\delta _m \psi (t)\), and we can apply Nelson’s lemma to it [26], saying that all moments of \(\delta _m \psi (t)\) are bounded up to a constant multiplier by its second moment. Therefore,
Combining the bounds (8.12), (8.13) together with Lemma 8.4, we derive
Since for \(\gamma < 1\), \(\gamma \ne 0\), the space \(\mathcal {C}^\gamma \) coincides with the Besov space \(\mathcal {B}^\gamma _{\infty , \infty }\), we obtain
which is finite if \(\gamma < \alpha - \frac{1}{p}\). Finally, we can notice that for any \(\gamma < \alpha \), we can choose \(p \ge 1\) large enough such that \(\gamma < \alpha - \frac{1}{p}\), so that
for every \(\gamma < \alpha \). Repeating the same argument for \(\delta _m \psi (t) - \delta _m \psi (s)\), we derive
We finish the proof by applying the Banach space-valued version of the Kolmogorov continuity criterion [22], which gives the estimate (8.11) from (8.14) and (8.15). \(\square \)
The following Lemma provides a bound on the product of two distributions from certain Hölder spaces.
Lemma 8.6
Let \(\varphi \in \mathcal {C}^\alpha \) and \(\psi \in \mathcal {C}^\beta \), where \(\beta < 0 < \alpha < 1\) with \(\alpha + \beta > 0\). Then there is a constant \(C = C(\alpha , \beta )\) such that
The proof of this result can be found in [2, Theorem 2.85].
Appendix 2: Regularity properties of the semigroups
In this appendix we list some properties of the heat semigroup \(S_t = e^{t\Delta }\), defined as a convolution on the circle \(\mathbb {T}\) with the heat kernel (3.3), and the approximate heat semigroup \(S^{(\varepsilon )}_t = e^{t\Delta _\varepsilon }\), which is defined as a convolution with the approximate heat kernel (4.2).
The following Lemma provides the regularising property of the heat semigroup \(S_t\) in the Hölder spaces.
Lemma 8.7
Let \(\alpha < \beta \), \(\beta \ge 0\), then for \(t >0\) one has \(\Vert S_t \Vert _{\mathcal {C}^\alpha \rightarrow \mathcal {C}^\beta } \lesssim t^{\frac{\alpha - \beta }{2}}\).
For \(\alpha \le 0\) and integer \(\beta \), one can easily show this bound by the definition of the Hölder spaces. For non-integer \(\beta \) the bound follows by interpolation. A proof of the Lemma for \(\alpha \ge 0\) and \(\beta \le \alpha + 1\) can be found in [13, Lemma 47]. For larger values of \(\beta \), the estimate can be shown by using the semigroup property of \(S_t\).
The following results provide the regularizing properties of the approximate semigroup \(S_\varepsilon \), defined in the beginning of Sect. 4. All the missing proofs can be found in [21, Sect. 6]. We assume that Assumption 1 holds in order to derive these bounds. First, we give a bound on the difference between \(S_t\) and \(S^{(\varepsilon )}_t\).
Lemma 8.8
Let \(\lambda \in [0,1]\) and \(\alpha \le \gamma +\lambda \). Then for \(\kappa > 0\) sufficiently small and \(t > 0\) one has \(\Vert S_t - S^{(\varepsilon )}_t \Vert _{\mathcal {C}^{\alpha } \rightarrow \mathcal {C}^{\gamma }} \lesssim t^{-\frac{1}{2}(\gamma - \alpha + \lambda + \kappa )} \varepsilon ^{\lambda }\).
The following result is analogous to the regularisation property of the heat semigroup.
Lemma 8.9
For any \(\gamma , \bar{\gamma } \ge 0\), any \(t > 0\) and any \(\kappa > 0\) sufficiently small one has \(\sup _{\varepsilon \in (0,1)} \Vert S^{(\varepsilon )}_t \Vert _{\mathcal {C}^{\bar{\gamma }} \rightarrow \mathcal {C}^{\bar{\gamma } + \gamma - \kappa }} \lesssim t^{-\frac{\gamma }{2}}\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hairer, M., Matetski, K. Optimal rate of convergence for stochastic Burgers-type equations. Stoch PDE: Anal Comp 4, 402–437 (2016). https://doi.org/10.1007/s40072-015-0067-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40072-015-0067-5



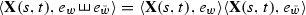 , for any
, for any