Abstract
The purpose of this study was to develop and validate prediction equations for fillet traits in Asian sea bass. Ninety-day old fish (average weight = 9.48 ± 0.35 g; length = 8.78 ± 0.6 cm) from four hatchery stocks (Chachoengsao, Chon Buri, Chumphon, and Samut Songkram) were raised in earthen ponds. After 300 days, weight and body measurement data of live fish (n = 400) were collected. Mean individual weight was greatest for the Chacheongsao stock (1166.32 ± 23.42 g) and was similar for the other stocks, ranging from 982.96 ± 25.07 to 997.44 ± 24.71 g. Fillet percentage varied slightly from 47.33 to 49.88%. Positive high correlations were observed for weight and body measurements with fillet weight, whereas there were significant but weak correlations for body measurements with fillet yield. Prediction equations developed from body weight using simple linear regression models yielded R2 values of 0.97–0.98 for fillet weight for each stock. Correlations between values predicted from the body weight models and actual values were 0.98–0.99 for fillet weight. Stepwise regression was performed to develop prediction models for fillet yield from body measurements. The best fillet yield prediction models identified length and an additional 2–3 measurement as potential predictors depending on the population. Prediction biases were close to zero despite low to moderate (r values of 0.20–0.51) degrees of predictive power of the models. However, prediction models for fillet yield should be further developed to increase predictability and be applicable to new data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Asian sea bass, also known as barramundi (Lates calcarifer), is the predominant fish species used for coastal aquaculture in Thailand. It is a significant fishery commodity representing 10% of all seafood production. Asian sea bass production increased by 51% from 8004 metric tons in 2001 to 16,501 tons in 2014 as reported by the Thailand Department of Fisheries (DOF 2016). Farmed sea bass is normally sold as whole fish at 500–700 g for local markets, with a retail price of 150 baht/kg (4.50 USD/kg). The consumer preference is increasingly leaning towards value-added and convenience products, such as frozen fish and fish fillets. Therefore, the production of larger fish (1000–2000 g) has increased during the past decade. These types of products are also exported to Taiwan, Singapore, Malaysia and Australia (Food and Agriculture Organization 2017). Value addition is one of the approaches expected to increase profitability of the sea bass farming and processing industries (Department of Fisheries 2016).
Improvement in production traits, including growth performance and yield, is considered the most important breeding goals in fish farming (Gjedrem 1997, 2000; Kause et al. 2002; Thodesen et al. 2012). Several studies have been conducted comparing growth performance and fillet percentage for various fish strains utilizing body weight and volume measurements, as well as body shape, e.g., Nile tilapia Oreochromis niloticus (Rutten et al. 2004; Rutten et al. 2005; Peterman and Phelps 2012), striped bass Morone spp. (Bosworth et al. 1998), common carp Cyrpinus carpio (Cibert et al. 1999) and catfish Ictalurus spp. (Argue et al. 2003; Bosworth et al. 2001). Fillet yield, an economically important trait for the fish processing industry, however, is difficult to measure with high accuracy without sacrificing the animal and cannot be used as a criterion during broodstock selection. A more practical approach is through selection of candidates on phenotypic characteristics that are highly correlated with fillet traits. Studies have evaluated the ability of total weight and various body shape measurements to predict fillet traits and found body weight to be an accurate predictor of fillet weight (Rutten et al. 2004; Kause et al. 2007; Nguyen et al. 2010; Gjerde et al. 2012; Thodesen et al. 2012). By contrast, most studies obtained modest to low prediction accuracies for fillet percentage models developed from body measurements, although a few have shown potentially useful prediction power (Bosworth et al. 2001; Sang et al. 2009).
Prediction models for fillet yields are typically developed using relationships between growth metrics and fillet yields. There is a lack of information regarding phenotypic correlations between growth traits and processing characteristics for Asian sea bass stocks in Thailand. Therefore, the objective of this study was to investigate the potential for total weight and body measurements of live fish to predict fillet weights and fillet yields in four different stocks of Asian sea bass and to develop prediction equations for these traits.
Materials and methods
Fish origin and fry production
Sea bass fingerlings at approximately 90 days post-hatch (dph) were obtained from private hatcheries, including Chachoengsao (CHAC), Chon Buri (CHON), Chumphon (CHUM), and Samut Songkram (SAMU). The CHAC and SAMU stocks originated from wild populations of the Bang Pakong and Meklong Rivers, respectively, in the upper Gulf of Thailand. The CHON stock was founded from broodstock obtained from cage culture operations along the east coast of the Gulf of Thailand, mainly in Chon Buri Province. The CHUM stock originated from wild populations of the Chumphon River, which runs through the west coast of the Gulf of Thailand. These hatchery populations represent primary sources of seed stocks for Asian sea bass farming in Thailand (Department of Fisheries 2016; Senanan et al. 2015). In general, the hatcheries produced sea bass fry from group mating with a sex ratio of 1:2 (male:female). About 18–24 brood fish, aged 3–5 years with body weight of 4–5 kg were stocked in each spawning tank (2 × 4 × 2.5 m3). They were injected with 1 ml of synthetic hormone (Suprefact) under the dorsal fin, in the afternoon, to induce gamete maturation. Spawning normally took place 24–28 h post-injection (second night). Eggs were collected at 38–40 h (second morning) post-spawning and transferred to nursing tanks (1.5 × 2.5 × 1 m3), where larvae were reared until 20 dph. Fry were then transferred to concrete tanks (2 × 4 × 1 m3) and size graded at 30 and 60 dph at the hatcheries to minimize cannibalism.
Fish culture
The grow-out experiment was conducted at the Kasetsart University Fisheries Research Station in Samut Songkram Province. Four 1 m deep earthen ponds (20 m × 40 m or 800 m2) were each equipped with four, 36 m2 stationary cages (6 × 6 × 1.2 m), providing a randomized complete block design (RCBD). In each pond (block), populations were randomly assigned to cages, each with 50 fish (a density of 1.4 fish per m2). Average size at stocking ranged from 9.48 ± 0.62 to 9.74 ± 0.16 g and 8.13 ± 0.82 to 9.04 ± 0.90 cm total lengths. The cages were covered with netting to exclude predatory birds. Aeration was provided through polyethylene pipes on the pond bottoms below the cages to maintain sufficient dissolved oxygen concentration. Water was supplied from a brackish water canal connected to the Meklong River. Fresh well water was used to dilute brackish water to obtain salinities within 10–25 ppt. There was no water exchange during grow-out, but the ponds were topped off regularly to compensate for evaporation, maintaining the water depth within the cages at 80–90 cm. The cage netting was cleaned regularly to allow water flow through the cages.
Fish were fed to apparent satiation with a 40% protein commercial floating feed (Betagro Feed Mills, Bangkok, Thailand) twice daily at 07:00 and 17:00 h. Feed consumption was closely monitored and uneaten was removed prior to the next feeding. Fish health was observed and mortalities were immediately removed during feedings. Temperature and other water quality parameters were checked twice daily. Dissolved oxygen (DO) was measured using a portable model YSI 550A meter (Yellow Springs Instruments, Inc.; Yellow Springs, OH, USA) and pH using a model YSI EcoSense pH 100A meter (Yellow Springs Instruments, Inc.; Yellow Springs, OH, USA). Salinity was measured weekly using a portable salinity refractometer (Atago, Co., Ltd.; Tokyo, Japan). Aquatic plants and algae that may interfere with fish growth were removed regularly from the ponds.
After 300 days of rearing, fish were harvested and transported to the Taiban Fishery processing plant in Samut Prakarn Province, approximately 70 km from the research station. Fish were weighed (W in grams) and tagged to identify stock. They were placed on a light-colored background on their left side and photographed using a Nikon D40X digital camera. A centimeter scale was included in the images to ensure calibration of body measurement to the nearest 0.01 cm. SigmaScan Pro 4.0 software (www.sigmaplot.com) was used to measure 12 distances between body locations as illustrated in Fig. 1. A total of 400 fish (100 from each stock) were filleted by four skilled processors (P) at the processing plant, with each processor filleting individuals from all four stocks. The filleting process was as follows: (1) scales were removed manually. (2) Fish were cut from the top of the head, down the side behind the pectoral fins and along the side of the dorsal fins, and (3) the fillet was removed by cutting along the backbone from head to tail. The weight of the two fillets with skin attached (FW) was measured and recorded in grams. Fillet yield (FY) was calculated as \({\text{FY}} = \left( {{\text{FW}}/W} \right) \times 100.\)
Body measurement in Asian sea bass: distances from anterior 1st dorsal-anterior 2nd dorsal (M12), anterior 1st dorsal-anterior anal (M17), anterior 1st dorsal-anterior pelvic (M18), anterior 2nd dorsal-posterior dorsal (M23), anterior 2nd dorsal-anterior anal (M27), anterior 2nd dorsal-anterior pelvic (M28), posterior dorsal–dorsal membrane of caudal fin (M34), posterior dorsal-posterior anal (M36), dorsal–ventral membrane from caudal fin (M45), ventral membrane of caudal fin-posterior anal (M56), posterior anal-anterior anal (M67), anterior anal-anterior pelvic (M78), and SL standard length
Statistical analysis
The distribution of data was examined using SAS PROC UNIVARIATE procedure (SAS Inst. Inc., Cary, NC, USA). The output indicated that all the analysis variables were normally distributed. Analysis of variance was performed to examine the effects of pond (block) and genetic factors (stock) on weight, standard length and condition factor of preprocessed fish. There was a significant genetic effect on fish weights (P < 0.0001), whereas a block effect was not significant. Consequently, fillet yield was analyzed with total weight fitted as a covariate using the general linear model procedure (PROC GLM: SAS). The fixed effects of processor and stock were added to the model as: \(y_{ijk} = \mu + P_{i} + S_{j} + \beta *W_{ijk} + e_{ijk}\), where \(y_{ijk}\) is an observation of FY, \(\mu\) is the overall mean, \(P_{i}\) is a fixed effect of processor, \(S_{j}\) is a fixed effect of stock, \(\beta\) is the regression coefficient of body weight, \(W_{ijk}\) is a co-variable of total weight and \(e_{ijk}\) is a random residual error. In addition, fillet weight was analyzed with the fixed effects of processor and stock as: \(y_{ijk} = \mu + P_{i} + S_{j} + e_{ijk}\), where \(y_{ijk}\) is an observation of FW and other parameters are as described previously.
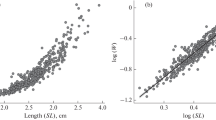
Scatter plots revealed relationships between total weight and fillet traits (Fig. 2). Data for body weight and body measurements were pooled across stocks and phenotypic correlations among traits were calculated using Pearson correlations with PROC CORR in SAS. Residual correlations were calculated after adjustments for systematic effects (Bosworth et al. 2001; Hung and Nguyen 2014). Collinearity of independent variables was tested using a variance inflation factor (VIF). Due to high correlations among predictors, fillet weight was predicted from total weight and length using simple linear regression models (PROG REG) in SAS. Because there were many independent variables to consider, stepwise regression was used to develop prediction equations for fillet yields. Goodness of fit for the models was assessed using coefficient of determination (R2). In addition, the best model was determined based on conceptual predictive criterion (Cp) and Akaike’s information criterion (AIC). Probability values < 0.05 were considered significant for estimates of parameters (intercept and beta). To assess the ability of these equations to predict new data, fillet records of each stock were evaluated using a fourfold cross-validation procedure. In the cross-validation, the data were randomly split into four subsets. Each iteration of the cross-validation used 75% of the records for training and the remaining 25% for testing. Predictive abilities of the equations were evaluated using the root mean squared error of prediction (RMSEP), calculated as the standard deviation of the residuals and the correlation between the predicted and the actual values (\(r\)) calculated for the best model. Prediction bias was calculated as the difference between the actual and the predicted values.
Results
Analyses of variance demonstrated highly significant differences in total weight and standard length among population samples of Asian sea bass (P < 0.0001) (Table 1). At 390 days of age, CHAC exhibited the highest weight (1166.32 ± 23.42 g). Least squares means for total weight among the remaining three stocks were similar and ranged from 997.44 ± 24.71 to 982.96 ± 25.07 g. Analysis of processing yields demonstrated significant differences among stocks. The CHAC samples exhibited the highest fillet weight of 596.23 ± 12.27 g, whereas weights among the remaining stocks were similar, ranging from 478.85 ± 13.32 to 491.53 ± 12.95 g. In addition, fillet yields differed among stocks with CHON (49.88 ± 0.19%) having the highest yield, followed by SAMU (48.24 ± 0.19%), CHUM (47.80 ± 0.20%), and CHAC (47.33 ± 0.19%).
Phenotypic correlations of total weight with body measurements and fillet traits are presented in Table 2. Positive high correlations were observed for weight, standard length, and body measurements with fillet weight (0.99, 0.93, and 0.40–0.91). Significant but weak correlations were observed for total weight, standard length and body measurements with fillet yield (0.21, 0.24, and 0.11–0.24). A modest relationship (0.34) was observed between fillet weight and fillet yield.
Regression equations for predicting fillet weight from total weight, standard length, and body measurement (M18) in each stock are presented in Table 3. Across populations, total weight accounted for 98% of the variation in fillet weight, whereas standard length and M18 accounted for 86–91 and 61–84% of the variability in fillet weight, respectively. The model predictive power (RMSEP) for fillet weight indicated that the regression models developed from total weight resulted in a prediction error of 14.84–21.86 g. The errors of prediction were higher using standard length (39.84–44.99 g) and M18 (51.60–71.58 g) as predictors. Correlation coefficients between actual and predicted fillet weights were high for total weight (0.99). Fillet weights were under-predicted by 10.6, 0.38, and 6.03 g for CHAC, CHON and CHUM stocks, and over-predicted by 0.42 g for SAMU stock. Results for fillet yield predictions are presented in Table 4. Table 5 provides validation statistics for model selection. The best models were chosen when the Cp approached the number of parameters and AIC was smallest. The R2 values were low for all predictors, which explained only 15–28% of the variation in fillet yield. The RMSEP ranged from 1.21 to 1.70%. Correlation coefficients between actual and predicted fillet yields were low for CHUM (0.20) and moderate for CHAC (0.49), CHON (0.51), and SAMU (0.39) stocks. Fillet yields were over-predicted by 0.03% for CHAC and under-predicted by 0.06, 0.04 and 0.06% for CHON, CHUM, and SAMU stocks, respectively.
Discussion
Results of the grow-out experiment indicated significant stock effects for all body size parameters. In particular, fillet weight varied significantly from 478.8 ± 13.32 g to 569.2 ± 12.27 g over the size range (960–1190 g) of fish examined. The CHAC stock exhibited greater total and fillet weights than the other stocks, but had the lowest fillet yield (47.3%). Interestingly, three stocks (CHON, CHUM and SAMU) exhibited similar weight were found to differ in fillet yields, among which CHON had the highest fillet percentage (49.88%). Such differences could result from variations in body shape among populations likely due to genetic composition and effects of selection within stocks. Differences in fillet yields (31–38%) between strains of Nile tilapia have been reported (Rutten et al. 2004; Peterman and Phelps 2012). Fillet percentages of Asian sea bass (47.3–49.8%) were similar to fillet yields observed in hybrid striped bass (49.7%) (Bosworth et al. 1998). This is not surprising as both species are anadromous perciformes fish, having slightly compressed, streamlined body shapes. In other species, fillet percentages varied from 35% for river catfish Pangasianodon hypophthalmus (Sang et al. 2009) and gilthead seabream Sparus auratus (Navarro et al. 2009) to 32–41% for common carp (Kocour et al. 2007; Bauer and Schlott 2009) and 42% for channel catfish (Argue et al. 2003). Fillet yields were as high as 58% for Coho salmon Oncorhynchus kisutch (Neira et al. 2004), 64% for rainbow trout O. mykiss (Kause et al. 2002), and 69% for Atlantic salmon Salmo salar (Powell et al. 2008). In giant freshwater prawn Macrobrachium rosenbergii, a meat yield of 45% was reported (Hung and Nguyen 2014). With regard to phenotypic correlations among growth metrics, fillet weight was closely related to fish weight, as well as standard length and body measurements, while there were weak correlations between fillet yield and fish size. Results were mostly in agreement with other previous studies, in that high correlations between fillet weight and total weight suggest that growing fish to a larger size is an efficient way to increase fillet weight.
Prediction equations developed in this study were based on simple linear regression, as some of the independent variables are highly correlated, e.g., total weight and standard length. In general, the most useful prediction equation is the one that accounts for the largest proportion of the variation (R2) in the predicted traits. An R2 of 1 would be a perfect prediction while an R2 of 0 would indicate no predictive power. The predictions of fillet weight from total weight gave R2 values of 0.98–0.99 and would be the equations recommended for use in practice for sea bass populations in this study. The proportion of variation explained by the prediction equations in our study using fish weight for fillet weight (0.98) was similar to the 0.95 R2 reported for tilapia by Rutten et al. (2004). Similarly, Sang et al. (2009) predicted river catfish fillet weight of from body weight, and obtained an R2 value of 0.86, which was lower than the values obtained in this study. However, a lesser degree of fit was exhibited when standard length (R2 values of 0.86–0.81) or body measurement (M18) (R2 values of 0.61–0.80) was used as predictors for fillet weight. In addition to R2 values, RMSEP and correlation coefficients between observed and predicted values (r) of the equations should be considered if predictions are to be made for Asian sea bass stocks other than those in this study. Validation of the model developed from body weight showed the highest correlation coefficients between predicted and observed fillet weights (0.98–0.99) and lowest RMSEP values (14.74–21.86 g), suggesting that these equations would be applicable to other Asian sea bass stocks.
Fillet yield, as a proportional trait consisting of fillet weight and total weight, showed weak relationships to total weight, standard length, and body measurements. Total weight is an important variable, normally included in prediction equations for fish fillet yield. The proportion of variation in fillet yield explained by the regression equation was low to moderate (R2 = 0.16–0.36) for total weight in tilapia (Rutten et al. 2004), but much higher for the ratio between body volume and body weight in river catfish (0.75) (Sang et al. 2009). However, only body measurement traits not total weight were included in the stepwise-developed regression equations in our study. The first included variable was standard length, which accounted for 12–20% of the variation in fillet yields, depending on the stock. Addition of other variables (M17, M18, M28 and M67) depending on the stock accounted for an additional 5–8% of the variation in fillet yields. Although the best model for each population gave a low to moderate degree of predictive ability for fillet yield, prediction bias was close to zero. The relationship between fish size and fillet yield in this study generally confirms the principle that larger fish provide higher fillet yield percentages. However, regarding the prediction equations, for example, the regression coefficient of standard length on fillet yield was 0.67 for the CHAC stock. This value represents the expected change in the predicted fillet yield for each unit change in fish length, when the remaining variables are fixed. Therefore, for each 1 cm increase in body length, an individual fillet yield is expected to increase 0.67%. This prediction ability for predict fillet yield is probably too low to be practical for predicting new data for the CHUM stock (r = 0.20). At this stage, it appears that our regression models for predicting fillet yields in three stocks are adequate (r values of 0.39–0.51). For future work, it would be useful to develop similar models for larger fish (1500–2000 g) using a larger data set to increase predictive power. With the use of up to 2700 records and a multiple regression models, Sang et al. (2009) obtained an r value of 0.86 for predicting fillet yield in river catfish.
In conclusion, total weight is the best single measurement for predicting fillet weight in Asian sea bass. Regression models developed in this study are applicable to fish weighing 960–1190 g from all populations sampled. Using separate models yielded similar prediction power and accuracy for fillet weight. This study demonstrates the use of various body measurements in predicting fillet yields. Despite relatively weak correlations between body measurements and fillet yields, we were able to develop useful prediction models for fillet yields in three stocks of Asian sea bass. Although fillet yield is the most important trait for fish processors, increased fillet percentages could be achieved along with increased fillet weights, given the positive correlation between the traits. The application of prediction models would allow for rapid genetic improvement via breeding to increase fillet yields and enable producers to be more competitive in the value-added markets of Asian sea bass.
References
Argue BJ, Liu Z, Dunham RA (2003) Dress-out and fillet yields of channel catfish, Ictalurus punctatus, blue catfish, Ictalurus furcatus, and their F1, F2 and backcross hybrids. Aquaculture 228:81–90
Bauer C, Schlott G (2009) Fillet yield and fat content in common carp (Cyprinus carpio) produced in three Austrian carp farms with different culture methodologies. J Appl Ichthyol 25:591–594
Bosworth BG, Libey GS, Notter DR (1998) Relationships among total weight, body shape, visceral components, and fillet traits in palmetto bass (striped bass female Morone saxatilis × white bass male M. chrysops) and paradise bass (striped Bass female M. saxatilis × yellow bass male M. mississippiensis). J World Aquacult Soc 29:40–50
Bosworth BG, Holland M, Brazil BL (2001) Evaluation of ultrasound imagery and body shape to predict carcass and fillet yield in farm-raised catfish. J Anim Sci 79:1483–1490
Cibert C, Fermon Y, Vallod D, Meunier FJ (1999) Morphological screening of carp Cyprinus carpio: relationship between morphology and fillet yield. Aquat Liv Resour 12:1–10
Department of Fisheries (2016) Fishery statistics analysis and research group. Information and Communication Technology Center, Department of Fisheries, no. 3/2016
Food and Agriculture Organization (2017) Fishstat Plus Version 2.30. FAO Fisheries and Aquaculture Department, Fishery Information, Data and Statistics Unit. www.fao.org/fishery/statistics/software/fishstat/en
Gjedrem T (1997) Flesh quality improvement in fish through breeding. Aquacult Int 5:197–206
Gjedrem T (2000) Genetic improvement of cold-water species. Aquacult Res 31:25–33
Gjerde B, Mengistu SB, Ødegård J, Johansen H, Altamirano DS (2012) Quantitative genetics of body weight, fillet weight and fillet yield in Nile tilapia (Oreochromis niloticus). Aquaculture 342–343:117–124
Hung D, Nguyen HN (2014) Modeling meat yield based on measurements of body traits in genetically improved giant freshwater prawn (GFP). Aquacult Int 22:619–631
Kause A, Ritola O, Paananen T, Mantysaari E, Eskelinen U (2002) Coupling body weight and its composition: a quantitative genetic analysis in rainbow trout. Aquaculture 211:65–79
Kause A, Paananen T, Ritola O, Koskinen H (2007) Direct and indirect selection of visceral lipid weight, fillet weight, and fillet percentage in a rainbow trout breeding program. J Anim Sci 85:3218–3227
Kocour M, Mauger S, Rodina M, Gela D, Linhart O, Vandeputte M (2007) Heritability estimates for processing and quality traits in common carp (Cyprinus carpio L.) using a molecular pedigree. Aquaculture 270:43–50
Navarro A, Zamorano MJ, Hildebrandt S, Gines R, Aguilera C, Afonso JM (2009) Estimates of heritabilities and genetic correlations for growth and carcass traits in gilthead seabream (Sparus auratus L.), under industrial conditions. Aquaculture 289:225–230
Neira R, Lhorente JP, Araneda C, Diaz N, Bustos E, Alert A (2004) Studies on carcass quality traits in two populations of Coho salmon (Oncorhynchus kisutch): phenotypic and genetic parameters. Aquaculture 24:117–131
Nguyen NH, Ponzoni RW, Abu-Bakar KR, Hamzah A, Khaw HL, Yee HY (2010) Correlated response in fillet weight and yield to selection for increased harvest weight in genetically improved farmed tilapia (GIFT strain), Oreochromis niloticus. Aquaculture 305:1–5
Peterman MA, Phelps RP (2012) Fillet yields from four strains of Nile Tilapia (Oreochromis niloticus) and a Red variety. J Appl Aquacult 24:342–348
Powell J, White I, Guy D, Brotherstone S (2008) Genetic parameters of production traits in Atlantic salmon (Salmo salar). Aquaculture e 274:225–231
Rutten MJM, Bovenhuis H, Komen H (2004) Modeling fillet traits based on body measurements in three Nile tilapia strains (Oreochromis niloticus L.). Aquaculture 231:113–122
Rutten MJM, Bovenhuis H, Komen H (2005) Genetic parameters for fillet traits and body measurements in Nile tilapia (Oreochromis niloticus L.). Aquaculture 246:125–132
Sang NV, Thomassen M, Klemetsdal G, Gjøen HM (2009) Prediction of fillet weight, fillet yield, and fillet fat for live river catfish (Pangasianodon hypophthalmus). Aquaculture 288:166–171
Senanan W, Pechsiri J, Sonkaew S, Na-Nakorn U, Sean-In N, Yashiro R (2015) Genetic relatedness and differentiation of hatchery populations of Asian seabass (Lates calcarifer) (Bloch, 1790) broodstock in Thailand inferred from microsatellite genetic markers. Aquacult Res 46:2897–2912
Thodesen J, Rye M, Wang YX, Bentsen HB, Gjedrem T (2012) Genetic improvement of tilapias in China: genetic parameters and selection responses in fillet traits of Nile tilapia (Oreochromis niloticus) after six generations of multi-trait selection for growth and fillet yield. Aquaculture 366–367:67–75
Acknowledgements
We would like to acknowledge the Center for Advanced Studies in Agriculture and Food (CASAF), Institute for Advanced Studies, Kasetsart University (Grant number CASAF 094) for providing a scholarship funding to the first author. We acknowledge the Kasetsart University Research and Development Institute (KURDI) for their support through grant number Kor-Sor (Dor) 34.59.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yenmak, S., Joerakate, W. & Poompuang, S. Prediction of fillet yield in hatchery populations of Asian sea bass, Lates calcarifer (Bloch, 1790) using body weight and measurements. Int Aquat Res 10, 253–261 (2018). https://doi.org/10.1007/s40071-018-0202-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40071-018-0202-9