Introduction

Tuna fishes, Scombridae family, are one of the most economically important marine resources for industrial fishing activities in the Persian Gulf and Oman Sea (Kamrani et al. 2010). The Scombridae is a family of 15 genera and about 50 species of epipelagic marine fishes (Block and Stevens 2001). The main tuna species caught in the Iranian waters of Persian Gulf and Oman Sea are: longtail tuna (Thunnus tonggol Bleeker, 1851), yellowfin tuna (Thunnus albacares Bonnaterre, 1788), skipjack tuna (Katsuwonus pelamis Linnaeus, 1758), kawakawa (Euthynnus affinis Cantor, 1849), frigate tuna (Auxis thazard Lacepede, 1800), Narrow-barred Spanish mackerel (Scomberomorus commerson Lacepede, 1800) and Indo-Pacific king mackerel (Scomberomorus guttatus Bloch & Schneider, 1801). Tuna fishes constitute around 50% of total landings of the Hormozgan province and total annual commercial landings of tuna fishes in Iranian waters of Persian Gulf and Oman Sea were around 175,000 tonnes. Longtail tuna represented 46% of total catch (Iran Fishery Organization 2013).

Longtail tuna is an epipelagic species inhabiting tropical to temperate regions of the Indo-Pacific, found almost exclusively in the neritic waters close to the shore, avoiding estuaries, turbid wasters and open Ocean. This species primarily caught by gillnet fleets operating in coastal waters with the highest reported catches from Iran, Indonesia, Pakistan, Malaysia and, to Oman, Yemen, India and Thailand (Pierre et al. 2014).

Knowledge of growth and mortality parameters is essential for understanding the population dynamics of different species. Several approaches were often used to determine the age and growth of the aquatic species, such as length–frequency analyses, tagging and recapture experiments and observations of the mark on the hard parts (scales, otoliths, spines and vertebrates) (Stequert et al. 1996). Particular morphometric measurements, such as length–weight relationship (LWR), are useful in fishery management and stock assessment models (Barría et al. 2014), and has been widely used in the environmental monitoring programs such as calculation of fish weight at a certain length and the conversion of an equation of growth in weight and vice versa, as well as the calculation of a condition index to allow for morphological comparisons of populations among different regions (Yoon et al. 2013; Oliveira et al. 2014). The general biology and population dynamics of the several tuna species have been researched in Iranian waters of Persian Gulf and Oman Sea (Kaymaram et al. 2010; Taghavi Motlagh et al. 2010; Hosseini and Ehsani 2014). Nevertheless, scanty information is available on growth and mortality characteristics of longtail tuna in this region http://www.jifro.ir/files/site1/user_files_eb12be/admin-A-10-1-11-532319e.pdf. Therefore, the specific objectives of present study were to determine: (1) the length and weight frequency structure (length–weight relationship), (2) the growth parameters (L ∞, K, T 0) using the length-based MULTIFAN method (3) the mortality parameters based on the length-converted catch curve and Pauly’s empirical equation, and (4) the exploitation rate of the longtail tuna in coastal waters of the northern Persian Gulf and Oman Sea, Iran.

Materials and methods

Study area and sampling

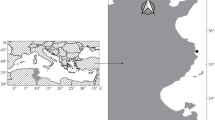
Using commercial gill nets, specimens of longtail tuna were collected monthly and randomly in coastal waters of the northern Persian Gulf and Oman Sea (Hormozgan province, Iran) from January to December 2014 (Fig. 1). Sampling was carried out from five different landing sites including Bandar lengeh (54°22′E and 26°39′N), Gheshm Island (55°41′E and 26°41′N), Bandar Abbas (56°15′E 27°11′N), Sirik (57°05′E and 26°20′N) and Jask (57°47′E and 25°39′N). A total of 2163 individuals were examined during the study period.

Fig. 1
figure 1

Map of study area and location of sampling ports for longtail tuna (northern Persian Gulf and Oman Sea, Iran)

Full size image

Length–weight relationship

The length frequency distribution of longtail tuna caught in different months was determined. For each specimen, the fork length (FL) was measured with a measuring board to the nearest 1 cm, and total body weight (TW) was measured on a digital scale to 1 g. The relationship between length and weight was calculated using the following equation (Ricker 1975):

$${\text{TW}} = a{\text{FL}}^{b}$$

where TW is the total weight (g), FL is the fork length (cm), a is the intercept of the regression and b is the regression coefficient indicating isometric growth when equal to 3. The best regression parameters were obtained by minimizing the residuals errors by the least square residuals method (Haddon 2011).

Student’s t test was utilized to confirm whether the declivity of regression (constant “b”) presented a significant difference with 3, indicating the type of growth: isometric (b = 3), positive allometric (b > 3) or negative allometric (b < 3) (Sokal and Rohlf 1987).

$$t_{\text{s}} = \frac{b - 3}{sb}$$

where t s is the t test value, b is the slope and sb is the standard error of the slope (b).

Growth parameters

Length frequency data were used to calculate the von Bertalanffy growth rate (k) and the asymptotic length (L ∞) by model progression analysis using the FiSAT program (Gayanilo et al. 1996) and ELEFAN I method (Pauly 1984). The best value of growth parameter (k) for the given value of L ∞ was identified by Shepherd’s method and scan of k values option from Assess menu. A classical von Bertalanffy growth function (VBGF) was fitted to the data using the following formula (Sparre and Venema 1998):

$$L_{\text{t}} = L_{\infty } (1 - \exp ( - k(t - t_{0} )))$$

In this equation, t 0 represents the theoretical age at length zero, L ∞ is the asymptotic length and L t is the length at age. Estimation of the t 0 parameter was determined by empirical equation proposed by Pauly (1983):

$${\text{Log}}10 ( - t_{0} ) = - 0.392 - 0.275{\text{Log}}10L_{\infty } - 1.038k$$

Mortality parameters

The length-converted catch curve was applied for the calculation of the instantaneous annual mortality rate (Z) (Pauly 1983). The growth performance index (ϕ′) was calculated using the following formulae (Pauly and Munro 1984):

$$\phi^{\prime } = \log K + 2\log L_{\infty } .$$

The natural mortality (M) was calculated by Pauly’s empirical equation:

$${\text{Log}}M = 0.1228 - 0.192{\text{Log}}L_{\infty } + 0.7485 {\text{Log}}K + 0.2391\log T,$$

where T is the mean annual temperature (in °C), which is assumed to reflect the locally sea surface temperature in the survey area (Pauly 1984) (in the present study, T = 27 °C).

For the calculation of the fishery mortality (F), the M value was subtracted from the Z value to get the fishing mortality (Appeldoom 1984).

$$F = Z - M$$

With the estimated values of F and Z, the rate of exploitation (U) was calculated using the following formulae (Gulland 1985):

$$E = \frac{{F}}{Z}$$

Results

The annual length frequency of longtail tuna is shown in Fig. 2. A total of 2163 specimens sampled in five landing sites. The fork length of longtail tuna was in the range of 27–107 cm. Along the length range analyzed, the highest length frequency obtained was in the range of 62–65 cm. The average length obtained was between 59 and 63 cm with no difference between months.

Fig. 2
figure 2

Annual fork length frequency distribution of longtail tuna in northern Persian Gulf and Oman Sea, Iran

Full size image

Figure 3 represents the length–weight relationships of longtail tuna during a 1 year period and in different seasons. The length–weight relationship during a 1 year period was estimated to be TW = 0.00003 × FL2.82 (R 2 = 0.84). The b value of relationship between length and weight was ranged from 2.70 (summer) to 2.89 (spring). According to the obtained b value and using the Student’s t test, isometric growth model was determined for longtail tuna in the study area (P > 0.05).

Fig. 3
figure 3

Length–weight relationships of longtail tuna during a 1 year period and different seasons in northern Persian Gulf and Oman Sea, Iran

Full size image

The von Bertalanffy growth curves of longtail tuna are shown in Fig. 4. The growth parameters estimated by ELEFAN I were as: L ∞ = 111.23 cm fork length, t 0 = −0.38 year, ϕ′ = 3.6. The k value was 0.3 year−1 (Fig. 5). The estimated age in different fork length classes is represented in Table 1.

Fig. 4
figure 4

The von Bertalanffy growth curves of longtail tuna in northern Persian Gulf and Oman Sea, Iran

Full size image
Fig. 5
figure 5

Shepherd’s method with maximum score (S max) appropriate to the best value of growth coefficient of longtail tuna in northern Persian Gulf and Oman Sea, Iran

Full size image
Table 1 Detailed data on relationship between fork length classes and estimated age for longtail tuna in northern Persian Gulf and Oman Sea, Iran
Full size table

The length-converted catch curve of longtail tuna is shown in Fig. 6. The estimated rates of total mortality (Z) and natural mortality rate (M) were 1.15 and 0.43 year−1, respectively. The fishing mortality (F) was 0.72 year−1. The exploitation rate (E) for population of longtail tuna was calculated as E = 0.63.

Fig. 6
figure 6

Length-converted catch curve for longtail tuna in northern Persian Gulf and Oman Sea, Iran

Full size image

Discussion

The length–frequency-based analysis is used widespread at the present time, especially in the tropical and subtropical regions (Sparre and Venema 1998). This method becomes important when other aging techniques are either not possible or very expensive (Wang and Ellis 2005). According to Zhu et al. (2011), the study of growth using length–frequency analysis has long been the most frequently used method.

Gulland and Rosenberg (1992) noted that sampling from large number of smaller samples than sampling from a limited number of larger samples will always give more information, while providing estimates with smaller variance. In this regard, two samples of 150 fish will always give more information than one of 300 fish, but will take more time. Furthermore, a sample of 50–150 fish/month and an annual sample of 1000–1500 fish provide the most reliable image on the biological characteristics of a specific species. To have most reliable understanding on the biology of longtail tuna distributed in coastal waters of the northern Persian Gulf and Oman Sea, sampling was done in five different landing sites and covered 12 months (180 fish/month).

According to IGFA (2001), the maximum fork length of longtail tuna was found to be 147 cm. The length frequency of long tail tuna captured from the traditional fishing was 26–130 cm (Darvishi et al. 2003). The author found significant differences in the length frequency of long tail tuna between the traditional and commercial fishing which might probably be governed by the sampling methods and fishing tools. Fish with mean length of 30 cm have been reported in the gillnet catches of long tail tuna in Oman Sea waters in October while the average size was found to be 36 and 46 cm for February and May, respectively.

Abdussamad et al. (2012) have reported that longtail tuna along the Indian Coast is supported by fishery having a length range of 23–111 cm and a mean length of 60.5 cm in gillnets fishery. Khorshidian and Carrara (1993) indicated the differences in size composition of longtail tuna between the Iranian and Omani fisheries on the northern and southern shores of the Oman Sea. Size-related migration or differences in the mesh size of the gill nets used were possibly contributed to this difference. No differences in the monthly length frequency of longtail tuna were observed. Moreover, the average length was lower than that at first sexual maturity, indicating overfishing or the use of small mesh size nets.

Among the biometric relations in fishes, the length–weight relationships are greatly presented by scientists and researchers as useful tools in fish biology (King 2007; Ferreira et al. 2008). Calculation of the length–weight relationship parameter is useful for the prediction of weight from length values, condition of fish, stock assessment, and estimation of biomass (Valset et al. 2007).

In our study, the length–weight relationship was estimated to be W = 0.00003 × FL2.82 (R 2 = 0.84). To verify if b was significantly different from the isometric value (b = 3), the Student’s t test (H 0: b = 3) was utilized. Results showed no difference between obtained b value (2.82) and 3 and isometric growth model was determined for longtail tuna in study area (P > 0.05). Biswass (1993) and Froese (2006) presented the acceptable range of b value between 2.5 and 3.5 that is in agreement with our estimation. Length–weight relationship for longtail tuna was estimated as W = 0.0148 × L 3.0 in waters of India (Abdussamad et al. 2012), indicating a perfect isometric pattern in growth that is in agreement with the results of our study. Griffiths et al. (2010) estimated the length–weight relationship of longtail tuna as W = 0.00005 × L 2.82 in tropical and temperate waters of the central Indo-Pacific that is completely in agreement with our findings.

The growth parameters of longtail tuna estimated by ELEFANI were as: L ∞ = 111.23 cm fork length, t 0 = −0.38 year, ϕ′ = 3.6. The k value was 0.3 year−1. Studies in different regions have indicated that the L ∞ of longtail tuna was differed from 55 cm in waters of Japan (Itoh et al. 1999) to 135.4 cm in Australia (Griffiths et al. 2010) and the range for k was 0.228 in Oman (Prabhakar and Dudley 1989) to 1.7 in waters of Japan (Itoh et al. 1999). The L ∞ estimated in our study for the longtail tuna was higher than the estimates given by some previous studies (Supongpan and Saikliang 1987; Yesaki 1989; Itoh et al. 1999) but lower than that by Griffiths et al. (2010) and Abdussamad et al. 2012.

Difference in the growth parameters estimated by other authors may be due to the fact that the data used for different analytical methods by them were obtained by different gears such as drift gillnets, hooks and lines, troll and trawls (Pillai et al. 2002). Taghavi Motlagh et al. (2010) declared that different values of L ∞ and k might be associated with sampling error, variation in fishing intensity or environmental conditions. Moreover, slight differences in growth patterns can be the results of differences in genetic structure, differences in temperature, density of food and diseases (Wootton 1998). Age at zero length (−t 0) was calculated to be −0.38 year and, according to King (2007), it means juveniles of longtail tuna grow more quickly than adults.

The total mortality for longtail tuna was 1.15 year−1. Abdussamad et al. 2012 presented a total mortality rate as 3.85 year−1 for longtail tuna in Indian waters that was considerably higher than our results. The instantaneous natural mortality coefficient (M) was 0.43 year−1 in the present study. Our result was lower than the instantaneous natural mortality coefficient estimated for the same species in the Indian waters, 0.77 year−1 (Abdussamad et al. 2012) and 0.8 year−1 (James et al. 1993). SU et al. (2003) declared that the estimation of natural mortality poses some difficulty because it may be affected by the selection of the estimation method and the study area.

The exploitation rate for population of longtail tuna (E = 0.63) in the present study was high. Gulland (1985) stated that in an optimally exploited stock, fishing mortality should be equal to natural mortality, resulting in an exploitation rate of 0.5. Patterson (1992) declared that the fishing rate satisfying optimal E level of 0.5 tended to reduce pelagic fish stock abundance and, hence, the former author suggested that E should be maintained at 0.4 for optimal exploitation of those stocks. The present estimate of E suggests that the population of longtail tuna in the waters of northern Persian Gulf and Oman Sea is being heavily exploited and overfished at a higher level than the optimum and a better management policy is necessary in this area. The decision making on fisheries management of longtail tuna cannot use only biological information; thus, the socioeconomic condition of small-scale fishermen in waters of the Persian Gulf and Oman Sea should be considered to achieve sustainable management of longtail tuna resources. Finally, results of this study are particularly helpful for drift gillnet fisheries management in the Persian Gulf and Sea of Oman.