Abstract
Numerous investigations of RC beams strengthened in shear with externally-bonded (EB) fibre-reinforced polymer (FRP) sheets, plates and strips have been successfully conducted in recent years. These valuable studies have highlighted a number of influencing parameters that are not captured by the design guidelines. The objective of this study was: (1) to highlight experimentally and analytically the influential parameters on the shear contribution of FRP to RC beams strengthened in shear using EB FRP sheets and strips; and (2) to develop a set of transparent, coherent, and evolutionary design equations to calculate the shear resistance of RC beams strengthened in shear. In the experimental part of this study, 12 tests were performed on 4,520-mm-long T-beams. The specimens were strengthened in shear using carbon FRP (CFRP) strips and sheets. The test variables were: (1) the presence or absence of internal transverse-steel reinforcement; (2) use of FRP sheets versus FRP strips; and (3) the axial rigidity of the EB FRP reinforcement. In the analytical part of this study, new design equations were proposed to consider the effect of transverse-steel in addition to other influential parameters on the shear contribution of FRP. The accuracy of the proposed equations has been verified in this study by predicting the FRP shear contribution of experimentally tested RC beams.
Similar content being viewed by others
1 Introduction
The last two decades have witnessed a growing demand for strengthening and rehabilitation of existing reinforced concrete (RC) structures. In the 1990s, researchers paid more attention to the potential applications and benefits of using fibre-reinforced polymer (FRP) material to strengthen RC elements. This enthusiasm was due to the attractive characteristics of FRP, such as high strength-to-density ratios, chemical and corrosion resistance, and easy construction and handling. Many valuable research studies on strengthening of RC beams with FRP composites have been conducted (e.g., Uji 1992; Al-Sulaimani et al. 1994; Sato et al. 1996; Taerwe et al. 1997; Täljsten 1997; Chaallal et al. 1998; Triantafillou 1998; Khalifa et al. 1998; Pellegrino and Modena 2008; Galal and Mofidi 2010; Chen et al. 2013; Mofidi et al. 2013a, b; and Pellegrino and Vasic 2013). However, recent findings have highlighted major influential parameters related to shear strengthening with externally-bonded (EB) FRP that have still not been captured by current predictive models, including standard codes and guidelines (Mofidi and Chaallal 2011a, b). The objectives of this study were: (1) to investigate experimentally and analytically the effect of the influential parameters which have been found to affect the shear resistance of EB FRP; and (2) to propose a set of transparent, rational, and evolutionary design equations to calculate the shear contribution of EB FRP to the shear resistance of strengthened RC beams.
In the experimental part of this study, 12 tests were performed on full-scale T-beams strengthened in shear using EB FRP sheets and strips. The variables examined in the experimental test matrix were: (1) the presence or absence of internal transverse-steel reinforcement, (2) the use of FRP sheets versus FRP strips, and (3) the axial rigidity of the EB FRP reinforcement.
In the analytical part of this study, the factors that showed the most significant effects on the shear resistance of RC beams retrofitted with EB FRP were highlighted. This investigation confirmed that the influence of internal transverse-steel on the contribution of FRP to shear resistance was significant. However, this effect has not yet been recognized by any existing design standard code or guidelines. In this paper, a new design method was developed that considers the effect of internal transverse-steel in addition to other parameters that affect the contribution of FRP to shear resistance.
2 Experimental tests
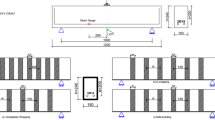
Twelve T-beams were tested in three-point load flexure. The specimens were purposely designed as under-reinforced in shear. All specimens had similar materials and geometry. The specimens were 4,520 mm long with an effective cross-sectional beam depth d = 350 mm (Fig. 1). The specimens with no internal transverse-steel stirrups were labelled NT. The specimens labelled WT were reinforced with internal transverse-steel reinforcement spaced at s = d/2. The transverse-steel reinforcing bars were 8 mm in diameter (area = 50 mm2) and were spaced at s = d/2 (Fig. 1). The reference T-beams not strengthened with CFRP sheets or strips were labelled RF, whereas the specimens retrofitted with CFRP sheets and strips were labelled SH and ST respectively. In addition, the percentage of the shear-span area that was covered by the strengthening FRP strips (the strip-width to strip-spacing ratio) was provided at the end of each specimen’s label. For example, specimen WT-ST-50 features a T-beam with transverse-steel spaced at d/2 = 175 mm which is retrofitted using CFRP strips with a strip-width to strip-spacing ratio of 0.5.
The 28-day concrete compressive strength on 152 mm diameter by 305 mm concrete cylinders reached an average value of 29 MPa. The average concrete compressive strength of the specimens in the test days was calculated by testing concrete cylinders for each concrete beam at the testing day. The average concrete compressive strengths of the tested specimens were relatively close to each other for the tested specimens and were equal to 31 MPa. The longitudinal-steel reinforcement included two layers of reinforcement each including two 25 M bars (diameter = 25.2 mm, modulus of elasticity = 187 GPa, and yield stress = 500 MPa), and the transverse-steel reinforcement consisted of deformed 8-mm bars (modulus of elasticity = 206 GPa and yield stress = 540 MPa). The steel reinforcement characteristics are reported based on the information gathered from the supplier.
The FRP sheets and strips used in this study were unidirectional carbon-fibre fabric epoxy-bonded over the shear span in a U-shaped configuration. The CFRP sheet had an ultimate tensile strength of 3,450 MPa, an elastic modulus of 230 GPa, and an ultimate strain of 1.5 %. The area weight and the fibre density of the CFRP fabric were equal to 6.10 N/m2 and 18 kN/m3 respectively. Table 1 presents the mechanical and elastic properties of the CFRP fabric as provided by the manufacturers.
2.1 Experimental procedure
All twelve tests were conducted using three-point load bending test setup. This loading configuration was selected since it enabled two tests to be performed on each specimen. While one end zone is being tested, the other end zone is overhung and unstressed (see Fig. 1a). The load is applied at a distance a = 3d from the closest support, which is representative of a slender beam (see Fig. 1a). The measurement equipments used for the project was carefully designed to meet the objective and the scope of this study. Linear variable differential transformers (LVDT) with a 100-mm stroke were used to measure the vertical displacement at the position under the applied load and at mid-span. Different types of strain gauges were installed on the longitudinal reinforcement, on the steel stirrups or embedded in concrete to measure the strains experienced by different materials as the load was applied and to monitor the yielding of the steel and the concrete cracking. The strain gauges on the transverse-steel reinforcement were positioned in different heights along the expected plane of shear fracture. Displacement sensors, also known as crack gauges, were utilized to measure the strain in the CFRP sheet. These gauges were installed vertically on the EB FRP sheets at the same location along the longitudinal axis as the strain gauges on the steel stirrups. Thus, the strains in the CFRP sheets and in their corresponding transverse-steel reinforcement can be compared throughout the loading stages. The load was applied using a 2,000 kN-capacity hydraulic jack.
2.2 Test descriptions and results
Table 2 presents the loads attained at rupture, the contributions to the shear resistance by the concrete, the transverse-steel, and the CFRP, the gain in capacity due to the CFRP, defined as (gain = V f /(Vtot − V f )), and the maximum deflection at failure under the load point. Note that the shear contributions of concrete and steel are calculated based on the results obtained from the reference specimens. Moreover, the following assumptions, which were implicitly admitted in the guidelines, are considered in deriving some of the values provided in Table 2: (i) the shear resistance due to concrete is the same whether or not the beam is retrofitted in shear with FRP and whether or not the retrofitted beam is reinforced with transverse-steel; and (ii) the contribution of transverse-steel is the same for both strengthened and unstrengthened beams. All the test specimens failed in shear. The specimens strengthened with CFRP failed by FRP debonding followed by shear diagonal tension failure (Figs. 2, 3, 4, 5). In addition, Figs. 6 and 7a show the applied load versus mid-span deflection curves for the tested specimens respectively. Details of specimen failures are described in the following paragraphs.
2.2.1 NT-RF-0
Control specimen NT-RF-0 exhibited a single shear-crack pattern. The shear crack initiated on the beam’s web, midway between the support and the point load, and propagated simultaneously toward both the beam flange and the support. As the crack reached the flange, it triggered immediate failure of the specimen. The crack propagated at an angle of approximately 42° in the web and became almost horizontal as it reached the beam flange. The failure load for the specimen NT-RF-0 specimen was equal to 122.7 kN (Fig. 2).
2.2.2 NT-ST-35
This specimen was strengthened with 40-mm wide U-jacket strips spaced at 115 mm. For all the beams without transverse-steel, cracking initiated at more or less the same load level, approximately 80 kN. The failure load for specimen NT-ST-35 was equal to 182.6 kN. The gain in shear capacity due to CFRP was 49 % (Fig. 3). All the specimens retrofitted with CFRP strips experienced local strip debonding during loading. Each local strip-debonding event resulted in a noticeable decrease in the load-carrying capacity of the beam in question (see Fig. 6), but the load continued to increase as the cracks propagated, engaging thereby the unloaded CFRP strips in their path.
2.2.3 NT-ST-50
The NT-ST-50 specimen was retrofitted with 87.5-mm-wide U-jacket strips spaced at 175 mm. The first cracks were observed at a load of 78 kN. At 170 kN, the third strip started to debond at the bottom. The failure load for specimen NT-ST-50 was equal to 203.1 kN. The gain in shear capacity due to CFRP was 66 %.
2.2.4 NT-ST-60
This specimen was retrofitted with 30-mm-wide U-jacket strips spaced at 50 mm. Formation of the first cracks was visible at 80 kN. The third strip from the left started to debond from the top at 165 kN. The failure load for specimen NT-ST-60 was equal to 197.9 kN. The gain in shear capacity due to CFRP was 61 %.
2.2.5 NT-ST-61
Specimen NT-ST-61 was retrofitted with 53-mm-wide U-jacket strips spaced at 87.5 mm. At 136 kN, the second strip started to debond. The failure load for specimen NT-ST-61 was equal to 204.9 kN. The gain in shear capacity due to CFRP was 67 %.
2.2.6 NT-ST-70
This specimen was strengthened with 87.5-mm-wide U-jacket strips spaced at 125 mm. At 85 kN, formation of cracks occurred between the strips. The failure load for specimen NT-ST-70 was equal to 227.3 kN. The gain in shear capacity due to CFRP was 85 %.
2.2.7 NT-SH-100
Specimen NT-SH-100 was retrofitted with a single layer of U-jacket CFRP sheet. At 175 kN, debonding occurred at the shear span, right after the first cracks were observed. The failure load for specimen NT-SH-100 was equal to 181.2 kN. The gain in shear capacity due to CFRP was 48 % (Fig. 4a). All the specimens strengthened with FRP sheet U-Jackets featured a progressive FRP debonding type of failure once local debonding initiated, as illustrated by the load-deflection graphs (Figs. 6, 7a).
2.2.8 NT-SH-200
This specimen was strengthened with double layers of U-jacket CFRP sheet. The failure load for specimen NT-ST-200 was equal to 183.8 kN. The addition of a second CFRP layer resulted in a modest gain in shear capacity for specimen NT-ST-200. The gain in shear capacity due to CFRP was 50 % (Fig. 4b).
2.2.9 WT-RF-0
Because of the presence of a transverse-steel reinforcement, reference specimen WT-RF-0 exhibited a cracking pattern different from that of the reference specimen NT-RF-0. In specimen WT-RF-0, the cracking pattern was more widespread and propagated at an angle of 39°. The failure load for specimen WT-RF-0 was equal to 350.6 kN (Fig. 5a).
2.2.10 WT-ST-50
This specimen was retrofitted with 87.5-mm-wide U-jacket strips spaced at 175 mm. In general, in the beams strengthened with transverse-steel reinforcement, two parallel diagonal cracks formed between 78 and 81 kN and propagated with increasing load from the support to the flange at an average angle of approximately 38°. As the load was reaching its ultimate value, these two diagonal cracks merged into a single crack which progressed horizontally in the RC beam flange. The failure load for specimen WT-ST-50 was equal to 372.5 kN. The gain in shear capacity due to CFRP was 6 %.
2.2.11 WT-ST-70
This specimen was retrofitted with 87.5-mm-wide U-jacket strips spaced at 125 mm. The failure load for specimen WT-ST-70 was equal to 383.4 kN. The addition of transverse-steel reinforcement resulted in a drastic decrease of the gain in shear capacity due to CFRP. The gain in shear capacity due to CFRP was 9 %.
2.2.12 WT-SH-100
This specimen was retrofitted with a single layer of U-jacket CFRP sheet. The failure load for specimen WT-SH-100 was equal to 378.3 kN. The gain in shear capacity due to CFRP was 8 % (Fig. 5b).
It should be mentioned that for the specimens with transverse-steel, shear failure took place after yielding of the steel stirrups intersecting the shear crack (Fig. 8). Similar results were observed by researchers in earlier investigations on RC beams retrofitted with CFRP material (e.g., Bousselham and Chaallal 2004; Chaallal et al. 2011; Mofidi et al. 2012a, b). It is believed that the presence of the strengthening FRP will not prevent the transverse-steel from yielding, provided that the major shear crack intercepts the transverse-steel (i.e., the spacing between the steel stirrups are not too wide). See Mofidi and Chaallal (2011c) for more detailed information.
However, few studies based on finite-element (FE) models have reported that the presence of FRP in shear-strengthened RC beams limits strain in the transverse-steel (e.g., Chen et al. 2010). The experimental results of the current study contradict the results of those FE studies. This discrepancy between the experimental results and those of the FE studies might occur since the mentioned FE studies consider a single crack pattern in the concrete beam web which does not comply with the multi-crack pattern observed in the shear-strengthened RC beam strengthened with internal transverse steel reinforcement (See Mofidi and Chaallal 2011c). Nevertheless, the matter related to yielding of transversal-steel reinforcement is still a subject of debate among the researchers in this area.
In the analytical part of this study, it is assumed that the transverse-steel yields in the shear-strengthened RC beams. Moreover, a design model is proposed to provide a clear rationale for the effects of transverse-steel on the shear contribution of FRP.
3 Design equations for FRP shear strengthening
The most probable governing failure mode for RC beams shear-strengthened with EB FRP is debonding of the FRP. Debonding of FRP mainly occurs in the side-bonded and U-jacket FRP configurations. Several major factors which influence debonding of FRP and hence the contribution of FRP to shear resistance have been identified (e.g., bond model, FRP effective strain, shear crack angle and FRP effective anchorage length). Most of the factors mentioned have been involved in the development of standard codes and guidelines. On the other hand, there are still a few key factors that have not yet been captured by standard codes and guidelines. Table 3 lists the major effecting parameters and the status of their application in the current major design standard codes and guidelines.
3.1 Cracking pattern of the RC beam
Experimental tests by Pellegrino and Modena (2002) and Chaallal et al. (2002) have illustrated that for RC strengthened or not strengthened beams with FRP, the shear-crack pattern tends to be more distributed in the shear span in the presence of internal transverse-steel compared to that for RC beams with little or no shear reinforcement. Figures 2, 4a, 5a and b show specimens NT-RF-0, NT-SH-100, WT-RF-0, and WT-SH-100 from the experimental section of the current study. The NT-RF-0 specimen (Fig. 2), with no shear reinforcement, failed along a single crack line. The NT-SH-100 specimen (Fig. 4b) was strengthened in shear with one layer of EB FRP sheet. This specimen failed with one major shear crack and a few extra surface shear cracks (in the concrete cover) that connected to the major shear crack in the concrete core. This resulted in debonding of the FRP attached to a chunk of concrete cover. The WT-RF-0 specimen (Fig. 5a), with transverse-steel reinforcement and without EB FRP, failed with one major shear crack and a few minor shear cracks. The WT-SH-100 specimen (Fig. 5b) was reinforced with both internal transverse-steel and one layer of FRP sheet. As is clearly illustrated in Fig. 5b, the WT-SH-100 specimen failed with a distributed shear multiple-crack pattern.
It follows that the debonding of EB FRP usually initiates from a shear crack in the concrete cracked zone. This occurs mainly because the FRP fibre anchorage is interrupted by the cracks. Meanwhile, bond stresses reach their maximum at the fibres intersecting with the shear crack. The concentrated bond stress is transferred away from the crack, developing thereby a locally debonded area. Ultimately, the FRP anchorage failure propagates until the remaining FRP anchorage length is smaller than the effective anchorage length of the FRP. The matter is more discussed in detail in Mofidi and Chaallal (2011c).
It is believed that cracking affects the debonding process because it results in a loss of bonding in the crack vicinity. Therefore, it can be concluded that a more distributed cracking pattern could accelerate FRP debonding and lead to premature shear failure.
Khalifa et al. (1998) showed that, assuming a single-crack line pattern, some fibres with an anchorage length less than the effective bond length debond earlier than the rest of the fibres. They recommended that these fibres should be ignored when calculating the shear contribution of FRP. Therefore, Khalifa et al. (1998) proposed an effective width, w fe , for a single-crack line pattern. With a multiple-line cracking pattern, the anchorage lengths of the FRP fibres cannot be calculated using the proposed equations for a single-line crack pattern because in a multiple-shear-crack pattern, there are several irregular intersections of fibres. This makes it hard to determine the effective width of the fibres that have the minimum effective anchorage length. In the present article, new equations are proposed to calculate FRP effective width assuming a multiple-shear-crack pattern in RC beams strengthened in shear using EB FRP. A new coefficient, k c , is introduced that transforms the effective width of a beam with a multiple-line cracking pattern to the equivalent effective width of a beam with a 45° single-line cracking pattern.
3.2 Effect of transverse-steel on shear contribution of FRP
Figure 7b shows the applied load versus strain in steel stirrups curves for the tested specimens with transverse-steel reinforcement. Experimental studies (Pellegrino and Modena 2002; Chaallal et al. 2002, 2011; Bousselham and Chaallal 2004; Mofidi and Chaallal 2011b; Mofidi et al. 2012a, b) have shown that the effectiveness of FRP composites is diminished with the presence of internal shear-steel reinforcement. It has been clearly established that the contribution of FRP to shear resistance depends on the amount of internal shear-steel reinforcement. However, as can be seen in Table 3, none of the standard codes and guidelines has yet considered the effect of transverse-steel on the equations for FRP shear contribution.
As mentioned earlier, the contribution of FRP to shear resistance is primarily related to the quality of the bond between the FRP and the concrete. The FRP-concrete bond is governed mainly by the FRP anchorage length. However, a greater amount of transverse reinforcement (steel + FRP) results in a more distributed cracking pattern and hence a shorter available anchorage length of FRP fibres. Therefore, for specimens strengthened with transverse-steel reinforcement, the bond force, and hence the EB FRP contribution to shear resistance, decrease compared to specimens with no transverse-steel reinforcement.
3.3 Proposed conceptual model
In this section, a design model is proposed to calculate the contribution of FRP to the shear resistance of RC beams strengthened in shear with EB FRP. In this model, the diminishing effect of internal transverse-steel and the distributed pattern of the shear cracks are quantified by the proposed equations.
Figure 9a and b present a schematic configuration of a beam retrofitted in shear with side-bonded EB FRP. Based on experimental observations (e.g., the failed specimen in the current study), the debonded FRP area can be defined as a trapezoidal area, as illustrated by the shaded area in Fig. 9a for side-bonded EB FRP and in Fig. 9c for U-jacket EB FRP. The schematic configuration shown in Fig. 9 is representative of a multiple-shear-crack pattern. It was previously mentioned that the bond effect of several cracks intersecting the FRP is not easy to determine and therefore not well documented. As an alternative, an equivalent rectangular area assuming a 45° single crack was used to replace the assumed trapezoidal bonding area in the distributed multiple-line shear-crack pattern (Fig. 9b, d). The dimensions of the equivalent rectangular area are equal to the FRP effective length and the FRP effective width. The concept of FRP effective length has already been established and is defined as the length of the FRP beyond which the bond force will not increase. The effective bond length can be calculated using the Neubauer and Rostásy (1997) equation:
where f ct is the concrete tensile strength. In lieu of f ct , the equation by Mirza et al. (1979) can be calculated as a function of as follows:
In calculating the FRP effective width, w fe , the cracking pattern was assumed to be a function of the amount of internal transverse-steel and of external EB FRP shear reinforcement as measured by their respective axial rigidities. As previously mentioned, the cracking pattern greatly affects the anchorage length of the FRP fibres. As the cracking pattern becomes more distributed, fewer fibres will offer the full effective anchorage length. As a result, the effective width, that is, the width of those fibres which are long enough to attain the effective anchorage length, is reduced. Using a regression analysis based on experimental test results available in the literature (see Bousselham and Chaallal 2004 for the database), the effective width is defined as a function of the sum of the axial rigidities of the transverse-steel reinforcement and the EB FRP sheets (see Figs. 10, 11):
With w fe defined, the cracking modification factor can then be introduced as , i.e.,
The bond shear force between FRP and concrete can then be calculated by multiplying the equivalent rectangular bond area by the bond shear stress (τeff = ). The effects of k w , which incorporates the w f /s f ratio of the FRP strips, and of k L for beams with an anchorage length less than the effective length are considered in the equation for effective strain:
and hence:
The coefficients k L and k w can be calculated using Eqs. (10) and (11):
where w f and s f are the width and spacing of the EB FRP strips and Lmax the maximum available length of the FRP as given by:
The contribution of FRP to shear resistance is calculated as a function of ε fe using the following equation that accounts for the effect of the cracking angle, θ:
Note that in the case of a continuous FRP sheet, the FRP width, w f , and the spacing, s f , can be assumed equal to one.
For the full wrap configuration, the shear contribution of FRP can be calculated using Eq. (13), assuming the effective strain equal to 0.75ε u ≤ 0.005. The maximum effective strain in the FRP is limited to 0.005 according to CNR-DT200 (2004) provisions (clause 4.3.3.2).
4 Validation of design equations
To evaluate the accuracy of the proposed design equations, experimental test results from the current study were compared to the values predicted by the proposed equation. The contribution of CFRP to shear-resistance test results (see Table 2) was compared with the nominal shear resistance predicted by the following standard codes and guidelines: ACI 440.2R (2008) (based on Khalifa et al. 1998); fib-TG 9.3 (2001) (based on Triantafillou 1998); CAN/CSA-S806 (2002); HB 305-2008 (2008) (based on Chen and Teng 2003); and CNR-DT200 (2004) (based on Monti and Liotta 2006). Table 4 presents the calculated contribution of FRP to shear, Vf cal, using the proposed model and each of the standard codes and guidelines versus the experimental contribution of FRP to shear, Vf exp. Table 4 clearly shows that the proposed model (R2 = 0.819) is superior to the models available in the codes and guidelines. The proposed model was compared with the experimental results, assuming k c = 1 (i.e., the effect of transverse-steel was not considered) to verify the sensitivity of the proposed model to the effect of transverse-steel (cracking coefficient k c ). This resulted in a significant drop in the coefficients of determination (R2 = 0.008) and a considerable scatter in the proposed model’s predictions of V f . In addition, it was deemed useful to assess the effect of k c (a dimensionless parameter) on the calculated results from other standard codes and guidelines. A significant improvement in the accuracy of the predicted results for all the mentioned guidelines was observed when k c was used to calculate Vf cal (Table 4), demonstrating thereby the relevance of including k c in the equation for the contribution of FRP to shear resistance.
5 Conclusions
This paper presents the results of an experimental/analytical research study on twelve RC T-beams retrofitted in shear using EB CFRP strips and sheets. In the experimental part of this study, the test variables were chosen as the following: (1) the presence or absence of transverse-steel reinforcement; (2) the use of FRP sheets versus FRP strips; and (3) the axial rigidity of the EB FRP reinforcement. In the analytical part of this study, the major parameters which affect the shear contribution of EB FRP, but which are not accounted for in the standard codes and guidelines, were discussed. The main findings of this research are as follows:
-
The presence of internal transverse-steel resulted in a significant decrease in the gain due to FRP in the tested specimens. Moreover, the contribution of FRP to shear resistance was significantly greater for RC beams with no transverse-steel reinforcement than for beams with transverse-steel reinforcement.
-
All the tested specimens with transverse-steel failed in shear after the steel stirrups intersecting the shear crack yielded. Experimental tests in this and previous studies concur that the presence of strengthening FRP does not prevent the transverse-steel from yielding, provided that the major shear crack intercepts the transverse-steel (in other words, this is a matter of proper spacing between the steel stirrups).
-
The effect of internal transverse-steel on the contribution of FRP to shear resistance was found to be significant. So far, standard codes and guidelines have not considered internal transverse-steel when calculating the FRP contribution to shear resistance.
-
The effective width of the EB FRP strips and sheets, w fe , was defined based on a distributed shear-crack pattern to replace the bonding area of a beam with a multiple-line cracking pattern to an equivalent bonding area in a beam with a single-line cracking pattern.
-
A cracking coefficient (k c ) to address the effect of transverse-steel on the contribution of FRP to shear resistance was defined as a function of the sum of the axial rigidities of the internal transverse-steel reinforcement and of the EB FRP sheets or strips.
-
The coefficient k c can represent the effect of the internal transverse-steel on the V f design equations in standard codes and guidelines. Applying the cracking coefficient to the design equations of standard codes and guidelines resulted in a significantly improved correlation of the experimental results with the predicted results from those standard codes and guidelines.
Abbreviations
- d :
-
Effective depth of the concrete beam
- d f :
-
Distance from the extreme compression fiber to the centroid of tension reinforcement
- E f :
-
Elastic modulus of FRP in the principal fibre-orientation direction
- E s :
-
Elastic modulus of steel stirrups
- :
-
Cylindrical compressive strength of concrete
- f ct :
-
Concrete tensile strength
- k c :
-
Concrete-cracking coefficient based on transverse-steel and FRP rigidity values
- k L :
-
Coefficient to compensate for insufficient FRP anchorage length
- k w :
-
FRP-width-to-spacing-ratio coefficient
- L e :
-
Effective anchorage length of FRP
- L max :
-
Maximum available bond length
- P bond :
-
Bond shear force in the equivalent rectangular area
- P fe :
-
Effective resisting force in the FRP
- S:
-
Spacing between stirrups
- s f :
-
Spacing between FRP strips
- t f :
-
Thickness of FRP composite
- V f :
-
Contribution of FRP to shear
- V total :
-
Nominal shear resistance at the ultimate limit state
- w fe :
-
Effective FRP width
- α :
-
Angle of inclination of the FRP fibers
- β :
-
Shear-slip coefficient (set equal to 0.315 times the 95th percentile characteristic value of the bond strength proposed by Chen and Teng (2001))
- ε fe :
-
Effective strain of FRP
- λ :
-
Normalized maximum bond length
- θ :
-
Angle of concrete shear crack
- ρ f :
-
FRP strengthening ratio = (2n·tf/b)·(wf/sf)
- τ eff :
-
Average bond shear stress at failure
References
Al-Sulaimani, G. J., Sharif, A. M., Basunbul, I. A., Baluch, M. H., & Ghaleb, B. N. (1994). Shear repair for reinforced concrete by fibreglass plate bonding. ACI Structural Journal,91(3), 458–464.
American Concrete Institute (ACI). (2008). Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures. Report No. 440 2R-08, Farmington Hills, MI.
Bousselham, A., & Chaallal, O. (2004). Shear strengthening reinforced concrete beams with fibre-reinforced polymer: Assessment of influencing parameters and required research. ACI Structural Journal,101(2), 219–227.
CAN/CSA-S806-02. (2002). Design and construction of building components with fibre-reinforced polymer. Rexdale: Canadian Standards Association.
Chaallal, O., Mofidi, A., Benmokrane, B., & Neale, K. (2011). Embedded through-section FRP rod method for shear strengthening of RC beams: Performance and comparison with existing techniques. Journal of Composites for Construction,15(3), 374–383.
Chaallal, O., Nollet, M. J., & Perraton, D. (1998). Strengthening of reinforced concrete beams with externally bonded fibre-reinforced-plastic plates: Design guidelines for shear and flexure. Canadian Journal of Civil Engineering,25(4), 692–704.
Chaallal, O., Shahawy, M., & Hassan, M. (2002). Performance of reinforced concrete T-girders strengthened in shear with CFRP fabrics. ACI Structural Journal,99(3), 335–343.
Chen, J. F., & Teng, J. G. (2001). Anchorage strength models for FRP and steel plates bonded to concrete. Journal of the Structural Engineering,127(7), 784–791.
Chen, J. F., & Teng, J. G. (2003). Shear capacity of FRP-strengthened RC beams: FRP debonding. Construction and Building Materials,17(1), 27–41.
Chen, G. M., Teng, J. G., & Chen, J. F. (2013). Shear strength model for FRP-strengthened RC beams with adverse FRP-steel interaction. Journal of Composites for Construction,17(1), 50–66.
Chen, G. M., Teng, J. G., Chen, J. F., & Rosenboom, O. A. (2010). Interaction between steel stirrups and shear-strengthening FRP strips in RC beams. Journal of Composites for Construction,14(5), 498–509.
CNR-DT200 (2004). Guidelines for design, execution, and control of strengthening interventions by means of fibre-reinforced composites. Italy: National Research Council.
Galal, K., & Mofidi, A. (2010). Shear strengthening of RC T-beams using mechanically anchored unbonded dry carbon fibre sheets. Journal of Performance of Constructed Facilities,24(1), 31–39.
Khalifa, A., Gold, W. J., Nanni, A., & Aziz, A. (1998). Contribution of externally bonded FRP to shear capacity of RC flexural members. Journal of Composites for Construction,2(4), 195–203.
Mirza, S., MacGregor, J., & Hatzinikolas, M. (1979). Statistical descriptions of strength of concrete. Journal of the Structural Division,105(6), 1021–1037.
Mofidi, A., & Chaallal, O. (2011a). Renforcement à l’effort tranchant des poutres en béton armé à l’aide de matériaux composites collés en surface: Avancées et perspectives pour la norme CSA-S806. Canadian Journal of Civil Engineering,38, 556–569.
Mofidi, A., & Chaallal, O. (2011b). Shear strengthening of RC beams with externally bonded FRP composites: Effect of strip-width to strip-spacing ratio. Journal of Composites for Construction,15(5), 732–742.
Mofidi, A., & Chaallal, O. (2011c). Shear strengthening of RC beams with epoxy-bonded FRP—influencing factors and conceptual debonding model. Journal of Composites for Construction,15(1), 62–74.
Mofidi, A., Chaallal, O., Benmokrane, B., & Neale, K. W. (2012a). Performance of end-anchorage systems for RC beams strengthened in shear with epoxy-bonded FRP. Journal of Composites for Construction,16(3), 322–331.
Mofidi, A., Chaallal, O., Benmokrane, B., & Neale, K. W. (2012b). Experimental tests and design model for RC beams strengthened in shear using the embedded through-section FRP method. Journal of Composites for Construction,16(5), 540–550.
Mofidi, A., Chaallal, O., & Shao, Y. (2013a). Analytical design model for reinforced concrete beams strengthened in shear using L-shaped CFRP plates. ASCE, Journal of Composites for Construction. doi:10.1061/(ASCE)CC.1943-5614.0000433.
Mofidi, A., Thivierge, S., Chaallal, O., & Shao, Y. (2013b). Performance of reinforced concrete beams strengthened in shear using L-shaped CFRP plates: An experimental investigation. ASCE, Journal of Composites for Construction,. doi:10.1061/(ASCE)CC.1943-5614.0000398.
Monti, G., & Liotta, M. (2006). Tests and design equations for FRP strengthening in shear. Construction and Building Materials,21, 799–809.
Neubauer, U., & Rostásy, F. S. (1997). Design aspects of concrete structures strengthened with externally bonded CFRP plates (pp. 109–118). Edinburgh: ECS Publications.
Oehlers, D. J., Seracino, R., & Smith, S. T. (2008). Design guideline for RC structures retrofitted with FRP and metal plates: Beams and slabs, HB 305-2008. Sydney: Standards Australia. ISBN 0 7337 7831 3.
Pellegrino, C., & Modena, C. (2002). Fibre-reinforced polymer shear strengthening of RC beams with transverse-steel reinforcement. Journal of Composites for Construction,6(2), 104–111.
Pellegrino, C., & Modena, C. (2008). An experimentally based analytical model for shear capacity of FRP strengthened reinforced concrete beams. Mechanics of Composite Materials,44(3), 231–244.
Pellegrino, C., & Vasic, M. (2013). Assessment of design procedures for the use of externally bonded FRP composites in shear strengthening of reinforced concrete beams. Composites Part B Engineering,45(1), 727–741.
Sato, Y., Ueda, T., Kakuta, Y., & Tanaka, T. (1996). Shear reinforcing effect of carbon fibre sheet attached to side of reinforced concrete beam. In Proceedings, 2nd International Conference on Advanced Composite Materials in Bridges (ACMBS II), Montreal, Canada (pp. 621–637).
Taerwe, L., Khalil, H., & Matthys, S. (1997). Behaviour of RC beams strengthened in shear by external CFRP sheets. In Proceedings, 3rd International Symposium on Non-Metallic (FRP) Reinforcement for Concrete Structures, Sapporo, Japan (Vol. 1, pp. 507–514).
Täljsten, B. (1997). Strengthening of concrete structures for shear with bonded CFRP fabrics. In Proceedings, US–Canada–Europe Workshop on Bridge Engineering, organized by EMPA, Zurich, Switzerland (pp. 57–64).
Triantafillou, T. C. (1998). Shear strengthening of reinforced concrete beams using epoxy-bonded FRP composites. ACI Structural Journal,95(2), 107–115.
Uji, K. (1992). Improving shear capacity of existing reinforced concrete members by applying carbon fibre sheets. Transactions of the Japan Concrete Institute,14(253), 66.
Acknowledgments
The authors acknowledge the support provided by the Natural Sciences and Engineering Research Council of Canada through a postdoctoral fellowship to Dr. Mofidi and to Prof. Chaallal through a Discovery grant. The authors express appreciation to Sika Canada, Inc. (Pointe Claire, Quebec) for providing the FRP sheets and the epoxy. The efficient collaboration of John Lescelleur (senior technician) and Juan Mauricio Rios (technician) is acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Mofidi, A., Chaallal, O. Tests and Design Provisions for Reinforced-Concrete Beams Strengthened in Shear Using FRP Sheets and Strips. Int J Concr Struct Mater 8, 117–128 (2014). https://doi.org/10.1007/s40069-013-0060-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40069-013-0060-1