1 Introduction

A fractal represents a geometric development that’s self-comparable all through its structure. Fractals make a difference in thinking about and recognizing basic logical thoughts, such as solidifying water (snowflake) designs, microbes’ development, and brain waves. Sierpi’nski-type networks are considered in fractal hypothesis [25] and apply in various zones of science, i.e., in biology, chemical chart hypothesis, computer organizing, and physical sciences [11, 19, 20].

Functions and polynomials are powerful tools in computer mathematics for predicting the features of computer networks. Topological descriptors, frequently graph invariants, are numerical numbers that characterize the topology of a network. Multiple types of such invariants are examined and used in computer networking, pharmaceutical, and other branches of science [15, 18, 21]. The chemical structure under investigation is linked to qualities such as fracture toughness, boiling point, and heat of formation. In the discipline of chemical graph theory, this finding is significant [4]. Instead, a general method can directly produce a particular class’s different topological indices. Keeping this idea in mind, the concept of polynomials is introduced in graph theory. By constructing a general polynomial corresponding to a given structure, one can compute several topological indices by differentiating or integrating (or a different combination of both) the corresponding polynomial. Zagreb polynomials, F-polynomials, and Hosoya polynomials are all polynomials with one or two topological invariants [9, 17]. Hosoya polynomial has Wiener and super Wiener index [13].

The M-polynomial is a relatively new polynomial. It will yield innovative chemical graph discoveries and new insights into the study of degree-based topological descriptors [6]. In chemistry, algebraic polynomials [1] have a wide range of applications. The distance-related topological descriptor is calculated using the Wiener polynomial, also known as the Hosoya polynomial [12]. Similarly, when determining degree-related topological descriptors, the M-polynomial is critical [2].

2 Some literature review and basic definitions

In this paper, \({\mathcal {H}}\) is supposed to be a connected, finite and simple graph, the vertex set and edge set of graph \({\mathcal {H}}\) are \(V({\mathcal {H}})\) and \(E({\mathcal {H}})\) respectively, here \(\eta ^{v}\) denote the degree of vertex v.

Deutsch and Klavz̆ar [10] introduced the M-polynomial for \({\mathcal {H}}\) as follows

$$\begin{aligned} M({\mathcal {H}};x,y)=\sum \limits _{\delta \le c\le d \le \triangle }n_{cd}({\mathcal {H}})x^{c}y^{d} \end{aligned}$$
(1)

where \(\delta =\min {\eta ^{v}:v\in V({\mathcal {H}})}, \triangle =\max {\eta ^{v}:v\in V({\mathcal {H}})}\) and \(n_{cd}({\mathcal {H}})\) be the cardinality of edges \( uv\in E({\mathcal {H}})\).

The generalized Sierpiński network [7], is a graph of dimension t with vertex set \(V^t\), which is the set of all words \(v_1v_2...v_t\) of length t, where \(V=V\left( {\mathcal {H}}\right) \), denoted by \(S\left( {\mathcal {H}},t\right) \). Here \(v_p\in V\), \(1\le p \le t\), two vertices u, w associated by an edge in \(gS\left( {\mathcal {H}},t\right) \) if and only if there is \(i\in \{1,2,...,t\}\) such that

\(\bullet \) \(u_j=w_j\) if \(j<i\)

\(\bullet \) \(u_i\ne w_i\) and \({u_i,w_i}\in E\left( {\mathcal {H}}\right) \)

\(\bullet \) \(u_j=w_i\) and \(u_i=w_j\) if \(j>i\)

Above interpretation, shows that if \(uw\in E\left( S\left( {\mathcal {H}},t\right) \right) \) then \(xy\in E\left( {\mathcal {H}}\right) \) and a term z such that \(u=zxyy...y\) and \(w=zyxx...x\). A node of expression uu...u is called a extreme vertex and represented by \({\bar{w}}\). \(S\left( {\mathcal {H}},t\right) \) has always p extreme vertices, where p is the order of base graph \({\mathcal {H}}\). Furthermore, \(d_{\mathcal {H}}\left( u\right) +1=d_{S\left( {\mathcal {H}},t\right) }wuu...u\) and \(d_{\mathcal {H}}\left( w\right) +1=d_{S\left( {\mathcal {H}},t\right) }uww...w.\)

The Randic invariant [8], proposed by Milan Randić in 1975, was the first degree-related topological descriptor. It was later called molecular connectivity invariant [3] and is now known as Randic invariant. Bollobás et al. [5] refined a common form of the Randic index, stated as:

$$\begin{aligned} R_{\alpha }({\mathcal {H}})=\sum \limits _{uv\in E({\mathcal {H}})}\frac{1}{(\eta ^{u}\eta ^{v})^{\alpha }} \end{aligned}$$
(2)

where \(\eta ^{u}\) and \(\eta ^{v}\) represents the degree of vertices u and v, and \(\alpha \in R\). Chemists and mathematicians explored this invariant broadly, the result of which, the Randic invariant has been found to have a correlation. The inverse Randic invariant \(RR_{\alpha }(X)\) is defined as:

$$\begin{aligned} RR_{\alpha }({\mathcal {H}})=\sum \limits _{uv\in E({\mathcal {H}})}{(\eta ^{u}\eta ^{v})^{\alpha }} \end{aligned}$$
(3)

Clearly, these invariants can be established for a variety of distinct values of \(\alpha \).

The first \(M_{1}\) and second \(M_{2}\) Zagreb invariants invented by Gutman and Trinajstić [14, 16, 26] as follows:

$$\begin{aligned}{} & {} M_{1}({\mathcal {H}})=\sum \limits _{uv\in E({\mathcal {H}})}{(\eta ^{u}+\eta ^{v})} \end{aligned}$$
(4)
$$\begin{aligned}{} & {} M_{2}({\mathcal {H}})=\sum \limits _{uv\in E({\mathcal {H}})}{(\eta ^{u}\eta ^{v})} \end{aligned}$$
(5)

The modified Zagreb invariant can be defined as [27]:

$$\begin{aligned} M^{m}_{2}({\mathcal {H}})=\sum \limits _{uv\in E({\mathcal {H}})}\frac{1}{(\eta ^{u}\eta ^{v})} \end{aligned}$$
(6)

The symmetric division deg index \(SDD({\mathcal {H}})\) for connected graphs defined as follows:

$$\begin{aligned} SDD({\mathcal {H}})=\sum \limits _{uv\in E({\mathcal {H}})}\bigg (\frac{\min (\eta ^{u},\eta ^{v})}{\max (\eta ^{u},\eta ^{v})}+\frac{\max (\eta ^{u},\eta ^{v})}{\min (\eta ^{u},\eta ^{v})}\bigg ) \end{aligned}$$
(7)

One more adjustment of Randić invariant is the harmonic invariant expressed as:

$$\begin{aligned} H({\mathcal {H}})=\sum \limits _{uv\in E({\mathcal {H}})}\frac{2}{(\eta ^{u}+\eta ^{v})} \end{aligned}$$
(8)

The inverse sum indeg \(I({\mathcal {H}})\) invariant is defined as:

$$\begin{aligned} I({\mathcal {H}})=\sum \limits _{uv\in E({\mathcal {H}})}\frac{(\eta ^{u}\eta ^{v})}{(\eta ^{u}+\eta ^{v})} \end{aligned}$$
(9)
Table 1 dispersion of certain degree-related topological invariants
Full size table

In above table

\(D_{x}=\frac{\partial g(x,y)}{\partial x}\), \(D_{y}=\frac{\partial g(x,y)}{\partial y}\), \(S_{x}=\int _{0}^{x}\frac{ g(t,y)}{t}dt\), \(S_{y}=\int _{0}^{y}\frac{ g(x,t)}{t}dt\),

\(J g(x,y)= g(x,x)\), & \(Q_{\alpha } g(x,y)= x^{\alpha } g(x,y)\)

where \(D_x\) means derivative of a given function w.r.t x, while \(S_x\) represents the integral of a given function w.r.t x.

3 Main results

In this study, we constructed the M-polynomial of fractals, namely Sierpiński graphs, by considering cycle, star, and complete graph as a base graph \({\mathcal {H}}\). Moreover, we also calculate the topological indices for Sierpiński-type graphs using M-polynomial. In this article, l represents the order of a base graph \({\mathcal {H}}\).

Fig. 1
figure 1

Sierpiński graph S(\(C_4,2\))

Full size image

Theorem 3.1

Let \(S(C_l,t)\) be a Sierpiński graph, whose base graph is a cycle graph. Then for \(l\ge 3\) and \(t\ge 2\)

$$\begin{aligned} \begin{aligned} M(S(C_l,t);x,y)&=(l-4)l^{t-1}x^2y^2+4l(l-1)^{t-2}x^2y^3\\&\quad +\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{l-1}\right) x^3y^3\\ \end{aligned} \end{aligned}$$

Proof

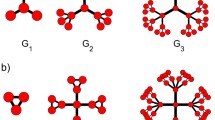
Let \(S(C_l,t)\) be a Sierpiński graph, whose base graph is a cycle graph. Then from Fig. 1, we have

$$\begin{aligned} \begin{aligned} |V(S(C_l,t))|&=l^t\\ |E(S(C_l,t))|&=\frac{l^{t+1}}{l-1} \end{aligned} \end{aligned}$$

Since, type of edges of \(S(C_l,t)\) w.r.t end vertices are

$$\begin{aligned} \begin{aligned} (2,2)&=(l-4)l^{t-1}=|E_1|\\ (2,3)&=4l(l-1)^{t-2}=|E_2|\\ (3,3)&=\frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{l-1}=|E_3|\\ \end{aligned} \end{aligned}$$

Hence, the M-polynomial of \(S(C_k,t)\) is computed as

$$\begin{aligned} \begin{aligned} M(S(C_l,t);x,y)&=\sum _{c\le d}n_{cd}(S(C_l,t))x^cy^d\\&=\sum _{uv\in E_{1}}n_{22}(S(C_l,t))x^2y^2 +\sum _{uv\in E_{2}}n_{23}(S(C_l,t))x^2y^3\\&\quad +\sum _{uv\in E_{3}}n_{33}(S(C_l,t))x^3y^3\\&= |E_{1}|x^2y^2+|E_{2}|x^2y^3+|E_{3}|x^3y^3 \\ M(S(C_l,t);x,y)&=(l-4)l^{t-1}x^2y^2+4l(l-1)^{t-2}x^2y^3\\&\quad +\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{l-1}\right) x^3y^3 \end{aligned} \end{aligned}$$

\(\square \)

Corollary 3.2

Let \(S(C_l,t)\) be a Sierpiński graph, whose base graph is a cycle graph. Then for \(l\ge 3\) and \(t\ge 2\)

$$\begin{aligned} \begin{aligned} M_{1}(S(C_l,t))&=\frac{4l^{t+1}+10l^t-4n(l-1)^{t-1}-8l^{t-1}-6l}{l-1} \\ M_{2}(S(C_l,t))&=\frac{4l^{t+1}+25l^t-12l(l-1)^{t-1}-20l^{t-1}-9l}{l-1} \\ M_{2}^{m}(S(C_l,t))&=\frac{9l^{t+1}-25l^t+8l(l-1)^{t-1}+20l^{t-1}-4l}{36(l-1)} \\ R_{\alpha }(S(C_l,t))&=\frac{1}{l-1}\bigg [2^{2\alpha }l^{t+1}+5(3^{2\alpha }-2^{2\alpha })l^t+4l(3^{\alpha }\cdot 2^{\alpha }-3^{2\alpha })(l-1)^{t-1}\\&\quad +4(2^{2\alpha }-3^{2\alpha })l^{t-1}-3^{2\alpha }l\bigg ] \\ RR_{\alpha }(S(C_l,t))&=\frac{1}{l-1}\bigg [\frac{1}{2^\alpha }l^{t+1}+5 \left( \frac{1}{3^{2\alpha }}-\frac{1}{2^{2\alpha }}\right) l^t+4 \left( \frac{1}{2^{2\alpha }}-\frac{1}{3^{2\alpha }}\right) l^{t-1}\\&\quad +4n \left( \frac{1}{3^{\alpha }\cdot 2^{\alpha }}-\frac{1}{3^{2\alpha }}\right) (l-1)^{t-1}-\frac{l}{3^{2\alpha }}\bigg ] \\ SSD(S(C_l,t))&=\frac{6l^{t+1}+2l(l-1)^{t-1}-6l}{3(l-1)} \\ H(S(C_l,t))&=\frac{20l^{t+1}-50l^t+40l^{t-1}+8n(l-1)^{t-1}-10l}{60(l-1)} \\ I(S(C_l,t))&=\frac{10l^{t+1}+25l^t-20l^{t-1}-12n(l-1)^{t-1}-15l}{(l-1)} \end{aligned} \end{aligned}$$

Proof

Since, the M-polynomial of cycle based Sierpiński graph is

$$\begin{aligned} \begin{aligned} M(S(C_l,t);x,y)&=(l-4)l^{t-1}x^2y^2+4l(l-1)^{t-2}x^2y^3\\&\quad +\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{l-1}\right) x^3y^3\\ \end{aligned} \end{aligned}$$

Then, for the derivation of different topological invariants, first we have to calculate the derivative, integral and combination of both operators of M-polynomial of cycle based Sierpiński network, which are as follows:

$$\begin{aligned} D_x(M(S(C_l,t);x,y))= & {} 2(l-4)l^{t-1}x^2y^2+8l(l-1)^{t-2}x^2y^3\\{} & {} +\left( \frac{15l^t-12l(l-1)^{t-1}-12l^{t-1}-3l}{l-1}\right) x^3y^3\\ D_y(M(S(C_l,t);x,y))= & {} 2(l-4)l^{t-1}x^2y^2+12l(l-1)^{t-2}x^2y^3\\{} & {} +\left( \frac{15l^t-12l(l-1)^{t-1}-12l^{t-1}-3l}{l-1}\right) x^3y^3\\ D_y D_x(M(S(C_l,t);x,y))= & {} 4(l-4)l^{t-1}x^2y^2+24l(l-1)^{t-2}x^2y^3\\{} & {} +\left( \frac{45l^t-36l(l-1)^{t-1}-36l^{t-1}-9l}{l-1}\right) x^3y^3\\ S_x(M(S(C_l,t);x,y)){} & {} =\frac{1}{2}(l-4)l^{t-1}x^2y^2+2l(l-1)^{t-2}x^2y^3\\{} & {} +\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-k}{3(l-1)}\right) x^3y^3\\ S_y(M(S(C_l,t);x,y))= & {} \frac{1}{2}(l-4)l^{t-1}x^2y^2+\frac{4}{3}l(l-1)^{t-2}x^2y^3\\{} & {} +\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{3(l-1)}\right) x^3y^3\\ S_x S_y(M(S(C_l,t);x,y))= & {} \frac{1}{4}(l-4)l^{t-1}x^2y^2+\frac{2}{3}k(l-1)^{t-2}x^2y^3\\{} & {} +\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{3(l-1)}\right) x^3y^3\\ D_{x}^{\alpha }D_{y}^{\alpha }(M(S(C_l,t);x,y))= & {} 2^{2\alpha }(l-4)l^{t-1}x^2y^2+3^\alpha \cdot 2^{\alpha +2}l(l-1)^{t-1}x^2y^3\\{} & {} +3^{2\alpha }\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{l-1}\right) x^3y^3\\ S_{x}^{\alpha }S_{y}^{\alpha }(M(S(C_l,t);x,y))= & {} \frac{1}{2^{2\alpha }}(l-4)l^{t-1}x^2y^2+\frac{1}{3^\alpha \cdot 2^{\alpha -2}}k(l-1)^{t-1}x^2y^3\\{} & {} +\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{3^{2\alpha }(l-1)}\right) x^3y^3\\ S_y D_x(M(S(C_l,t);x,y))= & {} (l-4)l^{t-1}x^2y^2+\frac{8}{3}k(l-1)^{t-2}x^2y^3\\{} & {} +\left( \frac{5l^t-4l(l-1)^{t-1}-4l^{t-1}-l}{(l-1)}\right) x^3y^3\\ S_x D_y(M(S(C_l,t);x,y))= & {} (l-4)l^{t-1}x^2y^2+6l(l-1)^{t-2}x^2y^3\\{} & {} +\left( \frac{5l^t-4n(l-1)^{t-1}-4l^{t-1}-l}{(l-1)}\right) x^3y^3\\ S_x J(M(S(C_l,t);x,y))= & {} \frac{1}{4}(l-4)l^{t-1}x^4+\frac{1}{5}4l(l-1)^{t-2}x^5\\{} & {} +\left( \frac{5l^t-4n(l-1)^{t-1}-4l^{t-1}-k}{6(l-1)}\right) x^6\\ S_x J D_x D_y(M(S(C_l,t);x,y))= & {} (l-4)l^{t-1}x^4+\frac{24}{5}l(l-1)^{t-2}x^5\\{} & {} +\left( \frac{15l^t-12l(l-1)^{t-1}-12l^{t-1}-3l}{2(l-1)}\right) x^6\\ \end{aligned}$$

Now, we will calculate the different topological invariants by applying algebraic operations on above operators

1. First Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{1}(S(C_l,t))&=(D_x+D_y) M(S(C_l,t);x,y)\mid _{x=y=1}\\&=\frac{4l^{t+1}+10l^t-4l(l-1)^{t-1}-8l^{t-1}-6l}{l-1} \end{aligned} \end{aligned}$$

2. Second Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{2}(S(C_l,t))&= (D_yD_x )M(S(C_l,t);x,y)\mid _{x=y=1}\\&=\frac{4l^{t+1}+25l^t-12l(l-1)^{t-1}-20l^{t-1}-9l}{l-1} \end{aligned} \end{aligned}$$

3. Modified Second Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{2}^{m}(S(C_l,t))&=(S_xS_y) M(S(C_l,t);x,y)\mid _{x=y=1}\\&=\frac{9l^{t+1}-25l^t+8l(l-1)^{t-1}+20l^{t-1}-4l}{36(l-1)} \end{aligned} \end{aligned}$$

4. Generalized Randic Index:

$$\begin{aligned} \begin{aligned} R_{\alpha }(S(C_l,t))&=(D_{x}^\alpha D_{y}^\alpha ) M(S(C_l,t);x,y)\mid _{x=y=1}\\&=\frac{1}{l-1}\bigg [2^{2\alpha }l^{t+1}+5(3^{2\alpha }-2^{2\alpha })l^t+4l(3^{\alpha }\cdot 2^{\alpha }-3^{2\alpha })(l-1)^{t-1}\\ {}&\quad +4(2^{2\alpha }-3^{2\alpha })l^{t-1}-3^{2\alpha }l\bigg ] \\ \end{aligned} \end{aligned}$$

5. Inverse Randic Index:

$$\begin{aligned} \begin{aligned} RR_{\alpha }(S(C_l,t))&=(S_{x}^\alpha S_{y}^\alpha ) M(S(C_l,t);x,y)\mid _{x=y=1}\\ {}&=\frac{1}{l-1}\bigg [\frac{1}{2^\alpha }l^{t+1}+5 \left( \frac{1}{3^{2\alpha }}-\frac{1}{2^{2\alpha }}\right) l^t+4 \left( \frac{1}{2^{2\alpha }}-\frac{1}{3^{2\alpha }}\right) l^{t-1}\\&\quad +4l \left( \frac{1}{3^{\alpha }\cdot 2^{\alpha }}-\frac{1}{3^{2\alpha }}\right) (l-1)^{t-1}-\frac{l}{3^{2\alpha }}\bigg ] \\ \end{aligned} \end{aligned}$$

6. Symmetric Division Deg Index:

$$\begin{aligned} \begin{aligned} SSD(S(C_l,t))&=(S_yD_x+S-xD_y) M(S(C_l,t);x,y)\mid _{x=y=1}\\&=\frac{6l^{t+1}+2l(l-1)^{t-1}-6l}{3(l-1)} \end{aligned} \end{aligned}$$

7. Harmonic Index:

$$\begin{aligned} \begin{aligned} H(S(C_l,t))&=2S_xJ (M(S(C_l,t);x,y))\mid _{x=1}\\&=\frac{20l^{t+1}-50l^t+40l^{t-1}+8l(l-1)^{t-1}-10l}{60(l-1)} \end{aligned} \end{aligned}$$

8. Inverse Sum Indeg Index:

$$\begin{aligned} \begin{aligned} I(S(C_l,t))&=2S_xJD_xD_y (M(S(C_l,t);x,y))\mid _{x=1}\\&= \frac{10l^{t+1}+25l^t-20l^{t-1}-12l(l-1)^{t-1}-15l}{(l-1)} \end{aligned} \end{aligned}$$

\(\square \)

Table 2 Topological indices of cycle based Sierpiński graph for distinct values of [l, t]
Full size table
Fig. 2
figure 2

Some topological indices of cycle based Sierpiński graph

Full size image

Figure 2 shows that all the topological indices increased gradually with the increase of values of l and t.

Fig. 3
figure 3

Sierpiński graph S(\(S_5,2\))

Full size image

Theorem 3.3

Let \(S(S_l,t)\) be a Sierpiński graph, whose base graph is a star graph. Then for \(l\ge 3\) and \(t\ge 2\)

$$\begin{aligned} M(S(S_l,t);x,y)&=((l-2)l^{t-1}+1)x^1y^l+(2l^{t-1}-l-1)x^2y^l+(l-1)x^2y^{l-1}x^2y^{l-1} \end{aligned}$$

Proof

Let \(S(S_l,t)\) be a Sierpiński graph, whose base graph is a star graph. Then from Fig. 3, we have

$$\begin{aligned} \begin{aligned} |V(S(S_l,t))|&=l^t\\ |E(S(S_l,t))|&=l^t-1\\ \end{aligned} \end{aligned}$$

Since, the type of edges of \(S(S_l,t)\) w.r.t end vertices are

$$\begin{aligned} \begin{aligned} (1,l)&=(l-2)l^{t-1}+1=|E_1|\\ (2,l)&=2l^{t-1}-l-1=|E_2|\\ (2,l-1)&=l-1=|E_3|\\ \end{aligned} \end{aligned}$$

Hence, the M-polynomial of \(S(S_l,t)\) is

$$\begin{aligned} \begin{aligned} M(S(S_l,t);x,y)&=\sum _{c\le d}n_{cd}(S(S_l,t))x^cy^d\\ M(S(S_l,t);x,y)&=\sum _{uv\in E_{1}}n_{1l}(S(S_l,t))x^1y^l +\sum _{uv\in E_{2}}n_{2l}(S(S_l,t))x^2y^l\\&\quad +\sum _{uv\in E_{3}}n_{2(l-1)}(S(S_l,t))x^2y^{l-1}\\ M(S(S_l,t);x,y)&= |E_{1}|x^1y^l+|E_{2}|x^2y^l+|E_{3}|x^2y^{l-1}\\ M(S(S_l,t);x,y)&=((l-2)l^{t-1}+1)x^1y^l+(2l^{t-1}-l-1)x^2y^l+(l-1)x^2y^{l-1} \end{aligned} \end{aligned}$$

\(\square \)

Corollary 3.4

Let \(S(S_l,t)\) be a Sierpiński graph, whose base graph is a star graph. Then for \(l\ge 3\) and \(t\ge 2\)

$$\begin{aligned} \begin{aligned} M_{1}(S(S_l,t))&=l^{t+1}+l^t+2l^{t-1}-2l-2 \\ M_{2}(S(S_l,t))&=l^{t+1}+2l^t-5l+2\\ M_{2}^{m}(S(S_l,t))&=\frac{2l^t-2l^{t-1}+1}{2l} \\ R_{\alpha }(S(S_l,t))&=(l-2-2^{\alpha +1})l^\alpha l^{t-1}+(1-2^\alpha l- 2^\alpha )l^\alpha +(l-1)^{\alpha +1}2^\alpha \\ RR_{\alpha }(S(S_l,t))&=\frac{1}{l^\alpha }(l^t-2l^{t-1}+1)+ \frac{1}{2^\alpha \cdot (l-1)^{\alpha -1}} +\frac{1}{2^\alpha \cdot l^\alpha }(2l^{t-1}-l-1)\\ SSD(S(S_l,t))&=\frac{2l^{t+3}-4l^{t+2}+4l^{t+1}-4l^t+8l^{t-1}+l^3-l^2+3l-4}{2l} \\ H(S(S_l,t))&=\frac{l^{t+1}+2l^t-2l^{t-1}-1}{(1+l)(2+l)} \\ I(S(S_l,t))&=\frac{2l^{t+2}+4l^{t}-4l^{t-1}-2}{(1+l)(2+l)}\\ \end{aligned} \end{aligned}$$

Proof

Since, the M-polynomial of star based Sierpiński network is

$$\begin{aligned} \begin{aligned} M(S(S_l,t);x,y)&=((l-2)l^{t-1}+1)x^1y^l+(2l^{t-1}-l-1)x^2y^l+(l-1)x^2y^{l-1} \end{aligned} \end{aligned}$$

Then, for the derivation of different topological invariants, first we have to calculate the derivative, integral and combination of both operators of M-polynomial of star based Sierpiński network, which are as follows:

$$\begin{aligned} D_x(M(S(S_l,t);x,y))= & {} ((l-2)l^{t-1}+1)x^1y^l+2(2l^{t-1}-l-1)x^2y^l+2(l-1)x^2y^{l-1}\\ D_y(M(S(S_l,t);x,y))= & {} l((l-2)l^{t-1}+1)x^1y^l+l(2l^{t-1}-l-1)x^2y^l+(l-1)x^2y^{l-1}\\ D_y D_x(M(S(S_l,t);x,y))= & {} l((l-2)l^{t-1}+1)x^1y^l+2l(2l^{t-1}-l-1)x^2y^l+2(l-1)x^2y^{l-1}\\ S_x(M(S(S_l,t);x,y))= & {} ((l-2)l^{t-1}+1)x^1y^l+\frac{1}{2}(2l^{t-1}-l-1)x^2y^l+\frac{1}{2}(l-1)x^2y^{l-1}\\ S_y(M(S(S_l,t);x,y))= & {} \frac{1}{l}((l-2)l^{t-1}+1)x^1y^l+\frac{1}{l}(2l^{t-1}-l-1)x^2y^l+x^2y^{l-1}\\ S_xS_y(M(S(S_l,t);x,y))= & {} \frac{1}{l}((l-2)l^{t-1}+1)x^1y^l+\frac{1}{2l}(2l^{t-1}-l-1)x^2y^l+\frac{1}{2}x^2y^{l-1}\\ D_{x}^{\alpha }D_{y}^{\alpha }(M(S(S_l,t);x,y))= & {} l^{\alpha }((l-2)l^{t-1}+1)x^1y^l+l^\alpha \cdot 2^{\alpha }(2l^{t-1}-l-1)x^2y^l\\{} & {} +2^{\alpha }\cdot (l-1)^\alpha (l-1)x^2y^{l-1}\\ S_{x}^{\alpha }S_{y}^{\alpha }(M(S(S_l,t);x,y))= & {} \frac{1}{l^\alpha }((l-2)l^{t-1}+1)x^1y^l+\frac{1}{2^\alpha \cdot l^\alpha }(2l^{t-1}-l-1)x^2y^l+\frac{l-1}{2^\alpha \cdot (l-1)^\alpha }x^2y^{l-1}\\ S_y D_x(M(S(S_l,t);x,y))= & {} \frac{1}{l}((l-2)l^{t-1}+1)x^1y^l+\frac{1}{k}(2l^{t-1}-l-1)x^2y^l+2x^2y^{l-1}\\ S_x D_y(M(S(S_l,t);x,y))= & {} l((l-2)l^{t-1}+1)x^1y^l+\frac{l}{2}(2l^{t-1}-l-1)x^2y^l+\frac{(l-1)^2}{2}x^2y^{l-1}\\ S_x J(M(S(S_l,t);x,y))= & {} \frac{1}{(1+l)}((l-2)l^{t-1}+l)x^{1+l}+\frac{1}{(2+l)}(2l^{t-1}-l-1)x^{2+l}\\ S_x J D_x D_y(M(S(S_l,t);x,y))= & {} \frac{1}{(1+l)}((l-2)l^{t}+l+2(l-1)^2)x^{1+l}+\frac{1}{(2+l)}(4l^t-2l^2-2l)x^{2+l} \end{aligned}$$

Now, we will calculate the different topological invariants by applying algebraic operations on above operators

1. First Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{1}(S(S_l,t))&=(D_x+D_y) M(S(S_l,t);x,y)\mid _{x=y=1}\\&= l^{t+1}+l^t+2l^{t-1}-2l-2 \\ \end{aligned} \end{aligned}$$

2. Second Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{2}(S(S_l,t))&=(D_yD_x) M(S(S_l,t);x,y)\mid _{x=y=1}\\&= l^{t+1}+2l^t-5l+2\\ \end{aligned} \end{aligned}$$

3. Modified Second Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{2}^{m}(S(S_l,t))&=(S_xS_y) M(S(S_l,t);x,y)\mid _{x=y=1}\\&=\frac{2l^t-2l^{t-1}+1}{2l} \\ \end{aligned} \end{aligned}$$

4. Generalized Randic Index:

$$\begin{aligned} \begin{aligned} R_{\alpha }(S(S_l,t))&=(D_{x}^\alpha D_{y}^\alpha ) M(S(S_l,t);x,y)\mid _{x=y=1}\\&=(l-2-2^{\alpha +1})l^\alpha l^{t-1}+(1-2^\alpha l- 2^\alpha )l^\alpha +(l-1)^{\alpha +1}2^\alpha \\ \end{aligned} \end{aligned}$$

5. Inverse Randic Index:

$$\begin{aligned} \begin{aligned} RR_{\alpha }(S(S_l,t))&=(S_{x}^\alpha S_{y}^\alpha ) M(S(S_l,t);x,y)\mid _{x=y=1}\\&=\frac{1}{l^\alpha }(l^t-2l^{t-1}+1)+ \frac{1}{2^\alpha \cdot (l-1)^{\alpha -1}}+\frac{1}{2^\alpha \cdot l^\alpha }(2l^{t-1}-l-1)\\ \end{aligned} \end{aligned}$$

6. Symmetric Division Deg Index:

$$\begin{aligned} \begin{aligned} SSD(S(S_l,t))&=(S_yD_x+S-xD_y) M(S(S_l,t);x,y)\mid _{x=y=1}\\&=\frac{2l^{t+3}-4l^{t+2}+4l^{t+1}-4l^t+8l^{t-1}+l^3-l^2+3l-4}{2l} \\ \end{aligned} \end{aligned}$$

7. Harmonic Index:

$$\begin{aligned} \begin{aligned} H(S(S_l,t))&=2S_xJ M(S(S_l,t);x,y))\mid _{x=1}\\&=\frac{l^{t+1}+2l^t-2l^{t-1}-1}{(1+l)(2+l)} \\ \end{aligned} \end{aligned}$$

8. Inverse Sum Indeg Index:

$$\begin{aligned} \begin{aligned} I(S(S_l,t))&=2S_xJD_xD_y M(S(S_l,t);x,y))))\mid _{x=1}\\&= \frac{2l^{t+2}+4l^{t}-4l^{t-1}-2}{(1+l)(2+l)}\\ \end{aligned} \end{aligned}$$

\(\square \)

Table 3 Topological indices of star based Sierpiński graph for various values of [l, t]
Full size table
Fig. 4
figure 4

Some topological indices of star based Sierpiński graph

Full size image

Figure 4 shows that all the topological indices increased with the increase of values of l and t.

Fig. 5
figure 5

Sierpiński graph S(\(K_4,2\))

Full size image

Theorem 3.5

Let \(S(K_l,t)\) be a Sierpiński graph, whose base graph is a complete graph. Then for \(l\ge 3\) and \(t\ge 2\)

$$\begin{aligned} M(S(K_l,t);x,y)&=l(l-1)x^{l-1}y^l+\left( \frac{l^{t+1}-2l^2+l}{2}\right) x^ly^l \end{aligned}$$

Proof

Let \(S(K_l,t)\) be a Sierpiński graph, whose base graph is a complete graph. Then from Fig. 5, we have

$$\begin{aligned} \begin{aligned} |V(S(K_l,t))|&=l^t\\ |E(S(K_l,t))|&=\frac{l^{t+1}-t}{2}\\ \end{aligned} \end{aligned}$$

Since, the type of edges of \(S(K_l,t)\) w.r.t end vertices are

$$\begin{aligned} \begin{aligned} (l-1,l)&=k(l-1)=|E_1|\\ (l,l)&=\frac{l^{t+1}-2l^2+l}{2}=|E_1| \end{aligned} \end{aligned}$$

Hence, the M-polynomial of \(S(K_l,t)\) is computed as

$$\begin{aligned} \begin{aligned} M(S(K_l,t);x,y)&=\sum _{c\le d}n_{cd}(S(K_l,t))x^cy^d\\&=\sum _{uv\in E_{1)}}n_{(l-1)l}(S(K_l,t))x^{l-1}y^l+\sum _{uv\in E_{2}}n_{ll}(S(K_l,t))x^ly^l\\&= |E_{1}|x^{l-1}y^l+|E_{2}|x^ly^l\\ M(S(K_l,t);x,y)&=l(l-1)x^{l-1}y^l+\left( \frac{l^{t+1}-2l^2+l}{2}\right) x^ly^l\\ \end{aligned} \end{aligned}$$

\(\square \)

Corollary 3.6

Let \(S(K_l,t)\) be a Sierpiński graph, whose base graph is a complete graph. Then for \(l\ge 3\) and \(t\ge 2\)

$$\begin{aligned} \begin{aligned} M_{1}(S(K_l,t))&=l^{t+2}-2l^2+l\\ M_{2}(S(K_l,t))&=\frac{l^{t+3}-3l^3+2l^2}{2}\\ M_{2}^{m}(S(K_l,t))&=\frac{l^{t+1}+1}{2l} \\ R_{\alpha }(S(K_l,t))&=\frac{2l^{\alpha +1}(l-1)^{\alpha +1}+l^{2\alpha }(l^{t+1}-2l^2+l )}{2} \\ RR_{\alpha }(S(K_l,t))&=\frac{1}{l^{\alpha -1}(l-1)^{\alpha -1}}+\frac{1}{2l^{2\alpha }}(l^{t+1}-2l^2+l)\\ SSD(S(K_l,t))&=l^{t+1}-l+1 \\ H(S(K_l,t))&=\frac{2l^{t+1}-l^t-1}{8l-4}\\ I(S(K_l,t))&=\frac{2l^{t+3}-l^{t+2}-4l^3+3l^2}{8l-4}\\ \end{aligned} \end{aligned}$$

Proof

Since, the M-polynomial of complete based Sierpiński network is

$$\begin{aligned} \begin{aligned} M(S(K_l,t);x,y)&=l(l-1)x^{l-1}y^l+\frac{l^{t+1}-2l^2+l}{2}x^ly^l \end{aligned} \end{aligned}$$

Then, for the derivation of different topological invariants, first we have to calculate the derivative, integral and combination of both operators of M-polynomial of cycle based Sierpiński network, which are as follows:

$$\begin{aligned} \begin{aligned} D_x(M(S(K_l,t);x,y))&=l(l-1)^2x^{l-1}y^l+\left( \frac{l^{t+2}-2l^3+l^2}{2}\right) x^ly^l\\\\ D_y(M(S(K_l,t);x,y))&=l^2(l-1)x^{l-1}y^l+\left( \frac{l^{t+2}-2l^3+l^2}{2}\right) x^ly^l\\\\ D_y D_x(M(S(K_l,t);x,y))&=l^2(l-1)^2x^{l-1}y^l+\left( \frac{l^{t+3}-2l^4+l^3}{2}\right) x^ly^l\\\\ S_x(M(S(K_l,t);x,y))&=lx^{l-1}y^l+\left( \frac{l^{t}-2l+1}{2}\right) x^ly^l\\\\ S_y(M(S(K_l,t);x,y))&=(l-1)x^{l-1}y^l+\left( \frac{l^{t}-2l+1}{2}\right) x^ly^l\\\\ S_x S_y(M(S(K_l,t);x,y))&=x^{l-1}y^l+\left( \frac{l^{t}-2l+1}{2l}\right) x^ly^l\\\\ D_{x}^{\alpha }D_{y}^{\alpha }(M(S(K_l,t);x,y))&=l^{\alpha +1}(l-1)^{\alpha +1}x^{l-1}y^l+l^{2\alpha } \left( \frac{l^{t+1}-2l^2+l}{2}\right) x^ly^l \end{aligned} \\ \begin{aligned} S_{x}^{\alpha }S_{y}^{\alpha }(M(S(K_l,t);x,y))&=\frac{1}{l^{\alpha +1}(l-1)^{\alpha -1}}x^{l-1}y^l+ \left( \frac{l^{t+1}-2l^2+l}{2l^{2\alpha }}\right) x^ly^l\\\\ S_y D_x(M(S(K_l,t);x,y))&=(l-1)^2x^{l-1}y^l+\left( \frac{l^{t+1}-2l^2+l}{2}\right) x^ly^l\\\\ S_x D_y(M(S(K_l,t);x,y))&=l^2x^{l-1}y^l+\left( \frac{l^{t+1}-2l^2+l}{2}\right) x^ly^l\\\\ S_x J(M(S(K_l,t);x,y))&=\frac{1}{(2l-1)}((l^2-l)x^{2l-1}+\left( \frac{l^{t+1}-2l^2+l}{4l}\right) x^{2l}\\\\ S_x J D_x D_y(M(S(K_l,t);x,y))&=\frac{1}{(2l-1)}((l^2(l-1)^2)x^{2l-1}+\left( \frac{l^{t+3}-2l^4+l^3}{4l}\right) x^{2l}\\ \end{aligned} \end{aligned}$$

Now, we will calculate the different topological invariants for complete based Sierpiński graph by applying algebraic operations on above operators

1. First Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{1}(S(K_l,t))&=(D_x+D_y) M(S(K_l,t);x,y)\mid _{x=y=1}\\&= l^{t+2}-2l^2+l\\ \end{aligned} \end{aligned}$$

2. Second Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{2}(S(K_l,t))&=(D_yD_x) M(S(K_l,t);x,y)\mid _{x=y=1}\\&= \frac{l^{t+3}-3l^3+2l^2}{2}\\ \end{aligned} \end{aligned}$$

3. Modified Second Zagreb Index:

$$\begin{aligned} \begin{aligned} M_{2}^{m}(S(K_l,t))&=(S_xS_y) M(S(K_l,t);x,y)\mid _{x=y=1}\\&=\frac{l^{t+1}+1}{2l} \\ \end{aligned} \end{aligned}$$

4. Generalized Randic Index:

$$\begin{aligned} \begin{aligned} R_{\alpha }(S(K_l,t))&=(D_{x}^\alpha D_{y}^\alpha ) M(S(K_l,t);x,y)\mid _{x=y=1}\\&=\frac{2l^{\alpha +1}(l-1)^{\alpha +1}+l^{2\alpha }(l^{t+1}-2l^2+l)}{2} \\ \end{aligned} \end{aligned}$$

5. Inverse Randic Index:

$$\begin{aligned} \begin{aligned} RR_{\alpha }(S(K_l,t))&=(S_{x}^\alpha S_{y}^\alpha ) M(S(K_l,t);x,y)\mid _{x=y=1}\\&=\frac{1}{l^{\alpha -1}(l-1)^{\alpha -1}}+\frac{1}{2l^{2\alpha }}(l^{t+1}-2l^2+l)\\ \end{aligned} \end{aligned}$$

6. Symmetric Division Deg Index:

$$\begin{aligned} \begin{aligned} SSD(S(K_l,t))&=(S_yD_x+S-xD_y) M(S(K_l,t);x,y)\mid _{x=y=1}\\&=l^{t+1}-l+1 \\ \end{aligned} \end{aligned}$$

7. Harmonic Index:

$$\begin{aligned} \begin{aligned} H(S(K_l,t))&=2S_xJ M(S(K_l,t);x,y))\mid _{x=1}\\&=\frac{2l^{t+1}-l^t-1}{8l-4}\\ \end{aligned} \end{aligned}$$

8. Inverse Sum Indeg Index:

$$\begin{aligned} \begin{aligned} I(S(K_l,t))&=2S_xJD_xD_y M(S(K_l,t);x,y))))\mid _{x=1}\\&= \frac{2l^{t+3}-l^{t+2}-4l^3+3l^2}{8l-4}\\ \end{aligned} \end{aligned}$$

\(\square \)

Table 4 Topological indices of complete based Sierpiński graph for distinct values of [l, t]
Full size table
Fig. 6
figure 6

Some topological indices of complete based Sierpiński graph

Full size image

Figure 6 shows that all the topological indices increased with the increase of values of l and t.

4 Conclusion

In this study, firstly, we obtained the M-polynomials of Sierpiński-type networks using cycle, star, and complete network as a base structure. Topological descriptors make it simpler and more accurate to identify these networks’ physical characteristics, chemical reactivity, and biological activities. Therefore, we calculate the formulae for some degree-related topological invariants, such as the first, second, modified, general, and inverse Randić invariants, symmetric division invariant, harmonic invariants and inverse sum invariant for Sierpiński graphs by using M-polynomial. Moreover, we compare the different topological invariants using a graph.

Future work

The “modified symmetric division deg index" and “harmonic-arithmetic index" are newly introduced invariants presented in [22,23,24]. In our next study, we will obtain these invariants for Sierpiński-type networks and compare them with the “symmetric division deg index" and “harmonic index."