1 Introduction

In recent decades, fractional calculus (FC) has played a significant role in science and engineering, and therefore, the scientists focused on its applications to model the real phenomena [2, 23, 24, 29]. The fractional derivative and integrals were recognized to be an efficient tool to describe the properties of complex dynamical processes more accurately than the standard integer derivative and integral [14, 17, 21, 27, 38]. Fractional partial differential equations (FPDEs) are a fascinating subject, because they are frequently used to explain a variety of phenomena in real-world situations, including signal processing control theory, fluid flow, potential theory, information theory, finance, and entropy [7, 9, 25, 32].

Samko in 1993 [29] introduces the VOFDEs. These fractional operators can be considered as a generalization of fractional operators of constant orders. Indeed, the variable-order FPDEs extend the fractional fixed-order PDEs and occur in problems in the areas of physics and engineering [11, 12, 26, 32, 34].

Many models of specific processes or dynamical systems in real-world problems exhibit neutral delay, which is always described using delay differential equations (DDEs) or time-delay systems [6, 18, 35]. Despite the fact that FPDEs have been considered by a few researchers [16, 22, 37] and the references therein, there has been no work done in the area of VFDPDEs to our knowledge. Therefore, this reason motivates us in this paper to propose a numerical technique to solve a class of VFDDEs using the collocation method and the OMs of the shifted Legendre–Laguerre polynomials.

A considerable advantage of the method is that the shifted Legendre–Laguerre polynomial coefficients of the solution are found very easily using computer programs. Also, according to the proposed model, the time of the occurrence of an event does not have fix domain. Therefore, for approximating the time functions in the problem, we apply the Laguerre polynomials, which defined in \([0,\infty ).\)

Finally, using a few terms of shifted Legendre–Laguerre functions, approximate solution converges to the exact solution.

2 Preliminaries

For the continuous function \(\delta :[0,\infty )\rightarrow (0,1)\) and \(m,\beta \in N\cup \{0\}.\) The variable-order fractional derivative and integration definitions, along with some of the fundamental definitions and properties, are introduced in this section and will be used throughout the paper [8, 11, 15, 31, 36].

Definition 2.1

The Riemann–Liouville variable-order fractional integral operator with order \(n-1<\delta ({\xi },{\tau })\le n,~ {\tau }>0\)  of \(\nu ({\xi },{\tau })\)  is defined as

$$\begin{aligned} I_{{\tau }}^{\delta ({\xi },{\tau })} \nu (\xi ,\tau )=\frac{1}{\Gamma (\delta (\xi ,\tau ))}\int _{0}^{\tau }(\tau -\rho )^{\delta (\xi ,\tau )}~\nu (\xi ,\rho )~{\text {d}}\rho , \end{aligned}$$
(2.1)

where \(\tau > 0\) and \(\Gamma (.)\) is the Gamma function. According to the above definition, variable-order fractional integration satisfies the following property:

$$\begin{aligned} I_{\tau }^{\delta (\xi ,\tau )}~\tau ^\beta =\left\{ \begin{array}{ll} \frac{\Gamma (\beta +1)}{\Gamma (\beta +\delta (\xi ,\tau )+1)}\tau ^{\beta + \delta (\xi ,\tau )},&{} \beta >-1\\ {0},&{} {\text {otherwise}}. \end{array} \right. \end{aligned}$$
(2.2)

Definition 2.2

[13] The fractional derivative of  \(\nu (\xi , \tau )\)  in the Caputo experience is described as

$$\begin{aligned} \begin{aligned} _{0}D_{\tau }^{\delta (\xi ,\tau )}\nu (\xi ,\tau )&=I_{\tau }^{n-\delta (\xi ,\tau )}~D_{\tau }^{n}~\nu (\xi ,\tau )\\&=\frac{1}{\Gamma (n-\delta (\xi ,\tau ))}~\int _{0}^{\tau }(\tau -\rho )^{n-\delta (\xi ,\tau )-1}~\frac{\partial ^{n} \nu (\xi ,\rho )}{\partial \rho ^{n}}~{\text {d}}\rho , \end{aligned} \end{aligned}$$
(2.3)

for  \(n-1<\delta (\xi ,\tau )\le n,~\tau >0,\) and \(n\in Z^{+}.\) It has the taking after valuable property

$$\begin{aligned} _{0}D_{\tau }^{\delta (\xi ,\tau )}~\tau ^{m}=\left\{ \begin{array}{ll} \frac{\Gamma (m+1)}{\Gamma (m-\delta (\xi ,\tau )+1)}\tau ^{m-\delta (\xi ,\tau )}, &{}n\le m\in N\\ {0}, &{}{\text {otherwise}}. \end{array} \right. \end{aligned}$$
(2.4)

3 Function approximation

Consider the basis function \(\Phi _{\tilde{m}\tilde{n}}(\xi ,\tau )\) which is two variable function and important to deal with VFDPDEs, and can be expanded as

$$\begin{aligned} \Phi _{\tilde{m}\tilde{n}}(\xi ,\tau )=G_{\tilde{m}}(\xi )~\ell _{\tilde{n}}(\tau ), ~~~(\xi ,\tau )\in \Delta =[0,1]\times [0,\infty ), \end{aligned}$$
(3.1)

where \(\tilde{m}=0,1, \ldots ,\tilde{M},~~~\tilde{n}=0,1, \ldots ,\tilde{N}, G_{\tilde{m}}(\xi )\) is the shifted Legendre polynomials defined on the interval [0, 1] and \( \ell _{n}(\tau )\) is the shifted Laguerre polynomials defined on the interval \([0,\infty )\).

The shifted Legendre–Laguerre polynomials are \(\bot \) w.r.t the weight function \( \Xi (\xi ,\tau )=exp({-\tau })\) in the \(\Delta \), i.e., [3,4,5]

$$\begin{aligned} \int _{0}^{\infty }\int _{0}^{1}\Xi (\xi ,\tau )\Phi _{\tilde{m}\tilde{n}}(\xi ,\tau )\Phi _{ij}(\xi ,\tau )~{\text {d}}\xi {\text {d}}\tau =\frac{1}{2\tilde{m}+1}\delta _{\tilde{m}i}\delta _{\tilde{n}j}, \end{aligned}$$
(3.2)

where  \( \delta _{\tilde{m}i}\)  and \(\delta _{\tilde{n}j}\)  are the Kronecker functions. Any function \(\nu (\xi ,\tau )\in L_{2}(\Omega )\) and may be decomposed as

$$\begin{aligned} \nu (\xi ,\tau )=\sum _{\tilde{m}=0}^{\tilde{M}}\sum _{\tilde{n}=0}^{\tilde{N}}\nu _{\tilde{m}\tilde{n}}\Phi _{\tilde{m}\tilde{n}}(\xi ,\tau )\simeq G^{\text {T}}(\xi )V ~\ell (\tau ), \end{aligned}$$
(3.3)

where

$$\begin{aligned} \nu _{\tilde{m}\tilde{n}}=(2\tilde{m}+1)\int _{0}^{\infty }\int _{0}^{1}\Xi (\xi ,\tau )\nu (\xi ,\tau )\Phi _{\tilde{m}\tilde{n}}(\xi ,\tau ){\text {d}}\xi {\text {d}}\tau \end{aligned}$$
(3.4)

and

$$\begin{aligned} V= & {} \begin{bmatrix} \nu _{00}&{}\nu _{01}&{}\nu _{02}&{}...&{}\nu _{0\tilde{N}}\\ \nu _{10}&{}\nu _{11}&{}\nu _{12}&{}...&{}\nu _{1\tilde{N}}\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ \nu _{\tilde{M}0}&{}\nu _{\tilde{M}1}&{}\nu _{\tilde{M}2}&{}...&{}\nu _{\tilde{M}\tilde{N}}\\ \end{bmatrix},\nonumber \\ G(\xi )= & {} [G_{0}(\xi ),~G_{1}(\xi ),\ldots G_{\tilde{M}}(\xi )]^{\text {T}},~~\ell (\tau )=[\ell _{0}(\tau ),~\ell _{1}(\tau ),\ldots \ell _{\tilde{N}}(\tau )]^{\text {T}}. \end{aligned}$$
(3.5)

4 Pseudo-operational matrix of integer order integral of the shifted Legendre and Laguerre polynomials

The purpose of this section is to find the OMs of the integer order quintessential of SLPs and the (S\(\ell \)Ps), respectively, using Taylor polynomials (TPs) [1, 28, 30], which is described as follows:

$$\begin{aligned} T_{k}(\xi )=\xi ^{k},~~~~k=0,1, \ldots ,M. \end{aligned}$$

The SLPs may be expressed by means of the TPs as

$$\begin{aligned} G(\xi )=D_{1}~T(\xi ), \end{aligned}$$

since

$$\begin{aligned} T(\xi )= & {} [1,\xi ,\xi ^{2},\ldots ,\xi ^{M}]^{\text {T}},~~~~D_{1}=[d_{\imath \jmath }^{1}]_{(M+1)\times (M+1)},\nonumber \\ d_{\imath \jmath }^{1}= & {} \left\{ \begin{array}{ll} \frac{(-1)^{\imath +\jmath }~(\imath +\jmath )!}{(\imath -\jmath )!~(\jmath !)^2}, &{} \imath \ge \jmath \\ {0}, &{}{\text {otherwise}}. \end{array} \right. \end{aligned}$$
(4.1)

Then, by integrating  \( G(\xi )\), the pseudo-operational matrix of the SLPs is obtained

$$\begin{aligned} \begin{aligned} \int _{0}^{\xi }G(\rho )~{\text {d}}\rho&=\int _{0}^{\xi }D_{1}T(\rho ) {\text {d}} \rho =D_{1}\int _{0}^{\xi }T(\rho ) {\text {d}} \rho \\&=\xi D_{1}\Lambda _{1}T(\xi )=\xi D_{1}\Lambda _{1}D_{1}^{-1}G(\xi )=\xi \vartheta _{1}G(\xi ), \end{aligned} \end{aligned}$$

where \(\vartheta _{1}=D_{1}\Lambda _{1}D_{1}^{-1}\) is the pseudo-operational matrix of the integer order integral of the SLPs and\(\Lambda _{1}\) is defined by [10, 20, 33]

$$\begin{aligned} \Lambda _{1}= \begin{bmatrix} 1&{}0&{}0&{}...&{}0\\ 0&{}1/2&{}0&{}...&{}0\\ 0&{}0&{}1/3&{}\ldots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}...&{}1/(M+1)\\ \end{bmatrix}. \end{aligned}$$

Similarly

$$\begin{aligned} \ell (\tau )=D_{2}T(\tau ), \end{aligned}$$
(4.2)

where

$$\begin{aligned} d_{\imath \jmath }^{2}=\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{(-1)^{\imath }~(\imath )!}{(\imath -\jmath )!~(\jmath !)^2},\imath \ge \jmath \\ &{}{0},~~~~~~~~~~~~~~~{\text {otherwise}}. \end{aligned} \end{array} \right. \end{aligned}$$
(4.3)

Also, with the aid of integrating \( \ell (\tau )\), we gain the operational matrix of integer integration of the (S\(\ell \)Ps) as

$$\begin{aligned} \begin{aligned} \int _{0}^{\tau }\ell (\rho )~{\text {d}}\rho&=\int _{0}^{\tau }D_{2}T(\rho ){\text {d}} \rho =D_{2}\int _{0}^{\tau }T(\rho ) {\text {d}}\rho \\&=\tau D_{2}\Lambda _{2}T(\tau )=\tau D_{2}\Lambda _{2}D_{2}^{-1}\ell (\tau )=\tau \vartheta _{2}\ell (\tau ), \end{aligned} \end{aligned}$$

where \(\vartheta _{2}=D_{2}\Lambda _{2}D_{2}^{-1}\) is the pseudo-operational matrix of the integer order integral of the shifted (S\(\ell \)Ps) and \(\Lambda _{2}\) is given by

$$\begin{aligned} \Lambda _{2}= \begin{bmatrix} 1&{}0&{}0&{}...&{}0\\ 0&{}1/2&{}0&{}...&{}0\\ 0&{}0&{}1/3&{}\ldots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}...&{}1/(N+1)\\ \end{bmatrix}. \end{aligned}$$

5 Pseudo-operational matrix of the variable-order fractional integral of the (S\(\ell \)Ps)

To obtain the operational matrix of the variable-order Riemann–Liouville fractional integration of order \(\delta (\xi ,\tau )>0\) of the vector \(\ell (\tau )\) defined in Eq. (3.5), we need to calculate first variable-order Riemann–Liouville fractional integral of the TPs which is written as

$$\begin{aligned} I_{\tau }^{\delta (\xi ,\tau )}~T(\tau )=\tau ^{\delta (\xi ,\tau )}~\gamma _{N}^{\delta (\xi ,\tau )}T(\tau ), \end{aligned}$$
(5.1)

where

$$\begin{aligned} \gamma _{N}^{\delta (\xi ,\tau )}= \begin{bmatrix} \frac{\Gamma (1)}{\Gamma (1+\delta (\xi ,\tau ))}&{}0&{}0&{}...&{}0\\ 0&{}\frac{\Gamma (2)}{\Gamma (2+\delta (\xi ,\tau ))}&{}0&{}...&{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}...&{}\frac{\Gamma (N+1)}{\Gamma (N+1+\delta (\xi ,\tau ))}\\ \end{bmatrix}. \end{aligned}$$

Also, we need to find

$$\begin{aligned} I_{\tau }^{\delta (\xi ,\tau )}~\tau T(\tau )=\tau ^{1+\delta (\xi ,\tau )}~\hat{\gamma }_{N}^{\delta (\xi ,\tau )}T(\tau ), \end{aligned}$$
(5.2)

where

$$\begin{aligned} \hat{\gamma }_{N}^{\delta (\xi ,\tau )}= \begin{bmatrix} \frac{\Gamma (2)}{\Gamma (2+\delta (\xi ,\tau ))}&{}0&{}0&{}...&{}0\\ 0&{}\frac{\Gamma (3)}{\Gamma (3+\delta (\xi ,\tau ))}&{}0&{}...&{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}...&{}\frac{\Gamma (N+2)}{\Gamma (N+2+\delta (\xi ,\tau ))}\\ \end{bmatrix}. \end{aligned}$$

Lemma 5.1

Let \(\ell (\tau )\) be the (S\(\ell \)Ps) vector defined in (3.5) and \(q-1<\delta (\xi ,\tau )\le q \in Z^{+}\) The pseudo-operational matrix of variable-order fractional integration of the vector \(\ell (\tau )\) can be expressed as

$$\begin{aligned} I_{\tau }^{\delta (\xi ,\tau )}\ell (\tau )=\tau ^{\delta (\xi ,\tau )}~\Theta _{N}^{\delta (\xi ,\tau )}T(\tau ), \end{aligned}$$
(5.3)

where \(\Theta _{N}^{\delta (\xi ,\tau )}=D_{2}~\gamma _{N}^{\delta (\xi ,\tau )}~D_{2}^{-1}.\)

Proof

A direct application of the relations (4.2) and (5.1) is given as

$$\begin{aligned} \begin{aligned} I_{\tau }^{\delta (\xi ,\tau )}~\ell (\tau )&=I_{\tau }^{\delta (\xi ,\tau )}D_{2}~T(\tau )=\tau ^{\delta (\xi ,\tau )}D_{2}~\gamma _{N}^{\delta (\xi ,\tau )}T(\tau )\\&=\tau ^{\delta (\xi ,\tau )}~D_{2}~\gamma _{N}^{\delta (\xi ,\tau )}~D_{2}^{-1}~\ell (\tau )\\&=\tau ^{\delta (\xi ,\tau )}~\Theta _{N}^{\delta (\xi ,\tau )}~\ell (\tau ). \end{aligned} \end{aligned}$$

\(\square \)

6 The approach

This section is devoted to finding the numerical solution of the following VFDPDEs:

$$\begin{aligned}{} & {} D_{\tau }^{\delta (\xi ,\tau )}~\nu (\xi ,\tau )-\eta ~\frac{\partial ^{2}\nu (\xi ,\tau )}{\partial ~\xi ^{2}}=f(\tau ,\nu (\xi ,\tau ),\nu (\xi ,\tau -\kappa )),\nonumber \\{} & {} \quad 0\le \xi \le 1, ~~~~ 0< \tau \le \infty \end{aligned}$$
(6.1)

subject to

$$\begin{aligned} \nu (0,\tau )=\nu _{0}(\tau ),~~~~ \nu (1,\tau )=\nu _{1}(\tau ). \end{aligned}$$
(6.2)

and

$$\begin{aligned} \nu (\xi ,0)=g_{0}(\xi ),~~~~~ \frac{\partial \nu (\xi ,0)}{\partial \tau }=g_{1}(\xi ). \end{aligned}$$
(6.3)

So that, \(\nu (\xi ,\tau )\) is an unknown function, the known functions\(~\nu _{0}(\tau ), \nu _{1}(\tau )~,g_{0}(\xi ) ~and ~g_{1}(\xi )\) are given continuous functions. Also, \( q=max_{(\xi ,\tau )\in \Omega }\{\delta (\xi ,\tau )\}~ and~ q\in Z^{+}\).

For this problem, assume that the easiest order of spinoff with appreciate to  \(\xi \) and\(~ \tau \) is 2. Therefore, we obtain the following approximate functions as:

$$\begin{aligned} \frac{\partial ^{4}\nu (\xi ,\tau )}{\partial \xi ^{2}\partial \tau ^{2}}\simeq G^{\text {T}}(\xi ) U \ell (\tau ), \end{aligned}$$
(6.4)

where the unknown matrix  U  is defined as follows:

$$\begin{aligned} U= \begin{bmatrix} u_{00}&{}u_{01}&{}u_{02}&{}...&{}u_{0N}\\ u_{10}&{}u_{11}&{}u_{12}&{}...&{}u_{1N}\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ u_{M0}&{}u_{M1}&{}u_{M2}&{}...&{}u_{MN}\\ \end{bmatrix}. \end{aligned}$$

By integrating of the above equation with (6.4) with respect to \(~\tau \) and using the initial condition (6.3), we have

$$\begin{aligned} \frac{\partial ^{3}\nu (\xi ,\tau )}{\partial \xi ^{2}\partial \tau }\simeq \tau G^{\text {T}}(\xi ) U \vartheta _{2} \ell (\tau )+\acute{\acute{g_{1}}}(\xi ). \end{aligned}$$
(6.5)

Integrating (6.5) with respect to \(\tau \) yields

$$\begin{aligned} \frac{\partial ^{2}\nu (\xi ,\tau )}{\partial \xi ^{2}}\simeq \tau ^{2} G^{\text {T}}(\xi ) U \vartheta _{2} \hat{\vartheta _{2}}\ell (\tau )+\tau \acute{\acute{g_{1}}}(\xi )+\acute{\acute{g_{0}}}(\xi ), \end{aligned}$$
(6.6)

where

$$\begin{aligned} \begin{aligned} \int _{0}^{\tau } \rho L(\rho ) d\rho&=\int _{0}^{\tau }\rho D_{2} T(\rho ) d\rho =D_{2}\int _{0}^{\tau }\rho T(\rho ) d\rho \\&=\tau ^{2}D_{2}\hat{\Lambda _{2}}T(\tau )=\tau ^{2} D_{2} \hat{\Lambda _{2}} D_{2}^{-1} \ell (\tau )= \tau ^{2} \hat{\vartheta _{2}}\ell (\tau ), \end{aligned} \end{aligned}$$
(6.7)

and

$$\begin{aligned} \hat{\Lambda }_{2}= \begin{bmatrix} 1/2&{}0&{}0&{}...&{}0\\ 0&{}1/3&{}0&{}...&{}0\\ 0&{}0&{}1/4&{}\ldots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}...&{}1/(N+2)\\ \end{bmatrix}. \end{aligned}$$

Now, by integrating (6.6) with respect to \(\xi \), we get

$$\begin{aligned} \begin{aligned} \frac{\partial \nu (\xi ,\tau )}{\partial \xi }&\simeq \xi ~\tau ^{2} G^{\text {T}}(\xi ) \vartheta _{1}^{\text {T}}U \vartheta _{2} \hat{\vartheta _{2}}\ell (\tau )+\tau (\acute{g_{1}}(\xi )-\acute{g_{0}}(0))+(\acute{g_{0}}(\xi )-\acute{g_{0}}(0))\\&+\frac{\partial \nu (0,\tau )}{\partial \xi }, \end{aligned} \end{aligned}$$
(6.8)

and

$$\begin{aligned} \begin{aligned} \nu (\xi ,\tau )&\simeq \xi ^{2} ~\tau ^{2} G^{\text {T}}(\xi ) \hat{\vartheta _{1}^{\text {T}}}~\vartheta _{1}^{\text {T}}U~\vartheta _{2} \hat{\vartheta _{2}}\ell (\tau )+\tau (g_{1}(\xi )-g_{1}(0) -\xi ~\acute{g_{1}}(0))\\&+(g_{0}(\xi )-g_{0}(0)-\xi ~\acute{g_{0}}(0))+\xi ~\frac{\partial \nu (\xi ,0)}{\partial \xi }+\nu _{0}(\tau ), \end{aligned} \end{aligned}$$
(6.9)

where

$$\begin{aligned} \begin{aligned} \int _{0}^{\xi } \rho P(\rho ) d\rho&=\int _{0}^{\xi } \rho D_{1} T(\rho ) d\rho = D_{1}\int _{0}^{\xi } \rho T(\rho ) d\rho \\&=\xi ^{2}D_{1}\hat{\Lambda _{1}}T(\xi )=\xi ^{2}D_{1}\hat{\Lambda _{1}}D_{1}^{-1}G(\xi )=\xi ^{2}\hat{\vartheta }_{1}G(\xi ), \end{aligned} \end{aligned}$$
(6.10)

and

$$\begin{aligned} \hat{\Lambda }_{1}= \begin{bmatrix} 1/2&{}0&{}0&{}...&{}0\\ 0&{}1/3&{}0&{}...&{}0\\ 0&{}0&{}1/4&{}\ldots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}...&{}1/(M+2)\\ \end{bmatrix}. \end{aligned}$$

Integrating (6.4) w.r.t. \( \xi \) and by the aid of the conditions (6.2) and (6.3) yields

$$\begin{aligned}{} & {} \frac{\partial ^{3}\nu (\xi ,\tau )}{\partial \xi \partial \tau ^{2}}\simeq \xi G^{\text {T}}(\tau ) \vartheta _{1}^{\text {T}} U \ell (\tau )+\frac{\partial ^{3}\nu (0,\tau )}{\partial x\partial \tau ^{2}}. \end{aligned}$$
(6.11)
$$\begin{aligned}{} & {} \frac{\partial ^{2}\nu (\xi ,\tau )}{\partial \tau ^{2}}\simeq \xi ^{2} G^{\text {T}}(\xi )\hat{\vartheta _{1}^{\text {T}}} \vartheta _{1}^{\text {T}} U \ell (\tau )+\xi ~\frac{\partial ^{3}\nu (0,\tau )}{\partial \xi \partial \tau ^{2}}+{\acute{\acute{\nu _{0}}}(\tau )}. \end{aligned}$$
(6.12)

It is remarkable that \(\frac{\partial ^{3}\nu (0,\tau )}{\partial \xi \partial \tau ^{2}}\) is unknown function, by integrating (6.11) from 0 to 1 with respect to  \(\xi \), we get

$$\begin{aligned} \frac{\partial ^{3}\nu (0,\tau )}{\partial \xi \partial \tau ^{2}}\simeq \acute{\acute{\nu _{1}}}(\tau )-\acute{\acute{\nu _{0}}}(\tau )-S^{\text {T}}D_{1}^{\text {T}}\vartheta _{1}^{\text {T}}U \ell (\tau ), \end{aligned}$$

where

$$\begin{aligned} \int _{0}^{1} \xi G^{\text {T}}(\rho ) d\xi =\int _{0}^{1} \xi T(\xi ) D_{1}^{\text {T}} d\xi =S^{\text {T}} D_{1}^{\text {T}}, \end{aligned}$$

and

$$\begin{aligned} S=\left[ \frac{1}{2},\frac{1}{3},\frac{1}{4}, \ldots \frac{1}{M+2}\right] ^{\text {T}}. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} \frac{\partial ^{2}\nu (\xi ,\tau )}{\partial \tau ^{2}}&\simeq \xi ^{2} G^{\text {T}}(\xi )\hat{\vartheta _{1}^{\text {T}}}\vartheta _{1}^{\text {T}}U \ell (\tau ) +x[\acute{\acute{\nu _{1}}}(\tau )-\acute{\acute{\nu _{0}}}(\tau )-S^{\text {T}}D_{1}^{\text {T}}\vartheta _{1}^{\text {T}} U \ell (\tau )]\\&+\acute{\acute{\nu _{0}}}(\tau ). \end{aligned} \end{aligned}$$
(6.13)

By integrating (6.13) for \(\tau \), we acquire to

$$\begin{aligned} \begin{aligned} \frac{\partial \nu (\xi ,\tau )}{\partial \tau }&\simeq \xi ^{2} \tau G^{\text {T}}(\xi )\hat{\vartheta _{1}^{\text {T}}}\vartheta _{1}^{\text {T}}U \vartheta _{2} \ell (\tau ) +\xi [\acute{\nu _{1}}(\tau )-\acute{\nu _{0}}(\tau )-\tau S^{\text {T}} D_{1}^{\text {T}}\vartheta _{1}^{\text {T}} U \vartheta _{2} \ell (\tau )]\\&+\acute{\nu _{0}}(\tau )+g_{1}(\tau ). \end{aligned} \end{aligned}$$
(6.14)

6.1 The operational matrix of the delay term

In this subsection, the delay term \(\nu (\xi ,\tau -\kappa )\) will be approximated using the operational matrix of the Laguerre polynomials as follows:

consider [10]

$$\begin{aligned} \nu (\xi ,\tau -\kappa )=G^{\text {T}}(\xi ) U \ell (\tau -\kappa ), \end{aligned}$$
(6.15)

where

$$\begin{aligned} \ell (\tau -\kappa )=H P^{\text {T}}(\tau -\kappa ), \end{aligned}$$
(6.16)

and

$$\begin{aligned} H= \begin{bmatrix} \frac{(-1)^{0}}{0!}(^{0}_{0})&{}0&{}0&{}...&{}0\\ \\ \frac{(-1)^{0}}{0!}(^{1}_{0})&{}\frac{(-1)^{1}}{1!}(^{1}_{1})&{}0&{}...&{}0\\ \\ \frac{(-1)^{0}}{0!}(^{2}_{0})&{}\frac{(-1)^{1}}{1!}(^{2}_{1})&{}\frac{(-1)^{2}}{2!}(^{2}_{2})&{}...&{}0\\ \\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ \\ \frac{(-1)^{0}}{0!}(^{N}_{0})&{}\frac{(-1)^{1}}{1!}(^{N}_{1})&{}\frac{(-1)^{2}}{2!}(^{N}_{2})&{}...&{}\frac{(-1)^{N}}{N!}(^{N}_{N})\\ \end{bmatrix}. \end{aligned}$$

To get \(P(\tau -k)\) by means of \(P(\tau )\), we must employ the next relation

$$\begin{aligned} P(\tau )= & {} [1, \tau , \tau ^{2},\ldots ,\tau ^{N}],~~~P(\tau -\kappa )=[1,\tau -\kappa , (\tau -k)^{2}, \ldots (\tau -k)^{N}].\nonumber \\ P(\tau -k)= & {} P(\tau ) B_{-k}^{\text {T}}, \end{aligned}$$
(6.17)

where

$$\begin{aligned} B_{-\kappa }^{\text {T}}= \begin{bmatrix} (^{0}_{0})(-\kappa )^{0}&{}(^{1}_{0})(-\kappa )^{1}&{}(^{2}_{0})(-\kappa )^{2}&{}\cdots &{}(^{N}_{0})(-\kappa )^{N}\\ \\ 0&{}(^{1}_{1})(-\kappa )^{0}&{}(^{2}_{1})(-\kappa )^{1}&{}\cdots &{}(^{N}_{1})(-\kappa )^{N-1}\\ \\ 0&{}0&{}(^{2}_{2})(-\kappa )^{0}&{}\cdots &{}(^{N}_{2})(-\kappa )^{N-2}\\ \\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ \\ 0&{}0&{}0&{}\cdots &{}(^{N}_{2})(-\kappa )^{0} \end{bmatrix}. \end{aligned}$$

Using Eqs. (6.15)–(6.17), we have

$$\begin{aligned} \nu (\xi ,\tau -\kappa )=G^{\text {T}}(\xi ) U B^{\text {T}}_{-\kappa } H^{\text {T}} \ell (\tau ). \end{aligned}$$
(6.18)

6.2 Computation of VFD of \(\nu (\xi ,\tau )\)

Here, we expand \(D^{\delta (\xi ,\tau )}_{\tau }, 0<\delta (\xi ,\tau )\le 1\) in terms of the (S\(\ell \)Ps), using Eq. (6.14), we get

$$\begin{aligned} D_{\tau }^{\delta (\xi ,\tau )}\nu (\xi ,\tau )&=I_{\tau }^{1-\delta (\xi ,\tau )} \left( \frac{\partial \nu (\xi ,\tau )}{\partial \tau } \right) \nonumber \\&\simeq \xi ^{2}\tau ^{2-\delta (\xi ,\tau )}G^{\text {T}}(\xi )\hat{\vartheta _{1}^{\text {T}}}\vartheta _{1}^{\text {T}} U~ \vartheta _{2}~\hat{\Theta }_{N}^{1-\delta (\xi ,\tau )}\ell (\tau )+\xi I_{\tau }^{1-\delta (\xi ,\tau )}(\acute{\nu _{1}}(\tau )-\acute{\nu _{0}}(\tau ))\nonumber \\&\quad -\xi \tau ^{2-\delta (\xi ,\tau )}S^{\text {T}}D_{1}^{\text {T}} \vartheta _{1}^{\text {T}}U \vartheta _{2}~\hat{\Theta }_{N}^{1-\delta (\xi ,\tau )}\ell (\tau )+\frac{\Gamma (1)}{\Gamma (2-\delta (\xi ,\tau )} \tau ^{1-\delta (\xi ,\tau )}g_{1}(\xi )\nonumber \\&\quad +I_{\tau }^{1-\delta (\xi ,\tau )}\acute{\nu }_{0}(\tau ). \end{aligned}$$
(6.19)

So that

$$\begin{aligned} I_{\tau }^{1-\delta (\xi ,\tau )}(\tau \ell (\tau ))\simeq \tau ^{2-\delta (\xi ,\tau )}\hat{\Theta }_{N}^{1-\delta (\xi ,\tau )} \ell (\tau ), \end{aligned}$$

since

$$\begin{aligned} \hat{\Theta }_{N}^{1-\delta (\xi ,\tau )}=D_{2}\hat{\vartheta }_{N}^{1-\delta (\xi ,\tau )}D_{2}^{-1}. \end{aligned}$$

Also, for \(1<\delta (\xi ,\tau )\le 2\)

$$\begin{aligned} D_{\tau }^{\delta (\xi ,\tau )}\nu (\xi ,\tau )&=I_{\tau }^{2-\delta (\xi ,\tau )}(\frac{\partial ^{2} \nu (\xi ,\tau )}{\partial \tau ^{2}}) \nonumber \\&\simeq \xi ^{2}\tau ^{2-\delta (\xi ,\tau )}G^{\text {T}}(\xi )\hat{\vartheta _{1}^{\text {T}}}\vartheta _{1}^{\text {T}} U~ \vartheta _{2}~\hat{\Theta }_{N}^{2-\delta (\xi ,\tau )}\ell (\tau )+\xi I_{\tau }^{2-\delta (\xi ,\tau )}(\acute{\acute{\nu _{1}}}(\tau )-\acute{\acute{\nu _{0}}}(\tau ))\nonumber \\&\quad -\xi \tau ^{2-\delta (\xi ,\tau )}S^{\text {T}}D_{1}^{\text {T}}\vartheta _{1}^{\text {T}} U \vartheta _{2}~\hat{\Theta }_{N}^{2-\delta (\xi ,\tau )}\ell (\tau ) +I_{\tau }^{2-\delta (\xi ,\tau )}\acute{\acute{\nu _{0}}}(\tau ). \end{aligned}$$
(6.20)

Substituting the approximations (6.6), (6.9) and (6.20) into Eq. (6.1) and the nodal points of Newton–Cotes [19], then we get an algebraic system of equations and using the Newton’s iterative method. We get the unknown matrix U.

Substituting U into Eq. (6.9), we attain the approximate solution of the problem (6.1)–(6.3).

7 Numerical examples

To demonstrate the ability of the proposed method for solving VFDDEs, two tested examples are given:

Example 7.1

Consider the VFDDEs (6.1) with \(\eta =1, \kappa =0.1\) and subject to

$$\begin{aligned} \nu (0,\tau )= & {} 0, ~~~~\nu (1,\tau )=0,~~~~\tau \in [0,\infty ), \end{aligned}$$
(7.1)
$$\begin{aligned} \nu (\xi ,0)= & {} 10\xi ^{2}~(1-\xi )^{2},~~~~~~~~~~~~~~~~~\frac{\partial \nu (\xi ,0)}{\partial \tau }=0, \end{aligned}$$
(7.2)

where

$$\begin{aligned}{} & {} f(\nu (\xi ,\tau ),\nu (\xi ,\tau -\kappa ))=10 \xi ^{2}(1-\xi )^{2}\frac{ \tau ^{2-\delta (\xi ,\tau )}}{\Gamma (3-\delta (\xi ,\tau ))}\\{} & {} \quad -20(6\xi ^{2}-6\xi +1)(\tau ^{2}+1)-10(\tau -0.1+1)^{2} \xi ^{2}(1-\xi )^{2}. \end{aligned}$$

This problem has an exact solution \(\nu (\xi ,\tau )=10\xi ^{2}(1-\xi )^{2}(\tau ^{2}+1)\)   and

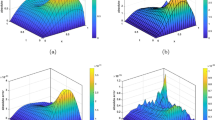
$$\begin{aligned} \delta (\xi ,\tau )=\frac{9}{5}-0.005~cos(\xi \tau )~sin(x). \end{aligned}$$

Figure 1 represents the AE of Example 7.1 for M=N=8 and distinct values of \(\delta (\xi ,\tau )\). Also, Fig.2 represents a comparison between the exact solution and the approximate solution using the proposed method.

Fig. 1
figure 1

AE of Example 7.1

Full size image
Fig. 2
figure 2

Approximate and exact solution of Example 7.1

Full size image

Example 7.2

Consider the VFDDEs (6.1) with \(\eta =1,~~\kappa =0.2\) and subject to

$$\begin{aligned} \nu (0,\tau )= & {} 0,~~~~~ \nu (1,\tau )=0,~~~~ \tau \in [0,\infty ), \end{aligned}$$
(7.3)
$$\begin{aligned} \nu (\xi ,0)= & {} \frac{\partial \nu (\xi ,0)}{\partial \tau }=5\xi ~(1-\xi ), \end{aligned}$$
(7.4)

where

$$\begin{aligned} f(\nu (\xi ,\tau ),\nu (\xi ,\tau -\kappa ))=5 \xi (1-\xi )\frac{ \tau ^{1-\delta (\xi ,\tau )}}{\Gamma (2-\delta (\xi ,\tau ))}-10\tau +5\xi (1-\xi )(\tau -0.2+1). \end{aligned}$$

This problem has a exact solution \(\nu (\xi ,\tau )=5\xi (1-\xi )(\tau +1)\)   and

$$\begin{aligned} \delta (\xi ,\tau )=2-0.2~{\text {cos}}(\tau )~{\text {sin}}(\xi ). \end{aligned}$$

Figure 3 represents AE of Example 7.2 for \(M=N=8\) and distinct values of \(\delta (\xi ,\tau )\). A comparison between the exact and the approximate solutions of Example 7.2 is given in Fig. 4.

Fig. 3
figure 3

AE of Example 7.2

Full size image
Fig. 4
figure 4

Approximate and exact solution of Example 7.2

Full size image

8 Conclusion

In this paper, we formulate the collocation method and the OMs of shifted Legendre–Laguerre polynomials to approximate the solutions of VFDDEs. The proposed method transform the VFDDEs to system of algebraic equations using the nodal points of Newton–Cots. By solving the algebraic system using Newton’s iterative methods, numerical solutions are obtained. The numerical results approved that the proposed method is accurate and has very high accuracy as M and N increased.