Analysis of entropy generation and nonlinear convection on unsteady flow of MHD Prandtl fluid with Soret and Dufour effects

Abstract

Here the assessment of entropy generation with Soret and Dufour impact in flow of MHD Prandtl fluid along an unsteady stretching surface has been measured. Nonlinear mixed convection and convective conditions for heat/mass transfer are imposed at the surface. The outcome of viscous dissipation and radiation is considered in heat transfer features. The obtained system of nonlinear PDEs is converted to ODEs by consuming dimensionless variables. Resulting systems are solved for the convergent solutions. Impacts of Prandtl fluid parameters, unsteadiness parameter, Soret and Dufour numbers, magnetic parameter, nonlinear thermal and concentration parameter, Prandtl number, radiation parameter, thermal and concentration Biot numbers, ratio of concentration to thermal buoyancy, Eckert number and Schmidt number are addressed. Skin friction coefficient, local Nusselt and Sherwood numbers are analyzed graphically. Unsteady parameter ${ \epsilon }$ has reverse behavior on the velocity and temperature profiles, velocity declines while temperature raises. Prandtl fluid parameter ${ \alpha }$ and ${ \beta }$ boost the velocity field. Mixed convection parameter le and N* (ratio of concentration and buoyancy force) enhance the velocity field and resultant boundary layer thickness. Magnetic parameter change its behavior on $f(\eta )$$\theta (\eta )$ and . Soret/Dufour number enhances the energy flux due to mass transfer rate and mass flux which radically increases the temperature. Far away from the wall entropy generation grows rapidly for greater values of a and b. Magnetic and radiation parameter increase the entropy generation while radiation parameter decreases.

1 Introduction

Unsteady flow over a stretching surface has been widely used in annealing and thinning of copper wires, paper production sheet from a dye, metals, and plastics, cooling of the metallic plate in a cooling bath, glass blowing and food processing. Boundary layer flow and heat transfer over a permeable unsteady stretching sheet with non-uniform heat source/sink is examined by Zheng et al. [34]. Unsteady boundary layer stagnation-point flow over a shrinking stretching surface has been reported by Bhattacharyya [9]. He considered that the sheet temperature depends on time; also he found out dual solutions for same values of velocity ratio parameter as well as unique solution of the problem. Mukhopadhyay [24, 25] reported Casson fluid flow over an unsteady stretching surface with a chemical reaction. They discuss that fluid velocity initially decreases with increasing values of time depending on parameter while temperature and concentration fields decay, because less heat and solute is moved from the sheet to fluid. Lin et al. [21] examined the flow and heat transfer of pseudoplastic nanoliquid in a finite slim film across an unsteady stretching sheet. They also considered variable thermal conductivity and viscous dissipation effects. Rosca and Pop [27] examined time dependent viscous flow across a curved stretching/shrinking surface with mass suction. They solved the dimensionless system numerically and performed stability analysis for solution. Also conclude that pressure cannot be negligible in curved surfaces. Lin et al. [22] numerically studied the magnetohydrodynamic (MHD) pseudoplastic flow of a nanofluid in a finite film over an unsteady stretching surface with internal heating effects. They consider water as base fluid with nanoparticles (Cu, $\hbox {A1}_2\hbox {0}_3$, CuO and $\textrm{TiO}_2$). They discussed that when time-dependent parameter goes to zero then film thickness approaches to infinity. The time-dependent 2D flow of non-Newtonian fluid across a stretching sheet with thermal radiation and variable thermal conductivity has been evaluated by Reddy [26]. He calculated that the rate of cooling for larger values of the time dependent parameter is significantly bigger than this rate in steady flows. Unsteady flow of Powell–Eyring fluid past an inclined stretching surface was discovered by Hayat et al. [15]. They also studied the collective effects of non-uniform heat source/sink and radiation.

The combined effect of heat/mass transfer is significant in different fields including moisture over the agriculture field, distribution of temperature, cooling towers and food processing and many others. The Soret/Dufour effects are very prominent in the analysis of heat/mass transfer. Therefore Hayat et al. [12] studied the effects of Soret/Dufour in mixed convection flow towards a vertical surface. Hayat et al. [13] also discussed Soret and Dufour impacts in three-dimensional boundary layer flow of viscoelastic fluid over a stretching surface. Tsai and Huang [31] explored Soret and Dufour impacts in Hiemeng flow through a stretching sheet. Zheng et al. [35] analyzed the unsteady heat and mass transfer in MHD fluid by an oscillatory stretching surface. They consider the effect of viscous dissipation and uniform magnetic field that applied in vertical direction of the flow. They studied that at the same time when we increase Dufour number and decrease Soret number, temperature field increases while spices decays. Wang et al. [33] explained the influence of thermo-solutal buoyancies with Soret and Dufour belongings. In this study, they found that the flow composition of various aspects ratios develops from condition-controlled to steady convection-controlled and complete growth of Rayleigh number increases. Radiative heat and mass transfer flow with Soret and Dufour effects have been reported by Vedavathi et al. [32]. They solve OD Eq by using shooting method along with Runge–Kutta fourth order integration scheme. They conclude that radiation parameter enhances the velocity and temperature profile while it decays the heat transfer rate. Hayat et al. [14] explored the Soret/Dufour impacts in the MHD rotating flow of viscoelastic fluid. They model three dimension flow in the rotating frame of reference . Series solution is obtained and described that result for porous channel. The flow behavior is different for upper and lower plate.

The present communication is to analyze the entropy generation flow of non-Newtonian fluid induced over an unsteady stretching surface with Soret/Dufour effects. Constitutive relations for MHD Prandtl fluid are considered. Viscous dissipation nonlinear mixed convection and thermal radiation are also taken into account. Convective heat and mass conditions were imposed. The coupled highly nonlinear equations are solved analytically. The effects of physical parameters on the velocity, temperature and concentration profiles are deliberated. Skin friction, local Nusselt and Sherwood numbers are also discussed.

2 Problem formulation

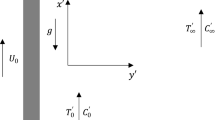
Consider the flow of Prandtl fluid across an unsteady stretching surface with heat/mass transfer. It is assumed that the surface is stretched with two equal and opposite forces along the x-axis keeping the origin fixed. The x-axis is taken along the sheet and y-axis normal to it. Radiation, Soret/Dufour effects and viscous dissipation are deliberated. Convective heat and mass conditions are considered at the stretching sheet. Fig. a. Flow diagram

The governing equations of the velocity, temperature and concentration fields are as follows

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left[ \frac{A}{\rho \bar{C}}\frac{\partial ^{2}u}{\partial y^{2}}+\frac{A}{2\rho \bar{C}^{3}}\left( \frac{\partial u}{\partial y} \right) ^{2}\frac{\partial ^{2}u}{\partial y^{2}}\right] -\frac{\sigma B_{0} }{\rho }u+g\left\{ \Omega _{1}(T-T_{\infty })+\Omega _{2}(T-T_{\infty })^{2}\right\} \nonumber \\&\displaystyle g\left\{ \Omega _{3}(C-C_{\infty })+\Omega _{4}(C-C_{\infty })^{2}\right\} , \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha ^{*}\frac{\partial ^{2}T}{\partial y^{2}}-\frac{1}{ \rho c_{p}}\frac{\partial q_{r}}{\partial y}+\frac{1}{\rho c_{p}}\left[ \frac{A}{C}\left( \frac{\partial u}{\partial y}\right) ^{2}+\frac{A}{6C^{3}} \left( \frac{\partial u}{\partial y}\right) ^{4}\right] +\frac{D_{m}k_{T}}{ c_{p}c_{f}}\frac{\partial ^{2}C}{\partial y^{2}}+\sigma B_{0}u^{2},\nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle \frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_{m}\frac{\partial ^{2}C}{\partial y^{2}}+\frac{D_{m}k_{T}}{ T_{m}}\frac{\partial ^{2}T}{\partial y^{2}}, \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle u=U_{w}\left( x,t\right) ,\text { }v=0,\text { }-k\frac{\partial T}{\partial y} =h\left( T_{f}-T\right) ,-D_{m}\frac{\partial C}{\partial y} =k_{m}\left( C_{f}-C\right) \text { at }y=0, \nonumber \\&\displaystyle u\rightarrow 0,\text { }T\rightarrow T_{\infty }\text {, }C\rightarrow C_{\infty }\text { as }y\rightarrow \infty , \end{aligned}$$

(5)

where u and v represent the velocity components along the x and $y-$directions respectively, $U_{w}\left( x,t\right)$ $=\frac{cx}{\left( 1-at\right) }$ is the stretching velocity of sheet, $\left( \text {where }a \text { and }c\text { are positive constants}\right) , A$ and $\bar{C}$ are the material constant of Prandtl fluid, $\nu =\frac{\mu }{\rho }$ is the kinematic viscosity, T is the fluid temperature, $T_{\infty }$ is the ambient fluid temperature, C is the fluid concentration, $C_{\infty }$ is the ambient fluid concentration, $\alpha ^{*}$ is the thermal diffusivity, k is the thermal conductivity, $\Omega _{1}$ and $\Omega _{2}$ is the linear and nonlinear thermal expansion coefficients, $c_{p}$ is the specific heat, $q_{r}=-\frac{16\sigma T_{\infty }^{3}}{3k^{*}}\frac{ \partial T}{\partial y}$ is the radiative heat flux, $k^{*}$ is the mean absorption coefficient, $\sigma$ is the Stefan–Boltzmann constant, $c_{f}$ is the concentration susceptibility, $D_{m}$ is the molecular diffusivity of the species concentration, g is the gravitational acceleration, $k_{T}$ is the thermal diffusion ratio, h is the wall heat transfer coefficient, $\Omega _{3}$ and $\Omega _{4}$ is the linear and nonlinear concentration expansion coefficients, $k_{m}$ is the wall mass transfer coefficient, $T_{m}$ is the mean fluid temperature and convective heating process is characterized by temperature $T_{f}$ and concentration near the surface is $C_{f}$.

The transformations are defined as follows:

$$\begin{aligned} u= & {} \frac{cx}{\left( 1-at\right) }f^{\prime }(\eta ),v=-\sqrt{ \frac{c\nu }{\left( 1-at\right) }}f(\eta )\text {, } \nonumber \\ \theta (\eta )= & {} \frac{T-T_{\infty }}{T_{f}-T_{\infty }},\text { }\phi \left( \eta \right) =\text { }\frac{C-C_{\infty }}{C_{f}-C_{\infty }} ,\text { }\eta =\sqrt{\frac{c}{\nu \left( 1-at\right) }}y. \end{aligned}$$

(6)

Now Eq. (1) is identically satisfied and Eqs. (2–5) yield

$$\begin{aligned}&\displaystyle \alpha f^{\prime \prime \prime }+ff^{\prime \prime }-f^{\prime 2}-\epsilon \left( f^{\prime }+\frac{\eta }{2}f^{\prime \prime }\right) +\beta f^{\prime \prime }f^{\prime \prime \prime }-Mf^{\prime }+\lambda (1+\beta _{t}\theta )\theta +\lambda N^{*}(1+\beta _{c}\phi )\phi =0, \end{aligned}$$

(7)

$$\begin{aligned}&\displaystyle \left( 1+\frac{4}{3}R\right) \theta ^{\prime \prime }+\Pr \left( f\theta ^{\prime }-\lambda \frac{\eta }{2}\theta ^{\prime }\right) +\Pr Du\phi ^{\prime \prime }+\Pr Ec\left( \alpha f^{\prime \prime 2}+\frac{\beta }{3} f^{\prime \prime 4}\right) +\Pr EcMf^{\prime 2}=0, \end{aligned}$$

(8)

$$\begin{aligned}&\displaystyle \phi ^{\prime \prime }+ScSr\theta ^{\prime \prime }+Sc\left( f\phi ^{\prime }-\lambda \frac{\eta }{2}\phi ^{\prime }\right) =0, \end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle f=0, f^{\prime }=1,\text { }\theta ^{\prime }\left( 0\right) =-Bi_{1}\left( 1-\theta \left( 0\right) \right) ,\text { }\phi ^{\prime }\left( 0\right) =-Bi_{2}\left( 1-\phi \left( 0\right) \right) \text { at }\eta =0, \nonumber \\&\displaystyle f^{\prime }=0,\text { }\theta =0,\text { }\phi =0\text { at }\eta =\infty , \end{aligned}$$

(10)

where $\epsilon$ is the unsteadiness parameter, $\alpha$ and $\beta$ are the Prandtl fluid parameters, $\Pr$ is the Prandtl number, Du is the Dufour number, Sr is the Soret number, $\lambda$ is the mixed convection parameter, $N^{*}$ is the ratio of concentration to thermal buoyancy forces, Sc is the Schmidt number, $\beta _{t}$ and $\beta _{c}$ is the nonlinear thermal and concentration parameters, M is the magnetic parameter, Ec is the Eckert number, $Bi_{1}$ is the thermal Biot number, $Bi_{2}$ is the concentration Biot number and R is the radiation parameter. The definitions of these parameters are

$$\begin{aligned} \begin{array}{ccc} \epsilon =\frac{a}{c}, &{} \alpha =\frac{A}{\mu \bar{C}},M=\frac{\sigma B_{0}}{\rho c}, &{} \beta =x^{2}\frac{c^{3}}{\nu \left( 1-at^{3}\right) }, \\ \Pr =\frac{\nu }{\alpha ^{*}}, &{} Sr=\frac{D_{m}k_{T}(T_{f}-T_{\infty })}{\nu T_{m}(C_{f}-C_{\infty })}, &{} Ec=\frac{U_{w}^{2}\left( x\right) }{ c_{p}\left( T_{f}-T_{\infty }\right) }, \\ Sc=\frac{\nu }{D_{m}}, &{} Bi_{1}=\frac{h}{k}\sqrt{\frac{\nu \left( 1-at\right) }{c}}, &{} Du=\frac{D_{m}k_{T}(C_{f}-C_{\infty })}{\nu c_{\rho }c_{f}(T_{f}-T_{\infty })}, \\ R=\frac{4\sigma T_{\infty }^{3}}{kk^{*}}, &{} Bi_{2}=\frac{k_{m}}{D_{m}} \sqrt{\frac{\nu \left( 1-at\right) }{c}}. &{} \lambda =\frac{Gr}{\textrm{Re} _{x}^{2}} \end{array} \end{aligned}$$

(11)

The physical quantities of interest are the skin-friction coefficient $C_{f_{x}}$, local Nusselt number $Nu_{x}$ and local Sherwood number $Sh_{x}.$ These are defined by

$$\begin{aligned}{} & {} C_{f_{x}}=\frac{2\tau _{w}}{\rho U_{w}^{2}},\text { }\tau _{w}=\left. \frac{A }{\bar{C}}\frac{\partial u}{\partial y}+\frac{A}{6\bar{C}^{3}}\left( \frac{ \partial u}{\partial y}\right) ^{3}\right| _{y=0}, \end{aligned}$$

(12)

$$\begin{aligned}{} & {} Nu_{x}=\frac{xq_{w}}{k(T_{f}-T_{\infty })},\text { }q_{w}=\left. -k\frac{ \partial T}{\partial y}-\frac{16\sigma T_{\infty }^{3}}{3k^{*}}\frac{ \partial T}{\partial y}\right| _{y=0}, \end{aligned}$$

(13)

$$\begin{aligned}{} & {} Sh_{x}=\frac{J_{w}x}{D_{m}\left( C_{f}-C_{\infty }\right) },\text { } J_{w}=\left. -D_{m}\frac{\partial C}{\partial y}\right| _{y=0}, \end{aligned}$$

(14)

where $\tau _{w}$ is the local wall shear stress and $q_{w}$ is the surface heat flux. Above equations in dimensionless variables yield

$$\begin{aligned}&\displaystyle \frac{1}{2}C_{f_{x}}Re_{x}^{1/2}=\left( \alpha f^{\prime \prime }\left( 0\right) +\frac{\beta }{3}f^{\prime \prime 3}\left( 0\right) \right) , \end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle Nu_{x}/Re_{x}^{1/2}=-\left( 1+\frac{4}{3}R\right) \theta ^{\prime }(0), \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle Sh_{x}/Re_{x}^{1/2}=-\phi ^{\prime }\left( 0\right) , \end{aligned}$$

(17)

in which $Re_{x}=\frac{U_{w}\left( x,t\right) x}{\nu }$ is the local Reynolds number.

Fig. 1

$\hslash _{f}$ − curve for velocity field

Fig. 2

$\hslash _{\theta }$ − curve for temperature field

Fig. 3

$\hslash _{\phi }$ − curve for concentration field

3 Convergence analysis

Convergence of constructed series solutions clearly depends upon the $h_{f},$ $h_{\theta }$ and $h_{\phi }$. Therefore we plot $h-$curves for the velocity, temperature and concentration fields. Figures 1, 2, 3 depict the h − curves of $f^{\prime \prime }(0),$ $\theta ^{\prime }(0)$ and $\phi ^{\prime }(0)$ for different values of involved physical parameters. Here admissible ranges of $h_{f},$ $h_{\theta }$ and $h_{\phi }$ are $-1.8<h_{f}<-0.1$, $-1.5<h_{\theta }<-0.1$ and $-1.6<h_{\phi }<-0.1$ respectively.Obviously the series solutions converge in the whole region of $\eta$ when $h_{f}=-1$, $h_{\theta }=-9$ and $h_{\phi }=-8.$ Table 1 ensures the convergence of HAM solutions for different order of approximations. Here the $25\textrm{th}$-order of approximations are sufficient for the convergent series solutions.

Table 1 Convergence of series solutions for different order of approximations

4 Entropy generation

This sector is associated with the influence of MHD Prandtl fluid with heat transfer on entropy generation. Local volumetric rate of entropy generation is defined as

$$\begin{aligned} S_{gen}^{\prime \prime \prime }= & {} \frac{k}{T_{\infty }^{2}}\left[ \left( \frac{\partial T}{\partial y}\right) ^{2}+\frac{16\sigma ^{*}T_{\infty }^{3}}{3k^{*}}\left( \frac{\partial T}{\partial y}\right) ^{2}\right] + \frac{\sigma B_{0}^{2}u^{2}}{T_{\infty }}+\frac{D_{m}}{T_{\infty }}\left( \frac{\partial T}{\partial y}\frac{\partial C}{\partial y}\right) \nonumber \\{} & {} +\frac{\mu }{T_{\infty }}\left[ \frac{A}{C}\left( \frac{\partial u }{\partial y}\right) ^{2}+\frac{A}{6C^{3}}\left( \frac{\partial u}{\partial y }\right) ^{4}\right] +\frac{D_{m}}{C_{\infty }}\left( \frac{\partial C}{ \partial y}\right) ^{2}. \end{aligned}$$

(18)

Above equation is the combination of three different phenomena. First is heat transfer, second due to magnetic field and third one is due to viscous dissipation of Walter’s B fluid. Characteristics entropy generation rate is defined as

$$\begin{aligned} \dot{S}_{0}^{^{\prime \prime \prime }}=\frac{k(\Delta T)^{2}}{l^{2}T_{\infty }^{2}}, \end{aligned}$$

(19)

Thus, the dimensionless form of entropy generation is obtained by taking ratio of Eqs. (21) and (22).

$$\begin{aligned} N_{G}= & {} \frac{S_{gen}^{\prime \prime \prime }}{\dot{S}_{0}^{^{\prime \prime \prime }}}=\textrm{Re}\left[ \left( 1+\frac{4}{3}R\right) \theta ^{\prime \prime }\right] +\frac{1}{\theta _{f}^{2}}\textrm{Re}BrMf^{\prime 2} \\{} & {} -\frac{1}{\theta _{f}^{2}}\textrm{Re}Br\left[ \alpha f^{\prime \prime 2}+\beta f^{\prime \prime 4}\right] +\Lambda \textrm{Re}\left( \frac{1}{\theta _{f}}\phi ^{\prime 2}+\phi ^{\prime }\theta ^{\prime }\right) . \nonumber \end{aligned}$$

(20)

where $\textrm{Re}=\frac{U_{w}(x,t)x}{\upsilon },$ $Br=\frac{\mu (U_{w}(x,t))^{2}}{k\Delta T}$ $\Lambda =\frac{D_{m}T_{\infty }}{k}\left( \frac{\Delta C}{\Delta T}\right)$ and $\theta _{f}=\frac{\Delta T}{ T_{\infty }}.$

5 Results and discussion

Analysis and physical significance of Prandtl fluid parameters, unsteadiness parameter, radiation parameter, thermal and concentration Biot numbers, Prandtl number, Eckert number, Schmidt number and Soret and Dufour analysis. Figure 4 shows the plot of velocity profile $f^{\prime }(\eta )$ for different values of unsteadiness parameter $\epsilon$. It is clear from this Fig. that $\epsilon$ decreases the velocity profile. Physically an increase of time offers larger resistance to the flow which reduces the velocity field. The influence of Prandtl fluid parameters $\alpha$ and $\beta$ is shown in Figs. 5 and 6. It is seen that velocity enhances throughout the domain with increasing values of $\alpha$ and $\beta$. The momentum boundary layer also boost. Figure 7 shows the outcome of the mixed convection parameter on the velocity profile. Greater values of mixed convection parameter growths the velocity profile. Figure 8 represents the impact of the ratio of concentration and buoyancy force. For larger values of $N^{*}$ the velocity field enhanced. Larger values of M decays the velocity profile and boundary layer thickness. Because the growth in M corresponds to the increase in Lorentz force which creates the resistance in fluid flow, thus velocity reduces (see Fig. 9). While the opposite behavior is observed in Fig. 10. For the larger values of M. Figure 11 illustrates that temperature distribution is boosting the function of the unsteadiness parameter. This is since the rate of heat transfer increases which ultimately enhances the temperature boundary layer. Figure 12 display the increasing behavior of the concentration field for different values of $\epsilon$. Figure 13 indicates that the temperature enhances for larger $\beta$. Figure 14 captures the impact of R on the temperature field. Temperature boost with increasing value of R. Rate of heat transfer at the boundary layer region also increases. Figures 15, 16, 17, 18 are presented to compare the effects of Biot numbers on the temperature and concentration fields respectively. Temperature boundary layer is an raising function of $Bi_{1}$ and $Bi_{2}$. Figures 19 and 20 depict the Soret (”thermophoresis”) and Dufour (”diffusion thermo”) impacts on the temperature and concentration distributions. The values of Soret/Dufour effects are taken in such a way that their product is constant so that the mean temperature remains constant as well. The Dufour number Du (which indicates the energy flux due to mass concentration gradient) is increased for larger values of temperature and smaller values of Soret number Sr (which generates mass flux due to temperature gradient). Thus it enhances the energy flux due to mass transfer rate and mass flux which significantly increases the temperature. The reverse behavior of Sr and Du is noticed in Fig. 20. Figure 21 elucidates variation of Prandtl number (“ratio of momentum diffusivity to the thermal diffusivity”) on dimensionless temperature distribution $\theta (\eta )$. For larger values of Prandtl number the thermal diffusivity decreases and thus both temperature and thermal boundary layers are reduced. Figure 22 shows the influence of the concentration field on the Prandtl number. It shows monotonic behavior on $\phi (\eta )$. Prandtl number increases the concentration when it is closer to the sheet but away from the sheet it decreases and asymptotically approaches zero. Figures 23 and 24 discuss the effects of Eckert number on $\theta (\eta )$ and $\phi (\eta )$. Figure 23 reports that with an increase in Eckert number Ec both the temperature and thermal boundary layer thickness is enhanced. Monotonic behavior of the concentration field is noticed for larger values of Ec in Fig. 24. Near the wall it reduces and away from the wall it increases. Figure 25 illustrates the impact of the Schmidt number on $\phi (\eta )$. Concentration field decays when Sc increases.

Fig. 4

Impact of $\epsilon$ on $f^{\prime }(\eta )$

Fig. 5

Impact of $\alpha$ on $f^{\prime }(\eta )$

Fig. 6

Impact of $\beta$ on $f^{\prime }(\eta )$

Fig. 7

Impact of $\lambda$ on $f^{\prime }(\eta )$

Fig. 8

Impact of $N^{*}$ on $f^{\prime }(\eta )$

Fig. 9

Impact of M on $f^{\prime }(\eta )$

Fig. 10

Impact of M on $\theta (\eta )$

Fig. 11

Impact of $\epsilon$ on $\theta (\eta )$

Fig. 12

Impact of $\epsilon$ on $\phi (\eta )$

Fig. 13

Impact of $\beta$ on $\theta (\eta )$

Fig. 14

Impact of R on $\theta (\eta )$

Fig. 15

Impact of $Bi_{1}$ on $\theta (\eta )$ and $\theta ^{\prime }(\eta )$

Fig. 16

Impact of $Bi_{1}$ on $\phi \left( \eta \right)$ & $\phi ^{\prime }(\eta )$

Fig. 17

Impact of $Bi_{2}$ $\theta (\eta )$ & $\theta ^{\prime }(\eta )$

Figures 26, 27, 28, 30, 31 display the differences of physical parameters on the Nusselt and the Sherwood numbers respectively. Local Nusselt number reduces with an increase in the unsteadiness parameter (see Fig. 26). Figure 27 shows reverse behavior for larger values of R. A small deviation in local Nusselt number is observed for larger values of Eckert number Ec (see Fig. 28). Figures 29 and 30 depict the impact of $\gamma$ and Sc on the mass transfer rate. An increase in $\epsilon$ and Sr decreases the mass transfer rate at the surface. Figure 31 shows increasing behavior for Sherwood number when concentration Biot number is increased.

Figures 32 and 33 show the flow behavior of fluid parameter, no increment is observed near the wall but far away from the wall entropy generation increases rapidly for greater values of $\alpha$ and $\beta$. The dispersion of M on the entropy generation is displayed in Fig. 34. Magnetic parameter persuade Lorentz force which boost the entropy generation. The deviation of entropy generation with $\eta$ is depicted in Fig. 35 for diverse values of radiation parameter. An increase in radiation parameters leads to an increase in entropy generation. It is also detected that near the surface variation is almost negligible. Variation of entropy generation with Reynolds number is discussed in Fig. 36. It is noted that the entropy generation rises with larger Reynolds number, because larger Reynolds number corresponds to the larger inertia and smaller viscous force. The effect of $\theta _{f}$ on the entropy generation is display in Fig. 37. It is understood from this Fig. that entropy generation is decreased when the temperature ratio parameter enhances. The effect of Brickman number is discus in Fig. 38. Brickman number produced heat transport by viscous heating, which improves in entropy generation.

Table 2 investigates the variations of Prandtl fluid and unsteadiness parameters on the skin friction coefficient.The destructive values of the skin-friction coefficient revenues that the surface applies a drag force on the fluid. The amount of the skin-friction coefficient is enlarged for greater values of $\alpha$, $\beta$ and $\epsilon$ (Tables 2). Tables 3 shows the comparison between the results. We found good comparison for different values of Biot number when Pr = 0.72.

Fig. 18

Impact of $Bi_{2}$ on $\phi \left( \eta \right)$ and $\phi ^{\prime }(\eta )$

Fig. 19

Impact of Du and Sr on $\theta (\eta )$

Fig. 20

Impact of (Du, Sr) on $\phi (\eta )$

Fig. 21

Impact of $\Pr$ on $\theta (\eta )$

Fig. 22

Impact of $\Pr$ on $\phi (\eta )$

Fig. 23

Impact of and Ec $\theta (\eta )$

Fig. 24

Impact of Ec on $\phi (\eta )$

Fig. 25

Impact of Sc on $\phi (\eta )$

Fig. 26

Impact of $\lambda$ on $\theta ^{\prime }(0)$

Fig. 27

Impact of R on $\theta ^{\prime }(0)$

Fig. 28

Impact of Ec on $\theta ^{\prime }(0)$

Fig. 29

Impact of $\lambda$ on $\phi ^{\prime }(0)$

Fig. 30

Impact of Sr on $\phi ^{\prime }(0)$

Fig. 31

Impact of $Bi_{2}$ on $\phi ^{\prime }(0)$

Fig. 32

Impact of $\alpha$ on $N_{G}(\eta )$

Fig. 33

Impact of $\beta$ on $N_{G}(\eta )$

Fig. 34

Impact of M on $N_{G}(\eta )$

Fig. 35

Impact of R on $N_{G}(\eta )$

Fig. 36

Impact of $\textrm{Re}$ on $N_{G}(\eta )$

Fig. 37

Impact of $\theta _{w}$ on $N_{G}(\eta )$

Fig. 38

Impact of $B_{r}$ on $N_{G}(\eta )$

Table 2 Values of skin-friction coefficient $\frac{1}{2}Re_{x}^{1/2}C_{f_{x}}$ for different parameters

Table 3 Comparison with Aziz [6], Ishak [18] and Makinde & Olanrewaju [23] for (incompressible fluid) -3b8’(0) when Pr = 0.72

6 Conclusions

Radiative flow of MHD Prandtl fluid with nonlinear mixed convection, entropy generation and convective heat and mass conditions, over an unsteady stretching sheet is examined. The main observations are summarized through the following points.

• Velocity field $f^{\prime }\left( \eta \right)$ increases for larger values of Prandtl fluid parameters $\alpha$ and $\beta .$

• Unsteady parameter $\lambda$ reduces the velocity throughout the region whereas opposite behavior is observed for the temperature and concentration profiles.

• Parameter $\beta$ enhances the temperature and thermal boundary layer thickness.

• The temperature profile shows increasing behavior for larger values of radiation parameter R.

• The temperature field increases when Eckert number is in strength.

• The effects of Soret and Dufour on the thermal and concentration distributions are practically opposite.

• Thermal and concentration Biot numbers boost the temperature and concentration profiles.

• Prandtl and Eckert numbers have monotonic behavior on the concentration field.

• The concentration field decreases for larger values of Schmidt number Sc.

• The skin friction coefficient is boosted for increasing values of $\alpha ,$ $\beta$ and $\lambda .$

• Prandtl fluid parameters enhance the entropy generation rate.

• Entropy generation increase with magnetic parameter, Reynolds number and Brinkman number, while reverse behavior is observed for larger values of radiation parameter, temperature ratio parameter.