1 Introduction

From a practical point of view, external disturbances (e.g., temperature, wind, noise, and vibration) and internal uncertainties (e.g., unknown system parameters and model errors) are the commonly encountered factors threatening the performance of flexible structures, which may cause various dangerous effects on the system such as mechanical failure, and increase the control error and other undesirable effects [16, 17, 28, 35, 36]. Consequently, considering control solutions for systems with uncertainties is of great importance in the industrial control systems. Various control methods have been developed for controlling such systems, such as sliding mode control (SMC) for nonlinear systems with disturbances [2, 19], Lyapunov approach for beam systems with boundary disturbance [22, 23], internal model control for output regulation of systems with external disturbance [33]. Unfortunately, most of these control approaches focus on the worst case scenario that makes the controller rather conservative.

Since its introduction by Han [25], the Active Disturbance Rejection Control (ADRC) approach has become a valid and practical control method, which attracts considerable attention due to its effectiveness against external and internal uncertainties, as well as its practical simplicity. The basic framework of the ADRC approach can be summarized in its capability to online estimate the total disturbance of the system using state observers, which are designed, specifically, to account for the class of the system model and the type of the uncertainties as well. The estimation is, then, added to the feedback observer-based controller to enable real time cancellation of the total disturbance at the start of each loop. With this approach, the control energy is significantly reduced, which is confirmed by many engineering practices [38], although the rigorous theoretical analysis is still lacking. The numerous applications have been carried out in the last decade, [20, 21] for the disk-beam system, and [12, 13, 28] for the beam with tip mass system; moreover, the stabilization problems of the wind-turbines subject to varying-frequency periodic load disturbances in [18], torsional plants with sinusoidal uncertainties in [29], Seismically excited building structure in [34], and trajectory tracking problem of a two-degree of freedom helicopter system in [37].

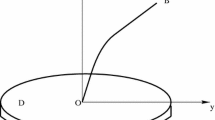
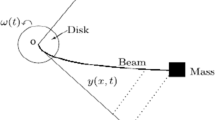
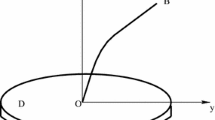
The rotating disk-beam system was introduced by Baillieul and Levi [4] to model some Aerospace systems. Then, Chentouf in [11], considered a rotating disk-beam-mass system which is a modified variant of that of Bailleul and Levi in [4]. As in [11], we assume that the disk (D) rotates freely about the x-axis with a time angular velocity and the beam (B) is clamped at the center of a disk and attached at its free end to a tip mass. The motion of the beam is confined to a x–y plane perpendicular to the disk and all the deflections are assumed to be parallel to the y-axis. The disk is supposed to rotate without friction. The system can be schematically shown in Fig. 1 (Chen et al. [14]). This system arises in the study of aerospace engineering applications, flexible robots arms and flexible marine risers. The system can be modeled as follows

$$\begin{aligned} \left\{ \begin{array}{ll} \rho y_{tt}(x,t)+EIy_{xxxx}(x,t)=\rho \bar{\omega }^2(t)y(x,t),&{} x\in (0,l), t>0,\\ y(0,t)=y_x(0,t)=0,&{} t>0,\\ my_{tt}(l,t)-EIy_{xxx}(l,t)=u(t)+d(t),&{} t>0\\ Jy_{xtt}(l,t)+EIy_{xx}(l,t)=r(t)+d_0(t),&{} t>0,\\ \frac{d}{dt}\left[ \omega (t)(I_d+\int ^l_0\rho y^2(x,t)dx)\right] ={\mathcal {T}}(t),&{} t>0,\\ y(x,0)=y_0(x),\;y_t(x,0)=y_1(x), &{} x\in (0,l),\\ \bar{\omega }(0)=\bar{\omega }_0. \end{array}\right. \end{aligned}$$
(1)

y represents the transverse displacement of the beam from its equilibrium state (i.e., the x-axis), all the subscripts on \(y_{x}\) and \(y_{t}\) denote the derivatives with respect to the position x and the time t variables, respectively. \(EI>0\) is the flexural rigidity, \(\rho >0\) is the mass per unit length of the beam, \(I_d\) is the disk’s moment of inertia, m is the mass of the tip mass, J is the moment of inertia of the tip mass and \(\bar{\omega }(t)\) is the angular velocity of the disk. r(t) is the boundary moment control and u(t) is the boundary control force exerting to the tip mass. \(d_0(t)\) and d(t) are the unknown non-uniformly bounded disturbances affecting the tip mass at \(x=l\). \({\mathcal {T}}(t)\) is the torque control applied on the disk which is chosen as \({\mathcal {T}}(t)=\lambda (\bar{\omega }(t)-\omega )\) where \(\lambda >0\) and \(\omega \) is the equilibrium point of \(\bar{\omega }(t)\).

Fig. 1
figure 1

Disk-beam-mass system (Chen et al.[14])

Full size image

In this paper, the dynamical term related to the mass is not neglected, but the dynamical term \(Jy_{xtt}(1,t)\) is so small that one can ignore it. In physical terms, this correspond to the case where the mass attached to the flexible beam, has high density. Furthermore, we assume that the angular velocity of a disk is constant \(\bar{\omega }(t)=\omega \) and only the control is acting on the shear force of the beam. Hereupon, the system is governed by the following linear system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho y_{tt}(x,t)+EIy_{xxxx}(x,t)=\rho \omega ^2y(x,t),&{} x\in (0,l),\, t>0,\\ y(0,t)=y_x(0,t)=y_{xx}(l,t)=0, &{} t>0,\\ my_{tt}(l,t)-EIy_{xxx}(l,t)=u(t)+d(t),&{} t>0,\\ y(x,0)=y_0(x),\;y_t(x,0)=y_1(x), &{} x\in (0,l). \end{array}\right. } \end{aligned}$$
(2)

The unknown external disturbance satisfies the following conditions:

Assumption 1.1

The disturbance d(t) is differentiable. Moreover, there exists two positive constants \( C, \delta > 0 \) such that

$$\begin{aligned} \arrowvert d(t)\arrowvert , \arrowvert \dot{d}(t)\arrowvert \le Ce^{\delta t},\;\;\; \forall t>0. \end{aligned}$$
(3)

In recent past decades, there existed many publications that contributed to dealing with beam systems with and without disturbance. Morgul [31] proved the exponential stability for an Euler-Bernoulli beam without a mass at the end. Laousy and Chentouf [26] have proved the exponential stability for Euler-Bernoulli flexible beam with tip mass, which describes the Scole model in the sense that the moment of inertia at \(x=l\) is neglected. This result is proved in [1, 8] for the non-homogeneous beam. In other hand, when \(my_{tt}(l,t)=0\) and the moment of inertia is accounted for, i.e., \(J>0\), the exponential stability is proved, in [5] for the homogeneous beam. Guo et al. [22] have proved the exponential stability for an Euler-Bernoulli beam with boundary disturbance. In turn, if a tip mass is attached at the free end with the moment of inertia of the mass is neglected, the exponential stability was proved in [28]. Chen and Jiang [12] have proved the exponential stability for an Euler-Bernoulli beam with mass and two disturbances affecting the tip mass. The exponential decay is proved for the rotating disk beam without mass and disturbance in [30] with a constant angular velocity. In the other case of a time-varying velocity, the exponential stability is proved in [15, 27] with static boundary controls and in [6, 9] with dynamic boundary controls. Similar achievement has been reached in [10] through the consideration of a linear direct strain controls, and in [7] by means of nonlinear controls. For a rotating disk beam with mass and without disturbance, Chen et al. [14] proved the exponential stability when \(my_{tt}(l,t)=0\). This result is proved by Aouragh and Segaoui [3] when \(Jy_{xtt}(l,t)=0\). When \(m=0\) and based on a constant gain for extended state observer (ESO), Guo and Wang [20] have proposed the feedback controller for the rotating disk-beam system with boundary input disturbances with \(\omega (t)\) variable and proved that the closed-loop system is exponentially stable when the disturbance and the derivative of disturbance are uniformly bounded, this assumption is avoided in [24] by proposing to estimate the uncertainties by time-varying gain ESO for the feedback control of a coupled heat and ordinary differential system subject to boundary control matched disturbance. This approach was used in [21] for a rotating disk beam with time-varying angular velocity.

The aim of this paper is to eliminate the vibrations caused by the external disturbance located at the tip mass of system (2). To this end, and since the disturbance d(t) and its derivative \(\dot{d}(t)\) are bounded by exponential, we employ the ADRC approach. Indeed, we design an extended state observer (ESO) to track the disturbance d(t), then, install the proposed control law which utilizes the generated estimation to cancel the effect of the disturbance in real-time. Thus, stabilizing problem (2).

The paper is organized as follows. In Sect. 2, we design a controller using the ADRC approach. To this end, we start by designing the state observer to track the boundary disturbance, then, we propose a control force to employ the estimation generated by the ESO to eliminate the disturbance. In Sect. 3, after reformulating the closed-loop system into an abstract evolution equation, we prove the well-posedness by the semigroup theory. Sect. 4 is dedicated to the stability result using a suitable Lyapunov function candidate. Furthermore, we conclude in Sect. 5 by providing simulation example to illustrate the validity of the theoretical results. Finally, we give some concluding remarks in Sect. 6.

2 Feedback controllers via ADRC

The high gain extended state observer (ESO) is designed in this section, and the ESO objective is to estimate the disturbance d(t) in real-time. First, we design the observer-based feedback control force of the following form

$$\begin{aligned} u(t)=-\alpha y_{t}(l,t)+EI\beta y_{xxxt}(l,t)+v(t), \end{aligned}$$
(4)

where v(t) is a new control variable that will be determined later in this section, and \(\alpha ,\beta >0\) satisfy the condition: \(\alpha \beta =m\).

Now, by substituting the control form (4) into the third equation in (2), we obtain

$$\begin{aligned} \beta \dot{\eta }(t)= d(t)-\eta (t)+v(t), \end{aligned}$$
(5)

where \(\eta \) is an auxiliary function, which has the following form

$$\begin{aligned} \eta (t)=-EIy_{x x x}(l, t)+\alpha y_{t}(l, t). \end{aligned}$$
(6)

Next, to estimate the disturbance d(t) affecting the tip mass, we design the following extended state observer for the ODE equation (5)

$$\begin{aligned} \left\{ \begin{array}{l} \beta \dot{{\hat{\eta }}}(t)=-{\hat{\eta }}(t)+v(t)+{\hat{d}}(t)+(a(t)-1)(\eta (t)-{\hat{\eta }}(t)),\\ \beta \dot{{\hat{d}}}(t)=a^{2}(t)(\eta (t)-{\hat{\eta }}(t)), \end{array}\right. \end{aligned}$$
(7)

where the function a(t) is a time varying high gain function.

Furthermore, to prove the exponential stability of the closed-loop system, we assume that the high gain function and its derivative are positive (i.e. \(a(t)>0\) and \(\dot{a}(t)>0\)), and satisfies the following conditions

$$\begin{aligned} \left\{ \begin{array}{l} \underset{t\ge 0}{\mathrm {sup}}\; \dfrac{\dot{a}(t)}{a(t)}=M_{0}<\infty ,\\ \underset{t\rightarrow \infty }{\mathrm {lim}}\; \dfrac{\mathrm {e}^{\delta t}}{a(t)}=0,\\ \underset{t\rightarrow \infty }{\mathrm {lim}}\; \dfrac{\arrowvert \dot{d}(t)\arrowvert }{a(t)}=0, \end{array}\right. \end{aligned}$$
(8)

where \(\delta \) is the same constant in (3) and \( M_{0} \) is a positive constant.

It is worth mentioning that from (8), we can see that the high gain function a(t) is of exponential type. Thus, there exists two constant \(\theta \) and \(\mu \) satisfying \(a(t)=\mu e^{\theta t}\).

The following lemma gives the asymptotic behavior of the solutions of extended state observer (7).

Lemma 2.1

Let \(({\hat{\eta }}(t), {\hat{d}}(t))\), be the solution of (7). If the disturbance condition (3) as well as the high gain function condition (8) hold, we have

$$\begin{aligned}&\underset{t\rightarrow \infty }{\mathrm {lim}} \arrowvert {\hat{\eta }}(t)-\eta (t)\arrowvert =\underset{t\rightarrow \infty }{\mathrm {lim}} \arrowvert d(t)-{\hat{d}}(t)\arrowvert =0, \end{aligned}$$
(9)
$$\begin{aligned}&a^{2}(t)\arrowvert {\hat{\eta }}(t)-\eta (t)\arrowvert ^{2}+\arrowvert d(t)-{\hat{d}}(t)\arrowvert ^{2}\le C_{2}e^{-2(\theta -\delta )t}, \end{aligned}$$
(10)

where \(\delta<\theta <M_0\), and \(C_2\) is some positive constant.

Proof

Set the errors \(({\tilde{\eta }},{\tilde{d}})\) as follows

$$\begin{aligned} \left\{ \begin{array}{l} {\tilde{\eta }}(t)=a(t)({\hat{\eta }}(t)-\eta (t)),\\ {\tilde{d}}(t)=d(t)-{\hat{d}}(t). \end{array}\right. \end{aligned}$$
(11)

Then, the following ODEs can be easily obtained from (5) and (7)

$$\begin{aligned} \left\{ \begin{array}{l} \dot{{\tilde{\eta }}}(t)=-\dfrac{a(t)}{\beta }({\tilde{\eta }}(t)+{\tilde{d}}(t))+\dfrac{\dot{a}(t)}{a(t)}{\tilde{\eta }}(t),\\ \dot{{\tilde{d}}}(t)=\dfrac{a(t)}{\beta }{\tilde{\eta }}(t)+\dot{d}(t). \end{array}\right. \end{aligned}$$
(12)

Thus, (9) and (10) can be easily obtained according to Theorem 2.1 and Corollary 2.1 in [28]. \(\square \)

From (9), we know that \({\hat{d}}(t),\) is the estimations of the disturbance d(t). Now, let us return to the already designed controller (4), setting \(v(t)=-{\hat{d}}(t)\) yields

$$\begin{aligned} \begin{array}{l} u(t)=-\alpha y_{t}(l,t)+EI\beta y_{x x x t}(l, t)-{\hat{d}}(t). \end{array} \end{aligned}$$
(13)

Therefore, system (2) becomes the following closed-loop system

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho y_{tt}(x,t)+EIy_{xxxx}(x,t)=\rho \omega ^2y(x,t),&{} x\in (0,l), t>0,\\ y(0,t)=y_x(0,t)=y_{xx}(l,t)=0, &{} t>0,\\ \beta \dot{\eta }(t)= d(t)-\eta (t)-{\hat{d}}(t), &{} t>0,\\ \eta (t)=-EIy_{x x x}(l, t)+\alpha y_{t}(l, t), &{} t>0,\\ \dot{{\tilde{\eta }}}(t)=-\dfrac{a(t)}{\beta }({\tilde{\eta }}(t)+{\tilde{d}}(t))+\dfrac{\dot{a}(t)}{a(t)}{\tilde{\eta }}(t), &{} t>0,\\ \dot{{\tilde{d}}}(t)=\dfrac{a(t)}{\beta }{\tilde{\eta }}(t)+\dot{d}(t), &{} t>0. \end{array}\right. } \end{aligned}$$
(14)

In the following sections, we discuss the well-posedness as well as the stability of the closed-loop system (14).

3 Formulation of the problem and the well-posedness of the closed-loop system (14)

This section is dedicated to the well-posedness of the closed-loop system (14). Clearly, if the existence and uniqueness of the \((y,\eta )\) variables is established, then the \(({\tilde{\eta }},{\tilde{d}})\)-part from system (14) (i.e. the ESO system (12)) admits a unique solution for any given initial value, since the Local Lipschitz condition of the right side of system (12) ensure the local existence and uniqueness of a solution for (12). Furthermore, we already established in Lemma 2.1 the convergence of said solution, which asserts two important results; from (9) the local solution of system (12) never blows up, so the global solution exist; also, from (10) we have the exponential stability of system (12). Therefore, the \(({\tilde{\eta }},{\tilde{d}})\)-part is no longer a concern and can be neglected in the following sections.

System (14), therefore, can be reduced to the following one

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho y_{tt}(x,t)+EIy_{xxxx}(x,t)=\rho \omega ^2y(x,t),&{} x\in (0,l), t>0,\\ y(0,t)=y_x(0,t)=y_{xx}(l,t)=0, &{} t>0,\\ \beta \dot{\eta }(t)= {\tilde{d}}(t)-\eta (t), &{} t>0,\\ \eta (t)=-EIy_{x x x}(l, t)+\alpha y_{t}(l, t), &{} t>0. \end{array}\right. } \end{aligned}$$
(15)

Let \(V_0^k:=\{y\in H^k(0,l)/y(0)=y_x(0)=0\}\) be the Sobolev spaces for \(k\in \{2,3,...\}\). We define the state space as

$$\begin{aligned} {\mathcal {X}}:=V_0^2\times L^2(0,l)\times {\mathbb {R}}, \end{aligned}$$

endowed with the new inner product

$$\begin{aligned} \langle (y_1,z_1,\eta _1),(y_2,z_2,\eta _2)\rangle = \int _0^l(EIy_1^{\prime \prime }y_2^{\prime \prime }-\rho \omega ^2y_1y_2+\rho z_1z_2)dx+ k\eta _1\eta _2, \end{aligned}$$
(16)

where \(k>\frac{\beta }{\alpha }\). Then, norm induced by the last inner product is equivalent to the usual one (see [27]) provided that

$$\begin{aligned} \vert \omega \vert < \frac{1}{l^{2}}\sqrt{\frac{12EI}{\rho }}. \end{aligned}$$
(17)

which is supposed to be valid throughout the paper. Then, we defined an unbounded linear operator A by

$$\begin{aligned} A\begin{bmatrix} y\\ z \\ \eta \\ \end{bmatrix} =\begin{bmatrix} z\\ -\frac{1}{\rho }(EIy_{xxxx}(x)-\rho \omega ^2y(x)) \\ -\frac{1}{\beta }\eta \\ \end{bmatrix}, \end{aligned}$$
(18)

for \((y,z,\eta )^T\in D(A)\) where

$$\begin{aligned} D(A)=\{ (y,z,\eta )^{T}\in V_0^4\times V_0^2\times {\mathbb {R}}\arrowvert y_{xx}(l)=0,\; \eta =-EIy_{xxx}(l)+\alpha z(l)\}. \end{aligned}$$
(19)

Now, we can reformulate the system (15) as a first-order evolution equation

$$\begin{aligned} \frac{d}{dt}\begin{bmatrix} y\\ z \\ \eta \\ \end{bmatrix} =A\begin{bmatrix} y\\ z \\ \eta \\ \end{bmatrix}+F(t), \end{aligned}$$
(20)

with the initial condition \((y_0,z_0,\eta _0)^T=(y_0(x),y_1(x),\eta (0)^T\), where

$$\begin{aligned} F(t)=\begin{bmatrix} 0\\ 0 \\ \frac{{\tilde{d}}(t)}{\beta }\\ \end{bmatrix}. \end{aligned}$$
(21)

The following theorem concerns the well-posedness of system.

Theorem 3.1

The operator A generates a C\(_0-\) semigroup of contraction \(e^{At}\) on the space \({\mathcal {X}}\). Hence, the system (20) is well-posed.

Proof

First, we show that A is dissipative. Let \(u=(y,z,\eta )^T\in D(A)\). Thanks to \(k>\frac{\beta }{\alpha }\), we have

$$\begin{aligned} \begin{aligned} \langle Au,u\rangle&= \int _0^lEI(z_{xx}y_{xx}-y_{xxxx}z)dx-EIy_{xxx}(l)z(l)-\frac{k}{\beta }\eta ^2,\\&=-EIy_{xxx}(l)z(l)-\frac{k}{\beta }\eta ^2,\\&=\left( \frac{1}{2\alpha }-\frac{k}{\beta }\right) \eta ^2-\frac{\alpha }{2}z^2(l)-\frac{EI^2}{2\alpha }y^2_{xxx}(l)\le 0. \end{aligned} \end{aligned}$$

Thus, A is dissipative in \({\mathcal {X}}\).

Next, we prove that \({\mathcal {R}}(\lambda I-A)={\mathcal {X}}\), for some \(\lambda >0\). It suffices to show that for any \(F=(f_1,f_2,f_3)\in {\mathcal {X}}\), there exits \(U=(y,z,\eta )\in D(A)\) such that \((\lambda I-A)U=F\). That is equivalent to the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} z=\lambda y-f_1,\\ \rho \lambda z+EIy_{xxxx}(x)-\rho \omega ^2y(x)=\rho f_2,\\ \beta \lambda \eta +\eta =\beta f_3,\\ \eta =-EIy_{xxx}(l)+\alpha z(l),\\ y(0)=y_x(0)=y_{xx}(l)=0. \end{array}\right. } \end{aligned}$$
(22)

Obviously, it suffices to find y. We multiply the second equation of (22) by a test function \(\varphi \in V^2_0 \). A simple integration by parts over [0, l] yields

$$\begin{aligned} \begin{aligned}&\int _0^l\rho (\lambda ^2-\omega ^2)y\varphi dx+\int _0^lEIy_{xx}\varphi _{xx} dx+\alpha \lambda y(l)\varphi (l)\\&\qquad =\int _0^l\rho (f_2+\lambda f_1)\varphi dx+\varphi (l)\left( \frac{\beta }{1+\lambda \beta } f_3+\alpha f_1(l)\right) , \end{aligned} \end{aligned}$$
(23)

which can be written as \(\Psi (y,\varphi )=L(\varphi )\), where \(\Psi (y,\varphi )\) is a continuous coercive bilinear form on \(V^2_0\times V^2_0 \) and \(L(\varphi )\) is a continuous linear form on \(V^2_0 \). Using Theorem of Lax-Milgram, there exists a unique solution \(y\in V^2_0\) of (23). Therefore, the operator A generates a C\(_0-\)semigroup of contraction \(e^{At}\) on the space \({\mathcal {X}}\) by the Lumer-Philips theorem (see [32]). Moreover, F(t) is local Lipschitz continuous on \({\mathbb {R}}^{+}\); thus, system (20) is well-posed. \(\square \)

4 Exponential stability

In this section, we discuss the exponential stability of the closed-loop system (15) using a suitable Lyapunov function. Before that we introduce the following important inequalities:

Lemma 4.1

(Young’s inequality) If a, b are non negative real numbers and p, q are positive numbers satisfying the condition \( \frac{1}{p} + \frac{1}{q} =1 \), then

$$\begin{aligned} ab \le \frac{1}{\zeta p}a^{p} + \frac{\zeta }{q}b^{q},\quad for\;any\quad \zeta >0. \end{aligned}$$

Lemma 4.2

Let w(x, t) be a function where \(x \in (0,l)\) and \(t \in (0,\infty )\) which satisfy the boundary conditions \(w(0,t)=w_{x}(0,t)=0\) for \(t \in (0,\infty )\), then we have

$$\begin{aligned}&{\arrowvert w(l,t) \arrowvert ^{2}\le \frac{l^{3}}{3}\int ^{l}_{0} \arrowvert w_{xx}(x,t) \arrowvert ^{2}dx,}\\&\arrowvert w_{x}(l,t) \arrowvert ^{2}\le l\int ^{l}_{0} \arrowvert w_{xx}(x,t) \arrowvert ^{2}dx,\\&\int ^{l}_{0} \arrowvert w(x,t) \arrowvert ^{2}dx\le l^{2}\int ^{l}_{0} \arrowvert w_{x}(x,t) \arrowvert ^{2}dx.\\&{\int ^{l}_{0} \arrowvert w(x,t) \arrowvert ^{2}dx\le \frac{l^{4}}{12}\int ^{l}_{0} \arrowvert w_{xx}(x,t) \arrowvert ^{2}dx.} \end{aligned}$$

We define the energy functional E(t) of system (15) as follows:

$$\begin{aligned} E(t) =\frac{1}{2}\int _{0}^{l} \rho y_{t}^{2}(x,t)+EI y_{xx}^{2}(x,t)\;dx-\frac{\omega ^{2}}{2}\int _{0}^{l}\rho y^{2}(x,t)\;dx+\frac{k}{2}\eta ^{2}(t). \end{aligned}$$
(24)

Now, we consider the following functionals

$$\begin{aligned} \left\{ \begin{array}{l} V_1(t) =\frac{1}{2}\int _{0}^{l} \rho y_{t}^{2}(x,t)+EI y_{xx}^{2}(x,t)\;dx-\frac{\omega ^{2}}{2}\int _{0}^{l}\rho y^{2}(x,t)\;dx,\\ V_2(t)=\frac{k}{2}\eta ^{2}(t),\\ V_3(t) =\chi \int _{0}^{l} xy_{x}(x,t) y_{t}(x,t)\;dx, \end{array}\right. \end{aligned}$$
(25)

where \(0<\chi <\min \left\{ \frac{1}{{\sigma }},\frac{\alpha }{l},{\frac{EI\rho }{l^{3}\alpha \vartheta }} \right\} \), \({\sigma }=\max \left\{ {\frac{12l^{3}}{3EI}},\frac{l}{\rho },1 \right\} \), \(k>\frac{\beta ^{2}}{m}\), and \(\vartheta >0\) a positive constant to be fixed later. Then, our Lyapunov function candidate has the following form

$$\begin{aligned} V(t)=V_1(t)+V_2(t)+V_3(t). \end{aligned}$$
(26)

Next, we show the boundedness of (26) in the following lemma.

Lemma 4.3

Let the Lyapunov function candidate V(t) be defined as in (25) and (26). If the constant velocity satisfies \({\omega ^{2}<\frac{9EI}{l^{4}\rho }}\), then there exist two positive constant \(\varrho _{1}\) and \(\varrho _{2}\), where

$$\begin{aligned} 0<\varrho _{1}(V_1(t)+\eta ^{2}(t))<V(t)< \varrho _{2}(V_1(t)+\eta ^{2}(t)), \end{aligned}$$
(27)

Proof

Using Young’s inequality, we get

$$\begin{aligned} \arrowvert V_3(t)\arrowvert \le \chi l \int _{0}^{l} {\frac{1}{2}}y_{x}^{2}(x,t) + {\frac{1}{2}}y_{t}^{2}(x,t) \;dx. \end{aligned}$$

Taking the forth inequality in Lemma 4.2 in mind, and the condition on \(\omega \) as well, i.e., \({\omega ^{2}<\frac{9EI}{l^{4}\rho }}\), we obtain

$$\begin{aligned} \arrowvert V_3(t)\arrowvert \le \chi l \int _{0}^{l} \frac{1}{2}y_{x}^{2}(x,t) + \frac{1}{2}y_{t}^{2}(x,t) \;dx +\chi \left[ \int _{0}^{l} {\frac{9EI}{24}}y_{xx}^{2}(x,t) - \frac{\rho \omega ^{2}}{2} y^{2}(x,t) \;dx \right] , \end{aligned}$$

Using the third inequality in Lemma 4.2 provides

$$\begin{aligned} \arrowvert V_3(t)\arrowvert&\le \chi l \int _{0}^{l} \frac{l^{2}}{2}y_{xx}^{2}(x,t) + \frac{1}{2}y_{t}^{2}(x,t) \;dx +\chi \left[ \int _{0}^{l} {\frac{9EI}{24}}y_{xx}^{2}(x,t) - \frac{\rho \omega ^{2}}{2} y^{2}(x,t) \;dx \right] \nonumber \\&\le \chi \max \left\{ {\frac{12l^{3}}{3EI}},\frac{l}{\rho },1 \right\} \left[ \int _{0}^{l} \frac{EI}{2}y_{xx}^{2}(x,t) + \frac{\rho }{2}y_{t}^{2}(x,t) \;dx - \frac{\rho \omega ^{2}}{2} y^{2}(x,t) \;dx \right] \nonumber \\&\le \chi {\sigma } V_1(t), \end{aligned}$$
(28)

where \( {\sigma }=\max \left\{ {\frac{12l^{3}}{3EI}},\frac{l}{\rho },1 \right\} \). Then, it follows directly from the last inequality (28) that

$$\begin{aligned} (1-\chi {\sigma }) V_1(t)+ \frac{k}{2}\eta ^{2}(t)<V(t)< (1+\chi {\sigma }) V_1(t)+ \frac{k}{2}\eta ^{2}(t). \end{aligned}$$

Since \( \chi <\frac{1}{{\sigma }} \), we finally obtain

$$\begin{aligned} 0<\varrho _{1}(V_1(t)+\eta ^{2}(t))<V(t)< \varrho _{2}(V_1(t)+\eta ^{2}(t)), \end{aligned}$$

where \(\varrho _{1}=\min \left\{ 1-\chi {\sigma },\; \frac{k}{2} \right\} \), \(\varrho _{2}=\max \left\{ 1+\chi {\sigma },\; \frac{k}{2} \right\} \). The proof is complete. \(\square \)

Theorem 4.4

Assume condition (17) holds. If the angular velocity \(\omega \), and the control gain \(\beta \) satisfy the following conditions:

$$\begin{aligned} {{\omega ^{2}<\frac{9EI}{l^{4}\rho }, \quad \beta ^{2}<km.}} \end{aligned}$$

Then, the closed-loop system (15) is exponentially stable.

Proof

A straightforward calculation yields

$$\begin{aligned} \dot{V}_{1}(t)&=\int _{0}^{l}\left[ EIy_{x x}(x, t) y_{x x t}(x, t)+\rho y_{t}(x, t) y_{t t}(x, t)\right] d x-\omega ^{2}\int _{0}^{l}\rho y(x,t)y_{t}(x,t) dx\nonumber \\&=-EIy_{x x x}(l, t) y_{t}(l, t)\nonumber \\&=\frac{1}{2 \alpha } \eta ^{2}(t)-\frac{(EI)^{2}}{2 \alpha } y_{x x x}^{2}(l,t)-\frac{\alpha }{2} y_{t}^{2}(l, t), \end{aligned}$$
(29)
$$\begin{aligned} \dot{V}_{2}(t)&=k \eta (t) \dot{\eta }(t)=-\frac{k}{\beta } \eta ^{2}(t)+\frac{k}{\beta } \eta (t) {\tilde{d}}(t). \end{aligned}$$
(30)

Moreover, we have

$$\begin{aligned} \dot{V}_{3}(t)&=\chi \left( \int _{0}^{l} x y_{t t}(x, t) y_{x}(x, t) d x+\int _{0}^{l} x y_{t}(x, t) y_{x t}(x, t) d x\right) \nonumber \\&=-\chi \dfrac{EI}{\rho }\int _{0}^{l} x y_{x x x x}(x, t) y_{x}(x, t) d x+\chi \int _{0}^{l} x y_{t}(x, t) y_{x t}(x, t) d x\nonumber \\&\quad +\chi \omega ^{2}\int _{0}^{l}xy_{x}(x,t)y(x,t)dx, \end{aligned}$$
(31)

where

$$\begin{aligned} \int _{0}^{l} x y_{t}(x, t) y_{x t}(x, t) d x&=\frac{l}{2} y_{t}^{2}(l, t)-\frac{1}{2} \int _{0}^{l} y_{t}^{2}(x, t) d x, \end{aligned}$$
(32)

similarly,

$$\begin{aligned} \int _{0}^{l}xy_{x}(x,t)y(x,t)dx = \frac{l}{2} y^{2}(l, t)-\frac{1}{2} \int _{0}^{l} y^{2}(x, t) d x, \end{aligned}$$
(33)

also,

$$\begin{aligned} \int _{0}^{l} x y_{x x x x}(x, t) y_{x}(x, t) d x =&x y_{x}(x, t) y_{x x x}(x, t)\arrowvert _{0} ^{l}-\int _{0}^{l} y_{x x x}(x, t)\left( y_{x}(x, t)+x y_{x x}(x, t)\right) d x \nonumber \\ =&x y_{x}(x, t) y_{x x x}(x, t)\arrowvert _{0} ^{l}-y_{x x}(x, t) y_{x}(x, t)\arrowvert _{0} ^{l}+\int _{0}^{l} y_{x x}^{2}(x, t) d x \nonumber \\&-\frac{x}{2} y_{x x}^{2}(x, t)\arrowvert _{0} ^{l}+\frac{1}{2} \int _{0}^{l} y_{x x}^{2}(x, t) d x \nonumber \\ =&\, ly_{x}(l, t) y_{x x x}(l, t)+\frac{3}{2} \int _{0}^{l} y_{x x}^{2}(x, t) d x. \end{aligned}$$
(34)

Reporting (32), (33), and (34) into (31) yields

$$\begin{aligned} \dot{V}_{3}(t)&=\frac{\chi l}{2} y_{t}^{2}(l, t)-\chi \frac{EIl}{\rho }y_{x}(l, t) y_{x x x}(l, t)-\frac{3 \chi }{2}\frac{EI}{\rho } \int _{0}^{l} y_{x x}^{2}(x, t) d x-\frac{\chi }{2} \int _{0}^{l} y_{t}^{2}(x, t) d x\nonumber \\&\quad +\frac{\chi \omega ^{2} l}{2} y^{2}(l, t)-\frac{\chi \omega ^{2}}{2} \int _{0}^{l} y^{2}(x, t) d x. \end{aligned}$$
(35)

Using Lemma 4.1 and the second inequality in 4.2, we get

$$\begin{aligned} \chi \frac{EIl}{\rho }y_{x}(l, t) y_{x x x}(l, t)\le \frac{\chi EI}{2\rho {\vartheta }}\int ^{l}_{0}y_{xx}^{2}(x,t)dx+\frac{\chi {\vartheta } EIl^{3}}{2\rho }y_{xxx}^{2}(l,t). \end{aligned}$$
(36)

where \(\vartheta >0\) is a positive constant. Thus, reporting (36) into (35) yields

$$\begin{aligned} \dot{V}_{3}(t)&\le \frac{\chi l}{2} y_{t}^{2}(l, t)+\frac{\chi EI}{2\rho {\vartheta }}\int ^{l}_{0}y_{xx}^{2}(x,t)dx+\frac{\chi {\vartheta } EIl^{3}}{2\rho }y_{xxx}^{2}(l,t)-\frac{3 \chi }{2}\frac{EI}{\rho } \int _{0}^{l} y_{x x}^{2}(x, t) d x\nonumber \\&\quad -\frac{\chi }{2} \int _{0}^{l} y_{t}^{2}(x, t) d x +\frac{\chi \omega ^{2} l}{2} y^{2}(l, t)-\frac{\chi \omega ^{2}}{2} \int _{0}^{l} y^{2}(x, t) d x. \end{aligned}$$
(37)

Obviously, a direct calculation yields

$$\begin{aligned} \dot{V}(t)=\dot{V}_1(t)+\dot{V}_2(t)+\dot{V}_3(t). \end{aligned}$$
(38)

Therefore, from (29),(30) and (37), we see that (38) becomes

$$\begin{aligned} \dot{V}(t)&\le -\left[ \frac{k}{\beta }-\frac{1}{2 \alpha }\right] \eta ^{2}(t)-\frac{EI}{2}\left[ \frac{EI}{ \alpha }-\frac{\chi \vartheta l^{3}}{\rho }\right] y_{x x x}^{2}(l,t)-\left[ \frac{\alpha }{2}-\frac{\chi l}{2}\right] y_{t}^{2}(l, t)\nonumber \\&\quad +\frac{\chi EI}{2\rho \vartheta }\int ^{l}_{0}y_{xx}^{2}(x,t)dx-\frac{3 \chi }{2}\frac{EI}{\rho } \int _{0}^{l} y_{x x}^{2}(x, t) d x-\frac{\chi }{2} \int _{0}^{l} y_{t}^{2}(x, t) d x \nonumber \\&\quad +\frac{\chi \omega ^{2} l}{2} y^{2}(l, t)-\frac{\chi \omega ^{2}}{2} \int _{0}^{l} y^{2}(x, t) d x+\frac{k}{\beta } \eta (t) {\tilde{d}}(t). \end{aligned}$$
(39)

According to the first inequality in Lemma 4.2 and Young’s inequality, we further have

$$\begin{aligned} \frac{\chi \omega ^{2} l}{2} y^{2}(l, t)&\le {\frac{\chi \omega ^{2} l^{4}}{6}}\int ^{l}_{0} y_{xx}^{2}(x, t)dx, \end{aligned}$$
(40)
$$\begin{aligned} \frac{k}{\beta } \eta (t) {\tilde{d}}(t)&\le \frac{k}{2\beta } \eta ^{2}(t)+\frac{k}{2\beta } {\tilde{d}}^{2}(t). \end{aligned}$$
(41)

Thus, estimate (39) becomes

$$\begin{aligned} \dot{V}(t)&\le -\left[ \frac{k}{2\beta }-\frac{1}{2 \alpha }\right] \eta ^{2}(t)-\frac{EI}{2}\left[ \frac{EI}{ \alpha }-\frac{\chi \vartheta l^{3}}{\rho }\right] y_{x x x}^{2}(l)-\left[ \frac{\alpha }{2}-\frac{\chi l}{2}\right] y_{t}^{2}(l, t)\nonumber \\&\quad +\frac{k}{2\beta } {\tilde{d}}^{2}(t)-\dfrac{\chi }{2\rho }\left[ 3EI-\frac{\omega ^{2}\rho l^{4}}{3}-\frac{EI}{\vartheta }\right] \int _{0}^{l} y_{x x}^{2}(x, t) d x-\frac{\chi }{2} \int _{0}^{l} y_{t}^{2}(x, t) d x\nonumber \\&\quad -\frac{\chi \omega ^{2}}{2} \int _{0}^{l} y^{2}(x, t) d x. \end{aligned}$$
(42)

Taking into account the condition \({\omega ^{2}<\frac{9EI}{l^{4}\rho }}\), we can choose \(\vartheta \) in order to have

$$\begin{aligned} {3EI-\frac{\omega ^{2}\rho l^{4}}{3}-\frac{EI}{\vartheta }>0}. \end{aligned}$$

Since \(k>\frac{\beta ^{2}}{m}\), \(0<\chi <\min \left\{ \frac{\alpha }{l},{\frac{EI\rho }{l^{3}\alpha \vartheta }} \right\} \), it holds that

$$\begin{aligned} \frac{k}{2\beta }-\frac{1}{2 \alpha }>0,\quad {\frac{EI}{ \alpha }-\frac{\chi \vartheta l^{3}}{\rho }\ge 0},\quad \frac{\alpha }{2}-\frac{\chi l}{2}\ge 0. \end{aligned}$$

Therefore, adding the term \( \frac{\delta _{1}\omega ^{2}\rho }{2} \int _{0}^{l} y^{2}(x, t) d x \) to (42), using estimate (27), and setting \(\delta _{1}=\min \left\{ \frac{k}{2\beta }-\frac{1}{2 \alpha }, \frac{\chi }{EI\rho }\right. \left. \left[ { 3EI-\frac{\omega ^{2}\rho l^{4}}{3}-\frac{EI}{\vartheta }}\right] ,\frac{\chi }{\rho } \right\} \) and \(\nu =\frac{\delta _{1}}{\varrho _{2}}\) yields

$$\begin{aligned} \dot{V}(t)&\le -\delta _{1} \left[ \eta ^{2}(t)+\frac{1}{2}\int _{0}^{l} EIy_{x x}^{2}(x, t) d x+\frac{1}{2}\int _{0}^{l} \rho y_{t}^{2}(x, t) d x-\frac{\omega ^{2}\rho }{2} \int _{0}^{l} y^{2}(x, t) d x\right] \nonumber \\&\quad +\frac{k}{2\beta } {\tilde{d}}^{2}(t)\nonumber \\&\le -\delta _{1}\left[ \eta ^{2}(t)+V_1(t)\right] +\frac{k}{2\beta } {\tilde{d}}^{2}(t)\nonumber \\&\le -\nu V(t) +\frac{k}{2\beta } {\tilde{d}}^{2}(t), \end{aligned}$$
(43)

Now, from estimates (43), (10), and according to Gronwall’s inequality, we obtain

$$\begin{aligned} V(t)&\le \frac{kC_{2}}{2\beta } \int _{0}^{t}e^{-\nu (t-s)}e^{-2(\theta -\delta )s}\;ds\nonumber \\&\quad +\mathrm {e} ^{-\nu t}V(0)\nonumber \\&\le \frac{kC_{2}}{2\beta }\frac{1}{2(\theta -\delta )-\nu } \left[ e^{-2(\theta -\delta )t}-e^{-\nu t}\right] \nonumber \\&\quad +\mathrm {e} ^{-\nu t}V(0)\nonumber \\&\le \delta '_{0} \max \left\{ e^{-2(\theta -\delta )t},e^{-\nu t}\right\} +\mathrm {e} ^{-\nu t}V(0), \end{aligned}$$
(44)

where \( \delta '_{0}=\frac{kC_{2}}{2\beta }\frac{1}{\arrowvert 2(\theta -\delta )-\nu \arrowvert } \). Set

$$\begin{aligned} \nu _{1}&=\min \arrowvert \nu , 2(\theta -\delta ) \arrowvert ,\\ \delta _{0}&=V(0)+\frac{kC_{2}}{2\beta }\frac{1}{\arrowvert 2(\theta -\delta )-\nu \arrowvert }. \end{aligned}$$

Hence,

$$\begin{aligned} V(t)\le \delta _{0}e^{-\nu _{1}t}. \end{aligned}$$

Moreover, it is evident that the energy function E(t) from (24) satisfies

$$\begin{aligned} \varrho '_{1}(V_1(t)+\eta ^{2}) \le E(t) \le \varrho '_{2} (V_1(t)+\eta ^{2}), \end{aligned}$$
(45)

where \( \varrho '_{1}=\min \left\{ 1,\frac{k}{2}\right\} \) and \( \varrho '_{2}=\max \left\{ 1,\frac{k}{2}\right\} \); thus, using (27), (44), and (45) yields

$$\begin{aligned} E(t)\le \frac{\varrho '_{2}}{\varrho _{1}} \delta _{0}\mathrm {e}^{-\nu _{1} t}. \end{aligned}$$

This ends the proof. \(\square \)

Fig. 2
figure 2

Displacement y(x, t) without control

Full size image

5 Numerical simulation

In this section, we present some numerical simulations for system (2) using finite difference method in time and space for the space-time domain \([0,1]\times [0,10]\). Here, we subdivided the spatial interval into \(N=10\) subintervals and the temporal interval into \(M=30000\) subintervals. The parameters, the initial data, disturbance and the time varying high gain function are chosen as

$$\begin{aligned} \left\{ \begin{array}{l} \rho =1,\; EI=1,\; \omega =-2,\; \alpha =2,\; \beta =1,\\ y(x,0)=0.2(-3x^2+2x^3),\\ y_t(x,0)=-0.2(-3x^2+2x^3),\\ d(t)=\frac{t^2}{60}\exp (0.08(t-1)),\\ a(t)=2\exp (0.2t). \end{array} \right. \end{aligned}$$

From Fig. 2, we can see that without control (i.e. \(\alpha =\beta =0\)) the displacement y(x, t) is not stabilized. Examining Fig. 3, we can notice that the vibration of the system is greatly suppressed when the developed control is applied to the system. From Fig. 4, we can observe that the disturbance d(t) and its estimation \({\hat{d}}(t)\) are almost the same only after 4s. Consequently, the estimation \({\hat{d}}(t)\) can be used to track the disturbance d(t) very fast.

Fig. 3
figure 3

Displacement y(x, t) with control

Full size image
Fig. 4
figure 4

Disturbance d(t), estimation \({\hat{d}}(t)\), and error \({\tilde{d}}(t)=d(t)-{\hat{d}}(t)\)

Full size image

6 Concluding remarks

In this paper, we studied the stabilization problem of a uniformly rotating disk-beam-mass system with a boundary disturbance. The ADRC approach was used to design the controller, where the extended state observer (ESO) was, first, constructed to estimate the disturbance, then, the control force uses these estimations to online cancel the disturbance effect. The well-posedness of the system is proved using the semigroup theory. Finally, we showed that the closed-loop system is exponentially stable by the Lyapunov method.

An interesting research problem would be the extension of the results presented in this paper to the time-varying angular velocity case and the non-uniform beam case. It would be, also, interesting to study the exponential stabilization for the system when the moment of inertia is accounted for. These will be the subject of future works.