Constraining spacetime deformation based on astrophysical observations from radio pulsars

Abstract

The present work is devoted to investigations of cut-off for plasma magnetospheric radiations around magnetized neutron stars in the presence of spacetime deformation. In this way, we first analysed behaviour deathline conditions of curvature radiations (CR), and inverse Compton scattering (ICS) around deformed neutron stars. Through the analyses, we have obtained upper limits for the deformation parameter which causes switchingof pulsars in radio to $\gamma$-rays bands of the electromagnetic spectrum. It is observed that the upper limits for the radio waves and $\gamma$-rays cut off are not the same, but they are different, the limit is higher for radio wave cut off than $\gamma$-rays. Moreover, our detailed analyses show that this limit also depends on the period of pulses from pulsars and its delay (period derivation). Finally, we have obtained upper limits for the deformation parameter for selected several millisecond pulsars using the deathline conditions.

Introduction

Testing gravity theories in measurements of observational parameters of pulsars and magnetars is one of the most important issues in neutron star physics. In fact, neutron stars being fast-rotating highly magnetized astrophysical relativistic compact object play a cosmic laboratory role in testing strong gravity regime physics. In fact, for electromagnetic radiations of neutron stars, several factors play a significant role: surface magnetic field strength, rotational period of neutron stars, and feature of the strong gravitational field around the neutron star. All factors can affect the switching of the pulsars.

For the first time, the vacuum magnetospheric model of rotating magnetized neutron stars have been studied by Deutch [7] in the non-relativistic case, and general relativistic effects have been taken into account in Refs. [31]. The study has also been carried out in alternative theories of gravity and modified gravity by numerous authors [2, 5, 25, 27, 35]. In fact, a strong magnetic field and fast rotation of neutron stars cause the formation of a plasma consisting of electron-positron pair, so it is called the plasma magnetospheric model. This model was first suggested by Goldreich and Julian [10]. In past years, the model has been developed by a number of authors in the frames of various gravity models [1, 18,19,20,21, 24, 26, 28, 30].

Co-rotation of magnetic field line can be extended up to the distance of so-called light cylinder, where the speed of magnetic field lines equals to speed of light in vacuum. Thus, the magnetic field line is divided mainly into two groups: closed and open field lines [4, 34]. In the observation of neutron stars, an important issue is a radiation by accelerated electrons and positrons in the open field line region, which comes from the region so-called polar cap [33, 36]. The physics of acceleration mechanisms in the polar cap region is studied and developed in Refs. [22, 23, 30]. In their works, depending on acceleration models, the acceleration region has been divided to three regions: polar cap, outer gap, and inner gap regions.

The polar cap acceleration model tells that electrons, pulled out from the polar cap of the neutron star, accelerate along open field due to parallel electric field and radiate high-energy photons ($\gamma$ rays), in turn, $\gamma$ rays in the high magnetic field create electron-positron pairs, then the cascade pair production fills out around the neutron star with plasma [32]. However, according to the rotation-powered neutron star model, the neutron star ages as it radiates electromagnetic waves, and it slows down. When the electric field becomes weak enough to carry on secondary plasma formation, and the radiation stops, it means the neutron star (pulsar) disappears from the observations. This cut off the observation defines by a condition, so-called deathline for ICS and CR [5, 15, 27].

One of the alternative approaches to finding spacetime metrics is a perturbation of an exact analytical solution, which is obtained in the GR framework. As a perturbation parameter one can express a series of small parameters and this approach is called parameterization of the spacetime [13, 14, 38]. Various properties of the spacetime obtained by Johannson and Psaltis in Ref. [14] have been studied by several authors in detail for the spacetime around neutron stars [3, 11, 27, 29, 30].

In pulsar observations, except mass and radii measurements, it is important to get information on the feature of spacetime around the neutron stars. In other words, which theory of gravity plays a dominant role around the neutron star. In our previous works [27, 30], we have studied electromagnetic fields and plasma magnetosphere around rotating dipolar magnetized neutron stars in deformed spacetime using Johannsen-Psaltis parametrized solution. Moreover, we have also been investigated behaviour of deathline for radio pulsars with respect to the variability of deformation parameters through ICS. In this work, we plan to extend our calculations to CR, which mostly corresponds to X and $\gamma$ rays band of electromagnetic waves. The main aim of this work is to constrain the deformation parameter of the spacetime around observed neutron stars using precious data from pulsars and magnetars observations.

Neutron stars in deformed spacetime

First, we would like to explain why neutron stars are considered as slowly rotating compact relativistic objects. In reality, a neutron star, with total mass M and radius R, has its proper spin parameter a and its ratio to mass can be estimated in the following form

$$\begin{aligned} \frac{a}{M}=\frac{J}{M^2c}=\frac{I\varOmega }{M^2}\simeq \frac{1}{15} \left( \frac{P}{1\ \mathrm ms}\right) ^{-1}\left( \frac{M}{1.4M_\odot }\right) ^{-1}\left( \frac{R}{10\ \mathrm km}\right) ^2, \end{aligned}$$

(1)

where J and I are the angular momentum and moment of inertia of the neutron star, respectively, and P is the period of the star correspondingly, the angular velocity of the star is $\varOmega =2\pi /P$. The estimation shows that the value of the square of dimensionless spin parameter even for millisecond pulsars (with mass 1.4 $M_\odot$ and radii 10 km) is about $\sim 0.0044$ ($\sim 0.4\%$), so we can neglect it. This estimation implies that neutron stars best fit to slow rotation approximation.

The deformed spacetime around slowly rotating neutron stars describes in the Hartle Thorne approximation through the Boyer–Lindquist coordinates ($t, r, \theta , \varphi$) in the following form [12, 14]:

$$\begin{aligned} \mathrm{d}s^2= & {} -N^2 (1+h) \mathrm{d}t^2+N^{-2}(1+h)\mathrm{d}r^2 +r^2 \mathrm{d}\theta ^2 +r^2\sin ^2\theta \mathrm{d}\varphi ^2\nonumber \\&\quad -2\omega _*(r)r^2\sin ^2\theta \mathrm{d}t \mathrm{d}\varphi , \end{aligned}$$

(2)

where

$$\begin{aligned} N^2=1-\frac{2M}{r}, \quad r \ge R, \end{aligned}$$

(3)

and

$$\begin{aligned} \omega _*(r)=\omega _\mathrm{LT}(1+h), \quad \omega _\mathrm{LT}=\frac{2aM}{r^3}, \end{aligned}$$

(4)

$\omega _\mathrm{LT}$ is the angular velocity of the dragging of inertial frames, so-called the Lense–Thirring angular velocity, and

$$\begin{aligned} h=\sum _{k=1}^{\infty }\epsilon _k \left( \frac{M}{r}\right) ^k \end{aligned}$$

(5)

is a small dimensionless parameter that corresponds to the perturbation of the spacetime. $\epsilon _0\ll 1$ and similarly $\epsilon _1 \ll M/r$ and $\epsilon _2\simeq 4.6\times 10^{-6}$ (it is obtained by the observational data of the Laser Lunar Ranging experiment [37] are also very small. The $\epsilon _3=\epsilon$ is called the deformation parameter, and it can be either positive and/or negative, describing oblate and prolate deformations respectively. Thus, $k=3$ [14]. In further calculations, we use $\epsilon _3$ as $\epsilon$.

The solution of the Maxwell equations for the deformed spacetime described by Eq. (2) have been found under the following assumptions: (i) the neutron star’s magnetic moment is constant ; (ii) the neutron star’s inner medium consists of a perfect fluid matter and infinite conductivity $\sigma \rightarrow \infty$, and (iii) the deformation of the relativistic star due to rotation is small enough to be neglected. Moreover, we will also work in the linear approximation in angular velocities (${\mathcal {O}}(\varOmega ^2)$ and ${\mathcal {O}}(\omega ^2)$).

Deathline condition for neutron star radiation in deformed spacetime

In fact, the energy source of neutron stars’ radiation can be either is their rotational kinetic energy (rotation powered pulsar model) [9] and high magnetic field (magnetically powered pulsars). According to these models, when a pulsar ages its magnetic field (quite) weakens and the rotation slows down. These (magnetic field and kinetic energy) losses reduce the decrease of accelerating parallel (to magnetic field lines) electric field in the polar cap region and the field can not be provided to the secondary plasma (pair) formation which is one of the source mechanisms of polar cap radiation. We are interested in which values of the deformation parameter the deathline condition satisfies and the pulsar radiation cuts out, disappearing from the pulsar observations at the given position and electromagnetic waveband.

According to the plasma magnetospheric model, radio pulsars can generate electromagnetic waves in the open magnetic field lines region under the process of producing plasma magnetosphere through the cascade generation of the electron-positron pairs. For this, the magnetic field could satisfy the following condition [16]:

$$\begin{aligned} B_{\mathrm{cr}}\ge B_{\mathrm{surf}}\ge B_{\mathrm{DL}} , \end{aligned}$$

(6)

where

$$\begin{aligned} B_{\mathrm{surf}} \simeq 6.4 \times 10^{19}\sqrt{P{\dot{P}}}, \end{aligned}$$

(7)

is given in Gauss, and it is the magnetic field of the neutron star’s surface which defines by pulsar’s spin period and period derivative, $B_{\mathrm{Schw}} = m^2 c^3/e \hbar \approx 4.4 \times 10^{13}\mathrm G$ is quantum Schwinger limit, which supports the cyclotron energy of electron equals to its rest mass-energy. Consequently, $B_{\mathrm{DL}}$ is the minimum value of the magnetic field corresponding to the "death line" regime that causes to switch off the pulsars, cutting out the pair production in the polar cap region. Death line for pulsars depend on first, configurations of the magnetic field at the surface of the neutron star and second, mechanism of origin of photons that carries out pair production by CR and/or ICS.

When Lorentz factors of the primary electrons pulled out from the neutron star surface is in the order $10^5 \div 10^7$, then they radiate high energetic $\gamma$ rays by curvature radiation and if it is about $10 \div 10^2$ then radiate thermal X-ray via ICS which in turn provides the pairs cascade production [17].

It implies that the effect of the deformation parameter of spacetime around neutron stars for ICS and CR processes should be different. Below, we investigate the deathline conditions for both radiation processes: ICS and CR processes in detail.

Constraining the deformation parameter of neutron stars by the deathline conditions

In this section, we study deathline conditions for pulsars in deformed spacetime and get upper limits for the deformation parameters of spacetime around pulsars. In fact, pulsar radiation comes from their polar cap region through ICS and CR processes. Below, we discuss the cut-off conditions separately for each radiation mechanism.

Inverse Compton scattering deathline

In this mechanism of radiation by ICS of photons, higher energy electrons increase the energy of scattered low-energy photons. When the electron energy is not enough to increase the low-energy photon that in turn create electron-positron pairs with less than $2m_ec^2$. Thus, the secondary pair production cuts out in the polar cap region. The total energy accelerated electron can be defined by their Lorentz Factor and the intensity of emitted the electromagnetic waves is also defined by the factor [15]

$$\begin{aligned} \gamma =\frac{e \varPhi }{m_e c^2}=10^6 \frac{B_{12}}{P_{s}^{2}}\left[ 1+h_1-\frac{1}{\eta ^3}(1+h)\right] , \end{aligned}$$

(8)

where the denotes $\varPhi$ is scalar potential [30]. Here we use new dimensionless radial coordinate, $\eta =r/R$ and impact parameter of neutron stars, $\varepsilon =2M/R$. In consequences, the perturbative function takes the form, $h=\epsilon \ \varepsilon ^3/(8\eta ^3)$ and its surface value, $h_1=\epsilon \ \varepsilon ^3/8$. $B_{12}=B/10^{12} \mathrm G$-normalized value of the magnetic field strength on $10^{12} \mathrm{G}$ and $P_s$ is rotational period of the neutron star normalized to a second. Thus, the deathline condition for the ICS mechanism in radio pulsars which allows getting upper limits for deformation parameter of the spacetime around the pulsars, take the form

$$\begin{aligned} 74 \frac{B_{12}^2}{P_s^{2.5}}=\frac{\eta ^2}{1+h_1-\frac{1}{\eta ^3}(1+h)}. \end{aligned}$$

(9)

One can find the critical distance where the pair production stops can be found as a solution of the equation which derivation right-hand side of Eq. (9) and equalling it to zero, and we had [27],

$$\begin{aligned} \eta _\mathrm{cr}^3=\frac{A}{4 \left( 1+h_1\right) }, \end{aligned}$$

(10)

where $A=5+\sqrt{5^2+4^3 h_1 \left( 1+h_1\right) }$. One can have the dependence of deathline condition from the deformation parameter, substituting the critical distance in Eq. (9). Thus, the equation of the deathline condition for the ICS mechanism in $P-{\dot{P}}$ space has the following form

$$\begin{aligned} \lg P=\frac{2}{3}\lg {\dot{P}}+3.046+\lg f(\epsilon ), \end{aligned}$$

(11)

where

$$\begin{aligned} f^{\frac{5}{2}}(\epsilon )=4.64 \left( 1+h_1\right) \left( \frac{1+h_1}{A}\right) ^{\frac{2}{3}} \frac{A+8 h_1 \left( 1+h_1\right) }{ A+6.4 h_1 \left( 1+h_1\right) } . \end{aligned}$$

(12)

Now, we will analyse effects of deformation parameter on the pulsar deathline.

Fig. 1

Deathline for pulsars in $P-{\dot{P}}$ space

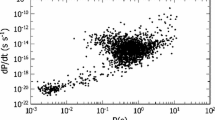
In Fig. 1 we have demonstrated deathline for radio pulsars in $P-{\dot{P}}$ space for the different values of the deformation parameter $\epsilon$. It is seen from the figure that positive values of the parameter shift down the deathline, while negatives of the parameter shift it up. Moreover, in this figure, we also have shown the positions of several pulsars. As an example, we have named some of them a, b, c and d with $\odot$ which are corresponding to the pulsars J2145-0750, J0024-7204D, J0024-7204H, and J0579-6523K, respectively. According to deathline conditions, pulsars can emit electromagnetic radiations only if their position lies above the deathline. Thus, if a pulsar lies under the line, the pulsar is invisible in the radio band. Using the deathline condition given in Eq. (11) we have calculated upper limits for the deformation parameter of spacetime around the above-mentioned pulsars numerically assuming in the limit the pulsar’s position lies on the deathline. The upper limit means that if the deformation parameter of a pulsar exceeds the limit, the pulsar disappears from the pulsar observations in the given band of electromagnetic waves. Our calculations show that the limit for the pulsar J2145-0750 is $\epsilon =-26.5$, and for pulsars J0024-7204D, J0024-7204H, and J0579-6523K, it is $\epsilon =-86.3,\ 4.273$ and 17.4, respectively.

Curvature radiation deathline

Now, we will carry on the deathline condition calculations for the CR cut off process. In this cut-off, if photons the energy less than $2m_ec^2$ produced by the accelerated charged particles, they can not be enough energy that produces any more electron-positron pairs. Thus, secondary pair production in the plasma magnetosphere around rotating neutron stars, due to slow rotation or/and weak magnetic field. To have estimations for limits for the deformation parameter by the deathline position of pulsars in the $P-{\dot{P}}$ diagram, we assume that the open magnetic field lines are plays a role in the curvature radius of accelerating charged particles [6, 32, 39]. The deathline condition in this approach,

$$\begin{aligned} \lg P\simeq \frac{4}{9}\lg {\dot{P}}-7.37+\frac{4}{9}\lg \rho _{6}\ , \end{aligned}$$

(13)

where, $\rho _{6}$ is the curvature radius of the open magnetic field lines normalized to the typical radius $10^6 \,\mathrm{cm}$ of the neutron star. In fact, it is hard to calculate the radius of the curvature of open field lines, however, they can minimum be equal to the critical distance from the surface of the star, $\rho _{6}\equiv \eta _{cr}$.

Here, we provide numerical calculations based on Eq. (13) using observational parameters of J2145-0750, J0024-7204D and J0024-7204H pulsars and get upper limits for the deformation parameter of their spacetime.

Table 1 Upper limits for the deformation parameters of spacetime around pulsars J2145-0750, J0024-7204D and J0024-7204H [8]

In Table 1 we have shown the observational parameters of pulsars J2145-0750, J0024-7204D and J0024-7204H, and corresponding upper limits for their spacetime’s deformation parameters. All the upper limits have been found numerically, it is seen that the upper limits for the deformation parameter are larger for ICS than CR. One can see that the upper limit large for the smaller period and period derivative of pulsars. Moreover, comparisons of the limits obtained in the ICS mechanism show that the upper limits in CR are bigger than it’s in ICS.

Conclusions

In this paper, we have investigated cut-off for plasma magnetospheric radiations around slowly rotating magnetized neutron stars in the presence of spacetime deformation. We have first shown that the square of rotation parameter for rotating neutron stars is very small, even for millisecond pulsars, the contribution is about 0.4 %. This estimation shows that the spacetime around neutron stars can be assumed as a slowly rotating spacetime. Then, we have analysed behaviour deathline conditions for pulsars’ radiations through curvature radiations (CR), and inverse Compton scattering (ICS) in the polar cap of the neutron stars. Using these analyses, we have been able to obtain upper limits for the deformation parameter around neutron stars that causes switching of pulsars in radio to $\gamma$-ray bands of the electromagnetic spectrum. It is obtained that the upper limits for the radio waves and $\gamma$ rays cut off are not the same, but they are different, the limit is higher for radio cut off than $\gamma$-ray. Moreover, our detailed analyses show that this limit also depends on the period of pulses from pulsars and its delay (period derivation). Finally, we have obtained upper limits for the deformation parameter of millisecond pulsars J2145-0750, J0024-7204D, J0024-7204H, and J0579-6523K using the deathline conditions in both ICS and CR mechanisms.