An improvised collocation algorithm to solve generalized Burgers’–Huxley equation

Abstract

In the proposed work, an improvised collocation technique with cubic B-spline as basis functions is applied to obtain the numerical solution of non-linear generalized Burgers’–Huxley equation, which has application in the soliton theory. In this technique, posteriori corrections are made to the cubic B-spline interpolant and its higher-order derivatives, which leads to enhancement in the order of convergence in the spatial domain. The temporal domain is discretized using a weighted finite difference scheme, to obtain the solution at each time level and the spatial domain is discretized using the improvised cubic B-spline collocation method. The stability analysis is carried out using the von Neumann scheme and the technique is found to be unconditionally stable. The theoretical proof of the order of convergence is discussed in detail using Green’s function approach. The $L_{2}$, $L_{\infty }$, and absolute error norms are calculated as well as compared with the results available in the literature, which shows the improvement and efficacy of the proposed technique over the existing ones.

1 Introduction

Consider the one-dimensional generalized Burgers’–Huxley (gBH) equation as follows:

$$\begin{aligned} z_{t} = z_{xx} + {\mathfrak {f}}(x,t,z,z_{x}),\quad \text {in}\ \varPhi = \varPhi _{x} \times \varPhi _{t}, \end{aligned}$$

(1.1)

with the following initial and boundary conditions:

$$\begin{aligned}&z = z^{0},\quad \text {in}\ \bar{\varPhi }_{x} \times \{t_{0}\}, \end{aligned}$$

(1.2)

$$\begin{aligned}&{\mathfrak {B}}z = \varOmega ,\quad \text {on}\ \partial \varPhi _{x} \times \varPhi _{t}. \end{aligned}$$

(1.3)

For further use, define Eq. (1.1) in the operator form as follows:

$$\begin{aligned} {\mathfrak {L}} \equiv z_{xx} - z_{t} + {\mathfrak {f}}(x,t,z,z_{x}), \end{aligned}$$

(1.4)

where ${\mathfrak {f}}(x,t,z,z_{x}) = -\beta z^{\delta } z_{x} + \gamma z (1-z^{\delta })(z^{\delta } - \eta )$, $\varPhi _{x} = (x_{L},x_{R})$, $\varPhi _{t} = (t_{0},T)$, ${\mathfrak {B}}$ is the boundary operator defined as ${\mathfrak {B}}z = a_{1}(x,t)z(x,t) + a_{2}(x,t)z_{x}(x,t)$. Here $\beta \ge 0$ is a real constant (coefficient of advection), $\gamma > 0$ (reaction coefficient), $\delta \ge 1$, and $\eta \in (0,1)$ is a real constant. This equation involves non-linear phenomenon such as convection effect, reaction mechanism as well as diffusion transport.

When $\beta =0$ and $\delta =1$, Eq. (1.1) represents the Huxley equation, which explains the mechanism of nerve pulse propagation and wall motion, inside the liquid crystals [32]. When $\gamma = 0$ and $\delta =1$, Eq. (1.1) reduces to the Burgers’ equation [3], which describes the dissipative systems with wave propagation. With $\beta =0$, $\gamma = 1$, and $\delta =1$, Eq. (1.1) turns out to be the FitzHugh–Nagoma equation [11] with its application in the transmission of nerve impulses. With $\delta =1$ and $\beta ,~ \gamma \ne 0$, Eq. (1.1) becomes the Burgers’–Huxley equation [15].

Initially, the generalized Burgers’–Huxley equation was investigated by Satsuma et al. [26] with its application in soliton theory. The wave solution of this equation was given by Wang et al. [32] using certain non-linear transformations. Ismail et al. [19] solved the Burgers’–Huxley and Burgers’–Fisher equation using the Adomian decomposition method. Hashim et al. [14] obtained a series solution without any discretization, linearization, or special transformation, using Adomian decomposition technique and established the sufficient condition for convergence. Batiha et al. [4] used the variational iterative scheme by incorporating a correction functional with a general Lagrange multiplier. Sari et al. [25] adapted up to tenth-order finite difference technique based on Taylor’s series expansion combined with the Runge–Kutta method to solve the gBH equation. Bratsos [5] applied the fourth-order implicit finite difference scheme for spatial domain and improved predictor-corrector method to solve the non-linear system of differential equations. Dehghan et al. [9] implemented methods based on interpolation scaling functions and a mixture of collocation and finite difference for solving the gBH equation.

A nodal Galerkin method was applied by El-Kady et al. [10] to discretize the spatial domain. Cardinal Chebyshev and Legendre polynomials were taken as basis functions with Chebyshev and Legendre Gauss–Lobatto points as nodal points. Gauss quadrature formula and El-Gendi method was used to convert the problem into a system of ODEs, which was further solved by RK method of fourth-order. Mittal and Tripathi [22] proposed the modified cubic B-spline collocation method (MCSCM), without discretizing the temporal domain. A system of first-order ODEs is obtained, which was solved using the SSP-RK54 scheme. An exponential finite difference (EFD) scheme was used by Inan and Bahadir [16] to solve the gBH equation. The application of the EFD method leads to a system of non-linear equations, which was linearized by Newton’s method at each time step and the system was solved by the Gauss elimination method. Singh et al. [31] applied the modified cubic B-spline differential quadrature method (MCBDQM) with the SSP-RK43 scheme to solve the gBH equation. Chen [6] discretized the spatial domain using the multiscale Galerkin technique (MGT) with multiscale orthonormal bases in $H^{1}_{0}(0,1)$. A third-order SSP-RK method was used to solve the system of differential equations. A hybrid B-spline collocation method (HSCM) was used by Wasim et al. [33] in which the temporal domain is discretized using the Crank–Nicolson scheme. A cardinal B-spline wavelet approach was followed by Shiralashetti and Kumbinarasaiah [30] and hyperbolic-trigonometric tension B-spline method was implemented by Alinia and Zarebnia [2] to solve the gBH equation.

A hybrid form of cubic B-spline collocation method was applied to solve the different types of differential equations such as third-order Emden–Flower type equations [17], non-linear singular boundary value problems [18], third-order Korteweg–de Vries equation [1], second-order singular boundary value problems [34], etc. In the present work, an improvised collocation method is used to solve the gBH equation. To date, different equations have been solved using the proposed improvised technique such as RLW and MRLW equation [27], modified Burgers’ equation [28], singularly perturbed boundary value problems [29], etc. The motivation behind the paper is to solve such an important equation having large applications, with better accuracy in results as well as higher-order of convergence.

The paper is organized as, in Sect. 2 the properties and also posteriori improvements of cubic B-spline interpolant and its derivatives are discussed. Then, spatial convergence analysis is established. In Sect. 3, the temporal domain is discretized and its convergence is discussed. The stability analysis of the technique using the von Neumann method is presented in Sect. 4. In Sect. 5, suitable examples are considered to show the efficacy of the proposed method and its improvement over the results available in the literature. In Sect. 6, the conclusion part of the paper is given. The key points for applying the improvised collocation technique with cubic B-spline are to solve the non-linear partial differential equation with better accuracy in results, higher-order of convergence and less computational time.

2 Improvised cubic B-spline collocation method

In the standard B-spline collocation method, the unknown function and its derivatives are just replaced by the spline interpolant and its higher-order derivatives. But the second-order derivative approximation of the unknown function can be improved by forcing the cubic B-spline to satisfy the interpolatory and some special end conditions. As with the standard B-spline collocation approach, the optimal order of convergence could not be obtained, so to overcome this deficiency, optimal order of splines are obtained. The properties and subsequent improvements of cubic B-spline interpolant are discussed below:

2.1 Properties of cubic B-spline interpolant

Consider the equispaced partition of the spatial domain $\varLambda _{x}\equiv \{x_{L} = x_{0}<x_{1}<\cdots <x_{N}=x_{R}\}$ in $\bar{\varPhi }_{x}$ with the node points $x_{j} = x_{L} + j\hat{h}, ~j = 0, 1,\ldots , N,$ with the spatial step size $\hat{h} = (x_{R}-x_{L})/N$ or $\hat{h}= x_{j+1}-x_{j},$ where N is the number of node points. Four extra node points are required outside $\bar{\varPhi }_{x}$, which are positioned as $x_{-2}< x_{-1} < x_{0}$ and $x_{N}< x_{N+1}< x_{N+2}$. The cubic B-spline basis functions can be found in [23], which are as follows:

$$\begin{aligned} \hat{B}_{j}(x)=\frac{1}{\hat{h}^3}\left\{ \begin{array}{ll} (x-x_{j-2})^3, &{}\quad x\in [x_{j-2},x_{j-1}) \\ \hat{h}^3+3\hat{h}^2(x-x_{j-1})+3\hat{h}(x-x_{j-1})^2-3(x-x_{j-1})^3, &{}\quad x\in [x_{j-1},x_j)\\ \hat{h}^3+3\hat{h}^2(x_{j+1}-x)+3\hat{h}(x_{j+1}-x)^2-3(x_{j+1}-x)^3, &{}\quad x\in [x_j,x_{j+1})\\ (x_{j+2}-x)^3, &{}\quad x\in [x_{j+1},x_{j+2}]\\ 0, &{}\quad \hbox {Otherwise}. \end{array} \right. \end{aligned}$$

(2.1)

The collection of cubic B-spline functions $\hat{B}_{j}(x)=\{\hat{B}_{-1}(x), \hat{B}_{0}(x), \hat{B}_{1}(x), \ldots , \hat{B}_{N+1}(x)\}$, forms the basis for the subspace ${\mathbb {X}}$ of ${\mathbb {C}}^{2}(\bar{\varPhi }_{x})$ with $(N+3)$ dimension over the domain $\bar{\varPhi }_{x}$. The approximate solution U(x, t), corresponding to the exact solution z(x, t) can be expressed as follows:

$$\begin{aligned} U(x,t) = \sum \limits _{j=-1}^{N+1}c_{j}(t)\hat{B}_{j}(x), \end{aligned}$$

(2.2)

where $c_{j}(t)$’s are the unknown time dependent parameters to be determined from the collocation form and boundary conditions.

2.2 Posteriori correction to cubic B-spline interpolant

Assume that the cubic B-spline interpolant (CSI) satisfy the following conditions:

(I) the interpolation condition, for $j = 0, 1,\ldots , N$:

$$\begin{aligned} U(x_{j},t) = z(x_{j},t), \end{aligned}$$

(2.3)

(II) at end node points ($j = 0, N$):

$$\begin{aligned} U_{xx}(x_{j},t) = z_{xx}(x_{j},t) - \frac{\hat{h}^{2}}{12}z_{xxxx}(x_{j},t). \end{aligned}$$

(2.4)

Theorem 2.1

Let U(x, t) be the CSI of z(x, t),  where $z(x,.) \in {\mathbb {C}}^{6}(\bar{\varPhi }_{x})$ and satisfy Eqs. (2.3) and (2.4). Then for $j = 0, 1,\ldots , N,$ the following results hold : 

$$\begin{aligned}&U_{xx}(x_{j},t) = z_{xx}(x_{j},t) - \frac{\hat{h}^{2}}{12}z_{xxxx}(x_{j},t) + O(\hat{h}^{4}), \end{aligned}$$

(2.5)

$$\begin{aligned}&U_{x}(x_{j},t) = z_{x}(x_{j},t) + O(\hat{h}^{4}). \end{aligned}$$

(2.6)

In addition, 

$$\begin{aligned} \parallel U^{(k)} - z^{(k)} \parallel _{\infty }\, = O(\hat{h}^{4-k}),\quad k=0,1,2, \end{aligned}$$

(2.7)

where $U^{(k)}$ and $z^{(k)}$ represents the kth derivative w.r.t. ‘x’.

Proof

Reported in [7, 21].$\square$

Lemma 2.2

If $z(x,.) \in {\mathbb {C}}^{6}(\bar{\varPhi }_{x}),$ then the following relations hold : 

$$\begin{aligned}&\text {For}\ j=0{:}\\&\quad z_{xxxx}(x_{0},t)=\frac{1}{\hat{h}^2}\left[ 2U_{xx}(x_{0},t) - 5U_{xx}(x_{1},t) + 4U_{xx}(x_{2},t) - U_{xx}(x_{3},t)\right] + O(\hat{h}^{2}).\\&\text {For}\ j = 1, 2, \ldots , N-1{:}\\&\quad z_{xxxx}(x_{j},t)=\frac{1}{\hat{h}^2}\left[ U_{xx}(x_{j-1},t) - 2U_{xx}(x_{j},t) + U_{xx}(x_{j+1},t)\right] + O(\hat{h}^{2}).\\&\text {For}\ j=N{:}\\&\quad z_{xxxx}(x_{N},t)=\frac{1}{\hat{h}^2}\left[ 2U_{xx}(x_{N},t) - 5U_{xx}(x_{N-1},t) + 4U_{xx}(x_{N-2},t) - U_{xx}(x_{N-3},t)\right] \\&\quad + O(\hat{h}^{2}). \end{aligned}$$

Proof

Finite differences and Taylor’s expansion can be used to prove the above relations [7]. $\square$

Corollary 2.3

If $z(x,.) \in {\mathbb {C}}^{6}(\bar{\varPhi }_{x}),$ then the given relations hold : 

$$\begin{aligned}&\text {For}\ j = 0, 1,\ldots , N{:}\\&\quad z_{x}(x_{j},t) = U_{x}(x_{j},t) + O(\hat{h}^{4}).\\&\text {For}\ j = 0{:}\\&\quad z_{xx}(x_{0},t)=\frac{1}{12}\left[ 14U_{xx}(x_{0},t) - 5U_{xx}(x_{1},t) + 4U_{xx}(x_{2},t) - U_{xx}(x_{3},t)\right] + O(\hat{h}^{4}).\\&\text {For}\ j = 1, 2, \ldots , N-1{:}\\&\quad z_{xx}(x_{j},t) =\frac{1}{12}\left[ U_{xx}(x_{j-1},t) + 10U_{xx}(x_{j},t) + U_{xx}(x_{j+1},t)\right] + O(\hat{h}^{4}). \\&\text {For}\ j = N{:}\\&\quad z_{xx}(x_{N},t)=\frac{1}{12}\left[ 14U_{xx}(x_{N},t) - 5U_{xx}(x_{N-1},t) + 4U_{xx}(x_{N-2},t) - U_{xx}(x_{N-3},t)\right] \\&\qquad + O(\hat{h}^{4}). \end{aligned}$$

Proof

See [7]. $\square$

2.3 System of equations

At the node points of $\varLambda _{x}$, Eq. (1.1) can be written as follows:

$$\begin{aligned}&z_{t}(x_{j},t)=z_{xx}(x_{j},t) + {\mathfrak {f}}(x_{j},t,z(x_{j},t),z_{x}(x_{j},t)),\quad x_{j} \in \bar{\varPhi }_{x}, \end{aligned}$$

(2.8)

$$\begin{aligned}&{\mathfrak {B}}(z(x_{j},t)) = \varOmega (x_{j},t),\quad x_{j} \in \partial \varPhi _{x}. \end{aligned}$$

(2.9)

Substituting the values of $z(x_{j},t)$, $z_{x}(x_{j},t)$, and $z_{xx}(x_{j},t)$ in the above equations:

$$\begin{aligned} \frac{\partial }{\partial t}U(x_{0},t)= & {} \frac{1}{12}[14U_{xx}(x_{0},t) - 5U_{xx}(x_{1},t) + 4U_{xx}(x_{2},t) - U_{xx}(x_{3},t)] \nonumber \\&+{\mathfrak {f}}(x_{0},t,U(x_{0},t),U_{x}(x_{0},t)) + O(\hat{h}^{4}), \end{aligned}$$

(2.10)

$$\begin{aligned} \frac{\partial }{\partial t}U(x_{j},t)= & {} \frac{1}{12}[U_{xx}(x_{j-1},t) + 10U_{xx}(x_{j},t) + U_{xx}(x_{j+1},t)] \nonumber \\&+ {\mathfrak {f}}(x_{j},t,U(x_{j},t),U_{x}(x_{j},t)) + O(\hat{h}^{4}),\quad j=1, 2, \ldots , N-1, \end{aligned}$$

(2.11)

$$\begin{aligned} \frac{\partial }{\partial t}U(x_{N},t)= & {} \frac{1}{12}[14U_{xx}(x_{N},t) - 5U_{xx}(x_{N-1},t) + 4U_{xx}(x_{N-2},t) \nonumber \\&- U_{xx}(x_{N-3},t)] + {\mathfrak {f}}(x_{N},t,U(x_{N},t),U_{x}(x_{N},t)) + O(\hat{h}^{4}), \end{aligned}$$

(2.12)

and the boundary conditions:

$$\begin{aligned} a_{1}(x_{j},t)U(x_{j},t) + a_{2}(x_{j},t)U_{x}(x_{j},t) = \varOmega (x_{j},t)+ O(\hat{h}^{4}),\quad j=0,N. \end{aligned}$$

(2.13)

The above relations forms a non-linear system of first-order initial value problems with Eq. (1.2) as initial condition.

2.4 Spatial convergence analysis

The convergence analysis is based on the work of [7, 12, 13]. Let $\hat{{\mathfrak {L}}}$ and $\hat{{\mathfrak {B}}}$ be the perturbation operators of ${\mathfrak {L}}$ and ${\mathfrak {B}}$ respectively after collocation. Then for the cubic B-spline approximate solution U(x, t), the following relation holds:

$$\begin{aligned}&\text {For}\ j = 0{:} \nonumber \\&\quad \hat{{\mathfrak {L}}} U(x_{0},t) \equiv {\mathfrak {L}}(U(x_{0},t), U_{x}(x_{0},t),U_{xx}(x_{0},t) + \frac{1}{12}[2U_{xx}(x_{0},t) \nonumber \\&\qquad - 5U_{xx}(x_{1},t) + 4U_{xx}(x_{2},t) - U_{xx}(x_{3},t)]).\nonumber \\&\text {For}\ j = 1, 2,\ldots , N-1{:}\nonumber \\&\quad \hat{{\mathfrak {L}}} U(x_{j},t) \equiv {\mathfrak {L}}(U(x_{j},t), U_{x}(x_{j},t),U_{xx}(x_{j},t) + \frac{1}{12}[U_{xx}(x_{j-1},t) \nonumber \\&\qquad - 2U_{xx}(x_{j},t) + U_{xx}(x_{j+1}, t)]).\nonumber \\&\text {For}\ j = N{:}\nonumber \\&\quad \hat{{\mathfrak {L}}} U(x_{N},t) \equiv {\mathfrak {L}}(U(x_{N},t), U_{x}(x_{N},t),U_{xx}(x_{N},t)+\frac{1}{12}[2U_{xx}(x_{N},t) \nonumber \\&\qquad - 5U_{xx}(x_{N-1},t)+4U_{xx}(x_{N-2},t)-U_{xx}(x_{N-3},t)]). \end{aligned}$$

(2.14)

$$\begin{aligned}&\quad \hat{{\mathfrak {B}}}U_{j}(t)= {\mathfrak {B}}U_{j}(t),\quad j=0,N. \end{aligned}$$

(2.15)

For the unique CSI U(x, t) of z(x, t), which satisfy Eqs. (2.3)–(2.4), the following relations hold at the node points:

$$\begin{aligned} \hat{{\mathfrak {L}}}U(x_{j},t) = O(\hat{h}^{4}),\quad j=0, 1, \ldots , N;\qquad \hat{{\mathfrak {B}}}U(x_{j},t) = O(\hat{h}^{4}),\quad j=0, N. \end{aligned}$$

(2.16)

This method is based on finding a cubic B-spline solution $\hat{z}(x,t)$, which satisfies the following:

$$\begin{aligned} \hat{{\mathfrak {L}}}\hat{z}(x_{j},t) = 0,\quad j=0, 1, \ldots , N;\qquad \hat{{\mathfrak {B}}}\hat{z}(x_{j},t)=0,\quad j=0,N. \end{aligned}$$

(2.17)

Further, a Green’s function approach is used to establish the error bounds of the proposed technique. The following lemma is required in the convergence analysis.

Lemma 2.4

The inverse of the coefficient matrix of the proposed method applied to $z_{xx}=g(x,t)$ with the homogenous boundary conditions,  exists and has a finite norm.

Proof

By the procedure of the formation, the coefficient matrix $\gimel$ of the problem $z_{xx}=g(x,t)$ is as follows:

$$\begin{aligned} \gimel =\frac{1}{12} \left[ \begin{array}{cccccccccc} 14 &{} -5 &{} 4 &{}-1 &{} 0 &{} \ldots &{} 0 \\ 1 &{} 10 &{} 1 &{} 0 &{} 0 &{} \ldots &{} 0 \\ 0 &{} 1 &{} 10&{} 1 &{} 0 &{} \ldots &{} 0 \\ . &{} . &{} . &{} . &{} . &{} \ldots &{} . \\ . &{} . &{} . &{} . &{} . &{} \ldots &{} . \\ 0 &{} \ldots &{} 0 &{} 1 &{} 10&{} 1 &{} 0\\ 0 &{} \ldots &{} 0 &{} 0 &{} 1 &{} 10 &{} 1 \\ 0 &{} \ldots &{} 0 &{}-1 &{} 4 &{} -5 &{} 14 \\ \end{array} \right] . \end{aligned}$$

As the above coefficient matrix is diagonally dominant and hence invertible. Using the definition of norm:

$$\begin{aligned} \Vert \gimel ^{-1}\Vert _{\infty } \le \max _{0\le j \le N }\frac{1}{\varDelta _{j}\gimel }, \end{aligned}$$

where

$$\begin{aligned} {\varDelta _{j}\gimel } = \mid \gimel _{jj}\mid - \sum _{k\ne j}\mid \gimel _{jk}\mid >0\quad \text {for}\ j = 0, 1, \ldots , N. \end{aligned}$$

So,

$$\begin{aligned} \Vert \gimel ^{-1}\Vert _{\infty } \le \frac{1}{\min _{0\le j \le N}\varDelta _{j}(\gimel )} = \frac{12}{14 - ( 5 + 4 + 1)} = 3, \end{aligned}$$

which completes the proof of lemma.$\square$

Now onwards, $U^{(k)}$, $z^{(k)}$, and $\hat{z}^{(k)}$ represents the kth derivative with respect to ‘x’. Let $\hat{\gimel }$ represents the coefficient matrix of $U^{(1)}(x,t)$ in Eqs. (2.10)–(2.13), which is invertible with finite norm of inverse matrix. As the BVP of form (1.1) with the boundary conditions (1.3) can be converted into second-order Fredholm integral equation. According to Russell and Shampine [24] if the equation $z_{xx}=0$ with the B.C’s ${\mathfrak {B}}(z) = 0$ is uniquely solvable, then there exists a Green’s function ${\mathcal {G}}(x,t)$ corresponding to this problem. Let $z^{(2)}=v$ and $\hat{z}^{(2)} = w$ such that v and w satisfies the boundary conditions (1.3). Then z and $\hat{z}$ can be reconstructed using the Green’s function as follows:

$$\begin{aligned}&z^{(k)}(x,t) = \int _{x_{L}}^{x_{R}}\frac{\partial ^{k}{\mathcal {G}}(x,t,s)}{\partial x^{k}} v(s,t){\mathrm{d}}s,\quad k=0,1, \end{aligned}$$

(2.18)

$$\begin{aligned}&\hat{z}^{(k)}(x,t) = \int _{x_{L}}^{x_{R}}\frac{\partial ^{k}{\mathcal {G}}(x,t,s)}{\partial x^{k}} w(s,t){\mathrm{d}}s,\quad k=0,1. \end{aligned}$$

(2.19)

Let $\xi$ be any continuously differentiable function in the article. The necessary operators required to establish the convergence analysis are given hereunder:

$$\begin{aligned} {\mathcal {P}} : {\mathbb {C}}(\bar{\varPhi })\longrightarrow {\mathbb {C}}(\bar{\varPhi })\quad \text{ such } \text{ that }\ {\mathcal {P}}\xi = G_{0}\xi _{t} - {\mathfrak {f}}(x,t,G_{0}\xi ,G_{1}\xi ), \end{aligned}$$

(2.20)

where $G_{k}\xi = \int _{x_{L}}^{x_{R}}\frac{\partial ^{k}{\mathcal {G}}(x,t,s)}{\partial x^{k}} \xi (s,t){\mathrm{d}}s$, $k=0,1$ are the operators from $\bar{\varPhi }$ onto $\bar{\varPhi }$. Lets denote the unique piecewise linear interpolation operator by ${\mathcal {D}}$ at the node points $\{(x_{j},t)\}_{j=0}^{N}$. Define a projection operator as follows:

$$\begin{aligned}&{\mathcal {S}} : {\mathbb {C}}(\bar{\varPhi })\longrightarrow {\mathbb {R}}^{n+1}\quad \text{ such } \text{ that }\ {\mathcal {S}}\xi = [\xi (x_{0},t),\xi (x_{1},t), \ldots , \xi (x_{N},t)]^{\mathrm {T}}. \end{aligned}$$

(2.21)

$$\begin{aligned}&{\mathcal {H}} : {\mathbb {C}}(\bar{\varPhi })\longrightarrow {\mathbb {C}}(\bar{\varPhi }),\quad \text{ such } \text{ that }\ {\mathcal {H}}\xi = [{\mathcal {H}}_{0}\xi , {\mathcal {H}}_{1}\xi , \ldots , {\mathcal {H}}_{N}\xi ]^{\mathrm {T}}, \end{aligned}$$

(2.22)

$$\begin{aligned}&\text {where}\quad {\mathcal {H}}_{j}\xi = G_{0}\xi _{t} - {\mathfrak {f}}(x,t,G_{0}\xi , {\mathcal {E}}_{j}{\mathcal {S}} G_{1}\xi ){,} \end{aligned}$$

(2.23)

where ${\mathcal {E}}_{j}$ represents the jth row of coefficient matrix corresponding to $z_{x}(x,t)$. Using the above definitions, Eqs. (1.1) and (2.17) can be written in the form of operators as follows:

$$\begin{aligned}&(I-{\mathcal {P}})v = 0, \end{aligned}$$

(2.24)

$$\begin{aligned}&(\gimel {\mathcal {S}}-{\mathcal {H}})w = 0. \end{aligned}$$

(2.25)

As the matrix $\gimel$ is invertible, so:

$$\begin{aligned} ({\mathcal {S}}- \gimel ^{-1}{\mathcal {H}})w = 0. \end{aligned}$$

(2.26)

As w is a linear polynomial, so ${\mathcal {D}} {\mathcal {S}}w=w$:

$$\begin{aligned} (I- {\mathcal {D}}\gimel ^{-1}{\mathcal {H}})w = 0. \end{aligned}$$

(2.27)

Lemma 2.5

For the equispaced partition $\varLambda _{x}$ of $[x_{L},x_{R}]$ and any continuous function $\xi ,$ $\parallel {\mathcal {D}}\gimel ^{-1}{\mathcal {H}}\xi - {\mathcal {P}}\xi \parallel _{\infty } \rightarrow 0$ as $\hat{h} \rightarrow 0.$

Proof

$$\begin{aligned} \parallel {\mathcal {D}}\gimel ^{-1}{\mathcal {H}}\xi - {\mathcal {P}}\xi \parallel _{\infty }\le & {} \parallel {\mathcal {D}}\gimel ^{-1}{\mathcal {H}}\xi - {\mathcal {D}}{\mathcal {S}}{\mathcal {P}}\xi \parallel _{\infty } + \parallel {\mathcal {D}}{\mathcal {S}}{\mathcal {P}}\xi - {\mathcal {P}}\xi \parallel _{\infty }\\\le & {} \parallel {\mathcal {D}}\parallel _{\infty }\parallel \gimel ^{-1}\parallel _{\infty }\parallel {\mathcal {H}}\xi - \gimel {\mathcal {S}}{\mathcal {P}}\xi \parallel _{\infty } + \parallel {\mathcal {D}}{\mathcal {S}}{\mathcal {P}}\xi - {\mathcal {P}}\xi \parallel _{\infty }\\\le & {} \parallel {\mathcal {H}}\xi - \gimel {\mathcal {S}}{\mathcal {P}}\xi \parallel _{\infty } + O(\hat{h}^{2}). \end{aligned}$$

(As $\parallel \gimel ^{-1}\parallel _{\infty }$ is finite and $\parallel {\mathcal {D}}\parallel _{\infty } = 1$). By the modulus of continuity of functions $\xi$ and Green’s function ${\mathcal {G}}$ over a width of $6\hat{h}$, the term $\parallel {\mathcal {H}}\xi - \gimel {\mathcal {S}}{\mathcal {P}}\xi \parallel _{\infty }$ can be dominated. As $\xi$ and ${\mathcal {G}}$ are continuous functions, so $\parallel {\mathcal {D}}\gimel ^{-1}{\mathcal {H}}\xi - {\mathcal {P}}\xi \parallel _{\infty } \rightarrow 0$ as $\hat{h}\rightarrow 0$. $\square$

Theorem 2.6

[8] Consider the curve ${\mathrm {C}} = {(x,t,z,z_{x}) \in {\mathbb {R}}^{4}, (x,t) \in \bar{\varPhi }}$ and let $z(x,.) \in {\mathbb {C}}^{6}[x_{L},x_{R}]$ be the solution of the Eq. (1.1) with boundary condition (1.3), ${\mathfrak {f}}(x,t,u,y)$ be sufficiently smooth near z and the following linear problem : 

$$\begin{aligned} z_{xx} - \frac{\partial }{\partial y}(u_{t} - {\mathfrak {f}}(x,t,u,y))z_{x} - \frac{\partial }{\partial u}(u_{t} - {\mathfrak {f}}(x,t,u,y))z=0, \end{aligned}$$

(2.28)

with the boundary conditions (1.3) is uniquely solvable and possesses Green’s function ${\mathcal {G}}(x,t,s)$. Then,  there exist constants $\epsilon ,~\wp > 0$ such that

• (I) there does not exists any other solution $\hat{w}$ of problem (1.1) with B.C (1.3) satisfying $\parallel z_{xx} - \hat{w}_{xx}\parallel < \wp ,$

• (II) for $\hat{h} < \epsilon ,$ the Eq. (2.27) has a unique solution $U(x,.) \in B_{j,3}(\varLambda _{x})$ in the same neighborhood of z.

• (III) Newton’s method converges quadratically in some neighborhood of z for $\hat{h} < \epsilon$, which is used for numerically solving the Eq. (2.27).

Theorem 2.7

Suppose the assumptions of Theorem 2.6 holds. Then the following error bounds exists : 

$$\begin{aligned} \parallel z^{(k)}(x,.) - \hat{z}^{(k)}(x,.)\parallel _\infty= & {} O(\hat{h}^{4-k}),\quad k=0,1,2,\nonumber \\ \mid z^{(k)}(x,.) - \hat{z}^{(k)}(x,.)\mid _{x_{j}}= & {} O(\hat{h}^{4}),\quad k=0,1,\nonumber \\ \mid z^{(2)}(x,.) - \hat{z}^{(2)}(x,.)\mid _{x_{j}}= & {} O(\hat{h}^{2}). \end{aligned}$$

(2.29)

Proof

Consider the problem $U^{(2)}=\hat{\mu }$, ${\mathfrak {B}}U=O(\hat{h}^{4}).$ By Theorem 2.6, there exists a linear polynomial $\bar{w}$, such that:

$$\begin{aligned} {\mathfrak {B}}\bar{w} ={\mathfrak {B}}U = O(\hat{h}^{4}),\quad \parallel \bar{w}^{(k)}\parallel _{\infty } = O(\hat{h}^{4}),\quad k=0,1. \end{aligned}$$

(2.30)

As $(U^{(2)}-\bar{w}^{(2)})=\hat{\mu }$, ${\mathfrak {B}}(U - \bar{w}) = 0$ is uniquely solvable. So, by Theorem 2.6:

$$\begin{aligned} (I +{\mathcal {D}}\gimel ^{-1}{\mathcal {H}})(U^{(2)} - \bar{w}^{(2)}) = O(\hat{h}^{4}). \end{aligned}$$

(2.31)

Subtracting Eq. (2.27) from (2.31):

$$\begin{aligned} (I +{\mathcal {D}}\gimel ^{-1}{\mathcal {H}})(U^{(2)} - \bar{w}^{(2)} - \hat{z}^{(2)}) = O(\hat{h}^{4}). \end{aligned}$$

(2.32)

As $(I +{\mathcal {D}}\gimel ^{-1}{\mathcal {H}})$ is bounded:

$$\begin{aligned} \parallel U^{(2)}- \bar{w}^{(2)} - \hat{z}^{(2)}\parallel _{\infty } = O(\hat{h}^{4}). \end{aligned}$$

(2.33)

By Theorem 2.6, the problem $(U - \bar{w} - \hat{z})^{(2)}=\bar{\eta }$, ${\mathfrak {B}}(U - \bar{w} - \hat{z}) = 0$ is uniquely solvable, so there exists a Green’s function such that:

$$\begin{aligned} \mid (U - \bar{w} - \hat{z})^{(k)} \mid = \int _{x_{L}}^{x_{R}}\frac{\partial ^{k}{\mathcal {G}}(x,t,s)}{\partial x^{k}}(U^{(2)} - \bar{w}^{(2)} - \hat{z}^{(2)}) {\mathrm{d}}s,\quad k=0,1. \end{aligned}$$

Thus,

$$\begin{aligned} \parallel (U - \bar{w} - \hat{z})^{(k)}\parallel _{\infty } = O(\hat{h}^4),\quad k=0, 1. \end{aligned}$$

So,

$$\begin{aligned} \parallel (U - \hat{z})^{(k)}\parallel _{\infty } \le \parallel (U - \bar{w} - \hat{z})^{(k)}\parallel _{\infty } + \parallel \bar{w}^{(k)}\parallel _{\infty } = O(\hat{h}^4),\quad k=0, 1,2. \end{aligned}$$

(2.34)

Using Theorem 2.1, Eq. (2.34) and triangular inequality:

$$\begin{aligned} \parallel (z - \hat{z})^{(k)}\parallel _\infty \le \parallel (z - U)^{(k)}\parallel _\infty + \parallel (U - \hat{z})^{(k)}\parallel _\infty = O(\hat{h}^{4-k}),\quad k=0,1,2. \end{aligned}$$

Using Theorem 2.1, local error bounds can also be obtained, which completes the proof. $\square$

3 Temporal discretization

Substituting the values of $z,~z_{x}$, and $z_{xx}$ in Eq. (1.1), a system of initial value problem is obtained as follows:

$$\begin{aligned} {\mathcal {Q}}_{1}\frac{{\mathrm{d}}}{{\mathrm{d}}t}{\mathcal {C}}(t) = \frac{1}{\hat{h}^{2}}{\mathcal {Q}}_{2}{\mathcal {C}}(t) + {\mathfrak {F}}(t,{\mathcal {C}}(t)),\quad t \in \varPhi _{t}, \end{aligned}$$

(3.1)

with the initial condition:

$$\begin{aligned} {\mathcal {Q}}_{1}{\mathcal {C}}(t_{0}) = z^{0}, \end{aligned}$$

(3.2)

where ${\mathcal {Q}}_{1}=\hbox {tri}[1,4,1]$ is a diagonal matrix, ${\mathcal {C}}(t) = [c_{0}(t),c_{1}(t), \ldots , c_{N}(t)]^{\mathrm{T}}$, $z^{0} = [z(x_{0},t_{0}), z(x_{1},t_{0}), \ldots , z(x_{N},t_{0})]^{\mathrm{T}}$, ${\mathfrak {F}}(t,{\mathcal {C}}(t))$ is a column vector with the elements ${\mathfrak {f}}(t,{\mathcal {Q}}_{1j}{\mathcal {C}}(t), {\mathcal {Q}}_{3j}{\mathcal {C}}(t))$, where ${\mathcal {Q}}_{3} = \frac{1}{3\hat{h}}\hbox {tri}[-1,0,1]$ and the matrix ${\mathcal {Q}}_{2}$ is as follows:

$$\begin{aligned} {\mathcal {Q}}_{2}=\frac{1}{2} \left[ \begin{array}{cccccccccc} 14 &{}-33 &{} 28 &{}-14 &{} 6 &{}-1 &{} 0 &{} \ldots &{} 0 \\ 1 &{} 8 &{}-18 &{} 8 &{} 1 &{} 0 &{} 0 &{} \ldots &{} 0 \\ 0 &{} 1 &{} 8 &{}-18 &{} 8 &{} 1 &{} 0 &{} \ldots &{} 0 \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} \ldots &{} . \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} \ldots &{} . \\ 0 &{} \ldots &{} 0 &{} 1 &{} 8 &{}-18&{} 8 &{} 1 &{} 0 \\ 0 &{} \ldots &{} 0 &{} 0 &{} 1 &{} 8 &{}-18&{} 8 &{} 1 \\ 0 &{} \ldots &{} 0 &{}-1 &{} 6 &{}-14&{} 28&{} -33 &{} 14 \\ \end{array} \right] . \end{aligned}$$

Consider the equispaced partition of temporal domain as $\Gamma _{t}\equiv \{t^{i}\}_{i=0}^{m}$ of $\varPhi _{t}$ with the step size $\varDelta t = t^{n+1} - t^{n}$. Discretize Eq. (3.1) by using the weighted finite difference scheme, as used in [13] depending on a parameter $\theta$ as follows with the identity matrix I:

$$\begin{aligned} {\mathcal {Q}}_{1}I\frac{\delta _{t}}{\varDelta t(1-\varTheta \delta _{t})}{\mathcal {C}}^{n} = \frac{1}{\hat{h}^{2}}{\mathcal {Q}}_{2}{\mathcal {C}}^{n} + {\mathfrak {F}}(t,{\mathcal {C}}^{n}),\quad n=1,2,\ldots , \end{aligned}$$

(3.3)

$$\begin{aligned} \left[ {\mathcal {Q}}_{1}I - \frac{\varDelta t}{\hat{h}^{2}}(1-\varTheta ){\mathcal {Q}}_{2}I\right] {\mathcal {C}}^{n} - \varDelta t(1-\varTheta ){\mathfrak {F}}^{n} = \left[ {\mathcal {Q}}_{1}I + \frac{\varDelta t}{\hat{h}^{2}}\varTheta {\mathcal {Q}}_{2}I\right] {\mathcal {C}}^{n-1} + \varDelta t \varTheta {\mathfrak {F}}^{n-1}, \end{aligned}$$

(3.4)

$$\begin{aligned} {\mathcal {Q}}_{1}{\mathcal {C}}^{0} = z^{0}. \end{aligned}$$

(3.5)

Lemma 3.1

Let $z(.,t) \in {\mathbb {C}}^{3}(\bar{\varPhi }_{t})$ be the exact solution of Eq. (1.1). Then for $\varTheta = \frac{1}{2},$ the above given time discretization scheme has second-order and for $\varTheta \in \left( \frac{1}{2},1\right]$ scheme has first-order of convergence.

Proof

Given in [20], Theorem 2.6. $\square$

So the proposed technique is fourth-order convergence in spatial domain and second-order convergent in temporal domain for $\varTheta = \frac{1}{2}$, which is used in whole computation.

4 Stability analysis

Von Neumann method is applied for stability analysis of the proposed improvised collocation method. For this, take z as a local constant $m=\hbox {max} ~z$ to linearize the non-linear terms and further discretize the temporal domain using the weighted finite difference scheme with $\varTheta = \frac{1}{2}$:

$$\begin{aligned} \frac{z^{n+1}_{j} - z^{n}_{j}}{\varDelta t}= & {} \frac{(z_{xx})^{n+1}_{j} + (z_{xx})^{n}_{j}}{2} - \beta m^{\delta } \left[ \frac{(z_{x})^{n+1}_{j} + (z_{x})^{n}_{j}}{2}\right] + \gamma (1 - m^{\delta })(m^{\delta } - \eta )\nonumber \\&\times \left[ \frac{z^{n+1} + z^{n}}{2} \right] . \end{aligned}$$

(4.1)

Put $\gamma (1 - m^{\delta })(m^{\delta } - \eta ) = l_{1}$ and separate the $(n+1)$th and nth time level terms:

$$\begin{aligned} \left( \frac{1}{\varDelta t} - \frac{l_{1}}{2}\right) z^{n+1}_{j} + \frac{\beta m^{\delta }}{2} (z_{x})^{n+1}_{j} - \frac{(z_{xx})^{n+1}_{j}}{2}= \left( \frac{1}{\varDelta t} + \frac{l_{1}}{2}\right) z^{n}_{j} - \frac{\beta m^{\delta }}{2} (z_{x})^{n}_{j} + \frac{(z_{xx})^{n}_{j}}{2}. \end{aligned}$$

(4.2)

Put

$$\begin{aligned} a_{1}=\frac{1}{\varDelta t} - \frac{l_{1}}{2};\quad b_{1}=\frac{\beta m^{\delta }}{2};\quad a_{2}= \frac{1}{\varDelta t} + \frac{l_{1}}{2};\quad b_{2}=-\frac{\beta m^{\delta }}{2}. \end{aligned}$$

With the above substitution, Eq. (4.2) becomes:

$$\begin{aligned} a_{1}z^{n+1}_{j} + b_{1}(z_{x})^{n+1}_{j}- \frac{(z_{xx})^{n+1}_{j}}{2} = a_{2}z^{n}_{j} + b_{2}(z_{x})^{n}_{j}+ \frac{(z_{xx})^{n}_{j}}{2}. \end{aligned}$$

(4.3)

Substitute the value of $z,~z_{x}$, and $z_{xx}$ using the improvised cubic B-splines:

$$\begin{aligned}&a_{1} (c_{j-1}^{n+1} + 4c_{j}^{n+1} + c_{j+1}^{n+1}) - \frac{3b_{1}}{\hat{h}} (c_{j-1}^{n+1} - c_{j+1}^{n+1}) - \frac{1}{4 \hat{h}^{2}}(c_{j-2}^{n+1} + 8c_{j-1}^{n+1} - 18c_{j}^{n+1} \nonumber \\&\quad + 8c_{j+1}^{n+1} + c_{j+2}^{n+1})= a_{2} (c_{j-1}^{n} + 4c_{j}^{n} + c_{j+1}^{n}) - \frac{3b_{2}}{\hat{h}} (c_{j-1}^{n} - c_{j+1}^{n}) + \frac{1}{4 \hat{h}^{2}}(c_{j-2}^{n} + 8c_{j-1}^{n} \nonumber \\&\quad - 18c_{j}^{n} + 8c_{j+1}^{n} + c_{j+2}^{n}). \end{aligned}$$

(4.4)

After simplifying, Eq. (4.4) becomes:

$$\begin{aligned} y_{1}c_{j-2}^{n+1} + y_{2} c_{j-1}^{n+1} + y_{3} c_{j}^{n+1} + y_{4} c_{j+1}^{n+1} + y_{1} c_{j+2}^{n+1} = -y_{1} c_{j-2}^{n} + y_{5} c_{j-1}^{n} + y_{6} c_{j}^{n} + y_{7} c_{j+1}^{n} -y_{1} c_{j+2}^{n}, \end{aligned}$$

where

$$\begin{aligned}&y_{1} = - \frac{1}{4 \hat{h}^{2}}, ~y_{2} = a_{1} -\frac{3 b_{1}}{\hat{h}} - \frac{2}{\hat{h}^{2}}, ~y_{3} = 4 a_{1} + \frac{9}{2 \hat{h}^{2}}, ~y_{4} = a_{1} + \frac{3 b_{1}}{\hat{h}} - \frac{2}{\hat{h}^{2}}, \\&y_{5} = a_{2} -\frac{3 b_{2}}{\hat{h}} + \frac{2}{ \hat{h}^{2}}, y_{6} = 4 a_{2} - \frac{9}{2\hat{h}^{2}},~ y_{7} = a_{2} + \frac{3 b_{2}}{\hat{h}} + \frac{2}{ \hat{h}^{2}}. \end{aligned}$$

Put $c_{j}^{n} = E \alpha ^{n} \text {exp}(ij\phi \hat{h})$, where E is the amplitude, $i = \sqrt{-1}$, $\hat{h}$ is the spatial step length and $\phi$ is mode number:

$$\begin{aligned} \alpha= & {} \frac{-y_{1}\text {exp}(-2i\phi \hat{h}) + y_{5}\text {exp}(-i\phi \hat{h}) + y_{6} + y_{7}\text {exp}(i\phi \hat{h}) - y_{1}\text {exp}(2i\phi \hat{h})}{y_{1}\text {exp}(-2i\phi \hat{h}) + y_{2}\text {exp}(-i\phi \hat{h}) + y_{3} + y_{4}\text {exp}(i\phi \hat{h}) + y_{1}\text {exp}(2i\phi \hat{h})},\\= & {} \frac{-2y_{1}\text {cos}(2\phi \hat{h}) + y_{6} + (y_{5} + y_{7})\text {cos}(\phi \hat{h}) + i(y_{7} - y_{5})\text {sin}(\phi \hat{h})}{2y_{1}\text {cos}(2\phi \hat{h}) + y_{3} + (y_{2} + y_{4})\text {cos}(\phi \hat{h}) + i(y_{4} - y_{2})\text {sin}(\phi \hat{h})},\\= & {} \frac{F_{1} + iG_{1}}{F_{2} + iG_{2}}, \end{aligned}$$

where

$$\begin{aligned}&F_{1}=\frac{1}{2\hat{h}^{2}} \text {cos}(2\phi \hat{h}) + \left( 2a_{2}+\frac{4}{\hat{h}^{2}}\right) \text {cos}(\phi \hat{h}) + 4a_{2} - \frac{9}{2\hat{h}^{2}},\\&G_{1} = \frac{6b_{2}}{\hat{h}}\text {sin}(\phi \hat{h}),\\&F_{2}=-\frac{1}{2\hat{h}^{2}} \text {cos}(2\phi \hat{h}) + \left( 2a_{1}-\frac{4}{\hat{h}^{2}}\right) \text {cos}(\phi \hat{h}) + 4a_{1} + \frac{9}{2\hat{h}^{2}},\\&G_{2}= \frac{6b_{1}}{\hat{h}}\text {sin}(\phi \hat{h}). \end{aligned}$$

For the stability of the technique, it is need to prove that $|\alpha | \le 1$, i.e., $F_{1}^{2} + G_{1}^{2} \le F_{2}^{2} + G_{2}^{2}$. As $b_{1} = -b_{2}$, $G_{1}^{2} = G_{2}^{2}$. Next it is proved that $F_{2}\ge F_{1}$ i.e., $F_{2}-F_{1} \ge 0$.

$$\begin{aligned} F_{2}-F_{1}= & {} -\frac{\text {cos}(2\phi \hat{h})}{\hat{h}^{2}} + \left( 2(a_{1} - a_{2}) - \frac{8}{\hat{h}^{2}}\right) \text {cos}(\phi \hat{h}) + 4(a_{1} - a_{2}) + \frac{9}{\hat{h}^{2}}\\= & {} -\frac{2}{\hat{h}^{2}} \text {cos}^{2}(\phi \hat{h}) + \left( 2(a_{1} - a_{2}) - \frac{8}{\hat{h}^{2}}\right) \text {cos}(\phi \hat{h}) + 4(a_{1} - a_{2}) + \frac{10}{\hat{h}^{2}}. \end{aligned}$$

For the minimum possible value of $F_{2}-F_{1}$, take $\text {cos}(\phi \hat{h}) =1$. So, $F_{2}-F_{1} = 6(a_{1} - a_{2})$, but $a_{1} \ge a_{2}$ as $l_{1}$ is negative. With this, $F_{2}^{2} \ge F_{1}^{2}$. Hence, the proposed technique is unconditionally stable.

Table 1 Comparison of absolute error of Ex.1 with $\beta =1$, $\gamma =1$, $\eta =0.001$, $\varDelta t=0.0001$, and $\delta =2$

5 Numerical examples

Few examples of generalized Burgers’–Huxley equation are solved numerically by improvised collocation technique to demonstrate the applicability of the proposed technique. The numerically obtained results are given in the form of tables and are compared with the results available in the literature and also with the exact solution. The $L_{\infty }$, $L_{2}$, and relative error norms are calculated, which are as follows:

$$\begin{aligned}&L_{\infty } = \max _{0\le j \le N }|z_{j} - \hat{z}_{j}|,\nonumber \\&L_{2} = \sqrt{\hat{h}\sum \limits _{j=0}^{N}(z_{j} - \hat{z}_{j})^{2}},\nonumber \\&\text {Relative error} = \bigg |\frac{z_{j}-\hat{z}_{j}}{z_{j}} \bigg |, \end{aligned}$$

(5.1)

where $z_{j}$ and $\hat{z}_{j}$ represents the exact and numerical solutions at any node point $x_{j}$. The order of convergence is calculated using the following formula:

$$\begin{aligned} \hbox {Order} = \frac{\log (\hbox {err}(N_{2})/\hbox {err}(N_{1}))}{\log (N_{1}/N_{2})}, \end{aligned}$$

where $\hbox {err}(N_{1})$ and $\hbox {err}(N_{2})$ represents the $L_{\infty }$ and $L_{2}$ errors with $N_{1}$ and $N_{2}$ number of partitions of the spatial domain.

The wave solution of Eq. (1.1) was given by Wang et al. [32]:

$$\begin{aligned} z(x,t)=\frac{\eta }{2}\left[ {1 + \text {tanh}(k(x-bt))}\right] ^{\frac{1}{\delta }}, \end{aligned}$$

(5.2)

where

$$\begin{aligned} b=\frac{\beta \eta }{\delta +1} - \frac{(1+\delta - \eta )(-\beta + \sqrt{\beta ^{2} + 4\gamma (\delta + 1)})}{2(\delta + 1)}{,} \end{aligned}$$

(5.3)

and

$$\begin{aligned} k=\frac{\eta \delta (-\beta + \sqrt{\beta ^{2} + 4\gamma (\delta + 1)})}{4(\delta + 1)}{.} \end{aligned}$$

(5.4)

Example 5.1

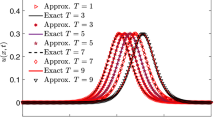
Consider the gBH Eq. (1.1) and the wave solution Eq. (5.2) in the interval [0, 1] with $\beta =1$, $\gamma =1$, $\eta =0.001$, and $\hat{h} = 0.1$. In Table 1, a comparison of absolute error with $\delta =2$ is given, which demonstrates that the results with the present technique are better than the exponential finite difference scheme [16], hybrid B-spline collocation method [33], and hyperbolic-trigonometric tension B-spline collocation method [2]. In Table 2, the $L_{\infty }$ error is calculated for different values of $\delta$ at $t=0.2$ and $t=1$. The comparison shows that the results are better than the modified cubic B-spline collocation technique [22], modified cubic B-spline differential quadrature method [6], and hyperbolic-trigonometric tension B-spline collocation method [2]. The $L_{\infty }$ and $L_{2}$ errors are calculated in Table 3 with $\varDelta t =0.01$ and $\delta =2$ at different time levels. In Table 4, the order of convergence is calculated numerically which agrees with the theoretical results. Figure 1 depicts the numerical behavior of the solution with $N=50$ and $\varDelta t=0.01$ and Fig. 2 shows the absolute error at different time levels.

Table 2 Comparison of $L_\infty$ error of Ex.1 with $\beta =1$, $\gamma =1$, $\eta =0.001$, and $\varDelta t=0.001$ for different values of $\delta$

Table 3 Comparison of errors of Ex.1 with $\beta =1$, $\gamma =1$, $\eta =0.001$, $\varDelta t=0.01$, and $\delta =2$ at different time levels

Table 4 Computation of order of convergence of Ex.1 with $\beta =1$, $\gamma =1$, $\eta =0.001$, $\varDelta t=0.01$, and $\delta =2$

Fig. 1

Numerical behavior of Ex.1 with $N=50$ and $\varDelta t=0.01$

Fig. 2

Absolute error of Ex.1 for different values of time levels

Example 5.2

Consider the gBH Eq. (1.1) and the wave solution Eq. (5.2) in the interval [0, 1] with $\beta =0.1$, $\gamma =0.001$, $\eta =0.0001$, and $\hat{h} = 0.1$. Table 5 shows the improvement in results by reduction in absolute error in comparison to results given by [2, 16, 33] with $\delta =2$ at $t=0.5$ and $t=0.8$. The $L_{\infty }$ error norm for different values of $\delta$ is reported in Table 6 and results with the ICSCM are found to be better than [6, 22], and [2] for large values of $\delta$. In Table 7, the order of convergence is reported. Figure 3 gives the surface plot of the numerical solution and Fig. 4 shows the behavior of absolute error at different time levels.

Table 5 Comparison of absolute error of Ex.2 with $\beta =0.1$, $\gamma =0.001$, $\eta =0.0001$, $\varDelta t=0.0001$, and $\delta =2$

Table 6 Comparison of $L_\infty$ error of Ex.2 with $\beta =0.1$, $\gamma =0.001$, $\eta =0.0001$, and $\varDelta t=0.001$ for different values of $\delta$

Table 7 Computation of order of convergence of Ex.2 with $\beta =0.1$, $\gamma =0.001$, $\eta =0.0001$, $\varDelta t=0.01$, and $\delta =2$

Fig. 3

Numerical behavior of Ex.2 with $N=50$ and $\varDelta t=0.01$

Fig. 4

Absolute error of Ex.2 for different values of time levels

Table 8 Comparison of absolute error of Ex.3 with $\beta =5$, $\gamma =10$, $\eta =0.0001$, $\varDelta t=0.0001$, and $\delta =2$

Table 9 Comparison of absolute error of Ex.3 with $\beta =5$, $\gamma =10$, $\eta =0.00001$, $\varDelta t=0.0001$, and $\delta =2$

Table 10 Computation of order of convergence of Ex.3 with $\beta =5$, $\gamma =10$, $\eta =0.0001$, $\varDelta t=0.01$, and $\delta =2$

Fig. 5

Numerical behavior of Ex.3 with $N=50$ and $\varDelta t=0.01$

Table 11 Comparison of absolute error of Ex.4 with $\beta =0$, $\gamma =1$, $\eta =0.001$, and $\delta =2$

Table 12 Comparison of absolute error of Ex.4 with $\beta =0$, $\gamma =1$, $\eta =0.001$, and $\delta =3.$

Table 13 Computation of order of convergence of Ex.4 with $\beta =0$, $\gamma =1$, $\eta =0.001$, $\varDelta t=0.01$ and $\delta =2$

Table 14 Computation of relative error with $\hat{h}=0.1$, $\varDelta t=0.01$, and $\delta =2$

Example 5.3

Consider the gBH Eq. (1.1) and the wave solution Eq. (5.2) in the interval [0, 1] with $\beta =5$, $\gamma =10$, and $\hat{h} = 0.1$. Tables 8 and 9 shows the improvement in results with the present technique over the existing techniques [2, 16]. The comparison of absolute error with $\delta =2$ and $\eta =0.0001$ is shown in Table 8, and with $\eta =0.00001$ is shown in Table 9. Also, [2, 16] have taken $\varDelta t=0.0001$, but in the present case the error is calculated with $\varDelta t=0.01$, which implies that the present technique is computationally efficient too. The order of convergence is calculated numerically and is reported in Table 10. Figure 5 gives the surface plot of the numerical solution and Fig. 6 shows the absolute error in 2D at different time levels.

Example 5.4

Consider the gBH Eq. (1.1) and the wave solution Eq. (5.2) in the interval [0, 1] with $\beta =0$, $\gamma =1$, $\eta = 0.001$, $\hat{h} = 0.1$, and $\varDelta t=0.01$. Table 11 shows that the results with ICSCM are better than the Adomian decomposition method [19], fourth-order implicit finite difference scheme [5], Galerkin method with cardinal Chebyshev and Legendre as basis functions [10], and modified cubic B-spline differential quadrature method [31] with $\delta =2$. In Table 12, the absolute error is calculated and compared with $\delta =3$. In Table 13, the order of convergence is calculated numerically. In Table 14, the relative error is computed for all four cases of gBH equation. Figure 7 gives the surface plot of the numerical solution and Fig. 8 shows absolute error at different time levels.

Fig. 6

Absolute error of Ex.3 for different values of time levels

Fig. 7

Numerical behavior of Ex.4 with $N=50$ and $\varDelta t=0.01$

Fig. 8

Absolute error of Ex.4 for different values of time levels

6 Conclusion

An improvised cubic B-spline collocation technique in collaboration with weighted finite-difference scheme has been successfully applied to solve the gBH equation. Suitable examples have been solved with the proposed technique to show the efficacy and improvement in the numerical results. The comparisons in the form of $L_{2}$ and $L_{\infty }$ error norms, demonstrates that the results with the proposed method is better than many existing ones such as by exponential finite-difference scheme, hybrid B-spline, and hyperbolic-trigonometric tension B-spline collocation method, Adomian decomposition method, fourth-order implicit FDM, Galerkin method with cardinal Chebyshev and Legendre as basis functions, MCBDQM, etc. Also, the technique is proved to be unconditionally stable with von-Neumann method. The theoretical results of the order of convergence and numerically computed order agree with each other. A major improvement of the present work is that results are better even for less number of divisions of the temporal domain, which makes the technique computationally efficient than others.