1 Introduction and motivation

The continuous probability distributions with bounded support are always a treasure for applied statisticians. They make it possible to model bounded characteristics by exploiting a maximum of information underlying the data. In the literature of reliability and survival analysis, lifetime distributions with unbounded support are very large in number, but not much work is available in the case of support equal to (0, 1). Uniform distribution, truncated normal distribution, beta distribution, Kumaraswamy distribution (see [12]), power distribution (see [2]), beta-power distribution (see [7]), log-Lindley distribution (see [10]), unit inverse Gaussian distribution (see [9]), unit Rayleigh distribution (see [3]), unit power-log distribution (see [6]), etc. are some available examples of distributions with bounded support. However, none of these distributions can claim to be able to model all potential characteristics with unit values efficiently; novel distributions with unique properties still have a place.

In this context, we consider an interesting new distribution with support equal to (0, 1), just like the beta and Kumaraswamy distributions. It has many of the same properties as the existing distributions but has some benefits in terms of flexibility. Before presenting it in detail, a retrospective on the inverse cosine function is necessary. Basically, the inverse cosine function or “arccosine” function, denoted by \(\arccos (x)\), is a classic mathematical function satisfying \(\arccos (\cos (x))=\cos (\arccos (x))=x\). It is involved in all the branches of mathematics, engineering and mathematical physics. The purpose of this note is based on a remark that does not appear to have been addressed in the literature: the arccosine function defined as \(g(x)=\arccos (x)\) for \(x\in (0,1)\) and \(g(x)=0\) elsewhere has the properties of a true probability density function (pdf). Indeed, it is continuous over \(\mathbb {R}/\{1\}\), satisfies \(g(x)\ge 0\) and is of integral equal to one, i.e., \(\int _{\mathbb {R}}g(x)\mathrm{{d}}x=\mid x\arccos (x)-\sqrt{1-x^2} \mid _{x=0}^{x=1}=1\). It is also decreasing and concave, which is not a frequent property among pdfs with support equal to (0, 1). The motivation of this study stems from the lack of information regarding the arccosine function as pdf and its possible uses in Probability and Statistics. We thus introduce the Arccos distribution defined by the following simple and flexible one-parameter extension of g(x) as pdf: \(f(x;\alpha )=\alpha x^{\alpha -1}g(x^{\alpha })\) where \(\alpha >0\) denotes a shape parameter. That is

$$\begin{aligned} f(x; \alpha )= \alpha x^{\alpha -1} \arccos (x^{\alpha }), \quad x\in (0,1), \end{aligned}$$
(1)

and \(f(x; \alpha )=0\) for \(x\not \in (0,1)\). Hence, for any event A, the probability that a random variable X with the Arccos distribution belongs to A is given by \(P(X\in A)=\int _{A}f(x)\mathrm{{d}}x\), where P denotes the probability operator. Therefore, in this paper, we study the main properties of the Arccos distribution. We begin with the analytical form expressions and characteristics of its cumulative distribution function (cdf), survival function (sf) and hazard rate function (hrf). Asymptotes and shape analysis are examined, revealing the role of \(\alpha \), and also the “round mesokurtic” and “left skewed” nature. Also, a complete part is devoted to various types of moments, skewness and kurtosis, expressing them with the use of the standard gamma function. In our statistical investigations, as the main competitor, the power distribution is considered. Power distribution is important in lifetime data analysis, particularly in environmental policy, public health, and financial engineering. In this regard, we may refer the reader to [4, 15]. Keeping these applications in mind, two real data applications are considered and show that the Arccos distribution performs favorably against the power distribution.

The rest of the sections are composed as follows. Section 2 is devoted to the main functions and properties of the Arccos distribution. Section 3 focuses on interesting statistical applications. The article ends with concluding discussions and remarks.

2 Properties

Here, we examine some fundamental properties of the Arccos distribution.

2.1 Functions of the proposed distribution

The Arccos distribution is formally defined by the pdf presented in (1). Therefore, the cdf of the Arccos distribution is obtained as

$$\begin{aligned} F(x; \alpha )=\int _{-\infty }^{x}f(t; \alpha )\mathrm{{d}}t=x^{\alpha } \arccos ( x^{\alpha })+1-\sqrt{1- x^{2 \alpha }},\quad x\in (0,1), \end{aligned}$$
(2)

with \(F(x; \alpha )=0\) for \(x\le 0\) and \(F(x; \alpha )=1\) for \(x\ge 1\). Immediately, we can derive the corresponding sf as

$$\begin{aligned} S(x; \alpha )=1-F(x; \alpha )=\sqrt{1-x^{2 \alpha }}- x^{\alpha } \arccos ( x^{\alpha }),\quad x\in (0,1), \end{aligned}$$

with \(S(x; \alpha )=1\) for \(x\le 0\) and \(S(x; \alpha )=0\) for \(x\ge 1\). The analytical form expressions of these two functions are advantages of the Arccos distribution for various purposes. They are involved in survival, reliability and diverse statistical analysis, among others. The same remark holds for the corresponding hrf specified by

$$\begin{aligned} h(x; \alpha )=\frac{f(x; \alpha )}{S(x; \alpha )}=\frac{ \alpha x^{\alpha -1} \arccos ( x^{\alpha })}{\sqrt{1- x^{2 \alpha }}- x^{\alpha } \arccos ( x^{\alpha })},\quad x\in (0,1), \end{aligned}$$

with \(h(x; \alpha )=0\) for \(x\not \in (0,1)\). In particular, the analytical behavior of \(h(x; \alpha )\) plays a determinant role for understanding the statistical features of the Arccos distribution, mainly for data fitting purposes. See, for instance, [1]. The determination of the asymptotes and the analysis of the shapes of these functions are performed in the next subsection.

2.2 Shape analysis

The asymptotically-equivalent functions and limits of the functions of the Arccos distributions are now determined. First, when x is in the neighborhood of 0, we have

$$\begin{aligned} f(x;\alpha )\sim \frac{\pi }{2}\alpha x^{\alpha -1}, \quad F(x;\alpha )\sim \frac{\pi }{2}x^{\alpha }, \quad h(x;\alpha )\sim \frac{\pi }{2}\alpha x^{\alpha -1} . \end{aligned}$$

Therefore, for \(\alpha \in (0,1)\), we have \(\lim _{x\rightarrow 0}f(x;\alpha )=\lim _{x\rightarrow 0}h(x;\alpha )=+\infty \), for \(\alpha =1\), \(f(x;\alpha )=h(x;\alpha )=\pi /2\), and, for \(\alpha >1\), \(\lim _{x\rightarrow 0}f(x;\alpha )=\lim _{x\rightarrow 0}h(x;\alpha )=0\). Obviously, we have \(\lim _{x\rightarrow 0}F(x;\alpha )=0\) in all circumstances. Now, when x is in the neighborhood of 1, we have

$$\begin{aligned} f(x;\alpha )\sim \alpha ^{3/2} \sqrt{2} \sqrt{1-x}, \quad F(x;\alpha )\sim 1-\alpha ^{3/2}\frac{2\sqrt{2}}{3} (1-x)^{3/2}, \quad h(x;\alpha )\sim \frac{3}{2} (1-x)^{-1}. \end{aligned}$$

Thus, in all circumstances, we have \(f(1;\alpha )=0\), \(\lim _{x\rightarrow 1}h(x;\alpha )=+\infty \) and, obviously, \(\lim _{x\rightarrow 1}F(x;\alpha )=1\).

For the analytical study of \(f(x;\alpha )\), one can notice that

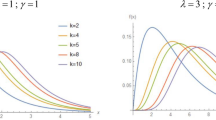
Therefore, if \(\alpha \in (0,1]\), we have \(\mathrm{{d}} f(x;\alpha )/\mathrm{{d}}x<0\), implying that \(f(x;\alpha )\) is decreasing. According to the asymptotes of \(f (x; \alpha ) \), the maximum is reached at \(x=0\), which is finite if and only if \(\alpha =1 \). In the case \(\alpha >1\), the function has a unique maximum point over (0, 1) given as the solution \(x_m\) of the following nonlinear equation: \( (\alpha -1) \sqrt{1-x_m^{2\alpha }} \arccos (x_m^{\alpha })= \alpha x_m^{\alpha }\). Numerical techniques are needed to determine \(x_m\). Thus, the Arccos distribution is unimodal. All these mathematical facts are illustrated in Fig. 1.

Fig. 1
figure 1

Graphs of the pdf of the Arccos distribution for different values of \( \alpha \)

Full size image

In Fig. 1, as anticipated, various shapes for the pdf are observed, with maximum in \(x=0\) or \(x=x_m\), depending on the values of \(\alpha \). We also note various decreasing and left-skewed shapes, which are advantageous for the analysis of data sets presenting such tendencies.

The hrf is more complicated to study from the analytical point of view. We thus perform a graphical analysis to understand its shape behavior. The graphs of the hrf for different values for \( \alpha \) are given in Fig. 2.

Fig. 2
figure 2

Graphs of the hrf of the Arccos distribution for different values of \( \alpha \)

Full size image

From Fig. 2, it is evident that the hrf of the Arccos distribution can be increasing and bathtub shaped.

2.3 Raw moments

Let X be a random variable following the Arccos distribution, i.e., with pdf and cdf given as (1) and (2), respectively. Then, since the support of X is equal to (0, 1), the raw moments of X always exist. The following proposition provides their mathematical expression in terms of the standard gamma function.

Proposition 2.1

The r-th raw moment of X is given by

$$\begin{aligned} \upsilon ^{\prime }_r&=E(X^r)=\frac{\alpha ^{2}\sqrt{\pi }}{(\alpha +r)^2}\frac{\Gamma \left( r/(2\alpha )+1\right) }{\Gamma \left( r/(2\alpha )+1/2\right) }, \end{aligned}$$

where E denotes the expectation operator and \(\Gamma (x)\) denotes the gamma function (i.e., \(\Gamma (x)=\int _{0}^{+\infty }t^{x-1}e^{-t}\mathrm{{d}}t\), \(x>0\)).

Proof

Owing to the definition of \(\upsilon ^{\prime }_r\) and an integration by part, we get

$$\begin{aligned} \upsilon ^{\prime }_r&=\int _{\mathbb {R}}x^r f(x;\alpha )\mathrm{{d}}x= \alpha \int _{0}^{1}x^r x^{\alpha -1} \arccos (x^{\alpha })\mathrm{{d}}x\\&=\alpha \left[ \frac{x^{\alpha +r}}{\alpha +r}\arccos (x^{\alpha })\mid _{x=0}^{x=1} - \int _{0}^{1}\frac{x^{\alpha +r}}{\alpha +r}\left\{ -\alpha x^{\alpha -1}\left( 1-x^{2\alpha }\right) ^{-1/2}\right\} \mathrm{{d}}x\right] \\&= \frac{\alpha ^2}{\alpha +r}\int _{0}^{1} x^{2\alpha +r-1}\left( 1-x^{2\alpha }\right) ^{-1/2}\mathrm{{d}}x. \end{aligned}$$

Now, with the change of variable \(y=x^{2\alpha }\), we get

$$\begin{aligned} \int _{0}^{1} x^{2\alpha +r-1}\left( 1-x^{2\alpha }\right) ^{-1/2}\mathrm{{d}}x&= \frac{1}{2\alpha }\int _{0}^{1} y^{r/(2\alpha )}(1-y)^{-1/2}\mathrm{{d}}y=\frac{1}{2\alpha }B\left( r/(2\alpha )+1, 1/2\right) , \end{aligned}$$

where B(x, y) denotes the beta function (i.e., \(B(x,y)=\int _{0}^{1}t^{x-1}(1-t)^{y-1}\mathrm{{d}}t\), \(x,y>0\)). Now, using the following well-known properties: \(B(x,y)=\Gamma (x)\Gamma (y)/\Gamma (x+y)\) and \(\Gamma (x+1)=x\Gamma (x)\), we get

$$\begin{aligned} B\left( r/(2\alpha )+1,1/2\right) =\frac{\Gamma \left( r/(2\alpha )+1\right) \Gamma \left( 1/2\right) }{\Gamma \left( r/(2\alpha )+3/2\right) }, \end{aligned}$$

with \(\Gamma (1/2)=\sqrt{\pi }\) and \(\Gamma \left( r/(2\alpha )+3/2\right) =\left( r/(2\alpha )+1/2\right) \Gamma \left( r/(2\alpha )+1/2\right) \). By putting all the above equalities together, we get

$$\begin{aligned} \upsilon ^{\prime }_r&= \frac{\alpha ^2}{\alpha +r}\int _{0}^{1} x^{2\alpha +r-1}\left( 1-x^{2\alpha }\right) ^{-1/2}\mathrm{{d}}x= \frac{\alpha ^2}{\alpha +r}\frac{1}{2\alpha } \frac{\Gamma \left( r/(2\alpha )+1\right) \sqrt{\pi }}{\left( r/(2\alpha )+1/2\right) \Gamma \left( r/(2\alpha )+1/2\right) }\\&= \frac{\alpha ^{2}\sqrt{\pi }}{(\alpha +r)^2} \frac{\Gamma \left( r/(2\alpha )+1\right) }{\Gamma \left( r/(2\alpha )+1/2\right) }. \end{aligned}$$

This proves Proposition 2.1. \(\square \)

From Proposition 2.1, by taking \(r=1\), the mean of X becomes explicit, and it is given as

$$\begin{aligned} \upsilon =\upsilon ^{\prime }_1&=\frac{\alpha ^{2}\sqrt{\pi }}{(\alpha +1)^2}\frac{\Gamma \left( 1/(2\alpha ) +1\right) }{\Gamma \left( 1/(2\alpha )+1/2\right) }, \end{aligned}$$

and, by using \(r=2\) and the equation above, the variance of X can be expressed as

$$\begin{aligned} \sigma ^2=\upsilon ^{\prime }_2-\upsilon ^2&=\frac{\alpha ^{2}\sqrt{\pi }}{(\alpha +2)^2} \frac{\Gamma \left( 1/\alpha +1\right) }{\Gamma \left( 1/\alpha +1/2\right) } -\left[ \frac{\alpha ^{2}\sqrt{\pi }}{(\alpha +1)^2}\frac{\Gamma \left( 1/(2\alpha ) +1\right) }{\Gamma \left( 1/(2\alpha )+1/2\right) }\right] ^2. \end{aligned}$$

The standard deviation specified by \(\sigma \) follows by taking the square-root of the above equation. Also, one can express the classical skewness and kurtosis coefficients of X (CS and CK) by applying Proposition 2.1 with well-chosen values of r; they are given by

$$\begin{aligned} \mathrm{CS}=\frac{\upsilon ^{\prime }_3-3\upsilon ^{\prime }_2 \upsilon +2 \upsilon ^3}{\sigma ^3}, \quad \mathrm{CK}=\frac{\upsilon ^{\prime }_4-4 \upsilon ^{\prime }_3 \upsilon +6 \upsilon ^{\prime }_2 \upsilon ^2- 3\upsilon ^4}{\sigma ^4}. \end{aligned}$$

respectively. Table 1 indicates numerical values for the four first raw moments, variance, CS and CK, for some selected values of \(\alpha \).

Table 1 Numerical values of the moment measures of the Arccos distribution for some selected values of \(\alpha \)
Full size table

From Table 1, we see that, when \( \alpha >1 \), the value of \(\sigma ^2\) decreases as \( \alpha \) increases, and when \( \alpha <1\), the value of \(\sigma ^2\) increases as \( \alpha \) increases. On the other hand, the values of CS are decreasing as the values of \( \alpha \) gets larger (when either \( \alpha >1 \) or \( \alpha <1 \)). Furthermore, the values of CK decrease as the values of \(\alpha \) increase when \(\alpha <1\) and increase when the values of \(\alpha \) increase when \(\alpha > 1\). Also, positive and negative values for CS are observed, showing that the Arccos distribution can be right and left-skewed. The value of CK can be close to 3, a bit smaller, or very far away, demonstrating the flexibility of the tailness of the Arccos distribution.

2.4 Incomplete moments

Again, let X be a random variable following the Arccos distribution, i.e., with pdf and cdf given as (1) and (2), respectively. The incomplete moment of X always exists and is involved in a multitude of important probability functions, such as the residual life function with its raw moments, the revered residual life function with its raw moments, the Lorenz curve, etc. The complete list can be found in [8].

Here, we determine the expression of the incomplete moments of X in an analytical way.

Proposition 2.2

The r-th incomplete moments of X at \(t\in [0,1]\) is given by

$$\begin{aligned} \upsilon ^{\prime }_r(t)&=E(X^r1_{\{X\le t\}})\\ {}&=\frac{\alpha }{(\alpha +r)(r+2\alpha )}t^{\alpha +r}\left[ (r+2\alpha )\arccos (t^{\alpha }) +\alpha t^{\alpha } {}_2F_1\left( \frac{1}{2}, \frac{r}{2\alpha }+1; \frac{r}{2\alpha }+2; t^{2\alpha } \right) \right] , \end{aligned}$$

where \(1_{\{X\le t\}}=1\) if \(X\le t\) and \(1_{\{X\le t\}}=0\) otherwise, \({}_2F_1(a,b;c;x)\) denotes the Gauss hypergeometric function (i.e., \({}_2F_1(a,b;c;x)=B(b,c-b)^{-1}\int _{0}^{1}t^{b-1}(1-t)^{c-b-1}(1-xt)^{-a}\mathrm{{d}}t\). Note that, if \(c-b=1\), we have \(B(b,c-b)\)=1/b).

Proof

We follow the lines of the proof of Proposition 2.1. Owing to the definition of \(\upsilon ^{\prime }_r(t)\) and an integration by part, we get

$$\begin{aligned} \upsilon ^{\prime }_r(t)&=\int _{-\infty }^{t}x^r f(x;\alpha )\mathrm{{d}}x= \alpha \int _{0}^{t}x^r x^{\alpha -1} \arccos (x^{\alpha })\mathrm{{d}}x\\&=\alpha \left[ \frac{x^{\alpha +r}}{\alpha +r}\arccos (x^{\alpha })\mid _{x=0}^{x=t} - \int _{0}^{t}\frac{x^{\alpha +r}}{\alpha +r}\left\{ -\alpha x^{\alpha -1}\left( 1-x^{2\alpha }\right) ^{-1/2}\right\} \mathrm{{d}}x\right] \\&= \frac{\alpha }{\alpha +r}t^{\alpha +r}\arccos (t^{\alpha }) +\frac{\alpha ^2}{\alpha +r}\int _{0}^{t} x^{2\alpha +r-1}\left( 1-x^{2\alpha }\right) ^{-1/2}\mathrm{{d}}x. \end{aligned}$$

Applying the change of variable \(y=(x/t)^{2\alpha }\), we obtain

$$\begin{aligned} \int _{0}^{t} x^{2\alpha +r-1}\left( 1-x^{2\alpha }\right) ^{-1/2}\mathrm {{d}}x&= \frac{1}{2\alpha }t^{r+2\alpha }\int _{0}^{1} y^{r/(2\alpha )}(1-t^{2\alpha } y)^{-1/2}\mathrm {{d}}y\\ {}&= \frac{1}{2\alpha }t^{r+2\alpha } \frac{1}{r/(2\alpha )+1} {}_2F_1\left( \frac{1}{2}, \frac{r}{2\alpha }+1; \frac{r}{2\alpha }+2; t^{2\alpha } \right) . \end{aligned}$$

By combining the above equalities, we get

$$\begin{aligned} \upsilon ^{\prime }_r(t)&= \frac{\alpha }{\alpha +r}t^{\alpha +r}\arccos (t^{\alpha }) +\frac{\alpha ^2}{\alpha +r} \frac{1}{2\alpha } \frac{1}{r/(2\alpha )+1} t^{r+2\alpha } {}_2F_1\left( \frac{1}{2}, \frac{r}{2\alpha }+1; \frac{r}{2\alpha }+2; t^{2\alpha } \right) \\ {}&= \frac{\alpha }{(\alpha +r)(r+2\alpha )}t^{\alpha +r}\left[ (r+2\alpha )\arccos (t^{\alpha }) +\alpha t^{\alpha } {}_2F_1\left( \frac{1}{2}, \frac{r}{2\alpha }+1; \frac{r}{2\alpha }+2; t^{2\alpha } \right) \right] . \end{aligned}$$

This ends the proof of Proposition 2.2. \(\square \)

It should be noted that the Gauss hypergeometric function is implemented in most mathematical software; the numerical evaluation of \(\upsilon _r^{\prime }(t)\) is quite manageable. Also, as an example of application, one can use \(\upsilon _r^{\prime }(t)\) to define the mean reversed residual life function. In our context, this function is defined by

$$\begin{aligned} K(t)&=E(t-X \mid X\le t)=t -\frac{1}{F(t;\alpha )}\upsilon _1^{\prime }(t)\\&= t\left[ 1 -\frac{\alpha }{(\alpha +1)(1+2\alpha )} t^{\alpha } \frac{(1+2\alpha )\arccos (t^{\alpha }) +\alpha t^{\alpha } {}_2F_1\left( 1/2, 1/(2\alpha )+1; 1/(2\alpha )+2; t^{2\alpha } \right) }{t^{\alpha } \arccos ( t^{\alpha })+1-\sqrt{1- t^{2 \alpha }}}\right] . \end{aligned}$$

More considerations about the incomplete moments can be found in [8]. As a secondary remark, after some developments, one can show that \(\upsilon _r^{\prime }=\lim _{t\rightarrow +\infty }\upsilon _r^{\prime }(t)\).

The next result offers an alternative approach to Proposition 2.3; it presents a power series expansion for \(\upsilon ^{\prime }_r(t)\) that can be used for approximation purposes, among others.

Proposition 2.3

For \(t\in [0,1]\), we have

$$\begin{aligned} \upsilon ^{\prime }_r(t)&=\frac{\pi }{2}\alpha \frac{t^{\alpha +r}}{\alpha +r} -\alpha \sum _{k=0}^{+\infty }\frac{(2k)!}{(k ! 2^k)^2(2k+1)} \frac{t^{r+2\alpha (k+1)}}{r+2\alpha (k+1)}. \end{aligned}$$

Proof

First, let us notice that \(\arccos (x)=\pi /2-\arcsin (x)\). Thus, for \(x\in (0,1)\subseteq (-1,1)\), owing to a well-known series expansion for \(\arcsin (x)\), the following expansion holds:

$$\begin{aligned} \arccos (x)=\frac{\pi }{2}-\sum _{k=0}^{+\infty }\frac{(2k)!}{(k ! 2^k)^2(2k+1)} x^{2k+1}. \end{aligned}$$

Hence, upon integration, we get

$$\begin{aligned} \upsilon ^{\prime }_r(t)&=\int _{-\infty }^{t}x^r f(x;\alpha )\mathrm{{d}}x=\frac{\pi }{2}\alpha \int _{0}^{t}x^rx^{\alpha -1}\mathrm{{d}}x -\alpha \sum _{k=0}^{+\infty }\frac{(2k)!}{(k ! 2^k)^2(2k+1)} \int _{0}^{t}x^rx^{\alpha -1}x^{\alpha (2k+1)}\mathrm{{d}}x\\&=\frac{\pi }{2}\alpha \frac{t^{\alpha +r}}{\alpha +r} -\alpha \sum _{k=0}^{+\infty }\frac{(2k)!}{(k ! 2^k)^2(2k+1)} \frac{t^{r+2\alpha (k+1)}}{r+2\alpha (k+1)}. \end{aligned}$$

This proves Proposition 2.3. \(\square \)

Based on Proposition 2.3, the following simple approximation can be useful for practical aims:

$$\begin{aligned} \upsilon ^{\prime }_r(t)&\approx \frac{\pi }{2}\alpha \frac{t^{\alpha +r}}{\alpha +r} -\alpha \sum _{k=0}^{K}\frac{(2k)!}{(k ! 2^k)^2(2k+1)} \frac{t^{r+2\alpha (k+1)}}{r+2\alpha (k+1)}, \end{aligned}$$

with K large enough, and the following simple inequality holds: \(\upsilon ^{\prime }_r(t)\le (\pi /2)\alpha t^{\alpha +r}/(\alpha +r)\).

3 Applications

In this section, we show examples where the Arccos distribution is applicable. All computations were done using the R software, which is a free software environment for statistical computing and graphics (see [14]).

3.1 Data sets

We consider the two following real data sets to evaluate the fits of the Arccos distribution.

  • Data set 1: the source of the first data set is [11]. It is about the times to infection of kidney dialysis patients in months. The data set is: 2.5, 2.5, 3.5, 3.5, 3.5, 4.5, 5.5, 6.5, 6.5, 7.5, 7.5, 7.5, 7.5, 8.5, 9.5, 10.5, 11.5, 12.5, 12.5, 13.5, 14.5, 14.5, 21.5, 21.5, 22.5, 22.5, 25.5, 27.5. Now, following the spirit of [3], we perform a proportion operation on these data by dividing them by 30, yielding data ranging from 0 to 1. In this case, 30 is an arbitrary number chosen slightly higher than the maximum value of the data, which is 27.5; other numbers can be considered. After this transformation, the considered data set is given below: 0.08333333, 0.08333333, 0.11666667, 0.11666667, 0.11666667, 0.15000000, 0.18333333, 0.21666667, 0.21666667, 0.25000000, 0.25000000, 0.25000000, 0.25000000, 0.28333333, 0.31666667, 0.35000000, 0.38333333, 0.41666667, 0.41666667, 0.45000000, 0.48333333, 0.48333333, 0.71666667, 0.71666667, 0.75000000, 0.75000000, 0.85000000, 0.91666667.

  • Data set 2: As a second application, we consider a real data set on the failure times of the air conditioning system of an airplane (in hours), it has been received from [13]. The data set is: 23, 261, 87, 7, 120, 14, 62, 47, 225, 71, 246, 21, 42, 20, 5, 12, 120, 11, 3, 14, 71, 11, 14, 11, 16, 90, 1, 16, 52, 95. Again, we perform a proportion operation by dividing these data by 265 to obtain data ranging from 0 to 1, the maximum of the data being 261. The resulting data set is given below:

    0.086792453, 0.984905660, 0.328301887, 0.026415094, 0.452830189, 0.052830189, 0.233962264,

    0.177358491, 0.849056604, 0.267924528, 0.928301887, 0.079245283, 0.158490566, 0.075471698,

    0.018867925, 0.045283019, 0.452830189, 0.041509434, 0.011320755, 0.052830189, 0.267924528,

    0.041509434, 0.052830189, 0.041509434, 0.060377358, 0.339622642, 0.003773585, 0.060377358,

    0.196226415, 0.358490566.

For previous research on these data sets, see [3].

3.2 Criteria of comparison

Based on data sets 1 and 2, we aim to evaluate and compare the fits of the Arccos distribution with the fits of a distribution of reference: the power distribution. We recall that the power distribution has the following cdf:

$$\begin{aligned} G(x;\alpha ) =x^\alpha ,\quad x\in (0,1), \end{aligned}$$

and \(G(x;\alpha )=0\) for \(x \not \in (0,1)\), where \( \alpha >0 \) is a shape parameter. For \( \alpha = 1 \), we obtain as a special case the uniform distribution defined on the interval (0, 1).

We estimate the unknown parameters by the standard maximum likelihood method, and thus obtain the maximum likelihood estimates (MLEs). We use these estimates to derive estimates of the unknown functions (cdf, pdf,...) by the substitution method. The standard errors (SEs) of the MLEs are calculated. In order to judge whether the distribution is expedient, we compare the values of the −log likelihood (− logL), Akaike information criterion (AIC) and Bayesian information criterion (BIC), Kolmogorov–Smirnov (K–S) statistic, the corresponding p values, Anderson–Darling (\( A^* \)) and Cramér von Mises (\( W^* \)) statistics.

Some of the fundamentals of these mathematical approaches and tools are summarized below. In the setting of the Arccos distribution, the MLE of \(\alpha \) is obtained as \(\hat{\alpha }={{\,\mathrm{argmax}\,}}_{\alpha }L(\alpha )\), where \(L(\alpha )=\prod _{j=1}^n f(x_j;\alpha )\) and \(x_1,\ldots ,x_n\) denote the data. The SE corresponding to \({{\hat{\alpha }}}\) is equal to \([\{- \partial ^2 \log L(\alpha )/\partial \alpha ^2 \}^{-1}\mid _{\alpha =\hat{\alpha }}]^{1/2}\). We also have logL \(=\log L(\hat{\alpha })\), \(\text {AIC} = -2 \text { logL }+ 2 k\), and \(\text {BIC} = -2\text { logL }+ k \log (n)\), with \(k=1\) corresponding to the number of estimated parameter(s). The K–S statistic is specified by

$$\begin{aligned} \text {K-S} = \max \limits _{j=1,\ldots ,n}\left( \frac{j}{n} - F (x_{(j)} ; {\hat{\alpha }}) , F (x_{(j)} ; {\hat{\alpha }})-\frac{j-1}{n} \right) , \end{aligned}$$

where \(x_{(1)},\ldots , x_{(2)}\) are the ordered values of \(x_1,\ldots ,x_n\). Based on the null hypothesis \(H_0: \) “the dataset values are from the Arccos distribution”, the corresponding p value is defined as p value \(=P(K \ge \text {K-S})\), where K is random variable following the appropriate K–S distribution. Concerning the statistics \(A^*\) and W, they are defined by

$$\begin{aligned} A^*= - \sum \limits _{j=1}^{n}\frac{2j-1}{n}\left[ \log (F(x_{(j)} ; {\hat{\alpha }})) + \log (1-F(x_{(j)}; {\hat{\alpha }})) \right] -n \end{aligned}$$

and

$$\begin{aligned} W^*= \sum \limits _{j=1}^{n}\left( F(x_{(j)}; {\hat{\alpha }})-\frac{2j-1}{n}\right) ^2 +\frac{1}{12n}, \end{aligned}$$

respectively. We refer to [5] for more details on these statistical measures.

3.3 Analysis

Tables 2 and 3 provide the results of a descriptive summary for the fitted Arccos and power distributions for data sets 1 and 2, respectively.

Table 2 Estimated values, − logL, AIC, BIC, K–S, p value, \( A^* \) and \( W^* \) for data set 1
Full size table
Table 3 Estimated values, − logL, AIC, BIC, K–S, p value, \( A^* \) and \( W^* \) for data set 2
Full size table

From the obtained results, the smallest − logL, AIC, BIC, K–S, \( A^*\), \( W^* \) and the highest p values are acquired for the Arccos distribution. Therefore, the Arccos distribution gives significantly better fit to both datasets based on these measures and hence can be an adequate distribution for these data.

Moreover, Figs. 3a and 4a present the estimated pdfs for data sets 1 and 2, respectively. In addition, Figs. 3b and 4b show the comparison of the estimated cdfs for the two distributions with the empirical cdfs.

Fig. 3
figure 3

Plots of a estimated pdfs and b estimated cdfs of the considered distributions for data set 1

Full size image
Fig. 4
figure 4

Plots of a estimated pdfs and b estimated cdfs of the considered distributions for data set 2

Full size image

Apparently, for the two considered data sets, the Arccos distribution captures the general pattern of the histograms. The same holds for the estimated cdfs and the empirical cdfs. In summary, the Arccos distribution gives the best fit.

4 Conclusions

In this paper, we propose and study an original and intriguing distribution of (0, 1) , so-called the Arccos distribution. A detailed study of the asymptotes and shape properties of its main functions is obtained. There is a moments analysis, with analytical form expressions for the raw and incomplete moments. As previously stated, one notable feature of the Arccos distribution is the ability to have an increasing and bathtub-shaped hrf with a flat region, which may be very useful in applied areas. Therefore, it is much more flexible than the power distribution in some sense. This is supported in two applications to real data, where it is verified that the Arccos distribution provides consistently a better fit than the power distribution.