Abstract
In 1995, it was suggested that some of the baryonic dark matter in galaxies may be in the form of molecular hydrogen clouds, and a mechanism for observing them had been given. In the same year, a novel method of seeing the clouds was proposed, that is to look for a temperature asymmetry in the cosmic microwave background towards the M31 galaxy, due to a “Doppler effect” induced by the M31 halo rotation. This temperature asymmetry has since been seen and confirmed in M31 and other galaxies, and used to study the rotation of galactic haloes and map their dynamics. It had been questioned whether such clouds could actually exist, and in response, the clouds were modeled and shown to be possible. It then becomes necessary to trace the evolution of those clouds from their formation to the modern day. Here, the development of the ideas is reviewed.
Similar content being viewed by others
1 Introduction
According to the standard (\(\Lambda CDM\)) model of cosmology, the Universe is composed of about \((69.2\pm 1.2)\%\) dark energy, \((25.8\pm 1.1)\%\) non-baryonic dark matter and \((4.84\pm 0.1)\%\) baryonic matter [1]. As far as baryons are concerned, stars and the luminous part of galaxies account for about \(7\%\) of these baryons, \(\simeq 28\%\) is detected in the so-called \(ly-{\alpha }\) forest [17], \(\simeq 15\%\) is detected as warm-hot intergalactic gas at temperature \(\sim 10^5\div 10^7\) K, \(\simeq 5\%\) is in the circum-galactic medium, \(\simeq 4\%\) is present in the intra-cluster medium, and \(\simeq 2\%\) is observed to be relatively cold gas. This leaves about \(39\%\) of the baryonic matter unaccounted for [18]. “Where this matter is” is called the missing baryon problem. One might feel that it is unimportant, but it should be borne in mind that this is the bulk of matter as we know it, which lies in the standard (\(SU_C(3)\bigotimes SU_W(2)\bigotimes U_Y(1)\)) model of particle physics. While we know the deficit left over for the non-baryonic dark matter, we have no reliable candidates for it. It has even been suggested that there could be a problem with the law of gravitation and no non-baryonic dark matter is needed [13, 14, 20]. Though for the dark energy, we do have an excellent candidate, namely the cosmological constant (the \(\Lambda \) in \(\Lambda CDM\)), people are still searching for alternative candidates. This paper follows through one suggestion of where some of these missing baryons may lie. If we can locate them, maybe, we can put an upper bound on this portion of the missing baryons and start looking for the rest of the missing baryons.
There had been various hints that there should be more mass in galaxies than is seen, because it shines, or is inferred, because background radiation is absorbed by it. This was first called “missing mass”, but of course, it was not missing—it was very much there. It was the light from it that was missing. The better name for it soon came up as “dark matter”. The best evidence was provided by Vera Rubin, who studied the rotational dynamics of stars in the outer reaches of galaxies. If one takes the simplified model of all the mass of the galaxy lying in its core, and assumes that the core is of uniform density, one would expect a linear increase in the rotational velocity from the centre to the edge of the core of the galaxy. Beyond that one would expect the rotational speed to reduce as the square root of the distance. Allowing for a more realistic model, with a variation of density in the core, and the fact that there is no hard boundary for it, the curve gets smoothed out around the edge of the core. However, what she found [21, 22] was that beyond the edge, the rotation curves are generally flat, and may even rise for a bit. The only way to account for this would be to postulate dark matter whose density decreases inversely as the distance from the centre. Since this is not seen, it would have to be dark matter. To fit with the furthest visible stars, it is necessary that dark matter goes out to about ten times the radius of the core and much more lie in the outer part. This part was called the “galactic halo”, despite the fact that haloes are supposed to shine and these regions are dark. It turns out that more dark matter is required for binary galaxies, even more for systems of three galaxies and so on. Rich clusters of galaxies give the best estimate of how much dark matter there must be. While the galactic, or binary dark matter can easily be all baryonic, there has to be much more dark matter than the baryonic matter allowed by cosmic nucleosynthesis.
It had been proposed that some of the missing baryons may be present in molecular hydrogen clouds left over from the epoch of star formation [4]. To verify this suggestion, it was further proposed that one should look for gamma-ray scintillation from cosmic rays striking the hydrogen molecules in the clouds. However, the worry was that there would be numerous sources of gamma rays and it would be impossible to use the observation as any test for the existence of the clouds. An alternative proposal was to look at the CMB in the direction of our neighbouring galaxy, M31, called the Andromeda galaxy. Since it is rotating the clouds in the halo of the galaxy in the part rotating towards us would be blue-shifted, while those in the part rotating away from us would be red-shifted [3]. The prediction did not say how sharply visible such a shift would be, but it was clear that the resolution of the satellite observatories of the time was inadequate to see the prediction. With the observation that the prediction would have to wait for the next generation of satellites, the matter was left and we forgot all about it.
Sixteen years later, in 2011, while looking at the CMB data from WMAP the predicted antisymmetric frequency shift in the direction of M31 was seen in the CMB [5]. However, some doubt was expressed about the significance of the statistics, though it was at a 5-sigma level, on account of the procedure. Since the greatest rotational speed of the galaxy will be for the halo, assuming that it rotates with the rest of the galaxy, in 2012, it was pointed out that if the prediction is accepted as confirmed, the antisymmetric frequency shift would provide a measure of the rotation of the galactic halo in which it was seen [6]. Considering that the halo was originally proposed without being able to confirm its existence, it would be especially important to confirm the effect. By 2014, Planck data had become available in the open domain and the rotation was confirmed [7] at an \(11\sigma \)-level! Now, the question was raised whether the effect may, perhaps, be because of a hot spot giving the blue shift. However, we pointed out that the antisymmetry provided a red-shift the other side, and there would not be a cold spot absorbing the energy, exactly correlated with the supposed hot spot, on the other side of the galaxy. That “explanation” would have to be regarded as extremely forced and artificial.
Two more questions were raised that were not so trivial: (a) whether the antisymmetric frequency shift could ever be seen for any other galaxy, leave alone provide a means for studying halo rotations in a whole bunch of them; and (b) whether the postulated clouds could actually exist, or they would be unstable under gravitational collapse. In the next section, we will address the former question and in the subsequent section, the latter. In Sect. 1, we will discuss the future research under way and planned.
2 Seeing the galactic halo rotation
When the WMAP observation was in, we wanted to verify the presence of the clouds and the rotational “Doppler effect” in at least one other galaxy, so that the significance level would be doubled and the effect could be regarded as having been proved valid. To remind the reader, the relativistic Doppler effect (see, for example, [19]) is given by
where \(\delta \nu \) is the shift in the frequency \(\nu \), due to a relative speed of motion between the source and the observer at an angle \(\theta \) with the line of sight, and c is the speed of light. For \(\theta =0\), there is direct recession and for \(\theta =\pi \) direct approach, giving red and blue shifts, respectively. With the typical speeds and directions under considerations, there is a shift of \(\sim \pm 10^{-4}\). Even after the Planck confirmation of the antisymmetric frequency shift, there remained the worry that this was a one-off event, restricted to the Andromeda galaxy. Not only is it very close, our next-door neighbour as it were, it is also very large. The smaller the galaxy and the more distant it is, the finer the resolution required to see it. One idea had been to try to look for the clouds in our own galaxy. Unfortunately, we rotate along with the galaxy. All we could hope to see would be the differential rotation. One might have thought that the clouds on the other side of the galaxy would be moving in the opposite direction to us, and so, the effect should be dramatic. However, we would then only get the transverse Doppler effect, which would be negligible. Wherever we look, especially in view of our location in the galaxy, it turns out that there is no place where the effect would be very large. Furthermore, most of the galaxy is occluded by an intervening dust cloud near us. The Milky Way was a non-starter. Perforce, we had to look further afield. The Smaller and Larger Magellanic Clouds (our satellite galaxies, SLC and LMC) are too small to have haloes, and their own rotation is nowhere near enough to show an effect, even if they have managed to retain the clouds despite their comparatively low gravity. As such, we needed to go still further out into the Local Group.
For concreteness, the visible part of the Milky Way is about 32.41 kpc across and we are about 8.18 kpc from the Galactic centre; LMC is 2.15 kpc across and 48.50 kpc distant; SMC is 1.07 kpc across and 61.01 kpc distant; while M31 is 67.45 kpc across and 778 kpc distant; where \(1~\mathrm{kpc}=10^3\,\mathrm{pc}=3.262\times 10^3\,\mathrm{ly}=3.086\times 10^{16}\,\mathrm{km}\). Thus, M31 subtends an angle of \(0.0867~\mathrm{{rad}}~\sim 4.97^\circ \). It was first recorded by the Persian astronomer, Abd al-Rahman al-Sufi, as a “nebulous smear” in 964 AD. Of course, to see the rotational effect, we need that the galaxy not only has a large enough angular diameter, but it should be bright enough and be seen edge on. As M31 fulfills all these requirements admirably, it is eminently qualified to be seen. One of our closest regular (as opposed to dwarf) galactic neighbours is Centaurus A, which is \(\sim 3.8\times 10^3\) kpc distant and 29.74 kpc across, so that its angular diameter is \(\sim 0.45^\circ \). This is a factor of ten down from M31, but would still have been easily visible by Ulugh Beg’s observatory in Samarkand, in the early fifteenth century.
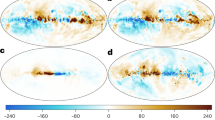
In 2015, while looking at the CMB in the direction of a lobe of Centaurus A, the predicted rotational effect was seen very clearly [8]. Ignoring what the cause of the antisymmetry in the frequency shifts in the Planck spectrum is, there was now little doubt of it being rotational in any case. For M31, it could, at a pinch, have been a one-off unlikely occurrence, say with a very low probability p. With the new observation, the chances became \(p^2\). If one had admitted that p was as large as one in a thousand, then for the two together, it would now be one in a million. When the “Doppler effect” showed up in the CMB [11] towards M82 (or NGC3034, the “cigar galaxy”), also in 2015, the chances of a random fit would jump down to one in a billion! By now, no one was objecting to its identification as a rotational effect. Soon thereafter, in 2016, it showed up in M33 (or NGC5128, the “triangulum galaxy”) [9], pushing the number down to one in a trillion. The point of the rotational effect was further driven home when it showed up in M81 [12] in 2018. It then appeared in M104, the “Sombero galaxy” [10], leaving no room for doubt. For completeness, we mention that M82 is 3,501 kpc distant and is 11.34 kpc across, so that it subtends an angle of \(0.1857^\circ \); M33 is 834.8 kpc distant and 18.40 kpc across, giving an angular diameter of \(1.263^\circ \); M81 is 3599 kpc distant and 27.594 kpc across, giving an angular diameter of \(0.439^\circ \).
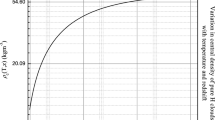
The next step was to use the asymmetric shifts to try to map the rotation of galactic haloes. What was needed was to model the distribution of the clouds in a galaxy using some standard distribution for interstellar matter and scan across the galaxy to see if the distribution fitted with observation. For this purpose, it is necessary that the resolution of the observations be adequate to see small parts of the galaxy. Now, the angular resolution of the Planck observatory depends on the frequency band in which one looks and gets to an accuracy of about 5–10 arc minutes. Given the angular diameters of the galaxies examined, it is clear that one can scan across the galaxy and see the antisymmetry clearly enough. The problem is that there is not one but many models that are commonly used for the distribution. What we needed was to see how robust our results would be under a change of the distributions used. We used the following three distributions: (a) the Navarro–Frenk–White [16]; (b) the Moore et al. [15]; and (c) the Burkert [2]. The distributions, given in terms of the core density, \(\rho _\mathrm{c}\) and the ratio of the distance to the core radius, \(x=r/r_\mathrm{c}\), are
Notice that the first two distributions can only work outside the sufficiently far from the galactic centre. One would normally use them outside the galactic core, but since we are interested in the halo, the problem is not very relevant.
We used the Planck data first for the M31 halo [24]. The calculation requires an estimate of the mass and radius of the clouds, which we will discuss in the next section. For the present purpose, we merely mention that, on the basis of the model used then, the cloud mass was taken to be \(\sim ~300\,M_{\odot }\), the central density of the clouds to be \(3.6\times 10^{-22}\) cm\(^{-3}\), the number of clouds in the halo to be \(\sim ~10^9\). The halo rotational velocity depends on the distance from the centre of the galaxy and turns out to vary between 20 and \(130\,\mathrm{km\, s}^{-1}\). For contrast, the galaxy itself has a rotational velocity of \(\sim ~250~\mathrm{km\, s}^{-1}\). More precisely, it gets up to about \(\sim ~260\,\mathrm{km\, s}^{-1}\) at \(\sim ~8\) kpc and goes down to \(\sim ~230\,\mathrm{km\, s}^{-1}\) at 35 kpc. The halo we trace goes from 41 to 104 kpc. The result is not unreasonable and gives a lot more detail about the halo if the reasoning is accepted. We used the same modeling next for NGC 5128, M33, M81, and M82 [23]. The results depended strongly on the frequency band considered. For NGC 5128, the rotational velocity varied from 15 to 90 \(\mathrm{km\,s}^{-1}\), for M33 from 30 to 150 \(\mathrm{km\,s}^{-1}\), for M81 from 250 to 450 \(\mathrm{km\,s}^{-1}\), and for M82 from 100 to 345 \(\mathrm{km\,s}^{-1}\). The results did not depend too much on which of the three distributions was used, but did depend crucially on the modeling adopted as the mass, radius and number of clouds would be altered. This brings us to the need for a better physical basis for our model. What keeps the clouds from undergoing gravitational collapse?
References
Ade, P.A.R.; et al., (Planck Collaboration).: Planck 2015 results XIII. Cosmological parameters. Astron. Astrophys. 594(A13), 1–63 (2016)
Burkert, A.: The structure of dark matter halos in dwarf galaxies. Astrophys. J. Lett. 447, L25–L28 (1995)
De Paolis, F.; et al.: Observing molecular hydrogen clouds and dark massive objects in galactic haloes. Astron. Astrophys. 299, 647–649 (1995)
De Paolis, F.; et al.: A case for a baryonic dark halo. Phys. Rev. Lett. 74, 14–17 (1995)
De Paolis, F.; et al.: Possible detection of the M31 rotation in WMAP data. Astron. Astrophys. 534(L8), 1–5 (2011)
De Paolis, F.; et al.: CMB as a possible new tool to study the dark baryons in galaxies. J. Phys. Conf. Ser. 354(012004), 1–8 (2012)
De Paolis, F.; et al.: Planck confirmation of the M31 disk and halo rotation. Astron. Astrophys. 565(L3), 1–4 (2014)
De Paolis, F.; et al.: Planck revealed bulk motion of centaurus A lobes. Astron. Astrophys. 580(L8), 1–4 (2015)
De Paolis, F.; et al.: Triangulum galaxy viewed by Planck. Astron. Astrophys. 593(A57), 1–7 (2016)
De Paolis, F.; et al.: Rotating baryonic dark halos. Astron. Astrophys. 629(A87), 1–5 (2019)
Gurzadyan, V.; et al.: Planck view of the M82 galaxy. Astron. Astrophys. 582(A77), 1–4 (2015)
Gurzadyan, V.; et al.: Messier 81’s Planck view versus its halo mapping. Astron. Astrophys. 609(A131), 1–4 (2018)
Harko, T.; et al.: \(f(R, T)\) gravity. Phys. Rev. D 84, 024020 (2011)
Milgrom, M.: A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 270, 365–370 (1983)
Moore, B.; et al.: Cold collapse and the core catastrophe. Mon. Not. R. Astron. Soc. 310, 1147–1152 (1999)
Navarro, J.F.; Frenk, C.S.; White, S.D.M.: The structure of cold dark matter halos. Astrophys. J. 462, 563–575 (1996)
Nicastro, F.; et al.: A decade of warm-hot intergalactic medium searches, where do we stand and where do we go? Astron. Nachr. 338, 281–286 (2017)
Nicastro, F.; et al.: Observations of the missing baryons in the warm-hot intergalactic medium. Nature 558, 406–409 (2018)
Qadir, A.: Relativity: An Instroduction to the Special Theory. World Scientific, Singapore (1989)
Qadir, A.; Lee, H.W.; Kim, K.Y.: Modified relativistic dynamics. Int. J. Mod. Phys. D 26, 1741001 (2017)
Rubin, V.C.: A century of galaxy spectroscopy. Astrophys. J. 451, 419–428 (1995)
Rubin, V.C.; Ford, W.K., Jr.: Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 159, 379–403 (1970)
Tahir, N.; De Paolis, F.; Qadir, A.; Nucita, A.A.: Virial clouds and the rotating M31 galactic halo. Astrophys. Space Sci. (Submitted to)
Tahir, N.; De Paolis, F.; Qadir, A.; Nucita, A.A.: Constraining baryons in the M31 galactic halo by Planck data. Int. J. Mod. Phys. D 28, 1950088 (2019)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qadir, A., De Paolis, F. Virial clouds and rotational asymmetry in galactic haloes. Arab. J. Math. 11, 91–95 (2022). https://doi.org/10.1007/s40065-021-00335-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40065-021-00335-z