1 Introduction

Statistical computation of optic flow proposed by Horn and Schunck [1] estimates the velocity field from a sequence of images. The constraint term is derived on the principle of conservation of intensity values over consecutive image patterns. In [1], a method for finding the optical flow pattern is presented which assumes that the apparent velocity of the brightness pattern varies smoothly almost everywhere in the image. Richard et al. [2] presented an approach to measure the fluid flow from some sequence of images. The physics of fluid mechanics is used to propose the algorithm of motion recovery. The paper depicts how extracted information from the physical activity of fluids affects the motion recovery algorithm. Next, the algorithm is applied on synthetic imagery and natural imagery and effectiveness of developed algorithm is discussed. Corpetti et al. [3] proposed an optical flow estimator based on image sequences representing fluid flow phenomenon. This technique is based on the adaptation of the data model and a smoothness term. Further extending his work, Corpetti [4] suggested a data model based on continuity equation for the density of fluid

$$\begin{aligned} \frac{\partial \rho }{\partial t} + {\nabla } \cdot (\rho \mathbf {v} ) = 0, \end{aligned}$$
(1)

where \(\rho \) is the density of the fluid and \(\mathbf {v} \) is the 3D velocity vector. Alternatively, through calculations, the continuity equation may be written as

$$\begin{aligned} \frac{d\rho }{dt} + \rho ({\nabla } \cdot \mathbf {v} ) = 0, \end{aligned}$$
(2)

where \( \frac{d\rho }{dt} = \frac{\partial \rho }{\partial t} + \mathbf {v} \cdot ({\nabla }\rho ) \). The equation is similar to 2D optical flow constraint on luminance when the divergence vanishes. Bruhn et al. [5] analysed the smoothing effects in local and global differential methods for optic flow computation. In [6], Ashish et al. presented the technique for modelling complex optical flow patterns using the Navier–Stokes equation for a turbulent fluid. The various terms that appear in the Navier–Stokes equation like controlling force, diffusion terms, nonlinear advection term, etc., have been implemented using discrete step-wise algorithms. In particular, the diffusion term has been implemented in the frequency domain because \(\nabla ^{2}\) becomes a multiplication operator in the spatial frequency domain. Before implementing the advection step, a Gaussian smoothing or the fluid flow has been performed. The diffusion step has been shown to be robust. In [7], Kharbat et al.  suggested to replace the individual intensity function of each pixel with a geometric moment of its neighbourhood. Every pixel is made invariant to fluctuations of intensity by doing normalisation. The algorithm was shown to be robust against reflections, shadows and varying illumination. Tianshu et al. [8] established the direct relation between the fluid flow and optical flow for visualisation of typical flow. Ashish et al. [9] proposed robust Hessian-based diffusion, advection and mass conservation for the formulation of stable fluid solver.

The proposed method is applied on synthetic field which is generated with the help of Navier–Stokes equations and it is used to model the complex optical flow using real images.

Feng et al. [10] presented modified Navier–Stokes potential flow method and also suggested models of brightness variation in fluid type motions. In optical flow estimation, the general assumption of constant brightness will not be applicable in case of smoke or cloud type motion. Dirichlet–Neumann operator (DNO) is applied to estimate the velocity potential of such images. Aaron et al. [11] used optical flow method to analyse the fluid transport dynamics. Stream function optical flow (SFOF) regularises variational optimisation problem.

Ashish and Adrian [12] applied anisotropic diffusion and local Hessian-based diffusion of viscous fluids to smooth images. Smoothing has also been achieved by interlacing diffusion with Gaussian kernel integration. In short, the physical laws that drive the Navier–Stokes equation after incorporating appropriate boundary conditions has been applied to image fields and accurate modelling of optical flows has thereby been achieved.

It would be interesting to see the random fluid flow produced by random fluctuation in the driving forces and to statistically characterise the random errors in the simulated image parameters due to the fluid. Our paper takes a step in this direction. We have incorporated the scheme suggested by Ashish [6, 12] for control forces having small random noisy components and calculated the statistical correlations in the simulated velocity fields via a Monte-Carlo method. This would enable us to calculate the mean square error between the given optical flow field and the simulated flow. We have assessed the impact of noise in the control force on the mean square error energy.

The rest of the paper is organised as follows. In Sect. 2, the Navier–Stokes and incompressibilty equations are used to define velocity field of fluid. In Sect. 3, the energy due to random forcing component is minimised. Section 4 presents the non-random model for the forcing field. The estimation of parameter vector \(\theta \) which minimises the average energy shift due to random forcing field \(\delta \) \(g\) is presented in Sect. 5. Section 6 includes the simulation results and concluding remarks.

2 Velocity field of fluid

In our work, optical flow has been modelled by representing the image intensity field E(t, x) as the fluid energy field and the image velocity field v(t, x) as the fluid velocity field. The rate of change of the energy calculated as the material derivative is given as

$$\begin{aligned} \frac{dE}{dt} = (\underline{\nabla }E,\underline{v}) + \frac{\partial E}{\partial t}. \end{aligned}$$
(3)

The velocity field \(\underline{w}(x,y) = u(x,y)\hat{x}+v(x,y)\hat{y}\) of a fluid inside the square \((x,\, y)\, \epsilon \,[0,L]\times [0,L]\) satisfies the Navier–Stokes equation [14].

$$\begin{aligned} (\underline{w}.\underline{\nabla })\underline{w}(x,y) = \frac{\nu }{\rho }\nabla ^{2}\underline{w}(x,y) - \frac{\underline{\nabla }\,p(x,y)}{\rho } + \frac{\underline{f}(x,y)}{\rho }, \end{aligned}$$
(4)

where the density \(\rho = 1\), \(\nu \) = viscosity and w(x, y) stands for the velocity field in \( \mathbb {R}^{{2}} \), (\( \underline{w}.\underline{\nabla } \)) is the operator \( w_{x}\frac{\partial }{\partial x} + w_{y}\frac{\partial }{\partial y}\), p is the pressure field and f is the external forcing field. Apart from (1), we have the equation of continuity for the incompressible fluid.

$$\begin{aligned} div\, \underline{w} = u_{,x} + v_{,y} = 0. \end{aligned}$$
(5)

The latter ensures the existence of a stream function \(\psi (x,y)\) so that

$$\begin{aligned} \underline{w} = \underline{\nabla }\times (\psi \hat{z}) = \underline{\nabla }\psi \times \hat{z}, \end{aligned}$$
(6a)

or equivalently,

$$\begin{aligned} u = \psi _{,y} , v = - \psi _{,x}. \end{aligned}$$
(6b)

By taking the curl of (4) and making use of (6a) and (6b), we arrive at the following equation for the stream function (7) and (8).

$$\begin{aligned} (\nabla ^{2}(\underline{\nabla }\psi )\times \underline{\nabla }\psi ,\hat{z})-\nu (\nabla ^{2})^{2}\psi +g=0, \end{aligned}$$
(7)

this is the same as

$$\begin{aligned} (\nabla ^{2}\psi _{,x})\psi _{,y}-(\nabla ^{2}\psi _{,y})\psi _{,x}-\nu (\nabla ^{2})^{2}\psi +g=0, \end{aligned}$$
(8)

where \(g = g\hat{z} = \underline{\nabla }\times \underline{f}\).

The derivation of the discretised form of curl operator has been mentioned in the appendix A.

3 Minimisation of energy function

Now, the standard method of estimating the velocity field \(\underline{w}\) of a flow is [11] by minimising an energy function E of the form

$$\begin{aligned} \mathbf {E}&=\frac{1}{2}\int _{D}[u(x,y), v(x,y), \underline{\nabla }u(x,y)^{T}, \underline{\nabla }v(x,y)^{T}]\mathrm {\underline{\underline{Q}}}(x,y)\nonumber \\&\quad \times [u(x,y), v(x,y), \underline{\nabla }u(x,y), \underline{\nabla }v(x,y)]^{T} \mathrm{d}x \,\mathrm{d}y \nonumber \\&\quad + \int _{D}\underline{\lambda }(x,y)^{T}[u(x,y), v(x,y), \underline{\nabla }u(x,y), \underline{\nabla }v(x,y)]^{T} \mathrm{d}x \,\mathrm{d}y, \end{aligned}$$
(9)

where \(\mathrm {\underline{\underline{Q}}}(x,\,y)\) is a \(6\times 6\) positive definite matrix and \(\underline{\lambda }(x,\,y)\) is a \(6\times 1\) vector \(\forall \) (x,y)\(\,\epsilon \) D. When the dynamics is given by (7), then \(u,\; v,\; \underline{\nabla }u,\,\underline{\nabla }v\) are expressed in terms of \(\psi _{x},\,\psi _{y},\,\psi _{xx},\,\psi _{xy},\,\psi _{yy}\) and (9) then becomes a linear quadratic function of \( \psi \). After integration by parts, this can be expressed as

$$\begin{aligned} \mathbf {E} = \frac{1}{2}\int _{D\times D}\mathrm {Q_{0}}(x,y|x^{\prime },y^{\prime })\psi (x,y)\psi (x^{\prime },y^{\prime })\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}x^{\prime }\,\mathrm{d}y^{\prime } + \int _{D}\lambda _{0}(x,y)\psi (x,y)\,\mathrm{d}x\,\mathrm{d}y, \end{aligned}$$
(10)

where \(\mathrm {Q_{0}} : \mathbb {R}^{2}\times \mathbb {R}^{2}\longrightarrow \mathbb {R}\) is a positive definite kernel. This linear quadratic form can be used to minimise the \( L^{2} \) distance between the simulated fluid velocity field and the true optical flow. Alternatively, it can also be used to minimise a weighted linear combination of the fluid energy and its \( L^{2} \) distance square from a desired optical flow. In this way, we would be able to simulate a given optical flow while keeping the simulated field energy small. The energy function (9) may equivalently be minimised w.r.t. g(x, y) by solving (7) for \(\psi \). We shall now describe a spatially discretised version of this problem. Divide the square \([0,L]\times [0,L]\) into pixels \((n\triangle ,\, m\triangle ), \, 0\le n,\, m \le N-1,\, N\triangle = L\) and write

$$\begin{aligned} \underline{\psi }= \sum _{n,m=0}^{N-1} (\psi (n\triangle , m\triangle )\underline{e}_{n}\otimes \underline{e}_{m})\,\epsilon \,\mathbb {R}^{N^{2}}. \end{aligned}$$
(11)

Here, \(\otimes \) denotes the standard Kronecker tensor product. function \(\underline{e}_{n}\,\epsilon \,\mathbb {R}^{N}\) has value 1 at \((n+1)^{th}\) position and 0s at all the other positions for \( 0 \leqslant n \leqslant N-1 \). Then, we can write (10) as (approximately since discretisation of the spatial integral has been applied)

$$\begin{aligned} \mathbf {E}(\psi )=\frac{1}{2}\underline{\psi }^{T} \mathrm {\underline{\underline{Q}}_{0}} \underline{\psi } + \underline{\lambda }_{0}^{T}\underline{\psi }, \end{aligned}$$
(12)

where \(\mathrm {\underline{\underline{Q}}_{0}}\) is an \(N^{2}\times N^{2}\) positive definite matrix and is approximately given by

$$\begin{aligned} \underline{\underline{Q}}_{0}=\triangle ^{2}.\sum _{n_{1},m_{1},n_{2},m_{2}=0}^{N-1} \mathrm {Q_{0}}(n_{1}\triangle ,m_{1}\triangle | n_{2}\triangle ,m_{2}\triangle )(\underline{e}_{n_{1}}\otimes \underline{e}_{m_{1}})(\underline{e}_{n_{2}}\otimes \underline{e}_{m_{2}})^{T} \epsilon \, \mathbb {R}^{N^{2}\times N^{2}}, \end{aligned}$$
(13)

and

$$\begin{aligned} \underline{{\lambda }}_{0} = \triangle .\sum _{n,m=0}^{N-1} ( \lambda _{0}(n\triangle ,m\triangle )\underline{e}_{n}\otimes \underline{e}_{m})\, \epsilon \, \mathbb {R}^{N^{2}\times 1}. \end{aligned}$$
(14)

4 Modelling of forcing field based on discretisation and optimisation

Now, we make use of the equation of the motion (7) and calculate \(\underline{g}\) using \(\underline{\psi }\) after minimising (10), i.e. \(\frac{\delta \mathbf {E}(\psi )}{\delta (\psi )} = 0 \) so that

$$\begin{aligned} \underline{\psi }=-\mathrm {\underline{\underline{Q}}_{0}}^{-1}\underline{\lambda }_{0}, \end{aligned}$$
(15)

we can express (7) as

$$\begin{aligned} \underline{\underline{A}}_{1}\underline{\psi }+\underline{\underline{A}}_{2}(\underline{\psi }\otimes \underline{\psi })=\underline{g}. \end{aligned}$$
(16)

This gives the value of \(\underline{g}\)

$$\begin{aligned} \underline{g}=-\underline{\underline{A}}_{1}\underline{\underline{Q}}_{0}^{-1}\underline{\lambda }_{0} + \underline{\underline{A}}_{2}(\underline{\underline{Q}}_{0}\otimes \underline{\underline{Q}}_{0})^{-1}(\underline{\lambda }_{0} \otimes \underline{\lambda }_{0}). \end{aligned}$$
(17)

In this formalism, we have used a non-random model for the forcing field \(\underline{g}\) and hence also for the velocity and stream function field. Here, the matrices \(\underline{\underline{A}}_{1}, \underline{\underline{A}}_{2}\) in (16) are calculated for (7) by first replacing \( \nabla ^{2}\) and \( (\nabla ^{2})^{2}\) by \( N^{2}\times N^{2}\) matrices:

$$\begin{aligned} \nabla ^{2}\psi (n\triangle ,m\triangle )&\thickapprox [\psi ((n+1)\triangle ,m\triangle )+\psi ((n-1)\triangle ,m\triangle )-2\psi (n\triangle ,m\triangle )\nonumber \\&\quad + \psi (n\triangle ,(m+1)\triangle ) +\psi (n\triangle ,(m-1)\triangle ) -2\psi (n\triangle ,m\triangle )]/ \triangle ^{2}\nonumber \\&= [\psi ((n+1)\triangle ,m\triangle )+\psi ((n-1)\triangle ,m\triangle )+\psi (n\triangle ,(m+1)\triangle )\nonumber \\&\quad +\psi (n\triangle ,(m-1)\triangle ) -4\psi (n\triangle ,m\triangle )]/ \triangle ^{2}, \end{aligned}$$
(18)

writing

$$\begin{aligned}&\sum _{n,m}\nabla ^{2}\psi (n\triangle ,m\triangle )\underline{e}_{n}\otimes \underline{e}_{m}=\underline{\underline{D}}\,\underline{\psi }, \end{aligned}$$
(19)
$$\begin{aligned}&\sum _{n,m}\psi _{,x}(n\triangle ,m\triangle )\underline{e}_{n}\otimes \underline{e}_{m}\equiv \sum _{n,m}\frac{(\psi ((n+1)\triangle ,m\triangle )-\psi (n\triangle ,m\triangle ))}{\triangle }\underline{e}_{n}\otimes \underline{e}_{m} \equiv \underline{\underline{P}}_{x}\,\underline{\psi }, \end{aligned}$$
(20)

and likewise

$$\begin{aligned} \sum _{n,m}\psi _{,y}(n\triangle ,m\triangle )\underline{e}_{n}\otimes \underline{e}_{m}=\underline{\underline{P}}_{y}\underline{\psi }, \end{aligned}$$
(21)

we can express (7) or (8) in discretised form as

$$\begin{aligned}&\sum _{n,m}(\underline{e}_{n}\otimes \underline{e}_{m})[(\underline{e}_{n}\otimes \underline{e}_{m})^{T}\underline{\underline{D}}\;\underline{\underline{P}}_{x}\underline{\psi }.(\underline{e}_{n}\otimes \underline{e}_{m})^{T}\underline{\underline{P}}_{y}\underline{\psi }]\nonumber \\&\quad -\sum _{n,m}(\underline{e}_{n}\otimes \underline{e}_{m})[(\underline{e}_{n}\otimes \underline{e}_{m})^{T}\underline{\underline{D}}\;\underline{\underline{P}}_{y}\underline{\psi }.(\underline{e}_{n}\otimes \underline{e}_{m})^{T}\underline{\underline{P}}_{x}\underline{\psi }]-\nu \underline{\underline{D}}^{2}\underline{\psi }+\underline{g}=0 \qquad \qquad . \end{aligned}$$
(22)

Equation (22) is derived from (8) by noting that \( (\underline{e}_{n}\otimes \underline{e}_{m})^{T}\underline{\underline{P}}_{x}\underline{\psi } \) given the \( (n+m)^{th} \) element of \(\frac{\partial \psi }{\partial x} \) and likewise for \( (\underline{e}_{n}\otimes \underline{e}_{m})^{T}\underline{\underline{P}}_{y}\underline{\psi } \). or equivalently, writing

$$\begin{aligned} \underline{\underline{S}}=\sum _{n,m}(\underline{e}_{n}\otimes \underline{e}_{m})[(\underline{e}_{n}\otimes \underline{e}_{m})^{T}\otimes (\underline{e}_{n}\otimes \underline{e}_{m})^{T}], \end{aligned}$$
(23)

we have

$$\begin{aligned} \underline{\underline{S}}( \underline{\underline{D}}\; \underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y}- \underline{\underline{D}}\; \underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x})(\underline{\psi }\otimes \underline{\psi })-\nu \underline{\underline{D}}^{2}\psi +\underline{g}=0. \end{aligned}$$
(24)

Comparing (16) and (24) gives \( \underline{\underline{A}}_{1} = -\nu \underline{\underline{D}}^{2} \), \( \underline{\underline{A}}_{2} = \underline{\underline{S}}(\underline{\underline{D}}\;(\underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y})-\underline{\underline{D}}\;(\underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x})) \).

5 Calculating the random shift in the stream function

We assume that the forcing field g is given a small random perturbation \(\delta g\) with statistics depending on an unknown parameter vector \(\theta \). We then apply perturbation theory to the equation of random motion (16) and calculate the shift \(\delta \psi \) in the stream function caused by the random shift \(\delta g\) in the forcing field g. Let \(\underline{g}=g_{0}+\delta g\) and \(\underline{\psi }=\underline{\psi }_{0}+\delta \underline{\psi }\). The unperturbed equation of motion is

$$\begin{aligned} \underline{\underline{S}}(\underline{\underline{D}}\;\underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y} - \underline{\underline{D}}\;\underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x})(\underline{\psi }_{0}\otimes \underline{\psi }_{0})-\nu \underline{\underline{D}}^{2}\psi _{0}+\underline{g}_{0}=0, \end{aligned}$$
(25)

and the perturbed equation is

$$\begin{aligned}&\underline{\underline{S}}(\underline{\underline{D}}\;\underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y} - \underline{\underline{D}}\;\underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x})(\underline{\psi }_{0}\otimes \underline{\underline{I}} + \underline{\underline{I}}\otimes \underline{\psi }_{0})\delta \underline{\psi }\nonumber \\&\quad +\underline{\underline{S}}(\underline{\underline{D}}\;\underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y} - \underline{\underline{D}}\;\underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x})(\delta \underline{\psi }\otimes \delta \underline{\psi })-\nu \underline{\underline{D}}^{2}\delta \underline{\psi }+\delta \underline{g}=0 \qquad \qquad \qquad . \end{aligned}$$
(26)

Neglecting second degree of smaller terms, (26) approximates to

$$\begin{aligned} \underline{\underline{S}}(\underline{\underline{D}}\;\underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y} - \underline{\underline{D}}\;\underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x})(\underline{\psi }_{0}\otimes \underline{\underline{I}} + \underline{\underline{I}}\otimes \underline{\psi }_{0})\delta \underline{\psi } -\nu \underline{\underline{D}}^{2}\delta \underline{\psi }+\delta \underline{g}=0. \end{aligned}$$
(27)

The exact perturbed equation (26) can be solved to the next degree of smallness. Let

$$\begin{aligned} \delta \underline{\psi }= & {} \delta \underline{\psi }^{(0)}+\epsilon \delta \underline{\psi }^{(1)}+O(\epsilon ^{2}), \nonumber \\ \underline{\underline{K}}_{0}= & {} -[\underline{\underline{S}}(\underline{\underline{D}}\;\underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y} - \underline{\underline{D}}\;\underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x})(\underline{\psi }_{0}\otimes \underline{\underline{I}} + \underline{\underline{I}}\otimes \underline{\psi }_{0}) -\nu \underline{\underline{D}}^{2}]^{-1}, \nonumber \\ \underline{\underline{S}}_{1}= & {} \underline{\underline{S}}(\underline{\underline{D}}\;\underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y} - \underline{\underline{D}}\;\underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x}). \end{aligned}$$
(28)

This gives the \(O(\epsilon ^{0})\) term,

$$\begin{aligned} \underline{\underline{S}}_{1}(\underline{\psi }_{0}\otimes \underline{\underline{I}} + \underline{\underline{I}}\otimes \underline{\psi }_{0})\underline{\delta \psi }^{(0)}-\nu \underline{\underline{D}}^{2}\underline{\delta \psi }^{(0)}=-\delta \underline{g}, \end{aligned}$$
(29)

so,

$$\begin{aligned} \underline{\delta \psi }^{(0)}=-[\underline{\underline{S}}_{1}(\underline{\psi }_{0}\otimes \underline{\underline{I}} + \underline{\underline{I}}\otimes \underline{\psi }_{0})-\nu \underline{\underline{D}}^{2}]^{-1}\delta \underline{g}\equiv \underline{\underline{K}}_{0}\delta \underline{g}, \end{aligned}$$
(30)

thus,

$$\begin{aligned} \mathbb {E}(\delta \underline{\psi }^{(0)})=0. \end{aligned}$$
(31)

Here, \( \mathbb {E} \) stands for the mathematical expectation with respect to the probability distribution of the random force and perturbation \( \delta \underline{g} \) or equivalently of \( \delta \underline{f} \) \( (i.e. \; \delta \underline{g} = \underline{\nabla }\times \delta \underline{f}) \).

Similarly, for the \(O(\epsilon ^{1})\) term,

$$\begin{aligned} \underline{\delta \psi }^{(1)}= \underline{\underline{K}}_{0}\underline{\underline{S}}(\underline{\underline{D}}\;\underline{\underline{P}}_{x}\otimes \underline{\underline{P}}_{y} - \underline{\underline{D}}\;\underline{\underline{P}}_{y}\otimes \underline{\underline{P}}_{x})(\underline{\underline{K}}_{0}\otimes \underline{\underline{K}}_{0})\delta \underline{g}\otimes \delta \underline{g} = \underline{\underline{K}}_{1}(\delta \underline{g}\otimes \delta \underline{g}), \end{aligned}$$
(32)

where

$$\begin{aligned} \underline{\underline{K}}_{1} = \underline{\underline{K}}_{0}\underline{\underline{S}}_{1}(\underline{\underline{K}}_{0}\otimes \underline{\underline{K}}_{0}). \end{aligned}$$
(33)

Now the average energy of the velocity field is

$$\begin{aligned} \langle \mathcal {E}\rangle&= \frac{1}{2}\mathbb {E}(\underline{\psi }_{0}+\delta \underline{\psi })^{T}\underline{\underline{Q}}_{0}(\underline{\psi }_{0}+\delta \underline{\psi })-\mathbb {E}({{\underline{\lambda }}_{0}}^{T}(\underline{\psi }_{0}+\delta \underline{\psi })) \nonumber \\&=\frac{1}{2}{\underline{\psi }_{0}}^{T}\underline{\underline{Q}}_{0}\underline{\psi }_{0}+\mathbb {E}(\delta {\underline{\psi }^{(1)}}^{T})\underline{\underline{Q}}_{0}\underline{\psi }_{0}+\mathbb {E}(\delta {\underline{\psi }^{(0)}}^{T}\underline{\underline{Q}}_{0}\delta \underline{\psi }^{(0)})-{\underline{\lambda }_{0}}^{T}\underline{\psi }_{0}-\underline{\lambda }_{0}^{T}\mathbb {E}(\delta \underline{\psi }^{(1)})\nonumber \\&\quad +O((\delta {\psi }^{(1)})^{2}) +\mathbb {E}(\delta {\underline{\psi }^{(0)}}^{T} \underline{\underline{Q}}_{0}\delta \underline{\psi }^{(1)})+ O((\delta \psi ^{(0)})^{4})\nonumber \\&= O((\delta g)^{4}). \end{aligned}$$
(34)

Note: We have removed the perturbation tag \(\epsilon \) because it is now clear that \(\delta \psi \) is \(O(\epsilon ),\) \(\delta \psi ^{(0)}\) is \(O(\epsilon )\) and \(\delta \psi ^{(1)}\) is \(O(\epsilon ^{2})\). It should be noted that (34) is a generalisation of the form \( \mathbb {E}(\underline{\psi }_{0} + \delta \underline{\psi } -\underline{\psi }^{(0)})^{2} \) that represents energy in the error between the simulated flow and the true optical flow. More generally, (34) is also a generalisation of a linear quadratic form that represents a weighted linear combination of the error energy and simulated flow energy. Thus, it accurately represents a problem in which we desire to minimise the error while simultaneously retaining the minimality of the simulated flow energy. In (34), \(\delta \psi = \delta \psi ^{(0)} + \delta \psi ^{(1)}\), where \( \delta \psi ^{(0)} \) is of the first order of smallness and \( \delta \psi ^{(1)} \) is of the second order of smallness. In deriving (34), we retain terms only upto cubic order of smallness i.e. by noting that a product of two \( \delta \psi ^{(0)} \)s is of second order as is \( \delta \psi ^{(1)} \), while a product of a \( \delta \psi ^{(0)} \) and a \( \delta \psi ^{(1)} \) is of cubic order, while a product of two \( \delta \psi ^{(0)} \)s is of fourth order of smallness.

5.1 Ornstein–Uhlenbeck process

In turbulent flows, Ornstein–Uhlenbeck (OU) [13] processes are used to model velocity components of fluid particles. The OU process is a stochastic process that satisfies the following stochastic differential equation:

$$\begin{aligned} dV = -\gamma V dt + \sigma dB, \end{aligned}$$
(35)

where \(\gamma \) is relaxation rate and \(\sigma \) is white noise. The first term in the right-hand side is a drift term that reduces fluctuations in V(t) process. The second term adds stochastic fluctuations in V(t) process and, therefore, counteracts the first term.

5.2 Estimating the shift in average error energy for calculating \(\theta \)

We evaluate the shift in the average energy function \( \langle \mathcal {E}\rangle \) caused by the random shift and calculate the parameter vector \(\underline{\theta }\) that minimises this average energy shift. Using the expressions (25) and (27) and defining \( \mathcal {E}_{0} = \frac{1}{2} \underline{\psi }_{0}^{T}\underline{\underline{Q}}_{0}\underline{\psi }_{0}-\underline{\lambda }_{0}^{T}\underline{\psi }_{0} \), we get

$$\begin{aligned} \langle \mathcal {E}\rangle - \mathcal {E}_{0}&= \mathbb {E}(\delta {\underline{\psi }^{(1)}}^{T}\underline{\underline{Q}}_{0}\underline{\psi }_{0}) + \mathbb {E}(\delta {\underline{\psi }^{(0)}}^{T}\underline{\underline{Q}}_{0}\delta \underline{\psi }^{(0)}) - {\underline{\lambda }_{0}}^{T}\mathbb {E}(\delta \underline{\psi }^{(1)})\quad \quad \nonumber \\&=\underline{{\psi }}_{0}^{T}\underline{\underline{Q}}_{0}\underline{\underline{K}}_{1}\mathbb {E}(\delta \underline{g}\otimes \delta \underline{g}) + Tr(\underline{\underline{K}}_{0}^{T}\underline{\underline{Q}}_{0}\underline{\underline{K}}_{0}\mathbb {E}(\delta \underline{g}\otimes \delta \underline{g}^{T}))- \underline{\lambda }_{0})^{T}\nonumber \\&\quad \times \underline{\underline{K}}_{1}\mathbb {E}(\delta \underline{g}\otimes \delta \underline{g}) + Tr(\underline{\underline{K}}_{0}^{T}\underline{\underline{Q}}_{0}\underline{\underline{K}}_{1}(\delta \underline{g}\otimes \delta \underline{g})\delta \underline{g}^{T}), \end{aligned}$$
(36)

the second and third moments \(\mathbb {E}(\delta \underline{g}\otimes \delta \underline{g})\) and \(\mathbb {E}((\delta \underline{g}\otimes \delta \underline{g}).\delta \underline{g}^{T})\) depend on parameter \(\underline{\theta }\) (variance) and \(\langle \mathcal {E}\rangle - \mathcal {E}_{0}\) is minimised w.r.t \(\underline{\theta }\) to get the optimal flow.

Remark 1

The third moment term in \( \delta {\underline{g}} \) arises from the factor \( \mathbb {E}(\delta {{\underline{\psi }}^{(0)}}^{T}\underline{\underline{Q}}_{0}\delta \underline{\psi }^{(1)}) \) in (34) after taking into account (30) and (32).

Remark 2

\( \mathcal {E}_{0} \) stands for the energy in the absence of the random force perturbation.

6 Results and conclusion

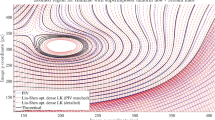
Simulations were done in Matlab R2015 on a PC INTEL CORE I5 to generate the true optical flow \(V_{ox}\) and \(V_{oy}\) by minimising the distance between the simulated stream function and the true stream function. The true stream function corresponds to optical flow subjected to an energy constraint on the fluid flow. Such a simulated optical flow has small energy and closely resembles to a given optical flow (as shown in Figs. 1, 2). In Fig. 1, the graphs titled \(V_{ox}\), \(V_{x}\), \(V_{ox}\)-\(V_{x}\) and \(V_{oy}\), \(V_{y}\), \(V_{oy}\)-\(V_{y}\) are x and y components of true velocity field, simulated velocity field and error velocity field, respectively.

6.1 Noise to signal ratio

Let \(\underline{\psi }_{0}\), \(\underline{\psi }\) be the true and simulated flow stream function and likewise \((V_{ox},V_{oy})\) and \((V_x,V_y)\) are the true and simulated velocity fields. We present in Table 1 the corresponding noise to signal ratio (NSR)s, here \(\mathrm{NSR} = \frac{||V_x-V_{0x}||^{2}}{||V_{0x}||^{2}}\), \(\mathrm{NSR}^{\prime } = \frac{||V_y-V_{0y}||^{2}}{||V_{0y}||^{2}}\) and \(\mathrm{NSR}^{\prime \prime } = \frac{||\psi -\psi _0||^{2}}{||\psi _0||^{2}}\), obtained from true and simulated stream function in x and y direction, respectively. The true and simulated optical flow velocities are of the order \( 10^{5} \), while the error between these two flows is of order \( 10^{-2} \) as shown in Fig. 1. In all cases, we get an \(\mathrm{NSR}<1\) showing the goodness of the energy minimisation technique. As time progresses, the NSR decreases showing that the time-varying transient simulated flow velocity converges close to the true optical flow.

6.2 Analysis of random velocity perturbation

Let \( (V_{0x}, \; V_{0y}) \) and \( (V_{x}, \; V_{y}) \) denote the true velocity field of optical flow and simulated flow respectively. Our method essentially matches \( V_{x}, \; V_{y} \) to \( V_{0x}, \; V_{0y} \) subject to the constraint that \( V_{x}, \; V_{y} \) satisfies the Navier–Stokes equation. Figures 1 and 2 justify the proposed statement. The experiment is carried out over the force field. The force field is varied so that we get a velocity which approximates the true optical flow.

The random forcing field, \(\underline{g}\), is calculated by energy minimisation using the stream function \(\underline{\psi }\). We then add a small random force \(\delta \underline{g}\) to \(\underline{g}\) and simulate the correction to the stream function \(\delta \psi \) using (34) and (35). The histogram for \(\delta \underline{g}\) (Fig. 3) shows a nearby normal distribution which justifies our linearised perturbation approximation. The value of parameter \(\underline{\theta }\) (mean, variance) obtained from simulation is 11.6 and 9.6171, respectively. The autocorrelation plot for \(\delta \) \(\underline{g}\) (Fig. 4) shows a exponentially decaying function with increasing spatial lag. This \(\delta \) \(\underline{g}\) is a spatial version of the OU(Ornstein–Uhlenbeck) process. This confirms the presence of both damping factors arising from viscosity and fluctuating factors arising from random white noise in \(\delta \underline{g}\) as in the OU process.

Remark  The simulation has been done based on the following computational steps:

  1. 1.

    Estimate the true stream function \( \underline{\psi }_{0} \) from measurements of the optical flow.

  2. 2.

    Calculate the force field in the Navier Stokes equation for approximating the true stream function \( \underline{\psi }_{0} \) by the simulated stream function \( \underline{\psi } \). To implement this step, we discretised the Navier–Stokes equation into spatial pixels and then optimise in the discrete domain. Optimisation yields the required driving force in the Navier–Stokes equation for optimal modelling.

  3. 3.

    Using perturbation theory outlined in the manuscript, evaluate the effect of a small random perturbation in the optimal force on the change in the modelled velocity field and the corresponding increase in the average modelling error energy.

Table 1 \(\mathrm{NSR}\), \(\mathrm{NSR}^{\prime }\) and \(\mathrm{NSR}^{\prime \prime }\) are noise to signal ratio values in x and y direction of velocity, respectively, and at five different time instants (in s)
Full size table
Fig. 1
figure 1

Simulation of optical flow using fluid flow by energy minimising the distance between simulated and true stream function

Full size image
Fig. 2
figure 2

True and simulated optical flow

Full size image
Fig. 3
figure 3

Histogram curve of small random force \(\delta \) g

Full size image
Fig. 4
figure 4

Autocorrelation curve of forcing field g

Full size image