1 Introduction

The time- and space-fractional Burgers’ equations arise in areas of many phenomena such as material science, hereditary effects on nonlinear acoustic waves, chemical reaction fluid mechanics, plasma physics, optical fibers, and finance [5, 17, 26, 32].

In this paper, let us consider time-fractional-coupled Burgers’ equation:

$$\begin{aligned} \dfrac{\partial ^{\alpha _{1}}}{\partial t^{\alpha _{1}}} Z_{1}= & {} \dfrac{\partial ^{2}}{\partial x^{2}}Z_{1}+ 2Z_{1} \dfrac{\partial ^{}}{\partial x^{}}Z_{1}-\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}Z_{2}),\qquad (0<\alpha _{1}\le 1),\end{aligned}$$
(1.1)
$$\begin{aligned} \dfrac{\partial ^{\beta _{1}}}{\partial t^{\beta _{1}}} Z_{2}= & {} \dfrac{\partial ^{2}}{\partial x^{2}}Z_{2}+2Z_{2} \dfrac{\partial ^{}}{\partial x^{}}Z_{2}-\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}Z_{2}),\qquad (0<\beta _{1}\le 1), \end{aligned}$$
(1.2)

and space-fractional-coupled Burgers’ equation:

$$\begin{aligned} \dfrac{\partial ^{}}{\partial t^{}} Z_{1}= & {} \dfrac{\partial ^{2}}{\partial x^{2}}Z_{1}+ 2Z_{1} \dfrac{\partial ^{\alpha _{2}}}{\partial x^{\alpha _{2}}}Z_{1}-\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}Z_{2}),\qquad (0<\alpha _{2}\le 1),\end{aligned}$$
(1.3)
$$\begin{aligned} \dfrac{\partial ^{}}{\partial t^{}} Z_{2}= & {} \dfrac{\partial ^{2}}{\partial x^{2}}Z_{2}+2Z_{2} \dfrac{\partial ^{\beta _{2}}}{\partial x^{\beta _{2}}}Z_{2}-\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}Z_{2}),\qquad (0<\beta _{2}\le 1). \end{aligned}$$
(1.4)

with initial condition:

$$\begin{aligned} Z_{1}(x,0) = f_{1}(x),~Z_{2}(x,0) = f_{2}(x),\qquad (x) \in \Omega , \end{aligned}$$

and boundary conditions:

$$\begin{aligned} Z_{1}(x_{L}t)= & {} g_{1}(t), ~~Z_{1}(x_{R},t) = g_{2}(t),~~ \quad t\in [0,1], \quad (x)\in \partial \Omega , \\ Z_{2}(x_{L},t)= & {} g_{3}(t), ~~Z_{2}(x_{R}, t) = g_{4}(t). \\ \end{aligned}$$

where \(\Omega ^{}= \left[ x_{L},x_{R}\right] ^{} \), \( \alpha _{1} \) and \( \beta _{1} \) are order of time-fractional derivative, and \( \alpha _{2} \) and \( \beta _{2} \) are order of space-fractional derivative.

In past years, several analytical and numerical methods have been developed for the time- and space-fractional coupled Burger’s equation. Kurt et al. [16] have proposed exp- function method and perturbation–iteration method for the analytical solutions of nonlinear time-fractional coupled Burgers’ equations. Senol et al. [27] have introduced residual power series method for the numerical solutions of time-fractional burgers’ type equation with conformable fractional derivative. Cenesiz et al. [7] have obtained new type exact solutions for time-fractional Burgers’ equation, modified Burgers’ equation, and Burgers’–Korteweg–de-Vries equation using first integral method. Islam et al. [15] have obtained extract exact solutions for space-time-fractional Burgers’ equation using rational fractional expansion method. Furthermore, authors have also employed exp-function method and the extended tanh method to construct the closed form solutions. Prakash et al. [25] have proposed fractional variational iteration method for the numerical solutions of time- and space-fractional coupled Burgers’ equations. Chen and Li An [8] have introduced the Adomian decomposition method for numerical solutions of coupled Burgers’ equations with time- and space-fractional derivatives. Yildirim and Kelleci [30] have proposed homotopy perturbation method for the numerical solutions of coupled Burgers’ equations with time- and space-fractional derivatives. Asgari and Hosseini [3] have proposed two semi-implicit Fourier spectral schemes for the numerical solution of generalized time-fractional Burger’s equation. In this method, the authors have shown unconditional stability and improve the computational cost. Momani [24] has obtained the non-perturbative analytical solutions of space- and time-fractional Burgers’ equations using Adomian decomposition method and describe the physical processes of unidirectional propagation of weakly nonlinear acoustic waves through a gas-filled pipe. Mohammadizadeh et al. [23] have obtained unique solutions under some special conditions for a special class of fractional Burgers’ equation. They have also found at least one optimal solution for this problem. Moreover, this equation was solved by many different numerical methods such as finite-difference method [18, 19], finite-element method [31, 33], variational iteration method [14], spectral method [4, 20,21,22], Adomian decomposition method [1], b-spline method [9, 11, 12], Galerkin method [6], homotopy algorithm [29], generalized exp-function method [10], finite volume method [13], residual power series method [34], and homotopy perturbation method [2], etc.

This paper is organized as follows. In Sect. 2, we describe some basic definitions and notations. Discretizing and description of the methods are presented in Sects. 3 and 4. In Sect. 5, we present the convergence analysis of time- and space-fractional coupled Burgers’ equation. In Sect. 5, we present numerical solutions and errors by the proposed scheme. Finally, the conclusion of our work is given in the last section.

2 Preliminary

In this section, the definition of the Caputo–Riemann–Liouville fractional derivative is introduced systematically.

Definition 2.1: The partial fractional derivatives of order \( n-1<\nu <n \) of a function \( \L _{M}(t) \), with respect to variable t, in the Caputo–Riemann–Liouville fractional derivative formula are defined by:

$$\begin{aligned} \L _{M}^{'}(t)= & {} \partial ^{\nu }_{t} \L _{M}(t)\nonumber \\= & {} \left\{ \begin{array}{ll} {\frac{1}{\Gamma (-\nu )}\int _{0}^{t}(t-\xi )^{-\nu -1}\left( \L _{M}(\xi )-\L _{M}(0)\right) \mathrm{d}\xi \, }, ~&{} \nu<0,\\ \frac{1}{\Gamma (1-\nu )} \frac{\partial }{\partial t}\int _{0}^{t}(t-\xi )^{-\nu }\left( \L _{M}(\xi )-\L _{M}(0)\right) \mathrm{d}\xi \,, ~&{} 0<\nu<1, \quad \forall M,\\ \frac{1}{\Gamma (n-\nu )} \frac{\partial ^{n}}{\partial t^{n}}\int _{0}^{t}(t-\xi )^{n-\nu -1}\left( \L _{M}(\xi )-\L _{M}(0)\right) \mathrm{d}\xi , &{} n-1\le \nu <n, \end{array}\right. \end{aligned}$$
(2.1)

where \( \nu \ge 0 \) is the order of derivative, \( \Gamma \) is the gamma function, and \( n=\lceil \nu \rceil +1 \) with \( \lceil \nu \rceil \) denoting the integral part of \( \nu \). Caputo–Riemann–Liouville fractional derivatives have some basic properties which are needed in this paper as follows:

$$\begin{aligned} \partial ^{\nu }_{t} C= & {} 0,~~~~ C~~ \text {is constant}, \\ \partial ^{\nu }_{t} t^{\upsilon }= & {} \left\{ \begin{array}{ll} {0}, ~~~~~~&{} \mathrm{for}~~ \upsilon \in N~~ \mathrm{and} ~~ \upsilon <\lceil \nu \rceil ,\\ \frac{\Gamma (\upsilon +1)}{\Gamma (\upsilon +1-\nu )} t^{\upsilon -\nu }, ~~~~~&{} \mathrm{for} ~~\upsilon \in N ~~\mathrm{and} ~~ \upsilon \ge \lceil \nu \rceil . \end{array}\right. \end{aligned}$$

Moreover, construction of the first-order Chebyshev fractional differential matrix is given as:

$$\begin{aligned} Q^{(\nu )}= \left[ \begin{array}{cccc} \L _{0}^{'}(t_{0}) &{} \dots &{} \dots &{} \L _{0}^{'}(t_{M})\\ \ddots &{} \ddots &{} \ddots &{} \ddots \\ \ddots &{} \ddots &{} \ddots &{} \ddots \\ \L _{M}^{'}(t_{0}) &{} \dots &{} \dots &{} \L _{M}^{'}(t_{M})\\ \end{array}\right] . \end{aligned}$$

3 Pseudospectral methodology

The method allows the representation of functions and their derivatives at given set of grid points and approximate solutions of nonlinear partial differential equations as a sum of basis functions in both space and time directions.

We seek a pseudospectral approximation F(x, t), as a finite linear combination of a chosen set of orthogonal basis functions for the one-dimensional form:

$$\begin{aligned} F(x,t) = \sum _{i=0}^{M_{}} \sum _{j=0}^{M_{}}{\tau _i(x) \tau _j(t)}~ { F(x_{i},t_{j})}, \end{aligned}$$
(3.1)

where the trial basis functions defined by:

$$\begin{aligned} \tau _k(z) = {\frac{P(z)}{Q(z_{k})~(z - z_{k})}} , ~~~~k = 0,\ldots ,M, \end{aligned}$$

and

$$\begin{aligned} P(z) = \prod _{k = 0}^{M} (z - z_{k}),~~~~~~~~~ Q(z) =\sum _{l=0}^{M} \prod _{k = 0,k\ne l}^{M} (z_{} - z_{k}). \end{aligned}$$

Here, z is a dummy variable and represents x in spatial and t in time direction, \(\tau _i(x)\) and \(\tau _j(t)\) are \(M^{th}\) degree Lagrange polynomials in spatial and time variables, and \( F(x_{i},t_{j}) \) are unknowns spectral coefficients. Let us define Chebyshev–Gauss–Lobatto points (CGL points):

$$\begin{aligned} z_{k} = -\cos (k\pi /M) , \, \, \forall ~~ k=0,\ldots ,M. \end{aligned}$$
(3.2)

These points are projection of equispaced points on upper half of unit circle on \( [ -1, 1] \) and make cluster at boundaries.

Next, define the Chebyshev differentiation matrix at CGL points \(\left\{ z_{0}, z_{1},\ldots ,z_{M} \right\} \), which is used to approximate the derivatives of F(x, t) in the spatial and time directions. The first derivative matrix \(D^{(1)}\) is defined by:

$$\begin{aligned} D^{(1)}_{ij}=\left\{ \begin{array}{ll} {\frac{P^{'}(z_{i})}{Q^{}(z_{j})~(z_{i} - z_{j})}}, &{} i \ne j, \\ \sum _{l=0,l \ne i}^{M} (z_{i} - z_{l})^{-1} , &{} i = j. \end{array}\right. \end{aligned}$$

Then, Eq. (3.1) can be expressed in the form of direct product as:

$$\begin{aligned} F(x,t)= & {} \tau _{0}(x)\left[ \tau _{0}(t)F_{00}+\cdots +\tau _{M}(t)F_{0M}\right] +\cdots + \tau _{M}(x)\left[ \tau _{0}(t)F_{M0}+\cdots +\tau _{M}(t)F_{MM}\right] , \nonumber \\= & {} \left[ (\tau _{0}(x), \ldots ,\tau _{M}(x)) \otimes (\tau _{0}(t), \ldots ,\tau _{M}(t)) \right] \mathbf{F }^{}, \nonumber \\= & {} \left( \Psi _{[0:M]}(x)\otimes \Psi _{[0:M]}(t)\right) ^{T} \mathbf{F }^{}, \end{aligned}$$
(3.3)

where

$$\begin{aligned} \mathbf{F }^{}= & {} \left[ F^{}_{00},\ldots ,F^{}_{0M}\mid \cdots \mid F^{}_{M0}, \ldots ,F^{}_{MM}\right] ^{T},\\ \Psi _{[0:M]}(z)= & {} \left[ \tau _{0}(z), \ldots ,\tau _{M}(z) \right] ^{T}. \end{aligned}$$

In this manner, first spatial derivative of the function can be defined as follows:

$$\begin{aligned} \frac{\partial F^{}}{\partial x}= & {} \left( \frac{\partial }{\partial x}\Psi _{[0:M]}^{T}(x)\otimes \Psi _{[0:M]}^{T}(t) \right) \mathbf{F }^{} = \left( \Psi _{[0:M]}^{T}(x)D^{(1)}_{\left[ 0:M,0:M\right] }\otimes \Psi _{[0:M]}^{T}(t) \right) \mathbf{F }^{}, \nonumber \\= & {} \left( \Psi _{[0:M]}(x) \otimes \Psi _{[0:M]}(t)\right) ^{T}\left( D^{(1)}_{[0:M,0:M]} \otimes I_{M+1}\right) \mathbf{F }^{}. \end{aligned}$$
(3.4)

In similar fashion, first spatial fractional derivative of the function can be defined as follows:

$$\begin{aligned} \frac{\partial ^{\nu } F^{}}{\partial x^{\nu }}= & {} \left( \Psi _{[0:M]}(x) \otimes \Psi _{[0:M]}(t)\right) ^{T}\left( Q^{(\nu )}_{[0:M,0:M]} \otimes I_{M+1}\right) \mathbf{F }^{}. \end{aligned}$$
(3.5)

Next, time derivative and time-fractional derivative of the function can be defined by:

$$\begin{aligned} \frac{\partial F^{}}{\partial t}= & {} \left( \Psi _{[0:M]}(x) \otimes \Psi _{[0:M]}(t)\right) ^{T}\left( I_{M+1} \otimes D^{(1)}_{[0:M,0:M]}\right) \mathbf{F }^{}. \nonumber \\ \frac{\partial ^{\nu } F^{}}{\partial t^{\nu }}= & {} \left( \Psi _{[0:M]}(x) \otimes \Psi _{[0:M]}(t)\right) ^{T}\left( I_{M+1} \otimes Q^{(\nu )}_{[0:M,0:M]}\right) \mathbf{F }^{}. \end{aligned}$$
(3.6)

Similarly, the second spatial derivative of the function is given by:

$$\begin{aligned} \frac{\partial ^{2} F^{}}{\partial x^{2}}= & {} \left( \frac{\partial ^{2}}{\partial x^{2}}\Psi _{[0:M]}^{T}(x)\otimes \Psi _{[0:M]}^{T}(t) \right) \mathbf{F }^{} = \left( \frac{\partial }{\partial x} \left( \frac{\partial }{\partial x}\Psi _{[0:M]}^{T}(x)\right) \otimes \Psi _{[0:M]}^{T}(t) \right) \mathbf{F }^{}, \nonumber \\= & {} \left( \left( \frac{\partial }{\partial x} \Psi _{[0:M]}^{T}(x)D^{(1)}_{\left[ 0:M,0:M\right] }\right) \otimes \Psi _{[0:M]}^{T}(t) \right) \mathbf{F }^{}, \nonumber \\= & {} \left( \left( \Psi _{[0:M]}^{T}(x)D^{(1)}_{\left[ 0:M,0:M\right] } \times D^{(1)}_{\left[ 0:M,0:M\right] }\right) \otimes \Psi _{[0:M]}^{T}(t) \right) \mathbf{F }^{}, \nonumber \\= & {} \left( \Psi _{[0:M]}(x) \otimes \Psi _{[0:M]}(t)\right) ^{T}\left( D^{(2)}_{[0:M,0:M]} \otimes I_{M+1}\right) \mathbf{F }^{}. \end{aligned}$$
(3.7)

where \( D^{(2)}= D^{(1)}\times D^{(1)}\).

4 Pseudospectral method-based discretization

Furthermore, let us consider following transformations which are used to transform the one-dimensional space \( [x_{L},x_{R}] \), \( [y_{L},y_{R}] \) and time [0, T] in to \( [-1,1] \). We obtain the time fractional coupled Burgers’ equation in new space and time interval:

$$\begin{aligned} \dfrac{\partial ^{\alpha _{1}}}{\partial t^{\alpha _{1}}} Z_{1}= & {} \frac{2^{(2-\alpha _{1})}T^{\alpha _{1}} }{(x_{R} -x_{L})^{2}}\dfrac{\partial ^{2}}{\partial x^{2}}Z_{1}+ \frac{2^{(1-\alpha _{1})}T^{\alpha _{1}} }{(x_{R} -x_{L})^{}}2Z_{1} \dfrac{\partial ^{}}{\partial x^{}}Z_{1} -Z_{1}\frac{2^{(1-\alpha _{1})}T^{\alpha _{1}} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Z_{2})-Z_{2}\frac{2^{(1-\alpha _{1})}T^{\alpha _{1}} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}),\\ \dfrac{\partial ^{\beta _{1}}}{\partial t^{\beta _{1}}} Z_{2}= & {} \frac{2^{(2-\beta _{1})}T^{\beta _{1}} }{(x_{R} -x_{L})^{2}}\dfrac{\partial ^{2}}{\partial x^{2}}Z_{2}+ \frac{2^{(1-\beta _{1})}T^{\beta _{1}} }{(x_{R} -x_{L})^{}}2Z_{2} \dfrac{\partial ^{}}{\partial x^{}}Z_{2} -Z_{1}\frac{2^{(1-\beta _{1})}T^{\beta _{1}} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Z_{2}) -Z_{2}\frac{2^{(1-\alpha _{1})}T^{\alpha _{1}}}{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}). \end{aligned}$$

and space-fractional coupled Burgers’ equation:

$$\begin{aligned} \dfrac{\partial ^{}}{\partial t^{}} Z_{1}= & {} \frac{2^{}T^{} }{(x_{R} -x_{L})^{2}}\dfrac{\partial ^{2}}{\partial x^{2}}Z_{1}+ \frac{2^{(\alpha _{2}-1)}T^{} }{(x_{R} -x_{L})^{\alpha _{2}}}2Z_{1} \dfrac{\partial ^{\alpha _{2}}}{\partial x^{\alpha _{2}}}Z_{1} -Z_{1}\frac{T^{} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Z_{2})- Z_{2}\frac{T^{} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}),\\ \dfrac{\partial ^{}}{\partial t^{}} Z_{2}= & {} \frac{2^{}T^{} }{(x_{R} -x_{L})^{2}}\dfrac{\partial ^{2}}{\partial x^{2}}Z_{2}+ \frac{2^{(\beta _{2}-1)}T^{} }{(x_{R} -x_{L})^{\beta _{2}}}2Z_{2} \dfrac{\partial ^{\beta _{2}}}{\partial x^{\beta _{2}}}Z_{2} -Z_{1}\frac{T^{} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Z_{2})- Z_{2}\frac{T^{} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}). \end{aligned}$$

with initial conditions:

$$\begin{aligned} Z_{1}(x,- 1) = p_{1}(x),~ Z_{2}(x,- 1) = p_{2}(x),\qquad x\in [- 1,1], \end{aligned}$$
(4.1)

and boundary conditions:

$$\begin{aligned} Z_{1}(- 1,t)= & {} q_{11}(t), ~~Z_{1}(1,t) = q_{12}(t),~~ \qquad t\in [- 1,1], \end{aligned}$$
(4.2)
$$\begin{aligned} Z_{2}(- 1,t)= & {} q_{21}(t), ~~Z_{2}(1,t) = q_{22}(t),~~ \qquad t\in [- 1,1]. \end{aligned}$$
(4.3)

Furthermore, we consider a mapping for converting the non-homogeneous initial and boundary values to homogeneous initial and boundary values:

$$\begin{aligned} \chi _{k}(x,t) = \frac{1-t}{2} p_{k}(x) + \frac{1-x}{2} q_{1k}(t) +\frac{1+x}{2} q_{2k}(t)- \frac{(1-t)(1-x)}{4} q_{1k}(- 1)- \frac{(1-t)(1+x)}{4}q_{2k}(-1). \nonumber \\ \end{aligned}$$
(4.4)

Define new variables \(Y_{k}(x,t),~\forall k=\left\{ 1,2\right\} \):

$$\begin{aligned} Z_{1}(x,t) = Y_{1}(x,t) +\chi _{1}(x,t),~~Z_{2}(x,t) = Y_{2}(x,t) +\chi _{2}(x,t), \end{aligned}$$
(4.5)

the above time-fractional coupled Burgers’ equation can be modified with new variables and obtained the residuals:

$$\begin{aligned} \dfrac{\partial ^{\alpha _{1}}}{\partial t^{\alpha _{1}}} (Y_{1} +\chi _{1})= & {} \frac{2^{(2-\alpha _{1})}T^{\alpha _{1}} }{(x_{R} -x_{L})^{2}}\dfrac{\partial ^{2}}{\partial x^{2}}(Y_{1} +\chi _{1})+ \frac{2^{(1-\alpha _{1})}T^{\alpha _{1}} }{(x_{R} -x_{L})^{}}2(Y_{1} +\chi _{1}) \dfrac{\partial ^{}}{\partial x^{}}(Y_{1} +\chi _{1})\\&-(Y_{1} +\chi _{1})\frac{2^{(1-\alpha _{1})}T^{\alpha _{1}} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Y_{2} +\chi _{2})-(Y_{2} +\chi _{2})\frac{2^{(1-\alpha _{1})}T^{\alpha _{1}} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Y_{1} +\chi _{1}),\\ \dfrac{\partial ^{\beta _{1}}}{\partial t^{\beta _{1}}} (Y_{2} +\chi _{2})= & {} \frac{2^{(2-\beta _{1})}T^{\beta _{1}} }{(x_{R} -x_{L})^{2}}\dfrac{\partial ^{2}}{\partial x^{2}}(Y_{2} +\chi _{2})+ \frac{2^{(1-\beta _{1})}T^{\beta _{1}} }{(x_{R} -x_{L})^{}}2(Y_{2} +\chi _{2}) \dfrac{\partial ^{}}{\partial x^{}}(Y_{2} +\chi _{2}) \\&-\,\,(Y_{1} +\chi _{1})\frac{2^{(1-\beta _{1})}T^{\beta _{1}} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Y_{2} +\chi _{2}) -(Y_{2} +\chi _{2})\frac{2^{(1-\alpha _{1})}T^{\alpha _{1}}}{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Y_{1} +\chi _{1}), \end{aligned}$$

and obtain the residuals of space-fractional coupled Burgers’ equation:

$$\begin{aligned} \dfrac{\partial ^{}}{\partial t^{}} (Y_{1} +\chi _{1})= & {} \frac{2^{}T^{} }{(x_{R} -x_{L})^{2}}\dfrac{\partial ^{2}}{\partial x^{2}}(Y_{1} +\chi _{1})+ \frac{2^{(\alpha _{2}-1)}T^{} }{(x_{R} -x_{L})^{\alpha _{2}}}2(Y_{1} +\chi _{1}) \dfrac{\partial ^{\alpha _{2}}}{\partial x^{\alpha _{2}}}(Y_{1} +\chi _{1})\\&-\,\,(Y_{1} +\chi _{1})\frac{T^{} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Y_{2} +\chi _{2})- (Y_{2} +\chi _{2})\frac{T^{} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Y_{1} +\chi _{1}),\\ \dfrac{\partial ^{}}{\partial t^{}} (Y_{2} +\chi _{2})= & {} \frac{2^{}T^{} }{(x_{R} -x_{L})^{2}}\dfrac{\partial ^{2}}{\partial x^{2}}(Y_{2} +\chi _{2})+ \frac{2^{(\beta _{2}-1)}T^{} }{(x_{R} -x_{L})^{\beta _{2}}}2(Y_{2} +\chi _{2}) \dfrac{\partial ^{\beta _{2}}}{\partial x^{\beta _{2}}}(Y_{2} +\chi _{2}) \\&-\,\,(Y_{1} +\chi _{1})\frac{T^{} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Y_{2} +\chi _{2})- (Y_{2} +\chi _{2})\frac{T^{} }{(x_{R} -x_{L})^{}}\dfrac{\partial ^{}}{\partial x^{}}(Y_{1} +\chi _{1}). \end{aligned}$$

Now, we apply CGL points and pseudospectral method in coupled equations and obtained the system of nonlinear algebraic equation:

$$\begin{aligned} G_{1}(Y_{1}|Y_{2}) =0 \qquad G_{2}(Y_{1}|Y_{2}) =0. \end{aligned}$$
(4.6)

The system of nonlinear equation (4.6) can be solved using Newton–Raphson method.

5 Convergence analysis

In this section, author study for the error analysis of the suggested expansion of Chebyshev polynomials is investigated.

Theorem 51

If the series \( \sum _{i=0}^{\infty } \sum _{k=0}^{\infty }{\tau _{i}(x) \tau _{k}(t) \varTheta _{ik}} \) converges uniformly to \( Z_{1}(x,t) \) on the interval \( [-1,1]^{2} \), then we have:

$$\begin{aligned} \varTheta _{ik}= & {} \dfrac{1}{ {\hat{h}}^{}_{i} {\hat{h}}^{}_{k}} \sum _{l=0}^{M} \sum _{n=0}^{M}\tau _{i}(x_{l}) \tau _{k}(t_{n}) w^{}_{l}~w^{}_{m}~w^{}_{n} {Z_{1}^{}(x_{i},t_{k})^{}}. \end{aligned}$$
(5.1)

Proof

We know that:

$$\begin{aligned} Z_{1}(x,t) = \sum _{i=0}^{\infty } \sum _{k=0}^{\infty }{\tau _{i}(x) \tau _{k}(t) \varTheta _{ik}}. \end{aligned}$$
(5.2)

Taking \( L_{w^{}}^{2}[- 1,1] \) norm both side, we get:

$$\begin{aligned} \Arrowvert Z_{1}(x,t)\Arrowvert ^{2}_{L^{2}_{w^{}}[-1,1]}= & {} \sum _{i=0}^{\infty } \sum _{k=0}^{\infty } \Arrowvert \tau _{i}(x) \tau _{k}(t) \varTheta _{ik}\Arrowvert ^{2}_{L^{2}_{w^{}}[-1,1]} =\sum _{i=0}^{\infty } \sum _{k=0}^{\infty } \Arrowvert \tau _{i}(x) \tau _{k}(t) \Arrowvert ^{2}_{L^{2}_{w^{}}[-1,1]} \arrowvert \varTheta _{ik}\arrowvert ^{2}, \\\le & {} \sum _{i=0}^{\infty } \sum _{k=0}^{\infty } \int _{-1}^1\int _{-1}^1 \tau ^{2}_{i}(x) \tau ^{2}_{k}(t) w^{}(x)w^{}(y) w^{}(t)\, dx\ dt\ \arrowvert \varTheta _{ik}\arrowvert ^{2}, \\\le & {} \sum _{i=0}^{\infty } \sum _{k=0}^{\infty } \tau ^{2}_{i}(x) w^{}(x) \, dx\ \int _{-1}^1 dy\ \int _{-1}^1 \tau ^{2}_{k}(t) w^{}(t)\, dt\ \arrowvert \varTheta _{ik}\arrowvert ^{2}, \\\le & {} \sum _{i=0}^{\infty } \sum _{k=0}^{\infty } \left[ \tau _{i}(x),\tau _{i}(x)\right] _{w^{}} \left[ \tau _{k}(t), \tau _{k}(t)\right] _{w^{}} \arrowvert \varTheta _{ik}\arrowvert ^{2}. \end{aligned}$$

Finally, put the value of discrete inner product, and we get:

$$\begin{aligned} \Arrowvert Z_{1}\Arrowvert ^{2}_{L^{2}_{w^{}}[-1,1]} \le \sum _{i=0}^{\infty } \sum _{k=0}^{\infty } {\hat{h}}^{}_{i} {\hat{h}}^{}_{k} \arrowvert \varTheta _{ik}\arrowvert ^{2}. \end{aligned}$$
(5.3)

Hence, function \( Z_{1}(x,t) \) is bounded. In a similar fashion, we can obtain function \( Z_{2}(x,t) \) is bounded. \(\square \)

6 Numerical results and discussion

In this section, to demonstrate the performance, the proposed method is implemented on test problems of time- and space-fractional Burgers’ equation. Error at different grid points will be expressed in terms of \( L_{2} \)- norm which is defined by:

$$\begin{aligned} L_{2} = \Arrowvert Z_{i}^\mathrm{exa}-Z_{i(\alpha ,\beta )}^\mathrm{num} \Arrowvert _{2}, \end{aligned}$$

where \(Z_{i}^\mathrm{exa}\) and \(Z_{i(\alpha ,\beta )}^\mathrm{num},~~~ \forall i\in {1,2},\) represent exact solutions and numerical solutions, respectively.

6.1 Example 1

Let us consider the time-fractional coupled Burgers’ equation:

$$\begin{aligned} \dfrac{\partial ^{\alpha _{1}}}{\partial t^{\alpha _{1}}} Z_{1}= & {} \dfrac{\partial ^{2}}{\partial x^{2}}Z_{1}+2Z_{1} \dfrac{\partial ^{}}{\partial x^{}}Z_{1}-\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}Z_{2}),\qquad (0<\alpha _{1}\le 1),\end{aligned}$$
(6.1)
$$\begin{aligned} \dfrac{\partial ^{\beta _{1}}}{\partial t^{\beta _{1}}} Z_{2}= & {} \dfrac{\partial ^{2}}{\partial x^{2}}Z_{2}+2Z_{2} \dfrac{\partial ^{}}{\partial x^{}}Z_{2}-\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}Z_{2}), \qquad (0<\beta _{1}\le 1) \end{aligned}$$
(6.2)

with initial condition:

$$\begin{aligned} Z_{1}(x,0) = \sin (x),~Z_{2}(x,0) = \sin (x),\qquad (x) \in \Omega , \end{aligned}$$

the exact solution for the problem is given: [1]

$$\begin{aligned} Z_{1}(x,t)= & {} \sin (x)-\sin (x)\frac{t^{\alpha _{1}}}{\Gamma (\alpha _{1}+1)}+(\sin (x)-2\sin (x)\cos (x))\frac{t^{2\alpha _{1}}}{\Gamma (2\alpha _{1}+1)}\\&2\sin (x)\cos (x)\frac{t^{\alpha _{1}+\beta _{1}}}{\Gamma (\alpha _{1}+\beta _{1}+1)}+\cdots \\ Z_{2}(x,t)= & {} \sin (x)-\sin (x)\frac{t^{\beta _{1}}}{\Gamma (\beta _{1}+1)}+(\sin (x)-2\sin (x)\cos (x))\frac{t^{2\beta _{1}}}{\Gamma (2\beta _{1}+1)}\\&2\sin (x)\cos (x)\frac{t^{\alpha _{1}+\beta _{1}}}{\Gamma (\alpha _{1}+\beta _{1}+1)}+\cdots \end{aligned}$$

When \( \alpha _{1}=\beta _{1}=1 \), then exact solution is:

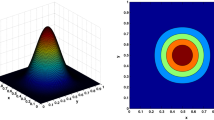
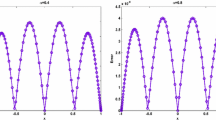
$$\begin{aligned} Z_{1}(x,t)=Z_{2}(x,t)=e^{-t}\sin (x). \end{aligned}$$

In this example, numerical solutions of the proposed method have obtained over the domain \( \Omega =[- 10,10]^{},~~ t \in [0,0.005] \) and fractional-order derivative \( 0< \alpha _{1},\beta _{1} \le 1 \). The error norms for different grid points and different fractional-order derivatives are presented in Table 1. In Table 1, it can be seen that the accuracy of the numerical results is increased along with the number of grid points. We are also depicted the 3D graph of numerical solutions \( Z_{1} \) and \( Z_{2} \) at time \( T= 0.005 \) and \( \alpha _{1}=0.5,\beta _{1}=0.25 \) in Fig.  1. Figure 2 illustrates the 2D curve of the numerical and exact solutions with different fractional-order derivatives at time \( T=0.005 \). In this figure, the solid line represents the exact solutions; however, the block represents the numerical solutions at various \( \alpha _{1} \) and \( \beta _{1} \). Accuracy of numerical solutions is merely seen in Fig. 2. Authors have discussed the numerical solutions of the equation with the different set of data, and for comparison purpose, we refer to [1, 8, 28, 30]. Furthermore, it is found that the results obtained by the proposed method show very good agreement with published results. Moreover, proposed method has obtained the eighth order of accuracy.

Table 1 Numerical solutions of proposed method at time \( T=0.005 \) with different \( \alpha _{1} \) \( \beta _{1} \) and grids points M for example 1
Full size table
Fig. 1
figure 1

Numerical solutions of \( Z_{1}(x,t) \) and \( Z_{2}(x,t) \) for example 1 when different \( \alpha _{1}=050, \beta _{1}=0.25\) and time \( T=0.005 \)

Full size image
Fig. 2
figure 2

Numerical and exact solutions of \( Z_{1}(x,t) \) and \( Z_{2}(x,t) \) for example 1 with different \( \alpha _{1}\) and \( \beta _{1}\) and time \( T=0.005 \)

Full size image

6.2 Example 2

Let us consider the space-fractional coupled Burgers’ equation:

$$\begin{aligned} \dfrac{\partial ^{}}{\partial t^{}} Z_{1}= & {} \dfrac{\partial ^{2}}{\partial x^{2}}Z_{1}+2Z_{1} \dfrac{\partial ^{\alpha _{2}}}{\partial x^{\alpha _{2}}}Z_{1}-\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}Z_{2}), \qquad (0<\alpha _{2}\le 1),\end{aligned}$$
(6.3)
$$\begin{aligned} \dfrac{\partial ^{}}{\partial t^{}} Z_{2}= & {} \dfrac{\partial ^{2}}{\partial x^{2}}Z_{2}+2Z_{2} \dfrac{\partial ^{\beta _{2}}}{\partial x^{\beta _{2}}}Z_{2}-\dfrac{\partial ^{}}{\partial x^{}}(Z_{1}Z_{2}), \qquad (0<\beta _{2}\le 1) \end{aligned}$$
(6.4)

with initial condition:

$$\begin{aligned} Z_{1}(x,0) = x^{2},~Z_{2}(x,0) = x^{3},\qquad (x) \in \Omega , \end{aligned}$$

the exact solution for the problem is given as: [8, 30]

$$\begin{aligned}&Z_{1}(x,t)=x^{2}+\left( 2-5x^{4}+f_{1}x^{(4-\alpha _{2})} \right) t\\&\quad +\frac{t^{2}}{2}\left( f_{2}x^{(6-2\alpha _{2})}+ f_{3}x^{(6-\alpha _{2})}+f_{4}x^{(2-\alpha _{2})}+f_{5}x^{(7-\beta _{2})}+20x^{6}+10x^{5}-72x^{2}\right) ,\\&Z_{2}(x,t)=x^{3}+\left( 6x-5x^{4}+g_{1}x^{(6-\beta _{2})} \right) t\\&\quad +\frac{t^{2}}{2}\left( g_{2}x^{(9-2\beta _{2})}+ g_{3}x^{(7-\beta _{2})}+g_{4}x^{(4-\beta _{2})}+g_{5}x^{(6-\alpha _{2})}+20x^{6}+10x^{5}-72x^{2}\right) , \end{aligned}$$

where

$$\begin{aligned} f(x)= & {} x^{2},~~f_{1}(x)=\frac{4}{\Gamma (3-\alpha _{2})},~~f_{2}(x)=\left[ \frac{4}{\Gamma (3-\alpha _{2})}+\frac{2 \Gamma (5-\alpha _{2})}{\Gamma (5-2\alpha _{2})} \right] f_{1},\\ f_{3}(x)= & {} (\alpha _{2}-4)f_{1} -\frac{20}{\Gamma (3-\alpha _{2})} -\frac{240}{\Gamma (5-\alpha _{2})},~~ f_{4}(x)=(4-\alpha _{2})(3-\alpha _{2})f_{1}+\frac{8}{\Gamma (3-\alpha _{2})},\\~ f_{5}(x)= & {} -2g_{1}(x).\\ g(x)= & {} x^{3},~~g_{1}(x)=\frac{12}{\Gamma (4-\beta _{2})},~~g_{2}(x)=\left[ \frac{12}{\Gamma (4-\beta _{2})}+\frac{2 \Gamma (7-\beta _{2})}{\Gamma (7-2\beta _{2})} \right] g_{1},\\ g_{3}(x)= & {} -2g_{1} -\frac{60}{\Gamma (4-\beta _{2})} -\frac{240}{\Gamma (5-\beta _{2})},~~ g_{4}(x)=(5-\beta _{2})(6-\beta _{2})g_{1}+\frac{12}{\Gamma (2-\beta _{2})}+\frac{72}{\Gamma (4-\beta _{2})},\\~ g_{5}(x)= & {} (\alpha _{2}-4)f_{1}(x).\\ \end{aligned}$$
Table 2 Numerical solutions of proposed method at time \( T=1.00 \) with different \( \alpha _{2} \) \( \beta _{2} \) and grid points M for example 2
Full size table
Fig. 3
figure 3

Numerical solutions of \( Z_{1}(x,t) \) and \( Z_{2}(x,t) \) for example 2 when a \( \alpha _{1}=0.25, \beta _{1}=0.50\), b \( \alpha _{1}=0.75, \beta _{1}=0.75\), and c \( \alpha _{1}=1.00, \beta _{1}=1.00\) at time \( T=1 \)

Full size image

In this example, numerical solutions of the proposed method have obtained over the domain \( \Omega =[0,10]^{},~~ t \in [0,1] \) and fractional-order derivative \( 0< \alpha _{2},\beta _{2} \le 1 \). The error norms for different grid points and different fractional order derivatives are presented in Table 2. In Table 2 , it can be seen that the accuracy of the numerical results is increased along with the number of grid points. In Fig.  3, we are also depicted the of numerical solutions \( Z_{1} \) and \( Z_{2} \) in the form of 3D graph for \( (a) \alpha _{1}=0.5, \beta _{1}=0.5\), (b) \( \alpha _{1}=0.75, \beta _{1}=0.75\) and (c) \( \alpha _{1}=1.00, \beta _{1}=1.00\) at time \( T=1 \). Authors have discussed the numerical solutions of the equation with the different set of data; for comparison purpose, we refer to [8, 28, 30]. Furthermore, it is found that the results obtained by the proposed method show very good agreement with published results. Moreover, proposed method has obtained the ninth order of accuracy.

7 Conclusion

In this paper, time–space Chebyshev pseudospectral method has been successfully employed to time- and space-fractional coupled Burgers’ equation. The fractional-order differentiation matrix has been established using Caputo–Riemann–Liouville derivative formula at CGL points for fractional-order derivative. It has shown that the numerical results of the proposed method are more close to exact solution. For the equation, convergence analysis of the proposed method has been presented. To demonstrate the performance, the method has been employed two test problems, first for time-fractional and other for space-fractional coupled Burgers’ equation. Reported numerical results are highly accurate which shows the efficiency of the proposed method.