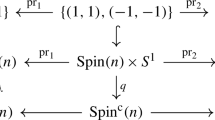Abstract
Let M be an orientable, simply-connected, closed, non-spin 4-manifold and let \({\mathcal {G}}_k(M)\) be the gauge group of the principal G-bundle over M with second Chern class \(k\in {\mathbb {Z}}\). It is known that the homotopy type of \({\mathcal {G}}_k(M)\) is determined by the homotopy type of \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\). In this paper we investigate properties of \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) when \(G=SU(n)\) that partly classify the homotopy types of the gauge groups.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let G be a simple, simply-connected, compact Lie group and let M be an orientable, simply-connected, closed 4-manifold. Then the isomorophism class of a principal G-bundle P over M is classified by its second Chern class \(k\in {\mathbb {Z}}\). In particular, if \(k=0\), then P is a trivial G-bundle. The associated gauge group \({\mathcal {G}}_k(M)\) is the topological group of G-equivariant automorphisms of P which fix M.
A simply-connected 4-manifold is spin if and only if its intersection form is even. In the case of simply-connected 4-manifolds, the spin condition is equivalent to all cup product squares being trivial in mod 2 cohomology. In this paper, we consider the homotopy types of gauge groups \({\mathcal {G}}_k(M)\), where M is a non-spin 4-manifold such as \({\mathbb {C}}{\mathbb {P}}^2\). When M is a spin 4-manifold, topologists have been studying the homotopy types of gauge groups over M extensively over the last twenty years. On the one hand, Theriault showed in [16] that there is a homotopy equivalence
where d is the second Betti number of M. Therefore to study the homotopy type of \({\mathcal {G}}_k(M)\) it suffices to study \({\mathcal {G}}_k(S^4)\). On the other hand, many cases of homotopy types of \({\mathcal {G}}_k(S^4)\)’s are known. For examples, there are 6 distinct homotopy types of \({\mathcal {G}}_k(S^4)\)’s for \(G=SU(2)\) [11], and 8 distinct homotopy types for \(G=SU(3)\) [5]. When localized rationally or at any prime, there are 16 distinct homotopy types for \(G=SU(5)\) [19] and 8 distinct homotopy types for \(G=Sp(2)\) [17].
When M is a non-spin 4-manifold, the author in [14] showed that there is a homotopy equivalence
so the homotopy type of \({\mathcal {G}}_k(M)\) depends on the special case \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\). Compared to the extensive work on \({\mathcal {G}}_k(S^4)\), only two cases of \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) have been studied, which are the SU(2)- and SU(3)-cases [12, 18]. As a sequel to [14], this paper investigates the homotopy types of \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\)’s in order to explore gauge groups over non-spin 4-manifolds.
A common approach to classifying the homotopy types of gauge groups is as follows. Atiyah, Bott and Gottlieb [1, 3] showed that the classifying space \(B{\mathcal {G}}_k(M)\) is homotopy equivalent to the connected component \({\text {Map}}_k(M, BG)\) of the mapping space \({\text {Map}}(M, BG)\) containing the map \(k\alpha \circ q\), where \(q:M\rightarrow S^4\) is the quotient map and \(\alpha \) is a generator of \(\pi _4(BG)\cong {\mathbb {Z}}\). The evaluation map \(ev:B{\mathcal {G}}_k(M)\rightarrow BG\) induces a fibration sequence
where \(\partial _k:G\rightarrow {\text {Map}}^*_k(M, BG)\) is the boundary map. The action of \(\pi _4(BG)\cong {\mathbb {Z}}\) on \({\text {Map}}^*_k(M, BG)\) induces a homotopy equivalence \({\text {Map}}^*_k(M,BG)\simeq {\text {Map}}^*_0(M, BG)\). Denote the composition \(G\overset{\partial _k}{\longrightarrow }{\text {Map}}^*_k(M,BG)\simeq {\text {Map}}^*_0(M, BG)\) also by \(\partial _k\) for convenience. For \(M=S^4\), \({\text {Map}}^*_0(M, BG)\simeq \Omega ^3_0G\) is an H-group so \([G, \Omega ^3_0G]\) is a group. The order of \(\partial _1:G\rightarrow \Omega ^3_0G\) is important for distinguishing the homotopy types of \({\mathcal {G}}_k(S^4)\).
Theorem 1.1
(Theriault, [17]) Let m be the order of \(\partial _1\). If \((m, k)=(m, l)\), then \({\mathcal {G}}_k(S^4)\) is homotopy equivalent to \({\mathcal {G}}_l(S^4)\) when localized rationally or at any prime.
For most cases of G, the exact value of the order of \(\partial _1\) is difficult to compute. When \(G=SU(n)\), the exact value or a partial result of the order of \(\partial _1\) was worked out for certain cases. For any number \(a=p^rq\) where q is coprime to p, the p-component of a is \(p^r\) and is denoted by \(\nu _p(a)\).
Theorem 1.2
([2, 5, 9, 11, 19, 20]) Let G be SU(n) and let m be the order of \(\partial _1\). Then
-
\(m=12\) for \(n=2\)
-
\(m=24\) for \(n=3\)
-
\(m=120\) for \(n=5\)
-
\(m=60\) or 120 for \(n=4\)
-
\(\nu _p(m)=\nu _p(n(n^2-1))\) for \(n<(p-1)^2+1\).
In Theorem 1.1, the g.c.d condition \((m,k)=(m,l)\) gives a sufficient condition for the homotopy equivalence \({\mathcal {G}}_k(S^4)\simeq {\mathcal {G}}_l(S^4)\). Conversely, there is a partial necessary condition for certain cases of \(G=SU(n)\).
Theorem 1.3
(Hamanaka and Kono [5]; Kishimoto, Kono and Tsutaya [9]) Let G be SU(n) and let p be an odd prime. If \({\mathcal {G}}_k(S^4)\) is homotopy equivalent to \({\mathcal {G}}_l(S^4)\), then
-
\((n(n^2-1),k)=(n(n^2-1),l)\) for n odd,
-
\(\nu _p(n(n^2-1),k)=\nu _p(n(n^2-1),l)\) for n less than \((p-1)^2+1\).
In this paper we consider gauge groups over \({\mathbb {C}}{\mathbb {P}}^2\). Take \(M={\mathbb {C}}{\mathbb {P}}^2\) in (1) and denote the boundary map by \(\partial '_k:G\rightarrow {\text {Map}}^*_0({\mathbb {C}}{\mathbb {P}}^2, BG)\). Since \({\text {Map}}^*_0({\mathbb {C}}{\mathbb {P}}^2, BG)\) is not an H-space, \([G,{\text {Map}}^*_0({\mathbb {C}}{\mathbb {P}}^2,BG)]\) is not a group so the order of \(\partial '_k\) makes no sense. However, we can still define an “order” of \(\partial '_k\) [18], which will be described in Sect. 2. We show that the “order” of \(\partial '_1\) helps distinguish the homotopy type of \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) as in Theorem 1.1.
Theorem 1.4
Let \(m'\) be the “order” of \(\partial '_1\). If \((m', k)=(m', l)\), then \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) is homotopy equivalent to \({\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\) when localized rationally or at any prime.
We study the SU(n)-gauge groups over \({\mathbb {C}}{\mathbb {P}}^2\) and use unstable K-theory to give a lower bound on the “order” of \(\partial '_1\) that is in the spirit of Theorem 1.2.
Theorem 1.5
When G is SU(n), the “order” of \(\partial '_1\) is at least \(\frac{1}{2}n(n^2-1)\) for n odd, and \(n(n^2-1)\) for n even.
Localized rationally or at an odd prime, we have \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\simeq {\mathcal {G}}_k(S^4)\times \Omega ^{2} G\) [16]. The homotopy types of \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) are then completely determined by that of \({\mathcal {G}}_k(S^4)\), which have been investigated in many cases when the localizing prime is relatively large [6, 7, 9, 10, 20]. A large part of the remaining cases can be understood by studying the 2-localized order of \(\partial '_1\), on which Theorem 1.5 gives bounds for the SU(n) case. For example, combining Theorem 1.5 with Lemma 2.2 implies the order of \(\partial '_1\) is either 120 or 60 for \(G=SU(5)\). Furthermore, when \(G=SU(4)\) since the order of \(\partial _1\) is either 120 or 60, the order of \(\partial '_1\) is either 60 or 120.
Finally we prove a necessary condition for the homotopy equivalence \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\simeq {\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\) similar to Theorem 1.3.
Theorem 1.6
Let G be SU(n). If \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) is homotopy equivalent to \({\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\), then
-
\((\frac{1}{2}n(n^2-1),k)=(\frac{1}{2}n(n^2-1),l)\) for n odd,
-
\((n(n^2-1),k)=(n(n^2-1),l)\) for n even.
The author would like to thank his supervisor, Professor Stephen Theriault, for his guidance in writing this paper, and thank the Referee for his careful reading and useful comments.
2 Some facts about boundary map \(\partial '_1\)
Take M to be \(S^4\) and \({\mathbb {C}}{\mathbb {P}}^2\) respectively in fibration (1) to obtain fibration sequences
There is also a cofibration sequence
where \(\eta \) is Hopf map and q is the quotient map. Due to the naturality of \(q^*\), we combine fibrations (2) and (3) to obtain a commutative diagram of fibration sequences

It is known, [13], that \(\partial _k\) is triple adjoint to Samelson product
where \(\imath :S^3\rightarrow SU(n)\) is the inclusion of the bottom cell and \(\langle {{\mathbb {1}},{\mathbb {1}}}\rangle \) is the Samelson product of the identity on G with itself. The order of \(\partial _k\) is its multiplicative order in the group \([G, \Omega ^3_0G]\).
Unlike \(\Omega ^3_0G\), \({\text {Map}}^*_0({\mathbb {C}}{\mathbb {P}}^2, BG)\) is not an H-space, so \(\partial '_k\) has no order. In [18], Theriault defined the “order” of \(\partial '_k\) to be the smallest number \(m'\) such that the composition
is null homotopic. In the following, we interpret the “order” of \(\partial '_k\) as its multiplicative order in a group contained in \([{\mathbb {C}}{\mathbb {P}}^2\wedge G, BG]\).
Apply \([-\wedge G, BG]\) to cofibration (4) to obtain an exact sequence of sets
All terms except \([{\mathbb {C}}{\mathbb {P}}^2\wedge G, BG]\) are groups and \((\Sigma \eta )^*\) is a group homomorphism since \(\Sigma \eta \) is a suspension. We want to refine this exact sequence so that the last term is replaced by a group. Observe that \({\mathbb {C}}{\mathbb {P}}^2\) is the cofiber of \(\eta \) and so there is a coaction \(\psi :{\mathbb {C}}{\mathbb {P}}^2\rightarrow {\mathbb {C}}{\mathbb {P}}^2\vee S^4\). We show that the coaction gives a group structure on \(Im(q^*)\).
Lemma 2.1
Let Y be a space and let \(A\overset{f}{\rightarrow }B\overset{g}{\rightarrow }C\overset{h}{\rightarrow }\Sigma A\) be a cofibration sequence. If \(\Sigma A\) is homotopy cocommutative, then \(Im(h^*)\) is an abelian group and
is an exact sequence of groups and group homomorphisms.
Proof
Apply \([-,Y]\) to the cofibration to get an exact sequence of sets
Note that \([\Sigma B, Y]\) and \([\Sigma A, Y]\) are groups, and \((\Sigma f)^*\) is a group homomorphism. We will replace [C, Y] by \(Im(h^*)\) and define a group structure on it such that \(h^*:[\Sigma A, Y]\rightarrow Im(h^*)\) is a group homomorphism.
For any \(\alpha \) and \(\beta \) in \([\Sigma A, Y]\), we define a binary operator \(\boxtimes \) on \(Im(h^*)\) by
To check this is well-defined we need to show \(h^*(\alpha +\beta )\simeq h^*(\alpha '+\beta )\simeq h^*(\alpha +\beta ')\) for any \(\alpha ,\alpha ',\beta ,\beta '\) satisfying \(h^*\alpha \simeq h^*\alpha '\) and \(h^*\beta \simeq h^*\beta '\).
First we show \(h^*(\alpha +\beta )\simeq h^*(\alpha '+\beta )\). By definition, we have
where \(\sigma :\Sigma A\rightarrow \Sigma A\vee \Sigma A\) is the comultiplication and \(\triangledown :Y\vee Y\rightarrow Y\) is the folding map. Since C is a cofiber, there is a coaction \(\psi :C\rightarrow C\vee \Sigma A\) such that \(\sigma \circ h\simeq (h\vee {\mathbb {1}})\circ \psi \).

Then we obtain a string of equivalences
The third line is due to the assumption \(h^*\alpha \simeq h^*\alpha '\). Therefore we have \(h^*(\alpha +\beta )\simeq h^*(\alpha '+\beta )\). Since \(\Sigma A\) is cocommutative, \([\Sigma A, Y]\) is abelian and \(h^*(\alpha +\beta )\simeq h^*(\beta +\alpha )\). Then we have
This implies \(\boxtimes \) is well-defined.
Due to the associativity of \(+\) in \([\Sigma A, Y]\), \(\boxtimes \) is associative since
Clearly the trivial map \(*:C\rightarrow Y\) is the identity of \(\boxtimes \) and \(h^*(-\alpha )\) is the inverse of \(h^*\alpha \). Therefore \(\boxtimes \) is indeed a group multiplication.
By definition of \(\boxtimes \), \(h^*:[\Sigma A, Y]\rightarrow Im(h^*)\) is a group homomorphism, and hence an epimorphism. Since \([\Sigma A, Y]\) is abelian, so is \(Im(h^*)\). We replace [C, Y] by \(Im(h^*)\) in (6) to obtain a sequence of groups and group homomorphisms
The exactness of (6) implies \(ker(h^*)=Im(\Sigma f)^*\), so the sequence is exact. \(\square \)
Applying Lemma 2.1 to cofibration \(\Sigma ^3G\rightarrow \Sigma ^2G\rightarrow {\mathbb {C}}{\mathbb {P}}^2\wedge G\) and the space \(Y=BG\), we obtain an exact sequence of abelian groups
In the middle square of (5) \(\partial '_k\simeq q^*\partial _k\), so \(\partial '_k\) is in \(Im(q^*)\). For any number m, \(q^*(m\partial _k)=mq^*\partial _k\), so the “order” of \(\partial '_k\) defined in [18] coincides with the multiplicative order of \(\partial '_k\) in \(Im(q^*)\). The exact sequence (7) allows us to compare the orders of \(\partial _1\) and \(\partial '_1\).
Lemma 2.2
Let m be the order of \(\partial _1\) and let \(m'\) be the order of \(\partial '_1\). Then m is \(m'\) or \(2m'\).
Proof
By exactness of (7), there is some \(f\in [\Sigma ^3G, BG]\) such that \((\Sigma \eta )^*f\simeq m'\partial _1\). Since \(\Sigma \eta \) has order 2, \(2m'\partial _1\) is null homotopic. It follows that \(2m'\) is a multiple of m. Since m is greater than or equal to \(m'\), m is either \(m'\) or \(2m'\). \(\square \)
When \(G=SU(2)\), the order m of \(\partial _1\) is 12 and the order \(m'\) of \(\partial '_1\) is 6 [12]. When \(G=SU(3)\), \(m=24\) and \(m'=12\) [18]. When \(G=Sp(2)\), \(m=40\) and \(m'=20\) [15]. It is natural to ask whether \(m=2m'\) for all G.
In the \(S^4\) case, Theorem 1.1 gives a sufficient condition for \({\mathcal {G}}_k(S^4)\simeq {\mathcal {G}}_l(S^4)\) when localized rationally or at any prime. In the \({\mathbb {C}}{\mathbb {P}}^2\) case, Theriault showed a similar counting statement, in which the sufficient condition depends on the order of \(\partial _1\) instead of \(\partial '_1\).
Theorem 2.3
(Theriault, [18]) Let m be the order of \(\partial _1\). If \((m,k)=(m,l)\), then \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) is homotopy equivalent to \({\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\) when localized rationally or at any prime.
Lemma 2.2 can be used to improve the sufficient condition of Theorem 2.3.
Theorem 2.4
Let \(m'\) be the order of \(\partial '_1\). If \((m',k)=(m',l)\), then \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) is homotopy equivalent to \({\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\) when localized rationally or at any prime.
Proof
By Lemma 2.2, m is either \(m'\) or \(2m'\). If \(m=m'\), then the statement is same as Theorem 2.3. Assume \(m=2m'\). Localize at an odd prime p. Let \(p^r\) be the p-component of m, that is \(m=p^r\cdot q\) where q is coprime to p. Observe that \(m\circ \partial _1\simeq (p^r\cdot q)\circ \partial _1\simeq p^r\circ \partial _1\) since the power map \(q:\Omega ^3_0G\rightarrow \Omega ^3_0G\) is a homotopy equivalence. Therefore \(p^r\) is the order of \(\partial _1\) after localization. The hypothesis \((m', k)=(m',l)\) implies \((p^r, k)=(p^r, l)\), so a homotopy equivalence \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\simeq {\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\) follows by Theorem 2.3. A similar argument works for rational localization. Now it remains to consider the case where \(m=2m'\) when localized at 2.
Assume \(m=2^n\) and \(m'=2^{n-1}\). For any k, \((2^{n-1},k)=2^i\) where i an integer such that \(0\le i\le n-1\). If \(i\le n-2\), then \(k=2^it\) for some odd number t and \((2^{n-1},k)=2^i\). The sufficient condition \((2^{n-1},k)=(2^{n-1},l)\) is equivalent to \((2^n,k)=(2^n,l)\). Again the homotopy equivalence \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\simeq {\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\) follows by Theorem 2.3. If \(i=n-1\), then \((2^n,k)\) is either \(2^n\) or \(2^{n-1}\). We claim that \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) has the same homotopy type for both \((2^n,k)=2^n\) or \((2^n,k)=2^{n-1}\).
Consider fibration (3)
If \((2^n,k)=2^n\), then \(k=2^nt\) for some number t. By linearity of Samelson products, \(\partial _k\simeq k\partial _1\). Since \(\partial '_k\simeq q^*k\partial _1\simeq q^*2^nt\partial _1\) and \(\partial _1\) has order \(2^n\), \(\partial '_k\) is null homotopic and we have
If \((2^n,k)=2^{n-1}\), then \(k=2^{n-1}t\) for some odd number t. Writing \(t=2s+1\) gives \(k=2^ns+2^{n-1}\). Since \(\partial '_k\simeq q^*k\partial _1\simeq q^*(2^ns+2^{n-1})\partial _1\simeq q^*2^{n-1}\partial _1\) and \(\partial '_1\) has order \(2^{n-1}\), \(\partial '_k\) is null homotopic and we have
The same is true for \({\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\) and hence \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\simeq {\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\). \(\square \)
3 Plan for the proofs of Theorems 1.5 and 1.6
From this section onward, we will focus on SU(n)-gauge groups over \({\mathbb {C}}{\mathbb {P}}^2\). There is a fibration
where \(p:SU(\infty )\rightarrow W_n\) is the projection and \(W_n\) is the symmetric space \(SU(\infty )/SU(n)\). Then we have
where \(x_{2n+1}\) has degree \(2n+1\), \(c_i\) is the \(i{\text {th}}\) universal Chern class and \(x_{2i+1}=\sigma (c_{i+1})\) is the image of \(c_{i+1}\) under the cohomology suspension \(\sigma \), and \(p^*(\bar{x}_{2i+1})=x_{2i+1}\). Furthermore, \(H^{2n}(\Omega W_n)\cong {\mathbb {Z}}\) and \(H^{2n+2}(\Omega W_n)\cong {\mathbb {Z}}\) are generated by \(a_{2n}\) and \(a_{2n+2}\), where \(a_{2i}\) is the transgression of \(x_{2i+1}\).
The \((2n+4)\)-skeleton of \(W_n\) is \(\Sigma ^{2n-1}{\mathbb {C}}{\mathbb {P}}^2\) for n odd, and is \(S^{2n+3}\vee S^{2n+1}\) for n even, so its homotopy groups are as follows:

The canonical map \(\epsilon :\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}\rightarrow SU(n)\) induces the inclusion \(\epsilon _*:H_*(\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1})\rightarrow H_*(SU(n))\) of the generating set. Let C be the quotient \({\mathbb {C}}{\mathbb {P}}^{n-1}/{\mathbb {C}}{\mathbb {P}}^{n-3}\) and let \(\bar{q}:\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}\rightarrow \Sigma C\) be the quotient map. Then there is a diagram

where \((\partial '_k)_*\) sends f to \(\partial '_k\circ f\) and the rows are induced by fibration (3). In particular, in the second row the map \(\epsilon :\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}\rightarrow SU(n)\) is sent to \((\partial '_k)_*(\epsilon )=\partial '_k\circ \epsilon \). In Sect. 4, we use unstable K-theory to calculate the order of \(\partial '_1\circ \epsilon \), giving a lower bound on the order of \(\partial '_1\). Furthermore, in [5] Hamanaka and Kono considered an exact sequence similar to the first row to give a necessary condition for \({\mathcal {G}}_k(S^4)\simeq {\mathcal {G}}_l(S^4)\). In Sect. 5 we follow the same approach and use the first row to give a necessary condition for \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\simeq {\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\).
We remark that it is difficult to use only one of the two rows to prove both Theorems 1.5 and 1.6. On the one hand, \(\partial '_1\circ \epsilon \) factors through a map \(\bar{\partial }:\Sigma C\rightarrow {\text {Map}}^*({\mathbb {C}}{\mathbb {P}}^2, BSU(n))\). There is no obvious method to show that \(\bar{\partial }\) and \(\partial '_1\circ \epsilon \) have the same orders except direct calculation. Therefore we cannot compare the orders of \(\bar{\partial }\) and \(\partial '_1\) to prove Theorem 1.5 without calculating the order of \(\partial '_1\circ \epsilon \). On the other hand, applying the method used in Sect. 5 to the second row gives a much weaker conclusion than Theorem 1.6. This is because \([\Sigma C,B{\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)]\) is a much smaller group than \([\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1},B{\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)]\) and much information is lost by the map \(\bar{q}^*\).
4 A lower bound on the order of \(\partial '_1\)
The restriction of \(\partial _1\) to \(\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}\) is \(\partial _1\circ \epsilon \), which is the triple adjoint of the composition
Since \(SU(n)\simeq \Omega BSU(n)\), we can further take its adjoint and get
where [ev, ev] is the Whitehead product of the evaluation map
with itself. Similarly, the restriction \(\partial '_1\circ \epsilon \) is adjoint to the composition
Since we will frequently refer to the facts established in [4, 5], it is easier to follow their setting and consider its adjoint
where \(T:\Sigma {\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1}\rightarrow {\mathbb {C}}{\mathbb {P}}^2\wedge \Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}\) is the swapping map and \(\tau :[\Sigma {\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},BSU(n)]\rightarrow [{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},SU(n)]\) is the adjunction. By adjunction, the orders of \(\partial '_1\circ \epsilon ,\rho '\) and \(\gamma \) are the same. We will calculate the order of \(\gamma \) using unstable K-theory to prove Theorem 1.5.
Apply \([{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},-]\) to fibration (8) to obtain the exact sequence
Since \({\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1}\) is a CW-complex with even dimensional cells, the last item \([{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},SU(\infty )]\cong {\tilde{K}}^1({\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1})\) is zero. First we identify the term \([{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},\Omega W_n]\).
Lemma 4.1
We have the following:
-
\([\Sigma ^{2n-4}{\mathbb {C}}{\mathbb {P}}^2,\Omega W_n]\cong {\mathbb {Z}}\);
-
\([\Sigma ^{2n-3}{\mathbb {C}}{\mathbb {P}}^2,\Omega W_n]=0\) for n odd;
-
\([\Sigma ^{2n-2}{\mathbb {C}}{\mathbb {P}}^2,\Omega W_n]\cong {\mathbb {Z}}\oplus {\mathbb {Z}}\).
Proof
First, apply \([\Sigma ^{2n-4}-, \Omega W_n]\) to cofibration (4) to obtain the exact sequence
We refer to Table (9) freely for the homotopy groups of \(W_n\). Since \(\pi _{2n-1}(W_n)\) and \(\pi _{2n}(W_n)\) are zero, \([\Sigma ^{2n-4}{\mathbb {C}}{\mathbb {P}}^{n-1},\Omega W_n]\) is isomorphic to \(\pi _{2n+1}(W_n)\cong {\mathbb {Z}}\).
Second, apply \([\Sigma ^{2n-3}-, \Omega W_n]\) to (4) to obtain
Since \(\pi _{2n}(W_n)\) and \(\pi _{2n+2}(W_n)\) are zero for n odd, so is \([\Sigma ^{2n-3}{\mathbb {C}}{\mathbb {P}}^2,\Omega W_n]\).
Third, apply \([\Sigma ^{2n-2}-, \Omega W_n]\) to (4) to obtain
where \(\eta _1\) and \(\eta _2\) are induced by Hopf maps \(\Sigma ^{2n}\eta :S^{2n+3}\rightarrow S^{2n+2}\) and \(\Sigma ^{2n-1}\eta :S^{2n+2}\rightarrow S^{2n+1}\), and j is induced by the inclusion \(S^{2n+1}\hookrightarrow \Sigma ^{2n-2}{\mathbb {C}}{\mathbb {P}}^2\) of the bottom cell. When n is odd, \(\pi _{2n+2}(W_n)\) is zero and \(\pi _{2n+1}(W_n)\) and \(\pi _{2n+3}(W_n)\) are \({\mathbb {Z}}\), so \([\Sigma ^{2n-2}{\mathbb {C}}{\mathbb {P}}^{n-1},\Omega W_n]\) is \({\mathbb {Z}}\oplus {\mathbb {Z}}\). When n is even, the \((2n+4)\)-skeleton of \(W_n\) is \(S^{2n+1}\vee S^{2n+3}\). The inclusions
generate \(\pi _{2n+1}(W_n)\) and the \({\mathbb {Z}}\)-summand of \(\pi _{2n+3}(W_n)\), and the compositions
generate \(\pi _{2n+2}(W_n)\) and the \({\mathbb {Z}}/2{\mathbb {Z}}\)-summand of \(\pi _{2n+3}(W_n)\) respectively. Since \(\eta _1\) sends \(j_1\) to \(j_2\), the cokernel of \(\eta _1\) is \({\mathbb {Z}}\). Similarly, \(\eta _2\) sends \(i_1\) to \(j_1\), so \(\eta _2:{\mathbb {Z}}\rightarrow {\mathbb {Z}}/2{\mathbb {Z}}\) is surjective. This implies the preimage of j is a \({\mathbb {Z}}\)-summand. Therefore \([\Sigma ^{2n-2}{\mathbb {C}}{\mathbb {P}}^2,\Omega W_n]\cong {\mathbb {Z}}\oplus {\mathbb {Z}}\). \(\square \)
Let C be the quotient \({\mathbb {C}}{\mathbb {P}}^{n-1}/{\mathbb {C}}{\mathbb {P}}^{n-3}\). Since \(\Omega W_n\) is \((2n-1)\)-connected, \([{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},\Omega W_n]\) is isomorphic to \([{\mathbb {C}}{\mathbb {P}}^2\wedge C,\Omega W_n]\) which is easier to determine.
Lemma 4.2
The group \([{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},\Omega W_n]\cong [{\mathbb {C}}{\mathbb {P}}^2\wedge C,\Omega W_n]\) is isomorphic to \({\mathbb {Z}}^{\oplus 3}\).
Proof
When n is even, C is \(S^{2n-2}\vee S^{2n-4}\). By Lemma 4.1, \([{\mathbb {C}}{\mathbb {P}}^2\wedge C, \Omega W_n]\) is \([\Sigma ^{2n-2}{\mathbb {C}}{\mathbb {P}}^2, \Omega W_n]\oplus [\Sigma ^{2n-4}{\mathbb {C}}{\mathbb {P}}^2, \Omega W_n]\cong {\mathbb {Z}}^{\oplus 3}\).
When n is odd, C is \(\Sigma ^{2n-6}{\mathbb {C}}{\mathbb {P}}^2\). Apply \([\Sigma ^{2n-6}{\mathbb {C}}{\mathbb {P}}^2\wedge -, \Omega W_n]\) to cofibration (4) to obtain the exact sequence
By Lemma 4.1, the first and the last terms \([\Sigma ^{2n-3}{\mathbb {C}}{\mathbb {P}}^2, \Omega W_n]\) are zero, while the second term \([\Sigma ^{2n-2}{\mathbb {C}}{\mathbb {P}}^2, \Omega W_n]\) is \({\mathbb {Z}}\oplus {\mathbb {Z}}\) and the fourth \([\Sigma ^{2n-4}{\mathbb {C}}{\mathbb {P}}^2, \Omega W_n]\) is \({\mathbb {Z}}\). Therefore \([{\mathbb {C}}{\mathbb {P}}^2\wedge C,\Omega W_n]\) is \({\mathbb {Z}}^{\oplus 3}\). \(\square \)
Define \(a:[{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1}, \Omega W_n]\rightarrow H^{2n}({\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1})\oplus H^{2n+2}({\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1})\) to be a map sending \(f\in [{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1}, \Omega W_n]\) to \(a(f)=f^*(a_{2n})\oplus f^*(a_{2n+2})\). The cohomology class \(\bar{x}_{2n+1}\) represents a map \(\bar{x}_{2n+1}:W_n\rightarrow K({\mathbb {Z}},2n+1)\) and \(a_{2n}=\sigma (\bar{x}_{2n+1})\) represents its loop \(\Omega \bar{x}_{2n+1}:\Omega W_n\rightarrow \Omega K({\mathbb {Z}},2n+1)\). Similarly \(a_{2n+2}=\sigma (\bar{x}_{2n+3})\) represents a loop map. This implies a is a group homomorphism. Furthermore, \(a_{2n}\) and \(a_{2n+2}\) induce isomorphisms between \(H^i(\Omega W_n)\) and \(H^i(K(2n,{\mathbb {Z}})\times K(2n+2,{\mathbb {Z}}))\) for \(i=2n\) and \(2n+2\). Since \([{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},\Omega W_n]\) is a free \({\mathbb {Z}}\)-module by Lemma 4.2, a is a monomorphism. Consider the diagram

In the left square, \(\Phi \) is defined to be \(a\circ p^*\). In the right square, \(\psi \) is the quotient map and b is defined as follows. Any \(f\in [{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},SU(n)]\) has a preimage \(\tilde{f}\) and b(f) is defined to be \(\psi (a(\tilde{f}))\). An easy diagram chase shows that b is well-defined and injective. Since b is injective, the order of \(\gamma \in [{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1}, SU(n)]\) equals the order of \(b(\gamma )\in Coker(\Phi )\). In [4], Hamanaka and Kono gave an explicit formula for \(\Phi \).
Theorem 4.3
(Hamanaka and Kono [4]) Let Y be a CW-complex. For any \(f\in {\tilde{K}}^0(Y)\) we have
where \(ch_{2i}(f)\) is the \(2i{\text {th}}\) part of ch(f).
Let u and v be the generators of \(H^2({\mathbb {C}}{\mathbb {P}}^2)\) and \(H^2({\mathbb {C}}{\mathbb {P}}^{n-1})\). For \(1\le i\le n-1\), denote \(L_i\) and \(L'_i\) as the generators of \({\tilde{K}}^0({\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1})\) with Chern characters \(ch(L_i)=u^2(e^v-1)^i\) and \(ch(L'_i)=(u+\frac{1}{2}u^2)\cdot (e^v-1)^i\). By Theorem 4.3 we have
where
Write an element \(xu^2v^{n-2}+yuv^{n-1}+zu^2v^{n-1}\in H^{2n}({\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1})\oplus H^{2n+2}({\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1})\) as (x, y, z). Then the coordinates of \(\Phi (L_i)\) and \(\Phi (L'_i)\) are \((n(n-1)A_i, 0, n(n+1)B_i)\) and \((\frac{n(n-1)}{2}A_i, nB_i, \frac{n(n+1)}{2}B_i)\) respectively.
Lemma 4.4
For \(n\ge 3\), \(Im(\Phi )\) is spanned by \((\frac{n(n-1)}{2},n,\frac{n(n+1)}{2})\), \((n(n-1),0,0)\) and (0, 2n, 0).
Proof
By definition, \(Im(\Phi )=span\{\Phi (L_i),\Phi (L'_i)\}^{n-1}_{i=1}\). For \(i=1\), \(A_1=B_1=1\). Then
Equivalently \((0,2n,0)=2\Phi (L'_1)-\Phi (L_1)\), so \(span\{\Phi (L_1),\Phi (L'_1)\}=span\{\Phi (L'_1),(0,2n,0)\}\). For other i’s,
is a linear combination of \(\Phi (L'_i)\) and (0, 2n, 0), so
We claim that \(span\{\Phi (L'_i)\}^{n-1}_{i=1}=span\{\Phi (L'_1), (n(n-1),0,0)\}\). Observe that
The difference
is even since each term \((j-1)j^{n-2}\) is even and \(n\ge 3\). Therefore \(\frac{A_i-B_i}{2}\) is an integer and \(\Phi (L'_i)\) is a linear combination of \(\Phi (L'_1)\) and \((n(n-1),0,0)\).
Furthermore,
and
For \(n=3\), \(B_2=2\) and \(\Phi (L'_2)=2\Phi (L'_1)-(n(n-1),0,0)\), so we have
For \(n\ge 4\), since \(2^{n-3}\) and \(3^{n-2}-3\cdot 2^{n-3}\) are coprime to each other, there exist integers s and t such that \(2^{n-3}s+(3^{n-2}-3\cdot 2^{n-3})t=1\) and
Therefore \((n(n-1),0,0)\) is a linear combination of \(\Phi (L'_1),\Phi (L'_2)\) and \(\Phi (L'_3)\). This implies \(span\{\Phi (L'_1),(n(n-1),0,0)\}=span\{\Phi (L'_i)\}^{n-1}_{i=1}\).
Combine all these together to obtain
\(\square \)
Back to diagram (10). The map \(\gamma \) has a lift \(\tilde{\gamma }:{\mathbb {C}}{\mathbb {P}}^2\wedge {\mathbb {C}}{\mathbb {P}}^{n-1}\rightarrow \Omega W_n\). By exactness, the order of \(\gamma \) equals the minimum number m such that \(m\tilde{\gamma }\) is contained in \(Im(p_*)\). Since a and b are injective, the order of \(\gamma \) equals the minimum number \(m'\) such that \(m'a(\tilde{\gamma })\) is contained in \(Im(\Phi )\).
Lemma 4.5
Let \(\alpha :\Sigma X\rightarrow SU(n)\) be a map for some space X. If \(\alpha ':{\mathbb {C}}{\mathbb {P}}^2\wedge X\rightarrow SU(n)\) is the adjoint of the composition
then there is a lift \(\tilde{\alpha }\) of \(\alpha '\) such that \(\tilde{\alpha }^*(a_{2i})=u^2\otimes \Sigma ^{-1}\alpha ^*(x_{2i-3})\), where \(\Sigma \) is the cohomology suspension isomorphism.

Proof
In [4, 5], Hamanaka and Kono constructed a lift \(\Gamma :\Sigma SU(n)\wedge SU(n)\rightarrow W_n\) of [ev, ev] such that \(\Gamma ^*(\bar{x}_{2i+1})=\sum _{j+k=i-1}\Sigma x_{2j+1}\otimes x_{2k+1}\). Let \(\tilde{\Gamma }\) be the composition
Then we have
where \(u_3\) is the generator of \(H^3(S^3)\).
Let \(T:\Sigma {\mathbb {C}}{\mathbb {P}}^2\wedge X\rightarrow {\mathbb {C}}{\mathbb {P}}^2\wedge \Sigma X\) be the swapping map and let \(\tau :[\Sigma {\mathbb {C}}{\mathbb {P}}^2\wedge X,W_n]\rightarrow [{\mathbb {C}}{\mathbb {P}}^2\wedge X,\Omega W_n]\) be the adjunction. Take \(\tilde{\alpha }:{\mathbb {C}}{\mathbb {P}}^2\wedge X\rightarrow \Omega W_n\) to be the adjoint of \(\tilde{\Gamma }\), that is \(\tilde{\alpha }=\tau (\tilde{\Gamma }\circ T)\). Then \(\tilde{\alpha }\) is a lift of \(\alpha '\). Since
we have \(\tilde{\alpha }^*(a_{2i})=u^2\otimes \Sigma ^{-1}\alpha ^*(x_{2i-3})\). \(\square \)
Lemma 4.6
In diagram (10), \(\gamma \) has a lift \(\tilde{\gamma }\) such that \(a(\tilde{\gamma })=u^2v^{n-2}\oplus u^2v^{n-1}\).
Proof
Recall that \(\gamma \) is the adjoint of the composition
Now we use Lemma 4.5 and take \(\alpha \) to be \(\epsilon :\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}\rightarrow SU(n)\). Then \(\gamma \) has a lift \(\tilde{\gamma }\) such that \(\tilde{\gamma }^*(a_{2i})=u^2\otimes \Sigma ^{-1}\epsilon ^*(x_{2i-3})=u^2\otimes v^{i-2}\). This implies
\(\square \)
Now we can calculate the order of \(\partial '_1\circ \epsilon \), which gives a lower bound on the order of \(\partial '_1\).
Theorem 4.7
When \(n\ge 3\), the order of \(\partial '_1\circ \epsilon \) is \(\frac{1}{2}n(n^2-1)\) for n odd and \(n(n^2-1)\) for n even.
Proof
Since \(\partial '_1\circ \epsilon \) is adjoint to \(\gamma \) , it suffices to calculate the order of \(\gamma \). By Lemma 4.4, \(Im(\Phi )\) is spanned by \((\frac{1}{2}n(n-1),n,\frac{1}{2}n(n+1)),(n(n-1),0,0)\) and (0, 2n, 0). By Lemma 4.6, \(a(\tilde{\gamma })\) has coordinates (1, 0, 1). Let m be a number such that \(ma(\tilde{\gamma })\) is contained in \(Im(\Phi )\). Then
for some integers s, t and r. Solve this to get
Since \(s=-2r\) is even, the smallest positive value of t satisfying \(s=t(n-1)\) is 1 for n odd and 2 for n even. Therefore m is \(\frac{1}{2}n(n^2-1)\) for n odd and \(n(n^2-1)\) for n even. \(\square \)
For SU(n)-gauge groups over \(S^4\), the order m of \(\partial _1\) has the form \(m=n(n^2-1)\) for \(n=3\) and 5 [5, 19]. If p is an odd prime and \(n<(p-1)^2+1\), then m and \(n(n^2-1)\) have the same p-components [9, 20]. These facts suggest it may be the case that \(m=n(n^2-1)\) for any \(n>2\). In fact, one can follow the method Hamanaka and Kono used in [5] and calculate the order of \(\partial \circ \epsilon \) to obtain a lower bound \(n(n^2-1)\) for n odd. However, it does not work for the n even case since \([S^4\wedge {\mathbb {C}}{\mathbb {P}}^{n-1},\Omega W_n]\) is not a free \({\mathbb {Z}}\)-module. An interesting corollary of Theorem 4.7 is to give a lower bound on the order of \(\partial _1\) for n even.
Corollary 4.8
When n is even and greater than 2, the order of \(\partial _1\) is at least \(n(n^2-1)\).
Proof
The order of \(\partial '_1\circ \epsilon \) is a lower bound on the order of \(\partial '_1\), which is either the same as or half of the order of \(\partial _1\) by Lemma 2.2. The corollary follows from Theorem 4.7. \(\square \)
5 A necessary condition for \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\simeq {\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\)
In this section we follow the approach in [5] to prove Theorem 1.6. The techniques used are similar to that in Sect. 4, except we are working with the quotient \(\Sigma C=\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}/\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}\) instead of \(\Sigma {\mathbb {C}}{\mathbb {P}}^{n-1}\). When n is odd, C is \(\Sigma ^{2n-6}{\mathbb {C}}{\mathbb {P}}^2\), and when n is even, C is \(S^{2n-2}\vee S^{2n-4}\). Apply \([\Sigma C,-]\) to fibration (3) to obtain the exact sequence
where \((\partial '_k)_*\) sends \(f\in [\Sigma C, SU(n)]\) to \(\partial '_k\circ f\in [\Sigma C, {\text {Map}}^*_0({\mathbb {C}}{\mathbb {P}}^2, BSU(n))]\). Since \(BSU(n)\rightarrow BSU(\infty )\) is a 2n-equivalence and \(\Sigma C\) has dimension \(2n-1\), \([\Sigma C, BSU(n)]\) is \({\tilde{K}}^0(\Sigma C)\) which is zero. Similarly, \([\Sigma C, SU(n)]\cong [\Sigma ^2C, BSU(n)]\) is \({\tilde{K}}^0(\Sigma ^2C)\cong {\mathbb {Z}}\oplus {\mathbb {Z}}\). Furthermore, by adjunction we have \([\Sigma C, {\text {Map}}^*_0({\mathbb {C}}{\mathbb {P}}^2,BSU(n))]\cong [\Sigma C\wedge {\mathbb {C}}{\mathbb {P}}^2, BSU(n)]\). The exact sequence becomes
This implies \([\Sigma C, B{\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)]\cong [C, {\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)]\) is \(Coker(\partial '_k)_*\). Also, apply \([{\mathbb {C}}{\mathbb {P}}^2\wedge C, -]\) to fibration (8) to obtain the exact sequence
Observe that \([{\mathbb {C}}{\mathbb {P}}^2\wedge C, \Omega SU(\infty )]\cong {\tilde{K}}^0({\mathbb {C}}{\mathbb {P}}^2\wedge C)\) is \({\mathbb {Z}}^{\oplus 4}\) and \([{\mathbb {C}}{\mathbb {P}}^2\wedge C, SU(\infty )]\cong {\tilde{K}}^1({\mathbb {C}}{\mathbb {P}}^2\wedge C)\) is zero. Combine exact sequences (11) and (12) to obtain the diagram

where \(a(f)=f^*(a_{2n})\oplus f^*(a_{2n+2})\) for any \(f\in [{\mathbb {C}}{\mathbb {P}}^2\wedge C, \Omega W_n]\), and \(\Phi \) is defined to be \(a\circ p_*\). By Lemma 4.2\([{\mathbb {C}}{\mathbb {P}}^2\wedge C,\Omega W_n]\) is free. Following the same argument in Sect. 4 implies the injectivity of a.
Our strategy to prove Theorem 1.6 is as follows. If \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) is homotopy equivalent to \({\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\), then \([C, {\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)]\cong [C, {\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)]\) and exactness in (12) implies that \(Im(\partial '_k)_*\) and \(Im(\partial '_l)_*\) have the same order in \([{\mathbb {C}}{\mathbb {P}}^2\wedge C, SU(n)]\), resulting in a necessary condition for a homotopy equivalence \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\simeq {\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\). To calculate the order of \(Im(\partial '_k)_*\), we will find a preimage \(\tilde{\partial }_k\) of \(Im(\partial '_k)_*\) in \([{\mathbb {C}}{\mathbb {P}}^2\wedge C,\Omega W_n]\). Since a is injective, we can embed \(\tilde{\partial }_k\) into \(H^{2n}({\mathbb {C}}{\mathbb {P}}^2\wedge C)\oplus H^{2n+2}({\mathbb {C}}{\mathbb {P}}^2\wedge C)\) and work out the order of \(Im(\partial '_k)_*\) there.
Let \(u, v_{2n-4}\) and \(v_{2n-2}\) be generators of \(H^2({\mathbb {C}}{\mathbb {P}}^2)\), \(H^{2n-4}(C)\) and \(H^{2n-2}(C)\). Then we write an element \(xu^2v_{2n-4}+yuv_{2n-2}+zu^2v_{2n-2}\in H^{2n}({\mathbb {C}}{\mathbb {P}}^2\wedge C)\oplus H^{2n+2}({\mathbb {C}}{\mathbb {P}}^2\wedge C)\) as (x, y, z). First we need to find the submodule Im(a).
Lemma 5.1
For n odd, Im(a) is \(\{(x, y, z)|x+y\equiv z\pmod {2}\}\), and for n even, Im(a) is \(\{(x, y, z)|y\equiv 0\pmod {2}\}\).
Proof
When n is odd, C is \(\Sigma ^{2n-6}{\mathbb {C}}{\mathbb {P}}^2\) and the \((2n+3)\)-skeleton of \(\Omega W_n\) is \(\Sigma ^{2n-2}{\mathbb {C}}{\mathbb {P}}^2\). To say \((x, y, z)\in Im(a)\) means there exists \(f\in [{\mathbb {C}}{\mathbb {P}}^2\wedge C,\Omega W_n]\) such that
Reducing to homology with \({\mathbb {Z}}/2{\mathbb {Z}}\)-coefficients, we have
Apply \(Sq^2\) to (13) to get \(x+y\equiv z\pmod {2}\). Therefore Im(a) is contained in \(\{(x, y, z)|x+y\equiv z\pmod {2}\}\). To show that they are equal, we need to show that (1, 0, 1), (0, 1, 1) and (0, 0, 2) are in Im(a). Consider maps
where \(q_1,q_2\) and \(q_3\) are quotient maps and \(\theta \) is the generator of \(\pi _{2n+3}(W_n)\). Their images are
respectively, so \(Im(a)=\{(x, y, z)|x+y\equiv z\pmod {2}\}\).
When n is even, C is \(S^{2n-2}\vee S^{2n-4}\) and the \((2n+3)\)-skeleton of \(\Omega W_n\) is \(S^{2n+2}\vee S^{2n}\). Reducing to homology with \({\mathbb {Z}}/2{\mathbb {Z}}\)-coefficients, \(Sq^2(v_{2n-4})=0\) and \(Sq^2(a_{2n})=0\). Apply \(Sq^2\) to (13) to get \(y\equiv 0\pmod {2}\). Therefore Im(a) is contained in \(\{(x, y, z)|y\equiv 0\pmod {2}\}\). To show that they are equal, we need to show that (1, 0, 0), (0, 2, 0) and (0, 0, 1) are in Im(a). The maps
where \(q'_1\) and \(q'_2\) are quotient maps and \(p_1\) and \(p_2\) are pinch maps, have images \(a(f'_1)=(1, 0, 0)\) and \(a(f'_2)=(0, 0, 1)\). To find (0, 2, 0), apply \([-\wedge S^{2n-2},\Omega W_n]\) to cofibration (4) to obtain the exact sequence
where \(i^*\) is induced by the inclusion \(i:S^2\hookrightarrow {\mathbb {C}}{\mathbb {P}}^2\) and \(\eta ^*\) is induced by Hopf map \(\eta \). The third term \(\pi _{2n+1}(W_n)\cong {\mathbb {Z}}\) is generated by \(i':S^{2n+1}\rightarrow W_n\), the inclusion of the bottom cell, and the fourth term \(\pi _{2n+2}(W_n)\cong {\mathbb {Z}}/2{\mathbb {Z}}\) is generated by \(i'\circ \eta \), so \(\eta ^*:{\mathbb {Z}}\rightarrow {\mathbb {Z}}/2{\mathbb {Z}}\) is a surjection. By exactness \([{\mathbb {C}}{\mathbb {P}}^2\wedge S^{2n-2},\Omega W_n]\) has a \({\mathbb {Z}}\)-summand with the property that \(i^*\) sends its generator g to \(2i'\). Therefore the composition
has image (0, 2, 0). It follows that \(Im(a)=\{(x, y, z)|y\equiv 0\pmod {2}\}\). \(\square \)
Now we split into the n odd and n even cases to calculate the order of \(Im(\partial '_k)_*\).
5.1 The order of \(Im(\partial '_k)_*\) for n odd
When n is odd, C is \(\Sigma ^{2n-6}{\mathbb {C}}{\mathbb {P}}^2\). First we find \(Im(\Phi )\) in Im(a). For \(1\le i\le 4\), let \(L_i\) be the generators of \({\tilde{K}}^0({\mathbb {C}}{\mathbb {P}}^2\wedge C)\cong {\mathbb {Z}}^{\oplus 4}\) with Chern characters
By Theorem 4.3, we have
By Lemma 5.1, Im(a) is spanned by (1, 0, 1), (0, 1, 1) and (0, 0, 2). Under this basis, the coordinates of the \(\Phi (L_i)\)’s are
We represent their coordinates by the matrix
where \(L=(n-2)!\). Then \(Im(\Phi )\) is spanned by the row vectors of \(M_{\Phi }\).
Next, we find a preimage of \(Im(\partial '_k)_*\) in \([{\mathbb {C}}{\mathbb {P}}^2\wedge C,\Omega W_n]\). In exact sequence (11) \({\tilde{K}}^0(\Sigma ^2C)\) is \({\mathbb {Z}}\oplus {\mathbb {Z}}\). Let \(\alpha _1\) and \(\alpha _2\) be its generators with Chern classes
Lemma 5.2
For \(i=1,2\), \((\partial '_k)_*(\alpha _i)\) has a lift \(\tilde{\alpha }_{i,k}:{\mathbb {C}}{\mathbb {P}}^2\wedge C\rightarrow \Omega W_n\) such that
Proof
For dimension and connectivity reasons, \(\alpha _i:\Sigma ^2C\rightarrow BSU(\infty )\) lifts through \(BSU(n)\rightarrow BSU(\infty )\). Label the lift \(\Sigma ^2C\rightarrow BSU(n)\) by \(\alpha _i\) as well. Let \(\alpha '_i:\Sigma C\rightarrow SU(n)\) be the adjoint of \(\alpha _i\). Then \((\partial '_k)_*(\alpha _i)\) is the adjoint of the composition
By Lemma 4.5, \((\partial '_k)_*(\alpha _i)\) has a lift \(\tilde{\alpha }_{i,k}\) such that \(\tilde{\alpha }_{i,k}^*(a_{2j})=ku^2\otimes \Sigma ^{-1}(\alpha ')^*(x_{2j-3})\). Since \(\sigma (c_{j-1})=x_{2j-3}\), we have \(\tilde{\alpha }_{i,k}^*(a_{2j})=ku^2\otimes \Sigma ^{-2}c_{j-1}(\alpha _i)\) and
\(\square \)
By Lemma 5.2, \((\partial '_k)_*(\alpha _1)\) and \((\partial '_k)_*(\alpha _2)\) have lifts
We represent their coordinates by the matrix
Let \(\tilde{\partial }_k=span\{\tilde{\alpha }_{1,k}, \tilde{\alpha }_{2,k}\}\) be the preimage of \(Im(\partial '_k)_*\) in \([{\mathbb {C}}{\mathbb {P}}^2\wedge C,\Omega W_n]\). Then \(\tilde{\partial }_k\) is spanned by the row vectors of \(M_{\partial }\).
Lemma 5.3
When n is odd, the order of \(Im(\partial '_k)_*\) is
Proof
Suppose \(n=4m+3\) for some integer m. Then
and
Transform \(M_{\Phi }\) into Smith normal form
where
The matrix B represents a basis change in Im(a) and A represents a basis change in \(Im(\Phi )\). Therefore \([{\mathbb {C}}{\mathbb {P}}^2\wedge C, SU(n)]\) is isomorphic to
We need to find the representation of \(\tilde{\partial }_k\) under the new basis represented by B. The new coordinates of \(\tilde{\alpha }_{1,k}\) and \(\tilde{\alpha }_{2,k}\) are the row vectors of the matrix
Apply row operations to get
Let \(\mu =(kL,0,-kL)\) and \(\nu =((4m+2)kL, (2m+1)kL,0)\). Then
If \(x\mu +y\nu \) and \(x'\mu +y'\nu \) are the same modulo \(Im(\Phi )\), then we have
These conditions are equivalent to
This implies that there are \(\displaystyle {\frac{(2m+2)(4m+3)(4m+2)}{((2m+2)(4m+3)(4m+2), k)}}\) distinct values of x and \(\displaystyle {\frac{4m+3}{(4m+3,k)}}\) distinct values of y, so we have
When \(n=4m+1\), we can repeat the calculation above to obtain
\(\square \)
5.2 The order of \(Im(\partial '_k)_*\) for n even
When n is even, C is \(S^{2n-2}\vee S^{2n-4}\). For \(1\le i\le 4\), let \(L_i\) be the generators of \({\tilde{K}}^0({\mathbb {C}}{\mathbb {P}}^2\wedge C)\cong {\mathbb {Z}}^{\oplus 4}\) with Chern characters
By Theorem 4.3, we have
By Lemma 5.1, Im(a) is spanned by (1, 0, 0), (0, 2, 0) and (0, 0, 1). Under this basis, the coordinates of the \(\Phi (L_i)\)’s are
We represent the coordinates of \(\Phi (L_i)\)’s by the matrix
Then \(Im(\Phi )\) is spanned by the row vectors of \(M_{\Phi }\).
In exact sequence (11) \({\tilde{K}}^0(\Sigma ^2C)\) is \({\mathbb {Z}}\oplus {\mathbb {Z}}\). Let \(\alpha _1\) and \(\alpha _2\) be its generators with Chern classes
By Lemma 5.2, \((\partial '_k)_*(\alpha _1)\) and \((\partial '_k)_*(\alpha _2)\) have lifts
We represent their coordinates by a matrix
Then the preimage \(\tilde{\partial }_k=span\{\tilde{\alpha }_{1, k}, \tilde{\alpha }_{2, k}\}\) of \(Im(\partial '_k)_*\) is spanned by the row vectors of \(M_{\partial }\). We calculate as in the proof of Lemma 5.3 to obtain the following lemma.
Lemma 5.4
When n is even, the order of \(Im(\partial '_k)_*\) is
5.3 Proof of Theorem 1.6
Before comparing the orders of \(Im(\partial '_k)_*\) and \(Im(\partial '_k)_*\), we prove a preliminary lemma.
Lemma 5.5
Let n be an even number and let p be a prime. Denote the p-component of t by \(\nu _p(t)\). If there are integers k and l such that
then \(\nu _p(n, k)=\nu _p(n,l)\).
Proof
Suppose p is odd. If p does not divide n, then \(\nu _p(n,k)=\nu _p(n,l)=1\), so the lemma holds. If p divides n, then \(\nu _p(\frac{1}{2}n,k)=\nu _p(n,k)\). The hypothesis becomes \(\nu _p(n,k)^2=\nu _p(n,l)^2\), implying that \(\nu _p(n, k)=\nu _p(n,l)\).
Suppose \(p=2\). Let \(\nu _2(n)=2^r\), \(\nu _2(k)=2^t\) and \(\nu _2(l)=2^s\). Then the hypothesis implies
To show \(\nu _2(n,k)=\nu _2(n,l)\), we need to show \(min(r,t)=min(r,s)\). Consider the following cases: (1) \(t,s\ge r\), (2) \(t,s\le r-1\), (3) \(t\le r-1,s\ge r\) and (4) \(s\le r-1,t\ge r\).
Case (1) obviously gives \(min(r,t)=min(r,s)\). In case (2), when \(t,s\le r-1\), equation (14) implies \(2t=2s\). Therefore \(t=s\) and \(min(r,t)=min(r,s)\).
It remains to show cases (3) and (4). For case (3) with \(t\le r-1,s\ge r\), equation (14) implies
Since \(s\ge r\), \(min(r-1,s)=r-1\) and the right hand side is \(2r-1\) which is odd. However, the left hand side is even, leading to a contradiction. This implies that this case does not satisfy the hypothesis. Case (4) is similar. Therefore \(\nu _2(n, k)=\nu _2(n, l)\) and the asserted statement follows. \(\square \)
Proof of Theorem 1.6
In exact sequence (11), \([C,{\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)]\) is \(Coker(\partial '_k)_*\). By hypothesis, \({\mathcal {G}}_k({\mathbb {C}}{\mathbb {P}}^2)\) is homotopy equivalent to \({\mathcal {G}}_l({\mathbb {C}}{\mathbb {P}}^2)\), so \(|Im(\partial '_k)_*|=|Im(\partial '_k)_*|\). The n odd and n even cases are proved similarly, but the even case is harder.
When n is even, by Lemma 5.4 the order of \(Im(\partial '_k)_*\) is
so we have
We need to show that
for all primes p. Suppose p does not divide \(\frac{1}{2}n(n^2-1)\). Equation (16) holds since both sides are 1. Suppose p divides \(\frac{1}{2}n(n^2-1)\). Since \(n-1\), n and \(n+1\) are coprime, p divides only one of them. If p divides \(n-1\), then \(\nu _p(\frac{1}{2}n,k)=\nu _p(n,k)=\nu _p(n+1,k)=1\). Equation (15) implies \(\nu _p(n-1,k)=\nu _p(n-1,l)\). Since
this implies equation (16) holds. If p divides \(n+1\), then equation (16) follows from a similar argument. If p divides n, then equation (15) implies \(\nu _p(\frac{1}{2}n,k)\cdot \nu _p(n,k)=\nu _p(\frac{1}{2}n,l)\cdot \nu _p(n,l)\). By Lemma 5.5\(\nu _p(n, k)=\nu _p(n,l)\), so equation (16) holds.
When n is odd, by Lemma 5.3 the order of \(Im(\partial '_k)_*\) is
so we have
We can argue as above to show that for all primes p,
\(\square \)
References
Atiyah, M., Bott, R.: The Yang–Mills equations over Riemann surfaces. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 308, 523–615 (1983)
Cutler, T., Theriault, S.: The homotopy types of \(SU(4)\)-gauge groups. J. Homotopy Relat. Struct. (submitted)
Gottlieb, D.: Applications of bundle map theory. Trans. Am. Math. Soc. 171, 23–50 (1972)
Hamanaka, H., Kono, A.: On \([X, U(n)]\) when \({\rm dim}X\) is \(2n\). J. Math. Kyoto Univ. 43–2, 333–348 (2003)
Hamanaka, H., Kono, A.: Unstable K-group and homotopy type of certain gauge groups. Proc. R. Soc. Edinb. A 136, 149–155 (2006)
Hasui, S., Kisihmoto, D., So, T., Theriault, S.: Odd primary homotopy types of the gauge groups of exceptional Lie groups. Proc. Am. Math. Soc. 147(4), 1751–1762 (2018). https://doi.org/10.1090/proc/14333
Kishimoto, D., Kono, A.: On the homotopy types of \(Sp(n)\) gauge groups.arXiv:1803.06477
Kishimoto, D., Kono, A., Theriault, S.: Refined gauge group decomposition. J. Math. Kyoto Univ. 54, 679–691 (2014)
Kishimoto, D., Kono, A., Tsutaya, M.: On \(p\)-local homotopy types of gauge groups. Proc. R. Soc. Edinburgh A 144, 149–160 (2014)
Kishimoto, D., Theriault, S., Tsutaya, M.: The homotopy types of \(G_2\)-gauge groups. Topol. Appl. 228, 92–107 (2017)
Kono, A.: A note on the homotopy type of certain gauge groups. Proc. R. Soc. Edinb. A 117, 295–297 (1991)
Kono, A., Tsukuda, S.: A remark on the homotopy type of certain gauge groups. J. Math. Kyoto Univ. 36, 115–121 (1996)
Lang, G.: The evaluation map and EHP sequences. Pac. J. Math. 44, 201–210 (1973)
So, T.: Homotopy types of gauge groups over non-simply-connected closed 4-manifolds. Glasgow Math J. (2018). https://doi.org/10.1017/S0017089518000241
So, T., Theriault, S.: The homotopy types of \(Sp(2)\)-gauge groups over closed, simply-connected four-manifolds. arXiv:1807.02337 (submitted to Proceedings of the Steklov Institute of Mathematics)
Theriault, S.: Odd primary homotopy decompositions of gauge groups. Algebr. Geom. Topol. 10, 535–564 (2010)
Theriault, S.: The homotopy types of \(Sp(2)\)-gauge groups. J. Math. Kyoto Univ. 50, 591–605 (2010)
Theriault, S.: Homotopy types of \(SU(3)\)-gauge groups over simply connected 4-manifolds. Publ. Res. Inst. Math. Sci. 48, 543–563 (2012)
Theriault, S.: The homotopy types of \(SU(5)\)-gauge groups. Osaka J. Math. 1, 15–31 (2015)
Theriault, S.: Odd primary homotopy types of \(SU(n)\)-gauge groups. Algebr. Geom. Topol. 17, 1131–1150 (2017)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Ronald Brown.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
So, T. Homotopy types of SU(n)-gauge groups over non-spin 4-manifolds. J. Homotopy Relat. Struct. 14, 787–811 (2019). https://doi.org/10.1007/s40062-019-00233-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-019-00233-4