Abstract
This paper introduces an inductive tree notation for all the faces of polytopes arising from a simplex by truncations, which allows viewing face inclusion as the process of contracting tree edges. These polytopes, known as hypergraph polytopes or nestohedra, fit in the interval from simplices to permutohedra (in any finite dimension). This interval was further stretched by Petrić to allow truncations of faces that are themselves obtained by truncations. Our notation applies to all these polytopes. As an illustration, we detail the case of Petrić’s permutohedron-based associahedra. As an application, we present a criterion for determining whether edges of polytopes associated with the coherences of categorified operads correspond to sequential, or to parallel associativity.
Similar content being viewed by others
1 Introduction
The topological significance of polytopes came to light in Stasheff’s work [19], where the family of associahedra was used as a parameter space for a homotopy-theoretic characterisation of based loop spaces. Since then, a variety of polytopes have been used for exploring different higher homotopies and related concepts of higher category theory and higher operad theory: higher homotopy commutativity, and higher homotopy associativity and commutativity are demonstrated by permutohedra [13, 21], and by permutoassociahedra [1, 9], respectively. The coherences of categorified operads [6] are displayed by associahedra, permutohedra, and hemiassociahedra. All these families of polytopes arise by truncation of simplices, and enjoy nice combinatorial descriptions, among which is the one developed by Došen and Petrić in the formalism of hypergraphs [5].
More precisely, Došen and Petrić investigate a family of polytopes that may be obtained by truncating the vertices, edges and other faces of simplices of any finite dimension. The permutohedra are limit cases in that family, where all possible truncations have been made. The limit cases at the other end, where no truncation has been made, are simplices. (Alternatively, one may choose the permutohedron as starting point, and reach the simplex by successive contractions, see e.g. [20]). Other independent (and even predating) approaches have been developed for combinatorial descriptions of the polytopes in this family [2, 4, 7, 8, 15, 16] and of their geometric realisations .
An easy example of a transition from a simplex to a permutohedron is obtained by truncating all the vertices of a 2-dimensional simplex (i.e., a triangle) to get a 2-dimensional permutohedron (i.e., a hexagon):

In higher dimensions, the number of possible truncations increases with the number of faces of different dimensions. For example, at dimension 3 we can truncate not only the vertices of a tetrahedron, but also its edges. The connected subsets of a hypergraph \({\varvec{H}}\) with n vertices act as truncating instructions to be applied to the simplex of dimension \(n-1\). The polytopes obtained in this manner are called hypergraph polytopes or nestohedra.
The variety of hypergraph polytopes (and beyond) arising in applications justifies an effort to provide an adequate labelling of their faces, analogous to, or extending, the well-known labelling of associahedra by parenthesisations of strings, and also by planar trees. As a matter of fact, a syntactically presented and inductively defined tree notation can be given for all polytopes arising as (iterated) truncations of the simplices, as we shall demonstrate.
In [5], the faces of hypergraph polytopes are named by combinatorial objects called constructs (also known as nested sets), for which we develop here a new approach. While they were originally defined in [5] as certain sets of connected subsets of a hypergraph, we define them as decorated trees obtained in an algorithmic manner; this dynamic point of view extends to the definition of the partial order on constructs (Sect. 2). We show the equivalence with the original definition of Došen and Petrić in Sect. 3, where we also provide an alternative proof for the main theorem of [5], stating the order-isomorphism between the poset of constructs and the poset of faces in the geometric realisation. Unlike the original proof, our proof builds the isomorphism explicitly.
Došen and Petrić developed hypergraph polytopes in connection to their work on the categorification of operads [6]. The coherences arising in this setting display themselves as faces of some hypergraph polytopes. We complement their work with a criterion for recognising whether edges in these polytopes arise from sequential or parallel associativity isomorphisms (Sect. 4).
Finally, in Sect. 5, we show how to extend our tree notation for constructs to cover iterated truncations, i.e., truncations of faces themselves obtained after (possibly iterated) truncations, as captured combinatorially in [14], and we illustrate it for the case of the permutohedron-based associahedron (underlying the coherences of symmetric monoidal categories). We present an ad hoc notation for the faces of this polytope (in any finite dimension), based on words with holes and directly suggested by our construct notation.
We have tried to give, as much as possible, a self-contained exposition of the material presented.
Terminology Classically, a (convex) polytope is defined as a bounded intersection of a finite set of half-spaces. More precisely, a polytope P is specified as the set of solutions to a system \(Ax\ge b\) of linear inequalities, where A is an \(m\times n\) matrix, x is an \(n\times 1\) column vector of variables, and b is an \(m\times 1\) column vector of constants. Here, n is the dimension of the ambient space containing P, and m is the number of half-spaces defining P. The actual dimension of P is the maximum dimension of an open ball contained in P.
A face of P is any intersection of P with one of its bounding hyperplanes (such a hyperplane intersects P and bounds a closed half-space containing P). Following usual terminology, the 0-dimensional (resp. 1-dimensional) faces of a polytope are called vertices (resp. edges), and if P is n-dimensional, we call its \((n-1)\)-dimensional faces facets. If the definition of a face is extended to allow the empty set to be considered as a face, then the faces of a convex polytope form a bounded lattice called its face lattice, the partial ordering being the set containment of faces. The whole polytope (resp. the empty set) is the maximum (resp. minimum) element of the lattice.
As opposed to the classically (or geometrically) defined polytopes, an abstract polytope is a structure that captures only the combinatorial properties of the face lattice of a polytope, ignoring some of its other properties, particularly measurable ones, such as angles, edge lengths, etc. An abstract polytope is given as a set of faces, together with an order relation that satisfies certain axioms reflecting the incidence properties of polytopes in the classical sense.
Throughout the paper, there will be trees (all rooted), graphs, hypergraphs, and polytopes, sometimes discussed next to each other. When speaking about “vertices” or “edges”, it should always be clear which of these structures we are referring to.
We shall use two notions of subtree. By a subtree of a constructT we shall mean a tree obtained by picking a node of T and taking all its descendants. But in the context of operadic trees\(\mathcal{T}\) (Sect. 4), we shall call subtree any connected subset of\(\mathcal{T}\).
Finally, for convenience, we also recall here some terminology used in rewriting theory. A set A equipped with a binary relation \(\mathcal{R}\) is called a rewriting system. A normal form is an element x of A such that there exists no y such that \(x\,\mathcal{R}\,y\). The relation is called terminating if there is no infinite sequence \(x_1\,\mathcal{R}\,x_2\,\mathcal{R}\,\ldots \,\mathcal{R}\,x_n\,\mathcal{R}\,x_{n+1},\ldots \,.\) The relation is called confluent if whenever \(x\,\mathcal{R} \,y_1\) and \(x\,\mathcal{R} \,y_2\), then there exists z such that \(y_1\,\mathcal{R}^*\,z\) and \(y_2\,\mathcal{R}^* \,z\) (where \(\mathcal{R}^*\) is the reflexive and transitive closure of \(\mathcal{R}\)).
2 Hypergraph polytopes and constructs
In this section, we recall the definition of a hypergraph and some basic related notions. Then we give our own definition of constructs and of the partial ordering between them, postponing to Sect. 3 the proof that these coincide up to isomorphism with the definitions given in [5].
2.1 Hypergraphs
A hypergraph is given by a set H of vertices (the carrier), and a subset \({\varvec{H}}\subseteq \mathcal{P}(H)\backslash \emptyset \) such that \(\bigcup {\varvec{H}}=H\). The elements of \({\varvec{H}}\) are called the hyperedges of \({\varvec{H}}\). We always assume that \({\varvec{H}}\) is atomic, by which we mean that \(\{x\}\in {\varvec{H}}\), for all \(x\in H\). Identifying x with \(\{x\}\), H can be seen as the set of hyperedges of cardinality 1, also called vertices. We shall always use the convention to give the same name to the hypergraph and to its carrier, the former being the bold version of the latter. A hyperedge of cardinality 2 is called an edge. Note that any ordinary graph (V, E) can be viewed as the atomic hypergraph \(\{\{v\}\!\mid \! v\in V\} \cup \{e\!\mid \! e\in E\}\) (with no hyperedge of cardinality \(\ge 3\)).
If \({\varvec{H}}\) is a hypergraph, and if \(X\subseteq H\), we set
We say that \({\varvec{H}}\) is connected if there is no non-trivial partition \(H=X_1\cup X_2\) such that \({\varvec{H}}={\varvec{H}}_{X_1}\cup {\varvec{H}}_{X_2}\). All our hypergraphs will be finite. It is easily seen that for each finite hypergraph there exists a partition \(H=X_1\cup \cdots \cup X_m\) such that each \({\varvec{H}}_{X_i}\) is connected and \({\varvec{H}}=\bigcup ({\varvec{H}}_{X_i})\). The \({\varvec{H}}_{X_i}\)’s are called the connected components of \({\varvec{H}}\). We shall also use the following notation:
As a (standard) abuse of terminology, we call a non-empty subset X of vertices connected (resp. a connected component) whenever \({\varvec{H}}_X\) is connected (resp. a connected component). We define the saturation of \({\varvec{H}}\) as the hypergraph
A hypergraph is called saturated when \({\varvec{H}}={ Sat}({\varvec{H}})\). Atomic and saturated hypergraphs are called building sets in the works of Postnikov et al. [15, 16], and are generalised, with the same name, from the present setting of \(\mathcal{P}(H)\) to that of arbitrary finite lattices in the works of Feichtner et al. [7, 8].
The notation
will mean that \(H_1,\ldots ,H_n\subseteq H\backslash X\) are the (resp. \( \{H_i\!\mid \! i\in I\}\) is the set of) connected components of \({\varvec{H}}\backslash X\). We shall write \({\varvec{H}}_i\) for \({\varvec{H}}_{H_i}\).
We call a quasi-partition of a setX a collection of disjoint (possibly empty) subsets whose union is X. We shall need the following (standard) property.
Lemma 1
Let \({\varvec{H}}\) be a connected hypergraph, and let \(Y\subseteq X\subseteq H\). Let \({\varvec{H}},Y\leadsto \{K_j\,|\,j\in J\}\) and \({\varvec{H}},X\leadsto \{H_i\,|\,i\in I\}\). Then the following two claims hold:
-
1.
If \( H_i\cap K_j\ne \emptyset \), then \(H_i\subseteq K_j\).
-
2.
There exists a quasi-partition \(\{I_j\,|\, j\in J\}\) of I, such that, for each \(j\in J\), \(K_j \backslash X=\bigcup _{i\in I_j} H_i\). Consequently, we have \({\varvec{K}}_j,X\leadsto \{H_i\,|\, i\in I_j\}\).
2.2 Constructs and constructions
A connected hypergraph \({\varvec{H}}\) gives rise to a set of constructs, which we define below inductively.
Definition 1
Let \({\varvec{H}}\) be a connected hypergraph and Y be an arbitrary non-empty subset of H:
-
If \(Y = H\), then the one-node tree decorated with H, written H, is a construct of \({\varvec{H}}\).
-
Otherwise, if \({\varvec{H}},Y \leadsto H_1,\ldots ,H_n\), and if \(T_1,\ldots ,T_n\) are constructs of \({\varvec{H}}_1,\ldots ,{\varvec{H}}_n\), respectively, then the tree whose root is decorated by Y, with n outgoing edges on which the respective \(T_i\,\)’s are grafted, written \(Y(T_1,\ldots ,T_n)\), is a construct.
A construction is a construct whose nodes are all decorated with singletons. We shall often use the letter V to denote a construction (since constructions denote vertices in the geometric realisation, see Sect. 3.2).
The intuition behind this definition is algorithmic: a construct is built by picking and removing a non-empty subset Yof H,then branching to the connected components of\({\varvec{H}}\backslash Y\)and continuing recursively in all the branches.
The notation \(T:{\varvec{H}}\) will mean that T is a construct of \({\varvec{H}}\). The following formal system summarises our definition of constructs:

We shall freely write x instead of \(\{x\}\) etc. for the labels of singleton nodes of constructs. For example, x(y, z) stands for \(\{x\}(\{y\},\{z\})\), etc.
In \(Y(T_1,\ldots ,T_n)\), the order of the constructs \(T_1,...,T_n\) is irrelevant. We shall write \(Y\{T_i\!\mid \! i\in I\}\) when the constructs \(T_i\) are indexed over some finite set I. When \(I=\emptyset \), we get that \(Y\{T_i\!\mid \! i\in I\}\) stands for Y, corresponding to the base case in Definition 1 (note that the only hypergraph whose set of connected components is empty is the empty one). It is also sometimes convenient to allow Y to be empty, with the understanding that \(\emptyset \{T_i\!\mid \! i\in I\}\), with \(I=\{i_0\}\), stands actually for \(T_{i_0}\) (indeed, removing the empty set is a non-action that leaves us with the original hypergraph).
The labels of the nodes of a construct of \({\varvec{H}}\) form a partition of H. We shall freely confuse the nodes with their labels, since they are a fortiori all distinct. For every node Y of T, we denote by  (or simply
(or simply  ) the union of the labels of the descendants of Y in T (all the way to the leaves), including Y. For every construct T of \({\varvec{H}}\) and every node Z of T, the subtree of S rooted at Z is a construct of
) the union of the labels of the descendants of Y in T (all the way to the leaves), including Y. For every construct T of \({\varvec{H}}\) and every node Z of T, the subtree of S rooted at Z is a construct of  .
.
We note that while the inductively-defined constructions in tree form appear in ([5], Sect. 3) and in ([15], Proposition 8.5) exactly like in Definition 1, these authors did not notice or exploit the fact that the tree notation could be extended to all constructs simply by replacing singletons with arbitrary subsets. As we shall see, this simple observation gives additional insights. In particular, it allows us to formulate various equivalent and useful characterisations of the partial order between constructs. The tree notation for all constructs appears in ([8], Proposition 3.17), but without an inductive characterisation.
2.3 Ordering constructs
We next define a partial order between constructs. The algorithmic intuition is that, given a construct S, one can get a larger construct by contracting an edge of S, and then merging the decorations of the two nodes related by that edge, as illustrated in the following picture:

Formally, the partial order \(\le ^{{\varvec{H}}}\) (or simply \(\le \), when \({\varvec{H}}\) is understood) is defined as the smallest partial order generated by the following rules:

This definition is well-formed, in the sense that, if \(S:{\varvec{H}}\) and if \(S\le T\) is inferred, then \(T:{\varvec{H}}\) can be inferred. The one-node construct H is maximum, while the constructions are the minimal elements (as all nodes are singletons, none of them can be split).
2.4 First examples of constructs
In this section, we provide some examples of hypergraphs and their constructs, conveying an intuitive understanding of their geometric realisation in terms of truncations (cf. Sect. 1). Došen and Petrić’s geometrical account of these truncations will be recalled in Sect. 3.2. More examples will be given in Sect. 2.6.
As our first example, we describe the \((n\!\!-\!\!1)\)-dimensional simplex:
All of its constructs have the form \(X(y_1,\ldots ,y_p),\) where \(X\subseteq \{x_1,\ldots ,x_n\}\) and \(\{y_1,\ldots ,y_p\}= \{x_1,\ldots ,x_n\}\backslash X\). Note that \({\varvec{H}}\) is indeed a hypergraph, and not just the discrete graph with n vertices, because we insist that the hyperedge \( \{x_1,\ldots ,x_n\}\) is included.
-
At dimension 2 and writing x, y, z instead of \(x_1,x_2,x_3\), we have 3 vertices, 3 edges or facets and the maximum face:
$$\begin{aligned} \begin{array}{llll} \text{ vertices } &{}&{}&{} x(y,z)\quad y(x,z)\quad z(x,y) \\ \text{ facets } &{}&{}&{} \{x,y\}(z)\quad \{y,z\}(x)\quad \{x,z\}(y) \\ \text{ whole } \text{ polytope } &{}&{}&{} \{x,y,z\} \end{array} \end{aligned}$$Note that \(x(y,z)\le \{x,y\}(z)\) and \(y(x,z)\le \{x,y\}(z)\), which says combinatorially that the edge \( \{x,y\}(z)\) connects the vertices x(y, z) and y(x, z).
-
At dimension 3, we get 4 vertices, 6 edges and 4 facets.
We illustrate now how the hypergraph structure allows us to make truncations. The desired effects of truncation will be obtained by adding hyperedges to the bare “simplex hypergraph”.
-
Truncation of a vertex, say x(y, z), of the 2-dimensional simplex (cf. Sect. 1). We add the hyperedge \(\{y,z\}\) to the simplex hypergraph:
$$\begin{aligned} {\varvec{H}}=\{\{x\},\{y\},\{z\},\{y,z\}, \{x,y,z\}\}. \end{aligned}$$Then x(y, z) is not a construction anymore, since \({\varvec{H}}_{\{y,z\}}\) is now connected. Instead, we have 3 new constructs (encoding two vertices and one edge):
$$\begin{aligned} x(y(z)) \quad x(z(y)) \quad x(\{y,z\}) \end{aligned}$$ -
Truncation of an edge, say \(\{x,y\}(u,z)\), of the 3-dimensional simplex. Similarly, we add the hyperedge \(\{u,z\}\) to the simplex hypergraph:
$$\begin{aligned} {\varvec{H}}=\{\{x\},\{y\},\{z\},\{u\},\{u,z\},\{x,y,z,u\}\}. \end{aligned}$$The edge \(\{x,y\}(u,z)\) and its end vertices are now replaced by a rectangular face (9 new constructs):
$$\begin{aligned} \begin{array}{c} x(y,u(z))\quad x(y,z(u))\quad y(x,u(z))\quad y(x,z(u))\\ x(y,\{u,z\})\quad y(x,\{u,z\})\quad \{x,y\}(u(z))\quad \{x,y\}(z(u))\\ \{x,y\}(\{u,z\}) \end{array} \end{aligned}$$

-
Truncation of a vertex, say x(y, z, u), of the 3-dimensional simplex. We achieve this by adding the hyperedge \(\{y,z,u\}\) to the simplex hypergraph:
$$\begin{aligned} {\varvec{H}}=\{\{x\},\{y\},\{z\},\{u\},\{y,z,u\} ,\{x,y,z,u\}\}. \end{aligned}$$This hypergraph disallows the construction x(y, z, u) since \({\varvec{H}}\backslash \{x\}\) is now connected, and replaces it by 3 vertices, 3 edges, and a facet:
$$\begin{aligned} \begin{array}{c} x(y(z,u))\quad x(z(y,u))\quad x(u(y,z))\\ x(\{y,z\}(u))\quad x(\{z,u\}(y))\quad x(\{u,y\}(z))\\ x(\{y,z,u\}) \end{array} \end{aligned}$$

2.5 Other characterisations of the partial order on constructs
The partial order \(\le \) admits two other equivalent definitions, for which we shall provisionally write \(\le ^{{\varvec{H}}}_2\) and \(\le ^{{\varvec{H}}}_3\) (shortly \(\le _2\) and \(\le _3\), respectively) before we prove that they define the same relation as \(\le ^{{\varvec{H}}}\). The formulation \(\le _2\) will allow us to prove the equivalence of our definitions with the original ones of [5], while, the formulation \(\le _3\) underlies an algorithm for enumerating all the vertices inferior to a given construct (see Sect. 2.7).
The definition of \(\le _2\) is given by two clauses (guided by Lemma 1):

The relation \(\le _2\) formalises the following intuition. As in the definition of \(\le \), given a construct \(S:{\varvec{H}}\), we want to know which constructs \(T:{\varvec{H}}\) lie above S in the partial order. If \(S=H\), then S is the maximum construct of \({\varvec{H}}\), hence \(H\le T\) boils down to \(T=H\). Otherwise, the root of S must be a subset of the root of T, and the task of showing \(S\le T\) is reduced to that of verifying that each \(S_j\) lies lower than an appropriate term.
For the definition of \(\le _3\), we need to introduce a variation of the notion of construct. We define the partial constructs of a connected hypergraph \({\varvec{H}}\) by adding one clause to the inductive definition of constructs:
-
The single-node tree decorated with \(\varOmega _H\) is a partial construct of \({\varvec{H}}\).
(and by replacing “construct” with “partial construct” in the original clauses).
To distinguish partial constructs from constructs, we use the font \(\mathbb {S},\mathbb {T},\ldots \) for the former. We summarise the definition of partial constructs as follows:

We define a partial construction to be a partial construct in which all the non-\(\varOmega \) nodes are labelled by singletons.
Note the difference between decorations X and \(\varOmega _X\) in a partial construct: the latter stands for “undefined”, in the spirit of Scott domain theory. We shall write \(\mathbb {T}[\varOmega _X\leftarrow \mathbb {S}]\) for the partial construct obtained from \(\mathbb {T}\) by replacing \(\varOmega _X\) with \(\mathbb {S}:{\varvec{H}}_X\).
We shall use the notation \(\mathbb {T} \blacktriangleright ^{{\varvec{H}}} X\) to indicate that X is the union of all non-\(\varOmega \)-decorations of \(\mathbb {T}\), and we shall say that \(\mathbb {T}\)spansX. Formally, this predicate is inductively defined as follows:

Lemma 2
If \(\mathbb {T}\blacktriangleright ^{{\varvec{H}}} X\), with \({\varvec{H}},X\leadsto H_1,\ldots ,H_n\), then, for each \(i\in \{1,\ldots ,n\}\), there exists exactly one occurrence of \(\varOmega _{H_i}\) in \(\mathbb {T}\), and these are all the occurrences of an \(\varOmega \) in \(\mathbb {T}\).
Proof
The proof is by structural induction on the proof of well-formedness of \(\mathbb {T}\). The case \(\mathbb {T}=Y(\mathbb {T}_1,\ldots ,\mathbb {T}_n)\) is settled by appealing to Lemma 1. \(\square \)
It follows from this lemma that the partial constructs (resp. constructions) that span the whole carrier H of a hypergraph \({\varvec{H}}\) are exactly the constructs (resp. constructions) of \({\varvec{H}}\).
Lemma 3
With the notations of Lemma 2, if \(S_1,\ldots ,S_n\) are constructs of \({\varvec{H}}_1,\ldots ,{\varvec{H}}_n\), respectively, then, for all \(1\le i\le n\), \(\mathbb {T}[\ldots ,\varOmega _{H_i}\leftarrow S_i,\ldots ]\) is a construct of \({\varvec{H}}\), and \(\mathbb {T}[\ldots , \varOmega _{H_i}\leftarrow S_i,\ldots ]\le X(S_1,\ldots ,S_n)\).
Proof
By structural induction on \(\mathbb {T}\). We treat the case \(\mathbb {T}=Y(\mathbb {T}_1,\ldots ,\mathbb {T}_m)\), with \(\mathbb {T}_j\) spanning \(Y_j\) for all j. Setting \(I_j=\{i\!\mid \! \varOmega _{H_i}\;\text{ occurs } \text{ in }\; \mathbb {T}_j\}\) and \(T'_j\) to be the result of replacing each \(\varOmega _{H_i}\) by \(S_i\) in \(\mathbb {T}_j\) (i ranging over \(I_j\)), we get by induction that \(T'_j\le Y_j\{S_i\!\mid \! i\in I_j\}\), and we conclude as follows:
\(\square \)
We have now all the prerequisites for our third presentation of the partial order. We define \(\le _3^{{\varvec{H}}}\) by the following two clauses:

Unlike for \(\le \) and \(\le _2\), the algorithmic reading of \(S\le _3 T\) answers the question of when S lies lower than some fixed T. If \(T=H\), then any construct of \({\varvec{H}}\) lies lower than T. Otherwise, S “starts by spanning X” (and recursively so).
Proposition 1
The relations \(\le \), \(\le _2\), and \(\le _3\) coincide.
Proof
That \(S\le T\) implies \(S\le _2 T\) is proved by showing that \(\le _2\) is closed under the rules that define \(\le \), including reflexivity and transitivity. Let us look at transitivity. Suppose that \({\varvec{H}},Y \leadsto K_1,\ldots ,K_m\), \({\varvec{H}},X \leadsto H_1,\ldots ,H_n\), \({\varvec{H}},Z\leadsto G_1,\ldots ,G_k\), and
We discuss only the case where \(m,n,k\ge 1\). We have to show that the two conditions allowing to deduce \(Y(S_1,\dots ,S_m)\le _2 Z(U_1,\dots ,U_k)\) hold. Collecting the first conditions in clause 2 of \(\le _2\), relative to our present two assumptions, we have that \(Y\subseteq X\) and \(X\subseteq Z\), and hence \(Y\subseteq Z\). We now show that the second condition holds. Let us fix \(j\in \{1,\dots ,m\}\) and let
We have to prove that
The second condition for our first assumption gives us that, for all j:
Now, for each \(T_i\), where \(i\in I_j\), the second condition for the second assumption gives us that
where \(M_i=\{m\in \{1,\ldots ,k\}\,|\, G_m\subseteq H_i\}\). Next, we have that
And, lastly, since \(K_j\backslash Z=(\bigcup _{i\in I_j} H_i)\backslash Z\), we have that
Finally, (1), (2), (3) and (4), together with the rules from the definition of \(\le \), give us that
Note that this proof is valid provided one has shown beforehand that \(\le _2\) is closed under the other defining clauses of
That \(S\le _2 T\) implies \(S\le _3 T\) (resp. \(S\le _3 T\) implies \(S\le T\)) is proved by induction on the proof of \(S\le _2 T\) (resp. of \(S\le _3 T\)). \(\square \)
2.6 More examples of hypergraphs and constructs
Continuing from Sect. 2.4, our next example is the family of associahedra. One of the standard labellings of the faces of the n-dimensional associahedron is by all the parenthesisations (partial or total) of a word of \(n+2\) letters. Here, the idea is to focus, not on the letters (or the leaves of the corresponding tree), but on the \(n+1\) “compositions of these letters” involved. These compositions are next to each other, as suggested in the following picture for dimension 3 (where \(a,b,c,\ldots \) are the letters and \(x,y,\ldots \) are the compositions):
-
At dimension 2, this suggests to take the following graph (in hypergraph form), expressing “x is next to y which is next to z”:
$$\begin{aligned} {\varvec{H}}=\{\{x\},\{y\},\{z\},\{x,y\},\{y,z\}\}. \end{aligned}$$(Note that the hyperedge \(\{x,y,z\}\) is no longer necessary to ensure that \({\varvec{H}}\) is connected.) The edges \(\{x,y\}\) and \(\{y,z\}\) are prescriptions for truncating two vertices of a triangle, yielding a pentagon. The 5 vertices are
$$\begin{aligned} x(y(z)) \quad x(z(y)) \quad y(x,z)\quad z(x(y))\quad z(y(x)) \end{aligned}$$ -
At dimension 3, we take
$$\begin{aligned} {\varvec{H}}=\{\{x\},\{y\},\{z\}, \{u\},\{x,y\},\{y,z\},\{z,u\}\}, \end{aligned}$$which seems like a prescription for truncating (only) three edges of the simplex. But look at what has become of the vertex u(x, y, z). It has been also truncated! Indeed, it has been split into 5 constructions (with corresponding edges and face):
$$\begin{aligned} u(x(y(z)))\quad u(x(z(y)))\quad u( y(x,z))\quad u(z(x(y))\quad u(z(y(x))) \end{aligned}$$To build these constructions, we have used that \({\varvec{H}}_{\{x,y,z\}}\) is connected. In fact, the truncation prescriptions are all hyperedges of \({ Sat}({\varvec{H}})\).
-
At dimension n, we take
$$\begin{aligned} {\varvec{H}}=\{\{x_1\},\ldots , \{x_{n+1}\},\{x_1,x_2\},\ldots ,\{x_n,x_{n+1}\}\}.\end{aligned}$$
Here is the recipe showing how to move between three equivalent presentations of the faces of the associahedra: partially parenthesised words, rooted (undecorated) planar trees (see e.g. [11]), and constructs.
-
From rooted planar trees to constructs. Label all the intervals beween the leaves of a tree with \(n+2\) leaves by \(x_1,\ldots ,x_{n+1}\) (from left to right). Consider the \(x_i\)’s as balls and let them fall. Label each node of the tree by the set of balls which fall to that node. Finally, remove all the leaves. For example:

-
From constructs to parenthesisations. Read a construct from the leaves to the root, and each node as an instruction for building a parenthesis. If the label is, for example, \(\{x_i,x_{i+2}\}\), then the instruction is to do an unbiased composition of three partially parenthesised words \(w_1,w_2,w_3\) “above” \(x_i\) and \(x_{i+2}\) (for example, a, (bc), d are above x and z in (4)), in one shot, resulting in \((w_1w_2w_3)\).
-
From parenthesisations to trees. This is standard.
For the 2-dimensional associahedron, the representation with planar rooted trees / constructs is given on the next picture:

Our final example is the family of permutohedra. Here we take the complete graph on the set of vertices as the hypergraph. We discuss directly the general case at dimension n:
Note that all the constructs of the permutohedra are filiform, i.e., are trees reduced to a branch. The faces of the permutohedra have been described in the literature as surjections, and also as planar rooted trees with levels. The three representations are related as follows:
-
From trees with levels to constructs. Consider again the \(x_i\)’s as balls being thrown in the successive intervals between the leaves, and let them fall. Then we form the construct \(Y_1(Y_2(\ldots (Y_m)\ldots ))\), where \(Y_i\) is the collection of balls that fall to level i (counting levels from the root). For example:

-
A construct \(Y_1(Y_2(\ldots (Y_m)\ldots ))\) defines a surjection from \(\{x_1,\ldots ,x_{n+1}\}\) to \(\{1,\ldots ,m\}\) mapping each \(x\in Y_i\) to i.
-
From surjections to trees with levels. We refer to [10].
For the 2-dimensional permutohedron, the representation with planar rooted trees with levels / constructs is given on the next picture:

2.7 Vertices of faces
As a preparation for the following section, given a hypergraph \({\varvec{H}}\) and a construct \(T:{\varvec{H}}\), we give a device for finding all constructions V such that \(V\le ^{{\varvec{H}}} T\). If T is a construction, then this set is reduced to T itself. We shall use the notation \(V \lessdot ^{{\varvec{H}}}T\) for “\(V \le ^{{\varvec{H}}} T\;\text{ and }\; V\;\text{ is } \text{ a } \text{ construction }\)”.
First, we notice that, by a straightforward tuning of the definition of \(\le _3\), the predicate \(\lessdot \) is defined by the following clauses:

where, in the second clause, \(\mathbb {V}_0\) is a partial construction.
This suggests an algorithm. For every node X of T, we should “zoom in” and replace it with a partial construction spanning X. Here is a formal device for searching all the partial constructions of \({\varvec{H}}\) spanning a given fixed set \(X\subseteq H\). One starts from \(\varOmega _H\), and one performs rewriting (non-deterministically), until exhaustion of X, as follows:

We shall say that a partial construction \(\mathbb {V}\) is accepted if \(\varOmega _H\longrightarrow _X\!\!{}^* \,\mathbb {V}\) and there exists no \(\mathbb {V}'\) such that \(\mathbb {V}\longrightarrow _X \mathbb {V}'\). As immediate observations, we have:
-
1.
If \(\mathbb {V}\longrightarrow _X \mathbb {V}'= V[\varOmega _K\leftarrow x(\varOmega _{K_1},\ldots ,\varOmega _{K_p})]\), then \(\mathbb {V}' \blacktriangleright ^{{\varvec{H}}} Y\cup \{x\}\), i.e., \(\mathbb {V}'\) is a partial construction spanning \(Y\cup \{x\}\).
-
2.
The rewriting system \(\longrightarrow _X\) is terminating, since the cardinality of the spanned subset increases by 1 at each step, while remaining a subset of X.
Lemma 4
(1) The accepted partial constructions are precisely the partial constructions spanning X. (2) For every element \(x\in X\), there exists a partial construction spanning X whose root is decorated by x.
Proof
If \(\mathbb {V}\) is accepted, then \(\mathbb {V}\) spans X by definition. Conversely, we proceed by induction on the cardinality of X. We can write \(\mathbb {V}\) as \(\mathbb {V}'[\varOmega _K \leftarrow x(\varOmega _{K_1},\ldots ,\varOmega _{K_p})]\), since every tree has a node all of whose outgoing edges are leaves, and then apply induction to \(\mathbb {V}'\), which spans \(X\backslash \{x\}\).
As for the second claim, given \(x\in X\), we can start the rewriting sequence with \(\varOmega _H\longrightarrow _X x(\varOmega _{K_1},\ldots , \varOmega _{K_p})\). Then any continuation of this sequence leads to a partial construction spanning X, and having x as a root. \(\square \)
Returning to our goal of finding all constructions V such that \(V\lessdot T\) (for fixed T), we transform our definition of \(\lessdot \) into an algorithmic one by replacing
in the second clause: we apply the device repetitively at all nodes of T.
Corollary 1
For each construct \(X(T_1,\ldots ,T_n)\) and each \(x\in X\), there exists at least one construction of the form \(x(S_1,\ldots ,S_m)\), such that \(x(S_1,\ldots ,S_m)\lessdot X(T_1,\ldots ,T_n)\).
3 Constructs as geometric faces
In this section, we recall the geometric realisation of hypergraph polytopes, following Došen and Petrić, and we provide a new proof of their theorem stating that the poset of constructs is isomorphic to the poset of geometric faces. The original proof in [5] relies on Birkhoff’s representation theorem, without providing an explicit description of the isomorphism. Our proof is constructive, in that it exhibits the isomorphism.
We first prove the equivalence between our notion of constructs and theirs. Then we recall the geometric realisation of hypergraph polytopes. Finally, we translate both formalisations in the language of simplicial complexes, which provides the environment for exhibiting the desired isomorphism.
3.1 Non-inductive characterisation of constructs
Let \({\varvec{H}}\) be a finite, atomic and connected hypergraph. We can define a map \(\psi \) from the set of constructs of \({\varvec{H}}\) to \(\mathcal{P}(\mathcal{P}(H)\backslash \emptyset )\backslash \emptyset \), as follows (with notation  from Sect. 2.2):
from Sect. 2.2):

We note that the Hasse diagram of \((\psi (T),\supseteq )\) is the same tree as T, replacing everywhere Y by  . We also observe that the old decoration can be recovered from the new one by noticing that
. We also observe that the old decoration can be recovered from the new one by noticing that

From these observations, one can easily conclude that \(\psi \) is injective.
Lemma 5
The map \(\psi \) is (contravariantly) monotonic and order-reflecting.
Proof
Monotonicity is easy, following the inductive definition of \(\le \). For the second part of the statement, we show that if \(\psi (T')\subseteq \psi (T)\), then \(T\le _2 T'\), by induction on the size of T. In what follows, for an arbitrary construct T, we will denote by \(\rho (T)\) the root of T.
If \(T=H\), then \(\psi (T)=\{H\}\) and  implies that also \(\psi (T')=\{H\}\), and hence \(T'=H\), and we conclude by clause 1 of the definition of \(\le _2\).
implies that also \(\psi (T')=\{H\}\), and hence \(T'=H\), and we conclude by clause 1 of the definition of \(\le _2\).
If \(T=Y(S_1,\dots ,S_m)\) (\(m\ge 1\)), let \(T'=X(T_1,\dots ,T_n)\) (\(n\ge 0\)). Since \(\psi (T')\subseteq \psi (T)\), we get

Denote by \(X_1,\dots ,X_n\) the nodes of T for which we have  , and let, for each \(1\le i\le n\), \(U_i\) be the subtree of T rooted at \(X_i\). Note that all \(X_i\)’s must be different from Y. Indeed, if we had that \(X_i=Y\) for some \(1\le i\le n\), i.e., that
, and let, for each \(1\le i\le n\), \(U_i\) be the subtree of T rooted at \(X_i\). Note that all \(X_i\)’s must be different from Y. Indeed, if we had that \(X_i=Y\) for some \(1\le i\le n\), i.e., that  , this would imply that
, this would imply that  , which is not possible. We now have
, which is not possible. We now have

Therefore, the first condition in the second clause defining \(\le _2\) holds for T and \(T'\). For the second condition, it is enough to establish (for all j)
which amounts to proving \(\psi (T_i)\subseteq \psi (S_j)\), for every i such that \(H_i\subseteq K_j\) . We have, on one hand, \(\psi (T_i)\subseteq \psi (T')\subseteq \psi (T)\), and, on the other hand, for each element Z of \(\psi (T_i)\), \(Z\subseteq H_i\subseteq K_j\), from which \(\psi (T_i)\subseteq \psi (S_j)\) follows, since every non-root node \(Z'\) of S, other than a node appearing in \(S_j\), appears in some other \(S_{j'}\), hence is included in \(K_{j'}\), and not in \(K_j\). \(\square \)
We now describe the image of \(\psi \). We shall characterise the constructs among all possible trees decorated with disjoint subsets of H, in a non-inductive way. We note that the definition of  makes sense for any such tree.
makes sense for any such tree.
Recall that an antichain in a poset is a subset of pairwise incomparable elements. We say that an antichain is proper if its cardinality is at least 2.
Lemma 6
Any of the following properties characterises constructs among trees T decorated with subsets of H:
-
1.
At every non-leaf node of T,
 are the connected components of
are the connected components of 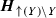 , where Y is the label of the node, and \(Y_1,\ldots ,Y_m\) are the labels of its child nodes.
, where Y is the label of the node, and \(Y_1,\ldots ,Y_m\) are the labels of its child nodes. -
2.
The following three conditions hold:
-
(A)
All labels of the nodes of T are pairwise disjoint and their union is H.
-
(B)
At each node X,
 is such that
is such that 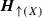 is connected.
is connected. -
(C’)
At every non-leaf node Y whose child nodes are \(Y_1,\ldots ,Y_m\), and any subset I of \(\{1,\ldots ,m\}\) of cardinality at least 2,
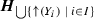 is not connected.
is not connected.
-
(A)
-
3.
Conditions (A) and (B) hold, together with:
-
(C)
For each set \(\{X_1,\ldots ,X_m\}\) of labels of T such that
 is a proper antichain,
is a proper antichain,  is not connected.
is not connected.
-
(C)
Proof
(1) is a paraphrase of our inductive definition of construct. We have that (3) obviously implies (2), since (C) a fortiori implies (C’).
We now prove that (1) implies (3). (A) and (B) are obvious through the equivalence of (1) with our definition of inductively defined constructs. We notice that (C) is vacuously true if T is reduced to one node. So let \(T=Y(T_1,\ldots ,T_p)\), with \({\varvec{H}},Y \leadsto H_1,\ldots ,H_p\). Let \(S=\{X_1,\ldots ,X_m\}\) be as specified in the statement, and suppose that  is connected. Then it is included in one of the \(H_i\)’s (note that
is connected. Then it is included in one of the \(H_i\)’s (note that  ). But then induction applies and we have a contradiction.
). But then induction applies and we have a contradiction.
Finally, we prove that (2) implies (1). By induction, it suffices to check the property (1) at the root of \(T=X(T_1,\ldots ,T_q)\). By (B), we have that every  (\(X_i\) root of \(T_i\), \(i\in \{1,\ldots ,q\}\)) is included in some \(H_j\). By (A), we have in fact that each \(H_j\) is a union of some
(\(X_i\) root of \(T_i\), \(i\in \{1,\ldots ,q\}\)) is included in some \(H_j\). By (A), we have in fact that each \(H_j\) is a union of some  ’s. Formally, there exists a non-empty set \(I_j\) such that
’s. Formally, there exists a non-empty set \(I_j\) such that  . But, by (C’), \(I_j\) must have cardinality 1 (for every j). Hence, up to permutation, we have \(p=q\) and it follows that (1) holds at the root of T. \(\square \)
. But, by (C’), \(I_j\) must have cardinality 1 (for every j). Hence, up to permutation, we have \(p=q\) and it follows that (1) holds at the root of T. \(\square \)
Proposition 2
The map \(\psi \) is a (contravariant) order-isomorphism between the set of constructs-as-decorated-trees and the collections of sets M of connected (non-empty) subsets of H, containing H, and satisfying the following property:
-
(C)
For each proper antichain \(S= \{X_1,\ldots ,X_m\}\subseteq M\), \({\varvec{H}}_{X_1 \cup \ldots \cup X_m}\) is not connected.
Proof
By Lemma 6, we have that, for any construct T, \(\psi (T)\) satisfies (C) (which we did not even care to rename!). Conversely, we first show that the Hasse diagram of a set M satisfying the conditions of the statement, ordered by reverse inclusion, is a tree. We note that if X, Y are in M and neither \(X \subseteq Y\) nor \(Y \subseteq X\), and thus \(\{X,Y\}\) is an antichain, then, by (C), \({\varvec{H}}\backslash X \cup Y\) is not connected. This entails in particular that \(X \cap Y\) is empty, as otherwise, since \({\varvec{H}}\backslash X\) and \({\varvec{H}}\backslash Y\) are connected by assumption, \({\varvec{H}}\backslash X \cup Y\) would be connected. It follows that there cannot be a Z above X and Y in the Hasse diagram, as this would imply \(Z \subseteq X \cap Y\), but all elements of M, and Z in particular, are non-empty: contradiction. Hence this Hasse diagram is a tree, with root H. Then, as remarked above, it is easy to find a decoration of the same tree where at each node the decoration X is such that  is the corresponding element in the Hasse diagram. Finally, we know from Lemma 6 that this tree is indeed a construct T, and we have \(\psi (T)=M\) by construction. \(\square \)
is the corresponding element in the Hasse diagram. Finally, we know from Lemma 6 that this tree is indeed a construct T, and we have \(\psi (T)=M\) by construction. \(\square \)
Remark 1
We collect here a few observations and comments about similar definitions in the literature.
-
1.
Sets as in Proposition 2 are called nested sets in [8, 15]. Proposition 2 thus states that constructs as inductively defined trees are in order-isomorphic correspondence with nested sets. In their work, Došen and Petrić adopt an intermediate viewpoint: they define constructions inductively, and they define constructs as subsets of \(\psi (V)\) containing H, for some construction V. They prove in [5][Proposition 6.13] that their definition is equivalent to that of nested set.
-
2.
When \({\varvec{H}}\) is a graph (or has its set of connected subsets unchanged if restricted to hyperedges of cardinality \(\le 2\)), the assumption (C) can be further relaxed to:
- \(\text{ C }_g\) :
-
For each antichain \(S=\{X_1,X_2\}\subseteq M\) (with respect to inclusion) of cardinality 2, we have that \({\varvec{H}}_{X_1 \cup X_2}\) is not connected.
Indeeed, if (referring to (C)) \({\varvec{H}}_{X_1 \cup \ldots \cup X_m}\) were connected, then since connectedness is path-connectedness in a graph, we would have that \({\varvec{H}}_{X_i \cup X_j}\) is connected, for every pair of distinct \(i,j\in \{1,\ldots ,m\}\) (actually, picking just one such pair is enough for proving that (\(\text{ C }_g\)) implies (C)).
Here is an example of why the stronger condition (C) is needed for general hypergraphs. Consider
Then (\(\text{ C }_g\)) holds, but \(\{\{x\},\{y\},\{z\}\}\) is a witness that (C) does not hold.
-
3.
Going back to graph polytopes, condition (\(\text{ C }_g\)) is equivalent to the conditions (1) and (2) below:
-
1.
If \(X_1,X_2\in M\) are such that \(X_1\cap X_2\ne \emptyset \), then \(X_1\subseteq X_2\) or \(X_2\subseteq X_1\).
-
2.
If \(X_1,X_2\in M\) are such that \(X_1\cap X_2=\emptyset \), then \({\varvec{H}}_{X_1 \cup X_2}\) is not connected.
That (1) and (2) together imply (\(\text{ C }_g\)) is obvious. Conversely, we get (the contraposite of) (1) by arguing as in the proof above, and since the implication \(((X_1\subseteq X_2\;\text{ or }\;X_2\subseteq X_1) \Rightarrow X_1\cap X_2\ne \emptyset )\) holds obviously, (1) is actually an equivalence, through which (2) can be rephrased as (\(\text{ C }_g\)). Conditions (1) and (2) are those given for tubings in [2].
-
1.
-
4.
We summarise the terminologies used in the literature in the following table (see also Sect. 3.2):

3.2 Geometric realisation
Following Došen and Petrić, given a hypergraph \({\varvec{H}}\), we show how to associate
-
actual half-spaces and hyperplanes to the connected subsets of \({{\varvec{H}}}\) (i.e., to the hyperedges of \({ Sat}({\varvec{H}})\)),
-
and a polytope to the whole hypergraph, whose poset of geometric faces is isomorphic to the poset of constructs of \({\varvec{H}}\).
Let \(H=\{x_1,\ldots ,x_n\}\). For every (non-empty) \(A\subseteq \{1,\ldots ,n\}\), we define two subsets of \(\mathbb {R}^n\), as follows:
where |A| is the cardinality of A. Then the polytope associated with \({\varvec{H}}\) is defined as follows:
For an arbitrary \(M\subseteq { Sat}({\varvec{H}})\), we define
The definition of \(\mathcal{G}({\varvec{H}})\) implements the truncation instructions encoded by the hypergraph \({\varvec{H}}\).
This construction extends the realisation of the associahedra and of the cyclohedra originally proposed in [17, 18]. In [2], graph-associahedra are also realised by means of truncations, although the concrete implementation of truncations is not described (interestingly, Devadoss gives a more precise realisation in terms of convex hulls in [4], that is also based on powers of 3).
In the setting of building sets (cf. Remark 1), a realisation that associates a linear inequality to every element of the building set, like in [5], can be found in [22]. On the other hand, Feichtner et al. use the elements of a building set as instructions for performing successive stellar subdivisions, starting from the simplex, while Postnikov et al. realise a building set by associating (via a fixed coordinate system) a simplex with each of its elements, and then by taking the Minkowski sum of these simplices. They call the resulting polytopes nestohedra.
3.3 Isomorphism between combinatorial and geometric faces
In this section, we exhibit an isomorphism between combinatorial faces (i.e. constructs) of \({\varvec{H}}\) and geometric faces of \(\mathcal{G}({\varvec{H}})\), which exploits the fact that \(\mathcal{G}({\varvec{H}})\) is a simple polytope.
For the sake of sparing on notation, we shall assume here without loss of generality that \({\varvec{H}}\) is saturated, i.e. that all connected subsets of \({\varvec{H}}\) are already in \({\varvec{H}}\).
We first give an alternative definition of a geometric face. We defined a face of a polytope as the intersection of the polytope with a single hyperplane. But by allowing the intersection with several hyperplanes, the choice of those hyperplanes can be restricted, as stated in the following proposition, which is often taken as an alternative definition of geometric face.
Proposition 3
Each non-empty face of a polytope P defined as the intersection of a collection \(\mathcal{S}\) of half-spaces is the intersection of P with some of the hyperplanes bounding the half-spaces in \(\mathcal{S}\).
We next introduce some notation. Given a polytope P, we let the letters F, G (resp. \(\varPhi \)) range over the geometric faces (resp. the facets) of P. We define a map \(\phi \) from faces to sets of facets as follows:
We shall use the following equivalent characterisations of the property, for a polytope P, to be simple (which are the item (iii) and a sharpened version of the item (v) of Proposition 2.16 of [23]):
-
S1
Each vertex of P belongs to exactly n facets of P, where n is the dimension of P.
-
S2
For every face F of P, the restriction of \(\phi \) to \(\{G\!\mid \! F\subseteq G\}\) is an order-isomorphism onto \(\mathcal{P}(\phi (F))\).
We shall also use the following properties, which are consequences of Lemmas 9.2, 9.4 and 9.5 of [5]:
-
H1
For every \(M\subseteq {\varvec{H}}\), if \(\varPi (M)\) is non-empty, then M satisfies condition (C) of Proposition 2.
-
H2
For every construction V, \(\varPi (\psi (V))\) is a vertex \(\{v\}\) of \(\mathcal{G}({\varvec{H}})\), and for every \(Y\in {\varvec{H}}\backslash \psi (V)\), we have \(v \not \in \pi _Y\). Conversely, every vertex of \(\mathcal{G}({\varvec{H}})\) is obtained as \(\varPi (\psi (V))\) for some construction V.
We take four steps in order to come up with the desired isomorphism.
A) The poset of (non-empty) faces of a simple polytope is isomorphic to an abstract simplicial complex.
This is well-known, but since we want to express our isomorphisms explicitly, we briefly review this correspondence. We start by some observations on polytopes (not necessarily simple). In any polytope, we have (cf. [23], Propositions 2.3 and 2.2):
-
Every face of a polytope is the convex hull of its vertices.
We shall exploit two consequences of this property.
-
P1
The map which associates with a face the set of all vertices that it contains is monotonic and order-reflecting, and by polarity (cf. [23], Sect. 2.3), it follows that the map \(\phi \) defined above is (contravariantly) monotonic and order-reflecting.
-
P2
Every non-empty face contains a vertex.
Let P be a polytope, with vertices \(\{v_1\},\ldots ,\{v_n\}\). By P2, the lattice of faces (minus the empty face) can be written as \(\mathbb {L} = \mathbb {L}_1 \cup \cdots \cup \mathbb {L}_n,\) where \(\mathbb {L}_i\) is the set of faces containing \(v_i\). If the polytope is simple, we know moreover by S2 that \(\phi \) restricts to an order-isomorphism between \(\mathbb {L}_i\) and \(\mathcal{P}(\phi (\{v_i\}))\).
Let us now define an abstract simplicial complex \(\mathbb {N}_P\) associated with P. Recall that a finite abstract simplicial complex (abbreviated here as simplicial complex) is given by specifying a set X, called the support, and subsets \(X_1,\ldots ,X_n\subseteq X\), called the bases, that are pairwise incomparable (w.r.t. inclusion), and are such that \(X=X_1\cup \cdots \cup X_n\). The simplicial complex associated to these data is by definition the set \(\mathcal{P}(X_1)\cup \cdots \cup \mathcal{P}(X_n)\), ordered by inclusion. The complex \(\mathbb {N}_P\) is defined as follows:
-
the support X of \(\mathbb {N}_P\) is the set of facets of P;
-
we take as bases the sets \(\phi (\{v_i\})\), for all \(1\le i\le n\).
Since the local isomorphisms between the \(\mathbb {L}_i\)’s and \(\mathcal{P}(\phi (\{v_i\}))\)’s are restrictions of the same function \(\phi \), it follows that \(\phi \) is an isomorphism from \(\mathbb {L}\) to \(\mathbb {N}_P\). We set \(\mathbb {N}=\mathbb {N}_{\mathcal{G}({\varvec{H}})}\).
B) The poset \(\mathcal{A}({\varvec{H}})\) of constructs of \({\varvec{H}}\) is isomorphic to a simplicial complex.
Indeed, the map \(T\mapsto \psi (T)\backslash \{H\}\) defines an order-isomorphism from \(\mathcal{A}({\varvec{H}})\) to the simplicial complex \(\mathbb {M}\)
-
whose support is \({\varvec{H}}\backslash \{H\}\),
-
and whose bases are the sets \(\psi (V)\backslash \{H\}\), where V ranges over the constructions of \({\varvec{H}}\).
This follows from the observation that any subset of a set satisfying condition (C) of Proposition 2 also satisfies that condition.
C) The complexes \(\mathbb {M}\) and \(\mathbb {N}\) are isomorphic.
Lemma 7
If T is a construct of \({\varvec{H}}\), and if \(X\in {\varvec{H}}\backslash \psi (T)\), then there exists a construction \(V \lessdot T\), such that \(X\in {\varvec{H}}\backslash \psi (V)\).
Proof
By induction on T. Let \(T=Y(T_1,\ldots , T_n)\) (possibly with \(n=0\)). We distinguish two cases:
-
1.
\(X\cap Y=\emptyset \). Then, \(n\ge 1\), and for each \(1\le i\le n\), since \(\psi (T_i)\subseteq \psi (T)\) for each i, we can apply induction to the \(T_i\)’s, and get \(V_i\lessdot T_i\) satisfying the statement relative to \(T_i\), for each i. Let then \(S'\) be an arbitrary partial construction spanning Y. By grafting the \(V_i\)’s on the corresponding occurrences of \(\varOmega \) of \(S'\), we get a construction \(V\lessdot T\), which satisfies the statement: this is clear for all nodes x coming from the \(V_i\)’s, while all nodes coming from \(S'\), being elements of Y, are such that
 , which implies
, which implies 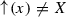 .
. -
2.
\(X\cap Y\ne \emptyset \). Let \(y\in X\cap Y\). By Corollary 1, we can choose a construction \(V\lessdot T\) whose root is decorated by y. Then \(\psi (V)\backslash \{H\} \) consists only of sets that do not contain y, hence none of them can be X.
\(\square \)
Lemma 8
The elements of \({\varvec{H}}\backslash \{H\}\) are in one-to-one correspondence with the facets of \(\mathcal{G}({\varvec{H}})\), through the map \(\chi \) defined by \(\chi (X) = \varPi (\{X\})\).
Proof
We need to show that \(\chi \) is both bijective and well-defined, in the sense that \(\varPi (\{X\})\) is actually a facet. We take the following steps.
-
1.
For all \(X, Y\in {\varvec{H}}\backslash \{H\}\), if \(X\ne Y\), then \(\chi (X)\) is not included in \(\chi (Y)\) (this a fortiori implies that \(\chi \) is injective). Since \(X\ne Y\), we have \(Y\not \in \psi ((H\backslash X)(X))\). Then, by Lemma 7, there exists a construction V such that \(V\le (H\backslash X)(X)\) and \(Y\not \in \psi (V)\). By (H2), we have \(\varPi (\psi (V))=\{v\}\) for some v such that \(v\not \in \pi _Y\), and therefore \(v\not \in \chi (Y)\). On the other hand, \(V\le (H\backslash X)(X)\) implies \(v\in \chi (X)\), which proves the claim.
-
2.
\(\chi (X)\) is a facet, for all X. Suppose that \(\chi (X) \subsetneq F\) for some face F of \(\mathcal{G}({\varvec{H}})\). It follows from Proposition 3 that every face is included in some \(\chi (Y)\) (just pick one of the hyperplanes in the statement). So we have \(F\subseteq \chi (Y)\) for some Y, and a fortiori \(\chi (X)\subseteq \chi (Y)\), from which we deduce \(X=Y\) by (1). But this forces \(\chi (X)=F\), contradicting our assumption.
-
3.
\(\chi \) is surjective. We already observed that every face is included in some \(\chi (Y)\), from which surjectivity follows.
\(\square \)
Lemma 9
A set N of facets belongs to \(\mathbb {N}\) if and only if \(\bigcap N\) is non-empty.
Proof
If \(N\in \mathbb {N}\), then \(N\subseteq \phi (\{v\})\), for some v, by definition of \(\mathbb {N}\). It follows that \(\bigcap \phi (\{v\})\subseteq \bigcap N\). But \(v\in \bigcap \phi (\{v\})\), by definition of \(\phi \), hence \(\bigcap N\) is not empty. Conversely, if \(\bigcap N\) is not empty, then, by (H1) and Proposition 2, \(\{X\!\mid \! \varPi (\{X\})\in N\}=\psi (T)\), for some construct \(T:{\varvec{H}}\). By Corollary 1, we can choose a construction \(V:{\varvec{H}}\), such that \(V\le T\). Moreover, by (H2), \(\varPi (\psi (V))\) is a vertex \(\{v\}\) of \(\mathcal{G}({\varvec{H}})\). Let now \(\chi (X)\) be a facet in N. Then \(X\in \psi (V)\) since \(\psi (T)\subseteq \psi (V)\), and therefore \(\{v\}=\varPi (\psi (V))\subseteq \chi (X)\), and hence \(N\subseteq \phi (\{v\})\). \(\square \)
Proposition 4
The map \(\mathcal{P}(\chi )\) is an isomorphism from \(\mathbb {M}\) to \(\mathbb {N}\).
Proof
By Lemma 8, \(\chi \) is a bijection from the support of \(\mathbb {M}\) to the support of \(\mathbb {N}\). We write \(\chi [M]\) for \(\mathcal{P}(\chi )(M)\), i.e. \(\chi [M]=\{\chi (X)\!\mid \! X\in M\}\). All what we have to do is to check that, for all subsets M of the support of \(\mathbb {M}\), we have \(M\in \mathbb {M}\Leftrightarrow \chi [M]\in \mathbb {N}\). Indeed, by Lemma 9, we have
So we are left to prove that M is of the form \(\psi (T)\backslash H\), for some construct \(T:{\varvec{H}}\), if and only if \(\varPi (M)\) is not empty. The “if” direction follows from (H1), and the “only if” direction follows from (H2) and Corollary 1. \(\square \)
D) \(\mathcal{G}({\varvec{H}})\) is simple.
First, we establish the dimension of \(\mathcal{G}({\varvec{H}})\).
Lemma 10
If H has cardinality \(n+1\), then \(\mathcal{G}({\varvec{H}})\) has dimension n.
Proof
It is enough to prove the statement in the case of the permutohedron, since \(\mathcal{G}({\varvec{H}})\) contains the permutohedron defined by the complete graph on H. Simple calculations prove that the point \((3^{n+1}/n+1,\ldots , 3^{n+1}/n+1)\) lies in \(\pi _H\) and in the interior of \(\pi _Y^+\) for all non-empty \(Y\subsetneq H\), from which one concludes easily. \(\square \)
We prove simplicity via condition S1, as follows. First, the dimension of \( \mathcal{G}({\varvec{H}})\) is \(|H|-1\), by Lemma 10. Second, we note that a construction V has always exactly |H| nodes, hence \(\psi (V)\) has exactly \(|H|-1\) elements different from H. Since, by (H2), every vertex can be written as \(\{v\}=\varPi (\psi (V))\), for some construction V, we conclude by observing that \(\varPi (\psi (V))\) is included by definition in all of the \(|H|-1\) facets \(\chi (X)\), for X ranging over \(\psi (V)\backslash \{H\}\), and in no other facet, by (H2) and Lemma 8.
Thus we can combine steps (A), (B) and (C).
Theorem 1
The map  is an order-isomorphism from \(\mathcal{A}({\varvec{H}})\) to the poset of geometric faces of \(\mathcal{G}({\varvec{H}})\).
is an order-isomorphism from \(\mathcal{A}({\varvec{H}})\) to the poset of geometric faces of \(\mathcal{G}({\varvec{H}})\).
Proof
Combining steps (A) and (C) gives us the isomorphism  . It can be shown that “taking the intersection” is inverse to \(\phi \). Thus we get (incorporating step (B)): \(\phi ^{-1}(\chi [\psi (T)\backslash \{H\}])=\varPi (\psi (T))\). \(\square \)
. It can be shown that “taking the intersection” is inverse to \(\phi \). Thus we get (incorporating step (B)): \(\phi ^{-1}(\chi [\psi (T)\backslash \{H\}])=\varPi (\psi (T))\). \(\square \)
4 Operadic coherences
In [6], Došen and Petrić have used hypergraph polytopes in the study of coherences arising when categorifying the notion of operad [11], i.e., when the axioms of sequential and parallel associativity are turned into coherent isomorphisms \(\beta \) and \(\theta \), the coherence conditions being naturally associated with suitable polytopes. We shall not need the precise definition of an operad, and shall rely instead on simple graphical intuitions.
4.1 Weak Cat-operads
In monoidal categories, a coherence condition is imposed on the associator \(\alpha _{A,B,C}:(A\otimes B)\otimes C\rightarrow A\otimes (B\otimes C)\), ensuring that all the diagrams made of instances of \(\alpha \) (possibly whiskered by identities), and their inverses, commute. This condition is expressed by the commutation of Mac Lane’s pentagon (see diagram (2) on the next page). In an operad, the role of the objects A, B of a monoidal category is now played by operations labelling the nodes of a rooted (non-planar) tree. We call such a tree, acting as a pasting scheme, an operadic tree. Any two neighbouring operations in an operadic tree may be composed (imagine that the edge connecting them is contracted in the process), and then composed with a neigbouring operation, etc. The axioms of operads guarantee that the overall composition of the operations in the tree does not depend on the order of compositions. Consider the two trees with three nodes:

The axiom of sequential (resp. parallel) associativity says that the two ways to build the tree on the left (resp. on the right) by means of grafting and to perform compositions accordingly, yield the same operation: first compose a with b, and then compose with (or insert) c, or first compose b with c and then insert a (resp. first compose a with b, or first compose a with c). In a weak Cat-operad, these identifications are turned into isomorphisms
(writing composition as juxtaposition).
To synthesise the coherence conditions that \(\beta \) and \(\theta \) have to satisfy, we need to consider the four possible shapes of operadic trees with four nodes:

Each of these trees guides the interpretation of parenthesised words such as ((ab)c)d as sequences of insertions, and each of the diagrams below (one for each tree) features the resolution of the critical pair (or overlapping)
interpreted diversely according to whether the associativities are parallel or sequential, as prescribed by the respective trees.


Remark 2
Before asking the question of distinguishing \(\beta \) and \(\theta \) edges in these “operadic polytopes” (and, in general, in operadic polytopes of arbitrary dimension), one must be able to systematically assign them labels. In Sect. 2.6, we have seen various ways to label all the faces of the pentagon and of the hexagon, that would work here for the pentagon made of \(\beta \)-arrows only and the hexagon made of \(\theta \)-arrows only. However, it is a priori not clear how we could do this for the other two mixed \(\beta /\theta \)-diagrams. This question will be addressed in Sect. 4.2.
By “lifting” the methodology of coherence chasing to the 3-dimensional setting, i.e., by considering trees with 5 nodes, we find 9 possible configurations. We shall draw only three of them:

The expression (((ab)c)d)e is now subject to a three-fold overlapping,
which is resolved differently for each of the 9 trees, leading to 9 “coherence conditions between coherences” (in a framework where the coherence equations would not hold up to equality), each described by a suitable 3-dimensional polytope.
For the first two trees above, we get the 3-dimensional permutohedron and associahedron, respectively, whose edges all stand for \(\theta \)-arrows in the first case, and \(\beta \)-arrows in the second. For the third one, we get a polytope called the hemiassociahedron, which, as we shall see, also belongs to the family of hypergraph polytopes. In Fig. 1, we labelled some of the vertices of this polytope, matching them with decompositions of our example tree (this matching will be spelled out in Proposition 5).
4.2 Graphs associated with operadic trees
To every rooted tree \(\mathcal{T}\) representing a pasting scheme for operadic operations, Došen and Petrić associate a graph \(\mathbb {G}(\mathcal{T})\), obtained as follows. Its vertices are the edges of \(\mathcal{T}\!\), and two vertices are connected whenever as edges of \(\mathcal{T}\) they share a common vertex.
It is clear that one can identify the edges of \(\mathcal{T}\) with the non-root nodes of \(\mathcal{T}\) (for example, in Fig. 2, there is a bijection mapping x to c, y to d, z to b, and u to e). By this identification, seeing now the nodes of \(\mathbb {G}(\mathcal{T})\) as the non-root nodes of \(\mathcal{T}\), all edges of \(\mathcal{T}\), apart from those stemming from the root, are in \(\mathbb {G}(\mathcal{T})\). All the other edges of \(\mathbb {G}(\mathcal{T})\) are edges witnessing that two edges of \(\mathcal{T}\) are siblings. We record the latter (resp. the former) by representing them with a dashed (resp. solid) line.
The graph \(\mathbb {G}(\mathcal{T})\) is connected and can be represented itself as a tree with some horizontal dashed edges such that, by construction, each dashed horizontal zone is a complete graph all of whose nodes are connected to their father node (if it exists) by solid edges. The nodes of \(\mathbb {G}(\mathcal{T})\) are thus organised in levels. We say that \(\mathbb {G}(\mathcal{T})\) has a root when there is no horizontal dashed layer at the bottom of \({\mathbb G}(\mathcal{T})\).
Figure 2 shows the graph associated to the third tree considered at the end of Sect. 4.1 (z, u are at level 1, and x, y are at level 2).
We insist that the dashed/solid information on the edges of \(\mathbb {G}(\mathcal{T})\) is not part of the graph structure \(\mathbb {G}(\mathcal{T})\): it provides additional data that we shall use to derive both the type (\(\beta \) or \(\theta \)) and (in the case of \(\beta \)) the orientation of all edges of the corresponding polytope (as dictated by \(\mathcal{T}\)).
Recall that, in the language of constructs, vertices are trees whose nodes are all labelled with singletons. An edge E is a tree whose nodes are all singletons, except one, which is a two-element set \(\{u_E,v_E\}\). We will show that \(\mathbb {G}(\mathcal{T})\), together with its bipartition of dashed and solid edges, determines the type (and the orientation) of E. Let us call a min-path of a graph a path of minimum length between two vertices (we will show that in \(\mathbb {G}(\mathcal{T})\) min-paths are always unique). Our criterion is the following:
- \(\dagger \) :
-
If the min-path between \(u_E\) and \(v_E\) in \(\mathbb {G}(\mathcal{T})\) is made only of solid edges, E corresponds to a \(\beta \)-arrow, oriented towards the vertex of E in which the label \(u_E\) appears below the label \(v_E\) if and only if the level of \(u_E\) is inferior to the level of \(v_E \) in \(\mathbb {G}(\mathcal{T})\). Otherwise, E witnesses a \(\theta \)-arrow.
As an example, let us derive the edge information for the mixed pentagon (4), out of the associated graph:

According to the criterion, the orientation of, say, the \(\beta \) edge connecting z(x(y)) and x(y, z) is dictated by the fact that x is below z in \(\mathbb {G}(\mathcal{T})\). The orientation of the \(\theta \) edges is then determined after choosing a starting vertex (one of the three upper vertices).
We now embark on the proof of soundness and completeness of this criterion. We shall formulate the criterion in different ways, and we shall exhibit the relationship between the connectedness properties of \(\mathcal{T}\) and of \(\mathbb {G}(\mathcal{T})\).
We first observe that for any two distinct vertices u, v of \(\mathbb {G}(\mathcal{T})\), exactly one of the following two situations occurs (referring to u, v as edges of \(\mathcal{T}\)):
- \(\bullet \) :
-
Type I: u is above v or conversely.
- \(\bullet \) :
-
Type II: u and v are situated in disjoint branches of a subtree of \(\mathcal{T}\). We will denote by \({ meet}(u,v)\) the node of \(\mathcal{T}\) at which the two branches diverge.
We can reformulate these two situations in \(\mathbb {G}(\mathcal{T})\), without reference to \(\mathcal{T}\):
- \(\bullet \) :
-
Type I: There is a descending path of solid edges (i.e., the level decreases by 1 at each node in the path) from u to v or from v to u (such a path will be called of type I);
- \(\bullet \) :
-
Type II: There exists a path \(p=p_1,u',v',p_2\) from u to v whose parts \(p_1,u'\) and \(v',p_2\) are descending and ascending, respectively (and therefore are made of solid edges only) and which is such that \((u',v')\) is a dashed edge (such a path will be called of type II).
That this indeed is a reformulation is obvious for type I, while for type II, the desired path in \(\mathbb {G}(\mathcal{T})\) is obtained by going down in \(\mathcal{T}\) from (the child vertex of) u all the way down to \(u'\) whose father node is \({ meet}(u,v)\), then through a dashed arrow to the branch carrying \(v'\), and then all the way up to (the child vertex of) v. Conversely, transcribing the path \(p_1,u',v',p_2\) in the language of \(\mathcal{T}\), we find a configuration of type II there.
In the next lemma, we show how to transform any path into a path of type I or II with the same end nodes. The transformations are specified by the following picture:

This specification is then used to define a rewriting system:
when x, y, z are in one of the four configurations at the top of the picture.
Lemma 11
This rewriting system is confluent and terminating. It is complete in the sense that any two paths between the same pair of end points are provably equal by a zigzag of such rewritings, and sound in the sense that any such zigzag always relates two paths with the same endpoints. The normal forms of the rewriting system are the paths of type I or II, and are the min-paths.
Proof
Termination is obvious, since the length decreases by 1 at each step. As for confluence, we list the critical pairs, which all admit immediate solutions (note that the sequence (x, y) solid, (y, z) dashed, (z, u) solid is excluded since one would then have \(x=u\), which contradicts the definition of a path):

That the paths of type I and II are in normal form is also immediate (there is no matching for the left hand sides of our rewriting rules). It remains to check that all normal forms are indeed of one of these two shapes. We proceed by induction on the length of the normal form p. Every path of length 1 is indeed of type I or II. Let now \(p=u,v,p_1\). We can assume by induction that \(p_1\) is of type I or II. There are three cases:
-
(u, v) is solid with v one level up from u. Then \(p_1\) can start neither with a solid edge going down, because then p would visit u twice, nor with a dashed edge, because p would then not be a normal form. Hence \(p_1\) is of type I, and moreover goes up (again because otherwise p would not be a path). Then adding (u, v) in front still results in a path of type I.
-
(u, v) is solid with v one down from u. Then \(p_1\) cannot start with a solid edge going up, since p would not be in normal form. Hence prefixing \(p_1\) with (u, v) yields a path of type I (resp. II) if \(p_1\) was of type I (resp. II).
-
(u, v) is dashed. Then \(p_1\) can start neither with a dashed edge nor with a solid edge going down, as p would then not be in normal form. Hence \(p_1\) has to be of type I, going up, which makes p a path of type II.
We now prove completeness. We have already observed the uniqueness of the paths of type I or II. Since we have established that the normal forms are the paths of type I or II, it follows that all paths in normal form from u to v coincide (notation \(\equiv \)), and we have, for any two paths \(p_1,p_2\) from u to v, and writing \({ nf}(p)\) for the normal form of a path p:
Conversely, the rewriting system leaves the endpoints of the path unchanged at each step, and hence any zigzag maintains this invariant, which establishes soundness.
That every minpath is normal is clear, since any rewriting step decreases the length of a path. For the converse, we use completeness. Suppose that p is normal, but is not a min-path, and let \(p_1\) be a min-path with the same endpoints as p. By completeness, there exists a zigzag between p and \(p_1\), or equivalently, by confluence, p and \(p_1\) have the same normal form. But \({ nf}(p_1)\) has a fortiori a length strictly smaller than \(p={ nf}(p)\): contradiction. \(\square \)
Summing up, the following are characterisations of “being of type I or II”, for two distinct vertices u, v of \(\mathbb {G}(\mathcal{T})\) (or equivalently, two edges u, v of \(\mathcal{T}\)):

Indeed, by Lemma 11, we know that the min-paths are exactly the paths of type I or II, and crossing or not a dashed edge is what distinguishes among min-paths those that are of type II or I, respectively.
Lemma 12
There is a one-to-one correspondence between the subtrees of \(\mathcal{T}\) and the connected subsets of \(\mathbb {G}(\mathcal{T})\).
Proof
The connected subset of \(\mathbb {G}(\mathcal{T})\) corresponding to a subtree \(\mathcal{T}'\) of \(\mathcal{T}\) is precisely \(\mathbb {G}(\mathcal{T}')\). In the other direction, let K be a connected subset of \(\mathbb {G}(\mathcal{T})\). By connectedness, for any u, v in K there exists a path p from u to v that is included in K. By Lemma 11, we know that \({ nf}(p)\) is also included in K. By this observation, through the transcription in \(\mathcal{T}\) of paths of type I or II of \(\mathbb {G}(\mathcal{T})\), we conclude that the subgraph of \(\mathcal{T}\) whose edges are precisely the vertices of K is a subtree. \(\square \)
In what follows, in the context of operadic trees, we shall say that a tree is non-Empty if it contains at least one edge (whence the capital “E”).
Clearly, all operadic trees relevant for describing operadic laws are non-Empty.
Lemma 13
If \(x_1,\ldots ,x_n\) are arbitrary distinct edges of \(\mathcal{T}\), then the following claims hold.
-
1.
By removing \(x_1,\ldots ,x_n\) from \(\mathcal{T}\), we obtain exactly \(n+1\) subtrees of \(\mathcal{T}\).
-
2.
The number k of non-Empty subtrees of \(\mathcal{T}\) obtained in this way is equal to the number of connected components of \(\mathbb {G}(\mathcal{T})\) obtained by removing the vertices \(x_1,\ldots ,x_n\), and \(k\in \{0,\ldots ,n+1\}\).
-
3.
Let \(\mathcal{T}'\) be one of the non-Empty subtrees of \(\mathcal{T}\) obtained by removing \(x_1,\ldots ,\)\(x_n\), and let K be the connected subset of \(\mathbb {G}(\mathcal{T})\) associated with \(\mathcal{T}\) by (2). Then, if y is an edge of \(\mathcal{T}'\) and a vertex of K, we have that \(\mathbb {G}(\mathcal{T}')=K\).
Proof
We consider only the case \(n=1\) (the general case follows easily by induction), and we write x for \(x_1\). Let a and b be the vertices adjacent to x, with a being the child vertex for b.
The first claim is standard: the subtrees obtained after the removal of x are the subtree \(\mathcal{T}_1\) rooted at a and containing all descendants of a, and the subtree \(\mathcal{T}_2\) obtained from \(\mathcal{T}\) by removing all of \(\mathcal{T}_1\). Note that b is a leaf of \(\mathcal{T}_2\).
We prove the other two claims in parallel, by looking at the possible configurations of \(\mathcal{T}\).
If x is the only edge of \(\mathcal{T}\), then \(\mathcal{T}_1\) and \(\mathcal{T}_{2}\) are the vertex a and the vertex b, respectively, and, therefore, \(k=0\). Suppose that x is not the only edge of \(\mathcal{T}\). Then, if x is on the highest level in \(\mathcal{T}\), \(\mathcal{T}_1\) is just the vertex a, while \( \mathcal{T}_2\) is clearly non-Empty, and, hence, \(k=1\). We also get \(k=1\) when x is the unique edge on the first level of \(\mathcal{T}\), in which case \(\mathcal{T}_1\) is non-Empty and \(\mathcal{T}_2\) is just the vertex b. In all other situations, we have \(k=2\).
Let us now prove that k is also the number of connected components of \(\mathbb {G}(\mathcal{T})\) obtained by removing the vertex x. We examine only the case \(k=2\). Let \(K_1=\mathbb {G}(\mathcal{T}_1)\) and \(K_2=\mathbb {G}(\mathcal{T}_2)\). Since \(K_1\) and \(K_2\) are connected and disjoint and \(\mathbb {G}(\mathcal{T})\backslash \{x\}=K_1\cup K_2\), we only have to show that the set of edges of \(\mathbb {G}(\mathcal{T})\backslash \{x\}\) is also the (disjoint) union of sets of edges of \(K_1\) and \(K_2\). For this, we use the fact that the removal of x from \(\mathbb {G}(\mathcal{T})\) involves the removal of all edges of \(\mathbb {G}(\mathcal{T})\) that have x as one of its adjacent vertices. Let e be an edge of \(\mathbb {G}(\mathcal{T})\), with y and z being its adjacent vertices.
Suppose first that e is an edge of \(\mathbb {G}(\mathcal{T})\backslash \{x\}\). We then know that both y and z are different from x, and share a common vertex v when considered as edges of \(\mathcal{T}\). Since \(\mathcal{T}_1\) and \(\mathcal{T}_2\) form a partition of the set of vertices of \(\mathcal{T}\), let us assume, say, that v is a vertex of \(\mathcal{T}_1\). If \(v\ne a\), we can immediately conclude that y and z are edges of \(\mathcal{T}_1\), and, if \(v=a\), then, since both y and z are different from x, it must be the case that v is the parent vertex for both y and z, which also implies that y and z are edges of \(\mathcal{T}_1\). Therefore, y and z are both vertices of \(K_1\), and, hence, e is an edge of \(K_1\).
Conversely, if e is an edge of \(K_1\), then y and z are edges of \(\mathcal{T}_1\), and therefore must both be different from x. Since they share a common vertex in \(\mathcal{T}_1\), and, hence, in \(\mathcal{T}\), we conclude that e is an edge of \(\mathbb {G}(\mathcal{T})\backslash \{x\}\). \(\square \)
The following proposition is only implicit in [6].
Proposition 5
For every operadic tree \(\mathcal{T}\), the constructions of \(\mathbb {G}(\mathcal{T})\) (considered as a hypergraph) are in one-to-one correspondence with the (fully) parenthesised words that denote decompositions of \(\mathcal{T}\).
Proof
To every decomposition/parenthesisation of \(\mathcal{T}\), one can associate a tree each of whose nodes is decorated by an edge of \(\mathcal{T}\): one proceeds from the most internal parentheses to the most external ones, recording each insertion on the way.
Formally, the fully parenthesised words are declared by the syntax \(w:: a \mid \!\!\mid (ww)\), where a ranges over the nodes of \(\mathcal{T}\) (all named with different letters).
Not all words correspond to decompositions of \(\mathcal{T}\). When this is the case, we say that w is admissible for \(\mathcal{T}\) (the precise definition of admissibility can be easily reconstructed from the inductive construction below).
Since we deal with non-Empty trees, our base case is that of a word (ab) corresponding to a single edge operadic tree connecting a and b. Then there is only one decomposition and one construction, hence the statement holds.
Otherwise, we have a word \(w=(w_1w_2)\), where at least one of the words \(w_1\) or \(w_2\) is not reduced to a letter. We proceed by structural induction on w, providing both the decorated tree and the proof that it is indeed a construction. Let us call \(\mathcal{T}_1\), \(\mathcal{T}_2\) the trees decomposed by \(w_1\), \(w_2\), respectively (cf. Lemma 13). Let x be the edge on which \(\mathcal{T}_1\) is grafted on the tree \(\mathcal{T}_2\). We distinguish three cases.
-
1.
If neither \(w_1\) nor \(w_2\) are reduced to a letter, then \(\mathbb {G}(\mathcal{T}_1)\) and \(\mathbb {G}(\mathcal{T}_2)\) are both non-empty, and are the connected components of \(\mathbb {G}(\mathcal{T})\backslash \{x\}\). We can thus apply induction: if \(V_1\) and \(V_2\) are the constructions associated with \(w_1\) and \(w_2\), then we associate \(x(V_1,V_2)\) with \((w_1w_2)\), which is a construction.
-
2.
If \(w_2=a\) is reduced to a letter and \(w_1\) is not reduced to a letter, then \(\mathbb {G}(\mathcal{T}_2)\) is empty, and x is a leaf of \(\mathbb {G}(\mathcal{T})\). We conclude by induction that the tree \(x(V_1)\) associated with \(((w_1)a)\) is a construction.
-
3.
If \(w_1=a\) is reduced to a letter, then \(\mathcal{T}\) is of the form \(a(\mathcal{T}_2)\), i.e. a is the root and has only one child which is the root of \(\mathcal{T}_2\). We conclude by induction that the tree \(x(V_2)\) associated with \((a(w_2))\) is a construction.
Note that case 1 (resp. cases 2 and 3) correspond to the situation where \(k=2\) (resp. \(k=1\)), while the base case is the case where \(k=0\) (in the terminology of Lemma 13).
The converse mapping is defined much in the same way. We observe that, for any \(\mathcal{T}\) (with at least 3 nodes), constructions of \(\mathbb {G}(\mathcal{T})\) can only be of the form x(V) or \(x(V_1,V_2)\). They are of the first (resp. second) form when the node x is either a leaf or the root of \(\mathbb {G}(\mathcal{T})\), (resp. when x is any other node). We can deploy induction on the number of nodes of \(\mathcal{T}\) and map constructions back to parenthesised words. By induction too, we can show that these are inverse transformations. \(\square \)
As an illustration, referring to Fig. 2, (ae)((bd)c) is mapped to z(x(y), u), obtained as follows: the leaf u records ae, while in parallel the leaf y records bd and then x(y) encodes (bd)c and, finally, the last insertion is along z. (Note that, following common practice, in examples, we do not write the most external parentheses.)
We are now in a position to conclude.
Theorem 2
The criterion \((\dagger )\) is sound and complete.
Proof
We write u, v for \(u_E,v_E\). Let \(E'\) be the subtree of E whose root is \(\{u,v\}\) and let K be the connected subset of \(\mathbb {G}(\mathcal{T})\) out of which \(E'\) arises as a construct. Let \(\mathcal{T}'\) be the subtree of \(\mathcal{T}\) that corresponds to K by Lemma 12.
The number of constructions grafted to \(\{u,v\}\) in \(E'\) is the number of connected components of \({\varvec{K}}\backslash \{u,v\}\). By Lemma 13, it is also the number of non-Empty subtrees of \(\mathcal{T}'\) obtained by removing the edges u and v. Moreover, there can be at most 3 such subtrees. Let us now introduce some names.
Let \(\mathcal{T}'_1, \mathcal{T}'_2\) and \(\mathcal{T}'_3\) be the subtrees of \(\mathcal{T}'\) obtained by removing u and v. Let \(I\subseteq \{1,2,3\}\) be such that \(i\in I\) if and only if \(\mathcal{T}'_i\) is non-Empty, and let \(J=\{1,2,3\}\backslash I\). Let, for all \(i\in I\), \(K_i\) be the connected component of \({\varvec{K}}\backslash \{u,v\}\) corresponding to \(\mathcal{T}'_i\), \(V_i\) be the construction of \(K_i\) that is grafted to \(\{u,v\}\) in \(E'\), and \(w_i\) be the decomposition of \(\mathcal{T}'_i\) corresponding to \(V_i\) according to Proposition 5. On the other hand, for all \(j\in J\), \(\mathcal{T}'_j\) is a vertex \(a_j\), and let \(w_j\) be precisely \(a_j\).
By analysing the case \(n=2\) of Lemma 13, we get that \(E'\) determines an (incomplete) decomposition W of \(\mathcal{T}'\), in which the insertions of u and v are the only ones not yet performed, and which has one of the following two shapes:

where \(\{k_1,k_2,k_3\}=I\cup J\), and where the words \(w_{k_i}\) are as defined above. The shape on the left arises in the case when there exists a sequence \(u=x_0,\dots ,x_n=v\) of edges in \(\mathcal{T}'\) such that the child vertex of \(x_{i-1}\) is a parent vertex of \(x_i\), for all \(1\le i \le n\), and the one on the right when there exists a subtree of \(\mathcal{T}'\) that has u and v on different branches. We observe that \(\{u,v\}\) is of type I (resp. of type II) in \(\mathcal{T}'\) (and hence in \(\mathcal{T}\)) if W has the shape on the left (resp. on the right).
Now, if \(V_1\) and \(V_2\) are the vertices of \(P_\mathcal{T}\) adjacent to E, then, in order to get complete decompositions of \(\mathcal{T}'\) corresponding to \(V_1\) and \(V_2\), it remains to add u and v (in a way dictated by \(V_1\) and \(V_2\), respectively) in the sequence of insertions obtained previously from \(E'\). More precisely, if we assume that u is the child of v (resp. v is the child of u) in \(V_1\) (resp. \(V_2\)), then in the decomposition of \(\mathcal{T}'\) guided by \(V_1\) (resp. \(V_2\)), the insertion of v (resp. u) will be applied last. We then conclude by examining the two possible shapes of W.
-
In the type I case, \(V_1\) and \(V_2\) differ only by the subwords \((w_{k_1} w_{k_2})w_{k_3}\) and \(w_{k_1} (w_{k_2}w_{k_3})\), respectively. Hence \(E'\) features a \(\beta \)-arrow. Moreover, the orientation prescribed in the statement of the criterion tells us that the edge should be oriented from \(V_1\) to \(V_2\), given our (arbitrary) choice of placing u under v in our drawing on the left.
-
In the type II case, \(V_1\) and \(V_2\) differ only by the subwords \((w_{k_1} w_{k_2})w_{k_3}\) and \((w_{k_1} w_{k_3})w_{k_2}\), respectively. Hence \(E'\) features a \(\theta \)-arrow.
\(\square \)
We illustrate the constructions of the proof below, with \(E',K,\mathcal{T}'\) as follows:

The subtrees we get after removing u and v from \(\mathcal{T}'\) are

and the corresponding decompositions are
Hence, \(E'\) corresponds to the following decomposition of \(\mathcal{T}'\):

For this example, the vertices \(V_1\) and \(V_2\) adjacent to E induce decompositions (a(bc))((de)(fg)) and a((bc)((de)(fg))), respectively, and E features a \(\beta \)-arrow from \(V_1\) to \(V_2\).
5 Iterated truncations
In this section, we recast the iterated truncations of [14] in our setting. Hypergraph polytopes allow us to describe all the polytopes in the interval between the simplex and the permutohedron. The hypergraph specifies at once all truncations to be made to reach a particular polytope in this interval. But what about truncating a new face that was not present in the original simplex, i.e. a face already obtained as a result of a truncation? We shall build a whole “tree” of polytopes, each polytope in the tree giving rise to a whole interval of truncations which are all its child nodes in the tree. A polytope at distance n of the root will be obtained through n rounds of truncations. The root is occupied by the simplex. Our tree notation for constructs extends to this setting.
5.1 Setting up the scene
Let \(\mathcal{X}\) be a set (whose elements stand for the facets of the initial simplex). All the work will be carried out within \(\mathcal{M}^f(\mathcal{X})\), the set of finite multisets of elements of \(\mathcal{X}\).
Recall that a multiset is a set with multiplicities, for which a convenient notation is that of formal (commutative) sums of elements with strictly positive integers as coefficients. For example, if \(\{y,z\}\subseteq Y\), then \(3z+y\in \mathcal{M}^f(Y)\) is the multiset where y, z have respective multiplicities 1, 3, while all other elements of Y have multiplicity 0. Note that we have written 1y simply as y, but it will be also useful to refrain to do so in the sequel, for the sake of precision. A finite multiset is one in which elements with non-zero multiplicity are in finite number. For every set Y, we have an obvious coercion \(\iota \) from \(\mathcal{P}^f(Y)\) (the set of finite subsets of Y) to \(\mathcal{M}^f(Y)\), given by assigning multiplicity 1 to every element. For example, \(\iota (\{y,z\})= 1y+1z\).
The finite multiset construction gives rise to a monad, whose unit is given by inclusion, and whose multiplication is given by flattening and multiplying and adding multiplicities:
Finally, let us recall that the powerset functor is defined elementwise as follows: if \(f:Y\rightarrow Z\) and if \(Y'\subseteq Y\), then \(\mathcal{P}(f)(Y')=\{f(y')\!\mid \! y'\in Y'\}\). In particular, for \(X\subseteq \mathcal{X}\), we have \(\mathcal{P}(\eta )(X)=\{1x\!\mid \! x\in X\}\).
With this notation, we are ready to describe our rounds of truncation. At each round, we are given
-
a non-empty set \(H\subseteq \mathcal{M}^f(\mathcal{X})\) (whose elements stand for the facets of the polytope that is to be truncated);
-
a hypergraph \({\varvec{H}}^v\) (whose hyperedges stand for the vertices of the same polytope);
-
an atomic and connected hypergraph \({\varvec{H}}^t\) (whose connected subsets give instructions for the truncations to be performed at this round).
We require that \((\cup {\varvec{H}}^v) = H = (\cup {\varvec{H}}^t).\) We also require \({\varvec{H}}^v\) to satisfy the following property:
(P) \(\forall x\in H,\,\exists V\in {\varvec{H}}^v,\, x\in V.\)
The intuition is that \({\varvec{H}}^v\) serves to tame the constructs of \({\varvec{H}}^t\). This is crucial to guarantee that the polytopes that we are building in this way are simple (this is a consequence of ([14], Proposition 9.3). We just recall here that one of the equivalent definitions of simplicity is that the local view from every vertex is that of a simplex, which suggests to ask for every face at round \(n+1\) to be traced to at least one vertex at round n.
To this effect, we modify the definition of construct (and construction) as follows. Constructs are defined exactly as in Sect. 2, except for the root, for which one has to pick, not an arbitrary non-empty subset Y of H, but one which contains the complement of some hyperedge V of \({\varvec{H}}^v\). Unrestricted constructs in the “old sense” will be called plain constructs in this context. Here is the full definition.
Pick an arbitrary subset \(Y\subseteq H\) such that \((H\backslash V)\subseteq Y\) for some \(V\in {\varvec{H}}^v\).
-
If \(Y = H\), then the one node tree decorated with Y, and written Y, is a construct of \({\varvec{H}}^t\) tamed by V.
-
Otherwise, if \({\varvec{H}}^t ,Y \leadsto H_1,\ldots ,H_n\), and if \(T_1,\ldots ,T_n\) are plain constructs of \({\varvec{H}}_1,\ldots ,{\varvec{H}}_n\), respectively, then \(Y(T_1,\ldots ,T_n)\), is a construct of \({\varvec{H}}^t\) tamed by V.
Note that the taming is only performed at the root, and that a construct of \({\varvec{H}}^t\) tamed by V is also a plain construct of \({\varvec{H}}^t\).
We say that a construct of \({\varvec{H}}^t\) is rel to \({\varvec{H}}^v\) if it is tamed by some \(V\in {\varvec{H}}^v\). We denote by \(\mathcal{A}_{{\varvec{H}}^v}({\varvec{H}}^t)\) the set of constructs rel to \({\varvec{H}}^v\), with the induced partial order.
The definition of construction is also slightly modified: it is a tree where all non-root nodes are decorated by singletons, while the root is decorated exactly by the complement of some hyperedge of \({\varvec{H}}^v\).
5.2 Successive rounds of truncations
The initial round of truncations is along the simplex-permutohedron interval. We take:
-
\(H_1=\mathcal{P}(\eta )(\mathcal{X})\),
-
\({\varvec{H}}_1^v=\{\mathcal{P}(\eta )(\mathcal{X}\backslash \{x\})\!\mid \! x\in \mathcal{X}\}\),
-
\({\varvec{H}}_1^t\) is any atomic connected hypergraph on \(H_1\).
In plain words, the carrier \(H_1\) consists of all elements x of \(\mathcal{X}\), considered as multisets 1x, and the hyperedges of \({\varvec{H}}_1^v\) correspond to the vertices of a simplex (recall that the constructions of the hypergraph \(\{\{1x\}\!\mid \! x\in \mathcal{X}\}\) are of the form \(\{1x\}(\ldots ,\{1y\},\ldots )\), where y ranges over \(\mathcal{X}\backslash \{x\}\), cf. Sect. 2.4). Note that the constructs of \({\varvec{H}}_1^t\) rel to \({\varvec{H}}_1^v\) are all the constructs of \({\varvec{H}}_1^t\) (no taming yet).
We explain now how round \(n+1\) is prepared from round n. From \(H_n\subseteq \mathcal{M}^f(\mathcal{X})\), \({\varvec{H}}_n^v\), \({\varvec{H}}_n^t\), we generate a set \(H_{n+1}\subseteq \mathcal{M}^f(\mathcal{X})\) and a hypergraph \( {\varvec{H}}_{n+1}^v\) with carrier \(H_{n+1}\), as follows:
-
The maximal elements of \(\mathcal{A}_{{\varvec{H}}_n^v}({\varvec{H}}_n^t) \backslash \{H_n\}\), which we shall call constrs, are all of the form X(Y), where \(X \cup Y = H_n\), and hence are entirely characterized by Y. We set
$$\begin{aligned} H_{n+1}= \{(\mu _{\mathcal{X}}\circ \iota _{\mathcal{M}^f(\mathcal{X})})(Y)\,|\, (H\backslash Y)(Y) \;\text{ is } \text{ a } \text{ constr } \text{ of }\; {\varvec{H}}_n^t\; \text{ rel } \text{ to }\; {\varvec{H}}_n^v \}. \end{aligned}$$Alternatively, unfolding the definition of construct of \({\varvec{H}}_n^t\) rel to \({\varvec{H}}_n^v\), we have
$$\begin{aligned} H_{n+1}= \{(\mu _{\mathcal{X}}\circ \iota _{\mathcal{M}^f(\mathcal{X})})(Y)\,|\, \exists V\in {\varvec{H}}_n^v\;\, Y\cap V=\emptyset \}. \end{aligned}$$ -
\({\varvec{H}}_{n+1}^v\) is in bijection with the set of constructions of \({\varvec{H}}_n^t\) rel to \({\varvec{H}}_n^v\):
$$\begin{aligned} \begin{array}{rcl} {\varvec{H}}_{n+1}^v&{} = &{} \{ \mathcal{P}(\mu _{\mathcal{X}}\circ \iota _{\mathcal{M}^f(\mathcal{X})})(\psi (T)\backslash \{H_n\}) \, |\, \\ &{}&{} T \;\text{ is } \text{ a } \text{ construction } \text{ of }\; {\varvec{H}}_n^t \;\text{ rel } \text{ to }\; {\varvec{H}}_n^v\} . \end{array} \end{aligned}$$
In summary, \(H_{n+1}\) and the set of hyperedges of \({\varvec{H}}_{n+1}^v\) are in bijection with the set of constrs and the set of constructions of \({\varvec{H}}_n^t\) rel to \({\varvec{H}}_n^v\), respectively.
While \(H_{n+1}\) and \({\varvec{H}}_{n+1}^v\) are induced by the preceding round, the third component \({\varvec{H}}_{n+1}^t\) is freely chosen:
-
\({\varvec{H}}_{n+1}^t\) is any atomic and connected hypergraph having \(H_{n+1}\) as carrier.
Proposition 6
-
1.
\({\varvec{H}}_{n+1}^v\) is indeed a subset of \(\mathcal{P}(H_{n+1})\), and \(\mu _{\mathcal{X}}\circ \iota _{\mathcal{M}^f(\mathcal{X})}\) is bijective on the subsets to which it is applied.
-
2.
At every round, \({\varvec{H}}_n^v\) satisfies property (P).
-
3.
At every round, we have \(H_n\subseteq H_{n+1}\).
Proof
For (1), we refer (mutatis mutandis) to ([14], Sects. 6 and 7). We prove (3) first. In terms of constructs, we have to show that for each \(y\in H_n\), \((H_n\backslash \{y\})(y)\) is a construct rel to \({\varvec{H}}_n^v\), i.e. that there exists V such that \((H_n\backslash \{y\})\supseteq (H\backslash V)\) which is statement (2) (at round n). We now prove (2) at round \(n+1\). Let Y be such that \((H_{n+1}\backslash Y)(Y)\) is a constr of \({\varvec{H}}_n^t\) rel to \({\varvec{H}}_n^v\). By an easy adaptation of the devices described in Sect. 2.7, we can obtain at least one construction V of \({\varvec{H}}_n^t\) rel to \({\varvec{H}}_n^v\) such that \(V\le (H\backslash Y)(Y)\), which entails \(Y\in \psi (V)\).\(\square \)
Remark 3
The use of multisets and of the associated monad structure is not needed for the purpose of describing the family of polytopes arising by iterated truncations of a simplex, but it nicely avoids a combinatorial explosion in terms of nested sets. More precisely, we could take \(H_{n+1}\subseteq \mathcal{P}^n\mathcal{X}\), and avoid any use of \(\iota ,\eta ,\mu \) above, but we would loose a lot in readability. That nothing is lost by using \(\mu \) as a compressing device is precisely what part 1 of Proposition 6 says.
As an illustration, here is how to recast the example of [14][p. 11]. We take \(\mathcal{X}=\{x,y,z,u\}\). We set (up to identification of 1x with x, etc.):
resulting in the following truncation of the 3-dimensional simplex (decorating the vertices as in \({\varvec{H}}_2^v\), by anticipation):

For example, \(\{x,x+y,u\}\) is obtained from the construction \(V= z(y(x),u)\) as prescribed by the specification of \({\varvec{H}}_2^v\): we have
from which we get \(\{x,x+y,u\}\) by applying \(\iota \) elementwise. Notice that the multiplication \(\mu \) is applied silently here, since in fact, at this stage, \(x+y\) stands for an element of \(\mathcal{M}^f(\mathcal{M}^f(X))\), namely the multiset formed by 1x with multiplicity 1 and 1y with multiplicity 1, and indeed we have \(\mu (1(1x)+1(1y))=1x+1y\).
The first round induces
and let the second round be instructed by
This results in the following polytope:

in which the new edge between x and \(x+y\) (created after the first round) has been itself truncated. This induces
Here, say, \(\{x+y,2x+y,u\}\) corresponds to \(\{y,z\}(x(x+y),u)\) (note the use of \(\mu \) on \(x+(x+y)\)).
We could continue and truncate the new edge between the faces x and \(2x+y\), and create the new face \(3x+y\), etc. By Proposition 6, the flattening from \(x+(x+y)\) to \(2x+y\) (or of \(x+(2x+y)\) to \(3x+y\)) incurs no loss of information, provided the traces of the rounds (i.e., the successive pairs of hypergraphs) are recorded.
5.3 The permutohedron-based associahedron
As a more sophisticated example of iterated truncations, we now describe the combinatorics of the family of permutohedron-based associahedra \(\mathbf{PA}_n\), which are polytopes describing the coherences of symmetric monoidal categories (see Figs. 3 and 4). They were introduced in [14], and further studied in [1]. These polytopes are different from the permutoassociahedra \(\mathbf{KP}_n\), which were introduced for the same purpose in [9], and which are not simple polytopes. The reason for this diversity is that different choices of generating isomorphisms lead to different combinatorial/geometrical interpretations of the same coherence theorem.
To stress this difference, the polytopes that we are about to describe have been renamed as simple permutoassociahedra in [1], but we prefer to stick to the original name of permutohedron-based associahedra, which stresses the two rounds of truncations involved.
We take \(\mathcal{X}=\{x_1,\ldots ,x_{n+1}\}\). The first round of truncation is that producing the permutohedron of dimension n, taking as truncation hypergraph the complete graph over \(\mathcal{X}\):
Recall from Sect. 2.6 that all constructs of the permutohedra are filiform. Thus constrs are in bijection with proper subsets of \(\mathcal{X}\) (different from \(\mathcal{X}\)), and the set of constructions is in bijection with the symmetric group \(S_{n+1}\). More precisely, a construction \(x_{\sigma (n+1)}(\ldots (x_{\sigma (2)}(x_{\sigma (1)}))\ldots )\) is encoded as
where \(\sigma \in S_{n+1}.\) This leads us to
We shall write \(x_I=\varSigma _{i\in I}x_i\). The second (and final) round of truncations is defined by
We note that, for each \(V\in {\varvec{H}}_2^v\), \(({\varvec{H}}_2^t)_V\) is the hypergraph specifying the associahedron of dimension \(n-1\) (since the cardinality of each \(x_\sigma \) is n):
(In particular, \(({\varvec{H}}_2^t)_{x_\sigma }\) is connected.)
We now proceed to analyse the poset of constructs of \({\varvec{H}}_2^t\) rel \({\varvec{H}}_2^v\), which is the lattice of faces of \(\mathbf{PA}_n\). As a first step, one sees easily that the constructs of \({\varvec{H}}_2^t\) that start with \(H_2\backslash x_\sigma \) have the form \((H_2\backslash x_\sigma )(S)\), where S is a construct of \(({\varvec{H}}_2^t)_{x_\sigma }\).
Now, recall from Sect. 2.6 that in the setting of associahedra we have a bijective correspondence between (fully) parenthesized words and constructions, which in the present case is guided by the following picture:

Putting these observations together, we have a naming scheme for this particular subset of constructs of \({\varvec{H}}_2^t\) rel \({\varvec{H}}_2^v\), by means of parenthesisations of the word \(x_{\sigma (1)}\ldots x_{\sigma (n+1)}\).
For \(n=3\), this takes care of all 24 pentagons (corresponding to all possible permutations \(\sigma \)) of Fig. 3. For example, if \(\sigma (1)=3, \sigma (2)=1,\sigma (3)=2,\sigma (4)=4\), then the construct \(((H_2\backslash x_\sigma )\cup \{x_3\})(\{x_3+x_1,x_3+x_1+x_2\})\) (which is an edge) is transcribed as \(x_3(x_1x_2x_4)\).
We next introduce our naming device for the remaining edges and faces for \(\mathbf{PA}_3\).
-
Let us set \(a=x_1, b=x_1+x_2, c= x_1+x_2+x_3, d=x_1+x_3\). Then
$$\begin{aligned} \left. \begin{array}{r}(H_2\backslash \{a,b,c\})(b(a,c))\\ (H_2\backslash \{a,c,d\})(d(a,c)) \end{array}\right\} \; \text{ correspond } \text{ to }\; \left\{ \begin{array}{l} (x_1x_2)(x_3x_4)\\ (x_1x_3)(x_2x_4). \end{array}\right. \end{aligned}$$There is an edge between these two vertices, named by \((H_2\backslash \{a,c\})(a,c)\). Here is a way to name it in the style of parenthesized words:
$$\begin{aligned} ((x_1{\varvec{\cdot }}_1)({\varvec{\cdot }}_1x_4)\,,\, ({\varvec{\cdot }}_1\mapsto \{x_2,x_3\})). \end{aligned}$$The notation here is a way to formalise the surjection that maps \(x_1\) to \(x_1\), \(x_2,x_3\) to \({\varvec{\cdot }}_1\), and \(x_4\) to \(x_4\), via its inverse that maps \({\varvec{\cdot }}_1\) to the set of its preimages. Here, \({\varvec{\cdot }}_1\) is a name for the unique non-singleton element of the partition \((\{x_1\},\{x_2,x_3\},\{x_4\})\) of \(\mathcal{X}\), whence the term “surjection”, as under this perspective our map is just the canonical map from \(\mathcal{X}\) to its quotient under the equivalence relation described by the partition. Thus, our notation features a mix of the notation for associahedra and permutohedra, i.e., a mix of parenthesisations and surjections. In this way, we account for all single edges relating two pentagons.
-
We now account for parallel edges between two pentagons, and the corresponding rectangular faces:
$$\begin{aligned} \begin{array}{l} \left. \begin{array}{r} \!\!({\varvec{\cdot }}_1({\varvec{\cdot }}_1(x_3x_4)),({\varvec{\cdot }}_1\!\mapsto \! \{x_1,\!x_2\}))\\ \!\!({\varvec{\cdot }}_1(({\varvec{\cdot }}_1x_3)x_4),({\varvec{\cdot }}_1\!\mapsto \! \{x_1,\!x_2\})) \end{array}\right\} \text{ for } \text{ the } \text{ edge } \left\{ \begin{array}{l} x_1(x_2(x_3x_4)) -x_2(x_1(x_3x_4))\\ x_1((x_2x_3)x_4) - x_2((x_1x_3)x_4) \end{array}\right. \\ \\ \quad ({\varvec{\cdot }}_1({\varvec{\cdot }}_1x_3x_4), ({\varvec{\cdot }}_1\!\mapsto \! \{x_1,\!x_2\}))\;\;\text{ for }\;\; (H_2\backslash \{b,c\})(\{b,c\}) \end{array} \end{aligned}$$and
$$\begin{aligned}\begin{array}{l} \left. \begin{array}{r} \!\!((x_1(x_2{\varvec{\cdot }}_1)){\varvec{\cdot }}_1,({\varvec{\cdot }}_1\!\mapsto \! \{x_3,\!x_4\}))\\ \!\!(((x_1x_2){\varvec{\cdot }}_1){\varvec{\cdot }}_1,({\varvec{\cdot }}_1\!\mapsto \! \{x_3,\!x_4\})) \end{array}\right\} \text{ for } \text{ the } \text{ edge } \left\{ \begin{array}{l} (x_1(x_2x_3))x_4 - (x_1(x_2x_4))x_3\\ ((x_1x_2)x_3)x_4 - ((x_1x_2)x_4)x_3 \end{array}\right. \\ \\ \quad ((x_1x_2{\varvec{\cdot }}_1){\varvec{\cdot }}_1 ,({\varvec{\cdot }}_1\!\mapsto \! \{x_3,\!x_4\}))\;\;\text{ for }\;\; (H_2\backslash \{a,b\})(\{a,b\}). \end{array}\end{aligned}$$ -
We are left with the remaining faces. The eight dodecagons are named by
$$\begin{aligned} ((x_i{\varvec{\cdot }}_1){\varvec{\cdot }}_1{\varvec{\cdot }}_1,({\varvec{\cdot }}_1\mapsto (H_2\backslash \{x_i\}))\text{ and } ({\varvec{\cdot }}_1{\varvec{\cdot }}_1({\varvec{\cdot }}_1 x_i) , ({\varvec{\cdot }}_1\mapsto (H_2\backslash \{x_i\})), \end{aligned}$$standing for \((H_2\backslash \{x_i\})(x_i)\) and \((H_2\backslash \{\sum _{j\ne i}x_j\})(\sum _{j\ne i}x_j)\), respectively, and the 6 octagons by, say:
$$\begin{aligned} ({\varvec{\cdot }}_1({\varvec{\cdot }}_1{\varvec{\cdot }}_2){\varvec{\cdot }}_2,({\varvec{\cdot }}_1\mapsto \{x_1,x_2\},\,{\varvec{\cdot }}_2\mapsto \{x_3,x_4\})). \end{aligned}$$Indeed, this octagon should contain the following four edges (which are sides of four pentagons), for each of which we give the corresponding construct:
$$\begin{aligned}\begin{array}{lll} x_1(x_2x_3)x_4 &{}&{}(H_2\backslash \{a,b,c\})(\{a,c\})(b))\\ x_1(x_2x_4)x_3 &{}&{}(H_2\backslash \{a,b,f\})(\{a,f\})(b))\\ x_2(x_1x_3)x_4 &{}&{}(H_2\backslash \{e,b,c\})(\{e,c\})(b))\\ x_2(x_1x_4)x_3 &{}&{}(H_2\backslash \{e,b,f\})(\{e,f\})(b)), \end{array}\end{aligned}$$where \(a= x_1\), \(b=x_1+x_2\), \(c=x_1+x_2+x_3\), \(e=x_2\), \(f=x_1+x_2+x_4\). The least upper bound of these constructs is \((H_2\backslash \{b\})(b)\), and all that this construct specifies is that we should do the operation b as innermost operation. It is a “Mastermind” kind of partial information:

Note that b, being the sum of two letters, has to be the central node, and that it being the sum of \(x_1\) and \(x_2\) entails that \(?_1\) is \(x_1\) or \(x_2\), and \(?_2\) is \(x_1+x_2+x_3\) or \(x_1+x_2+x_4\). The same information is carried out by our encoding.
Summarising, we have named all the faces of \(\mathbf{PA}_3\) by pairs \((W,\pi )\) consisting of a parenthesised word W over an alphabet made of elements of \(\mathcal{X}\) and special letters \({\varvec{\cdot }}_1,{\varvec{\cdot }}_2,\ldots \), and a mapping \(\pi \) associating a subset of elements of \(\mathcal{X}\) to each \({\varvec{\cdot }}_i\) appearing in W (a more precise description will be given below).
The notation can be systematised in any finite dimension. Let us thus revert back from \(n=3\) to arbitrary n. We shall describe an algorithm transforming any construct \(T=(H_2\backslash Y)(T_1,\ldots , T_p)\) of \({\varvec{H}}_2^t\) rel to \({\varvec{H}}_2^v\) into such a pair \((W,\pi )\). We can write
We can encode the information provided by Y through the following map \(\tilde{\pi }_Y\):
We associate with \(\tilde{\pi }_Y\) the word \(\tilde{w}_Y\) starting with \(|I_1|\) occurrences of the letter \({\varvec{\cdot }}_1\), followed by \(|I_2\backslash I_1|\) occurrences of the letter \({\varvec{\cdot }}_2\),..., ending with \(|[1,n+1]\backslash I_k|\) occurrences of \({\varvec{\cdot }}_{k+1}\). We then perform a bit of “makeup”: we replace in \(\tilde{w}_Y\) all letters \({\varvec{\cdot }}_i\) occurring only once by the unique element of \(\tilde{\pi }_Y(i)\); we also renumber the remaining letters \({\varvec{\cdot }}_j\), and we reindex \(\tilde{\pi }_Y\) accordingly. We denote the new word by \(w_Y\) and the new map by \(\pi _Y\). We call the \(\cdot _j\)’s and the \(x_i\)’s holes and determined letters, respectively. For example, if
then \({\varvec{\cdot }}_1{\varvec{\cdot }}_2{\varvec{\cdot }}_2{\varvec{\cdot }}_2{\varvec{\cdot }}_3{\varvec{\cdot }}_4{\varvec{\cdot }}_4{\varvec{\cdot }}_5{\varvec{\cdot }}_6{\varvec{\cdot }}_6\) becomes
and we have
We complete the makeup by placing parentheses in \(w_Y\):
-
around every subword \({\varvec{\cdot }}_j x_{i_1}\ldots x_{i_l} {\varvec{\cdot }}_{j+1}\) (l may be 0), and, if this applies,
-
around the prefix of \(w_Y\) of the form \(x_{i_1}\ldots x_{i_l} {\varvec{\cdot }}_1\) (\(l>0\)),
-
and around the suffix of \(w_Y\) of the form \({\varvec{\cdot }}_k x_{i_1}\ldots x_{i_l} \) (\(l>0\)).
(with all letters in the \(\ldots \)’s determined). We denote the obtained parenthesised word by \((w_Y\!)^{ st}\) (for standardisartion). We use square brackets for writing the parentheses in \((w_Y\!)^{ st}\), to distinguish them (visually only) from further parentheses that will be induced by \(T_1,\ldots ,T_p\). For our example, we get:
We now examine how to encode the information provided by \(T_1,\ldots ,T_p\). The square brackets in \((w_Y\!)^{ st}\) delimit the zones of \(w_Y\) that correspond to the connected components of \(({\varvec{H}}_2^t)_Y\), which have the form
We examine first the two degenerate cases:
-
\(Y=\emptyset \). Then \(k=0\), and we set by convention \(I_0=\emptyset \), so that \(\pi (1)=\{1,\ldots ,n+1\}\backslash I_0=\{1,\ldots ,n+1\}\). Then \((w_Y\!)^{ st}= w_Y={\varvec{\cdot }}_1\ldots {\varvec{\cdot }}_1\) (with length \(n+1\)), which encodes the maximum face, i.e., the entire polytope.
-
\(Y=x_\sigma \) for some \(\sigma \). Then all sets \(I_1\), \(I_2\backslash I_1\),..., \(\{1,\ldots ,n+1\}\backslash I_k\) are singletons, and we have that \((w_{x_\sigma }\!)^{ st}= w_{x_\sigma }=x_{\sigma (1)}\,\ldots \,x_{\sigma (n+1)}\). This case has been discussed above: we have that \(( {\varvec{H}}_2^t)_Y= ({\varvec{H}}_2^t)_{x_\sigma }\) generates an associahedron, and that the construct T is of the form \((H_2\backslash x_\sigma )(S)\), where S is a construct of \(({\varvec{H}}_2^t)_{x_\sigma }\), determining a parenthesisation of \(w_{x_\sigma }\).
In the non-degenerate cases, if we fix a permutation \(\sigma \) such that \(\emptyset \subsetneq Y\subsetneq x_\sigma \), we have that \((x_\sigma \backslash Y)(T_1,\ldots ,T_p)\) is a construct of \({\varvec{H}}_{x_\sigma }\), hence the data \(T_1\),..., \(T_p\) amount to giving parenthesisations in the p zones delimited by the square parentheses, resulting in a parenthesised word which we denote by \(W_T\). It can be shown easily that the synthesis of \(W_T\) does not depend on the choice of \(\sigma \) such that \(Y\subsetneq x_\sigma \).
Our analysis also identifies the target of the translation associating \(W_T\) and \(\pi _Y\) to \(T=(H_2\backslash Y)(T_1,\ldots , T_p)\). It consists of all pairs \((W,\pi )\), where
-
\(\pi \) is a map from \(\{1,\ldots ,q\}\) to the set of subsets of \(\mathcal{X}\) of cardinality at least 2, for some q,
-
W is a parenthesised word over \(\mathcal{X}\cup \{{\varvec{\cdot }}_1,\ldots ,{\varvec{\cdot }}_{q}\}\) such that, writing \(\overline{W}\) for the word obtained by removing all parentheses from W:
-
each letter \(x_i\) appears at most once in \(\overline{W}\);
-
for all \(i\in \{1,\ldots ,q\}\), all the occurrences of \({\varvec{\cdot }}_i\) appear as a block of length \(|\pi (i)|\) in \(\overline{W}\), and before any occurrence of \({\varvec{\cdot }}_{i+1}\) (if \(i<q\));
-
the sets \(\pi (r)\) (for r ranging over \(\{1,\ldots ,q\}\)) and the singletons \(\{x_i\}\) such that \(x_i\) appears in \(\overline{W}\) form a partition of \(\mathcal{X}\);
-
all the parentheses of W are within the scope of some parentheses of \((\overline{W})^{{ st}}\) (as defined above), and W carries all the parentheses of \((\overline{W})^{{ st}}\).
As an example, in reference to the above example of standardisation,
$$\begin{aligned}{}[x_9 {\varvec{\cdot }}_1]{\varvec{\cdot }}_1[{\varvec{\cdot }}_1(x_3{\varvec{\cdot }}_2)][{\varvec{\cdot }}_2 x_6 {\varvec{\cdot }}_3]{\varvec{\cdot }}_3, \end{aligned}$$respects the last condition. unlike the word \((x_1x_2)({\varvec{\cdot }}_1 {\varvec{\cdot }}_1)\), which is not accepted since \((x_1x_2{\varvec{\cdot }}_1 {\varvec{\cdot }}_1)^{ st}= [x_1x_2{\varvec{\cdot }}_1]{\varvec{\cdot }}_1\).
-
We leave to the reader the proof that the translation is well defined and bijective, and that it is actually an isomorphism, with the target partial order defined as the smallest partial order such that:
-
\((W,\pi )\le (W',\pi )\) if \(W'\) has one pair of parentheses (other than the standard ones) less than W;
-
\((W,\pi )\le (W',\pi ')\), if W inherits the parentheses of \(W'\), and if \(\pi \) is an elementary refinement of \(\pi '\), i.e., \(\pi (1)=\pi '(1),\ldots ,\pi (i-1)=\pi '(i-1)\), \(\pi (i)\cup \pi (i+1)=\pi '(i)\), \(\pi (i+2)=\pi '(i+1),\ldots \), up to makeup.
For example, we have:
We detail the derivation of \({\varvec{\cdot }}_1(({\varvec{\cdot }}_1 x_3)x_4) < {\varvec{\cdot }}_1({\varvec{\cdot }}_1{\varvec{\cdot }}_2){\varvec{\cdot }}_2\): the refinement splits \(\pi '(2)=\{x_3,x_4\}\), yielding the standardised word \({\varvec{\cdot }}_1({\varvec{\cdot }}_1x_3 x_4)\), and because parentheses are inherited, we indeed get \({\varvec{\cdot }}_1(({\varvec{\cdot }}_1 x_3)x_4) \) as a predecessor.
6 Directions for future work
We plan to apply hypergraph polytopes to study other coherence problems. In recent work [3], the first two authors have identified the coherence conditions for categorified cyclic operads, but it is not yet clear what the relevant polytopes are in this setting. The third author is working on giving precise geometric realisations of the polytopes obtained by iterated truncations.
The case of the permutohedron-based associahedra has already been settled in [1].
References
Baralić, D., Ivanović, J., Petrić, Z.: A simple permutoassociahedron. arXiv:1708.02482
Carr, M., Devadoss, S.: Coxeter complexes and graph-associahedra. Topol. Appl. 153(12), 2155–2168 (2006)
Curien, P.-L., Obradović, J.: Categorified cyclic operads. arXiv:1706.06788v2
Devadoss, S.: A realization of graph-associahedra. Discret. Math. 309, 271–276 (2009)
Došen, K., Petrić, Z.: Hypergraph polytopes. Topol. Appl. 158, 1405–1444 (2011). arXiv:1010.5477
Došen, K., Petrić, Z.: Weak Cat-operads. Log. Methods Comput. Sci. 11(1), 1–23 (2015). arXiv:1005.4633v8
Feichtner, E.M., Kozlov, D.N.: Incidence combinatorics of resolutions. Sel. Math. 10, 37–60 (2004)
Feichtner, E.M., Sturmfels, B.: Matroid polytopes, nested sets and Bergman fans. Port. Math. 62, 437–468 (2005)
Kapranov, M.: The permutoassociahedron, Mac Lane’s coherence theorem and asymptotic zones for the KZ equation. J. Pure Appl. Algebra 85(2), 119–142 (1993)
Loday, J.-L., Ronco, M.: Permutads. J. Comb. Theory Ser. A 120(2), 340–365 (2011)
Loday, J.-L., Vallette, B.: Algebraic Operads. Springer, Berlin (2012)
Mac Lane, S.: Categories for the Working Mathematician, 2nd edn. Springer, Berlin (1978)
Milgram, R.J.: Iterated loop spaces. Ann. Math. 2(84), 386403 (1966)
Petrić, Z.: On stretching the interval simplex-permutohedron. J. Algebraic Comb. 39, 99–125 (2014)
Postnikov, A., Reiner, V., Williams, L.: Faces of generalized permutohedra. Doc. Math. 13, 207–273 (2008)
Postnikov, A.: Permutohedra, associahedra, and beyond. Int. Math. Res. Not. IMRN 2009, 1026–1106 (2009)
Shnider, S., Sternberg, S.: Quantum Groups: From Coalgebras to Drinfeld Algebras Graduate Texts in Mathematical Physiscs. International Press, Vienna (1994)
Stasheff, J.D.: From operads to “physically” inspired theories, operads: proceedings of renaissance conferences. In: Loday, J.-L., Stasheff, J.D., Voronov, A.A. (eds.) Contemporary Math, vol. 202, pp. 53–81. American Mathematical Society Publications, Washington, DC (1997)
Stasheff, J.D.: Homotopy associativity of H-spaces. Trans. Am. Math. Soc. 108, 275–312 (1963)
Tonks, A.: Relating the associahedron and the permutohedron. In: Loday, J.-L., Stasheff J.D., Voronov A.A. (eds.) Operads: Proceedings of Renaissance Conferences (Hartford, CT/Luminy, 1995). Contemporary Mathematics, vol. 202, pp. 33–36. American Mathematical Society, Providence, RI (1997)
Williams, F.D.: Higher homotopy-commutativity. Trans. Am. Math. Soc. 139, 191206 (1969)
Zelevinsky, A.: Nested complexes and their polyhedral realizations. Pure Appl. Math. Q. 2, 655–671 (2006)
Ziegler, G.: Lectures on Polytopes, 2nd edn. Springer, Berlin (1998)
Acknowledgements
The authors wish to thank Zoran Petrić and our deeply missed colleague Kosta Došen (1954–2017) for enlightening discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Tim Porter.
Rights and permissions
About this article
Cite this article
Curien, PL., Obradović, J. & Ivanović, J. Syntactic aspects of hypergraph polytopes. J. Homotopy Relat. Struct. 14, 235–279 (2019). https://doi.org/10.1007/s40062-018-0211-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-018-0211-9





 are the connected components of
are the connected components of 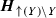 , where Y is the label of the node, and
, where Y is the label of the node, and  is such that
is such that 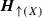 is connected.
is connected.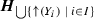 is not connected.
is not connected. is a proper antichain,
is a proper antichain,  is not connected.
is not connected. , which implies
, which implies 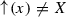 .
.


