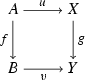Frobenius pairs in abelian categories

Abstract

We revisit Auslander–Buchweitz approximation theory and find some relations with cotorsion pairs and model category structures. From the notion of relative generators, we introduce the concept of left Frobenius pairs $({\mathcal {X}},\omega )$ in an abelian category ${\mathcal {C}}$. We show how to construct from $({\mathcal {X}},\omega )$ a projective exact model structure on ${\mathcal {X}}^\wedge$, the subcategory of objects in ${\mathcal {C}}$ with finite ${\mathcal {X}}$-resolution dimension, via cotorsion pairs relative to a thick subcategory of ${\mathcal {C}}$. We also establish correspondences between these model structures, relative cotorsion pairs, Frobenius pairs, and Auslander–Buchweitz contexts. Some applications of this theory are given in the context of Gorenstein homological algebra, and connections with perfect cotorsion pairs, covering subcategories and cotilting modules are also presented and described.

1 Introduction

The study of relative homological dimensions, obtained by replacing the projective or injective modules by certain subcategories of an abelian category, was initiated by Eilenberg and Moore in [12], which was the starting point for what is nowadays called relative homological algebra. Several years later, an important branch of relative homological algebra was developed by Auslander and Buchweitz in their paper [2]. The concepts and results in this seminal work comprise what is usually known as Auslander–Buchweitz approximation theory (to which we refer as “AB theory”, for short), which roughly speaking consists of methods for obtaining (pre-)covers and (pre-)envelopes, that is, right and left approximations, from generators and cogenerators of a full subcategory of an abelian category. These methods allowed Auslander and Buchweitz to prove, among other results, that for every finitely generated left R-module N (with R a commutative noetherian Cohen–Macaulay ring) there exists a maximal Cohen–Macaulay left R-module M which is mapped onto N and such that any other surjection from a maximal Cohen–Macaulay module onto N factors over it; in other words, N has a maximal Cohen–Macaulay pre-cover. Recently, H. Holm reproves this result in [28] for Cohen–Macaulay local rings, showing that the class of maximal Cohen–Macaulay modules is the left half of a complete and hereditary cotorsion pair in the abelian category of finitely generated modules over such rings. Note that, in these two cases where R is a commutative noetherian Cohen–Macaulay ring or a Cohen–Macaulay local ring, the existence of the mentioned pre-covers and of complete hereditary cotorsion pairs is restricted to a certain subcategory of the left R-modules: those which are finitely generated. Then, the problem of obtaining approximations for modules over such rings is tackled locally . In this paper, we will propose the concept of relative cotorsion pair as a method to find right and left approximations locally in thick subcategories of an abelian category.

It is worth saying that the importance of approximations is not only constrained to the context of modules over Cohen–Macaulay rings, but that it also lies in the fact that the existence of approximations is a prerequisite for computing relative dimensions. For instance, this can be appreciated in Holm’s work [27], where he constructs Gorenstein-projective pre-covers and Gorenstein-injective pre-envelopes for certain modules over an arbitrary ring, from which it is possible to define Gorenstein homological dimensions and Gorenstein derived functors. Holm’s results point out the strong relation between the existence of complete cotorsion pairs and approximations.

In recent years, a powerful machinery for producing approximations via complete cotorsion pairs has been developed by Eklof, Trlifaj, Enochs, Jenda and Göbel in [13, 14, 24]. So it is not surprising that AB theory provides a good setting for investigating relative Gorenstein objects in abelian categories which, as we will prove, are also cofibrant and fibrant objects of certain model categories, a notion that comes from algebraic topology. This last assertion will be a consequence of a one-to-one correspondence between complete cotorsion pairs and model category structures on abelian categories, developed by Hovey in [32] and later generalized by Gillespie in [19] for weakly idempotent complete exact categories. This result, to which we refer as Hovey–Gillespie correspondence, has turned out to be, citing verbatim Gillespie’s words in [20], “a powerful method for constructing model struc tures in algebraic settings and for transporting ideas from topology into algebra”.

The main purpose of this paper is to use AB theory in order to develop, in the general setting provided by an abelian category ${\mathcal {C}}$, the theory of left and right Frobenius pairs, which are concepts we will construct from the notions of generators and cogenerators (in the sense of Auslander and Buchweitz [2]). We will use Frobenius pairs to construct relative cotorsion pairs, seeking to bring the Hovey–Gillespie correspondence between complete cotorsion pairs and model structures to AB theory. Specifically, from a certain type of Frobenius pairs $({\mathcal {X}},\omega )$ in ${\mathcal {C}}$, we will obtain model category structures (to which we will name Auslander–Buchweitz model structures) on the thick subcategory ${\mathcal {X}}^\wedge \subseteq {\mathcal {C}}$ of objects in ${\mathcal {C}}$ with finite resolution dimension relative to ${\mathcal {X}}$. Once we have obtained these model structures, we compute their homotopy categories, aiming to represent the homological algebra made up of generators and cogenerators as certain stable categories. As an application, we will show how several known homotopy categories coming from relative Gorenstein objects, such as Gorenstein-projective, Ding-projective and Gorenstein AC-projective modules (and their duals), can be represented as homotopy categories of Auslander–Buchweitz model structures. This bridge between AB theory and model structures via Frobenius pairs is also related to the notion of Auslander–Buchweitz contexts. We will see how this relation gives rise to generalizations of some methods for constructing approximations in Auslander–Reiten theory and cotilting theory.

This paper is organized as follows. We begin recalling in Sect. 2 some results from AB theory. We also present in Definition 2.5 the notion of (left and right) Frobenius pairs, which constitutes the main subject studied in this work. Later in Sect. 3, we recall the concept of cotorsion pairs in exact categories. In the particular case where ${\mathcal {S}} \subseteq {\mathcal {C}}$ is a thick subcategory, a complete cotorsion pair in ${\mathcal {S}}$ is what we will call in Definition 3.4 an ${\mathcal {S}}$-cotorsion pair (or a cotorsion pair relative to ${\mathcal {S}}$). We provide in Proposition 3.5 an alternative description of ${\mathcal {S}}$-cotorsion pairs, from which we induce such pairs from generators and cogenerators in AB theory. Motivated by the interplay between cotorsion pairs and model categories, we show how to obtain from a strong left Frobenius pair $({\mathcal {X}},\omega )$ tw o compatible and complete cotorsion pairs in the subcategory ${\mathcal {S}}:= {\mathcal {X}}^\wedge$, which are examples of relative cotorsion pairs. We then apply in Sect. 4 the Hovey–Gillespie correspondence to obtain in Theorem 4.1 the main homotopical construction in this paper: the projective Auslander–Buchweitz model structure associated to $(\mathcal {X},\omega )$, that is, an exact model structure on the exact subcategory ${\mathcal {X}}^\wedge \subseteq {\mathcal {C}}$, whose classes of cofibrant, fibrant and trivial objects are given by ${\mathcal {X}}$, ${\mathcal {X}}^\wedge$ and $\omega ^\wedge$, respectively. In Sect. 5 we recall the notion of Auslander–Buchweitz contexts, and present some (one-to-one) correspondences with Frobenius pairs, relative cotorsion pairs, and exact model structures (see Theorems 5.4, 5.11,  5.13, 5.27,  and 5.29). One important application of these correspondences is stated in Proposition 5.20, where we reprove in a categorical context an important theorem by M. Auslander and I. Reiten which establishes a bijective correspondence between basic cotilting modules in ${\mathsf{mod}}(\varLambda )$ (the category of finitely generated left modules over an Artin algebra $\varLambda$), resolving pre-covering subcategories ${\mathcal {F}}\subseteq {\mathsf{mod}}(\varLambda )$ satisfying ${\mathcal {F}}^\wedge = {\mathsf{mod}}(\varLambda )$, and coresolving pre-enveloping subcategories ${\mathcal {G}}\subseteq {\mathsf{mod}}(\varLambda )$ with finite injective dimension. Finally, in Sect. 6 we provide some important applications to appreciate the utility of Frobenius pairs when it comes to interchange properties between homological and homotopical structures appearing in Gorenstein homologica l algebra and representation theory. We also revise some known results on which the theory of Frobenius pairs is motivated. First, we will show how part of the theory of Gorenstein projective, Ding projective and Gorenstein AC-projective modules fits in the context of Frobenius pairs and AB model structures. Some relations with several model structures found by Bravo, Gillespie and Hovey [10, 18, 23, 32] will be commented, along with a couple of open questions (see Propositions 6.1, 6.10 and 6.12). In the more general setting of abelian categories, in Proposition 6.4 we present Gorenstein subcategories, in the sense of Sather-Wagstaff et al. [43], as part of a strong Frobenius pair. Other appealing applications include characterizations of certain special rings. In Proposition 6.13 we will show that a ring R is perfect if, an d only if, the classes of Ding projective and flat R-modules form a left Frobenius pair. For local commutative rings R, we will prove in Corollary 6.6 that R is nonregular, Iwanaga–Gorenstein and artinian if, and only if, R is quasi-Frobenius and with infinite global dimension. At the end of this paper, we will use Gorenstein flat modules and Frobenius pairs to state a characterization for GF-closed rings. Namely, we will prove in Proposition 6.17 that having a GF-closed ring R is equivalent to saying that the classes of Gorenstein flat and flat-cotorsion R-modules form a left Frobenius pair.

1.1 Conventions

Throughout this paper, ${\mathcal {C}}$ will always denote an abelian category, unless otherwise stated. One example of such categories considered in this paper will be the category $\mathsf{Mod}(R)$ of R-modules, where R is an associative ring with unity. By R-modules we will mean left R-modules. In a few occasions, we will consider the category $\mathsf{Mod}(R{}^\mathrm{op})$ of right R-modules. The term “subcategory” will mean a full subcategory. Any class of objects in a category will be thought as a (full) subcategory. Finally, the definitions and results presented in this paper have their corresponding dual statements, which will be omitted for simplicity.

1.2 Notations

The symbol ${\mathcal {X}}\subseteq {\mathcal {C}}$ will mean that ${\mathcal {X}}$ is a class of objects of ${\mathcal {C}}$. On the other hand, $M \in {\mathcal {C}}$ will mean that M is an object of ${\mathcal {C}}$. In the case we are given another subcategory ${\mathcal {Y}}\subseteq {\mathcal {C}}$, then $M \in {\mathcal {Y}}$ and ${\mathcal {X}}\subseteq {\mathcal {Y}}$ have a similar meaning.

2 Auslander–Buchweitz approximation theory, revisited

We start this section by collecting all the background material that will be necessary in the sequel. First, we recall the notions of relative projective dimension and resolution dimension of a given class of objects in an abelian category ${\mathcal {C}}$. Later, we also recall definitions and basic properties we need from AB theory. In all that follows, we are taking as the main reference for consulting approximation theory the paper [2] by Auslander and Buchweitz.

Auslander and Buchweitz, in some of their results in [2], worked with a resolving and additively closed subcategory ${\mathcal {X}}\subseteq {\mathcal {C}}$, which is also closed under direct summands (in ${\mathcal {C}}$). In a very carefully revision of some of these results, one can see that some of these properties assumed for ${\mathcal {X}}$ are not used. In order to give nice applications of AB theory to Gorenstein homological algebra and to more general contexts, we give a review by putting in each statement the minimum needed hypotheses. For instance, subcategories ${\mathcal {X}}\subseteq {\mathcal {C}}$ need not be additive or closed under isomorphisms either, and there are results in which it is not necessary to assume that ${\mathcal {X}}$ is closed under direct summands or resolving.

2.1 Preliminaries from relative homological algebra

Let M and N be two objects of ${\mathcal {C}}$, ${\mathcal {X}}$ and ${\mathcal {Y}}$ be subcategories of an abelian category ${\mathcal {C}}$, and $i > 0$ be a positive integer. We set the following notation:

• 1. Orthogonality relative to Ext: We set $\mathsf{Ext}^i_{{\mathcal {C}}}({\mathcal {X}}, \mathcal {Y}) = 0$ whenever $\mathsf{Ext}^i_{{\mathcal {C}}}(X,Y) = 0$ for every $X \in {\mathcal {X}}$ and $Y \in \mathcal {Y}$. In the cases ${\mathcal {X}}:= \{ M \}$ and ${\mathcal {Y}}:= \{ N \}$, we write $\mathsf{Ext}^i_{{\mathcal {C}}}(M, \mathcal {Y}) = 0$ and $\mathsf{Ext}^i_{{\mathcal {C}}}({\mathcal {X}}, N) = 0$, respectively.

• 2. Relative projective and injective dimensions: We recall from [1, 2, 37] the notions and notations of relative projective and injective dimensions. Denote by $\mathsf{pd}_{{\mathcal {X}}}(M)$ the ${\mathcal {X}}$-projective dimension of M (or the projective dimension of Mrelative to${\mathcal {X}}$), defined as

  $$\begin{aligned} \mathsf{pd}_{{\mathcal {X}}}(M) := \mathrm{inf} \{ n \ge 0 : \mathsf{Ext}^i_{{\mathcal {C}}}(M,{\mathcal {X}}) = 0 \text{ for } \text{ every } i > n \}. \end{aligned}$$

  In the case ${\mathcal {X}}:= {\mathcal {C}}$, we obtain the absolute projective dimension of M, denoted $\mathsf{pd}(M)$. For relative dimensions of a subcategory ${\mathcal {Y}}$, we denote by $\mathsf{pd}_{{\mathcal {X}}}({\mathcal {Y}})$ the ${\mathcal {X}}$-projective dimension of ${\mathcal {Y}}$, defined as

  $$\begin{aligned} \mathsf{pd}_{{\mathcal {X}}}({\mathcal {Y}}) := \mathrm{sup} \{ \mathsf{pd}_{{\mathcal {X}}}(M) : M \in {\mathcal {Y}}\}. \end{aligned}$$

  The notions of ${\mathcal {X}}$-injective dimension of M, injective dimension of M and ${\mathcal {X}}$-injective dimension of${\mathcal {Y}}$ are defined similarly, and denoted by $\mathsf{id}_{{\mathcal {X}}}(M)$, $\mathsf{id}(M)$ and $\mathsf{id}_{{\mathcal {X}}}({\mathcal {Y}})$, respectively. In the case ${\mathcal {X}}:= {\mathcal {C}}$, we just write $\mathsf{pd}({\mathcal {Y}})$ and $\mathsf{id}({\mathcal {Y}})$ for the projective and injective dimension of ${\mathcal {Y}}$, respectively. It can be seen that

  $$\begin{aligned} \mathsf{pd}_{\mathcal {X}}({\mathcal {Y}}) = \mathsf{id}_{\mathcal {Y}}({\mathcal {X}}), \end{aligned}$$

  which turns out to be a very useful property to shift between relative dimensions, and which will be used a lot in the sequel.

• 2. Resolution and coresolution dimension: We recall also from [1, Sect. 1] the notions of resolution and coresolution dimensions. Denote by $\mathsf{resdim}_{{\mathcal {X}}}(M)$ the ${\mathcal {X}}$-resolution dimension of M, that is, the smallest non-negative integer n such that there is an exact sequence

  $$\begin{aligned} {\varvec{\xi }} :0 \rightarrow X_n \rightarrow X_{n-1} \rightarrow \cdots \rightarrow X_1 \rightarrow X_0 \rightarrow M \rightarrow 0 \end{aligned}$$

  with $X_i \in {\mathcal {X}}$ for every $0 \le i \le n$. The sequence ${\varvec{\xi }}$ is said to be a finite ${\mathcal {X}}$-resolution of M. If such n does not exist, we set $\mathsf{resdim}_{{\mathcal {X}}}(M) := \infty$. The ${\mathcal {X}}$-resolution dimension of a subcategory ${\mathcal {Y}}\subseteq {\mathcal {C}}$ is defined as

  $$\begin{aligned} \mathsf{resdim}_{\mathcal {X}}({\mathcal {Y}}) := \mathrm {sup} \{ \mathsf{resdim}_{\mathcal {X}}(Y) : Y \in {\mathcal {Y}}\}. \end{aligned}$$

  Dually, we have the ${\mathcal {X}}$-coresolution dimension of M and ${\mathcal {Y}}$, denoted by $\mathsf{coresdim}_{{\mathcal {X}}}(M)$ and $\mathsf{coresdim}_{{\mathcal {X}}}({\mathcal {Y}})$, respectively. We denote by ${\mathcal {X}}^\wedge$ the full subcategory of objects in ${\mathcal {C}}$ having a finite ${\mathcal {X}}$-resolution. The subcategory ${\mathcal {X}}^\vee$ of objects having a finite ${\mathcal {X}}$-coresolution is defined dually.

The proof of the following lemma, relating the injective and resolution dimensions, can be found in Mendoza and Saenz [37].

Lemma 2.1

For any two subcategories ${\mathcal {X}}, {\mathcal {Y}}\subseteq {\mathcal {C}}$, the equality $\mathsf{id}_{{\mathcal {X}}}({\mathcal {Y}}^\wedge ) = \mathsf{id}_{{\mathcal {X}}}({\mathcal {Y}})$ holds.

• 4. Orthogonal classes: We denote by

  $$\begin{aligned} {\mathcal {X}}^{\perp _i} := \{ N \in {\mathcal {C}}: \mathsf{Ext}^i_{\mathcal {C}}({\mathcal {X}}, N) = 0 \}\quad \text{ and } \quad {\mathcal {X}}^\perp := \bigcap _{i > 0} {\mathcal {X}}^{\perp _i} \end{aligned}$$

  the partial and total right orthogonal subcategories of ${\mathcal {X}}$. Dually, we have the partial and total left orthogonal subcategories of${\mathcal {X}}$, denoted ${}^{\perp _i}{\mathcal {X}}$ and ${}^{\perp }{\mathcal {X}}$, respectively.

• 5. Right and left approximations: The notions of pre-covering and pre-enveloping classes were first introduced, for the category of finitely generated modules over an Artin R-algebra, in [4, p. 81] by Auslander and Smalø, where they are referred to as contravariantly finite and covariantly finite classes, respectively. For a modern and detailed approach to pre-covers and pre-envelopes, we refer the reader to Enochs and Jenda [14, Definitions 5.1.1, 7.1.6]. Although these concepts are presented in [14] for the category $\mathsf{Mod}(R)$ of R-modules, they carry over to the context of abelian categories.

  Recall that a morphism $f :X \rightarrow M$ with $X \in {\mathcal {X}}$ is said to be an ${\mathcal {X}}$-pre-cover (or a right${\mathcal {X}}$-approximation) ofM if for every morphism $f' :X' \rightarrow M$ with $X' \in {\mathcal {X}}$, there exists a morphism $h :X' \rightarrow X$ such that $f' = f \circ h$. If in addition, in the case $X' = X$ and $f' = f$ the equality $f = f \circ h$ can only be satisfied by automorphisms h of X, then the ${\mathcal {X}}$-pre-cover f is called an ${\mathcal {X}}$-cover. Furthermore, an ${\mathcal {X}}$-pre-cover $f :X \rightarrow M$ is special if $\mathrm{CoKer}\,(f) = 0$ and $\mathrm {Ker}\,(f) \in {\mathcal {X}}^{\perp _1}$. A subcategory ${\mathcal {X}}$ is said to be pre-covering if every object of ${\mathcal {C}}$ has an ${\mathcal {X}}$-pre-cover. Similarly, we can define covering and special pre-covering subcategories of ${\mathcal {C}}$. Dually, we have the notions of ${\mathcal {X}}$-pre-envelopes (or left${\mathcal {X}}$-approximations), ${\mathcal {X}}$-envelopes and special${\mathcal {X}}$-pre-envelopes in ${\mathcal {C}}$, along with the corresponding notio ns of pre-enveloping, enveloping and special pre-enveloping subcategories.

• 6. We will frequently consider several closure properties for classes of objects in an abelian or an exact category. Namely, given a class ${\mathcal {X}}$ of objects of ${\mathcal {C}}$, we may ask that: (1) ${\mathcal {X}}$ is closed under direct summands, (2) ${\mathcal {X}}$ is closed under extensions, (3) ${\mathcal {X}}$ is closed under taking kernels of epimorphisms between its objects, or that (4) ${\mathcal {X}}$ is closed under taking cokernels of monomorphisms between its objects. For the reader convenience and simplicity, below we suggest some new terminology for certain special subcategories ${\mathcal {X}}\subseteq {\mathcal {C}}$ which will be employed in a lot of descriptions.

Let us denote by $\mathsf{Proj}({\mathcal {C}})$ and $\mathsf{Inj}({\mathcal {C}})$ the classes of projective and injective objects of ${\mathcal {C}}$, respectively.

Definition 2.2

(subcategories of interest) Let ${\mathcal {X}}$ be a subcategory of ${\mathcal {C}}$. We say that ${\mathcal {X}}$ is a pre-resolving subcategory of ${\mathcal {C}}$ if it is closed under extensions and under taking kernels of epimorphisms between its objects. If in addition $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}$, then ${\mathcal {X}}$ is said to be a resolving subcategory of ${\mathcal {C}}$. If the dual properties hold true, then we get the concepts of pre-coresolving and coresolving subcategory (that is, pre-coresolving + $\mathsf{Inj}({\mathcal {C}}) \subseteq {\mathcal {X}}$).

We say that a pre-resolving subcategory ${\mathcal {X}}$ of ${\mathcal {C}}$ is left thick if it is also closed under direct summands in ${\mathcal {C}}$. Dually, we get the concept of right thick subcategory of ${\mathcal {C}}$. If ${\mathcal {X}}$ is both left and right thick, then ${\mathcal {X}}$ is said to be a thick subcategory of ${\mathcal {C}}$.

We say that a left thick subcategory ${\mathcal {X}}$ of ${\mathcal {C}}$ is left saturated if also $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}$. Dually, we get the concept of right saturated subcategory of ${\mathcal {C}}$. Finally, we say that ${\mathcal {X}}$ is saturated if ${\mathcal {X}}$ is both left and right saturated.

${\mathcal {X}}$ is	Closed under				${\mathcal {X}}$ contains
	Direct smds.	Exts.	Kernels of epis.	Cokernels of monos.	$\mathsf{Proj}({\mathcal {C}})$	$\mathsf{Inj}({\mathcal {C}})$
Pre-resolving		$\checkmark$	$\checkmark$
Resolving		$\checkmark$	$\checkmark$		$\checkmark$
Pre-coresolving		$\checkmark$		$\checkmark$
Coresolving		$\checkmark$		$\checkmark$		$\checkmark$
Left thick	$\checkmark$	$\checkmark$	$\checkmark$
Right thick	$\checkmark$	$\checkmark$		$\checkmark$
Thick	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$
Left saturated	$\checkmark$	$\checkmark$	$\checkmark$		$\checkmark$
Right saturated	$\checkmark$	$\checkmark$		$\checkmark$		$\checkmark$
Saturated	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$

If ${\mathcal {X}}$ is a subcategory of ${\mathcal {C}}$, we will denote by $\mathsf{Thick}^-({\mathcal {X}})$ the smallest left thick subcategory of ${\mathcal {C}}$ that contains ${\mathcal {X}}$. The notations $\mathsf{Thick}^+({\mathcal {X}})$ and $\mathsf{Thick}({\mathcal {X}})$ will have a similar meaning.

Remark 2.3

• 1. The concepts from 1. to 6. have their analogues in the context of exact categories, and as such will be also used in Sects. 3 and 4. For an approach to these notions in additive categories, we recommend Beligiannis [6]. With respect to the ${\mathcal {X}}$-(co)resolution dimension, Beligiannis uses a more general notion of ${\mathcal {X}}$-(co)resolutions in [6, Sect. 2], but with the restriction that such resolutions have to be covariantly (resp., contravariantly) ${\mathcal {X}}$-exact. For our purposes, it will suffice to consider ${\mathcal {X}}$-(co)resolutions as in Angeleri-Hügel and Mendoza [1, Sect. 1]. (Co)resolutions, as considered in this work, coincide with Beligiannis’ in the abelian or exact cases if the subcategory ${\mathcal {X}}$ is pre-covering (resp., ${\mathcal {X}}$ is pre-enveloping). This coincidence occurs, for instance, if ${\mathcal {X}}$ is part of a left Frobenius pair $({\mathcal {X}},\omega )$, where ${\mathcal {X}}$ is pre-covering in ${\mathcal {X}}^\wedge$ (see Definition 2.5 below).

• 2. This paper deals with partial and total orthogonal subcategories, ${}^{\perp _i}{\mathcal {X}}$ and ${}^{\perp }{\mathcal {X}}$ (or ${\mathcal {X}}^{\perp _i}$ and ${\mathcal {X}}^\perp$), separately, especially the case $i = 1$. Other studies on relative homological algebra only consider total orthogonal subcategories (see [6], for instance).

2.2 Fundamental results from AB theory

Keeping in mind the terminology and notation we have presented so far, we are ready to recall the necessary background from AB theory.

Let ${\mathcal {X}}$ and $\omega$ be two subcategories of ${\mathcal {C}}$. It is said that $\omega$ is ${\mathcal {X}}$-injective if $\mathsf{id}_{\mathcal {X}}(\omega ) = 0$. The subcategory $\omega$ is a relative cogenerator in ${\mathcal {X}}$ if $\omega \subseteq {\mathcal {X}}$ and for any $X \in {\mathcal {X}}$ there exists a short exact sequence $0 \rightarrow X \rightarrow W \rightarrow X' \rightarrow 0$ with $W \in \omega$ and $X' \in {\mathcal {X}}$. Dually, we have the notions of ${\mathcal {X}}$-projective subcategories and relative generators in ${\mathcal {X}}$.

Remark 2.4

• ${\mathcal {X}}$-injective relative cogenerators are also known as injective cogenerators or Ext-injecti-ve cogenerators in part of the literature. To avoid confusion with the absolute injective dimension, we have preferred to use the adjective “${\mathcal {X}}$-injective” instead.

• Relative generators and cogenerators are also considered in [6, Definition 2.9] for additive categories, although in a slightly different way. These notions provide the setting to define a sort of Frobenius category in a relative sense. Let us be more specific about this in what follows.

Definition 2.5

Let ${\mathcal {X}}$ and $\omega$ be two subcategories of ${\mathcal {C}}$. We say that $({\mathcal {X}},\omega )$ is a left Frobenius pair in ${\mathcal {C}}$ if the following three conditions are satisfied:

• 1. ${\mathcal {X}}$ is left thick, that is, ${\mathcal {X}}= \mathsf{Thick}^{-}({\mathcal {X}})$.

• 2. $\omega$ is closed under direct summands in ${\mathcal {C}}$.

• 3. $\omega$ is an ${\mathcal {X}}$-injective relative cogenerator in ${\mathcal {X}}$.

If in addition, $\omega$ is also an ${\mathcal {X}}$-projective relative generator in ${\mathcal {X}}$, then we say that $({\mathcal {X}},\omega )$ is a strong left Frobenius pair in ${\mathcal {C}}$.

We refer to the dual concept as (strong) right Frobenius pair, for which we use the notation $(\nu ,{\mathcal {Y}})$, where $\nu \subseteq {\mathcal {Y}}$.

Remark 2.6

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in ${\mathcal {C}}$. Then, ${\mathcal {X}}$ is a Frobenius category in the usual sense, that is, ${\mathcal {X}}$ is an exact category with enough projectives and injectives, where the subcategories of projective and injective objects in ${\mathcal {X}}$ coincide. In this case:

• The exact structure on ${\mathcal {X}}$ is “inherited” from ${\mathcal {C}}$ since ${\mathcal {X}}$ is closed under extensions. Specifically, if $\tau _{{\mathcal {X}}}$ is the class of (admissible) short exact sequences $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ with $A, B, C \in {\mathcal {X}}$, then $({\mathcal {X}},\tau _{{\mathcal {X}}})$ is an exact category.

• The projective = injective objects are given by the objects in $\omega$.

The proof of the following result can be found in Mendoza and Saenz [37, Lemma 2.13]. Part 1. follows by Lemma 2.1, and part 2. is a consequence of Auslander and Buchweitz [2, Lemmas 3.7, 4.3].

Proposition 2.7

Let ${\mathcal {X}}$ and $\omega$ be two subcategories of ${\mathcal {C}}$ such that $\omega$ is ${\mathcal {X}}$-injective. Then, the following conditions hold true:

• 1. $\omega ^\wedge$ is ${\mathcal {X}}$-injective.

• 2. If in addition $\omega$ is a relative cogenerator in ${\mathcal {X}}$ which is closed under direct summands in ${\mathcal {C}}$, then the following equalities hold:

  $$\begin{aligned} \omega&= \{ X \in {\mathcal {X}}: \mathsf{id}_{\mathcal {X}}(X) = 0 \} = {\mathcal {X}}\cap \omega ^\wedge , \end{aligned}$$

  (1)
  $$\begin{aligned} {\mathcal {X}}\cap \omega ^{\vee }&= \{X \in {\mathcal {X}}: \mathsf{id}_{\mathcal {X}}(X) < \infty \}. \end{aligned}$$

  (2)

  Furthermore, we have that $\mathsf{id}_{\mathcal {X}}(M) = \mathsf{coresdim}_\omega (M)$, for every $M \in {\mathcal {X}}\cap \omega ^{\vee }$.

In the following result, the expression $\mathsf{resdim}_\omega (K) = -1$ just means that $K = 0$. A proof can be found in [2, Theorem 1.1]. On the other hand, Holm gives a different proof in [27, Theorem 2.10] in the particular setting where ${\mathcal {X}}$ and $\omega$ are the classes of Gorenstein projective and projective R-modules, respectively (see Sect. 6.1 for more details).

Theorem 2.8

Let ${\mathcal {X}}$ and $\omega$ be subcategories of ${\mathcal {C}}$ such that ${\mathcal {X}}$ is closed under extensions, $0 \in {\mathcal {X}}$, and $\omega$ is a relative cogenerator in ${\mathcal {X}}$. Then, for any $C \in {\mathcal {C}}$ with $\mathsf{resdim}_{\mathcal {X}}(C) = n < \infty$, there exist short exact sequences

$$\begin{aligned} 0&\rightarrow K\rightarrow X\xrightarrow {\varphi } C \rightarrow 0, \end{aligned}$$

(3)

$$\begin{aligned} 0&\rightarrow C \xrightarrow {\varphi '} H \rightarrow X' \rightarrow 0, \end{aligned}$$

(4)

in ${\mathcal {C}}$ with $X, X' \in {\mathcal {X}}$, $\mathsf{resdim}_\omega (K) = n - 1$ and $\mathsf{resdim}_\omega (H) \le n$. Moreover, if $\omega$ is ${\mathcal {X}}$-injective, then the following statements hold true:

• 1. $\varphi :X \rightarrow C$ is an ${\mathcal {X}}$-pre-cover and $K \in {\mathcal {X}}^\perp$.

• 2. $\varphi ' :C \rightarrow H$ is a $\omega ^\wedge$-pre-envelope and $X' \in {}^\perp (\omega ^\wedge )$.

Corollary 2.9

Let ${\mathcal {X}}$ and $\omega$ be two subcategories of ${\mathcal {C}}$ such that ${\mathcal {X}}$ is closed under extensions and direct summands in ${\mathcal {C}}$, and $\omega$ is a relative cogenerator in ${\mathcal {X}}$. If $\mathsf{resdim}_{{\mathcal {X}}}(C) \le 1$ and $C \in {}^{\perp _1}\omega$, then $C \in {\mathcal {X}}$.

Proof

For every $C \in {}^{\perp _1}\omega$ with $\mathsf{resdim}_{{\mathcal {X}}}(C) \le 1$, we have from Theorem 2.8 a short exact sequence as (3), say $0 \rightarrow W \rightarrow X \rightarrow C \rightarrow 0$ with $W \in \omega$ and $X \in {\mathcal {X}}$, which is split since $C \in {}^{\perp _1}\omega$. Hence, $C \in {\mathcal {X}}$ since ${\mathcal {X}}$ is closed under direct summands. $\square$

The following result, whose proof can be found in [2, Proposition 2.1], relates the concepts of relative projective and resolution dimensions for relative injective cogenerators.

Theorem 2.10

Let ${\mathcal {X}}\subseteq {\mathcal {C}}$ be a subcategory closed under extensions and direct summands in ${\mathcal {C}}$, and $\omega \subseteq {\mathcal {C}}$ be an ${\mathcal {X}}$-injective relative cogenerator in ${\mathcal {X}}$ that is closed under direct summands in ${\mathcal {C}}$. Then, the equality

$$\begin{aligned} \mathsf{pd}_{\omega ^{\wedge }}(C) = \mathsf{pd}_{\omega }(C) = \mathsf{resdim}_{{\mathcal {X}}}(C) \end{aligned}$$

holds for every object $C\in {\mathcal {X}}^{\wedge }$.

So far the reader may have already noticed that for any left Frobenius pair $({\mathcal {X}},\omega )$ in ${\mathcal {C}}$, the subcategories ${\mathcal {X}}^\wedge$ and $\omega ^\wedge$ have special properties related to the existence of approximations, and so to the computation of relative projective and injective dimensions. The former subcategory will turn out to be an exact subcategory of ${\mathcal {C}}$ in which we will get cotorsion pairs and model structures involving the subcategory ${\mathcal {X}}^\wedge$ itself, along with $\omega ^\wedge$. For this reason, it is important to devote the rest of this section recalling some descriptions of ${\mathcal {X}}^\wedge$ and $\omega ^\wedge$, from which one can deduce, among other things, that ${\mathcal {X}}^\wedge$ is indeed exact.

In what follows, given a class ${\mathcal {X}}\subseteq {\mathcal {C}}$ of objects of ${\mathcal {C}}$, we will denote by $\mathsf{add}\,({\mathcal {X}})$ the subcategory of all objects isomorphic to direct summands of finite direct sums of objects in ${\mathcal {X}}$. The following two results can be found in [2, Propositions 3.4, 3.5 and 3.6].

Theorem 2.11

Let ${\mathcal {X}}\subseteq {\mathcal {C}}$ be a pre-resolving subcategory and $\omega \subseteq {\mathcal {C}}$ be an ${\mathcal {X}}$-injective relative cogenerator in ${\mathcal {X}}$. Then, the following conditions hold true:

• 1. ${\mathcal {X}}^{\wedge }$ is the smallest pre-resolving and pre-coresolving subcategory of ${\mathcal {C}}$ containing ${\mathcal {X}}$.

• 2. If $\omega$ and ${\mathcal {X}}$ are closed under direct summands, then $\mathsf{add}\,({\mathcal {X}}^\wedge ) = {\mathcal {X}}^\wedge$.

In particular, if $({\mathcal {X}},\omega )$ is a left Frobenius pair, then ${\mathcal {X}}^\wedge = \mathsf{Thick}\,({\mathcal {X}})$.

Remark 2.12

It follows from the previous theorem that if $({\mathcal {X}},\omega )$ is a left Frobenius pair in ${\mathcal {C}}$, then ${\mathcal {X}}^\wedge$ is an exact category with the class of admissible short exact sequences given by $\tau _{{\mathcal {X}}^\wedge }$ (see Remark 2.6 above).

Proposition 2.13

Let ${\mathcal {X}}$ and $\omega$ be subcategories of ${\mathcal {C}}$ such that ${\mathcal {X}}$ is closed under extensions and $\omega$ is closed under direct summands in ${\mathcal {C}}$. If $\omega$ is ${\mathcal {X}}$-injective relative cogenerator in ${\mathcal {X}}$, then the equality

$$\begin{aligned} \omega ^\wedge = {\mathcal {X}}^\perp \cap {\mathcal {X}}^\wedge \end{aligned}$$

(5)

holds.

Given a left Frobenius pair $({\mathcal {X}},\omega )$ in ${\mathcal {C}}$, from the previous proposition we can note that the subcategory $\omega ^\wedge$ is closed under direct summands, extensions and cokernels of monomorphisms between its objects. However, $\omega ^\wedge$ is not necessarily closed under kernels of epimorphisms. The following three results sort of measure how far is $\omega ^\wedge$ from being thick.

Proposition 2.14

The equalities

$$\begin{aligned} {\mathcal {X}}^\wedge \cap {}^{\perp }\omega&= {\mathcal {X}}= {\mathcal {X}}^\wedge \cap {}^\perp (\omega ^\wedge ). \end{aligned}$$

(6)

hold for every left Frobenius pair $({\mathcal {X}},\omega )$ in ${\mathcal {C}}$.

Proof

By part 1. in Proposition 2.7, we know that ${\mathcal {X}}\subseteq {}^\perp \omega$ and ${\mathcal {X}}\subseteq {}^\perp (\omega ^\wedge )$. We assert that ${\mathcal {X}}^{\wedge } \cap {}^{\perp }(\omega ^{\wedge }) \subseteq {\mathcal {X}}$. Indeed, let $C \in {\mathcal {X}}^{\wedge } \cap {}^{\perp }(\omega ^{\wedge })$. Then, by Theorem 2.8 there exists a short exact sequence as (3), say $0 \rightarrow C \rightarrow Y \rightarrow X \rightarrow 0$ where $X \in {\mathcal {X}}\subseteq {}^\perp (\omega ^{\wedge })$ and $Y \in \omega ^{\wedge }$. Since $C \in {}^\perp (\omega ^{\wedge })$, it follows that $Y \in {}^\perp (\omega ^{\wedge })$. Now using Theorem 2.10, we get that $\mathsf{resdim}_{{\mathcal {X}}}(Y) = \mathsf{pd}_{\omega ^{\wedge }}(Y) = 0$, and thus $Y \in {\mathcal {X}}$. Hence, $C \in {\mathcal {X}}$ since ${\mathcal {X}}$ is pre-resolving. The inclusion ${\mathcal {X}}^{\wedge } \cap {}^{\perp }\omega \subseteq {\mathcal {X}}$ follows similarly. $\square$

We get a description of the subcategory $\mathsf{Thick}(\omega )$.

Theorem 2.15

Let ${\mathcal {X}}$ be a pre-resolving subcategory of ${\mathcal {C}}$, and $\omega \subseteq {\mathcal {C}}$ be an ${\mathcal {X}}$-injective relative cogenerator in ${\mathcal {X}}$. Then, the equality

$$\begin{aligned} (\omega ^\wedge )^\vee = \{ C \in {\mathcal {X}}^\wedge : \mathsf{id}_{{\mathcal {X}}}(C) < \infty \} \end{aligned}$$

(7)

holds. If in addition, ${\mathcal {X}}$ and $\omega$ are closed under direct summands in ${\mathcal {C}}$, then the equality

$$\begin{aligned} \mathsf{Thick}(\omega ) = (\omega ^\wedge )^\vee \end{aligned}$$

(8)

is also true.

Proof

The equality (7) follows by [2, Proposition 4.2]. To show (8), first note by Theorem 2.11 that ${\mathcal {X}}^\wedge = \mathsf{Thick}({\mathcal {X}})$, and thus $(\omega ^\wedge )^\vee = \{ C \in {\mathcal {X}}^\wedge : \mathsf{id}_{{\mathcal {X}}}(C) < \infty \}$ is a thick subcategory of ${\mathcal {C}}$. Now assume that ${\mathcal {B}}$ is a thick subcategory of ${\mathcal {C}}$ containing $\omega$. Since ${\mathcal {B}}$ is closed under cokernels of monomorphisms in ${\mathcal {B}}$, it follows that $\omega ^\wedge \subseteq {\mathcal {B}}$, which in turn implies, using now that ${\mathcal {B}}$ is closed under kernels of epimorphisms in ${\mathcal {B}}$, that $(\omega ^\wedge )^\vee \subseteq {\mathcal {B}}$. Therefore, (8) follows. $\square$

The next theorem is originally due to Auslander, Buchweitz and Reiten [2, 3]. The statement given below is a simplification of the one given in [26, Theorem 1.12.10] by M. Hashimoto, and adapted to our terminology and notation.

Theorem 2.16

Let ${\mathcal {X}}\subseteq {\mathcal {C}}$ be a left thick subcategory of ${\mathcal {C}}$, and ${\mathcal {Y}}\subseteq {\mathcal {C}}$ be a right thick subcategory of ${\mathcal {C}}$ contained in ${\mathcal {X}}^\wedge$, such that $\omega := {\mathcal {X}}\cap {\mathcal {Y}}$ is an ${\mathcal {X}}$-injective relative cogenerator in ${\mathcal {X}}$. Then, the following equalities hold:

$$\begin{aligned} {\mathcal {Y}}= \omega ^\wedge = {\mathcal {X}}^\wedge \cap {\mathcal {X}}^\perp = {\mathcal {X}}^\wedge \cap {\mathcal {X}}^{\perp _1} = \{ C \in {\mathcal {X}}^\wedge \cap \omega ^\perp : \mathsf{id}_{{\mathcal {X}}}(C) < \infty \}. \end{aligned}$$

Proof

We split the proof into several parts.

• By Proposition 2.13, we have the equality $\omega ^\wedge = {\mathcal {X}}^\wedge \cap {\mathcal {X}}^\perp$.

• We now show that $\omega ^\wedge = {\mathcal {Y}}$. Indeed, since $\omega \subseteq {\mathcal {Y}}$ we have that $\omega ^\wedge \subseteq {\mathcal {Y}}^\wedge$, and since ${\mathcal {Y}}$ is pre-coresolving we obtain ${\mathcal {Y}}^\wedge = {\mathcal {Y}}$. Thus, the inclusion $\omega ^\wedge \subseteq {\mathcal {Y}}$ follows. Now let $Y \in {\mathcal {Y}}$. Knowing that ${\mathcal {Y}}\subseteq {\mathcal {X}}^\wedge$, we get a short exact sequence as (3) in Theorem 2.8, say

  $$\begin{aligned} 0 \rightarrow K \rightarrow X \rightarrow Y \rightarrow 0 \end{aligned}$$

  with $X \in {\mathcal {X}}$ and $K \in \omega ^\wedge \subseteq {\mathcal {Y}}$. Since ${\mathcal {Y}}$ is closed under extensions, we have that $X \in {\mathcal {X}}\cap {\mathcal {Y}}=: \omega$. It follows that $Y \in \omega ^\wedge$, that is, ${\mathcal {Y}}\subseteq \omega ^\wedge$. So far, we have proven the equalities ${\mathcal {Y}}= \omega ^\wedge = {\mathcal {X}}^\wedge \cap {\mathcal {X}}^\perp$.

• For the third equality ${\mathcal {X}}^\wedge \cap {\mathcal {X}}^\perp = {\mathcal {X}}^\wedge \cap {\mathcal {X}}^{\perp _1}$, note that the containment ${\mathcal {X}}^\wedge \cap {\mathcal {X}}^\perp \subseteq {\mathcal {X}}^\wedge \cap {\mathcal {X}}^{\perp _1}$ is clear. Now let $C \in {\mathcal {X}}^\wedge \cap {\mathcal {X}}^{\perp _1}$. By Theorem 2.8 (4), there is a short exact sequence

  $$\begin{aligned} 0 \rightarrow C \rightarrow W \rightarrow X \rightarrow 0 \end{aligned}$$

  with $W \in \omega ^\wedge$ and $X \in {\mathcal {X}}$. Since $\mathsf{Ext}^1_{{\mathcal {C}}}(X, C) = 0$, we have that C is a direct summand of $W \in \omega ^\wedge = {\mathcal {Y}}$, and so $C \in {\mathcal {Y}}= {\mathcal {X}}^\wedge \cap {\mathcal {X}}^\perp$. Hence, the equality ${\mathcal {X}}^\wedge \cap {\mathcal {X}}^\perp = {\mathcal {X}}^\wedge \cap {\mathcal {X}}^{\perp _1}$ holds.

• It is only left to prove the equality $\mathcal {Y} = \{ C \in {\mathcal {X}}^\wedge \cap \omega ^\perp : \mathsf{id}_{{\mathcal {X}}}(C) < \infty \}$. Note that we already have ${\mathcal {Y}}\subseteq {\mathcal {X}}^\perp \subseteq \omega ^\perp$, and by the equality (7) in Theorem 2.15 we know that ${\mathcal {Y}}= \omega ^\wedge \subseteq (\omega ^\wedge )^\vee = \{ C \in {\mathcal {X}}^\wedge : \mathsf{id}_{{\mathcal {X}}}(C) < \infty \}$. So it follows that the containment ${\mathcal {Y}}\subseteq \{ C \in {\mathcal {X}}^\wedge \cap \omega ^\perp : \mathsf{id}_{{\mathcal {X}}}(C) < \infty \}$ holds. Now consider an object $M \in {\mathcal {X}}^\wedge \cap \omega ^\perp$ with $\mathrm {id}_{{\mathcal {X}}}(M) = k < \infty$. We use induction on k to prove $M \in {\mathcal {Y}}$. Suppose $k \le 1$. Given $X \in {\mathcal {X}}$, there is a short exact sequence

  $$\begin{aligned} 0 \rightarrow X \rightarrow W \rightarrow X' \rightarrow 0 \end{aligned}$$

  with $W \in \omega$ and $X' \in {\mathcal {X}}$. Then, we have an induced sequence

  $$\begin{aligned} \mathsf{Ext}^1_{{\mathcal {C}}}(W,M) \rightarrow \mathsf{Ext}^1_{{\mathcal {C}}}(X,M) \rightarrow \mathsf{Ext}^2_{{\mathcal {C}}}(X',M) \end{aligned}$$

  of abelian groups where $\mathsf{Ext}^1_{{\mathcal {C}}}(W,M) = 0$ since $M \in \omega ^\perp$ , and $\mathsf{Ext}^2_{{\mathcal {C}}}(X', M) = 0$ since $\mathsf{id}_{{\mathcal {X}}}(M) \le 1$. It follows that $M \in {\mathcal {X}}^\wedge \cap {\mathcal {X}}^{\perp _1} = {\mathcal {Y}}$. Now if $\mathsf{id}_{{\mathcal {X}}}(M) = k$, then in a similar way we can show that $\mathsf{Ext}^{k-1}_{{\mathcal {C}}}(X, M) = 0$ for every $X \in {\mathcal {X}}$. Repeating this procedure, we finally get that $M \in {\mathcal {X}}^{\perp _1}$.

$\square$

3 Relative cotorsion pairs

This section is devoted to present the notion of cotorsion pairs relative to a thick subcategory ${\mathcal {S}}$ of an abelian category ${\mathcal {C}}$. We begin this section recalling the concept of cotorsion pairs in exact categories, and then we introduce the relative ${\mathcal {S}}$-cotorsion pairs as complete cotorsion pairs in ${\mathcal {S}}\subseteq {\mathcal {C}}$. Later, we provide a characterization for this concept which, along with the results presented in Sect. 2, allows us to construct relative cotorsion pairs from Frobenius pairs.

The notion of cotorsion pairs was first introduced by Salce in [42]. It is the analog of a torsion pair where the functor $\mathsf{Hom}_{\mathcal {C}}(-,-)$ is replaced by $\mathsf{Ext}^1_{\mathcal {C}}(-,-)$. Roughly speaking, two classes ${\mathcal {A}}$ and ${\mathcal {B}}$ of objects in ${\mathcal {C}}$ form a cotorsion pair if they are complete with respect to the orthogonality relation defined by the vanishing of the functor $\mathsf{Ext}^1_{{\mathcal {C}}}(-,-)$.

An important part of the homological algebra done for abelian categories carries over to exact categories, and this can be appreciated in the detailed survey [11] of exact categories written by Bühler. So it is not surprising that the notion of cotorsion pairs, among others, has sense in the context of exact categories (see Definition 3.2).

3.1 Cotorsion pairs in exact categories

Let $({\mathcal {E}}, \tau )$ be an exact category, that is, an additive category ${\mathcal {E}}$ with a class $\tau$ of admissible short exact sequences satisfying a series of axioms (as in Bühler [11]). Given two objects $A, C \in {\mathcal {E}}$, we denote by $\mathsf{Ext}^1_{\tau }(C, A)$ the collection of equivalence classes of admissible short exact sequences

$$\begin{aligned} {\varvec{\varepsilon }} :0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0 \end{aligned}$$

in $\tau$, where the zero element is given by the class of the split exact sequence

$$\begin{aligned} 0 \rightarrow A \rightarrow A \oplus C \rightarrow C \rightarrow 0. \end{aligned}$$

Every morphism $A \rightarrow B$ appearing in short exact sequences in $\tau$, as ${\varvec{\varepsilon }}$, is called an admissible monomorphism. Dually, we have the admissible epimorphisms. The collection of i-extensions $\mathsf{Ext}^i_{\tau }(C,A)$ has a similar description, and the reader can check Sieg’s thesis [44, Chapter IV] for a detailed explanation. For any class ${\mathcal {X}}$ of objects of ${\mathcal {E}}$, we denote its orthogonal subcategories with respect to $\mathsf{Ext}^1_{\tau }(-,-)$ by ${\mathcal {X}}^{\perp _{1,\tau }}$, ${}^{\perp _{1,\tau }}{\mathcal {X}}$, which are defined in the same way as in the context of abelian categories. Recall that an object $I \in {\mathcal {E}}$ is $\tau$-injective if any admissible monomorphism $I \rightarrow B$ splits, or equivalently, if $\mathsf{Ext}^1_{\tau }({\mathcal {E}},I) = 0$. $\tau$-Projective objects in ${\mathcal {E}}$ have a dual description. An exact category $({\mathcal {E}},\tau )$ is said to have enough$\tau$-injectives if for every object $X \in {\mathcal {E}}$ there exists an admissible monomorphism $X \rightarrow I$, where I is a $\tau$-injective object of ${\mathcal {E}}$. If ${\mathcal {E}}$ satisfies the dual property, ${\mathcal {E}}$ is said to have enough$\tau$-projectives. We will denote by $\mathsf{Proj}({\mathcal {E}})$ the class of $\tau$-projective objects of ${\mathcal {E}}$. Note that $\mathsf{Proj}({\mathcal {E}}) = {}^{\perp _{1,\tau }}{\mathcal {C}}$. The next example presents the main two exact categories that we will be using in the sequel.

Example 3.1

Let ${\mathcal {C}}$ be an abelian category.

• 1. ${\mathcal {C}}$ is exact with $\tau$ formed by the family of all short exact sequences in ${\mathcal {C}}$. Note that in this case, $\mathsf{Proj}({\mathcal {C}})$ is the class of projective objects of ${\mathcal {C}}$.

• 2. Let ${\mathcal {Y}}\subseteq {\mathcal {C}}$ be a subcategory of ${\mathcal {C}}$ that is closed under extensions. Then, ${\mathcal {Y}}$ is an exact subcategory of ${\mathcal {C}}$, with the exact structure $({\mathcal {Y}},\tau _{{\mathcal {Y}}})$ from Remark 2.6. In this case, for any ${\mathcal {X}}\subseteq {\mathcal {C}}$, we denote the orthogonal subcategories by ${}^{\perp _{1,\tau _{{\mathcal {Y}}}}}{\mathcal {X}}= {}^{\perp _{1,{\mathcal {Y}}}}{\mathcal {X}}$ and ${\mathcal {X}}^{\perp _{1,\tau _{{\mathcal {Y}}}}} = {\mathcal {X}}^{\perp _{1,{\mathcal {Y}}}}$. Note that

  $$\begin{aligned} {}^{\perp _{1,{\mathcal {Y}}}}{\mathcal {X}}= {}^{\perp _1}{\mathcal {X}}\cap {\mathcal {Y}}\quad \text{ and } \quad {\mathcal {X}}^{\perp _{1,{\mathcal {Y}}}} = {\mathcal {X}}^{\perp _1} \cap {\mathcal {Y}}. \end{aligned}$$

  In the particular case where ${\mathcal {Y}}:= {\mathcal {S}}$ is a thick subcategory of ${\mathcal {C}}$, we have that ${\mathcal {S}}$ is also an exact category. However, ${\mathcal {S}}$ is not necessarily abelian. In fact, ${\mathcal {S}}$ is abelian if, and only if, ${\mathcal {S}}$ is an admissible subcategory of ${\mathcal {C}}$, in the sense of Marcos et al. [35, Proposition 2.3].

We recall the concept of cotorsion pairs in exact categories, due to Krause and Solberg [34].

Definition 3.2

Let $({\mathcal {E}}, \tau )$ be an exact category. Two subcategories ${\mathcal {F}}$ and ${\mathcal {G}}$ of ${\mathcal {E}}$ are said to form a cotorsion pair$(\mathcal {F,G})$ in ${\mathcal {E}}$ if ${\mathcal {F}}= {}^{\perp _{1,\tau }}{\mathcal {G}}$ and ${\mathcal {G}}= {\mathcal {F}}^{\perp _{1,\tau }}$.

A cotorsion pair $(\mathcal {F,G})$ in ${\mathcal {E}}$ is said to be complete if for every object $X \in {\mathcal {E}}$, there exist short exact sequences

$$\begin{aligned} 0 \rightarrow G \rightarrow F \rightarrow X \rightarrow 0 \quad \text{ and } \quad 0\rightarrow X \rightarrow G' \rightarrow F' \rightarrow 0 \end{aligned}$$

with $F, F' \in \mathcal {F}$ and $G, G' \in {\mathcal {G}}$.

Finally, we say that a cotorsion pair $(\mathcal {F,G})$ in ${\mathcal {E}}$ is left hereditary if ${\mathcal {F}}$ is resolving in ${\mathcal {E}}$. Dually, we have the notion of right hereditary cotorsion pair in ${\mathcal {E}}$. A hereditary cotorsion pair in ${\mathcal {E}}$ is a cotorsion pair that is both left and right hereditary.

Proposition 3.3

Let $({\mathcal {F}},{\mathcal {G}})$ be a cotorsion pair in an exact category $({\mathcal {E}},\tau )$ with enough $\tau$-projectives and $\tau$-injectives. Then, the following conditions are equivalent:

• (a) $(\mathcal {F,G})$ is left hereditary.

• (b) $(\mathcal {F,G})$ is right hereditary.

• (c) $\mathsf{Ext}^2_\tau ({\mathcal {F}},{\mathcal {G}}) = 0$.

• (d) $\mathsf{Ext}^i_\tau ({\mathcal {F}},{\mathcal {G}}) = 0$ for every integer $i \ge 2$.

3.2 Cotorsion pairs relative to thick subcategories

From now on, we focus on a special type of complete cotorsion pairs in a thick subcategory ${\mathcal {S}}$ of an abelian category ${\mathcal {C}}$.

Definition 3.4

Let ${\mathcal {S}}$ be a thick subcategory of an abelian category ${\mathcal {C}}$, and ${\mathcal {F}}$ and ${\mathcal {G}}$ be two subcategories of ${\mathcal {S}}$ (thought as an exact category). We say that $({\mathcal {F}},{\mathcal {G}})$ is a left${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$ if ${\mathcal {F}}= {}^{\perp _{1,{\mathcal {S}}}}{\mathcal {G}}$ and if for every object $S \in {\mathcal {S}}$ there exists a short exact sequence

$$\begin{aligned} 0 \rightarrow G \rightarrow F \rightarrow S \rightarrow 0 \end{aligned}$$

with $F \in {\mathcal {F}}$ and $G \in {\mathcal {G}}$. Similarly, we have the definitions of right${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$. Finally, by an ${\mathcal {S}}$-cotorsion pair$(\mathcal {F,G})$ in ${\mathcal {C}}$ we mean that $(\mathcal {F,G})$ is both a left and right ${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$.

Proposition 3.5

Let ${\mathcal {S}}$, ${\mathcal {F}}$ and ${\mathcal {G}}$ be subcategories of ${\mathcal {C}}$, where ${\mathcal {S}}$ is thick. Then, $({\mathcal {F}},{\mathcal {G}})$ is a left ${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$ if, and only if, the following conditions hold true:

• 1. ${\mathcal {F}}$ and ${\mathcal {G}}$ are subcategories of ${\mathcal {S}}$, and ${\mathcal {F}}$ is closed under direct summands in ${\mathcal {C}}$.

• 2. $\mathsf{Ext}^1_{\mathcal {C}}({\mathcal {F}},{\mathcal {G}}) = 0$.

• 3. For every $S \in {\mathcal {S}}$, there exists an epic ${\mathcal {F}}$-pre-cover $\varphi :F \rightarrow S$ with $\mathrm {Ker}(\varphi ) \in {\mathcal {G}}$.

Proof

The “only if” part is clear. For the “if” part, suppose that ${\mathcal {F}}, {\mathcal {G}}\subseteq {\mathcal {C}}$ satisfy conditions 1., 2. and 3. It is clear that ${\mathcal {F}}\subseteq {}^{\perp _{1,{\mathcal {S}}}}{\mathcal {G}}$. Now let $S \in {}^{\perp _{1,{\mathcal {S}}}}{\mathcal {G}}$ and $\varphi :F \rightarrow S$ as in condition 3. Then, we have that $\mathsf{Ext}^1_{{\mathcal {C}}}(S,\mathrm {Ker}(\varphi )) = 0$, which implies that $\varphi$ splits. It follows that S is a direct summand of $F \in {\mathcal {F}}$, and so we have $S \in {\mathcal {F}}$ by condition 1. Hence the inclusion ${}^{\perp _{1,{\mathcal {S}}}}{\mathcal {G}}\subseteq {\mathcal {F}}$ follows. $\square$

3.3 Relative cotorsion pairs from Frobenius pairs

The characterization of (left and right) ${\mathcal {S}}$-cotorsion pairs given in Proposition 3.5 allows us to construct easily cotorsion pairs from Frobenius pairs. (Recall Definition 2.5). Later on, we will study correspondences between these two notions.

Theorem 3.6

If $({\mathcal {X}},\omega )$ is a left Frobenius pair in ${\mathcal {C}}$, then $({\mathcal {X}},\omega ^\wedge )$ is an ${\mathcal {X}}^\wedge$-cotorsion pair in ${\mathcal {C}}$. Moreover, the equalities $\omega = {\mathcal {X}}\cap \omega ^\wedge$ and $\omega ^\wedge = {\mathcal {X}}^\perp \cap {\mathcal {X}}^\wedge$ from Propositions 2.7 (1) and 2.13 (5) hold true. In particular, $\omega ^\wedge$ is a right thick subcategory of ${\mathcal {C}}$.

Proof

We check conditions 1., 2. and 3. in Proposition 3.5, along with their dual statements, to show that $({\mathcal {X}},\omega ^\wedge )$ is an ${\mathcal {X}}^\wedge$-cotorsion pair in ${\mathcal {C}}$. By Theorem 2.11, ${\mathcal {X}}^\wedge \subseteq {\mathcal {C}}$ is a thick subcategory. On the other hand, we have $\mathsf{id}_{\mathcal {X}}(\omega ^\wedge ) = \mathsf{id}_{\mathcal {X}}(\omega ) = 0$ by Lemma 2.1, and so condition 2. follows. Furthermore, Proposition 2.13 gives us that $\omega ^{\wedge } = {\mathcal {X}}^{\perp } \cap {\mathcal {X}}^{\wedge }$, and hence $\omega ^{\wedge }$ is closed under direct summands. Then, the dual of condition 1. follows, while 1. holds since ${\mathcal {X}}$ is closed under direct summands. Note that condition 3. and its dual hold by Theorem 2.8, and hence we conclude that $({\mathcal {X}},\omega ^\wedge )$ is an ${\mathcal {X}}^\wedge$-cotorsion pair in ${\mathcal {C}}$. $\square$

If we impose an exact condition on $({\mathcal {X}},\omega )$ in the previous theorem, then it is possible to construct another ${\mathcal {X}}^\wedge$-cotorsion pair in ${\mathcal {C}}$.

Theorem 3.7

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in ${\mathcal {C}}$. Then, the following assertions hold true:

• 1. $(\omega ,{\mathcal {X}}^\wedge )$ is a ${\mathcal {X}}^\wedge$-cotorsion pair in ${\mathcal {C}}$.

• 2. $\omega ^\wedge = \mathsf{Thick}(\omega )$.

Proof

For part 1., we check again conditions 1., 2. and 3. in Proposition 3.5, along with their duals statements. Conditions 1. and its dual are straightforward. To show condition 2., it suffices to use Lemma 2.1 and the property $\mathsf{pd}_{{\mathcal {X}}}(\omega ) = 0$, so that we have the equalities $\mathsf{id}_{\omega }({\mathcal {X}}^\wedge ) = \mathsf{id}_{\omega }({\mathcal {X}}) = \mathsf{pd}_{{\mathcal {X}}}(\omega ) = 0$. Moreover, note that the dual of condition 3. is trivial. Finally, for 3. let $Y \in {\mathcal {X}}^\wedge$. By Theorem 3.6, there exists an epimorphism $\beta :X \rightarrow Y$ with $\mathrm {Ker}(\beta ) \in \omega ^\wedge$ and $X \in {\mathcal {X}}$. On the other hand, there exists an epimorphism $p :W \rightarrow X$ with $\mathrm {Ker}(p) \in {\mathcal {X}}$ and $W \in \omega$, since $\omega$ is a relative generator in ${\mathcal {X}}$. By Snake Lemma and the fact that p is epic, we obtain a short exact sequence

$$\begin{aligned} 0 \rightarrow \mathrm {Ker}(p) \rightarrow \mathrm {Ker}(\beta \circ p) \rightarrow \mathrm {Ker}(\beta ) \rightarrow 0, \end{aligned}$$

where $\mathrm {Ker}(p) \in {\mathcal {X}}$ and $\mathrm {Ker}(\beta ) \in \omega ^\wedge \subseteq {\mathcal {X}}^\wedge$. Then, $\mathrm {Ker}(\beta \circ p) \ in {\mathcal {X}}^\wedge$ since ${\mathcal {X}}^\wedge$ is thick. Hence, we have a short exact sequence

$$\begin{aligned} 0 \rightarrow \mathrm {Ker}(\beta \circ p) \rightarrow W \xrightarrow {\beta \circ p} Y \rightarrow 0, \end{aligned}$$

where $W \in \omega$ and $\mathrm {Ker}(\beta \circ p) \in {\mathcal {X}}^\wedge$.

We now focus on showing the equality $\omega ^\wedge = \mathsf{Thick}(\omega )$ in part 2. Indeed, by the equalities (7) and (8) in Theorem 2.15, we have that ${\mathcal {X}}\cap \mathsf{Thick}(\omega ) = \{ X \in {\mathcal {X}}: \mathsf{id}_{{\mathcal {X}}}(X) < \infty \}$. On the one hand, by (2) in Proposition 2.7 we have the equality ${\mathcal {X}}\cap \mathsf{Thick}(\omega ) = {\mathcal {X}}\cap \omega ^\vee$. On the other hand, since $\omega$ is an ${\mathcal {X}}$-projective relative generator in ${\mathcal {X}}$, we can use the dual version of the equality (1) in Proposition 2.7, that is, ${\mathcal {X}}\cap \omega ^\vee = \omega$. Hence, ${\mathcal {X}}\cap \mathsf{Thick}(\omega ) = \omega$ holds. Setting ${\mathcal {Y}}:= \mathsf{Thick}(\omega )$ in Theorem 2.16, it follows that $\omega ^\wedge = \mathsf{Thick}(\omega )$. $\square$

Knowing that a strong left Frobenius pair $({\mathcal {X}},\omega )$ gives rise to the complete cotorsion pair $(\omega ,{\mathcal {X}}^\wedge )$ in the exact category ${\mathcal {X}}^\wedge$, allows us to write $\omega = {}^{\perp _{1,{\mathcal {X}}^\wedge }}({\mathcal {X}}^\wedge )$, and thus proving the following result.

Corollary 3.8

If $({\mathcal {X}},\omega )$ is a strong left Frobenius pair in ${\mathcal {C}}$, then $\omega$ is the subcategory of projective objects in the exact subcategory ${\mathcal {X}}^\wedge \subseteq {\mathcal {C}}$. Moreover, ${\mathcal {X}}^\wedge$ has enough $\tau _{{\mathcal {X}}^\wedge }$-projectives, that is, for every $C \in \mathcal {X}^\wedge$ there exists an epimorphism $W \rightarrow C$ in ${\mathcal {C}}$ with $W \in \omega$ and kernel in ${\mathcal {X}}^\wedge$.

So far we know that the concept of ${\mathcal {S}}$-cotorsion pair is a description of the completeness of cotorsion pairs in ${\mathcal {S}}$. As many complete cotorsion pairs in the literature are hereditary, we will introduce in the next section the corresponding property of “being strongly hereditary” for ${\mathcal {S}}$-cotorsion pairs, and compare it with the standard definition of hereditary cotorsion pairs in ${\mathcal {S}}$ (that is, Definition 3.2).

3.4 Hereditary relative cotorsion pairs

We now study two notions of hereditary cotorsion pairs in the relative context, one of them corresponding to the standard one, and the other one being stronger. These two notions are not always equivalent. Some of the results appearing later on in this work will provide some conditions under which the ${\mathcal {X}}^\wedge$-cotorsion pairs obtained in Theorems 3.6 and 3.7 are hereditary and strongly hereditary in the sense of the following definition.

Definition 3.9

Let $({\mathcal {F}},{\mathcal {G}})$ be an ${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$. We say that $({\mathcal {F}},{\mathcal {G}})$ is:

• 1. left hereditary if ${\mathcal {F}}$ is a resolving subcategory of ${\mathcal {S}}$;

• 2. left strongly hereditary if ${\mathcal {F}}$ is a resolving subcategory in ${\mathcal {C}}$.

The notions of right (strongly) hereditary and (strongly) hereditary${\mathcal {S}}$-cotorsion pairs in ${\mathcal {C}}$ are defined similarly.

Note in Definition 3.9 that in both concepts 1. and 2., ${\mathcal {F}}$ is closed under extensions and under taking kernels of epimorphisms between its objects. The difference between them is that $\mathsf{Proj}({\mathcal {S}}) \subseteq {\mathcal {F}}$ is valid in 1., while $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {F}}$ holds for 2.

As noticed, the fact that causes that the notions of left hereditary and left strongly hereditary ${\mathcal {S}}$-cotorsion pairs are not the same is that the projective objects of ${\mathcal {S}}$, thought as an exact subcategory, are not necessarily the projective objects of ${\mathcal {C}}$. So it is natural to ask whether it is possible to establish conditions under which the projective objects of ${\mathcal {C}}$ and ${\mathcal {S}}$ coincide. This question is settled in the following result, whose proof is straightforward.

Proposition 3.10

Let ${\mathcal {S}}\subseteq {\mathcal {C}}$ be a thick subcategory of ${\mathcal {C}}$. If $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {S}}$ and ${\mathcal {C}}$ has enough projectives, then $\mathsf{Proj}({\mathcal {S}}) = \mathsf{Proj}({\mathcal {C}})$.

As a consequence, we have the following.

Remark 3.11

Let $({\mathcal {F}},{\mathcal {G}})$ be a cotorsion pair in ${\mathcal {S}}.$ If ${\mathcal {C}}$ has enough projectives, then ${\mathcal {F}}$ is resolving in ${\mathcal {C}}$ if, and only if, ${\mathcal {F}}$ is resolving in ${\mathcal {S}}$ and $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {F}}$.

The following theorem presents a method to obtain left and right Frobenius pairs from a left strongly hereditary ${\mathcal {S}}$-cotorsion pair. Before giving its statement and proof, we need to introduce the notation we will use for syzygies and cosyzygies.

Suppose ${\mathcal {C}}$ has enough projectives. Let $C \in {\mathcal {C}}$ and

$$\begin{aligned} {\varvec{P}} = \cdots \rightarrow P_1 \rightarrow P_0 \rightarrow C \rightarrow 0 \end{aligned}$$

be a projective resolution of C. We denote by $\varOmega ^i(C) := \mathrm {Ker}(P_{i-1} \rightarrow P_{i-2})$ the ith syzygy ofCoccurring in${\varvec{P}}$ for any integer $i \ge 1$, where $P_{-1} := C$. For $i = 0$, we set $\varOmega ^0(C) := C$.

Theorem 3.12

Let $({\mathcal {F}},{\mathcal {G}})$ be a left strongly hereditary ${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$, and set $\omega := {\mathcal {F}}\cap {\mathcal {G}}$. If ${\mathcal {C}}$ has enough projectives, then the following statements hold true:

• 1. $\mathsf{Ext}^i_{\mathcal {C}}({\mathcal {F}},{\mathcal {G}}) = 0$ for every $i\ge 1$.

• 2. $({\mathcal {F}},\omega )$ is a left Frobenius pair in ${\mathcal {C}}$.

• 3. $(\omega ,{\mathcal {G}})$ is a right Frobenius pair in ${\mathcal {C}}$.

• 4. If ${\mathcal {G}}\subseteq {\mathcal {F}}^{\wedge }$, then $({\mathcal {F}},{\mathcal {G}})$ is an ${\mathcal {F}}^{\wedge }$-cotorsion pair in ${\mathcal {C}}$. Moreover, the following equalities hold:

  $$\begin{aligned} {\mathcal {G}}&= \omega ^{\wedge } = {\mathcal {F}}^{\wedge } \cap {\mathcal {F}}^{\perp }, \end{aligned}$$

  (9)
  $$\begin{aligned} {\mathcal {F}}&= {\mathcal {F}}^{\wedge } \cap {}^{\perp }\omega = {\mathcal {F}}^{\wedge } \cap {}^{\perp }(\omega ^{\wedge }). \end{aligned}$$

  (10)

Proof

• 1. For every $F \in {\mathcal {F}}$, $G \in {\mathcal {G}}$ and $i \ge 1$, we have a natural isomorphism $\mathsf{Ext}^i_{\mathcal {C}}(F,G) \simeq \mathsf{Ext}^1_{\mathcal {C}}(\varOmega ^{i-1}(F), G) = 0$ where $\varOmega ^{i-1}(F) \in {\mathcal {F}}$ since ${\mathcal {F}}$ is resolving in ${\mathcal {C}}$.

• 2. The subcategory ${\mathcal {F}}= {}^{\perp _1}{\mathcal {G}}\cap {\mathcal {S}}$ is resolving and closed under direct summands in ${\mathcal {C}}$. On the other hand, note also that $\omega$ is closed under direct summands. So it remains to check that $\omega$ is an ${\mathcal {F}}$-injective relative cogenerator in ${\mathcal {F}}$. Part 1. implies that $\omega$ is ${\mathcal {F}}$-injective, since $\mathsf{id}_{\mathcal {F}}(\omega ) \le \mathsf{id}_{\mathcal {F}}({\mathcal {G}}) = 0$. Now let $F \in {\mathcal {F}}$. By the dual of condition 3. in Proposition 3.5, there exists a short exact sequence

  $$\begin{aligned} 0 \rightarrow F \rightarrow W \rightarrow F' \rightarrow 0 \end{aligned}$$

  in ${\mathcal {C}}$ with $F' \in {\mathcal {F}}$ and $W \in {\mathcal {G}}$. Since ${\mathcal {F}}$ is closed under extensions, we obtain that $W \in {\mathcal {F}}\cap {\mathcal {G}}=: \omega$, proving that $\omega$ is a relative cogenerator in ${\mathcal {F}}$.

• 3. The equality ${\mathcal {G}}= {\mathcal {F}}^{\perp _1} \cap {\mathcal {S}}$ implies that ${\mathcal {G}}$ is closed under extensions and direct summands in ${\mathcal {C}}$. Now consider an admissible exact sequence

  $$\begin{aligned} 0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0 \end{aligned}$$

  in ${\mathcal {S}}$, with $A, B \in {\mathcal {G}}$. We have an induced exact sequence

  $$\begin{aligned} \mathsf{Ext}^1_{\mathcal {C}}(F,B) \rightarrow \mathsf{Ext}^1_{\mathcal {C}}(F,C) \rightarrow \mathsf{Ext}^2_{\mathcal {C}}(F,A) \end{aligned}$$

  of abelian groups for each $F \in {\mathcal {F}}$, where $\mathsf{Ext}^1_{{\mathcal {C}}}(F,B) = 0$ and $\mathsf{Ext}^2_{{\mathcal {C}}}(F,A) = 0$ by part 1. Hence, it follows that $C \in {\mathcal {F}}^{\perp _1} \cap {\mathcal {S}}= {\mathcal {G}}$. Thus, we have that ${\mathcal {G}}$ is pre-coresolving and closed under direct summands in ${\mathcal {C}}$. The rest of the proof follows as part 2.

• 4. Note that ${\mathcal {F}}$ and ${\mathcal {G}}$ are subcategories of ${\mathcal {F}}^\wedge$ with ${\mathcal {F}}$ closed under direct summands in ${\mathcal {C}}$, and we already know that $\mathsf{Ext}^1_{{\mathcal {C}}}({\mathcal {F}},{\mathcal {G}}) = 0$. On the other hand, since ${\mathcal {F}}$ is resolving in ${\mathcal {C}}$ and ${\mathcal {F}}\subseteq {\mathcal {S}}$, we have that ${\mathcal {F}}^\wedge \subseteq {\mathcal {S}}$. So every $S \in {\mathcal {F}}^\wedge$ has an epic ${\mathcal {F}}$-pre-cover with kernel in ${\mathcal {G}}$, and a monic ${\mathcal {G}}$-pre-envelope with cokernel in ${\mathcal {F}}$. Hence, $({\mathcal {F}},{\mathcal {G}})$ is an ${\mathcal {F}}^\wedge$-cotorsion pair in ${\mathcal {C}}$.

  To show the equalities (9) and (10), we start noting by part 2. and by Theorem 3.6, the equalities $\omega ^{\wedge } = {\mathcal {F}}^{\wedge } \cap {\mathcal {F}}^{\perp }$ and ${\mathcal {F}}^{\wedge }\cap {}^{\perp }\omega = {\mathcal {F}}= {\mathcal {F}}^{\wedge } \cap {}^{\perp }(\omega ^{\wedge })$, thus having (10). We assert that ${\mathcal {G}}= \omega ^{\wedge }$. Indeed, by part 3. we get that $\omega ^\wedge \subseteq {\mathcal {G}}$. And in order to prove that ${\mathcal {G}}\subseteq \omega ^{\wedge }$, it suffices to see that ${\mathcal {G}}\subseteq {\mathcal {F}}^{\wedge } \cap {\mathcal {F}}^{\perp }$, which follows by part 1. since ${\mathcal {G}}\subseteq {\mathcal {F}}^{\wedge }$. Hence, (9) also follows.

The following result, whose proof is straightforward, shows how to obtain strongly hereditary relative cotorsion pairs from hereditary cotorsion pairs in abelian categories.

Corollary 3.13

Let $({\mathcal {F}},{\mathcal {G}})$ be a left hereditary complete cotorsion pair in ${\mathcal {C}}$ and set $\omega := {\mathcal {F}}\cap {\mathcal {G}}$. If ${\mathcal {C}}$ has enough projectives, then $({\mathcal {F}}, {\mathcal {G}}\cap {\mathcal {F}}^{\wedge })$ is a left strongly hereditary ${\mathcal {F}}^\wedge$-cotorsion pair in ${\mathcal {C}}$.

We close this section presenting some conditions under which the ${\mathcal {X}}^\wedge$-cotorsion pairs $({\mathcal {X}}, \omega ^\wedge )$ and $(\omega , {\mathcal {X}}^\wedge )$ are strongly hereditary.

Theorem 3.14

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in ${\mathcal {C}}$. Then, the following conditions are equivalent:

• (a) $\mathsf{Proj}({\mathcal {C}}) \subseteq \omega$ and $\mathsf{Inj}({\mathcal {C}}) \subseteq {\mathcal {X}}^\wedge$.

• (b) $(\omega ,{\mathcal {X}}^\wedge )$ is a strongly hereditary ${\mathcal {X}}^\wedge$-cotorsion pair in ${\mathcal {C}}$.

• (c) $({\mathcal {X}}, \omega ^\wedge )$ is a strongly hereditary ${\mathcal {X}}^\wedge$-cotorsion pair in ${\mathcal {C}}$.

Proof

We know by Theorems 3.6 and 3.7 that $({\mathcal {X}},\omega ^\wedge )$ and $(\omega ,{\mathcal {X}}^\wedge )$ are ${\mathcal {X}}^\wedge$-cotorsion pairs in ${\mathcal {C}}$, where the class $\omega ^\wedge$ is thick. These facts, along with the equalities $\omega = {\mathcal {X}}\cap \omega ^\wedge = {}^{\perp _1}({\mathcal {X}}^\wedge ) \cap {\mathcal {X}}^\wedge$ and $\omega ^\wedge = {\mathcal {X}}^\perp \cap {\mathcal {X}}^\wedge$, suffice to note the corresponding equivalences. $\square$

4 Model category structures in approximation theory

Given a strong left Frobenius pair $({\mathcal {X}}, \omega )$ in ${\mathcal {C}}$, recall from Example 3.1 that $\mathcal {X}^\wedge$ is an exact subcategory of ${\mathcal {C}}$. We will obtain an exact model structure on $\mathcal {X}^\wedge$ whose homotopy category represents, in a certain sense that specified below, a generalization of the stable module category of a ring.

4.1 Exact model structures from Frobenius pairs

Our first goal in this section is to show the following result.

Theorem 4.1

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in ${\mathcal {C}}$. Then, there exists a unique exact model structure on ${\mathcal {X}}^\wedge$, referred as the (projective) Auslander–Buchweitz model structure associated to $({\mathcal {X}},\omega )$, such that ${\mathcal {X}}$ is the subcategory of cofibrant objects, ${\mathcal {X}}^\wedge$ is the subcategory of fibrant objects, and $\omega ^\wedge$ is the subcategory of trivial objects. We will denote this model structure by

$$\begin{aligned} {\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega ) := ({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge ). \end{aligned}$$

The concept of model category structure was introduced by Quillen [39] in 1967. There are two modern approaches to this definition considered nowadays: one given by Hovey in [31, Chapter 1], and the other one by Beligiannis and Reiten in [7, Chapter VIII]. These two approaches are slightly different between them, and differ from the original definition given by Quillen. Due to the purpose of this paper, model structures will always be considered on exact categories (unless otherwise specified), although the definition given below covers more general situations.

We recall from [7] that a model structure on an exact category ${\mathcal {E}}$ is given by three classes ${\mathfrak {F}}$, ${\mathfrak {C}}$ and ${\mathfrak {T}}$ of morphisms of ${\mathcal {E}}$, called fibrations, cofibrations and weak equivalences, respectively, that satisfy a series of axioms, which we recall for the reader’s convenience:

• [M1] ${\mathfrak {T}}$ has the 2-out-of-3 property with respect to the composition.

• [M2] ${\mathfrak {F}}$, ${\mathfrak {C}}$ and ${\mathfrak {T}}$ are closed under retractions.

• [M3] Given a commutative diagram

  

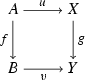
  in ${\mathcal {E}}$, if either f is a trivial cofibration (that is, $f \in {\mathfrak {C}} \cap {\mathfrak {T}}$) and g is a fibration, or f is a cofibration and g is a trivial fibration (that is, $g \in {\mathfrak {F}} \cap {\mathfrak {T}}$), then there exists a morphism $d :B \rightarrow X$ such that $d \circ f = u$ and $g \circ d = v$.

• [M4] Every morphism f in ${\mathcal {E}}$ admits a factorization $f = p \circ i = q \circ j$, where $i \in {\mathfrak {C}}$, $j \in {\mathfrak {C}} \cap {\mathfrak {T}}$, $p \in {\mathfrak {F}} \cap {\mathfrak {T}}$ and $q \in {\mathfrak {F}}$.

For more details concerning these axioms, see [31, Definition 1.1.3] or [7, Sect. 1 of Chapter VIII]. By a model category we will mean an exact category ${\mathcal {E}}$ equipped with a model structure ${\mathcal {M}} = ({\mathfrak {C,T,F}})$ on ${\mathcal {E}}$.

Remark 4.2

We need to point out some considerations about this definition of model category. In the sense of Hovey, a model category is a category ${\mathcal {E}}$ with (small) limits and colimits, that is equipped with a model structure such that factorizations in axiom [M4] are functorial. In Beligiannis and Reiten’s definition, on the other hand, ${\mathcal {E}}$ is only assumed to be an additive category with kernels and cokernels.

So our definition of model category is more similar to that of Beligiannis and Reiten, with the only detail that exact categories may not have all kernels and cokernels, according to the definition proposed by Quillen in [40]. However, this will not represent a problem in our setting. Indeed, the particular part of the theory of model categories considered in this paper will only require ground categories ${\mathcal {E}}$ such that: (1) ${\mathcal {E}}$ has terminal and initial objects, (2) the product $X \prod X$ and coproduct $X \coprod X$ of any object $X \in {\mathcal {E}}$ with itself exist, and (3) the pushouts of all cofibrations and pullbacks of all fibrations exist. This is in particular the case of exact categories. With only these three requirements, it will be possible to use some important basic results of homotopy theory. Let us be more specific about this.

A model structure provides to the category on which it is defined a general setting for doing homotopy theory. By this we mean that every model category $(\mathcal {E,M})$ has an associated homotopy category, denoted $\text {Ho}_{{\mathcal {M}}}({\mathcal {E}})$, that is defined by formally inverting the weak equivalences of ${\mathcal {M}}$. In other words, $\text {Ho}_{{\mathcal {M}}}({\mathcal {E}})$ is obtained after localizing ${\mathcal {E}}$ at the class ${\mathfrak {T}}$ of weak equivalences (see Hovey [31, Sect. 1.2] for details). It is important to mention that the construction of $\text {Ho}_{{\mathcal {M}}}({\mathcal {E}})$ does not require that ${\mathcal {E}}$ has finite limits and colimits, but only conditions (1), (2) and (3) in Remark 4.2, as explained again by Gillespie in [19, Sect. 1 and Fact 4.2].

We are interested in a particular family of model structures on exact categories that are called exact. For such models, the classes of cofibrant, fibrant and trivial objects play a more important role than the classes of cofibrations, fibrations and weak equivalences. On the one hand, recall that an object $X \in {\mathcal {E}}$ in a model category $(\mathcal {E,M})$ is said to be:

• cofibrant if the only morphism $0 \rightarrow X$ is a cofibration.

• fibrant if the only morphism $X \rightarrow 0$ is a fibration.

• trivial if the only morphism $0 \rightarrow X$ is a weak equivalence.

We will denote the classes of cofibrant, fibrant and trivial objects by ${\mathcal {Q}}$, ${\mathcal {R}}$ and ${\mathcal {T}}$, respectively, and in some occasions the model structure ${\mathcal {M}}$ may be displayed as the triple ${\mathcal {M}} = (\mathcal {Q,T,R})$. On the other hand, exact model structures were defined by Gillespie in [19, Definition 3.1] as those model structures on an exact category ${\mathcal {E}}$ such that:

• 1. f is a cofibration if, and only if, f is an admissible monomorphism and $\mathrm{CoKer}(f) \in {\mathcal {Q}}$.

• 2. g is a fibration if, and only if, g is an admissible epimorphism and $\mathrm {Ker}(g) \in {\mathcal {R}}$.

Such model structures have an appealing interplay with certain triples of subcategories of ${\mathcal {E}}$. Three subcategories ${\mathcal {F}}, {\mathcal {G}}, \mathcal {W} \subseteq {\mathcal {E}}$ form a Hovey triple$(\mathcal {F,W,G})$ in ${\mathcal {E}}$ if $({\mathcal {F}}\cap \mathcal {W},{\mathcal {G}})$ and $({\mathcal {F}},{\mathcal {G}}\cap \mathcal {W})$ are complete cotorsion pairs in ${\mathcal {E}}$, and if $\mathcal {W}$ is thick. Gillespie proved in [19, Theorem 3.3] that there is a one-to-one correspondence between exact model structures on ${\mathcal {E}}$ and Hovey triples in ${\mathcal {E}}$, provided that ${\mathcal {E}}$ is a weakly idempotent complete exact category, that is, every split monomorphism has a cokernel and every split epimorphism has a kernel (see [19, Definition 2.2]). This result is a generalization of a similar correspondence proved by Hovey in the context of abelian categories [32, Theorem 2.2], and will be referred to as the Hovey–Gillespie correspondence. It is worth mention ing that a similar approach to this interplay between model structures and cotorsion pairs in the abelian case was developed independently by Beligiannis and Reiten in [7, Chapter VIII] but in a different context, and giving rise to different results. We will also consider this other point of view later on in Sect. 5 due to its applications to basic cotilting modules.

Now given a strong left Frobenius pair $(\mathcal {X},\omega )$ in an abelian category ${\mathcal {C}}$, the exact subcategory $\mathcal {X}^\wedge \subseteq {\mathcal {C}}$ is weakly idempotent complete. We then have by Theorems 3.6 and 3.7 two ${\mathcal {X}}^\wedge$-cotorsion pairs $({\mathcal {X}}, \omega ^\wedge )$ and $(\omega , {\mathcal {X}}^\wedge )$ with $\omega = {\mathcal {X}}\cap \omega ^\wedge$. These are complete cotorsion pairs in the thick (and so exact) subcategory ${\mathcal {X}}^\wedge \subseteq {\mathcal {C}}$, thus forming a Hovey triple $(\mathcal {X},\omega ^\wedge ,\mathcal {X}^\wedge )$. Then, the Hovey–Gillespie correspondence produces the exact model structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega ) = ({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge )$ on ${\mathcal {X}}^\wedge$ described in Theorem 4.1. This model structure is projective, in the sense that every object in ${\mathcal {X}}^\wedge$ is fibrant.

Remark 4.3

Another observation about our definition of model category is that we do not consider functorial factorizations. In fact, we are not aware if factorizations in the AB model structure from Theorem 4.1 are functorial. As this model structure is exact, and exact model structures are in one-to-one correspondence with Hovey triples, we can note that ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega ) = ({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge )$ has functorial factorizations if, and only if, the associated cotorsion pairs $({\mathcal {X}},\omega ^\wedge )$ and $(\omega ,{\mathcal {X}}^\wedge )$ in ${\mathcal {X}}^\wedge$ are functorially complete in the sense of Hovey [32]. The latter condition occurs, for instance, when these cotorsion pairs are cogenerated by a set. In many cases, to show that a cotorsion pair $(\mathcal {F,G})$ in an exact category ${\mathcal {E}}$ is cogenerated by a set requires to construct for every direct summand of every object in $\mathcal {F}$ a filtration by a set, and this in t urn needs the existence of small colimits in ${\mathcal {E}}$. Notice that this is not necessarily the case of $\mathcal {X}^\wedge$.

The following result provides an easy method to get exact model structures from certain strongly hereditary ${\mathcal {S}}$-cotorsion pairs.

Corollary 4.4

Let $({\mathcal {F}},{\mathcal {G}})$ be an ${\mathcal {S}}$-cotorsion pair in an abelian category ${\mathcal {C}}$ with enough projectives and injectives. If ${\mathcal {F}}$ is resolving in ${\mathcal {C}}$, ${\mathcal {G}}$ coresolving in ${\mathcal {C}}$ and ${\mathcal {G}}\subseteq {\mathcal {F}}^\wedge$, then $({\mathcal {F}},{\mathcal {G}})$ and $({\mathcal {F}}\cap {\mathcal {G}}, {\mathcal {F}}^\wedge )$ are ${\mathcal {F}}^\wedge$-cotorsion pairs in ${\mathcal {C}}$. In other words, $({\mathcal {F}},{\mathcal {G}},{\mathcal {F}}^\wedge )$ is a Hovey triple in ${\mathcal {F}}^\wedge$.

4.2 Some remarks on submodel structures

We begin this section with the following definition.

Definition 4.5

We say that a Hovey triple $(\mathcal {F,W,G})$ in an exact category ${\mathcal {E}}$ is left hereditary if the cotorsion pairs $({\mathcal {F}}, {\mathcal {G}}\cap \mathcal {W})$ and $({\mathcal {F}}\cap \mathcal {W}, {\mathcal {G}})$ are both left hereditary, that is, the subcategories ${\mathcal {F}}$ and ${\mathcal {F}}\cap \mathcal {W}$ are both resolving in ${\mathcal {E}}$. Similarly, we have the definition of right hereditary and hereditary Hovey triples.

In the case where ${\mathcal {E}}$ is an exact subcategory of an abelian category ${\mathcal {C}}$, we say that a Hovey triple $(\mathcal {F,W,G})$ in ${\mathcal {E}}$ is left strongly hereditary if the cotorsion pairs $({\mathcal {F}}, {\mathcal {G}}\cap \mathcal {W})$ and $({\mathcal {F}}\cap \mathcal {W}, {\mathcal {G}})$ in ${\mathcal {E}}$ are left strongly hereditary. Right strongly hereditary and strongly hereditary Hovey triples are defined similarly (see Definition 3.9).

Let us recall from Gillespie [19, Definition 5.3] the notion of submodel structure. Given an exact category ${\mathcal {E}}$ with an exact model structure ${\mathcal {M}} = (\mathcal {Q,T,R})$ on it, and a fully exact subcategory ${\mathcal {E}}_0 \subseteq {\mathcal {E}}$, an exact model structure ${\mathcal {M}}_0 = ({\mathcal {Q}}_0,{\mathcal {T}}_0,{\mathcal {R}}_0)$ on ${\mathcal {E}}_0$ is a submodel structure of ${\mathcal {M}}$ if the following two conditions hold:

• 1. The inclusion functor $i :{\mathcal {E}}_0 \hookrightarrow {\mathcal {E}}$ preserves the model structure ${\mathcal {M}}_0$, that is, every cofibration, fibration and weak equivalence in ${\mathcal {M}}_0$ is a cofibration, fibration and weak equivalence in ${\mathcal {M}}$, respectively.

• 2. The induced functor $\mathrm{Ho}(i) :\mathrm{Ho}_{{\mathcal {M}}_0}({\mathcal {E}}_0) \longrightarrow \mathrm{Ho}_{{\mathcal {M}}}({\mathcal {E}})$ is an equivalence of categories.

Condition 1. above is equivalent to saying that ${\mathcal {Q}}_0$, ${\mathcal {R}}_0$ and ${\mathcal {T}}_0$ are full subcategories of ${\mathcal {Q}}$, ${\mathcal {R}}$ and ${\mathcal {T}}$, respectively.

In [19], Gillespie constructs from a hereditary Hovey triple $(\mathcal {F,W,G})$ in ${\mathcal {E}}$, submodel structures (of the unique model structure on ${\mathcal {E}}$ resulting from $(\mathcal {F,W,G})$) on the full subcategories ${\mathcal {Q}} = {\mathcal {F}}$, ${\mathcal {R}} = {\mathcal {G}}$ and ${\mathcal {Q}} \cap {\mathcal {R}} = {\mathcal {F}}\cap {\mathcal {G}}$ of cofibrant, fibrant, and cofibrant-fibrant objects, respectively. The first property obtained after assuming that $(\mathcal {F,W,G})$ is hereditary, is that the resulting subcategories ${\mathcal {Q}}$, ${\mathcal {R}}$ and ${\mathcal {Q}} \cap {\mathcal {R}}$ are exact and weakly idempotent complete (see [19, Lemma 5.1, Proposition 5.2]). The resulting submodel structures on ${\mathcal {Q}}$, ${\mathcal {R}}$ and ${\mathcal {Q}} \cap {\mathcal {R}}$ are described in [19, Proposition 5.2]. In this section, we apply this result to check which are the submodel structures obtained from a strong left Frobenius pair.

Proposition 4.6

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in ${\mathcal {C}}$. Then, $({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge )$ is a hereditary Hovey triple in ${\mathcal {X}}^\wedge$. Moreover, $({\mathcal {X}}, \omega ^\wedge , {\mathcal {X}}^\wedge )$ is a strongly hereditary Hovey triple in ${\mathcal {X}}^\wedge$ if, and only if, $\mathsf{Proj}({\mathcal {C}}) \subseteq \omega$ and $\mathsf{Inj}({\mathcal {C}}) \subseteq {\mathcal {X}}^\wedge$.

Proof

The fact that $({\mathcal {X}},{\mathcal {X}}^\wedge ,\omega ^\wedge )$ is a hereditary Hovey triple in ${\mathcal {X}}^\wedge$ follows easily from the properties of the two cotorsion pairs $({\mathcal {X}},\omega ^\wedge )$ and $(\omega ,{\mathcal {X}}^\wedge )$ in the exact subcategory ${\mathcal {X}}^\wedge \subseteq {\mathcal {C}}$. The characterization of $({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge )$ as a strongly hereditary Hovey triple is a consequence of Theorem 3.14. $\square$

Remark 4.7

If ${\mathcal {C}}$ has enough projectives, the inclusion $\mathsf{Proj}({\mathcal {C}}) \subseteq \omega$ in the previous statement can be replaced by $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}^\wedge$, since Proposition 3.10 asserts $\mathsf{Proj}({\mathcal {C}}) = \mathsf{Proj}({\mathcal {X}}^\wedge )$, and so $\mathsf{Proj}({\mathcal {C}}) \subseteq \omega$. Notice that $\mathsf{Proj}({\mathcal {X}}^\wedge ) \subseteq \omega$ since $(\omega ,{\mathcal {X}}^\wedge )$ is a cotorsion pair in ${\mathcal {X}}^\wedge$.

After applying Proposition 4.6, along with [19, Proposition 5.2], we obtain the following submodel structures from a strong left Frobenius pair.

Proposition 4.8

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in ${\mathcal {C}}$. Then, there exist a submodel structure of ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}, \omega )$, defined on the subcategory $\mathcal {X}$ of cofibrant-fibrant objects, where the cofibrant and fibrant objects are given by ${\mathcal {X}}$, and the trivial objects by $\omega$.

In [19, Proposition 5.2], the resulting submodel structure on ${\mathcal {R}} := {\mathcal {X}}^\wedge$ coincides with ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}, \omega )$. This happens because ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}, \omega )$ is a projective model structure. On the other hand, the resulting submodel structures on ${\mathcal {Q}} := {\mathcal {X}}$ and on ${\mathcal {Q}} \cap {\mathcal {R}} := \mathcal {X}$ coincide.

Example 4.9

The model structure in Proposition 4.8 is an example of what Gillespie [19] calls a Frobenius model structure, that is, every object in the corresponding exact category is cofibrant and fibrant. Note that in every Frobenius category ${\mathcal {E}}$, $({\mathcal {E}},\mathsf{Proj}({\mathcal {E}}),{\mathcal {E}})$ is a Hovey triple, which gives rise to a Frobenius model structure with $\mathsf{Proj}({\mathcal {E}})$ as the subcategory of trivial objects.

4.3 The homotopy category of an Auslander–Buchweitz model structure

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in ${\mathcal {C}}$. For simplicity, let us write the homotopy category of the AB model structure on ${\mathcal {X}}^\wedge$ as

$$\begin{aligned} \mathrm{Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^{\wedge }) := \mathrm{Ho}_{{\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega )}({\mathcal {X}}^{\wedge }). \end{aligned}$$

In this section, we present an explicit description of $\text {Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^\wedge )$, and note how this homotopy category is equivalent to the stable category of a Frobenius subcategory of ${\mathcal {C}}$.

Exact model structures serve as descriptions, from a homotopical point of view, of several important categories considered in relative homological algebra, such as derived categories and stable categories. For instance, it is well known that the derived category of a ring is equivalent to the homotopy category of the projective model structure on the category of chain complexes over an arbitrary ring R, described by Hovey in [31, Sect. 2.3]. Another example occurs in case R is quasi-Frobenius, where the stable module category of R is equivalent to the homotopy category of the stable model structure on $\mathsf{Mod}(R)$ described in [31, Sect. 2.2]. So we can note that exact model structures can contain several types of homological and homotopical information depending on which class of weak equivalences we are localizing at.

In this occasion, our theoretical framework favors the construction of models of more general stable categories. Let us be more specific about this assertion by computing the homotopy category associated to the Auslander–Buchweitz model structure of a strong left Frobenius pair $({\mathcal {X}},\omega )$.

Recall that given an exact model structure ${\mathcal {M}} = (\mathcal {Q,T,R})$ on an exact category ${\mathcal {E}}$, two morphisms $f, g :X \rightarrow Y$ in ${\mathcal {E}}$ are right homotopic if, and only if, $g - f$ factors through an object in ${\mathcal {Q}} \cap {\mathcal {T}}$. Dually, f and g are left homotopic if, and only if, $g - f$ factors through an object in ${\mathcal {R}} \cap {\mathcal {T}}$. This was proven by Gillespie in [19, Proposition 4.4]. If the Hovey triple $(\mathcal {Q,T,R})$ is hereditary, then the submodel structures on ${\mathcal {Q}}$, ${\mathcal {R}}$ and ${\mathcal {Q}} \cap {\mathcal {R}}$ are fully equivalent submodel structures of ${\mathcal {E}}$, that is:

• 1. The inclusions $i_{{\mathcal {Q}}} :{\mathcal {Q}} \hookrightarrow {\mathcal {E}}$, $i_{{\mathcal {R}}} :{\mathcal {R}} \hookrightarrow {\mathcal {E}}$ and $i_{{\mathcal {Q}} \cap {\mathcal {R}}} :{\mathcal {Q}} \cap {\mathcal {R}} \hookrightarrow {\mathcal {E}}$ preserve the corresponding model structures.

• 2. The induced functors in homotopy $\text {Ho}(i_{{\mathcal {Q}}}) :\text {Ho}({\mathcal {Q}}) \rightarrow \text {Ho}({\mathcal {E}})$, $\text {Ho}(i_{{\mathcal {R}}}) :\text {Ho}({\mathcal {R}}) \rightarrow \text {Ho}({\mathcal {E}})$ and $\text {Ho}(i_{{\mathcal {Q}} \cap {\mathcal {R}}}) :\text {Ho}({\mathcal {Q}} \cap {\mathcal {R}}) \rightarrow \text {Ho}({\mathcal {E}})$ are equivalences of categories.

These two results were proven in [19, Proposition 5.2, Corollary 5.4], and we can apply them to the Hovey triple associated to the AB model structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}, \omega )$. Indeed, by Proposition 4.6 it follows that if ${\mathcal {X}}^\wedge$ is equipped with the projective AB model structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega )$, then the subcategory of cofibrant-fibrant objects ${\mathcal {Q}} \cap {\mathcal {R}} = {\mathcal {X}}$ is equipped with the submodel structure ${\mathcal {M}}_\mathrm{cf} = ({\mathcal {X}},\omega ,{\mathcal {X}})$ of ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega )$ described in Proposition 4.8, and the corresponding homotopy categories $\text {Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^\wedge )$ and $\text {Ho}_{{\mathcal {M}}_\mathrm{cf}}({\mathcal {X}})$ are equivalent. One advantage of this fact is that $\text {Ho}_{{\mathcal {M}}_\mathrm{cf}}({\mathcal {X}})$ is easier to describe than $\text {Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^\wedge )$. First of all, on the subcategory ${\mathcal {Q}} \cap {\mathcal {R}} = {\mathcal {X}}\subseteq {\mathcal {X}}^\wedge$, the relations of being left and right homotopic (denoted $\sim$) coincide. On the other hand, by Hovey [31, Theorem 1.2.10 (i)], there is an equivalence of categories $\text {Ho}_{{\mathcal {M}}_\mathrm{cf}}({\mathcal {X}}) \cong ({{\mathcal {Q}} \cap {\mathcal {R}}) / \sim } = {\mathcal {X}}/ \sim$. By Remark 2.6, ${\mathcal {X}}$ is a Frobenius category, and for any two morphisms $f, g :X \rightarrow Y$, we have that $f \sim g$ if and only if $g - f$ factors through a projective object in ${\mathcal {X}}$ (that is, an object in $\omega$). Hence, the quotient ${\mathcal {X}}/ \sim$ is the stable category of ${\mathcal {X}}$.

The description of $\text {Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^\wedge )$ involves some knowledge about cofibrant and fibrant replacements. If X is an object in an exact category ${\mathcal {E}}$ with an exact model structure ${\mathcal {M}}$, we can factor the morphism $0 \rightarrow X$ as a cofibration $0 \rightarrow QX$ followed by a trivial fibration $QX \rightarrow X$. The object QX is then cofibrant, and it is called a cofibrant replacement of X. Dually, one has the notion of fibrant replacements of X, usually denoted as RX. In case ${\mathcal {M}}$ is the AB model structure ${\mathcal {M}}_\mathrm{AB}^\mathrm{proj}({\mathcal {X}}^\wedge )$, we have by [31, Theorem 1.2.10 (ii)] that for every $X, Y \in {\mathcal {X}}^\wedge$ there is a natural isomorphism

$$\begin{aligned} \mathsf{Hom}_{\text {Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^\wedge )}(X,Y) \cong \mathsf{Hom}_{{\mathcal {X}}^\wedge }(QX, RY) / \sim . \end{aligned}$$

Since every object in ${\mathcal {X}}^\wedge$ is fibrant, we can take $RY = Y$. We summarize these facts in the following result.

Proposition 4.10

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in ${\mathcal {C}}$. For the projective AB model structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega ) = ({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge )$ on ${\mathcal {X}}^\wedge$, there is a natural isomorphism

$$\begin{aligned} \mathsf{Hom}_{\mathrm{Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^\wedge )}(X,Y) \cong \mathsf{Hom}_{{\mathcal {X}}^\wedge }(QX, Y) / \sim \end{aligned}$$

for every $X, Y \in {\mathcal {X}}^\wedge$, where $f \sim g$ if and only if $g - f$ factors through an object in $\omega$. Moreover, $\mathrm{Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^\wedge )$ is equivalent to the stable category ${\mathcal {X}}/ \sim$.

Remark 4.11

Given a strong left Frobenius pair $({\mathcal {X}},\omega )$ in ${\mathcal {C}}$, we know by Proposition 4.10 that $\mathrm{Ho}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}}^\wedge )$ is equivalent to the stable category ${\mathcal {X}}/ \sim$. On the other hand, by Remark 2.6 we also know that ${\mathcal {X}}$ is a Frobenius category, and hence ${\mathcal {X}}/ \sim$ is indeed triangulated by Happel [25, Theorem I.2.6]. This last fact about ${\mathcal {X}}/ \sim$ can also be deduced from Beligiannis [6, Theorem 2.11], since ${\mathcal {X}}\subseteq {}^\perp \omega$ and $\omega$ is a cogenerator of ${\mathcal {X}}$.

It is important to declare that the concept of triangulated category employed here is the classical one defined by Verdier [46]. One can be tempted to say that $(\mathcal {X}^\wedge ,{\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathcal {X}^\wedge ))$ is a stable model category in the sense of Hovey’s [31, Chapter 7], that is, it is a model category whose homotopy category is triangulated. However, one must be careful with this terminology. The definition of triangulated category in [31] is relatively new and stronger than the classical one, and also requires the modern treatment of model categories that uses small (co)limits. We can only assert that $(\mathcal {X}^\wedge ,{\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathcal {X}^\wedge ))$ is an exact model category with projective model structure whose homotopy category is a stable classical triangulated category, but not necessarily triangulated in Hovey’s sense.

5 Auslander–Buchweitz contexts and their correspondence with relative cotorsion pairs, Frobenius pairs and model structures

We continue this paper presenting one-to-one correspondences between Frobenius pairs, relative cotorsion pairs and AB model structures. Auslander–Buchweitz contexts will play an important role in this section, as they will also appear in these correspondences.

5.1 AB contexts vs. Frobenius pairs vs. relative cotorsion pairs

The following definition is taken from Hashimoto [26, Theorem 1.1.2.10], but it is written according to the terminology we have been using so far.

Definition 5.1

Let $({\mathcal {A}},{\mathcal {B}})$ be a pair of classes of objects in ${\mathcal {C}}$ and $\omega := {\mathcal {A}}\cap {\mathcal {B}}$. We say that $({\mathcal {A}},{\mathcal {B}})$ is a left weak Auslander–Buchweitz pre-context (left weak AB pre-context for short) in ${\mathcal {C}}$ if:

• 1. $({\mathcal {A}}, \omega )$ is a left Frobenius pair in ${\mathcal {C}}$.

• 2. ${\mathcal {B}}= \mathsf{Thick}^{+}({\mathcal {B}})$, that is, $\mathcal {B}$ is right thick.

If in addition:

• $({\mathcal {A}},{\mathcal {B}})$ satisfies ${\mathcal {B}}\subseteq {\mathcal {A}}^\wedge$, then we say that $({\mathcal {A}},{\mathcal {B}})$ is a left weak AB context in ${\mathcal {C}}$;

• $({\mathcal {A}},{\mathcal {B}})$ satisfies ${\mathcal {A}}^\wedge = {\mathcal {C}}$, then we say that $({\mathcal {A}},{\mathcal {B}})$ is a left AB context in ${\mathcal {C}}$.

The notions of right weak AB pre-context, right weak AB context and right AB context in ${\mathcal {C}}$ are defined dually.

Example 5.2

In Theorem 2.16, the pair $({\mathcal {X}},{\mathcal {Y}})$ is a left weak AB context.

Remark 5.3

There are slightly different notions of AB contexts in the literature, such as the one considered in Beligiannis [6, Definition 4.4]. For example, Beligiannis works with ${\mathcal {A}}$ being $\omega$-resolving and ${\mathcal {B}}$ being closed under extensions of$\omega$-admissible sequences. Another difference is that we ask ${\mathcal {A}}= \mathsf{Thick}^{-}({\mathcal {A}})$ and ${\mathcal {B}}= \mathsf{Thick}^{+}({\mathcal {B}})$. Although in Definition 5.1, the class ${\mathcal {A}}$ is $\mathsf{Proj}({\mathcal {C}})$-resolving and ${\mathcal {B}}$ is closed under extensions of $\mathsf{Proj}({\mathcal {C}})$-admissible sequences in the sense of [6], it is not true in general that the subcategories $\mathsf{Proj}({\mathcal {C}})$ and $\omega$ coincide, as we will see in Sect. 6.4.

The goal of this section is to study the relation that left weak AB contexts have with left Frobenius pairs and relative cotorsion pairs. Specifically, we will focus on proving the following correspondence theorem.

Theorem 5.4

Let ${\mathcal {C}}$ be an abelian category. Consider the following classes of objects in the product category ${\mathcal {C}}\times {\mathcal {C}}$:

$$\begin{aligned} {\mathfrak {F}}&:= \{ ({\mathcal {X}}, \omega ) \subseteq {\mathcal {C}}\times {\mathcal {C}}{ \mathrm : } ({\mathcal {X}},\omega ) \text{ is } \text{ a } \text{ left } \text{ Frobenius } \text{ pair } \text{ in } {\mathcal {C}}\}, \\ {\mathfrak {C}}&:= \{ ({\mathcal {A}},{\mathcal {B}}) \subseteq {\mathcal {C}}\times {\mathcal {C}}{ \mathrm : } ({\mathcal {A}},{\mathcal {B}}) \text{ is } \text{ a } \text{ left } \text{ weak } \text{ AB } \text{ context } \text{ in } {\mathcal {C}}\}, \\ {\mathfrak {P}}&:= \{ ({\mathcal {F}},{\mathcal {G}}) \subseteq {\mathcal {C}}\times {\mathcal {C}}{ \mathrm : } ({\mathcal {F}},{\mathcal {G}}) \text{ is } \text{ a } \mathsf{Thick}({\mathcal {F}})\text{-cotorsion } \text{ pair } \text{ in } {\mathcal {C}} \text{ with } \mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0 \}. \end{aligned}$$

Then, the following conditions hold true:

• 1. There exists a one-to-one correspondence

  $$\begin{aligned} \varPhi :{\mathfrak {F}} \longrightarrow {\mathfrak {C}} \text{ given } \text{ by } ({\mathcal {X}},\omega ) \mapsto ({\mathcal {X}}, \omega ^\wedge ), \end{aligned}$$

  with inverse

  $$\begin{aligned} \varPsi :{\mathfrak {C}} \longrightarrow {\mathfrak {F}} \text{ given } \text{ by } ({\mathcal {A}},{\mathcal {B}}) \mapsto ({\mathcal {A}}, {\mathcal {A}}\cap {\mathcal {B}}). \end{aligned}$$

• 2. ${\mathfrak {C}} = {\mathfrak {P}}$.

First, we show how to obtain relative cotorsion pairs from left weak AB contexts.

Proposition 5.5

Let $({\mathcal {A}},{\mathcal {B}})$ be a left weak AB context in ${\mathcal {C}}$, and set $\omega := {\mathcal {A}}\cap {\mathcal {B}}$. Then, the following assertions hold true:

• 1. $({\mathcal {A}},{\mathcal {B}})$ is a ${\mathcal {A}}^\wedge$-cotorsion pair in ${\mathcal {C}}$ with $\mathsf{id}_{{\mathcal {A}}}({\mathcal {B}}) = 0$.

• 2. $\omega = {\mathcal {A}}\cap {\mathcal {A}}^\perp$ and ${\mathcal {B}}= \omega ^\wedge$.

Proof

On the one hand, by Theorem 3.6 we have an ${\mathcal {A}}^\wedge$-cotorsion pair $({\mathcal {A}}, \omega ^\wedge )$ with $\omega = {\mathcal {A}}\cap \omega ^\wedge = {\mathcal {A}}\cap ({\mathcal {A}}^\perp \cap {\mathcal {A}}^\wedge ) = {\mathcal {A}}\cap {\mathcal {A}}^\perp$. On the other hand, $\omega \subseteq {\mathcal {B}}$ and ${\mathcal {B}}= \mathsf{Thick}^{+}({\mathcal {B}})$ imply $\omega ^\wedge \subseteq {\mathcal {B}}$. We now show the remaining inclusion. Let $N \in {\mathcal {B}}$. Then $N \in {\mathcal {A}}^\wedge$ since ${\mathcal {B}}\subseteq {\mathcal {A}}^\wedge$, and so we can obtain an exact sequence

$$\begin{aligned} 0 \rightarrow K \rightarrow A \rightarrow N \rightarrow 0 \end{aligned}$$

with $A \in {\mathcal {A}}$ and $K \in \omega ^\wedge$, that is, as (3) in Theorem 2.8. Since $\omega ^\wedge \subseteq {\mathcal {B}}$, we have that $A \in {\mathcal {B}}$. Then $A \in \omega$ since ${\mathcal {B}}$ is closed under extensions. It follows that $N \in \omega ^\wedge$. Hence, we obtain ${\mathcal {B}}= \omega ^\wedge$, and so $({\mathcal {A}},{\mathcal {B}})$ is an ${\mathcal {A}}^\wedge$-cotorsion pair in ${\mathcal {C}}$. Finally, the latter equality ${\mathcal {B}}= \omega ^\wedge$ and Lemma 2.1 imply that $\mathsf{id}_{{\mathcal {A}}}({\mathcal {B}}) = 0$. $\square$

The following lemma is straightforward.

Lemma 5.6

If $({\mathcal {F}},{\mathcal {G}})$ is a left ${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$ such that $\mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$, then the equality ${\mathcal {F}}= \mathsf{Thick}^{-}({\mathcal {F}})$ holds.

Proposition 5.7

If $({\mathcal {F}},{\mathcal {G}})$ is an ${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$ with $\mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$, then $({\mathcal {F}},{\mathcal {G}})$ is a left and right weak AB pre-context in ${\mathcal {C}}$.

Proof

The equalities ${\mathcal {F}}= \mathsf{Thick}^{-}({\mathcal {F}})$ and ${\mathcal {G}}= \mathsf{Thick}^{+}({\mathcal {G}})$ follow by Lemma 5.6 and its dual. Now set $\omega := {\mathcal {F}}\cap {\mathcal {G}}$. Let us show that $\omega$ is an ${\mathcal {F}}$-injective relative cogenerator in ${\mathcal {F}}$. On the one hand, $\mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$ implies $\mathsf{id}_{{\mathcal {F}}}(\omega ) = 0$. On the other hand, for each $F \in {\mathcal {F}}\subseteq {\mathcal {S}}$ there exists a short exact sequence

$$\begin{aligned} 0 \rightarrow F \rightarrow G \rightarrow F' \rightarrow 0 \end{aligned}$$

with $F' \in {\mathcal {F}}$ and $G \in {\mathcal {G}}$. Since ${\mathcal {F}}$ is closed under extensions, we get $G \in {\mathcal {F}}\cap {\mathcal {G}}=: \omega$. Dually, one can show that $\omega$ is a ${\mathcal {G}}$-projective relative generator in ${\mathcal {G}}$. Notice that $\mathsf{pd}_{{\mathcal {G}}}({\mathcal {F}}) = \mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$ and $\omega \subseteq {\mathcal {F}}$ imply $\mathsf{pd}_{{\mathcal {G}}}(\omega ) = 0$. $\square$

The previous proposition, along with Theorem 2.11, provide the following way to obtain left weak AB contexts from relative cotorsion pairs.

Theorem 5.8

Let $({\mathcal {F}},{\mathcal {G}})$ be a $\mathsf{Thick}({\mathcal {F}})$-cotorsion pair in ${\mathcal {C}}$ with $\mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$. Then, the following conditons hold true:

• 1. $({\mathcal {F}},{\mathcal {G}})$ is a left weak AB context in ${\mathcal {C}}$.

• 2. $\mathsf{Thick}({\mathcal {F}}) = {\mathcal {F}}^\wedge$.

Proof

By Proposition 5.7, $({\mathcal {F}},{\mathcal {G}})$ is a left weak AB pre-context in ${\mathcal {C}}$. Then, $({\mathcal {F}},\omega )$ is a left Frobenius pair, and so Theorem 2.11 implies ${\mathcal {F}}^\wedge = \mathsf{Thick}({\mathcal {F}})$. Finally, note that ${\mathcal {G}}\subseteq \mathsf{Thick}({\mathcal {F}}) = {\mathcal {F}}^\wedge$. $\square$

Proof of Theorem 5.4

We first show that the mapping $\varPhi$ is well defined. Let $({\mathcal {X}},\omega ) \in {\mathfrak {F}}$ and set ${\mathcal {A}}:= {\mathcal {X}}$ and ${\mathcal {B}}:= \omega ^\wedge$. By (1) in Proposition 2.7, we have that $({\mathcal {A}}, {\mathcal {A}}\cap {\mathcal {B}}) = ({\mathcal {X}}, {\mathcal {X}}\cap \omega ^\wedge ) = ({\mathcal {X}},\omega )$, and so $({\mathcal {A}}, {\mathcal {A}}\cap {\mathcal {B}})$ is a left Frobenius pair in ${\mathcal {C}}$. Thus, it is only left to show that ${\mathcal {B}}= \mathsf{Thick}^{+}({\mathcal {B}})$ and that ${\mathcal {B}}\subseteq {\mathcal {A}}^\wedge$. By (5) in Proposition 2.13, we have that ${\mathcal {B}}= \omega ^\wedge = {\mathcal {X}}^\perp \cap {\mathcal {X}}^\wedge$, where ${\mathcal {X}}^\perp$ and ${\mathcal {X}}^\wedge$ are both pre-coresolving and closed under direct summands. Then ${\mathcal {B}}= \mathsf{Thick}^{+}({\mathcal {B}})$, and the inclusion ${\mathcal {B}}\subseteq {\mathcal {A}}^\wedge$ follows.

With respect to the inverse of $\varPhi$, first note that $\varPsi$ is well defined by the definition of left weak AB context. We show that $\varPsi \circ \varPhi = \mathsf{id}_{{\mathfrak {F}}}$ and $\varPhi \circ \varPsi = \mathsf{id}_{{\mathfrak {C}}}$. On the one hand, if $({\mathcal {X}},\omega )$ is a left Frobenius pair, then $\varPsi \circ \varPhi ({\mathcal {X}},\omega ) = ({\mathcal {X}}, {\mathcal {X}}\cap \omega ^\wedge ) = ({\mathcal {X}}, \omega )$ where ${\mathcal {X}}\cap \omega ^\wedge = \omega$ by (1) in Proposition 2.7. On the other hand, if $({\mathcal {A}},{\mathcal {B}})$ is a left weak AB context, we have that $\varPhi \circ \varPsi ({\mathcal {A}},{\mathcal {B}}) = ({\mathcal {A}}, ({\mathcal {A}}\cap {\mathcal {B}})^\wedge ) = ({\mathcal {A}}, {\mathcal {B}})$ where $({\mathcal {A}}\cap {\mathcal {B}})^\wedge = {\mathcal {B}}$ by Proposition 5.5. Hence, we have a one-to-one correspondence between ${\mathfrak {F}}$ and ${\mathfrak {C}}$.

Now we focus on showing part 2. Let $({\mathcal {A}},{\mathcal {B}}) \in {\mathfrak {C}}$ be a left weak AB context. Then by part 1. in Proposition 5.5, we have that $({\mathcal {A}},{\mathcal {B}})$ is a ${\mathcal {A}}^\wedge$-cotorsion pair with $\mathsf{id}_{{\mathcal {A}}}({\mathcal {B}}) = 0$, where ${\mathcal {A}}^\wedge = \mathsf{Thick}({\mathcal {A}})$ by Theorem 2.11. Hence $({\mathcal {A}},{\mathcal {B}}) \in {\mathfrak {P}}$, and ${\mathfrak {C}} \subseteq {\mathfrak {P}}$. The remaining inclusion ${\mathfrak {C}} \supseteq {\mathfrak {P}}$ follows directly by Theorem 5.8. $\square$

5.2 Relative cotorsion pairs vs. covering subcategories

It is important to recall at this point how cotorsion pairs are related to covering and enveloping classes. A cotorsion pair $({\mathcal {F}},{\mathcal {G}})$ in ${\mathcal {C}}$ is said to be perfect if ${\mathcal {F}}$ is covering and ${\mathcal {G}}$ is enveloping. In this section, we propose the relative analogue of perfect cotorsion pairs, and show its relation with covering and enveloping classes.

Definition 5.9

A left ${\mathcal {S}}$-cotorsion pair $({\mathcal {F}},{\mathcal {G}})$ in ${\mathcal {C}}$ is said to be perfect if every object in ${\mathcal {S}}$ has a ${\mathcal {F}}$-cover. Perfect right${\mathcal {S}}$-cotorsion pairs and perfect${\mathcal {S}}$-cotorsion pairs in ${\mathcal {C}}$ are defined similarly.

As perfect cotorsion pairs can be obtained from certain complete cotorsion pairs, it is not surprising that their analogues relative to a thick subcategory ${\mathcal {S}}\subseteq {\mathcal {C}}$ come from special classes which are pre-covering and pre-enveloping in ${\mathcal {S}}$. Indeed, the class

$$\begin{aligned} {\mathfrak {G}} := \left\{ {\mathcal {F}}\subseteq {\mathcal {C}}: \begin{array}{ll} {\mathcal {F}} \text{ is } \text{ a } \text{ resolving } \text{ subcategory } \text{ of } {\mathcal {C}} \text{ and } \text{ closed } \text{ under } \\ \text{ direct } \text{ summands, } \text{ and } \text{ pre-covering } \text{ in } \mathsf{Thick}({\mathcal {F}}) \end{array} \right\} . \end{aligned}$$

plays an important role in Theorem 5.4 when we impose some extra conditions on ${\mathcal {C}}$ that make ${\mathcal {C}}$ into a Krull–Schmidt category. For such categories, it is possible to study some interplay between ${\mathfrak {G}}$ and the class

$$\begin{aligned} {\mathfrak {P}}' := \left\{ ({\mathcal {F}},{\mathcal {G}}) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} ({\mathcal {F}},{\mathcal {G}}) \text{ is } \text{ a } \text{ perfect } \text{ left } \mathsf{Thick}({\mathcal {F}})\text{-cotorsion } \\ \text{ pair } \text{ in } {\mathcal {C}}, \text{ with } \mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0 \text{ and } \mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {F}}\end{array} \right\} \subseteq {\mathfrak {P}}. \end{aligned}$$

For, we first show how to map elements from ${\mathfrak {P}}'$ to ${\mathfrak {G}}$. Let $\varTheta$ be the projection mapping

$$\begin{aligned} \varTheta :{\mathfrak {P}}' \longrightarrow {\mathfrak {G}} \text{ given } \text{ by } ({\mathcal {F}},{\mathcal {G}}) \mapsto {\mathcal {F}}. \end{aligned}$$

This mapping $\varTheta$ is well defined by the following result, which is a consequence of Proposition 3.5 and Lemma 5.6.

Proposition 5.10

Let $({\mathcal {F}},{\mathcal {G}})$ be a left $\mathsf{Thick}({\mathcal {F}})$-cotorsion pair in ${\mathcal {C}}$ such that $\mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$. Then, ${\mathcal {F}}$ is a left thick and a pre-covering subcategory of $\mathsf{Thick}({\mathcal {F}})$.

A right inverse for $\varTheta$ can be constructed in the case where ${\mathcal {C}}$ is Krull–Schmidt. Recall that a category is Krull–Schmidt if it is additive and if every object decomposes into a finite direct sum of objects having local endomorphism rings.

Theorem 5.11

Let ${\mathcal {C}}$ be an abelian Krull–Schmidt category with enough projectives. Then, there is an injection

$$\begin{aligned} \varOmega :{\mathfrak {G}} \longrightarrow {\mathfrak {P}}' \text{ given } \text{ by } {\mathcal {F}}\mapsto ({\mathcal {F}}, {\mathcal {G}}), \end{aligned}$$

where ${\mathcal {G}}:= {\mathcal {F}}^\perp \cap \mathsf{Thick}({\mathcal {F}})$.

Indeed, the mapping $\varOmega$ satisfies the equality $\varTheta \circ \varOmega = \mathrm{id}_{{\mathfrak {G}}}$. So $\varOmega$ will define an injection from ${\mathfrak {G}}$ to ${\mathfrak {P}}'$ as long as it is well defined. This is a consequence of the following result.

Proposition 5.12

Let ${\mathcal {C}}$ be a Krull–Schmidt abelian category with enough projectives, and ${\mathcal {S}}$ be a thick subcategory of ${\mathcal {C}}$. If ${\mathcal {F}}$ is a pre-covering subcategory of ${\mathcal {S}}$, and a left saturated subcategory of ${\mathcal {C}}$, then the following conditions hold:

• 1. For each $S \in {\mathcal {S}}$, there exists an exact sequence

  $$\begin{aligned} {\varvec{\eta }} :0 \rightarrow \mathrm {Ker}(\varphi ) \rightarrow F \xrightarrow {\varphi } S \rightarrow 0 \end{aligned}$$

  where $\varphi$ is an ${\mathcal {F}}$-cover and $\mathrm {Ker}(\varphi ) \in {\mathcal {F}}^{\perp _1}$.

• 2. ${\mathcal {F}}^\perp = {\mathcal {F}}^{\perp _1}$.

• 3. The subcategories ${\mathcal {F}}$ and ${\mathcal {G}}:= {\mathcal {F}}^\perp \cap {\mathcal {S}}$ form a perfect left ${\mathcal {S}}$-cotorsion pair $({\mathcal {F}},{\mathcal {G}})$ in ${\mathcal {C}}$ with $\mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$.

Proof

Part 2. follows by the fact that ${\mathcal {C}}$ has enough projectives and that ${\mathcal {F}}$ is resolving in ${\mathcal {C}}$, while part 3. is a direct consequence of 1. and 2. So we only focus on proving 1. Let $S \in {\mathcal {S}}$. On the one hand, S has an ${\mathcal {F}}$-pre-cover. Since ${\mathcal {C}}$ is a Krull–Schmidt category, by Krause [33, Corollary 4.4] we have that the endomorphism ring $\mathrm{End}_{{\mathcal {C}}}(S)$ is semi-perfect. On the other hand, using Göbel and Trlifaj [24, Corollary 2.1.10 (b)], it follows that S has an ${\mathcal {F}}$-cover, say $\varphi$, which also can be taken epic since $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {F}}$. Thus, we obtain a short exact sequence as ${\varvec{\eta }}$. Finally, by using Wakamatsu Lemma, we can conclude that $\mathrm {Ker}(\varphi ) \in {\mathcal {F}}^{\perp _1}$. (For a proof of this lemma that works in any abelian category, see [24, Lemma 5.12]). $\square$

It is natural to ask whether it is possible to restrict $\varTheta$ on a subclass of ${\mathfrak {P}}'$, in such a way that this restriction defines a one-to-one correspondence to a subclass of ${\mathfrak {G}}$. We settle this in the following result.

Theorem 5.13

Let ${\mathcal {C}}$ be a Krull–Schmidt abelian category with enough projectives and injectives. Consider the following classes:

$$\begin{aligned} {\tilde{{\mathfrak {P}}}}&:= \left\{ ({\mathcal {F}},{\mathcal {G}}) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} ({\mathcal {F}},{\mathcal {G}}) \text{ is } \text{ a } \text{ perfect } \mathsf{Thick}({\mathcal {F}})\text{-cotorsion } \text{ pair } \text{ in } {\mathcal {C}} \text{ with } \\ \mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0, \mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {F}}, \text{ and } \mathsf{Inj}({\mathcal {C}}) \subseteq \mathsf{Thick}({\mathcal {F}}) \end{array} \right\} \subseteq {\mathfrak {P}}', \\ {\tilde{{\mathfrak {G}}}}&:= \left\{ {\mathcal {F}}\subseteq {\mathcal {C}}: \begin{array}{ll} {\mathcal {F}} \text{ is } \text{ a } \text{ left } \text{ saturated } \text{ subcategory } \text{ of } {\mathcal {C}}, \text{ pre-covering } \\ \text{ in } \mathsf{Thick}({\mathcal {F}}), \text{ and } \text{ such } \text{ that } \mathsf{Inj}({\mathcal {C}}) \subseteq \mathsf{Thick}({\mathcal {F}}) \end{array} \right\} \subseteq {\mathfrak {G}}. \end{aligned}$$

Then, there is a there is a one-to-one correspondence $\tilde{\varTheta } := \varTheta |_{{\tilde{{\mathfrak {P}}}}} :{\tilde{{\mathfrak {P}}}} \longrightarrow {\tilde{{\mathfrak {G}}}}$ given by the restriction of $\varTheta$ on ${\tilde{{\mathfrak {P}}}}$, with inverse given by the restriction $\tilde{\varOmega } := \varOmega |_{{\tilde{{\mathfrak {G}}}}} :{\tilde{{\mathfrak {G}}}} \longrightarrow {\tilde{{\mathfrak {P}}}}$ of $\varOmega$ on ${\tilde{{\mathfrak {G}}}}$.

Proof

First, it is clear that every pair $({\mathcal {F}},{\mathcal {G}})$ in ${\tilde{{\mathfrak {P}}}}$ is mapped to ${\tilde{{\mathfrak {G}}}}$ via $\varTheta$. On the other hand, let ${\mathcal {F}}\in {\tilde{{\mathfrak {G}}}}$. By Proposition 5.12 we have that $({\mathcal {F}}, {\mathcal {G}})$ is a perfect left $\mathsf{Thick}({\mathcal {F}})$-cotorsion pair in ${\mathcal {C}}$ with $\mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$, the inclusion $\mathsf{Inj}({\mathcal {C}}) \subseteq \mathsf{Thick}({\mathcal {F}})$ is true by hypothesis, and $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {F}}$ holds since ${\mathcal {F}}$ is resolving in ${\mathcal {C}}$. It is only left to show that $({\mathcal {F}},{\mathcal {G}})$ is a perfect right $\mathsf{Thick}({\mathcal {F}})$-cotorsion pair in ${\mathcal {C}}$. We split the rest of the proof into several parts:

• First, note that for ${\mathcal {G}}:= {\mathcal {F}}^\perp \cap \mathsf{Thick}({\mathcal {F}})$ the containment $\mathsf{Inj}({\mathcal {C}}) \subseteq {\mathcal {G}}$ is clear.

• Now we prove that $({\mathcal {F}},{\mathcal {G}})$ is a right $\mathsf{Thick}({\mathcal {F}})$-cotorsion pair in ${\mathcal {C}}$. Note that we only verify the pre-envelope condition in the dual of Proposition 3.5, that is, we show that for any $S \in \mathsf{Thick}({\mathcal {F}})$ there exists a short exact sequence

  $$\begin{aligned} {\varvec{\varepsilon }} :0 \rightarrow S \rightarrow G \rightarrow F \rightarrow 0 \end{aligned}$$

  where $F \in {\mathcal {F}}$ and $G \in {\mathcal {G}}$. On the one hand, since ${\mathcal {C}}$ has enough injectives and $\mathsf{Inj}({\mathcal {C}}) \subseteq \mathsf{Thick}({\mathcal {F}})$, there exists a short exact sequence

  $$\begin{aligned} \varvec{\iota } :0 \rightarrow S \rightarrow I \rightarrow C \rightarrow 0\end{aligned}$$

  where $I \in \mathsf{Inj}({\mathcal {C}}) \subseteq {\mathcal {G}}$ and $C \in \mathsf{Thick}({\mathcal {F}})$. On the other hand, since $({\mathcal {F}},{\mathcal {G}})$ is a left $\mathsf{Thick}({\mathcal {F}})$-cotorsion pair, for $C \in \mathsf{Thick}({\mathcal {F}})$ we can find a short exact sequence

  $$\begin{aligned} \varvec{\rho } :0 \rightarrow G' \rightarrow F \rightarrow C \rightarrow 0 \end{aligned}$$

  with $F \in {\mathcal {F}}$ and $G' \in {\mathcal {G}}$. Taking the pullback of $I \rightarrow C$ in $\varvec{\iota }$ and $F \rightarrow C$ in $\varvec{\rho }$, we obtain a short exact sequence as ${\varvec{\varepsilon }}$.

• Finally, we show that ${\mathcal {G}}$ is a right saturated subcategory of ${\mathcal {C}}$. We already know that ${\mathcal {G}}$ contains the injective objects of ${\mathcal {C}}$. Note also that ${\mathcal {G}}:= {\mathcal {F}}^\perp \cap \mathsf{Thick}({\mathcal {F}})$ is clearly closed under direct summands in ${\mathcal {C}}$, extensions and cokernels of monomorphisms between its objects.

Having proved the previous three facts, note also that ${\mathcal {G}}$ is pre-enveloping in $\mathsf{Thick}({\mathcal {F}})$. Then, by the dual of Proposition 5.12, it follows that ${\mathcal {G}}$ is the right half of a perfect right $\mathsf{Thick}({\mathcal {F}})$-cotorsion pair in ${\mathcal {C}}$, and so ${\mathcal {G}}$ is actually enveloping in $\mathsf{Thick}({\mathcal {F}})$. Therefore, $({\mathcal {F}},{\mathcal {G}})$ is a perfect $\mathsf{Thick}({\mathcal {F}})$-cotorsion pair in ${\mathcal {C}}$, and thus $\tilde{\varOmega }$ is well defined. The proof that $\tilde{\varOmega }$ is the inverse of $\tilde{\varTheta }$ is straightforward. $\square$

Using Theorem 5.13, the correspondence from Theorem 5.4 can be extended in the case where ${\mathcal {C}}$ is a Krull–Schmidt abelian category with enough projectives and injectives. Specifically, we have the following result.

Corollary 5.14

Let ${\mathcal {C}}$ be a Krull–Schmidt abelian category with enough projectives and injectives. Then, there exists a one-to-one correspondence between the classes ${\tilde{{\mathfrak {P}}}}$, ${\tilde{{\mathfrak {G}}}}$ and

$$\begin{aligned} \tilde{{\mathfrak {F}}} := \left\{ ({\mathcal {X}}, \omega ) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} ({\mathcal {X}},\omega ) \text{ is } \text{ a } \text{ left } \text{ Frobenius } \text{ pair } \text{ in } {\mathcal {C}}, \\ \text{ with } \mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}, \text{ and } \mathsf{Inj}({\mathcal {C}}) \subseteq {\mathcal {X}}^\wedge \end{array} \right\} . \end{aligned}$$

Moreover, ${\tilde{{\mathfrak {P}}}}$ is equal to the class

$$\begin{aligned} {\tilde{\mathfrak {C}}} := \left\{ ({\mathcal {A}},{\mathcal {B}}) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} ({\mathcal {A}},{\mathcal {B}}) \text{ is } \text{ a } \text{ left } \text{ weak } \text{ AB } \text{ context } \text{ in } {\mathcal {C}}, \\ \text{ with } \mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {A}}, \text{ and } \mathsf{Inj}({\mathcal {C}}) \subseteq \mathsf{Thick}({\mathcal {A}}) \end{array} \right\} . \end{aligned}$$

5.3 Some remarks on perfect cotorsion pairs

The problem of obtaining covers by subcategories of modules has had an increasing interest recently in homological algebra and representation theory of algebras. This in part has been motivated by the Flat Cover Conjecture, settled by Bican et al. [9], which states that every module over an arbitrary ring has a flat cover. Several authors have studied conditions under which it is possible to obtain covers. For example, it is known that every module over a perfect ring has a projective cover. This result is also valid in the category ${\mathsf{mod}}(\varLambda )$ of finitely generated modules over an Artin R-algebra $\varLambda$, where R is a commutative Artinian ring with identity. In a more general context, Holm and Jørgensen have established in [29, Theorem 3.4] certain conditions under which a subcategory ${\mathcal {F}}$ of R-modules is covering. Namely, if ${\mathcal {F}}$ contains the ground ring R and is closed under extensions , direct sums, pure submodules, and pure quotient of modules, then $({\mathcal {F}},{\mathcal {F}}^{\perp _1})$ is a perfect cotorsion pair in $\mathsf{Mod}(R)$, and hence ${\mathcal {F}}$ is covering. In the following result, which is a consequence of Proposition 3.3 and Theorem 5.13, we provide other conditions under which a subcategory of objects in an abelian category is covering.

Corollary 5.15

Let ${\mathcal {C}}$ be a Krull–Schmidt abelian category with enough projectives and injectives. Then, there is a one-to-one correspondence between the following classes:

$$\begin{aligned} {\tilde{{\mathfrak {P}}}}({\mathcal {C}})&:= \left\{ ({\mathcal {F}},{\mathcal {G}}) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} ({\mathcal {F}},{\mathcal {G}}) \text{ is } \text{ a } \text{ perfect } \text{ hereditary } \text{ cotorsion } \\ \text{ pair } \text{ in } {\mathcal {C}} \text{ with } \mathsf{Thick}({\mathcal {F}}) = {\mathcal {C}}\end{array} \right\} , \\ {\tilde{{\mathfrak {G}}}}({\mathcal {C}})&:= \left\{ {\mathcal {F}}\subseteq {\mathcal {C}}: \begin{array}{ll} {\mathcal {F}} \text{ is } \text{ a } \text{ left } \text{ saturated } \text{ and } \text{ a } \text{ pre-covering } \text{ subcategory } \text{ of } {\mathcal {C}}, \\ \text{ such } \text{ that } \mathsf{Thick}({\mathcal {F}}) = {\mathcal {C}}\end{array} \right\} . \end{aligned}$$

Remark 5.16

As an application, consider the case ${\mathcal {C}}:= {\mathsf{mod}}(\varLambda )$, where $\varLambda$ is an Artin algebra. Auslander and Reiten proved in [3, Proposition 3.3] that $({\mathcal {F}},{\mathcal {F}}^\perp )$ is a perfect and hereditary cotorsion pair in ${\mathsf{mod}}(\varLambda )$ with ${\mathcal {F}}^\wedge = {\mathsf{mod}}(\varLambda )$, whenever ${\mathcal {F}}$ is a left saturated and a pre-covering subcategory of ${\mathsf{mod}}(\varLambda )$ such that ${\mathcal {F}}^\wedge = {\mathsf{mod}}(\varLambda )$. The previous corollary states that these two assertions are in fact equivalent.

5.4 Relationship with some Auslander–Reiten correspondence theorems

We give some remarks on the relation between perfect cotorsion pairs, pre-enveloping subcategories, and cotilting modules, within the framework of the correspondences we have studied so far. Our motivation for this comes from the following correspondence theorem proved by Auslander and Reiten in their seminal paper [3].

For every $C \in {\mathsf{mod}}(\varLambda )$, we denote by [C] the isoclass of C.

Theorem 5.17

Let $\varLambda$ be an Artin R-algebra. Then, there exist one-to-one correspondences between:

• (a) the isoclasses of basic finitely generated cotilting $\varLambda$-modules;

• (b) the pre-covering and left saturated subcategories ${\mathcal {F}}\subseteq {\mathsf{mod}}(\varLambda )$ with ${\mathcal {F}}^\wedge = {\mathsf{mod}}(\varLambda )$;

• (c) the complete cotorsion pairs $({\mathcal {F}},{\mathcal {G}})$ with ${\mathcal {F}}$ left saturated and ${\mathcal {F}}^\wedge = {\mathsf{mod}}(\varLambda )$;

• (d) the pre-enveloping and right saturated subcategories of $\mathsf{inj}_{\infty }(\varLambda )$, where $\mathsf{inj}_{\infty }(\varLambda )$ denotes the subcategory of finitely generated left $\varLambda$-modules with finite injective dimension.

The correspondence (a) $\leftrightarrow$ (b) is given by $[C] \mapsto {}^\perp C$, with inverse ${\mathcal {F}}\mapsto [C_{\mathcal {F}}]$, where $C_{\mathcal {F}}$ is the finitely generated basic cotilting $\varLambda$-module defined as the direct sum of indecomposable ${\mathcal {F}}$-injective finitely generated $\varLambda$-modules. The proof of this can be found in [41, Theorem VIII.2.2 (c)] or in [3, Theorem 5.5 (a)]. On the other hand, we have a mapping (a) $\rightarrow$ (c) given by $[C] \mapsto ({}^\perp C, \mathsf{add}(C)^\wedge )$, with inverse $({\mathcal {F}},{\mathcal {G}}) \mapsto [C_{{\mathcal {F}}\cap {\mathcal {G}}}]$, where $C_{{\mathcal {F}}\cap {\mathcal {G}}}$ is the direct sum of pairwise non-isomorphic indecomposable finitely generated $\varLambda$-modules in ${\mathcal {F}}\cap {\mathcal {G}}$. This fact is proven in [41, Corollary VIII.2.3 (b)]. Finally, in [3, Theorem 5.5 (b)] or [41, Theorem VIII.2.2 (d)], one can check that the correspondence between (a) and (d) is defined by mappings $[C] \mapsto \mathsf{add}(C)^\wedge$ and ${\mathcal {G}}\mapsto [C_{\mathcal {G}}]$, where $C_{{\mathcal {G}}}$ is the di rect sum of pairwise non-isomorphic indecomposable ${\mathcal {G}}$-projective finitely generated $\varLambda$-modules.

Remark 5.18

In the case the Artin algebra $\varLambda$ is basic, the correspondence (a) $\leftrightarrow$ (b) $\leftrightarrow$ (c) in Theorem 5.17 can be extended to a class of model structures on ${\mathsf{mod}}(\varLambda )$ satisfying a series of four conditions (see Beligiannis and Reiten [7, Theorem VIII 5.8] for details). We tackle this point of model structures again and in a different way in Sect. 5.5, where we establish a one-to-one correspondence between projective AB model structures, strong left Frobenius pairs, and certain ${\mathcal {S}}$-cotorsion pairs. The approach in Sect. 5.5 will be different to the one presented in this section, as these ${\mathcal {S}}$-cotorsion pairs will be relative to ${\mathcal {S}}:= \mathsf{Thick}({\mathcal {F}})$ and satisfying $\mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0$ and ${\mathcal {F}}\cap {\mathcal {G}}= \mathsf{Proj}({\mathcal {C}})$, and so not necessarily in ${\tilde{{\mathfrak {P}}}}({\mathcal {C}})$.

Theorem 5.17 is one of the motivations of Corollary 5.15. This can be more appreciated if we explain how to present this theorem in a more general context. Before that, recall that if $\varLambda$ is an Artin R-algebra, a finitely generated $\varLambda$-module $M \in {\mathsf{mod}}(\varLambda )$ is called:

• cotilting provided that:

  • 1. $\mathsf{id}(C) < \infty$,

  • 2. $\mathsf{Ext}^i_R(C,C) = 0$ for every $i > 0$, and

  • 3. $\mathsf{resdim}_{\mathsf{add}(C)}(I) < \infty$ for any finitely generated injective $\varLambda$-module I;

• basic if in a direct sum decomposition of C, no indecomposable module appears more than once.

Let $\mathsf{Inj}_\infty ({\mathcal {C}})$ denote the class of objects of ${\mathcal {C}}$ with finite injective dimension. Let us present the following definition in order to simplify some statements and notations.

Definition 5.19

We say that an abelian category ${\mathcal {C}}$ with enough projectives and injectives is an IP-finite category if for any right saturated and special pre-enveloping subcategory ${\mathcal {X}}\subseteq {\mathcal {C}}$, the following equivalence holds true:

$$\begin{aligned} {\mathcal {X}}\subseteq \mathsf{Inj}_\infty ({\mathcal {C}}) \text{ if, } \text{ and } \text{ only } \text{ if, } ({}^\perp {\mathcal {X}})^\wedge = {\mathcal {C}}. \end{aligned}$$

Proposition 5.20

For any IP-finite category ${\mathcal {C}}$, the following statements hold:

• 1. For the classes

  $$\begin{aligned} {\tilde{{\mathfrak {G}}}}_\mathrm{IP}({\mathcal {C}})&:= \left\{ {\mathcal {G}}\subseteq \mathsf{Inj}_\infty ({\mathcal {C}}) : \begin{array}{ll} {\mathcal {G}} \text{ is } \text{ a } \text{ right } \text{ saturated } \text{ and } \text{ a } \text{ special } \\ \text{ pre-enveloping } \text{ subcategory } \text{ of } {\mathcal {C}}\end{array} \right\} , \\ {\tilde{{\mathfrak {P}}}}_\mathrm{IP}({\mathcal {C}})&:= \left\{ ({\mathcal {F}},{\mathcal {G}}) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} ({\mathcal {F}},{\mathcal {G}}) \text{ is } \text{ a } \text{ complete } \text{ hereditary } \text{ cotorsion } \\ \text{ pair } \text{ in } {\mathcal {C}} \text{ with } \mathsf{Thick}({\mathcal {F}}) = {\mathcal {C}}\end{array} \right\} , \end{aligned}$$

  there is a one-to-one correspondence

  $$\begin{aligned} \tilde{\varOmega }_\mathrm{IP} :{\tilde{{\mathfrak {G}}}}_\mathrm{IP}({\mathcal {C}}) \longrightarrow {\tilde{{\mathfrak {P}}}}_\mathrm{IP}({\mathcal {C}}) \text{ given } \text{ by } {\mathcal {G}}\mapsto ({}^\perp {\mathcal {G}},{\mathcal {G}}), \end{aligned}$$

  with inverse given by the projection $(\mathcal {F,G}) \mapsto {\mathcal {G}}$ for any $({\mathcal {F}},{\mathcal {G}}) \in {\tilde{{\mathfrak {P}}}}_\mathrm{IP}({\mathcal {C}})$.

• 2. For the class

  $$\begin{aligned} {\tilde{\mathfrak {C}}}_\mathrm{IP}({\mathcal {C}}) := \{ (\mathcal {A,B}) \subseteq {\mathcal {C}}\times {\mathcal {C}}{ \mathrm : } (\mathcal {A,B}) \text{ is } \text{ a } \text{ left } \text{ AB } \text{ context } \text{ in } {\mathcal {C}}\}, \end{aligned}$$

  the equality ${\tilde{{\mathfrak {P}}}}_\mathrm{IP}({\mathcal {C}}) = {\tilde{\mathfrak {C}}}_\mathrm{IP}({\mathcal {C}})$ holds true.

• 3. For the class

  $$\begin{aligned} \tilde{{\mathfrak {F}}}_\mathrm{IP}({\mathcal {C}}) := \{ ({\mathcal {X}},\omega ) \subseteq {\mathcal {C}}\times {\mathcal {C}}{ \mathrm : } ({\mathcal {X}},\omega ) \text{ is } \text{ a } \text{ left } \text{ Frobenius } \text{ pair } \text{ in } {\mathcal {C}} \text{ such } \text{ that } {\mathcal {X}}^\wedge = {\mathcal {C}}\}, \end{aligned}$$

  there is a one-to-one correspondence

  $$\begin{aligned} \tilde{\varPsi }_\mathrm{IP} :{\tilde{\mathfrak {C}}}_\mathrm{IP}({\mathcal {C}}) \longrightarrow \tilde{{\mathfrak {F}}}_\mathrm{IP}({\mathcal {C}}) \text{ given } \text{ by } (\mathcal {A,B}) \mapsto ({\mathcal {A}},{\mathcal {A}}\cap {\mathcal {B}}) \end{aligned}$$

  with inverse

  $$\begin{aligned} \tilde{\varPhi }_\mathrm{IP} :\tilde{{\mathfrak {F}}}_\mathrm{IP}({\mathcal {C}}) \longrightarrow {\tilde{\mathfrak {C}}}_\mathrm{IP}({\mathcal {C}}) \text{ given } \text{ by } ({\mathcal {X}},\omega ) \mapsto ({\mathcal {X}},\omega ^\wedge ). \end{aligned}$$

Proof

• 1. Let us check that the mapping $\tilde{\varOmega }_{\mathsf{IP}}$ is well defined. It suffices to show that $({}^\perp {\mathcal {G}},{\mathcal {G}})$ is indeed a cotorsion pair in ${\mathcal {C}}$ for any ${\mathcal {G}}\in {\tilde{{\mathfrak {G}}}}_\mathrm{IP}({\mathcal {C}})$ with $\mathsf{Thick}({}^\perp {\mathcal {G}}) = {\mathcal {C}}$. The fact that $({}^\perp {\mathcal {G}},{\mathcal {G}})$ is complete and hereditary will follow from the hypothesis that ${\mathcal {C}}$ has enough projectives and injectives, and from the properties of ${\mathcal {G}}$. First, note that the subcategories ${}^\perp {\mathcal {G}}$ and ${\mathcal {G}}$ are left thick and right thick, respectively, where ${\mathcal {G}}\subseteq {\mathcal {C}}= ({}^\perp {\mathcal {G}})^\wedge$ since ${\mathcal {G}}\subseteq \mathsf{Inj}_\infty ({\mathcal {C}})$ and ${\mathcal {C}}$ is an IP-finite category. On the one hand, ${}^\perp {\mathcal {G}}\cap {\mathcal {G}}$ is clearly a ${}^\perp {\mathcal {G}}$-injective relative cogenerator in ${}^\perp {\mathcal {G}}$. Thus, using Theorem 2.16 we have that the equality ${\mathcal {G}}= ({}^\perp {\mathcal {G}})^\wedge \cap ({}^\perp {\mathcal {G}})^{\perp _1} = ({}^\perp {\mathcal {G}})^{\perp _1}$, that is, $({}^\perp {\mathcal {G}},{\mathcal {G}})$ is a cotorsion pair in ${\mathcal {C}}$. On the other hand, Theorem 2.11 implies that that $({}^\perp {\mathcal {G}})^\wedge = \mathsf{Thick}({}^\perp {\mathcal {G}})$.

• 2. The containments ${\tilde{{\mathfrak {P}}}}_{\mathsf{IP}}({\mathcal {C}}) \supseteq {\tilde{\mathfrak {C}}}_{\mathsf{IP}}({\mathcal {C}})$ and ${\tilde{{\mathfrak {P}}}}_{\mathsf{IP}}({\mathcal {C}}) \subseteq {\tilde{\mathfrak {C}}}_{\mathsf{IP}}({\mathcal {C}})$ follow by Proposition 5.5 and Theorem 5.8, respectively.

• 3. Finally, it is not hard to see that the mappings $\tilde{\varPhi }_\mathrm{AR}$ and $\tilde{\varPsi }_\mathrm{AR}$ are well defined and inverse to each other.

$\square$

Remark 5.21

Consider the category ${\mathsf{mod}}(\varLambda )$ of finitely generated left modules over an Artin algebra $\varLambda$. In [3, Propositions 5.3, 5.5], Auslander and Reiten proved that if ${\mathcal {G}}$ is a coresolving and pre-enveloping subcategory of ${\mathsf{mod}}(\varLambda )$, closed under direct summands in ${\mathsf{mod}}(\varLambda )$, and ${}^\perp {\mathcal {G}}$ is the associated resolving and pre-covering subcategory of ${\mathsf{mod}}(\varLambda )$, then $({}^\perp {\mathcal {G}})^\wedge = {\mathsf{mod}}(\varLambda )$ if and only if ${\mathcal {G}}\subseteq \mathsf{inj}_{\infty }(\varLambda )$.

The following result is a categorical version of Theorem 5.17. It is a consequence of Proposition 5.20 and Corollary 5.15. Recall from Corollary 5.15 the definitions of the classes ${\tilde{{\mathfrak {P}}}}({\mathcal {C}})$ and ${\tilde{{\mathfrak {G}}}}({\mathcal {C}})$.

Corollary 5.22

Let ${\mathcal {C}}$ be an IP-finite and Krull–Schmidt category. Then, the following conditions hold true:

• 1. ${\tilde{{\mathfrak {P}}}}_{\mathsf{IP}}({\mathcal {C}}) = {\tilde{{\mathfrak {P}}}}({\mathcal {C}})$.

• 2. There exists a one-to-one correspondence between the classes ${\tilde{{\mathfrak {G}}}}_{\mathsf{IP}}({\mathcal {C}})$ and ${\tilde{{\mathfrak {G}}}}({\mathcal {C}})$.

Proof

By Corollary 5.15 and Proposition 5.20, we have already established one-to-one correspondences ${\tilde{{\mathfrak {G}}}}_{\mathsf{IP}}({\mathcal {C}}) \leftrightarrow {\tilde{{\mathfrak {P}}}}_{\mathsf{IP}}({\mathcal {C}})$ and ${\tilde{{\mathfrak {P}}}}({\mathcal {C}}) \leftrightarrow {\tilde{{\mathfrak {G}}}}({\mathcal {C}})$. On the other hand, it is clear that ${\tilde{{\mathfrak {P}}}}({\mathcal {C}}) \subseteq {\tilde{{\mathfrak {P}}}}_\mathrm{IP}({\mathcal {C}})$, while the remaining inclusion ${\tilde{{\mathfrak {P}}}}_\mathrm{IP}({\mathcal {C}}) \subseteq {\tilde{{\mathfrak {P}}}}({\mathcal {C}})$ holds by Proposition 5.12 and its dual, by setting ${\mathcal {S}}:= {\mathcal {C}}$. Hence, 1. and 2. follow. $\square$

The following result gives us a characterization of perfect and hereditary cotorsion pairs in ${\mathsf{mod}}(\varLambda )$ as cotilting cotorsion pairs, as a consequence of Corollary 5.22.

Corollary 5.23

Let $\varLambda$ be an Artin R-algebra. Then, a cotorsion pair $({\mathcal {F}},{\mathcal {G}})$ in ${\mathsf{mod}}(\varLambda )$ is perfect and hereditary with ${\mathcal {F}}^\wedge = {\mathsf{mod}}(\varLambda )$ if, and only if, it is of the form $({}^\perp C,({}^\perp C)^\perp )$ for some finitely generated cotilting $\varLambda$-module C. Moreover, for every finitely generated cotilting $\varLambda$-module C, one has the equality $\mathsf{add}(C)^\wedge = ({}^\perp C)^\perp$ in ${\mathsf{mod}}(\varLambda )$.

5.5 Strong Frobenius pairs vs. Hovey triples vs. AB model structures

We devote the last part of this section to complement the correspondences studied before, now involving the AB model structures in the interplay. We restrict out attention to the following subclass of ${\mathfrak {F}}$,

$$\begin{aligned} \text {s}{\mathfrak {F}} := \left\{ ({\mathcal {X}}, \omega ) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} ({\mathcal {X}},\omega ) \text{ is } \text{ a } \text{ strong } \text{ left } \text{ Frobenius } \text{ pair } \text{ in } {\mathcal {C}}\\ \text{ such } \text{ that } \mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}^\wedge \end{array} \right\} , \end{aligned}$$

and show how this class is in one-to-one correspondence with the AB model structures.

Proposition 5.24

Let ${\mathcal {C}}$ be an abelian category with enough projectives. If $({\mathcal {X}},\omega )$ is a strong left Frobenius pair in ${\mathcal {C}}$ with $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}^\wedge$, then the ${\mathcal {X}}^\wedge$-cotorsion pairs $({\mathcal {X}},\omega ^\wedge )$ and $(\omega ,{\mathcal {X}}^\wedge )$ in ${\mathcal {C}}$ are both left strongly hereditary in ${\mathcal {C}}$.

Proof

By Proposition 4.6, we already know that $({\mathcal {X}},\omega ^\wedge )$ and $(\omega ,{\mathcal {X}}^\wedge )$ are hereditary ${\mathcal {X}}^\wedge$-cotorsion pairs in ${\mathcal {C}}$. On the one hand, by Proposition 3.10 we have $\mathsf{Proj}({\mathcal {C}}) = \mathsf{Proj}({\mathcal {X}}^\wedge )$. On the other hand, $\mathsf{Proj}({\mathcal {X}}^\wedge ) \subseteq {\mathcal {X}}, \omega$. Hence, $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}, \omega$. The fact that ${\mathcal {X}}$ and $\omega$ are resolving in ${\mathcal {C}}$ follows by Remark 3.11. $\square$

Consider the following class:

$$\begin{aligned} {\mathfrak {T}} := \left\{ ({\mathcal {X}},\omega ) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} \omega \subseteq {\mathcal {X}} \text{ is } \text{ closed } \text{ under } \text{ direct } \text{ summands } \text{ in } {\mathcal {X}}, \\ {\mathcal {X}}^\wedge \text{ is } \text{ an } \text{ exact } \text{ subcategory } \text{ of } {\mathcal {C}}, \text{ and } ({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge ) \\ \text{ is } \text{ a } \text{ left } \text{ strongly } \text{ hereditary } \text{ Hovey } \text{ triple } \text{ in } {\mathcal {X}}^\wedge \end{array} \right\} . \end{aligned}$$

In the next lines, we prove that the classes $\text {s}{\mathfrak {F}}$ and ${\mathfrak {T}}$ coincide. We begin with the following property of Hovey triples.

Proposition 5.25

Let ${\mathcal {C}}$ be an abelian category with enough projectives, and ${\mathcal {S}}\subseteq {\mathcal {C}}$ be a thick subcategory of ${\mathcal {C}}$. If $(\mathcal {F,W,S})$ is a left strongly hereditary Hovey triple in ${\mathcal {S}}$, then $({\mathcal {F}}, {\mathcal {F}}\cap \mathcal {W})$ is a strong left Frobenius pair in ${\mathcal {C}}$ where ${\mathcal {F}}\cap \mathcal {W} = \mathsf{Proj}({\mathcal {C}})$.

Proof

Set $\omega := {\mathcal {F}}\cap \mathcal {W}$. By hypothesis, $({\mathcal {F}}, \mathcal {W})$ is a left strongly hereditary ${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$. Now by part 2. in Theorem 3.12, $({\mathcal {F}}, \omega )$ is a left Frobenius pair in ${\mathcal {C}}$. On the other hand, by condition 3. in Proposition 3.5 applied to the ${\mathcal {S}}$-cotorsion pair $(\omega , {\mathcal {S}})$, we have that for every $F \in {\mathcal {F}}\subseteq {\mathcal {S}}$ there exists a short exact sequence

$$\begin{aligned} 0 \rightarrow F' \rightarrow W \rightarrow F \rightarrow 0 \end{aligned}$$

where $W \in \omega$ and $F' \in {\mathcal {S}}$. Using that ${\mathcal {F}}$ is closed under kernels of epimorphisms between its objects, we have $F' \in {\mathcal {F}}$. It follows that $\omega$ is a relative generator in ${\mathcal {F}}$. It is only left to show $\mathsf{pd}_{{\mathcal {F}}}(\omega ) = 0$ in order to conclude that $({\mathcal {F}},\omega )$ is a strong left Frobenius pair in ${\mathcal {C}}$. This will follow after proving ${\mathcal {F}}\cap \mathcal {W} = \mathsf{Proj}({\mathcal {C}})$.

From the left strongly hereditary ${\mathcal {S}}$-cotorsion pair $(\omega , {\mathcal {S}})$ in ${\mathcal {C}}$, it is clear that $\omega = \mathsf{Proj}({\mathcal {S}})$. On the other hand, since ${\mathcal {C}}$ has enough projectives, we have by Proposition 3.10 that $\mathsf{Proj}({\mathcal {S}}) = \mathsf{Proj}({\mathcal {C}})$. Therefore, the result follows. $\square$

Remark 5.26

The previous proposition is also valid if we replace ${\mathcal {S}}$ by an exact subcategory ${\mathcal {E}} \subseteq {\mathcal {C}}$. However, it is stated and proven in terms of ${\mathcal {S}}$ due to the simplicity of its proof and the purposes of this paper.

Theorem 5.27

The equality $\text {s}{\mathfrak {F}} = {\mathfrak {T}}$ holds true in any abelian category ${\mathcal {C}}$ with enough projectives.

Proof

Let $({\mathcal {X}},\omega ) \in \text {s}{\mathfrak {F}}$, that is, $({\mathcal {X}},\omega )$ is a strong left Frobenius pair in ${\mathcal {C}}$ such that $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}^\wedge$. By Proposition 5.24, the ${\mathcal {X}}^\wedge$-cotorsion pairs $({\mathcal {X}},\omega ^\wedge )$ and $(\omega , {\mathcal {X}}^\wedge ) = ({\mathcal {X}}\cap \omega ^\wedge , {\mathcal {X}}^\wedge )$ are left strongly hereditary. Then the Hovey triple $({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge )$ is left strongly hereditary, and hence $({\mathcal {X}},\omega ) \in {\mathfrak {T}}$.

Now let $({\mathcal {X}},\omega ) \in {\mathfrak {T}}$, that is, $({\mathcal {X}},\omega ^\wedge ,{\mathcal {X}}^\wedge )$ is a left strong hereditary Hovey triple in the exact category ${\mathcal {X}}^\wedge$ such that $\omega \subseteq {\mathcal {X}}$ is closed under direct summands in ${\mathcal {X}}$. Then by Proposition 5.25, we have that $({\mathcal {X}}, {\mathcal {X}}\cap \omega ^\wedge )$ is a strong left Frobenius pair in ${\mathcal {C}}$. It is only left to show that $\omega = {\mathcal {X}}\cap \omega ^\wedge$. The inclusion $\omega \subseteq {\mathcal {X}}\cap \omega ^\wedge$ is clear. Now suppose $X \in {\mathcal {X}}\cap \omega ^\wedge$. Since $X \in \omega ^\wedge$, there exists a short exact sequence

$$\begin{aligned} 0 \rightarrow W' \rightarrow W \rightarrow X \rightarrow 0 \end{aligned}$$

with $W \in \omega$ and $W' \in \omega ^\wedge$. On the other hand, $X \in {\mathcal {X}}$ and $({\mathcal {X}}, \omega ^\wedge )$ is a cotorsion pair in ${\mathcal {X}}^\wedge$, and so the previous sequence splits (as a short exact sequence in ${\mathcal {X}}^\wedge$), which implies that X is a direct summand of $W \in \omega$, and so $X \in \omega$. Therefore, ${\mathcal {X}}\cap \omega ^\wedge \subseteq \omega$. $\square$

The following result is a consequence of Proposition 5.25 and Theorem 5.27.

Corollary 5.28

Let $({\mathcal {X}},\omega )$ be a strong left Frobenius pair in an abelian category ${\mathcal {C}}$ with enough projectives. If $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {X}}^\wedge$, then $\omega = \mathsf{Proj}({\mathcal {C}})$.

To conclude this section, we show that there exists a one-to-one correspondence between $\text {s}{\mathfrak {F}} = {\mathfrak {T}}$ and the following collection of exact model structures:

$$\begin{aligned} \mathfrak {M} := \left\{ ({\mathcal {S}},{\mathcal {M}}) : \begin{array}{ll} {\mathcal {S}} \text{ is } \text{ a } \text{ thick } \text{ subcategory } \text{ of } {\mathcal {C}} \text{ and } {\mathcal {M}} = (\mathcal {Q,T,R}) \text{ is } \\ \text{ a } \text{ projective } \text{ exact } \text{ model } \text{ structure } \text{ on } {\mathcal {S}} \text{ such } \text{ that } {\mathcal {Q}} \text{ is } \\ \text{ resolving } \text{ in } {\mathcal {C}}, \text{ and } {\mathcal {T}} \subseteq {\mathcal {Q}}^\wedge \end{array} \right\} . \end{aligned}$$

Theorem 5.29

Let ${\mathcal {C}}$ be an abelian category with enough projectives. Then, the mapping

$$\begin{aligned} \varXi :\text {s}{\mathfrak {F}} \longrightarrow \mathfrak {M} \text{ given } \text{ by } ({\mathcal {X}}, \omega ) \mapsto ({\mathcal {X}}^\wedge ,{\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega )) \end{aligned}$$

defines a one-to-one correspondence, with inverse

$$\begin{aligned} \varGamma :\mathfrak {M} \longrightarrow \text {s}{\mathfrak {F}} \text{ given } \text{ by } ({\mathcal {S}},{\mathcal {M}}) \mapsto ({\mathcal {Q}}, {\mathcal {Q}} \cap {\mathcal {T}}). \end{aligned}$$

Proof

First, note that the map $\varXi$ is well defined since the exact model structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {X}},\omega )$ on ${\mathcal {X}}^\wedge$ is unique by Hovey–Gillespie correspondence. Also, we have that ${\mathcal {X}}$ is resolving in ${\mathcal {C}}$ by Theorem 5.27.

We now check $\varGamma$ is well defined. If ${\mathcal {M}} = (\mathcal {Q,T,R})$ is a projective exact model structure on ${\mathcal {S}}$, then ${\mathcal {R}} = {\mathcal {S}}$, and by Hovey–Gillespie correspondence we have that $(\mathcal {Q,T,S})$ is a Hovey triple. On the other hand, the cotorsion pair $({\mathcal {Q}} \cap {\mathcal {T}}, {\mathcal {S}})$ in ${\mathcal {S}}$ is clearly left hereditary in ${\mathcal {S}}$, and $(\mathcal {Q,T})$ is also a left hereditary cotorsion pair in ${\mathcal {S}}$ since ${\mathcal {Q}}$ is resolving in ${\mathcal {S}}$. Since ${\mathcal {S}}$ is thick, we have ${\mathcal {Q}}$ and ${\mathcal {Q}} \cap {\mathcal {T}}$ are both pre-resolving in ${\mathcal {C}}$. In order to show that the Hovey triple $(\mathcal {Q,T,S})$ is left strongly hereditary in ${\mathcal {S}}$ and apply Proposition 5.25 to conclude that $({\mathcal {Q}}, {\mathcal {Q}} \cap {\mathcal {T}})$ is a strong left Frobenius pair in ${\mathcal {C}}$, it is only left to show that $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {Q}}, {\mathcal {Q}} \cap {\mathcal {T}}$. By definition of $\mathfrak {M}$, we have $\mathsf{Proj}({\mathcal {C}}) \ subseteq {\mathcal {Q}}$. On the other hand, by Proposition 3.10, we have that $\mathsf{Proj}({\mathcal {C}}) = \mathsf{Proj}({\mathcal {S}})$, where $\mathsf{Proj}({\mathcal {S}}) = {\mathcal {Q}} \cap {\mathcal {T}}$ since the pair $({\mathcal {Q}} \cap {\mathcal {T}}, {\mathcal {S}})$ is a cotorsion pair in ${\mathcal {S}}$. It follows that $({\mathcal {Q}}, {\mathcal {Q}} \cap {\mathcal {T}}) \in \text {s}{\mathfrak {F}}$.

Finally, to check that $\varXi$ and $\varGamma$ are inverse to each other, we first need to check the equalities ${\mathcal {S}}= {\mathcal {Q}}^\wedge$ and ${\mathcal {T}} = ({\mathcal {Q}} \cap {\mathcal {T}})^\wedge$, for every $({\mathcal {S}},(\mathcal {Q,T,R})) \in \mathfrak {M}$.

• To prove ${\mathcal {S}}= {\mathcal {Q}}^\wedge$, note that we have ${\mathcal {Q}}^\wedge \subseteq {\mathcal {S}}$ since ${\mathcal {S}}$ is thick. Now let $S \in {\mathcal {S}}$. Since the pair $(\mathcal {Q,T})$ is complete in ${\mathcal {S}}$, there exists an exact sequence

  $$\begin{aligned} 0 \rightarrow T \rightarrow Q \rightarrow S \rightarrow 0 \end{aligned}$$

  with $Q \in {\mathcal {Q}}$ and $T \in {\mathcal {T}} \subseteq {\mathcal {Q}}^\wedge$. It follows that $S \in {\mathcal {Q}}^\wedge$.

• Now for the proof of ${\mathcal {T}} = ({\mathcal {Q}} \cap {\mathcal {T}})^\wedge$, note that $(\mathcal {Q,T})$ is a ${\mathcal {S}}$-cotorsion pair in ${\mathcal {C}}$ and that ${\mathcal {Q}}$ is revolving subcategory of ${\mathcal {C}}$. Then, ${\mathcal {Q}} \cap {\mathcal {T}} \subseteq {\mathcal {T}} = {\mathcal {Q}}^{\perp _1} \cap {\mathcal {S}}= {\mathcal {Q}}^\perp \cap {\mathcal {S}}$. In particular, $\mathsf{Ext}^i_{{\mathcal {C}}}({\mathcal {Q}},{\mathcal {Q}} \cap {\mathcal {S}}) = 0$ for every $i > 0$. Thus, the hypothesis in Proposition 2.13 hold for ${\mathcal {X}}:= {\mathcal {Q}}$ and $\omega := {\mathcal {Q}} \cap {\mathcal {T}}$. Therefore, $({\mathcal {Q}} \cap {\mathcal {T}})^\wedge = {\mathcal {Q}}^\perp \cap {\mathcal {Q}}^\wedge = {\mathcal {Q}}^\perp \cap {\mathcal {S}}= {\mathcal {T}}$.

Thus, the equalities $\varXi \circ \varGamma ({\mathcal {S}},(\mathcal {Q,T,R})) = ({\mathcal {Q}}^\wedge ,{\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {Q}}, {\mathcal {Q}} \cap {\mathcal {T}})) = ({\mathcal {S}},(\mathcal {Q, T, S}))$ follow. Now if $({\mathcal {X}}, \omega ) \in \text {s}{\mathfrak {F}}$, we have that $\varGamma \circ \varXi ({\mathcal {X}},\omega ) = ({\mathcal {X}}, {\mathcal {X}}\cap \omega ^\wedge ) = ({\mathcal {X}},\omega )$, where ${\mathcal {X}}\cap \omega ^\wedge = \omega$ holds by Theorem 3.6. Therefore, $\varXi \circ \varGamma = \mathrm{id}_{\mathfrak {M}}$ and $\varGamma \circ \varXi = \mathrm{id}_{\text {s}{\mathfrak {F}}}$. $\square$

We close this section by complementing the correspondence given in Theorem 5.4 for abelian categories with enough projectives, when we restrict to the subclass $\text {s}{\mathfrak {F}}$.

Corollary 5.30

Let ${\mathcal {C}}$ be an abelian category with enough projectives. Then, there exists a one-to-one correspondence between the classes $\text {s}{\mathfrak {F}}$, $\mathfrak {M}$ and

$$\begin{aligned} \text {s}{\mathfrak {P}}&:= \left\{ ({\mathcal {F}},{\mathcal {G}}) \subseteq {\mathcal {C}}\times {\mathcal {C}}: \begin{array}{ll} ({\mathcal {F}},{\mathcal {G}}) \text{ is } \text{ a } \mathsf{Thick}({\mathcal {F}})\text{-cotorsion } \text{ pair } \text{ in } {\mathcal {C}}\\ \text{ with } \mathsf{id}_{{\mathcal {F}}}({\mathcal {G}}) = 0 \text{ and } {\mathcal {F}}\cap {\mathcal {G}}= \mathsf{Proj}({\mathcal {C}}) \end{array} \right\} \subseteq {\mathfrak {P}}. \end{aligned}$$

Namely, the restriction of the mapping $\varPhi$ from part 1. in Theorem 5.4 on $\text {s}{\mathfrak {P}}$ defines a one-to-one correspondence

$$\begin{aligned} \text {s}\varPhi := \varPhi |_{\text {s}{\mathfrak {F}}} :\text {s}{\mathfrak {F}} \longrightarrow \text {s}{\mathfrak {P}} \text{ given } \text{ by } ({\mathcal {X}},\omega ) \mapsto ({\mathcal {X}},\omega ^\wedge ), \end{aligned}$$

with inverse

$$\begin{aligned} \text {s}\varPsi := \varPsi |_{\text {s}{\mathfrak {P}}} :\text {s}{\mathfrak {P}} \longrightarrow \text {s}{\mathfrak {F}} \text{ given } \text{ by } ({\mathcal {F}},{\mathcal {G}}) \mapsto ({\mathcal {F}},{\mathcal {F}}\cap {\mathcal {G}}). \end{aligned}$$

Proof

By Theorems 5.4 and 5.29, we only need prove that $\text {s}\varPhi$ and $\text {s}\varPsi$ are well defined.

Consider $({\mathcal {X}},\omega ) \in \text {s}{\mathfrak {F}} \subseteq {\mathfrak {F}}$. We show that $\varPhi ({\mathcal {X}},\omega ) = ({\mathcal {X}},\omega ^\wedge ) \in \text {s}{\mathfrak {P}}$. First, we already know that $({\mathcal {X}},\omega ^\wedge )$ is a ${\mathcal {X}}^\wedge$-cotorsion pair in ${\mathcal {C}}$ with $\mathsf{id}_{{\mathcal {X}}}(\omega ^\wedge ) = 0$. On the other hand, since ${\mathcal {C}}$ has enough projectives, we can apply Corollary 5.28 and obtain ${\mathcal {X}}\cap \omega ^\wedge = \omega = \mathsf{Proj}({\mathcal {C}})$, thus proving $({\mathcal {X}},\omega ^\wedge ) \in \text {s}{\mathfrak {P}}$.

Now let $({\mathcal {F}},{\mathcal {G}}) \in \text {s}{\mathfrak {P}}$. On the one hand, we already know that $\varPsi ({\mathcal {F}},{\mathcal {G}}) = ({\mathcal {F}}, {\mathcal {F}}\cap {\mathcal {G}})$ is a left Frobenius pair in ${\mathcal {C}}$. Then, it is only left to show that $\omega := {\mathcal {F}}\cap {\mathcal {G}}$ is an ${\mathcal {F}}$-projective relative generator in ${\mathcal {F}}$ with $\mathsf{Proj}({\mathcal {C}}) \subseteq {\mathcal {F}}^\wedge$. This follows by the facts that ${\mathcal {F}}\cap {\mathcal {G}}= \mathsf{Proj}({\mathcal {C}})$, that ${\mathcal {C}}$ has enough projectives, and that ${\mathcal {F}}$ is pre-resolving and closed under direct summands. $\square$

6 Examples in relative Gorenstein homological algebra

In this section, we present a series of examples in relative Gorenstein homological algebra, in order to see the scope of the theory of Frobenius pairs and its connections with model category theory and Auslander–Buchweitz contexts.

The following concept will comprise several types of Gorenstein modules. Let us consider a class ${\mathcal {X}}$ of objects in an abelian category ${\mathcal {C}}$. It is said that a chain complex ${\varvec{C}} = (C_m, \partial ^{{\varvec{C}}}_m :C_m \rightarrow C_{m-1})_{m \in \mathbb {Z}}$ of objects and morphisms in ${\mathcal {C}}$ is $\mathsf{Hom}_{{\mathcal {C}}}({\mathcal {X}},-)$-acyclic if the induced complex $\mathsf{Hom}_{{\mathcal {C}}}(X,{\varvec{C}}) = (\mathsf{Hom}_R(X,C_m),\mathsf{Hom}_{{\mathcal {C}}}(X,\partial ^{{\varvec{C}}}_m))_{m \in \mathbb {Z}}$ of abelian groups and group homomorphisms is exact for any $X \in {\mathcal {X}}$. There is also a dual notion of $\mathsf{Hom}_{{\mathcal {C}}}(-,{\mathcal {X}})$-acyclic complexes.

6.1 A generalization of Gorenstein abelian model structures

Recall that an R-module M is Gorenstein projective if $M = Z_0({\varvec{P}}) = \mathrm{Ker}(\partial ^{{\varvec{P}}}_0)$ for some $\mathsf{Hom}_R(-,\mathsf{Proj}(R))$-acyclic and exact complex ${\varvec{P}}$ of projective R-modules. Let us denote by $\mathsf{GProj}(R)$ the subcategory of $\mathsf{Mod}(R)$ formed by all the Gorenstein projective R-modules.

It is easy to note from the previous definition that $\mathsf{Proj}(R)$ is a $\mathsf{GProj}(R)$-injective relative cogenerator in $\mathsf{GProj}(R)$. On the other hand, $\mathsf{Proj}(R)$ is clearly also a $\mathsf{GProj}(R)$-projective relative generator in $\mathsf{GProj}(R)$. Moreover, in Holm [27, Theorem 2.5] it is proven that $\mathsf{GProj}(R)$ is a resolving subcategory of $\mathsf{Mod}(R)$ that is also closed under direct summands. Hence, we have the following result.

Proposition 6.1

$(\mathsf{GProj}(R),\mathsf{Proj}(R))$ is a strong left Frobenius pair in $\mathsf{Mod}(R)$, for an arbitrary ring R.

Let us review some facts about Gorenstein projective R-modules from the properties of left Frobenius pairs applied to the pair $(\mathsf{GProj}(R),\mathsf{Proj}(R))$ from the previous proposition.

• First, we note that the pair $(\mathsf{Proj}(R),\mathsf{GProj}(R))$ is not necessarily a right Frobenius pair in $\mathsf{Mod}(R)$, since $\mathsf{GProj}(R)$ is not coresolving in general. However, in some particular cases one can assert that $\mathsf{GProj}(R)$ is closed under taking cokernels of monomorphisms. Specifically, setting ${\mathcal {X}}:= \mathsf{GProj}(R)$ and $\omega := \mathsf{Proj}(R)$ in Corollary 2.9 gives another way to show Holm [27, Corollary 2.11]. That is, if

  $$\begin{aligned} 0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0 \end{aligned}$$

  is a short exact sequence in $\mathsf{Mod}(R)$ with $A, B \in \mathsf{GProj}(R)$, and $\mathsf{Ext}^1_R(C,P) = 0$ for every projective R-module P, then $C \in \mathsf{GProj}(R)$.

• The pair $(\mathsf{GProj}(R), \mathsf{Proj}(R))$ satisfies the hypotheses in Proposition 2.7. So part 1. implies that $\mathsf{id}_{\mathsf{GProj}(R)}(\mathsf{Proj}(R)^\wedge ) = 0$. Note also that $\mathsf{Proj}(R)^\wedge$ coincides with the subcategory of R-modules with finite projective dimension. Thus, we obtain the well known fact that if M is a Gorenstein projective R-module, then $\mathsf{Ext}^i_R(M, W) = 0$ for every R-module W with finite projective dimension and every integer $i > 0$. This property is also stated in Holm [27, Proposition 2.3]. On the other hand, part 2. of Proposition 2.7 implies another important relation between the classes $\mathsf{GProj}(R)$ and $\mathsf{Proj}(R)$, namely, that $\mathsf{Proj}(R) = \mathsf{GProj}(R) \cap \mathsf{Proj}(R)^\wedge$. In other words, the projective dimension of a Gorenstein projective R-module is either 0 or infinite. Thus, we have another proof of Enochs and Jenda [14, Proposition 10.2.3]. These conclusions can also be obtained from the exact category approach present ed by Beligiannis in [6, Theorem 4.3].

• Using Theorem 2.11 and the fact that $(\mathsf{GProj}(R),\mathsf{Proj}(R))$ is a left Frobenius pair in $\mathsf{Mod}(R)$, we have that $\mathsf{GProj}(R)^\wedge$ is a thick subcategory of $\mathsf{Mod}(R)$. Recall from Enochs and Jenda [14, Chapter XI] that the Gorenstein projective dimension of an R-module M is defined as $\mathsf{Gpd}(M) := \mathsf{resdim}_{\mathsf{GProj}(R)}(M)$. So $\mathsf{GProj}(R)^\wedge$ is precisely the subcategory of $\mathsf{Mod}(R)$ formed by the modules with finite Gorenstein projective dimension. In the case where R is an Iwanaga–Gorenstein ring (that is, R is a two-sided noetherian ring with finite self-injective dimension at both sides) it is known that $(\mathsf{GProj}(R), \mathsf{Proj}(R)^\wedge )$ is a complete cotorsion pair in $\mathsf{Mod}(R)$. One way to see this is noticing that for such R one has $\mathsf{GProj}(R)^\wedge = \mathsf{Mod}(R)$, and then apply Theorem 2.8.

• Certain homological dimensions are defined as projective or injective dimensions relative to a certain subcategory of modules, such as the FP-injective (or absolutely pure) dimension. There are others, such as the Gorenstein projective dimension just mentioned, which are defined as a resolution dimension relative to a subcategory of modules. In the former case, the FP-injective dimension cannot be expressed as a coresolution dimension, unless we assume R is a coherent ring. This is not an inconvenience for the Gorenstein projective dimension, as indicated in Holm [27, Theorem 2.20]. This result can be obtained as a consequence of Theorem 2.10. Specifically, if we are given an R-module M with finite Gorenstein projective dimension, then

  $$\begin{aligned} \mathsf{Gpd}(M) = \mathsf{pd}_{\mathsf{Proj}(R)}(M) = \mathsf{pd}_{\mathsf{Proj}(R)^\wedge }(M). \end{aligned}$$

  In other words, we have that the following conditions are equivalent for every $n \ge 0$:

  • (a) $\mathsf{Gpd}(M) \le n$.

  • (b) $\mathsf{Ext}^i_R(M,L) = 0$ for every $i > n$ and every R-module L such that $\mathsf{pd}(L) < \infty$.

  • (c) $\mathsf{Ext}^i_R(M,P) = 0$ for every $i > n$ and every projective R-module P.

Concerning cotorsion pairs and model structures involving the class $\mathsf{GProj}(R)$, we have by Proposition 6.1 and Theorems 3.6 and 3.7 that the pairs $(\mathsf{GProj}(R), \mathsf{Proj}(R)^\wedge )$ and $(\mathsf{Proj}(R),\mathsf{GProj}(R)^\wedge )$ are $\mathsf{GProj}(R)^\wedge$-cotorsion pairs in $\mathsf{Mod}(R)$. These pairs are not in general right strongly hereditary, since the inclusions $\mathsf{Inj}(R) \subseteq \mathsf{GProj}(R)^\wedge$ and $\mathsf{Inj}(R) \subseteq \mathsf{Proj}(R)^\wedge$ are not necessarily true. However, note that these pairs are (left and right) hereditary as cotorsion pairs in the exact subcategory $\mathsf{GProj}(R)^\wedge \subseteq \mathsf{Mod}(R)$. Moreover, these two notions of hereditary cotorsion pairs coincide in the case R is an Iwanaga–Gorenstein ring, where the equalities $\mathsf{GProj}(R)^\wedge = \mathsf{Mod}(R)$ and $\mathsf{Proj}(R)^\wedge = \mathsf{Inj}(R)^\vee$ hold. Then, we have another way to obtain Enochs and Jenda [14, Remark 11.5.10]. Namely, if $\mathsf{GProj}(R)^\wedge = \mathsf{Mod}(R)$, then $(\mathsf{GProj}(R), \mathsf{Proj}(R)^\wedge )$ is a hereditary complete cotorsion pair in $\mathsf{Mod}(R)$.

We close our summary of Gorenstein homological algebra presenting an example of Auslander–Buchweitz model structures, which turns out to be a generalization of a well known projective abelian model structure on $\mathsf{Mod}(R)$.

From the strong left Frobenius pair $(\mathsf{GProj}(R),\mathsf{Proj}(R))$ in $\mathsf{Mod}(R)$, we obtain the projective AB model structure

$$\begin{aligned} {\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}(R), \mathsf{Proj}(R)) = (\mathsf{GProj}(R),\mathsf{Proj}(R)^\wedge ,\mathsf{GProj}(R)^\wedge ) \end{aligned}$$

on the subcategory $\mathsf{GProj}(R)^\wedge \subseteq \mathsf{Mod}(R)$. This model structure generalizes Hovey’s projective abelian model structure [32, Theorem 8.6] on $\mathsf{Mod}(R)$, in the case where R is an Iwanaga–Gorenstein ring. Notice we have not imposed any condition on the ground ring R in order to get ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}(R),\mathsf{Proj}(R))$. However, we do not get an abelian but an exact model structure on $\mathsf{GProj}(R)^\wedge$, an exact subcategory of $\mathsf{Mod}(R)$. On the other hand, we have already mentioned that if R is an Iwanaga–Gorenstein ring, then $\mathsf{GProj}(R)^\wedge$ coincides with $\mathsf{Mod}(R)$, and in this case, ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}(R), \mathsf{Proj}(R))$ is precisely the abelian model structure described in [32, Theorem 8.6].

Now consider the homotopy category $\mathsf{Ho}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}(R)^\wedge )$ of ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}(R), \mathsf{Proj}(R))$. By Proposition 4.10, we have that two morphisms $f, g :X \rightarrow Y$ in $\mathsf{GProj}(R)^\wedge$ are homotopic if, and only if, their difference $g - f$ factors through a projective module. The homotopy category of this model structure is the projective stable module category $\mathsf{GProj}(R) / \sim$, which is also the homotopy category of the Hovey’s projective abelian model structure $(\mathsf{GProj}(R),\mathsf{Proj}(R)^\wedge ,\mathsf{Mod}(R))$ on $\mathsf{Mod}(R)$, when R is an Iwanaga–Gorenstein ring (see [32, Sect. 9]). This stable module category coincides with the usual stable module category $\mathsf{Stmod}(R)$ in the case where R is a quasi-Frobenius ring, that is, a 0-Iwanaga–Gorenstein ring. The latter is a well known example of a Frobenius category. In the case R is arbitrary, another example of such categories is given by $\mathsf{GProj}(R)$. As a matter of fact, $\mathsf{GProj}(R) = \mathsf{Mod}(R)$ if R is quasi-Frobenius. It follows that there is a unique Frobenius model structure on $\mathsf{GProj}(R)$ with $\mathsf{Proj}(R)$ as the subcategory of trivial objects, which can also be obtained by setting ${\mathcal {C}}:= \mathsf{Mod}(R)$, ${\mathcal {X}}:= \mathsf{GProj}(R)$ and $\omega := \mathsf{Proj}(R)$ in Proposition 4.8.

Note that we can follow a dual approach to the previous results and comments, by considering the strong right Frobenius pair $(\mathsf{Inj}(R),\mathsf{GInj}(R))$ in $\mathsf{Mod}(R)$, where $\mathsf{GInj}(R)$ denotes the category of Gorenstein injective R-modules. The corresponding injective AB model structure ${\mathcal {M}}^\mathrm{inj}_\mathrm{AB}(\mathsf{Inj}(R),\mathsf{GInj}(R)) := (\mathsf{GInj}(R)^\vee ,\mathsf{Inj}(R)^\vee , \mathsf{GInj}(R))$ on $\mathsf{GInj}(R)^\vee$, coincides with Hovey’s injective model structure [32, Theorem 8.6] in the case where R is an Iwanaga–Gorenstein ring.

6.2 Left Frobenius pairs from Gorenstein subcategories

This example represents a slight generalization of the previous one and is motivated by the paper entitled “Stability of Gorenstein categories” by Sather-Wagstaff et al. [43]. We will show that $({\mathcal {G}}(\omega ),\omega )$ is a strong left Frobenius pair in an abelian category ${\mathcal {C}}$. Here, $\omega$ is a subcategory of ${\mathcal {C}}$ satisfying a series of conditions specified below, and ${\mathcal {G}}(\omega )$ denotes the Gorenstein subcategory associated to $\omega$, defined as the class of objects $M \in {\mathcal {C}}$ such that $M \simeq \mathrm{CoKer}(\partial ^{\varvec{W}}_1)$ for some $\mathsf{Hom}_{{\mathcal {C}}}(\omega ,-)$-acyclic and $\mathsf{Hom}_{{\mathcal {C}}}(-,\omega )$-acyclic chain complex $\varvec{W}$ such that $W_m \in \omega$ for every integer $m \in \mathbb {Z}$.

We list from [43] some conditions on $\omega$ that make $({\mathcal {G}}(\omega ),\omega )$ into a strong left Frobenius pair in ${\mathcal {C}}$. First, by [43, Corollaries 4.5, 4.7, and Proposition 4.11] we have that if $\mathsf{Ext}^i_{{\mathcal {C}}}(\omega ,\omega ) = 0$ for every integer $i \ge 1$, then ${\mathcal {G}}(\omega )$ is closed under extensions and direct summands, and $\omega$ is a ${\mathcal {G}}(\omega )$-injective relative cogenerator and a ${\mathcal {G}}(\omega )$-projective relative generator in ${\mathcal {G}}(\omega )$. If in addition $\omega$ is closed under taking kernels of epimorphisms between its objects, by [43, Theorem 4.12] we have the same closure property for ${\mathcal {G}}(\omega )$.

Proposition 6.2

Let $\omega$ be a class of objects in an abelian category ${\mathcal {C}}$ that is closed under direct summands and under taking kernels of epimorphisms between its objects, and such that $\mathsf{Ext}^i_{{\mathcal {C}}}(\omega ,\omega ) = 0$ for every integer $i \ge 1$. Then, $({\mathcal {G}}(\omega ),\omega )$ is a strong left Frobenius pair in ${\mathcal {C}}$.

We can deduce several properties from the previous result, complementing thus the properties of Gorenstein subcategories already discovered in [43]. Suppose $\omega$ is a class of objects in ${\mathcal {C}}$ satisfying the hypotheses of the previous proposition. First, we know by Propositions 2.7, 2.13 and 2.14 the following interactions between the classes ${\mathcal {G}}(\omega )$ and $\omega$.

Proposition 6.3

Let $\omega$ be a class of objects in ${\mathcal {C}}$ satisfying the conditions in Proposition 6.2. Then, the following conditions hold true:

• 1. $\omega = {\mathcal {G}}(\omega ) \cap \omega ^\wedge = {\mathcal {G}}(\omega ) \cap \omega ^\vee$.

• 2. ${\mathcal {G}}(\omega )^\wedge \cap {}^{\perp }\omega = {\mathcal {G}}(\omega ) = {\mathcal {G}}(\omega )^\wedge \cap {}^\perp (\omega ^\wedge )$.

• 3. $\omega ^\wedge = {\mathcal {G}}(\omega )^\perp \cap {\mathcal {G}}(\omega )^\wedge$.

Concerning cotorsion pairs and exact model structures, we have the following result from Theorem 4.1 and Proposition 4.10.

Proposition 6.4

Let $\omega$ be a class of objects in ${\mathcal {C}}$ satisfying the conditions in Proposition 6.2. Then, $({\mathcal {G}}(\omega ),\omega ^\wedge )$ and $(\omega ,{\mathcal {G}}(\omega )^\wedge )$ are complete cotorsion pairs in the exact subcategory ${\mathcal {G}}(\omega )^\wedge$. Moreover, there exists a unique exact model structure on ${\mathcal {G}}(\omega )^\wedge$ given by the Hovey triple

$$\begin{aligned} {\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {G}}(\omega ),\omega ) := ({\mathcal {G}}(\omega ),\omega ^\wedge ,{\mathcal {G}}(\omega )^\wedge ), \end{aligned}$$

whose homotopy category is equivalent to the stable category ${\mathcal {G}}(\omega ) / \sim$.

In what remains of this example, let R be a commutative noetherian ring, so that the category ${\mathsf{mod}}(R)$ of finitely generated R-modules is abelian. We apply the previous result in order to obtain finitely generated versions of the Frobenius model structure (see [31, Sect. 2.2] or Example 4.9 setting ${\mathcal {E}} := \mathsf{Mod}(R)$ with R a quasi-Frobenius ring) and the Gorenstein projective model structure (see [32, Theorem 8.6]).

Let ${\mathsf{proj}}(R)$ denote the class of finitely generated projective R-modules. It is an easy exercise to note that ${\mathsf{proj}}(R)$ is closed under direct summands and under kernels of epimorphisms in ${\mathsf{proj}}(R)$, while the condition $\mathsf{Ext}^i_R({\mathsf{proj}}(R),{\mathsf{proj}}(R)) = 0$ is clear for every integer $i > 0$. Thus, by Proposition 6.4 we have the exact model structure

$$\begin{aligned} {\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {G}}({\mathsf{proj}}(R)),{\mathsf{proj}}(R)) := ({\mathcal {G}}({\mathsf{proj}}(R)),{\mathsf{proj}}(R)^\wedge ,{\mathcal {G}}({\mathsf{proj}}(R))^\wedge ) \end{aligned}$$

on ${\mathcal {G}}({\mathsf{proj}}(R))^\wedge$ from the strong left Frobenius pair $({\mathcal {G}}({\mathsf{proj}}(R)),{\mathsf{proj}}(R))$ in $\mathsf{Mod}(R)$. Moreover, by [47, Proposition 1.4] we have that ${\mathcal {G}}({\mathsf{proj}}(R)) = \mathsf{GProj}(R) \cap {\mathsf{mod}}(R)$, and so the existence of ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathcal {G}}({\mathsf{proj}}(R)),{\mathsf{proj}}(R))$ represents somehow Hovey’s [32, Theorem 8.6] in the context of finitely generated modules.

Remark 6.5

If in addition R is a local nonregular Iwanaga–Gorenstein artinian ring, we have by [43, Example 5.7] that ${\mathcal {G}}({\mathsf{proj}}(R)) = {\mathsf{mod}}(R)$. Then, by Proposition 6.4, we have the Frobenius model structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}({\mathsf{mod}}(R),{\mathsf{proj}}(R)) := ({\mathsf{mod}}(R),{\mathsf{proj}}(R)^\wedge ,{\mathsf{mod}}(R))$ on ${\mathsf{mod}}(R)$. Note in this case, by Proposition 6.3, that ${\mathsf{proj}}(R) = {\mathsf{proj}}(R)^\wedge$. In particular, the (left) little finitistic dimension of R, defined as the value

$$\begin{aligned} \mathrm{fin.dim}(R) := \mathrm{sup}\{ \mathsf{pd}(M) : M \in {\mathsf{mod}}(R) \text{ with } \mathsf{pd}(M) < \infty \}, \end{aligned}$$

is zero. By a result due to Bass and Foxby [5, 17], we have that R is a self-injective ring. This in turn implies that R must be a 0-Iwanaga–Gorenstein ring, and so, R is a quasi-Frobenius ring by [14, Theorem 9.1.10]. On the other hand, using Matsumura’s [36, Theorem 19.2], we also have that R has infinite global dimension. The following characterization holds.

Corollary 6.6

Let R be a local commutative ring. Then, the following conditions are equivalent.

• (a) R is nonregular Iwanaga–Gorenstein and artinian.

• (b) R is quasi-Frobenius with infinite global dimension.

Moreover, if one of the above conditions holds, then $\mathrm{fin.dim}(R) = 0$.

6.3 Exact model structures from Gorenstein modules relative to duality pairs

We construct examples of Frobenius pairs involving relativizations of Gorenstein projective and Gorenstein injective modules with respect to duality pairs, a concept due to Holm and Jørgensen [30]. Two classes ${\mathcal {L}} \subseteq \mathsf{Mod}(R)$ and ${\mathcal {R}} \subseteq \mathsf{Mod}(R{}^\mathrm{op})$ form a duality pair$(\mathcal {L,R})$ over R if the following two conditions hold:

• 1. $L \in {\mathcal {L}}$ if, and only if, $L^+ \in {\mathcal {R}}$, where $L^+ := \mathsf{Hom}_R(L,\mathbb {Q / Z})$.

• 2. ${\mathcal {R}}$ is closed under direct summands and finite direct sums.

If in addition, ${\mathcal {L}}$ contains R and is closed under coproducts and extensions, then $(\mathcal {L,R})$ is said to be a perfect duality pair. One can also interchange the roles of the classes ${\mathcal {L}}$ and ${\mathcal {R}}$ and say that $(\mathcal {R,L})$ is a (perfect) duality pair over R.

For the relative versions of Gorenstein modules, one considers a particular type of duality pairs firstly studied by Bravo, Gillespie and Hovey in [10, Appendix A] in the context of model structures. Namely, a symmetric duality pair over R is given by a pair of classes $\{ \mathcal {L,R} \}$ with ${\mathcal {L}} \subseteq \mathsf{Mod}(R)$ and ${\mathcal {R}} \subseteq \mathsf{Mod}(R{}^\mathrm{op})$ such that $(\mathcal {L,R})$ and $(\mathcal {R,L})$ are duality pairs over R. If in addition $(\mathcal {L,R})$ is perfect, then the symmetric duality pair $\{ \mathcal {L,R} \}$ is said to be complete.

Example 6.7

• 1. By Enochs and Jenda [14, Sect. 3.2], if R is a right coherent ring, then we can note that $\{ \mathsf{Flat}(R),\mathsf{Inj}(R{}^\mathrm{op}) \}$ is a complete duality pair over R, where $\mathsf{Flat}(R)$ denotes the class of flat R-modules. By [16], we can assert that the same holds for the pair $\{ \mathsf{Flat}(R), \text {FP-}\mathsf{Inj}(R{}^\mathrm{op}) \}$, where $\text {FP-}\mathsf{Inj}(R{}^\mathrm{op})$ denotes the class of FP-injective (or absolutely pure) right R-modules (see Stenström [45]).

• 2. Let us recall the notions of level and $\text {FP}_\infty$-injective R-modules introduced in [10, Definition 2.6]. These are flat and injective R-modules relative to modules of type $\text {FP}_\infty$. Specifically, an R-module Q is of type$\mathrm{FP}_\infty$ if there is an exact sequence

  $$\begin{aligned} \cdots \rightarrow F_1 \rightarrow F_0 \rightarrow Q \rightarrow 0 \end{aligned}$$

  where $F_k$ is finitely generated and free, for every $k \ge 0$ (see [10, Definition 2.2]). Then, an R-module E is $\text {FP}_\infty$-injective (or absolutely clean) if $\mathsf{Ext}^1_R(Q,E) = 0$ for every R-module Q of type $\text {FP}_\infty$. Similarly, an R-module L is level if $\mathsf{Tor}^R_1(Q,L) = 0$ for every right R-module Q of type $\text {FP}_\infty$. Let us denote by $\mathsf{Lev}(R)$ and $\mathsf{FP}_\infty \text{- }\mathsf{Inj}(R)$ the classes of level and $\text {FP}_\infty$-injective R-modules, respectively. In [10], it is proved that $\{ \mathsf{Lev}(R),\mathsf{FP}_\infty \text{- }\mathsf{Inj}(R\ op) \}$ is a complete duality pair over R.

Gorenstein modules relative to duality pairs were recently introduced by Gillespie in [21, Definitions 4.1, 4.2]. Let $\{ \mathcal {L,R} \}$ be a complete duality pair over R. An R-module M is Gorenstein$(\mathcal {L,R})$-projective if $M = Z_0({\varvec{P}})$ for some exact complex ${\varvec{P}}$ of projective R-modules that is also $\mathsf{Hom}_R(-,{\mathcal {L}})$-acyclic. There is a dual notion of Gorenstein$(\mathcal {L,R})$-injectiveR-modules, defined as cycles of exact and $\mathsf{Hom}_R({\mathcal {R}},-)$-acyclic complexes of injective right R-modules. Let us denote these classes of modules by $\mathsf{GProj}_{(\mathcal {L,R})}(R)$ and $\mathsf{GInj}_{(\mathcal {L,R})}(R{}^\mathrm{op})$.

Example 6.8

• 1. If we set ${\mathcal {L}} := \mathsf{Flat}(R)$ and ${\mathcal {R}} := \text {FP-}\mathsf{Inj}(R{}^\mathrm{op})$ in the definition of Gorenstein $(\mathcal {L,R})$-projective and $(\mathcal {L,R})$-injective modules, we obtain the concepts of Ding-projective left R-modules and Ding-injective right R-modules, introduced by Gillespie in [18, Definitions 3.2, 3.7]. Although we need R to be a right coherent ring so that the pair $\{ \mathsf{Flat}(R), \text {FP-}\mathsf{Inj}(R{}^\mathrm{op}) \}$ can be a complete duality pair, these concepts hold for any arbitrary ring R.

  Ding projective and Ding injective modules are generalizations of Gorenstein projective and Gorenstein injective modules, respectively. If we denote by $\mathsf{DProj}(R)$ the class of Ding projective left R-modules and by $\mathsf{DInj}(R{}^\mathrm{op})$ the class of Ding injective right R-modules, it is clear that $\mathsf{DProj}(R) \subseteq \mathsf{GProj}(R)$ and $\mathsf{DInj}(R{}^\mathrm{op}) \subseteq \mathsf{GInj}(R{}^\mathrm{op})$, although the converse containments do not necessarily hold true for arbitrary rings. So far it is known from Gillespie [18, Remarks 3.3, 3.8] that $\mathsf{DProj}(R) = \mathsf{GProj}(R)$ when R is a Gorenstein ring, and $\mathsf{DInj}(R{}^\mathrm{op}) = \mathsf{GInj}(R{}^\mathrm{op})$ when R is noetherian.

• 2. Further generalizations of Gorenstein projective and Gorenstein injective modules, that cover Ding projective and Ding injective modules, were defined by Bravo, Gillespie and Hovey in [10, Sects. 5, 8]. They are known as Gorenstein AC-projective and Gorenstein AC-injective (left and right) R-modules, and are obtained after setting ${\mathcal {L}} := \mathsf{Lev}(R)$ and ${\mathcal {R}} := \text {FP}_\infty \text{- }\mathsf{Inj}(R{}^\mathrm{op})$ in the definition of Gorenstein $(\mathcal {L,R})$-projective and $(\mathcal {L,R})$-injective modules. In what follows, we denote by $\mathsf{GProj}_\mathrm{AC}(R)$ the class of Gorenstein AC-projective left R-modules, and by $\mathsf{GInj}_\mathrm{AC}(R{}^\mathrm{op})$ the class of Gorenstein AC-injective right R-modules.

Remark 6.9

Gorenstein-projective R-modules are an example of what Beligiannis [6, Definition 2.12] calls ${\mathcal {X}}$-Gorenstein objects, if we set ${\mathcal {X}}:= \mathsf{Proj}(R)$. However, this general approach cannot be applied to either Ding-projective or Gorenstein AC-projective R-modules.

Let us check how $\mathsf{GProj}_{(\mathcal {L,R})}(R)$ is part of a left Frobenius pair.

Proposition 6.10

The pair $(\mathsf{GProj}_{(\mathcal {L,R})}(R),\mathsf{Proj}(R))$ is a strong left Frobenius pair in $\mathsf{Mod}(R)$ for every complete duality pair $\{\mathcal {L,R}\}$ over R.

Proof

By the projective version of [21, Lemma 4.5], we have that the class $\mathsf{GProj}_{(\mathcal {L,R})}(R)$ is left thick. The rest of the conditions in Definition 2.5 are immediate. We only mention that $\mathsf{Ext}^i_R(M,P) = 0$ holds for every $M \in \mathsf{GProj}_{(\mathcal {L,R})}(R)$, $P \in \mathsf{Proj}(R)$ and every integer $i > 0$, since $\mathsf{Proj}(R) \subseteq {\mathcal {L}}$ by [21, Proposition 2.3]. $\square$

As a consequence of Theorem 4.1 and Proposition 4.10, we have an exact projective model structure on $\mathsf{GProj}_{(\mathcal {L,R})}(R)^\wedge$ given by

$$\begin{aligned} {\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}_{(\mathcal {L,R})}(R),\mathsf{Proj}(R)) = (\mathsf{GProj}_{(\mathcal {L,R})}(R),\mathsf{Proj}(R)^\wedge ,\mathsf{GProj}_{(\mathcal {L,R})}(R)^\wedge ), \end{aligned}$$

whose homotopy category is equivalent to the stable category $\mathsf{GProj}_{(\mathcal {L,R})}(R) / \sim$.

Let us comment some applications derived from Example 6.8 and concerning the works [10, 18] by Bravo, Gillespie and Hovey. First, we have the following consequence of Proposition 6.10.

Corollary 6.11

For every arbitrary ring R, $(\mathsf{GProj}_\mathrm{AC}(R),\mathsf{Proj}(R))$ is a strong left Frobenius pair in $\mathsf{Mod}(R)$.

Although another immediate consequence of Proposition 6.10 and Examples 6.7 and 6.8 is that $(\mathsf{DProj}(R),\mathsf{Proj}(R))$ is a strong left Frobenius pair if R is a right coherent ring, this can be proved for any arbitrary ring by using a similar reasoning as in Sect. 6.1. In fact, the results from Holm [27] we cited in Sect. 6.1, along with the arguments proving them, carry over to the subcategories $\mathsf{DProj}(R)$ and $\mathsf{DInj}(R{}^\mathrm{op})$. We have the following result.

Proposition 6.12

For any arbitrary ring R, $(\mathsf{DProj}(R),\mathsf{Proj}(R))$ is a strong left Frobenius pair in $\mathsf{Mod}(R)$.

From the definition of Ding-projective R-modules, one could be tempted to set $\omega := \mathsf{Flat}(R)$ and assert incorrectly that $(\mathsf{DProj}(R),\mathsf{Flat}(R))$ is a left Frobenius pair in $\mathsf{Mod}(R)$. For, one can note that the pair $(\mathsf{DProj}(R),\mathsf{Flat}(R))$ satisfies almost all of the conditions in Definition 2.5. Specifically, $(\mathsf{DProj}(R),\mathsf{Flat}(R))$ is a left Frobenius pair in $\mathsf{Mod}(R)$ if, and only if, the inclusion $\mathsf{Flat}(R) \subseteq \mathsf{DProj}(R)$ holds true. In [18, Proposition 3.8] it is proven that a Ding projective R-module is either projective or has infinite flat dimension, that is, the equality $\mathsf{Proj}(R) = \mathsf{DProj}(R) \cap \mathsf{Flat}(R)^\wedge$ holds. It follows that non-projective flat modules are not Ding projective, and so the containment $\mathsf{Flat}(R) \subseteq \mathsf{DProj}(R)$ is not necessarily true. For this reason, we have set $\omega := \mathsf{Proj}(R)$ instead of $\omega := \mathsf{Flat}(R)$ in order to obtain the left Frobenius pair $(\mathsf{DProj}(R),\mathsf{Proj}(R))$. However, we can get the following characterization of perfect rings in terms of the pair $(\mathsf{DProj}(R),\mathsf{Flat}(R))$.

Proposition 6.13

Let R be an arbitrary ring. Then, R is left perfect if, and only if, the pair $(\mathsf{DProj}(R),\mathsf{Flat}(R))$ is a left Frobenius pair in $\mathsf{Mod}(R)$.

Proof

The “only if” part is clear since $\mathsf{Flat}(R) = \mathsf{Proj}(R)$ holds for every perfect ring R.

Now let us assume that $(\mathsf{DProj}(R),\mathsf{Flat}(R))$ is a left Frobenius pair in $\mathsf{Mod}(R)$ and let $F \in \mathsf{Flat}(R)$. On the one hand, since F is Ding projective, we have that there is a short exact sequence

$$\begin{aligned} 0 \rightarrow F \rightarrow P \rightarrow M \rightarrow 0 \end{aligned}$$

where P is projective and M is Ding projective. On the other hand, since $\mathsf{id}_{\mathsf{DProj}(R)}(\mathsf{Flat}(R)) = 0$ by Gillespie [18, Lemma 3.9]), we have that this sequence splits and so F is a direct summand of the projective R-module P. It follows that every flat R-module is projective, and hence R is a left perfect ring. $\square$

With respect to relative cotorsion pairs, we obtain from Proposition 6.12 and Theorems 3.6 and 3.7 (not necessarily strongly) hereditary $\mathsf{DProj}(R)^\wedge$-cotorsion pairs in $\mathsf{Mod}(R)$ of the form $(\mathsf{DProj}(R), \mathsf{Proj}(R)^\wedge )$ and $(\mathsf{Proj}(R), \mathsf{DProj}(R)^\wedge )$, where $\mathsf{DProj}(R)^\wedge$ is the subcategory of R-modules with finite Ding projective dimension (defined as the $\mathsf{DProj}(R)$-resolution dimension). In the case where R is a Ding–Chen ring, Gillespie obtained in [18, Proof of Theorem 4.7] another cotorsion pair involving the class $\mathsf{DProj}(R)$. Recall first from [18, Definition 4.1] that a ring R is a Ding–Chen ring if R is both left and right coherent and the FP-injective dimensions of R as a left and right R-module coincide. For such rings, Gillespie constructed in [18, Proof of Theorem 4.7] a complete and hereditary cotorsion pair $(\mathsf{DProj}(R),\mathsf{Flat}(R)^\wedge )$ in $\mathsf{Mod}(R)$.

At this point, we can note a difference between the study of Gorenstein homological algebra and Ding–Chen homological algebra from the point of view of Frobenius pairs. Namely:

• We are not aware if the $\mathsf{DProj}(R)^\wedge$-cotorsion pair $(\mathsf{DProj}(R),\mathsf{Proj}(R)^\wedge )$ and the cotorsion pair $(\mathsf{DProj}(R),\mathsf{Flat}(R)^\wedge )$ in $\mathsf{Mod}(R)$ coincide when R is a Ding–Chen ring. It is known that for such rings, $\mathsf{Flat}(R)^\wedge$ coincides with the class $\mathsf{FP}\text{- }\mathsf{Inj}(R)^\vee$ of R-modules with finite FP-injective dimension, but we do not know if the equality $\mathsf{Flat}(R)^\wedge = \mathsf{Proj}(R)^\wedge$ holds in this case. Another inconvenience is that we do not know if $\mathsf{DProj}(R)^\wedge = \mathsf{Mod}(R)$ when R is a Ding–Chen ring.

Open problem 6.14

In the case R is a Ding–Chen ring, do the equalities $\mathsf{Flat}(R)^\wedge = \mathsf{Proj}(R)^\wedge$, $\mathsf{DProj}(R)^\wedge = \mathsf{Mod}(R)$ and $\mathsf{DProj}(R)^\wedge = \mathsf{DInj}(R)^\vee$ hold true?

• For an arbitrary ring R, the strong left Frobenius pair $(\mathsf{DProj}(R), \mathsf{Proj}(R))$ in $\mathsf{Mod}(R)$ yields the projective AB model structure

  $$\begin{aligned} {\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{DProj}(R), \mathsf{Proj}(R)) = (\mathsf{DProj}(R),\mathsf{Proj}(R)^\wedge ,\mathsf{DProj}(R)^\wedge ) \end{aligned}$$

  on $\mathsf{DProj}(R)^\wedge$. In the case where R is a Ding–Chen ring, there is an abelian model structure $(\mathsf{DProj}(R),\mathsf{Flat}(R)^\wedge ,\mathsf{Mod}(R))$ on $\mathsf{Mod}(R)$ found by Gillespie in [18, Theorem 4.7]. For such rings, we are not aware if the latter model structure coincide with the exact structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{DProj}(R), \mathsf{Proj}(R))$. That would be the case if Problem 6.14 had a positive answer.

  Dually, there exists a unique exact model structure

  $$\begin{aligned} {\mathcal {M}}^\mathrm{inj}_\mathrm{AB}(\mathsf{Inj}(R),\mathsf{DInj}(R)) := (\mathsf{DInj}(R)^\vee ,\mathsf{Inj}(R)^\vee ,\mathsf{DInj}(R)) \end{aligned}$$

  on $\mathsf{DInj}(R)^\vee$ obtained from the right Frobenius pair $(\mathsf{Inj}(R),\mathsf{DInj}(R))$ in $\mathsf{Mod}(R)$. This structure generalizes Gillespie’s injective model structure [18, Theorem 4.7] in case there were a positive answer for the dual of Problem 6.14.

Regarding the subcategory $\mathsf{GProj}_\mathrm{AC}(R)$, we obtain from Corollary 6.11 and Theorems 3.6 and 3.7 two hereditary $\mathsf{GProj}_{\mathrm{AC}}(R)^\wedge$-cotorsion pairs $(\mathsf{GProj}_\mathrm{AC}(R),\mathsf{Proj}(R)^\wedge )$ and $(\mathsf{Proj}(R),\mathsf{GProj}_\mathrm{AC}(R)^\wedge )$ in $\mathsf{Mod}(R)$, which produce the projective model structure

$$\begin{aligned} {\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}_\mathrm{AC}(R),\mathsf{Proj}(R)) = (\mathsf{GProj}_\mathrm{AC}(R),\mathsf{Proj}(R)^\wedge ,\mathsf{GProj}_\mathrm{AC}(R)^\wedge ) \end{aligned}$$

on $\mathsf{GProj}_\mathrm{AC}(R)^\wedge$. Let us compare this structure with the abelian Gorenstein AC-projective model structure on $\mathsf{Mod}(R)$ (with R an arbitrary ring) described in [10, Theorem 8.5]. For the latter model structure, the subcategory of trivial objects has a description (see [10, Lemma 5.4]) that is not necessarily the same that the one given above for the structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}_\mathrm{AC}(R),\mathsf{Proj}(R))$. On the other hand, the authors are not aware if the subcategory $\mathsf{GProj}_\mathrm{AC}(R)^\wedge$ coincides with the whole category $\mathsf{Mod}(R)$ for an arbitrary ring R. If this turned out to be true, we would know another way to obtain the abelian Gorenstein AC-projective model structure.

Open problem 6.15

Let R be a ring. Under which conditions on R do the following statements hold true?

• 1. $\mathsf{Mod}(R) = \mathsf{GProj}_\mathrm{AC}(R)^\wedge$.

• 2. Any R-module has finite Gorenstein AC-projective dimension if, and only if, it has finite Gorenstein AC-injective dimension.

The homotopy category of the AB model structure ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}_\mathrm{AC}(R), \mathsf{Proj}(R))$ is exactly the homotopy category obtained in [10, Theorem 8.7]. So we can say that the model ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}_\mathrm{AC}(R),\mathsf{Proj}(R))$ and the Gorenstein AC-projective model structure “coincide” in the sense that they have the same homotopy category.

Remark 6.16

The model structures ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}(R),\mathsf{Proj}(R))$, ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{DProj}(R),\mathsf{Proj}(R))$ and ${\mathcal {M}}^\mathrm{proj}_\mathrm{AB}(\mathsf{GProj}_\mathrm{AC}(R),\mathsf{Proj}(R))$ can also be obtained from Corollary 4.4.

Dually, one can obtain the injective AB model structure

$$\begin{aligned} {\mathcal {M}}^\mathrm{inj}_\mathrm{AB}(\mathsf{Inj}(R),\mathsf{GInj}_\mathrm{AC}(R)) = (\mathsf{GInj}_\mathrm{AC}(R)^\vee ,\mathsf{Inj}(R),\mathsf{GInj}_\mathrm{AC}(R)) \end{aligned}$$

on $\mathsf{GInj}_\mathrm{AC}(R)^\vee$, with the same homotopy category as the Gorenstein AC-injective model structure in [10, Theorem 5.5].

6.4 Frobenius pairs from Gorenstein flat modules

In this last example, we will show that the class $\mathsf{GFlat}(R)$ of Gorenstein flat R-modules, and the class $\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1}$ of flat-cotorsion R-modules form a left Frobenius pair in $\mathsf{Mod}(R)$, under the assumption that R is a GF-closed ring.

Let us recall that an R-module M is Gorenstein flat if $M = Z_0({\varvec{F}})$ where ${\varvec{F}}$ is an exact complex of flat R-modules such that $I \otimes _R {\varvec{F}}$ is an exact complex of abelian groups for every injective right R-module $I \in \mathsf{Inj}(R{}^\mathrm{op})$. For the latter condition, one says that the complex ${\varvec{F}}$ is $(\mathsf{Inj}(R{}^\mathrm{op}) \otimes _R -)$-acyclic. Nowadays, it is an open problem to determine if the class $\mathsf{GFlat}(R)$ is always closed under extensions. Some advances in this direction are achieved by D. Bennis in [8], where he introduces the concept of (left) GF-closed rings, that is, rings R such that $\mathsf{GFlat}(R)$ is closed under extensions. Examples of such rings include right coherent rings and rings with finite weak dimension (see [8, Proposition 2.2]). Moreover, in [8, Example 3.6] Bennis constructs an example of a GF-closed ring that is not right coherent and with weak dimension equal to $\infty$.

The goal of this section is to show the following characterization of GF-closed rings.

Proposition 6.17

A ring R is GF-closed if, and only if, $(\mathsf{GFlat}(R),\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1})$ is a left Frobenius pair in $\mathsf{Mod}(R)$.

Proof

The “if” part is clear, so let us assume that R is a GF-closed ring for the rest of this section. Thus, the first implication is that $\mathsf{GFlat}(R)$ is closed under extensions. Now applying [8, Theorem 2.3], this is equivalent to saying that $\mathsf{GFlat}(R)$ is resolving. On the other hand, by [8, Corollary 2.6], we have that $\mathsf{GFlat}(R)$ is also closed under direct summands, while the same property is clearly satisfied by the class $\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1}$ of flat-cotorsion modules. In order to conclude that $(\mathsf{GFlat}(R),\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1})$ is a left Frobenius pair in $\mathsf{Mod}(R)$, it is only left to show that $\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1}$ is a $\mathsf{GFlat}(R)$-injective relative cogenerator in $\mathsf{GFlat}(R)$.

First, we show that $\mathsf{Ext}^i_R(M,W) = 0$ for every $M \in \mathsf{GFlat}(R)$, $W \in \mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1}$ and $i > 0$. We only argument the case $i = 1$, as the rest follows inductively. We have that there is an exact complex ${\varvec{F}}$ of flat R-modules with $M = Z_0({\varvec{F}})$ and such that $I \otimes _R {\varvec{F}}$ is an exact complex of abelian groups for every $I \in \mathsf{Inj}(R{}^\mathrm{op})$. By [38, Theorem 4.18], the latter condition is equivalent to saying that ${\varvec{F}}$ is $\mathsf{Hom}_R(-,\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1})$-acyclic. Thus, we can assert that there exists a short exact sequence

$$\begin{aligned} {\varvec{\eta }} :0 \rightarrow M' \rightarrow F \rightarrow M \rightarrow 0 \end{aligned}$$

with $M' \in \mathsf{GFlat}(R)$ and $F \in \mathsf{Flat}(R)$ such that $\mathsf{Hom}_R({\varvec{\eta }},W)$ is exact. Using this along with the fact that $\mathsf{Ext}^1_R(F,W) = 0$, we can get an exact sequence

$$\begin{aligned} 0 \rightarrow \mathsf{Hom}_R(M,W) \rightarrow \mathsf{Hom}_R(F,W) \xrightarrow {\varphi } \mathsf{Hom}_R(M',W) \rightarrow \mathsf{Ext}^1_R(M,W) \rightarrow 0 \end{aligned}$$

where the morphism $\varphi$ is surjective. It follows that $\mathsf{Ext}^1_R(M,W) = 0$. Therefore, we can conclude that $\mathsf{id}_{\mathsf{GFlat}(R)}(\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1}) = 0$.

Now consider again $M \in \mathsf{GFlat}(R)$. On the one hand, there is a short exact sequence

$$\begin{aligned} 0 \rightarrow M \rightarrow F \rightarrow M' \rightarrow 0 \end{aligned}$$

with $F \in \mathsf{Flat}(R)$ and $M' \in \mathsf{GFlat}(R)$. On the other hand, for $F \in \mathsf{Flat}(R)$ we can consider another short exact sequence

$$\begin{aligned} 0 \rightarrow F \rightarrow C \rightarrow F' \rightarrow 0 \end{aligned}$$

with $F' \in \mathsf{Flat}(R)$ and $C \in (\mathsf{Flat}(R))^{\perp _1}$. An standard argument shows that taking the pushout of $C \leftarrow F \rightarrow M'$ yields a short exact sequence

$$\begin{aligned} 0 \rightarrow M \rightarrow C \rightarrow N \rightarrow 0, \end{aligned}$$

where $C \in \mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1}$ since $\mathsf{Flat}(R)$ is closed under extensions, and $N \in \mathsf{GFlat}(R)$ by [8, Lemma 2.5]. Hence, the existence of this sequence implies that $\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1}$ is a relative cogenerator in $\mathsf{GFlat}(R)$. $\square$

The authors are not aware if $\mathsf{Flat}(R) \cap (\mathsf{Flat}(R))^{\perp _1}$ is a $\mathsf{GFlat}(R)$-projective relative generator in $\mathsf{GFlat}(R)$, so we cannot assert the existence of a projective AB model structure on $\mathsf{GFlat}(R)^\wedge$ with R a GF-closed ring. However, there is already an abelian model structure on $\mathsf{Mod}(R)$, called the Gorenstein flat model structure, where the (trivially) cofibrant objects are given by the class $\mathsf{GFlat}(R)$ (resp., $\mathsf{Flat}(R)$) and the (trivially) fibrant objects by the class $(\mathsf{Flat}(R))^{\perp _1}$ (resp., $(\mathsf{GFlat}(R))^{\perp _1}$). This model structure was first obtained in [23, Theorem 4.8] under the assumption that R is a Gorenstein ring, where it is possible to describe the trivial objects as those R-modules with finite injective dimension. A slightly more general result by Gillespie [18, Theorem 4.10] asserts the existence of the Gorenstein flat model structure assuming that R is a Ding–Chen ring. In this case, the trivia l objects are given by the class of modules with finite FP-injective dimension. Gillespie later proves in [22, Theorem 3.3] that this model also exists on modules over coherent rings by using a general method he developed in [20] for producing Hovey triples from certain hereditary complete cotorsion pairs in abelian categories. However, in this case one has a less explicit description for the trivial objects. Finally, it was recently proved in [15, Corollary 4.3] by Estrada, Iacob and the third author, using a method different from Gillespie’s, that the Gorenstein flat model structure also exists on modules over GF-closed rings.

We close this section mentioning a more general context in where the present example also holds.

Remark 6.18

Under certain conditions, it is possible to obtain a left Frobenius pair in $\mathsf{Mod}(R)$ of the form $(\mathsf{GFlat}_{{\mathcal {R}}}(R),\mathsf{Flat}(R))$, where $\mathsf{GFlat}_{{\mathcal {R}}}(R)$ is the class of Gorenstein flat modules relative to a duality pair $(\mathcal {L,R})$, that is, cycles of exact complexes ${\varvec{F}}$ of flat R-modules such that $B \otimes _R {\varvec{F}}$ is exact for every $B \in {\mathcal {R}}$. See [15] for details.