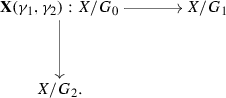Free and properly discontinuous actions of groups $G\rtimes {\mathbb {Z}}^m$ and $G_1*_{G_0}G_2$

Abstract

We estimate the number of homotopy types of orbit spaces for all free and properly discontinuous cellular actions of groups $G\rtimes {\mathbb {Z}}^m$ and $G_1*_{G_0}G_2$. In particular, homotopy types of orbits of $(2n-1)$-spheres $\Sigma (2n-1)$ for such actions are analysed, provided the groups $G_0, G_1, G_2$ and G are finite and periodic. This family of groups $G\rtimes {\mathbb {Z}}^m$ and $G_1*_{G_0}G_2$ contains properly the family of virtually cyclic groups. The possible actions of those groups on the top cohomology of the homotopy sphere are determined as well.

1 Introduction

Recall that a finite dimensional CW-complex $\Sigma (n)$ with the homotopy type of the n-sphere $\mathbb {S}^n$ is called an n-homotopy sphere for $n\ge 1$. The finite periodic groups, being the only finite groups acting freely on some homotopy sphere, have been fully classified by Suzuki–Zassenhaus, see e.g., [1, Chapter IV, Theorem 6.15].

A free action of a discrete (finite or infinite) group G on $\Sigma (n)$ induces a homomorphism $G \rightarrow {\text {Aut}}(H^{n}(\Sigma (n),\mathbb {Z}))$. Following [3, Chapter VII, Proposition 10.2], for any free action of a finite group G on $\Sigma (2n-1)$, the induced homomorphism $G \rightarrow {\text {Aut}}(H^{2n-1}(\Sigma (2n-1),\mathbb {Z}))$ is trivial.

The purpose of the paper [15] is to study free, properly discontinuous and cellular actions on a homotopy circle $\Sigma (1)$ by discrete infinite groups. There we need somewhat different methods than those used for $\Sigma (n)$ with $n>1$. We have addressed the following problems:

• when a group G acts;

• what is the minimal dimension of $\Sigma (1)$ on which G acts;

• the description of the action $G \rightarrow {\text {Aut}}(H^1(\Sigma (1),\mathbb {Z}))$

and determined all virtually cyclic groups G that act on $\Sigma (1)$ together with the induced action $G \rightarrow {\text {Aut}}(H^1(\Sigma (1),\mathbb {Z}))$, and we classified the orbit spaces $\Sigma (1)/G$.

In view of [25], the only finite groups acting freely on $\Sigma (2n)$ are, up to isomorphism, trivial or $\mathbb {Z}_2$ and the induced homomorphism $\mathbb {Z}_2\rightarrow {\text {Aut}}\,(H^{2n}(\Sigma (2n),\mathbb {Z}))$ is non-trivial. If the group G is infinite there are more possibilities for the induced homomorphism $G \rightarrow H^n(\Sigma (n),\mathbb {Z})$ than in the finite case. A characterization of those homomorphisms for $\Sigma (2n)$ is part of the problem studied in [16]. We have described all virtually cyclic groups G that act on $\Sigma (2n)$ together with the induced action $G \rightarrow {\text {Aut}}(H^{2n}(\Sigma (2n),\mathbb {Z}))$, and we classified the orbit spaces $\Sigma (2n)/G$.

The criterion [21, 28] due to Wall states: an infinite group G is virtually cyclic if and only if G is isomorphic to:

• (I) a semi-direct product $G_0\rtimes \mathbb {Z}$; or

• (II) $G_1\star _{G_0} G_2$, where $G_0<G_1,G_2$ and the index $[G_i:G_0]=2$ for $i=1,2$ with a finite group $G_0$.

If a virtually cyclic group G satisfies (I), we shall say that it is of Type I, while if it satisfies (II), we shall say that it is of Type II. An infinite virtually cyclic group is the middle term of a short exact sequence of the form $e\rightarrow \mathbb {Z }\rightarrow G \rightarrow G_0 \rightarrow e$, where $G_0$ is a finite group. Then, in view of [17, Proposition 19], it holds: if this extension is central then the group G is of type I, otherwise it is of type II.

The result [17, Theorem 7] presents the complete classification of infinite virtually cyclic subgroups of the braid group $B_n(\mathbb {S}^2)$ for all $n\ge 3$. Hence, by means e.g., [17, Proposition 10] those groups act on some $\Sigma (3)$ being the universal covering of $\widetilde{F_n(\mathbb {S}^2)}$ of the configuration space $F_n(\mathbb {S}^2)$ for $n\ge 3$.

The Farrell cohomology, $\hat{H}^*( -, {\mathbb {Z}})$ is a contravariant functor from groups to ${\mathbb {Z}}$-graded algebras, whenever the virtual cohomological dimension ${\text {vcd}}G < \infty$. If $\alpha \in \hat{H}^q(G,{\mathbb {Z}})$, an integer $q>0$, and the map $\alpha \cup -:\hat{H}^i(G, {\mathbb {Z}}) \longrightarrow \hat{H}^{i+q}(G, {\mathbb {Z}})$ is an isomorphism for all i we say that the group G has periodic Farell cohomology with period q.

In 1979 C.T.C. Wall raised [29, p. 518] the following problem: whether any countable group with periodic Farell cohomology can act freely and properly on some product $\mathbb {R}^m\times \mathbb {S}^n$? Wall’s problem was solved by Connolly and Prassidis (1989). Namely, [4, 1.4. Corollary] says: a discrete group G with ${\text {vcd}}G<\infty$ acts freely and properly on $\mathbb {R}^m\times \mathbb {S}^n$ for some m, n if and only if G is countable and the Farrell cohomology $\hat{H}^*(G,-)$ is periodic.

In view of the result [2] by Adem and Smith a discrete group G has periodic cohomology after d-steps with $d\ge 0$ if there is an integer $q>0$ and $\alpha \in H^q(G,\mathbb {Z})$ such that the cup product map $\alpha \cup -:H^i(G,M)\longrightarrow H^{i+q}(G,M)$ is an isomorphism for every G-module M and $i> d$.

Suppose that finite groups $G,G_0,G_1$ and $G_2$ are periodic. Then, one can show that:

$G_1*_{G_0}G_2$ is periodic;

$G\rtimes \mathbb {Z}^m$ is periodic (after d-steps for some d).

Applying constructions from [2] and [4] there are free and properly discontinuous actions of the groups $G_1*_{G_0}G_2$ and $G\rtimes \mathbb {Z}^m$ on $\mathbb {S}^n\times \mathbb {R}^k$ for some $k,n>0$.

Observe that the results from [2] and [4] provide neither any information about the dimension n of the homotopy sphere of which the group G acts nor the induced action $G \rightarrow {\text {Aut}}(H^{n}(\Sigma (n),\mathbb {Z}))$, nor the homotopy type of orbit spaces. Studies these problems are relevant points of the present work.

We assume throughout the paper that any space X is a CW-complex and an action $G\times X\rightarrow X$ of a discrete group G on X is free, properly discontinuous and cellular. The main aim of the present work is to analyse such actions on homotopy spheres $\Sigma (2n-1)$ of groups $G\rtimes {\mathbb {Z}}^m$ for $m\ge 1$ and $G_1*_{G_0}G_2$. Once n is fixed, induced actions of those groups on the top cohomology $H^{2n-1}(\Sigma (2n-1),\mathbb {Z})$ are studied and the number of homotopy type of orbit spaces is estimated. Observe that the family of the groups in question contains properly the family of all virtually cyclic groups.

Given actions $G_1\times \Sigma _1(2n-1)\rightarrow \Sigma _1(2n-1)$, $G_2\times \Sigma _2(2n-1)\rightarrow \Sigma _2(2n-1)$ and $G\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$, we not only present constructions of actions $(G_1*_{G_0}G_2)\times \Sigma '(2n-1)\rightarrow \Sigma '(2n-1)$ and $(G\rtimes \mathbb {Z}^m)\times \Sigma ''(2n-1)\rightarrow \Sigma ''(2n-1)$ but those actions leave explicitly dimensions of homotopy spheres involved as well.

This paper is organized into five sections, besides this Introduction.

Section 1 presents basic facts on homotopy colimits taking into a special account homotopy coequalizers and homotopy push-outs.

Let $\mathcal {K}^G_X$ be the quotient set of all homeomorphism classes of orbit spaces $X/\gamma$ with respect to all actions $\gamma :G\times X\rightarrow X$ by the homotopy relation. In particular, we write $\mathcal {K}^G_{2n-1}$ provided $X=\Sigma (2n-1)$ for the notion defined already in [8]. Section 2 aims to determine free, properly discontinuous and proper actions of groups $G\rtimes {\mathbb {Z}}^m$ on a space X by means of n-fold mapping tori studied in Sect. 1. Its main result stated in Theorem 1 estimates the set $\mathcal {K}^{G\rtimes {\mathbb {Z}}^m}_X$ of all homeomorphism classes of orbit spaces $X/\gamma$ by the homotopy relation with respect to all actions $\gamma : G\times X\rightarrow X$.

Section 3 takes up the systematic study free, properly discontinuous and proper actions of groups $G_1*_{G_0}G_2$ on a space X by means of homotopy push-outs studied in Sect. 1 and the result of [23]. Theorem 2 estimates $\mathcal {K}^{G_1*_{G_0}G_2}_X$ by means of $\mathcal {K}^{G_0}_X$, $\mathcal {K}^{G_1}_X$ and $\mathcal {K}^{G_2}_X$ as well.

Basic data on virtually cyclic groups are presented in Sect. 4. Then, Sect. 5 takes up the systematic study of properly discontinuous and proper actions of $G\rtimes {\mathbb {Z}}^m$ and $G_1*_{G_0}G_2$ on homotopy spheres $\Sigma (2n-1)$ provided the groups G and $G_i$ for $i=0,1,2$ are finite. For the sets $\mathcal {K}^{G\rtimes {\mathbb {Z}}^m}_{2n-1}$ and $\mathcal {K}^{G_1*_{G_0}G_2}_{2n-1}$ of all homeomorphism classes of orbit spaces $\Sigma (2n-1)/\gamma$ with respect to all actions $\gamma :(G\rtimes {\mathbb {Z}}^m)\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ and $\gamma :(G_1*_{G_0}G_2)\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ by the homotopy relation, are estimated in Corollary 4 and Corollary 6, respectively.

2 Prerequisites

Let $\mathbb {I}$ be a small category. Given an $\mathbb {I}$-diagram of topological (pointed) spaces $\mathbf {X}:\mathbb {I}\rightarrow \mathbb {T}op\,(\mathbb {T}op^*)$, we write ${\text {hocolim}}{\mathbf X}$ (${\text {hocolim}}^*{\mathbf X}$) for its (pointed) homotopy colimit. Constructions and other details on (pointed) homotopy colimit one can find in e.g., [7, Appendices] and [27]. The result [7, D.3.1 Corollary] yields:

Proposition 1

If $\mathbf {X} : \mathbb {I}\rightarrow \mathbb {T}op^*$ is an $\mathbb {I}$-diagram of pointed topological spaces and $\mathbf {B}\mathbb {I}$ the classifying space of the category $\mathbb {I}$ then there is a cofibration

$$\begin{aligned}\mathbf {B}\mathbb {I}\longrightarrow {\text {hocolim}}{\mathbf X}\longrightarrow {\text {hocolim}}^*{\mathbf X}.\end{aligned}$$

In particular, if the space $\mathbf {B}\mathbb {I}$ is contractible then the map ${\text {hocolim}}{\mathbf X}\longrightarrow {\text {hocolim}}^*{\mathbf X}$ is a homotopy equivalence.

Given an $\mathbb {I}$-diagram $\mathbf {X}:\mathbb {I}\rightarrow \mathbb {T}op$ ($\mathbb {T}op^*$), write $\mathbf {X}(i)=X_i$ for any object $i\in {\text {ob}}(\mathbb {I})$ and $\mathbf {X}(\varphi )=X_\varphi : X_{i_1}\rightarrow X_{i_2}$ for any morphism $\varphi \in {\text {Arr}}(\mathbb {I})$. Then, recall from [7, Appendices] and [27] the following homotopy invariance of homotopy limits.

Proposition 2

If $\mathbf {X},\mathbf {X}':\mathbb {I}\rightarrow \mathbb {T}op$ $(\mathbb {T}op^*)$ are $\mathbb {I}$-diagrams of topological (pointed) spaces and $g_i:X_i\rightarrow X'_i$ homotopy equivalences for all $i\in {\text {ob}}(\mathbb {I})$ such that the diagrams

are commutative (up to homotopy) for all $\varphi \in {\text {Arr}}(\mathbb {I})$ then there is a homotopy equivalence $\bar{g}:{\text {hocolim}}{\mathbf X}\rightarrow {\text {hocolim}}{\mathbf X'}$ such that the diagrams

commute (up to homotopy) for all $i\in \mathbb {I}$.

According to the construction presented in [27], the homotopy colimit ${\text {hocolim}}{\mathbf X}$ of the diagram of spaces

(called a homotopy coequalizer) is the quotient of the space

$$\begin{aligned} X_0\sqcup X_1 \sqcup X_0\times I\times \{0_f, 0_g\} \end{aligned}$$

under the identifications

$$\begin{aligned} \big <(x,1,0_f)\sim x\sim (x,1, 0_g),(x,0,0_f)\sim f(x),(x,0,0_g)\sim g(x)\big >, \end{aligned}$$

where $\{0_f,0_g\}$ is a two elements set and $I=[0,1]$ is the unit interval.

Then, by means of Proposition 2, the commutative (up to homotopy) diagram

leads to a map $\bar{h}:{\text {hocolim}}{\mathbf X}\rightarrow {\text {hocolim}}{\mathbf X'}$.

It is not difficult to see that the homotopy colimit ${\text {hocolim}}{\mathbf X}$ of the particular diagram

is homeomorphic to the mapping torus $T(f)=X\times I/(x,0)\sim (f(x),1)$.

The space T(f) is equipped with a canonical map

$$\begin{aligned} p: T(f)\longrightarrow \mathbb {S}^1=I/0\sim 1 \end{aligned}$$

given by $p([(x,t)])=[t]$ for $(x,t)\in X\times I$ and an injection $\imath :X\rightarrow T(f)$ such that $\imath (x)=[(x,1)]$ for $x\in X$. If X is an ANR-space and $f:X\rightarrow X$ a homotopy equivalence then by [6, Theorem A] the map $p:T(f)\rightarrow \mathbb {S}^1$ is an approximative fibration with X as the fibre. Then, in view of [5, Corollary 3.5], we can state:

Proposition 3

If X is a connected ANR-space and $f:X\rightarrow X$ a homotopy equivalence then there is an exact sequence

$$\begin{aligned} \cdots \rightarrow \pi _n(X)\xrightarrow {\imath _*}\pi _n(T(f))\xrightarrow {p_*}\pi _n(\mathbb {S}^1)\rightarrow \pi _{n-1}(X)\rightarrow \cdots . \end{aligned}$$

Consequently, we derive isomorphisms of homotopy groups $\pi _n(T(f))\cong \pi _n(X)$ for $n>1$ and a split short exact sequence $e\rightarrow \pi _1(X)\rightarrow \pi _1(T(f))\rightarrow {\mathbb {Z}}\rightarrow 0$. Now, fix a point $x_0\in X$, a path $\sigma ':I\rightarrow X$ such that $\sigma '(0)=f(x_0)$ and $\sigma '(1)=x_0$, and write $\sigma '_*:\pi _1(X,f(x_0))\rightarrow \pi _1(X,x_0)$ for the induced isomorphism. Then, the paths $\bar{\sigma }':I\rightarrow T(f)$ and $\bar{\sigma }'':I\rightarrow T(f)$ with $\bar{\sigma }'(t)=[(\sigma '(t),1)]$ and $\bar{\sigma }''(t)=[(x_0,1-t)]$ for $t\in I$, respectively lead to the loop $\sigma =\bar{\sigma }''\star \bar{\sigma }':I\rightarrow T(f)$ at the point $[(x_0,1)]\in T(f)$. By the construction of T(f), there is a homotopy $\sigma \star \tau \star \sigma ^{-1}\simeq \sigma '^{-1}\star (f\circ \tau )\star \sigma '$ for any loop $\tau :I\rightarrow X$. Consequently, we obtain an isomorphism $\pi _1(T(f))\cong \pi _1(X)\rtimes _\theta {\mathbb {Z}}$, where $\theta =\sigma '_*\circ f_*:\pi _1(X,x_0)\rightarrow \pi _1(X,x_0)$ is the automorphism with $f_*:\pi _1(X,x_0)\rightarrow \pi _1(X,f(x_0))$ induced by the homotopy equivalence $f:X\rightarrow X$.

In view of Proposition 2, commutative maps $f_1,f_2:X\rightarrow X$ yield a map $f_2^{(1)}:T(f_1)\rightarrow T(f_1)$. Then, we can define the space

$$\begin{aligned} T(f_1,f_2)=T({f}_2^{(1)}). \end{aligned}$$

More generally, given a sequence of mutually commutative (up to homotopy) maps $f_1,\ldots ,f_m:X\rightarrow X$, we define inductively the m-fold mapping torus $T(f_1,\ldots ,f_m)$ as follows: maps $f_2,\ldots ,f_m:X\rightarrow X$ lead to mutually commutative homotopy equivalences $f^{(1)}_2,\ldots ,f^{(1)}_m:T(f_1)\rightarrow T(f_1)$; given mutually commutative homotopy equivalences $f^{(i)}_{i+1},\ldots ,f^{(i)}_m:T(f_1,\ldots ,f_i)\rightarrow T(f_1,\ldots ,f_i)$ we define $T(f_1,\ldots ,f_{i+1})=T(f^{(i)}_{i+1})$ and mutually commutative homotopy equivalences $f^{(i+1)}_{i+2},\ldots ,f^{(i+1)}_m:T(f_1,\ldots ,f_{i+1})\rightarrow T(f_1,\ldots ,f_{i+1})$.

Then, $T(f_1,\ldots ,f_m)=T(f^{(m-1)}_m)$ is equipped with canonical maps

$$\begin{aligned} X\xrightarrow {\imath } T(f_1,\ldots ,f_m)\xrightarrow {p}\mathbb {T}^m, \end{aligned}$$

where $X\xrightarrow {\imath } T(f_1,\ldots ,f_m)$ stands for the composition of the maps $X\rightarrow T(f_1)\rightarrow T(f_1,f_2)\rightarrow \cdots \rightarrow T(f_1,\ldots ,f_m)$ and $\mathbb {T}^m$ for the m-torus.

Before we state the next result, consider a homomorphism $\varphi : G'\rightarrow {\text {Aut}}(G)$ for groups $G,G'$ and write ${\text {Aut}}_\varphi (G)=\{\psi \in {\text {Aut}}(G);\,\psi \varphi (g')=\varphi (g')\psi \text { for} g'\in G' \}$. Then, there is a canonical embedding ${\text {Aut}}_\varphi (G)\hookrightarrow {\text {Aut}}(G\rtimes _\varphi G')$ and one can easily show:

Lemma 1

Given groups $G,G'$ and $G''$, consider homomorphisms $\varphi ':G'\rightarrow {\text {Aut}}(G)$ and $\varphi '':G''\rightarrow {\text {Aut}}(G\rtimes _{\varphi '}G')$. If $\varphi '':G''\rightarrow {\text {Aut}}(G\rtimes _{\varphi '}G')$ factorizes through the embedding ${\text {Aut}}_{\varphi '}(G)\hookrightarrow {\text {Aut}}(G\rtimes _{\varphi '} G')$ and $\varphi '(g')\varphi ''(g'')=\varphi ''(g'')\varphi '(g')$ for $g'\in G'$, and $g''\in G''$ then there is an isomorphism of semi-direct products

$$\begin{aligned} (G\rtimes _{\varphi '}G')\rtimes _{\varphi ''}G''\cong G\rtimes _\varphi (G'\times G''), \end{aligned}$$

where the homomorphism $\varphi :G'\times G''\rightarrow {\text {Aut}}(G)$ is defined by $\varphi (g',g'')=\varphi '(g')\varphi ''(g'')$ for $g'\in G'$ and $g''\in G''$.

Now, we are in a position to state:

Proposition 4

If X is a connected ANR-space and $f_1,\ldots ,f_m:X\rightarrow X$ are mutually commutative (up to homotopy) homotopy equivalences then there are isomorphisms

$$\begin{aligned} \pi _n(T(f_1,\ldots ,f_m))\cong \pi _n(X)\text { for } n>1 \text {and } \pi _1(T(f_1,\ldots ,f_m))\cong \pi _1(X)\rtimes _\theta {\mathbb {Z}}^m, \end{aligned}$$

where the homomorphism $\theta :{\mathbb {Z}}^m\rightarrow {\text {Aut}}(\pi _1(X))$ is determined by (mutually commutative) automorphisms $\theta _i:\pi _1(X)\rightarrow \pi _1(X)$, where $\theta _i=\sigma '_{i*}\circ f_{i*}:\pi _1(X,x_0)\rightarrow \pi _1(X,x_0)$ are the automorphism with $f_{i*}:\pi _1(X,x_0)\rightarrow \pi _1(X,f_i(x_0))$ induced by the homotopy equivalences $f_i:X\rightarrow X$ and paths $\sigma '_i:I\rightarrow X$ with $\sigma '_i(0)=f_i(x_0)$, and $\sigma '_i(1)=x_0$ for a fixed $x_0\in X$ and $i=1,\ldots ,m$.

Proof

First, notice that, by inductive procedure, Proposition 3 leads to isomorphisms $\pi _n(X)\cong \pi _n(T(f_1,\ldots ,f_m))$ for $n>1$ and

$$\begin{aligned} \pi _1(T(f_1,\ldots ,f_m))\cong (\cdots ((\pi _1(X)\rtimes _{{\varphi _1}_*}{\mathbb {Z}})\rtimes _{{\varphi _2}_*}{\mathbb {Z}})\rtimes \cdots )\rtimes _{{\varphi _{m}}_*}{\mathbb {Z}}, \end{aligned}$$

where $\varphi _i :{\mathbb {Z}}\rightarrow {\text {Aut}}((\cdots ((\pi _1(X)\rtimes _{{\varphi _1}_*}{\mathbb {Z}})\rtimes _{{\varphi _2}_*}{\mathbb {Z}})\rtimes \cdots )\rtimes _{{\varphi _{i-1}}_*}{\mathbb {Z}})$ are homomorphisms determined by automorphisms $f_{i*}^{(i-1)}:\pi _1(T(f_1,\ldots ,f_{i-1}))\rightarrow \pi _1(T(f_1,\ldots ,f_{i-1}))$ for $i=1,\ldots ,m$.

Because $\varphi _i :{\mathbb {Z}}\rightarrow {\text {Aut}}((\cdots (\pi _1(X)\rtimes _{{\varphi _1}_*}{\mathbb {Z}})\rtimes _{{\varphi _2}_*}{\mathbb {Z}})\rtimes \cdots )\rtimes _{{\varphi _{i-1}}_*}{\mathbb {Z}})$ factors through ${\text {Aut}}_{\varphi _{i-1}}((\cdots (\pi _1(X)\rtimes _{{\varphi _1}_*}{\mathbb {Z}})\rtimes _{{\varphi _2}_*}{\mathbb {Z}})\rtimes \cdots )\rtimes _{{\varphi _{i-2}}_*}{\mathbb {Z}})$ for $i=1,\ldots ,m-1$, Lemma 1, by the inductive procedure, leads to an isomorphism

$$\begin{aligned} \pi _1(T(f_1,\ldots ,f_m))\cong \pi _1(X)\rtimes _\theta {\mathbb {Z}}^m, \end{aligned}$$

where $\theta :{\mathbb {Z}}^m\rightarrow {\text {Aut}}(\pi _1(X))$ is the associated homomorphism with the (mutually commutative) automorphisms $\theta _i:\pi _1(X)\rightarrow \pi _1(X)$, where $\theta _i=\sigma '_{i*}\circ f_{i*}:\pi _1(X,x_0)\rightarrow \pi _1(X,x_0)$ are the automorphisms with $f_{i*}:\pi _1(X,x_0)\rightarrow \pi _1(X,f(x_0))$ induced by the homotopy equivalences $f_i:X\rightarrow X$ and paths $\sigma '_i:I\rightarrow X$ with $\sigma '_i(0)=f_i(x_0)$, and $\sigma '_i(1)=x_0$ for a fixed $x_0\in X$ and $i=1,\ldots ,m$. This completes the proof. $\square$

Thus, Proposition 4 yields that the sequence

$$\begin{aligned} X\xrightarrow {\imath } T(f_1,\ldots ,f_m)\xrightarrow {p}\mathbb {T}^m \end{aligned}$$

implies the long exact sequence

$$\begin{aligned} \cdots \rightarrow \pi _n(X)\xrightarrow {\imath _*}\pi _n(T(f_1,\ldots ,f_m))\xrightarrow {p_*}\pi _n(\mathbb {T}^m)\rightarrow \pi _{n-1}(X)\rightarrow \cdots . \end{aligned}$$

Corollary 1

Let $f_1,\ldots ,f_m:X\rightarrow X$ be mutually commutative homotopy equivalences. Then, the lifting $\tilde{\imath } :\tilde{X}\rightarrow \widetilde{T(f_1,\ldots ,f_m)}$ of the inclusion map $\imath :X\rightarrow T(f_1,\ldots ,f_m)$ to a map of universal coverings is a homotopy equivalence and determines a homotopy equivalence

$$\begin{aligned} X\xrightarrow {\simeq }\widetilde{T (f_1,\ldots ,f_m)}/\pi _1(X). \end{aligned}$$

According to the construction presented in [27], the homotopy colimit ${\text {hocolim}}{\mathbf X}$ of a diagram of spaces

(called also a homotopy push-out or a homotopy Cartesian coproduct) is the quotient of the space

$$\begin{aligned}X_0\sqcup X_1\sqcup X_2 \sqcup X_0\times I\times \{0_{f_1},0_{f_2}\}\end{aligned}$$

under the identifications

$$\begin{aligned} \big <(x,1,0_{f_1})\sim x\sim (x,1,0_{f_2}),(x,0,0_{f_1})\sim f_1(x),(x,0, 0_{f_2})\sim f_2(x)\big > \end{aligned}$$

where $\{0_{f_1},0_{f_2}\}$ is a two elements set and $I=[0,1]$ is the unit interval.

This space is homeomorphic to the double mapping cylinder

$$\begin{aligned} X_1\sqcup (X_0\times I)\sqcup X_2/\big <f_1(x)\sim (x,0),\, f_2(x)\sim (x,1)\big > \end{aligned}$$

a familiar model for the homotopy push-out.

In particular, by means of [19, Chapter 2], the homotopy coequalizer of the diagram

is homeomorphic to the homotopy push-out of the associated diagram

where $\nabla :X_0\sqcup X_0 \rightarrow X_0$ is the codiagonal map. This implies that the mapping torus T(f) of a map $f:X\rightarrow X$ is homeomorphic to the homotopy push-out of the associated diagram

Because the indexing category contains $i_0$ as an initial object, the classifying space $\mathbf {B}\mathbb {I}$ is contractible and, in view of Proposition 1, the canonical map ${\text {hocolim}}{\mathbf X}\rightarrow {\text {hocolim}}^*{\mathbf X}$ is a homotopy equivalence provided $\mathbf {X}$ is an $\mathbb {I}$-diagram of pointed spaces.

As it is stated in Introduction, from now on, we assume throughout the paper that any space X is a CW-complex and an action $G\times X\rightarrow X$ of a discrete group G on X is free, properly discontinuous and cellular.

Remark 1

Notice that for an action $G\times X\rightarrow X$ there is a fibration $X\rightarrow X/G\rightarrow K(G,1)$. Consequently, there are isomorphisms $\pi _k(X)\cong \pi _k(X/G)$ for $k>1$ and an extension

$$\begin{aligned} e\rightarrow \pi _1(X)\rightarrow \pi _1(X/G)\rightarrow G\rightarrow e \end{aligned}$$

of groups.

In particular, for a homotopy n-sphere $\Sigma (n)$ there are isomorphisms $\pi _k(\Sigma (n))\cong \pi _k(\Sigma (n)/G)$ for $k>1$ and $n>1$, $\pi _1(\Sigma (n)/G)\cong G$ for $n>1$ and an extension

$$\begin{aligned} e\rightarrow {\mathbb {Z}}\rightarrow \pi _1(\Sigma (1)/G)\rightarrow G\rightarrow e \end{aligned}$$

of groups.

3 Actions of the group $G\rtimes {\mathbb {Z}}^m$

Given an action $(G\rtimes _\theta {\mathbb {Z}}^m)\times X\rightarrow X$ of the semidirect product $G\rtimes _\theta {\mathbb {Z}}^m$ on a space X, there is a fibration

$$\begin{aligned} X/G\xrightarrow {\jmath } X/(G\rtimes _\theta {\mathbb {Z}}^m)\xrightarrow {q}\mathbb {T}^m, \end{aligned}$$

where $\jmath :X/G\rightarrow X/(G\rtimes _\theta {\mathbb {Z}}^m)$ is determined by the inclusion $G\hookrightarrow G\rtimes _\theta {\mathbb {Z}}^m$.

Consider an action $G\times X\rightarrow X$ of a group G on a space X and mutually commutative (up to homotopy) homotopy equivalences $f_i:X/G\rightarrow X/G$ for $i=1,\ldots ,m$. Then, by Corollary 1, the inclusion map $\imath :X/G\rightarrow T(f_1,\ldots ,f_m)$ lifts to a homotopy equivalence of universal coverings $\tilde{\imath }:\widetilde{(X/G)}\xrightarrow {\simeq }\widetilde{T(f_1,\ldots ,f_m)}$. Further, the homotopy equivalence of the universal covering $\widetilde{(X/G)}\simeq \tilde{X}$ and the short exact sequence $e\rightarrow \pi _1(X)\rightarrow \pi _1(X/G)\rightarrow G\rightarrow e$ yield a homotopy equivalence $X\xrightarrow {\simeq } \widetilde{T(f_1,\ldots ,f_m)}/\pi _1(X)$ and an action

$$\begin{aligned} G\times \big (\widetilde{T(f_1,\ldots ,f_m)}/\pi _1(X)\big )\longrightarrow \widetilde{T(f_1,\ldots ,f_m)}/\pi _1(X). \end{aligned}$$

In view of Proposition 4 there is an isomorphism $\pi _1(T(f_1,\ldots ,f_m))\cong \pi _1(X/G)\rtimes _\theta \mathbb {Z}^m$ for a homomorphism $\theta :\mathbb {Z}^m\rightarrow {\text {Aut}}(\pi _1(X/G))$. Then, by the short exact sequence $e\rightarrow \pi _1(X)\rightarrow \pi _1(X/G)\rightarrow G\rightarrow e$, we derive a homomorphism $\bar{\theta }:\mathbb {Z}^m\rightarrow {\text {Aut}}(G)$ determined by $\theta :\mathbb {Z}^m\rightarrow {\text {Aut}}(\pi _1(X/G))$ and an action

$$\begin{aligned} (G\rtimes _{\bar{\theta }}\mathbb {Z}^m)\times (\widetilde{T(f_1,\ldots ,f_m)}/\pi _1(X)\big )\longrightarrow \widetilde{T(f_1,\ldots ,f_m)}/\pi _1(X) \end{aligned}$$

which yields a homotopy equivalence

$$\begin{aligned} T(f_1,\ldots ,f_m)\xrightarrow {\simeq }\big (\widetilde{T(f_1,\ldots ,f_m)}/\pi _1(X)\big )/(G\rtimes _{\bar{\theta }}\mathbb {Z}^m). \end{aligned}$$

Conversely:

Proposition 5

For any action $(G\rtimes _\theta {\mathbb {Z}}^m)\times X\rightarrow X$ there are mutually commutative homeomorphisms $h_1,\ldots ,h_m:X/G\rightarrow X/G$ and a homotopy equivalence

$$\begin{aligned}T(h_1,\ldots ,h_m)\xrightarrow {\simeq } X/(G\rtimes _\theta {\mathbb {Z}}^m).\end{aligned}$$

Proof

Given an action $(G\rtimes _\theta {\mathbb {Z}}^m)\times X\rightarrow X$, write $g_0=\jmath :X/G\rightarrow X/(G\rtimes _\theta {\mathbb {Z}}^m)$. Because G is a normal subgroup of $G\rtimes _\theta {\mathbb {Z}}^m$, the action $(G\rtimes _\theta {\mathbb {Z}}^m)\times X\rightarrow X$ leads to an action ${\mathbb {Z}}^m\times (X/G)\rightarrow X/G$. Then, generators of ${\mathbb {Z}}^m$ determine mutually commutative homeomorphisms $h_i:X/G\rightarrow X/G$ such that the diagrams

commute for $i=1,\ldots ,m$. In view of Proposition 2, the map $g_0:X/G\rightarrow X/(G\rtimes _\theta {\mathbb {Z}}^m)$ leads to $g_1:T(h_1)\rightarrow X/(G\rtimes _\theta {\mathbb {Z}}^m)$ such that the diagram

is commutative and mutually commutative homeomorphisms

$$\begin{aligned}h_2^{(1)},\ldots ,h_m^{(1)} : T(h_1)\rightarrow T(h_1).\end{aligned}$$

Inductively, given $g_i:T(h_1,\ldots ,h_i)\rightarrow X/(G\rtimes _\theta {\mathbb {Z}}^m)$ such that the diagram

commute and mutually commutative homeomorphisms

$$\begin{aligned} h_{i+1}^{(i)},\ldots ,h_m^{(i)} : T(h_1,\ldots ,h_i)\rightarrow T(h_1,\ldots ,h_i), \end{aligned}$$

we construct $T(h_1,\ldots ,h_{i+1})$ and a map $g_{i+1} : T(h_1,\ldots ,h_{i+1})\rightarrow X/(G\rtimes _\theta {\mathbb {Z}}^m)$ such that the diagram

commute and mutually commutative homeomorphisms

$$\begin{aligned} h_{i+2}^{(i+1)},\ldots ,h_m^{(i+1)} : T(h_1,\ldots ,h_{i+1})\rightarrow T(h_1,\ldots ,h_{i+1}).\end{aligned}$$

This yields a map $g_m : T(h_1,\ldots ,h_m)\rightarrow X/(G\rtimes _\theta {\mathbb {Z}}^m)$ such that the diagram

is commutative (up to homotopy). Because the diagram of fibrations

is commutative, the map

$$\begin{aligned}g_m : T(h_1,\ldots ,h_m)\xrightarrow {\simeq } X/(G\rtimes _\theta {\mathbb {Z}}^m)\end{aligned}$$

induces isomorphisms of homotopy groups and is the required homotopy equivalence, and the proof is complete. $\square$

Corollary 2

Let $f_1,\ldots ,f_m:X\rightarrow X$ be mutually commutative homotopy equivalences. Then, there are mutually commutative homeomorphisms

$$\begin{aligned}h_1,\ldots ,h_m:\widetilde{T(f_1,\ldots ,f_m)}/\pi _1(X)\rightarrow \widetilde{T(f_1,\ldots ,f_m)}/\pi _1(X)\end{aligned}$$

and a homotopy equivalence

$$\begin{aligned}T(h_1,\ldots ,h_m)\xrightarrow {\simeq }T(f_1,\ldots ,f_m).\end{aligned}$$

Let now $\mathcal {K}^G_X$ be the quotient set of all homeomorphism classes of orbit spaces $X/\gamma$ with respect to all actions $\gamma :G\times X\rightarrow X$ by the homotopy relation. Next, write $(\mathcal {E}^G_X)^m$ for the m-th Cartesian power of the homotopy self-equivalences of $X/\gamma$ and $SP^m(\mathcal {E}^G_X)$ for the quotient set with respect to the obvious action on $(\mathcal {E}^G_X)^m$ of the symmetric group on m letters. Given an action $G\times X\rightarrow X$ of a group G on a space X and mutually commutative (up to homotopy) homeomorphisms $h_i:X/G\rightarrow X/G$ for $i=1,\ldots ,m$, write $\tilde{\gamma }:(G\rtimes _\theta {\mathbb {Z}}^m)\times X\rightarrow X$ for the induced actions determined by Corollary 1. Summarizing the above, we can state the main result of this section.

Theorem 1

Let X be a space, G a group and $m\ge 1$. The assignment

$$\begin{aligned}\bigl ([X/\gamma ], ([h_1],\ldots ,[h_m])\bigr )\mapsto [X/\tilde{\gamma }] \end{aligned}$$

is a well defined map and determines a surjection

$$\begin{aligned} \mathcal {K}_X^G\times SP^m(\mathcal {E}^G_X)_c {\longrightarrow }\mathcal {K}_X^{G\rtimes {\mathbb {Z}}^m}, \end{aligned}$$

where $SP^m(\mathcal {E}^G_X)_c$ denotes the subset of $SP^m(\mathcal {E}^G_X)^m$ determined by n-tuples of homotopy classes of mutually commutative homotopy self-equivalences of $X/\gamma$.

Remark 2

The result above provides an upper bound for the number of homotopy types of orbit spaces once one can estimate the cardinality of the sets $\mathcal {K}_X^G$ and $(\mathcal {BE}^G_X)_c^m$. This will be further explored in Sect. 5.

4 Actions of the group $G_1*_{G_0}G_2$

Given groups $G_0,G_1$ and $G_2$ with monomorphic maps $G_1\mathop {\leftarrowtail }\limits ^{i_1} G_0\mathop {\rightarrowtail }\limits ^{i_2}G_2$, consider the push-out

in the category of groups. The group $G_1*_{G_0}G_2$ is usually called the free product of $G_1$ and $G_2$ with amalgamated subgroup $G_0$.

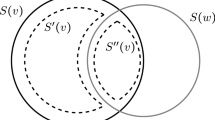
Let $\gamma _1:G_1\times X_1\rightarrow X_1$ and $\gamma _2:G_2\times X_2\rightarrow X_2$ be actions of $G_1$ and $G_2$ on 1-connected spaces $X_1$ and $X_2$, respectively, and the orbit spaces $X_1/G_0$ and $X_2/G_0$ have the same homotopy type. Then, consider the diagram

determined by monomorphic maps $G_1\mathop {\leftarrowtail }\limits ^{\imath _1} G_0\mathop {\rightarrowtail }\limits ^{\imath _2} G_2$ and a homotopy equivalence between $X_1/G_0$ and $X_2/G_0$, and its pointed homotopy colimit ${\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)$.

Conversely, given an action $\gamma :(G_1*_{G_0}G_2)\times X\rightarrow X$ of the group $G_1*_{G_0}G_2$ on a 1-connected space X, consider the associated diagram

determined by monomorphic maps $G_1\mathop {\leftarrowtail }\limits ^{\imath _1} G_0\mathop {\rightarrowtail }\limits ^{\imath _2} G_2$.

Given an action $\gamma :G\times X\rightarrow X$ and a subgroup $G_0<G$, write $\gamma _0:G_0\times X\rightarrow X$ for its restriction to $G_0$.

Proposition 6

• (1) If $\gamma :(G_1*_{G_0}G_2)\times X\rightarrow X$ is an action then the canonical map

  $$\begin{aligned} {\text {hocolim}}{\mathbf X}(\gamma )\longrightarrow X/(G_1*_{G_0}G_2) \end{aligned}$$

  is a homotopy equivalence.

• (2) Let $G_1\mathop {\leftarrowtail }\limits ^{i_1} G_0\mathop {\rightarrowtail }\limits ^{i_2}G_2$ be monomorphic maps of groups and consider actions $\gamma _1:G_1\times X\rightarrow X$ and $\gamma _2:G_2\times X\rightarrow X$ on a 1-connected space such that the orbit spaces $X/G_0$ and $X/\gamma _{2,0}$ have the same homotopy type. Then there is an action

  $$\begin{aligned}\tilde{\gamma }(\gamma _1,\gamma _2) : (G_1*_{G_0}G_2)\times (\widetilde{{\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)})\longrightarrow \widetilde{{\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)}\end{aligned}$$

  on the universal covering $\widetilde{{\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)}$ of ${\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)$. Further, there is a homotopy equivalence $X\xrightarrow {\simeq }\widetilde{{\text {hocolim}}^*{\mathbf X(\gamma _1,\gamma _2)}}$.

Proof

• (1) Because the indexing category $\mathbb {I}$ contains an initial object, the canonical map ${\text {hocolim}}{\mathbf X}\rightarrow {\text {hocolim}}^*{\mathbf X}$ is a homotopy equivalence. Therefore, it is sufficient to show that the canonical map

  $$\begin{aligned} {\text {hocolim}}^*{\mathbf X}(\gamma )\longrightarrow X/(G_1*_{G_0}G_2) \end{aligned}$$

  is a homotopy equivalence.

  But, the quotient maps $X/G_1\rightarrow X/(G_1*_{G_0}G_2)\leftarrow X/G_2$ determined by monomorphic maps monomorphic maps $G_1\rightarrowtail G_1*_{G_0}G_2\leftarrowtail G_2$, respectively lead to the canonical map

  $$\begin{aligned} \varphi : {\text {hocolim}}^*{\mathbf X}(\gamma )\longrightarrow X/(G_1*_{G_0}G_2). \end{aligned}$$

  Now, by [23, 1.2 Theorem], there is a spectral sequence

  $$\begin{aligned}E^2_{p,q}={\text {colim}}_p\pi _q({\mathbf X}(\gamma ))\Longrightarrow \pi _q({\text {hocolim}}^*{\mathbf X}(\gamma ))\end{aligned}$$

  with the value on the diagram of $\Pi$-algebras ${\text {colim}}_p\pi _q({\mathbf X}(\gamma ))$ of the p-th derived functor ${\text {colim}}_p$ of the direct limit functor ${\text {colim}}$.

  First, this implies an isomorphism

  $$\begin{aligned} \pi _1({\text {hocolim}}^*{\mathbf X}(\gamma ))\simeq G_1*_{G_0}G_2 \end{aligned}$$

  and consequently, an isomorphism $\pi _1(\varphi ): \pi _1({\text {hocolim}}^*{\mathbf X}(\gamma ))\xrightarrow {\simeq }\pi _1(X/G_1*_{G_0}G_2)$.

  Next, because the maps $X/G_1\rightarrow X/G_0 \leftarrow X/G_2$ are coverings, we get isomorphisms $\pi _q(X/G_1)\xleftarrow {\simeq }\pi _q(X/G_0)\xrightarrow {\simeq }\pi _q(X/G_1)$ for $q\ge 2$. Consequently, there are isomorphisms $\pi _q(X/G_1)\xrightarrow {\simeq }\pi _q({\text {hocolim}}^*{\mathbf X}(\gamma ))\xleftarrow {\simeq }\pi _q(X/G_2)$ and this leads to isomorphisms

  $$\begin{aligned} \pi _q(\varphi ): \pi _q({\text {hocolim}}^*{\mathbf X}(\gamma ))\xrightarrow {\simeq }\pi _q(X/G_1*_{G_0}G_2) \end{aligned}$$

  for $q\ge 2$ and the proof follows.

• (2) Let $G_1\mathop {\leftarrowtail }\limits ^{i_1} G_0\mathop {\rightarrowtail }\limits ^{i_2}G_2$ be monomorphic maps of groups and $\gamma _1:G_1\times X\rightarrow X$, and $\gamma _2:G_2\times X\rightarrow X$ actions on a 1-connected space such that the orbit spaces $X/\gamma _{1,0}$ and $X/\gamma _{2,0}$ have the same homotopy type, where $\gamma _{1,0}$ and $\gamma _{2,0}$ are restrictions of $\gamma _1$ and $\gamma _2$ to actions of the subgroup $G_0$ on X, respectively. Then the group $G_1*_{G_0}G_2$ acts on the universal covering $\widetilde{{\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)}$ of ${\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)$ for the diagram

  

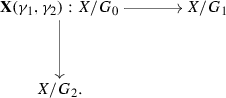
  By [23, 1.2 Theorem], there is an isomorphism $\pi _1({\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2))\cong G_1*_{G_0}G_2$, so the group $G_1*_{G_0}G_2$ acts on the universal covering $\widetilde{{\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)}$ of ${\text {hocolim}}^*{\mathbf X(\gamma _1,\gamma _2)}$.

  Because the canonical map $X\rightarrow {\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)$, by the arguments as above, leads to a homotopy equivalence $X\xrightarrow {\simeq }\widetilde{{\text {hocolim}}^*{\mathbf X}(\gamma _1,\gamma _2)}$, the proof is complete. $\square$

Given monomorphic maps $G_1\mathop {\leftarrowtail }\limits ^{i_1} G_0\mathop {\rightarrowtail }\limits ^{i_2}G_2$ of groups, consider actions $\gamma _1:G_1\times X\rightarrow X$ and $\gamma _2:G_2\times X\rightarrow X$ such that the orbit spaces $X/\gamma _{1,0}$ and $X/\gamma _{2,0}$ have the same homotopy type. Next, write $\mathcal {K}_X^{G_1}\times _{\mathcal {K}_X^{G_0}}\mathcal {K}_X^{G_2}$ for the quotient set of all homeomorphism classes of diagrams

by the homotopy relation, where the map $X/\gamma _{1,0}\rightarrow X_1/\gamma _1$ is determined by the monomorphism $G_0\rightarrowtail G_1$ and $X/\gamma _{1,0}\rightarrow X/\gamma _2$ by a homotopy equivalence $X/\gamma _{1,0}\simeq X/\gamma _{2,0}$ and the monomorphism $G_0\rightarrowtail G_2$. We identify an element of $\mathcal {K}_X^{G_1}\times _{\mathcal {K}_X^{G_0}}\mathcal {K}_X^{G_2}$ with a pair $([X/\gamma _1],[X/\gamma _2])$. Taking into account the above, in view of Proposition 6 we are in a position to state the main result of this section.

Theorem 2

Let X be a space and $G_1\mathop {\leftarrowtail }\limits ^{i_1} G_0\mathop {\rightarrowtail }\limits ^{i_2}G_2$ monomorphic maps of groups. The assignment

$$\begin{aligned} (\big [X/\gamma _1\big ], \big [X/\gamma _2\big ]) \mapsto \big [X/\tilde{\gamma }(\gamma _1,\gamma _2)\big ] \end{aligned}$$

is a well defined map and determines a surjection

$$\begin{aligned} \mathcal {K}_X^{G_1}\times _{\mathcal {K}_X^{G_0}}\mathcal {K}_X^{G_2}{\longrightarrow }\mathcal {K}_X^{G_1*_{G_0}G_2}. \end{aligned}$$

Remark 3

The theorem above can be used to provide an upper bound for the number of homotopy types of orbit space for the group $G_1*_{G_0}G_2$ once one can estimate the cardinality of the sets $\mathcal {K}_X^{G_1}, \mathcal {K}_X^{G_0}$ and $\mathcal {K}_X^{G_2}$, respectively. This will be further explored in Sect. 5.

5 Virtually cyclic groups

A virtually cyclic group is a group that has a cyclic subgroup of finite index. Every virtually cyclic group in fact has a normal cyclic subgroup of finite index (namely, the core of any cyclic subgroup of finite index), and virtually cyclic groups are therefore also known as cyclic-by-finite groups.

A finite-by-cyclic group (that is, a group G with a finite normal subgroup $G_0$ such that $G/G_0$ is cyclic) is always virtually cyclic. To see this, note that a finite-by-cyclic group is either finite, in which case it is certainly virtually cyclic, or it is finite-by-${\mathbb {Z}}$ for the infinite cyclic group ${\mathbb {Z}}$, in which case the extension $e\rightarrow F\rightarrow G\rightarrow \mathbb {Z}\rightarrow 0$ splits, where F is a finite group. Then $G=F\rtimes \mathbb {Z}=F\mathbb {Z}$ and so the subgroup $\mathbb {Z}$ of G has finitely many left cosets in G.

In fact, we have the following criterion due to Wall:

Theorem 3

([21, 28]) Let G be a group. Then the following are equivalent:

• (1) G is a group with two ends;

• (2) G is an infinite virtually cyclic group;

• (3) G has a finite normal subgroup $G_0$ such that $G/G_0$ is ${\mathbb {Z}}$ or ${\mathbb {Z}}_2\star {\mathbb {Z}}_2\cong D_\infty$, the infinite dihedral group.

Equivalently, G is of the form:

• (I) a semi-direct product $G_0\rtimes {\mathbb {Z}}$ or

• (II) $G_1\star _{G_0} G_2$, where $G_0<G_1,G_2$ and the index $[G_i:G_0]=2$ for $i=1,2$ with a finite group $G_0$.

If a virtually cyclic group G satisfies (I), we shall say that it is of Type I, while if it satisfies (II), we shall say that it is of Type II.

An infinite virtually cyclic group is the middle term of a short exact sequence of the form $e\rightarrow \mathbb {Z }\rightarrow G \rightarrow G_0 \rightarrow e$, where $G_0$ is a finite group. Then, in view of [17, Proposition 19], it holds: if this extension is central then the group G is of type I, otherwise it is of type II.

Given an action $G\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ of a finite group G on a homotopy sphere $\Sigma (2n-1)$, by means of [1, Chpater IV] and [3, Chapter VI], there is an isomorphism $H^{2n}(G,{\mathbb {Z}})\cong {\mathbb {Z}}/|G|$ and the homotopy type of $\Sigma (2n-1)/G$ is determined by the Postnikov invariant $k^{2n}(\Sigma (2n-1)/G)\in H^{2n}(G,{\mathbb {Z}}))$. Then, we get a skew-homomorphism ${\text {Aut}}(G)\rightarrow {\text {Aut}}(H^{2n}(G,{\mathbb {Z}}))\cong {\text {Aut}}({\mathbb {Z}}/|G|)$. Write $\varphi ^*$ for the image of $\varphi \in {\text {Aut}}(G)$ in the group ${\text {Aut}}({\mathbb {Z}}/|G|)$. It is well known that $\varphi ^*$ might be identified with a unit of the ring ${\mathbb {Z}}/|G|$ of integers mod |G|. Let now $\mathcal {K}^G_{2n-1}$ be the quotient set of all homeomorphism classes of orbit spaces $\Sigma (2n-1)/\gamma$ with respect to all actions $\gamma :G\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ by the homotopy relation. Details on $\mathcal {K}^G_{2n-1}$ and the group $\mathcal {E}^G_{2n-1}$ of homotopy self-equivalences $\Sigma (2n-1)/G$ for all finite periodic groups G classified by Suzuki–Zassenhaus and listed in [1, Theorem 6.15]) as follows: have been presented in a series of papers [8]–[14].

Family	Definition	Conditions
I	${\mathbb Z}/a\rtimes _\alpha {\mathbb Z}/b$	$(a,b)=1$
II	${\mathbb Z}/a\rtimes _\beta ({\mathbb Z}/b\times {\mathcal Q}_{2^i})$	$(a,b)=(ab,2)=1$
III	${\mathbb Z}/a\rtimes _\gamma ({\mathbb Z}/b\times T_i)$	$(a,b)=(ab,6)=1$
IV	${\mathbb Z}/a\rtimes _\tau ({\mathbb Z}/b\times O^*_i)$	$(a,b)=(ab,6)=1$
V	$({\mathbb Z}/a\rtimes _\alpha {\mathbb Z}/b)\times SL_2({\mathbb F}_p)$	$(a,b)=(a,p(p^2-1))=1$
VI	${\mathbb Z}/a\rtimes _\mu ({\mathbb Z}/b\times TL_2({\mathbb F}_p))$	$(a,b)=(ab,p(p^2-1))=1$

The following result was indicated by Swan in [24] and then completed by him in [26, Theorem A]:

Theorem 4

Let G be a finite group. Let d be the greatest common divisor of n and $\phi (n)$, $\phi$ being Euler’s $\phi$-function. Suppose G has period q. Then there exists a finite simplicial complex X of dimension $dq-1$ which has the homotopy type of a $(dq-1)$-sphere and on which G acts freely and simplicially.

Further, the results [3, Chapter VII, Proposition 10.2], [25] and [26] yield:

Proposition 7

Let a finite group G acts on $\Sigma (n)$. Then:

• (1) the group G is periodic;

• (2) if n is even then $G\cong {\mathbb {Z}}_2$ and the action of G reverses the orientation of $\Sigma (n)$;

• (3) if n is odd then:

  • (i) the action of G preserves the orientation of $\Sigma (n)$;

  • (ii) the least period d(G) being a divisor of $n+1$;

• (4) there is a bijection

  $$\begin{aligned} \mathcal {K}^G_{2n-1}\xrightarrow {\cong }{\text {Aut}}({\mathbb {Z}}/|G|)/\{\pm \varphi ^*;\;\varphi \in {\text {Aut}}(G)\}. \end{aligned}$$

In the light of Theorem 3 notations and the result from [26], we derive:

Corollary 3

Let a virtually cyclic group G acts on $\Sigma (2n-1)$. Then:

• (1) any its finite subgroup $G_0<G$ is isomorphic to a periodic finite group of period being a divisor of 2n;

• (2) there is an isomorphism $G\cong G_0\rtimes \mathbb {Z}$ for some finite group $G_0$ of period a divisor of 2n such that the period of G is a divisor of 4n provided G is virtually cyclic group of type I;

• (3) there is an isomorphism $G\cong G_1\star _{G_0} G_2$ for some $G_0,G_1, G_2$ finite periodic groups of period a divisor of 2n with $G_0<G_1,G_2$ and the index $[G_i:G_0]=2$ for $i=1,2$ provided G is of type II.

Proof

• (1): A free and cellular action $G\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ of a group G restricts to an action $G_0\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ for a finite subgroup $G_0<G$. Then, in light of Proposition 7, the claim follows.

• (2): For G being a virtually cyclic group of type I, by (1), we get an isomorphism $G \cong G_0\rtimes _\theta \mathbb {Z}$, the semi-direct product of some finite period subgroup $G_0<G$ with period dividing 2n and a homomorphism $\theta :\mathbb {Z}\rightarrow {\text {Aut}}(G_0)$. If the induced homomorphism $G_0\rtimes _\theta \mathbb {Z}\rightarrow {\text {Aut}}(H^{2n-1}(\Sigma (2n-1))\cong {\text {Aut}}(\mathbb {Z})$ is trivial then, in view of [2], the result is obvious. In fact the period d(G) divides 2n. If this homomorphism is not trivial, since restricted to $G_0$ is trivial, it follows that the action of a generator of $\mathbb {Z}$ is the multiplication by $-1$. Following [2], from the given action of $G_0\rtimes _\theta {\mathbb {Z}}$ on $\Sigma (2n-1)$ one can construct an action of $G_0\rtimes _\theta \mathbb {Z}$ on the joint $\Sigma (2n-1)*\Sigma (2n-1)\cong \Sigma (4n-1)$ with the trivial induced homomorphism $G_0\rtimes _\theta \mathbb {Z}\rightarrow {\text {Aut}}(H^{4n-1}(\Sigma (4n-1))\cong {\text {Aut}}(\mathbb {Z})$ and the result follows.

• (3): Now, consider a group G of type II. Then, $G\cong G_1\star _{G_0} G_2$ with $[G_i:G_0]=2$ for $i=1,2$. Because, in view of [22], the natural maps $G_i \rightarrow G_1\star _{G_0} G_2$ are injective for for $i=1,2$, it follows from (1) that the groups $G_0,G_1,G_2$ are periodic with period dividing 2n and the proof is complete. $\square$

In the next section, we aim to analyse actions on homotopy spheres $\Sigma (2n-1)$ of groups of the form $G\rtimes {\mathbb {Z}}^m$ for $m\ge 1$ and $G_1*_{G_0}G_2$, containing properly the family of all virtually cyclic groups, for $G, G_0, G_1, G_2$ finite. We point out that by [17, Proposition 10 and Theorem 70] some virtually cyclic groups $G_1*_{G_0}G_2$ act on a homotopy 3-sphere, which is an interesting case.

6 Actions of groups $G\rtimes {\mathbb {Z}}^m$ for $m\ge 1$ and $G_1*_{G_0}G_2$ on odd homotopy spheres

Consider an action $(G\rtimes {\mathbb {Z}}^m)\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ for a finite group G. Then, by means of Proposition 5, there are mutually commutative homeomorphisms $h_1,\ldots ,h_m:\Sigma (2n-1)/G\rightarrow \Sigma (2n-1)/G$ and a homotopy equivalence $T(h_1,\ldots ,h_m)\xrightarrow {\simeq }\Sigma (2n-1)/(G\rtimes {\mathbb {Z}}^m).$

On the other hand, given mutually commutative (up to homotopy) homotopy equivalences $f_1,\ldots ,f_m:\Sigma (2n-1)/G\rightarrow \Sigma (2n-1)/G$, in view of Corollary 1, there is a homotopy equivalence $\widetilde{T(f_1,\ldots ,f_m)}\simeq \Sigma '(2n-1)$ for some $(2n-1)$-homotopy sphere $\Sigma '(2n-1)$ and consequently,

$$\begin{aligned} T(f_1,\ldots ,f_m)\simeq \Sigma '(2n-1)/G\rtimes _\theta {\mathbb {Z}}^m, \end{aligned}$$

where the homomorphism $\theta :{\mathbb {Z}}^m\rightarrow {\text {Aut}}(G)$ is determined by (mutually commutative) automorphisms ${f_i}_*:G\rightarrow G$ induced by $f_i:\Sigma (2n-1)/G\rightarrow \Sigma (2n-1)/G$ with $\pi _1(\Sigma (2n-1)/G)\cong G$ for $i=1,\ldots ,m$.

Given a group G and an automorphism $\theta :G\rightarrow G$, the homomorphism $\varphi :{\mathbb {Z}}\rightarrow {\text {Aut}}(G)$ such that $\varphi (1)=\theta$ leads to the semi-direct product $G\rtimes _\theta {\mathbb {Z}}$. Write $\theta ^*:H^{2n}(G,{\mathbb {Z}})\rightarrow H^{2n}(G,{\mathbb {Z}})$ for the induced automorphism. In particular, if G is a finite periodic group then $\theta ^*$ might be identified with an invertible element of the ring ${\mathbb {Z}}/|G|$ of integers mod |G|. Notice that a group homomorphism $\theta :{\mathbb {Z}}^m\rightarrow {\text {Aut}}(G)$, yields mutually commutative automorphisms $\theta _1,\ldots ,\theta _m:G\rightarrow G$ of the group G.

Proposition 8

Let G be a finite periodic group of period d(G). The group $G\rtimes _\theta {\mathbb {Z}}^m$ acts on $\Sigma (2n-1)$ if and only if:

• (1) $d(G)\mid 2n$;

• (2) $\theta _i^*\equiv \pm 1\,(\bmod \,|G|)$ for $i=1,\ldots ,m$. Further, given an action $(G\rtimes _\theta {\mathbb {Z}}^m)\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$, the induced homomorphism $\varphi :G\rtimes _\theta {\mathbb {Z}}^m \rightarrow {\text {Aut}}(H^{2n-1}(\Sigma (2n-1),{\mathbb {Z}}))\cong {\mathbb {Z}}_2$ is given by $\varphi (g)={\text {id}}_{\mathbb {Z}}$ for $g\in G$ and $\varphi (\theta _i)=\theta _i^*$ for $i=1,\ldots ,m$.

Proof

First, suppose that the group $G\rtimes _\theta {\mathbb {Z}}^m$ acts on $\Sigma (2n-1)$.

• (1) The G-action on $\Sigma (2n-1)$ leads to $d(G)\mid 2n$.

• (2) Let ${\mathbb {Z}}^m=\big <t_1,\ldots ,t_m \big>$ and write $\bar{t}_i:\Sigma (2n-1)\rightarrow \Sigma (2n-1)$ for the induced strictly commutative G-homeomorphisms with $i=1,\ldots ,m$. Then, [8, Theorem 1.1] yields that $\pm 1=\deg \bar{t}_i\equiv \theta ^*\,(\bmod \,|G|)$ for $i=1,\ldots ,m$.

Conversely, because $d(G)\mid 2n$, we deduce from Theorem 4 that there is an action $G\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ for some $(2n-1)$-homotopy sphere $\Sigma (2n-1)$. By [8, Theorem 1.1], there are mutually commutative (up to homotopy) maps $f_i:\Sigma (2n-1)/G\rightarrow \Sigma (2n-1)/G$ (with a fixed point $x_0\in \Sigma (2n-1)$) such that $\pi _1(f_i)=\theta _i$ for the induced automorphisms $\pi _1(f_i):\pi _1(\Sigma (2n-1)/G)\rightarrow \pi _1(\Sigma (2n-1)/G)$ with $i=1,\ldots ,m$. If $\tilde{f_i}:\Sigma (2n-1)\rightarrow \Sigma (2n-1)$ is a lifting of $f_i:\Sigma (2n-1)/G\rightarrow \Sigma (2n-1)/G$ then $\deg \tilde{f_i}\equiv \theta _i^*\,(\bmod \,|G|)$ and $\theta _i^*\equiv \pm 1\,(\bmod \,|G|)$. Then, the result of [20] implies that $f_i:\Sigma (2n-1)/G\rightarrow \Sigma (2n-1)/G$ is a homotopy equivalence for $i=1,\ldots ,m$.

Next, by Corollary 1, the inclusion map $\imath :\Sigma (2n-1)/G\rightarrow T(f_1,\ldots ,f_m)$ determines a homotopy equivalence of the universal coverings $\tilde{i}:\Sigma (2n-1)\rightarrow \widetilde{T(f_1,\ldots ,f_m)}$ and the universal covering space $\widetilde{T(f_1,\ldots ,f_m)}$ is a $(2n-1)$-homotopy sphere with $\dim \widetilde{T(f_1,\ldots ,f_m)}=\dim \Sigma (2n-1)+m$. Certainly, there is an action of $\pi _1(T(f_1,\ldots ,f_m))\cong G\rtimes _\theta {\mathbb {Z}}^m$ on the space $\widetilde{T(f_1,\ldots ,f_m)}$ and the proof is complete. $\square$

Given an action $G\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ of a group G on a homotopy sphere $\Sigma (2n-1)$ and mutually commutative (up to homotopy) homeomorphisms $h_i:\Sigma (2n-1)/G\rightarrow \Sigma (2n-1)/G$ for $i=1,\ldots ,m$, write $\tilde{\gamma }:(G\rtimes _\theta {\mathbb {Z}}^m)\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$ for the induced actions determined by Corollary 1. Then, in virtue of Theorem 1, homotopy types of orbit spaces $\Sigma (2n-1)/(G\rtimes _\theta {\mathbb {Z}}^m)\xrightarrow {\simeq }T(h_1,\ldots ,h_m)$ might be estimated as follows:

Corollary 4

The assignment $(\big [\Sigma (2n-1)/\gamma \big ], ([h_1],\ldots ,[h_m]))\mapsto \big [\Sigma (2n-1)/\tilde{\gamma }\big ]$ determines a surjection

$$\begin{aligned} \mathcal {K}^G_{2n-1}\times (SP^m\mathcal {E}^G_{2n-1})_c {\longrightarrow } \mathcal {K}_{2n-1}^{G\rtimes {\mathbb {Z}}^m}, \end{aligned}$$

where $(SP^m\mathcal {E}^G_{2n-1})_c$ denotes the subset of the m-th Cartesian power $(PS^m\mathcal {E}^G_{2n-1})$ determined by n-tuples of homotopy classes of mutually commutative homotopy self-equivalences of $\Sigma (2n-1)/\gamma$.

To present a criterion on actions of groups $G_1*_{G_0}G_2$ on $\Sigma (2n-1)$, we constitute from Proposition 6:

Corollary 5

The group $G_1*_{G_0}G_2$ acts on a $(2n-1)$-homotopy sphere if and only if there are actions $G_1\times \Sigma _1(2n-1)\rightarrow \Sigma _1(2n-1)$ and $G_2\times \Sigma _2(2n-1)\rightarrow \Sigma _2(2n-1)$ such that the orbit spaces $\Sigma _1(2n-1)/G_0$ and $\Sigma _2(2n-1)/G_0$ have the same homotopy type.

Let now, $G_0,G_1$ and $G_2$ be finite groups with monomorphisms $G_1\mathop {\leftarrowtail }\limits ^{i_1} G_0\mathop {\rightarrowtail }\limits ^{i_2}G_2$ and consider an action $(G_1*_{G_0}G_2)\times \Sigma (2n-1)\rightarrow \Sigma (2n-1)$. Then, those groups are periodic and (see e.g., [3, Chapter VI, Exercise 4]) it holds $H^{2n-1}(G_i,{\mathbb {Z}})=0$ for $i=0,1,2$. Writing $\kappa _i : G_i\rightarrowtail G_1*_{G_0}G_2$ for the inclusion maps with $i=1,2$, the Mayer–Vietoris sequence [18, Chapter VI] leads to the short exact sequence

$$\begin{aligned} 0\rightarrow H^{2n}(G_1*_{G_0}G_2,{\mathbb {Z}})\xrightarrow {\kappa _*} H^{2n}(G_1,{\mathbb {Z}})\oplus H^{2n}(G_2,{\mathbb {Z}})\xrightarrow {\imath ^*} H^{2n}(G_0,{\mathbb {Z}})\rightarrow 0, \end{aligned}$$

where $\kappa ^*=(\kappa _1^*,\kappa _2^*)$ and $\imath ^*=(\imath _1^*,-\imath _2^*)$. Consequently, there is an isomorphism

$$\begin{aligned}H^{2n}(G_1*_{G_0}G_2,{\mathbb {Z}})\cong H^{2n}(G_1,{\mathbb {Z}})\times _{H^{2n}(G_0,{\mathbb {Z}})}H^{2n}(G_2,{\mathbb {Z}}).\end{aligned}$$

But periods of the groups $G_0,G_1$ and $G_2$ are divisors of 2n, so we conclude isomorphisms $H^{2n}(G_i,{\mathbb {Z}})\cong {\mathbb {Z}}/|G_i|$ for $i=0,1,2$. Notice that the short exact sequence above yields that the maps

$$\begin{aligned}\imath _i^*: H^{2n}(G_i,{\mathbb {Z}})\rightarrow H^{2n}(G_0,{\mathbb {Z}})\end{aligned}$$

(via isomorphisms $H^{2n}(G_i,{\mathbb {Z}})\cong {\mathbb {Z}}/|G_i|$) are the quotient maps ${\mathbb {Z}}/|G_i|\rightarrow {\mathbb {Z}}/|G_0|$ determined by the divisibility $|G_0|\mid |G_i|$ which induce epimorphisms

$$\begin{aligned}\imath _i^*: {\text {Aut}}({\mathbb {Z}}/|G_i|)\rightarrow {\text {Aut}}({\mathbb {Z}}/|G_0|)\end{aligned}$$

for $i=1,2$. Then, the Postnikov invariant $k^{2n}(\Sigma (2n-1)/(G_1*_{G_0}G_2))\in H^{2n}(G_1*_{G_0}G_2,{\mathbb {Z}})$ (and so the homotopy type of $\Sigma (2n-1)/(G_1*_{G_0}G_2)$) is determined by those $k^{2n}(\Sigma (2n-1)/G_0)\in H^{2n}(G_0,{\mathbb {Z}})$, $k^{2n}(\Sigma (2n-1)/G_1)\in H^{2n}(G_1,{\mathbb {Z}})$ and $k^{2n}(\Sigma (2n-1)/G_2)\in H^{2n}(G_2,{\mathbb {Z}})$ with

$$\begin{aligned}\imath _1^*k^{2n}(\Sigma (2n-1)/G_1)=k^{2n}(\Sigma (2n-1)/G_0)=\imath _2^*k^{2n}(\Sigma (2n-1)/G_2).\end{aligned}$$

Finally, in view of Theorem 2 and Proposition 7, we are in a position to evaluate the cardinality of the set $\mathcal {K}^{G_1*_{G_0}G_2}_{2n-1}$ by means of the cardinality of a quotient of ${\text {Aut}}({\mathbb {Z}}/|G_1|) \times _{{\text {Aut}}({\mathbb {Z}}/|G_0|)}{\text {Aut}}({\mathbb {Z}}/|G_2|)$.

Corollary 6

Let $G_0,G_1$ and $G_2$ be finite periodic groups with $G_1 \leftarrowtail G_0\rightarrowtail G_2$. Then, there is a surjection

$$\begin{aligned} {\text {Aut}}(\mathbb {Z}/|G_1|)\times _{{\text {Aut}}(\mathbb {Z}/|G_0|)} {\text {Aut}}(\mathbb {Z}/|G_2|)\longrightarrow K^{G_1*_{G_0}G_2}_{2n-1} \end{aligned}$$

which factors through the quotient of ${\text {Aut}}({\mathbb {Z}}/|G_1|)\times _{ {\text {Aut}}({\mathbb {Z}}/|G_0|)}{\text {Aut}}({\mathbb {Z}}/|G_2|)$ by its subset $\{(\pm \varphi _1^*,\pm \varphi _2^*);\; (\varphi _1,\varphi _2)\in {\text {Aut}}(G_1)\times {\text {Aut}}(G_2)\text { with } \imath _1^*(\varphi _1^*)=\imath _2^*(\varphi _2^*)\}$.