Common origin of dark matter, baryon asymmetry and neutrino masses in the standard model with extended scalars

Abstract

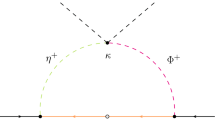
We propose a model that simultaneously addresses the existence of a dark matter candidate, baryon asymmetry and tiny neutrino masses and mixing by introducing two SU(2) triplet scalars and an inert SU(2) doublet scalar on top of the standard model. The two triplet scalars serve as mediators in generation of lepton asymmetry and determination of relic density of dark matter. They also play an essential role in the generation of tiny neutrino masses and inducing CP violation. The inert scalar is regarded as a dark matter candidate. The interference due to complex Breit–Wigner propagators for the triplets will result in CP-asymmetry that depends on the difference between their masses and a relative complex phase between their couplings to standard model leptons. Moreover, the production of lepton asymmetry will be closely tied to the evolution of dark matter, limiting the parameter space where the correct relic abundance and matter–antimatter asymmetry can be simultaneously accomplished.

Appendices

Apppendix A: Extended scalar sector

The scalar potential we consider includes two $SU(2)_L$ triplets, $\Delta _1$ and $\Delta _2$, and one inert $SU(2)_L$ doublet, $\Phi _2$, in addition to the Higgs doublet of the SM, $\Phi _1$. The decomposition of the scalar fields is given explicitly in Eq. (1). We also consider an additional $Z_2$ symmetry under which $\Phi _2$ is odd, while the rest of the fields are even. The most general potential can be written as:

$$\begin{aligned} V = {}&V_\textrm{IDM} + V_{\Delta } + V_{H\Delta } + V_\textrm{SB}, \end{aligned}$$

(25)

$$\begin{aligned} V_\textrm{IDM} = {}&- m_{\Phi 1}^2 \Phi _1^\dagger \Phi _1 + m_{\Phi 2}^2 \Phi _2^\dagger \Phi _2 \nonumber \\&+ \lambda _{\Phi 1} (\Phi _1^\dagger \Phi _1)^2 + \lambda _{\Phi 2} (\Phi _2^\dagger \Phi _2)^2 \nonumber \\&+ \lambda _{\Phi 12} \Phi _1^\dagger \Phi _1 \Phi _2^\dagger \Phi _2 \nonumber \\&+ \lambda '_{\Phi 12} \Phi _1^\dagger \Phi _2 \Phi _2^\dagger \Phi _1 + \lambda _5 \textrm{Re}\left[ (\Phi _1^\dagger \Phi _2)^2\right] \end{aligned}$$

(26)

$$\begin{aligned} V_{\Delta } = {}&\sum _{n=1}^2 \left\{ M_n^2 {{\,\textrm{Tr}\,}}\left( \Delta _n^\dagger \Delta _n\right) + \lambda _{\Delta n} {{\,\textrm{Tr}\,}}\left[ \left( \Delta _n^\dagger \Delta _n\right) ^2\right] \right. \nonumber \\&\left. + \lambda '_{\Delta n} \left[ {{\,\textrm{Tr}\,}}\left( \Delta _n^\dagger \Delta _n\right) \right] ^2\right\} \nonumber \\&+ \lambda _{\Delta 12} {{\,\textrm{Tr}\,}}(\Delta _1^\dagger \Delta _1 \Delta _2^\dagger \Delta _2)\nonumber \\&+ \lambda '_{\Delta 12} {{\,\textrm{Tr}\,}}(\Delta _1^\dagger \Delta _1) {{\,\textrm{Tr}\,}}(\Delta _2^\dagger \Delta _2) \nonumber \\&+ \lambda _{\Delta 21} {{\,\textrm{Tr}\,}}(\Delta _2^\dagger \Delta _1 \Delta _1^\dagger \Delta _2)\nonumber \\&+ \lambda '_{\Delta 21} {{\,\textrm{Tr}\,}}(\Delta _2^\dagger \Delta _1) {{\,\textrm{Tr}\,}}(\Delta _1^\dagger \Delta _2) \end{aligned}$$

(27)

$$\begin{aligned} V_{\Phi \Delta } = {}&\sum _{n=1}^{2}\sum _{k=1}^{2}\left[ \lambda _{\Phi k\Delta n} \Phi _k^\dagger \Phi _k {{\,\textrm{Tr}\,}}\left( \Delta _n^\dagger \Delta _n\right) \right. \nonumber \\&\left. + \lambda '_{\Phi k\Delta n} \Phi _k^\dagger \Delta _n \Delta _n^\dagger \Phi _k \right] \end{aligned}$$

(28)

$$\begin{aligned} V_\text {SB} = {}&\sum _{m=1}^2 \left\{ \sum _{n=1}^2 \mu _{nm} \Phi _m^T i\sigma ^2\Delta _n^\dagger \Phi _m \right. \nonumber \\&\left. + \lambda _{\Phi k\Delta 12} \Phi _m^\dagger \Phi _m {{\,\textrm{Tr}\,}}\left( \Delta _1^\dagger \Delta _2 \right) + \lambda '_{\Phi k\Delta 12} \Phi _m^\dagger \Delta _1 \Delta _2^\dagger \Phi _m\right\} \nonumber \\&M_{12}^2 {{\,\textrm{Tr}\,}}\left( \Delta _1^\dagger \Delta _2\right) + \sum _{ijkl} \left[ \lambda _{ijkl} {{\,\textrm{Tr}\,}}\left( \Delta _i^\dagger \Delta _j \Delta _k^\dagger \Delta _l\right) \right. \nonumber \\&\left. + \lambda '_{ijkl} {{\,\textrm{Tr}\,}}\left( \Delta _i^\dagger \Delta _j\right) \left( \Delta _k^\dagger \Delta _l\right) \right] + \text {H.c.} \end{aligned}$$

(29)

The terms in $V_{SB}$ break a global U(1) symmetry. The combination of indices (i, j, k, l) can take the values (2, 1, 1, 1), (1, 2, 1, 1), (1, 2, 2, 2), (2, 1, 2, 2) and (1, 2, 1, 2); other combinations belong to the H.c. part of the potential. After electroweak symmetry breaking, the scalar fields $\Phi _1$, $\Delta _1$ and $\Delta _2$ acquire VEVs of the form

$$\begin{aligned} \langle \Phi _1\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix} 0 \\ v \end{pmatrix},\quad \langle \Delta _{n}\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix} 0 &{} 0 \\ u_n &{} 0 \end{pmatrix}. \end{aligned}$$

(30)

Similarly to Ref. [19], we will use $u_1^2 + u_2^2 = u^2$, with $u_1 = u\cos \beta$, $u_2 = u\sin \beta$ and $\tan \beta = u_2/u_1$. The VEVs must follow the condition $v^2 + 2u^2 \approx (246\ \text {GeV})^2,$ which limits u to be below 8 GeV due to constraints on the $\rho$ parameter. From the first derivatives of the potential, we can find the following conditions:

$$\begin{aligned} 0 = {}&\lambda _{\Phi 1} v^2 - m^2_{\Phi 1} + u^2 \left( \lambda ^q_{\Phi 1 \Delta 1} \cos ^2\beta \right. \nonumber \\&\left. + \lambda ^q_{\Phi 1\Delta 2} \sin ^2\beta + 2 \lambda ^q_{\Phi 1 \Delta 12} \cos \beta \sin \beta \right) \nonumber \\&- \sqrt{2} u \left( \mu _{11} \cos \beta + \mu _{21} \sin \beta \right) , \end{aligned}$$

(31)

$$\begin{aligned} 0 = {}&u^3 \left[ (\lambda ^q_{12} + \lambda ^q_{1212}) \cos \beta \sin ^2\beta + \lambda ^q_1 \cos ^3\beta \right. \nonumber \\&\left. + 3 \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cos ^2\beta \sin \beta + \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \sin ^3\beta \right] \nonumber \\&+ u \left[ M^2_1 \cos \beta + M^2_{12} \sin \beta + \lambda ^q_{\Phi 1\Delta 12} v^2 \sin \beta \right. \nonumber \\&\left. + \lambda ^q_{\Phi 1\Delta 1} v^2 \cos \beta \right] - \frac{\mu _{11}}{\sqrt{2}} v^2 , \end{aligned}$$

(32)

$$\begin{aligned} 0 = {}&u^3 \left[ (\lambda ^q_{12} + \lambda ^q_{1212}) \cos ^2\beta \sin \beta + \lambda ^q_2 \sin ^3\beta \right. \nonumber \\&\left. + 3 \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \cos \beta \sin ^2\beta + \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cos ^3\beta \right] \nonumber \\&+ u \left[ M^2_2 \sin \beta + M^2_{12} \cos \beta + \lambda ^q_{\Phi 1\Delta 12} v^2 \cos \beta \right. \nonumber \\&\left. + \lambda ^q_{\Phi 1\Delta 2} v^2 \sin \beta \right] - \frac{\mu _{21}}{\sqrt{2}} v^2, \end{aligned}$$

(33)

where we used the following definitions:

$$\begin{aligned} \lambda ^q_n \equiv {}&\lambda _{\Delta n} + \lambda '_{\Delta n}, \end{aligned}$$

(34)

$$\begin{aligned} \lambda ^q_{\Phi 1\Delta n} \equiv {}&(\lambda _{\Phi 1\Delta n} + \lambda '_{\Phi 1\Delta n})/2, \end{aligned}$$

(35)

$$\begin{aligned} \lambda ^q_{12} \equiv {}&(\lambda _{\Delta 12} + \lambda _{\Delta 21} + \lambda '_{\Delta 12} + \lambda '_{\Delta 21})/2, \end{aligned}$$

(36)

$$\begin{aligned} \lambda ^q_{\Phi 1\Delta 12} \equiv {}&(\lambda _{\Phi 1\Delta 12} + \lambda '_{\Phi 1\Delta 12})/2, \end{aligned}$$

(37)

$$\begin{aligned} \lambda ^q_{1212} \equiv {}&\lambda _{1212} + \lambda '_{1212} \end{aligned}$$

(38)

$$\begin{aligned} \lambda ^q_{2111} \equiv {}&(\lambda _{2111} + \lambda _{1211})/2, \end{aligned}$$

(39)

$$\begin{aligned} \lambda ^{q\prime }_{2111} \equiv {}&(\lambda '_{2111} + \lambda '_{1211})/2, \end{aligned}$$

(40)

$$\begin{aligned} \lambda ^q_{1222} \equiv {}&(\lambda _{1222} + \lambda _{2122})/2, \end{aligned}$$

(41)

$$\begin{aligned} \lambda ^{q\prime }_{1222} \equiv {}&(\lambda '_{1222} + \lambda '_{2122})/2. \end{aligned}$$

(42)

From these conditions we can rewrite $m^2_{\Phi 1}$, $M^2_1$ and $M^2_2$ as

$$\begin{aligned} m^2_{\Phi 1} = {}&\lambda _{\Phi 1} v^2 + u^2 \left( \lambda ^q_{\Phi 1 \Delta 1} \cos ^2\beta \right. \nonumber \\&\left. + \lambda ^q_{\Phi 1\Delta 2} \sin ^2\beta + 2 \lambda ^q_{\Phi 1 \Delta 12} \cos \beta \sin \beta \right) \nonumber \\&- \sqrt{2} u \left( \mu _{11} \cos \beta + \mu _{21} \sin \beta \right) \end{aligned}$$

(43)

$$\begin{aligned} M^2_1 = {}&- u^2 \cos ^2\beta \left[ \lambda ^q_1 + 3 \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \tan \beta \right. \nonumber \\&\left. + (\lambda ^q_{12} + \lambda ^q_{1212}) \tan ^2\beta + \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan ^3\beta \right] \nonumber \\&- v^2 \left( \lambda ^q_{\Phi 1\Delta 1} + \lambda ^q_{\Phi 1\Delta 12} \tan \beta \right) \nonumber \\&- M^2_{12} \tan \beta + \frac{\mu _{11} v^2}{\sqrt{2}u \cos \beta } \end{aligned}$$

(44)

$$\begin{aligned} M^2_2 = {}&- u^2 \sin ^2\beta \left[ \lambda ^q_2 + 3 \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \cot \beta + (\lambda ^q_{12} + \lambda ^q_{1212}) \cot ^2\beta \right. \nonumber \\&\left. + \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot ^3\beta \right] \nonumber \\&- v^2 \left( \lambda ^q_{\Phi 1\Delta 2} + \lambda ^q_{\Phi 1\Delta 12} \cot \beta \right) \nonumber \\&- M^2_{12} \cot \beta + \frac{\mu _{21} v^2}{\sqrt{2}u \sin \beta }. \end{aligned}$$

(45)

1.1 Apppendix B: Neutral states masses

Consider the following expansion of the neutral states:

$$\begin{aligned} \delta ^0_n = \frac{\rho _n + i\eta _n}{\sqrt{2}}. \end{aligned}$$

(46)

We can take the base of the neutral states as $S^0_\textrm{even} = (h_1, \rho _1, \rho _2)$. In such a basis, we have a $3\times 3$ mass matrix for the CP-even neutral scalars, $M^2_\textrm{even}$, which is symmetric and has elements given by:

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{11} = {}&2 \lambda _{\Phi 1} v^{2} \end{aligned}$$

(47)

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{12} = {}&v \left[ 2 u \left( \lambda ^q_{\Phi 1\Delta 1} \cos \beta + \lambda ^q_{\Phi 1\Delta 12} \sin \beta \right) - \sqrt{2} \mu _{11}\right] \end{aligned}$$

(48)

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{13} = {}&v \left[ 2 u \left( \lambda ^q_{\Phi 1\Delta 2} \sin \beta + \lambda ^q_{\Phi 1\Delta 12} \cos \beta \right) - \sqrt{2} \mu _{21}\right] \end{aligned}$$

(49)

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{22} = {}&u^2 \cos ^2\beta \left[ 2 \lambda ^q_{1} + 3 \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \tan \beta \right. \nonumber \\&\left. - \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan ^3\beta \right] \nonumber \\&+ \frac{\mu _{11} v^2}{\sqrt{2} u \cos \beta } - (M^2_{12} + \lambda ^q_{\Phi 1\Delta 12} v^2) \tan \beta \end{aligned}$$

(50)

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{23} = {}&u^2 \cos \beta \sin \beta \left[ 2 (\lambda ^q_{12} + \lambda ^q_{1212}) + 3 \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan \beta \right. \nonumber \\&\left. + 3 \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot \beta \right] \nonumber \\&+ M^2_{12} + \lambda ^q_{\Phi 1\Delta 12} v^2 \end{aligned}$$

(51)

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{33} = {}&u^2 \sin ^2\beta \left[ 2 \lambda ^q_{2} + 3 \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \cot \beta \right. \nonumber \\&\left. - \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot ^3\beta \right] \nonumber \\&+ \frac{\mu _{21} v^2}{\sqrt{2} u \sin \beta } - (M^2_{12} + \lambda ^q_{\Phi 1\Delta 12}) \cot \beta . \end{aligned}$$

(52)

For the CP-odd states, we can take the basis $S^0_\textrm{odd} = (\eta _1, \eta _2)$, obtaining the mass matrix elements

$$\begin{aligned} \left( M^2_\textrm{odd}\right) _{11} = {}&- u^2 \sin ^2\beta \left[ 2 \lambda ^q_{1212} + \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan \beta \right. \nonumber \\&\left. + \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot \beta \right] \nonumber \\&+ \frac{\mu _{11} v^2}{\sqrt{2} u \cos \beta } - (M^2_{12} + \lambda ^q_{\Phi 1\Delta 12} v^2) \tan \beta , \end{aligned}$$

(53)

$$\begin{aligned} \left( M^2_\textrm{odd}\right) _{12} = {}&u^2 \cos \beta \sin \beta \left[ 2 \lambda ^q_{1212} + \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan \beta \right. \nonumber \\&\left. + \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot \beta \right] \nonumber \\&+ M^2_{12} + \lambda ^q_{\Phi 1\Delta 12} v^2, \end{aligned}$$

(54)

$$\begin{aligned} \left( M^2_\textrm{odd}\right) _{22} = {}&- u^2 \cos ^2\beta \left[ 2 \lambda ^q_{1212} + \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan \beta \right. \nonumber \\&\left. + \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot \beta \right] \nonumber \\&+ \frac{\mu _{21} v^2}{\sqrt{2} u \sin \beta } - (M^2_{12} + \lambda ^q_{\Phi 1\Delta 12} v^2) \cot \beta . \end{aligned}$$

(55)

The rest of the neutral scalars do not mix and the squared masses are given by the expressions:

$$\begin{aligned} m_{H^0}^2 = {}&u^2 \left[ \left( \lambda _{\Phi 2\Delta 1} + \lambda '_{\Phi 2\Delta 1}\right) \frac{\cos ^2\beta }{2} \right. \nonumber \\&\left. + \left( \lambda _{\Phi 2\Delta 2} + \lambda '_{\Phi 2\Delta 2}\right) \frac{ \sin ^2\beta }{2} + \left( \lambda _{\Phi 2\Delta 12} + \lambda '_{\Phi 2\Delta 12}\right) \cos \beta \sin \beta \right] \nonumber \\&- \sqrt{2} u (\mu _{12} \cos \beta + \mu _{22} \sin \beta ) + m^2_{\Phi 2} \nonumber \\&+ \frac{v^2}{2}\left( \lambda _{\Phi 12} + \lambda '_{\Phi 12} + \lambda _5\right) \end{aligned}$$

(56)

$$\begin{aligned} m_{A^0}^2 = {}&u^2 \left[ \left( \lambda _{\Phi 2\Delta 1} + \lambda '_{\Phi 2\Delta 1}\right) \frac{\cos ^2\beta }{2} \right. \nonumber \\&\left. + \left( \lambda _{\Phi 2\Delta 2} + \lambda '_{\Phi 2\Delta 2}\right) \frac{ \sin ^2\beta }{2} + \left( \lambda _{\Phi 2\Delta 12} + \lambda '_{\Phi 2\Delta 12}\right) \cos \beta \sin \beta \right] \nonumber \\&+ \sqrt{2} u (\mu _{12} \cos \beta + \mu _{22} \sin \beta )\nonumber \\&+ m^2_{\Phi 2} + \frac{v^2}{2}\left( \lambda _{\Phi 12} + \lambda '_{\Phi 12} - \lambda _5\right) . \end{aligned}$$

(57)

In this case, the difference between the masses of these two scalars is given by

$$\begin{aligned} m_{A^0}^2 - m_{H^0}^2 = - \lambda _5 v^2 + 2\sqrt{2} u (\mu _{12} \cos \beta + \mu _{22} \sin \beta ), \end{aligned}$$

(58)

which is positive (negative) when $H^0$ ($A^0$) is the DM candidate.

1.2 Charged states masses

In the scalar potentia,l we have three single charged scalars, $\Phi _2^\pm$, $\delta _1^\pm$ and $\delta _2^\pm$, and two doubly charged scalars, $\delta _1^{\pm \pm }$ and $\delta _2^{\pm \pm }$. The usual charged Higgs present in two Higgs doublet models does not mix with other charged scalars and its squared mass is given by

$$\begin{aligned} M_{\Phi _2^\pm }^2= & {} m_{\Phi 2}^2 + \frac{\lambda _{\Phi 12}}{2} v^2 + u^2 \sin \beta \cos \beta \nonumber \\{} & {} \left( \lambda _{\Phi 2\Delta 12} + \frac{\lambda _{\Phi 2\Delta 1}}{2} \cot \beta + \frac{\lambda _{\Phi 2\Delta 2}}{2} \tan \beta \right) . \end{aligned}$$

(59)

Note that the terms additional to the mass in the original IDM have a factor of $u^2$. Since we expect $u^2 \ll v^2$ these extra terms can be considered small corrections. The two single-charge scalars from the triplets mix and the $2\times 2$ matrix has the followings elements:

$$\begin{aligned} \left( M^2_{\delta ^\pm }\right) _{11} = {}&u^2 \sin ^2\beta \left[ \frac{\lambda '_{\Delta 12}}{4} - \frac{\lambda '_{\Delta 21}}{4} - \frac{\lambda ^q_{12}}{2} - \lambda ^q_{1212} \right. \nonumber \\&\left. - \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan \beta - \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot \beta \right] \nonumber \\&- M^2_{12} \tan \beta - v^2 \left( \lambda ^q_{\Phi 1\Delta 12} \tan \beta + \frac{\lambda '_{\Phi 1\Delta 1}}{4} \right) \nonumber \\&+ \frac{\mu _{11} v^2}{\sqrt{2} u \cos \beta }\,, \end{aligned}$$

(60)

$$\begin{aligned} \left( M^2_{\delta ^\pm }\right) _{12} = {}&u^2 \sin \beta \cos \beta \left( - \frac{\lambda '_{\Delta 12}}{4} + \frac{\lambda '_{\Delta 21}}{4} + \frac{\lambda ^q_{12}}{2} + \lambda ^q_{1212} \right. \nonumber \\&\left. + \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan \beta + \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot \beta \right) \nonumber \\&+M^2_{12} + v^2 \left( \lambda ^q_{\Phi 1\Delta 12} - \frac{\lambda '_{\Phi 1\Delta 12}}{4} \right) \,, \end{aligned}$$

(61)

$$\begin{aligned} \left( M^2_{\delta ^\pm }\right) _{22} = {}&u^2 \cos ^2\beta \left( \frac{\lambda '_{\Delta 12}}{4} - \frac{\lambda '_{\Delta 21}}{4} - \frac{\lambda ^q_{12}}{2} - \lambda ^q_{1212} \right. \nonumber \\&\left. - \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222}\right) \tan \beta - \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111}\right) \cot \beta \right) \nonumber \\&-M^2_{12} \cot \beta - v^2 \left( \lambda ^q_{\Phi 1\Delta 12} \cot \beta + \frac{\lambda '_{\Phi 1\Delta 2}}{4} \right) \nonumber \\&+ \frac{\mu _{21} v^2}{\sqrt{2} u \sin \beta } \,. \end{aligned}$$

(62)

The doubly charged scalars mix with each other resulting in the following matrix elements:

$$\begin{aligned} \left( M^2_{\delta ^{\pm \pm }}\right) _{11} = {}&u^2 \cos ^2\beta \bigg [ \lambda '_{\Delta 1} - \lambda ^q_1 - \tan \beta \left( 3 \lambda ^q_{2111} + \lambda ^{q\prime }_{2111} \right) \nonumber \\&- \tan ^2\beta \left( \lambda ^q_{12} + \lambda ^q_{1212} - \frac{\lambda '_{\Delta 12}}{2} \right) \nonumber \\&- \tan ^3\beta \left( \lambda ^q_{1222} + \lambda ^{q\prime }_{1222} \right) \bigg ] \nonumber \\&+ v^2 \left( \frac{\mu _{11}}{\sqrt{2} u \cos \beta } - \frac{\lambda '_{\Phi 1\Delta 1}}{2} - \lambda ^q_{\Phi 1\Delta 12} \tan \beta \right) \nonumber \\&- M^2_{12} \tan \beta , \end{aligned}$$

(63)

$$\begin{aligned} \left( M^2_{\delta ^{\pm \pm }}\right) _{12} = {}&u^2 \sin \beta \cos \beta \left[ \frac{\lambda '_{\Delta 21}}{2} + \lambda '_{1212} + \lambda ^{q\prime }_{1222} \tan \beta + \lambda ^{q\prime }_{2111} \cot \beta \right] \nonumber \\&+ M^2_{12} + v^2 \left( \lambda ^q_{\Phi 1\Delta 12} - \frac{\lambda '_{\Phi 1\Delta 12}}{2} \right) , \end{aligned}$$

(64)

$$\begin{aligned} \left( M^2_{\delta ^{\pm \pm }}\right) _{22} = {}&u^2 \sin ^2\beta \nonumber \\&\bigg [ \lambda '_{\Delta 2} - \lambda ^q_{2} - \cot \beta \left( 3 \lambda ^q_{1222} + \lambda ^{q\prime }_{1222} \right) \nonumber \\&- \cot ^2\beta \left( \lambda ^q_{12} + \lambda ^q_{1212} - \frac{\lambda '_{\Delta 12}}{2} \right) \nonumber \\&- \cot ^3\beta \left( \lambda ^q_{2111} + \lambda ^{q\prime }_{2111} \right) \bigg ] \nonumber \\&+ v^2 \left( \frac{\mu _{21}}{\sqrt{2} u \sin \beta } - \frac{\lambda '_{\Phi 1\Delta 2}}{2} - \lambda ^q_{\Phi 1\Delta 12} \cot \beta \right) \nonumber \\&- M^2_{12} \cot \beta . \end{aligned}$$

(65)

1.3 The no-mixing limit

In the case where $u \ll v$ and assuming that the couplings in $V_{SB}$ are smaller than other couplings in the potential, the non-diagonal terms in mass matrices shown in this appendix become subleading contributions. We can call this the no-mixing limit. A small value for u can be justified by the need of having small neutrino masses, while small couplings in $V_{SB}$ can be considered due to naturalness [36]. The leading contributions to the diagonal elements are

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{11}&= 2\lambda _{\Phi 1} v^2 \end{aligned}$$

(66)

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{22}&= \left( M^2_\textrm{odd}\right) _{11} = \left( M^2_{\delta ^{\pm }}\right) _{11} \nonumber \\&= \left( M^2_{\delta ^{\pm \pm }}\right) _{11} = \frac{\mu _{11} v^2}{\sqrt{2} u \cos \beta }, \end{aligned}$$

(67)

$$\begin{aligned} \left( M^2_\textrm{even}\right) _{33}&= \left( M^2_\textrm{odd}\right) _{22} = \left( M^2_{\delta ^{\pm }}\right) _{22} \nonumber \\&= \left( M^2_{\delta ^{\pm \pm }}\right) _{22} = \frac{\mu _{21} v^2}{\sqrt{2} u \sin \beta }, \end{aligned}$$

(68)

with all the diagonal elements suppressed either by u or couplings from $V_{SB}$. The squared mass of the SM-like Higgs, $m_h^2$, can be identified with $2\lambda _{\Phi 1} v^2$. For the triplets, all the masses of the fields in each triplet become degenerated and we can write $M_{\Delta 1}^2 = \mu _{11} v^2/\sqrt{2} u \cos \beta$ and $M_{\Delta 2}^2 = \mu _{21} v^2/\sqrt{2} u \sin \beta$, for all the scalars contained in the triplets. In the case of the masses for the dark scalars, $H^0$, $A^0$ and $\Phi _2^{\pm }$, it is easy to see that their masses fallback to the values in the original IDM.

Unitarity and CPT

It has been noted in the past that the amount of CP violation from 2-to-2 scatterings is constrained by unitarity and CPT [37,38,39]. In this appendix, we comment briefly on unitarity and CPT in the scatterings considered in Sect. 4. First of all, unitarity requires that all the scatterings with final or initial state $L_l L_m$ follow the condition

$$\begin{aligned} \sum _j |\mathcal {M}(j \rightarrow L_l L_m)|^2 = \sum _j |\mathcal {M}(L_l L_m \rightarrow j)|^2, \end{aligned}$$

(69)

where j represents possible initial and final states that have to be summed over, and l and m represent flavors in the corresponding state. Separating the $\Phi _2\Phi _2$ pairs from the sum (see Eqs. (13) to (15)), we can write

$$\begin{aligned} |\mathcal {M}&(\Phi _2\Phi _2 \rightarrow L_l L_m)|^2 + \sum _{j\ne \Phi _2 \Phi _2} |\mathcal {M}(j \rightarrow L_l L_m)|^2 \nonumber \\&= |\mathcal {M}(L_l L_m \rightarrow \Phi _2\Phi _2)|^2 + \sum _{j\ne \Phi _2 \Phi _2} |\mathcal {M}(L_l L_m \rightarrow j)|^2\,. \end{aligned}$$

(70)

Now the states summed over in j include scalars from $\Phi _1$, $\Delta _n$ and pairs of leptons. For example, considering processes mediated by $\Delta _n$, the scalars that are present in j belong to trilinear couplings that can be read off from the potential after expanding around VEVs. After using CPT invariance on the left-f-side of Eq. (70) and reordering terms we obtain

$$\begin{aligned} |\mathcal {M}&(\Phi _2\Phi _2 \rightarrow L_l L_m)|^2 - |\mathcal {M}(\Phi _2^*\Phi _2^* \rightarrow \bar{L}_l \bar{L}_m)|^2 \nonumber \\&= \sum _{j\ne \Phi _2 \Phi _2} |\mathcal {M}(j_\text {CPT} \rightarrow \bar{L}_l \bar{L}_m)|^2\nonumber \\&\quad - \sum _{j\ne \Phi _2 \Phi _2} |\mathcal {M}(j \rightarrow L_l L_m)|^2\,. \end{aligned}$$

(71)

Note that in the right-hand side of this equation, processes with $j = L_l L_m$ (same initial and final flavor) cancel each other. Considering that both sides of this equation have processes mediated by $\Delta _1$ and $\Delta _2$, the same effects from interferences due to the relative phase from $\xi$, ensure that both sides are non-zero. The left-hand side of Eq. (71) contributes to having non-zero scattering in Eq. (19). From the Boltzmann equation in Eq. (17), this leads to an accumulation of non-zero lepton asymmetry that builds-up as DM evolves toward freeze out.