Investigation of the propagation of coupled laser pulses in a plasma

Abstract

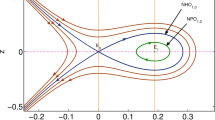
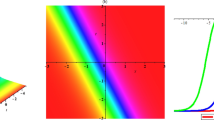
In this paper, the propagation of an electromagnetic pulse due to the interaction of laser pulse and plasma was investigated using a set of fluid relativistic equations and Maxwell’s equations in an unmagnetized collisionless common plasma. Using the multiple scale perturbation approach, the dispersion relation and the group velocity were derived, and finally it was shown that the evaluation of the components of vector potential is governed by two coupled-nonlinear Schrödinger (NLS) equations. It should be noted that using the relations of the phase and group velocities we understated that they are independent from plasma parameters. Then, using analytical methods, the solutions of the amplitude of the coupled Schrodinger equations for both components of the vector potential were obtained. Analytically, the modulation instability conditions in terms of plasma parameters have been investigated. Finally, by plotting the figures, the modulation stability and instability regions are numerically studied.

Appendix

Substitute $\xi =x-2pst$ and $\tau =t$ in Eqs. (26) and (27) and considering

$${a}_{x}(\xi ,\tau )={A}_{x}(\xi ){{\text{e}}}^{{\text{i}}(px+kt)}, {a}_{y}(\xi ,\tau )={A}_{y}(\xi ){{\text{e}}}^{{\text{i}}\left(px+kt\right),}$$

(36)

to obtain

$${Q}_{1}{{A}_{x}(\xi )}^{3}+{A}_{x}\left(\xi \right)\left(-k-{p}^{2}S+\left({Q}_{2}+{Q}_{3}\right){{A}_{y}\left(\xi \right)}^{2}\right)+S{A}_{x}^{^{\prime\prime} }\left(\xi \right)=0,$$

(37)

$$\left(-k-{p}^{2}S+\left({Q}_{2}+{Q}_{3}\right){{A}_{x}\left(\xi \right)}^{2}\right){A}_{y}\left(\xi \right)+{Q}_{1}{{A}_{y}\left(\xi \right)}^{3}+S{A}_{y}^{^{\prime\prime} }\left(\xi \right)=0,$$

(38)

Using the Jacobi elliptic function expansion method. One can assume ${A}_{x}\left(\xi \right)=\Phi \left(\xi \right)$ and ${A}_{y}\left(\xi \right)=\psi \left(\xi \right)$ as a finite series of Jacobi elliptic function (for example $cn$) and follow that method as [44,60]

$$\Phi \left(\xi \right)=\sum_{j=0}^{N}{a}_{j}{\varphi }^{j},$$

(39)

$$\uppsi \left(\xi \right)=\sum_{j=0}^{N}{b}_{j}{\varphi }^{j},$$

(40)

where $\varphi$ is considered as one of the Jacobi elliptic functions $sn\xi$, $cn\xi$ and $dn\xi$. By balancing between the highest order linear term and the nonlinear of eq. (A–1), one will realize that the value of $N$ should be $N=2$. Hence, the (A–1) equation may have the following form travelling wave equation

$$\Phi \left(\xi \right)={a}_{0}+{a}_{1}cn\xi +{a}_{2}{cn}^{2}\xi ,$$

(41)

$$\psi \left(\xi \right)={b}_{0}+{b}_{1}cn\xi +{b}_{2}{cn}^{2}\xi ,$$

(42)

Substituting eqs. (A–5) and (A–6) into (A–2) and (A–3), one can obtain

$$-k{a}_{0}-{p}^{2}S{a}_{0}+{Q}_{1}{{a}_{0}}^{3}+\left({Q}_{2}+{Q}_{3}\right){a}_{0}{{b}_{0}}^{2}+\left(-k{a}_{1}-{p}^{2}S{a}_{1}+3{Q}_{1}{{a}_{0}}^{2}{a}_{1}+\left({Q}_{2}+{Q}_{3}\right){a}_{1}{{b}_{0}}^{2}+2\left({Q}_{2}+{Q}_{3}\right){a}_{0}{b}_{0}{b}_{1}+S{a}_{1}{c}_{2}\right)cn\xi +\left(3{Q}_{1}{a}_{0}{{a}_{1}}^{2}+2\left({Q}_{2}+{Q}_{3}\right){a}_{1}{b}_{0}{b}_{1}+\left({Q}_{2}+{Q}_{3}\right){a}_{0}{{b}_{1}}^{2}\right){cn}^{2}\xi +{a}_{1}\left({Q}_{1}{{a}_{1}}^{2}+\left({Q}_{2}+{Q}_{3}\right){{b}_{1}}^{2}+2S{c}_{4}\right){cn}^{3}\xi ,$$

(43)

$$-k{b}_{0}-{p}^{2}S{b}_{0}+\left({Q}_{2}+{Q}_{3}\right){{a}_{0}}^{2}{b}_{0}+{Q}_{1}{{b}_{0}}^{3}+\left(2\left({Q}_{2}+{Q}_{3}\right){a}_{0}{a}_{1}{b}_{0}-k{b}_{1}-{p}^{2}S{b}_{1}+\left({Q}_{2}+{Q}_{3}\right){{a}_{0}}^{2}{b}_{1}+3{Q}_{1}{{b}_{0}}^{2}{b}_{1}+S{b}_{1}{c}_{2}\right)cn\xi +\left(\left({Q}_{2}+{Q}_{3}\right){{a}_{1}}^{2}{b}_{0}+2\left({Q}_{2}+{Q}_{3}\right){a}_{0}{a}_{1}{b}_{1}+3{Q}_{1}{b}_{0}{{b}_{1}}^{2}\right){cn}^{2}\xi +{b}_{1}\left(\left({Q}_{2}+{Q}_{3}\right){{a}_{1}}^{2}+{Q}_{1}{{b}_{1}}^{2}+2S{c}_{4}\right){cn}^{3}\xi =0,$$

(44)

and by substituting ${cn}^{2}\zeta =1-{sn}^{2}\zeta$ and $d{n}^{2}\zeta =1-{m}^{2}+{m}^{2}{cn}^{2}\zeta$, and with the aid of Mathematica we can determine the coefficients

$${a}_{0}={b}_{0}=0, {b}_{1}=-i{a}_{1}=\sqrt{-\frac{2S{c}_{4}}{{Q}_{1}+{Q}_{2}+{Q}_{3}}}, {a}_{2}={b}_{2}=0, {c}_{2}={p}^{2}+\frac{k}{S}, {c}_{4}=-{c}_{2},$$

(45)

where $p$ and $k$ are fixed and arbitrary values.