Response of mechanical and optoelectronic properties for InP_xAs_ySb_1–x–y/InAs system to composition

Abstract

The compositional dependence of optical, mechanical, thermal properties, and lattice vibrations of InP_xAs_ySb_1–x–y quaternary semiconductor alloys lattice-matched to InAs substrate has been studied. In this study, the physical properties of the binary elements InAs, InSb, and InP that make up the quaternary alloy were employed. Under the virtual crystal approximation (VCA), the empirical pseudo-potential model (EPM) was used to carry out the research. Our findings are in good agreement with the available experimental and theoretical values. In the literature, the composition effect on the optical, mechanical and thermal properties of the InP_xAs_ySb_1–x–y/InAs system has not been thoroughly investigated. As a result, we focused on these properties as a function of composition.

1 Introduction

Semiconductors that involve components from group III and group V of the periodic table, provide the main resources used in manufacturing great-speed electronics and optoelectronics [1,2,3,4,5]. The quaternary compounds of the III–V groups were liable to an enormous experimental and hypothetical examinations in the ongoing years, and the logical writing contains an enormous quantity of valuable information [6,7,8,9,10,11,12,13]. The understanding of the significance of phonons in electrical and thermal properties of materials requires knowledge of their frequency. They have an important role in the transport characteristics of technologically important semiconductors. Debye temperature relates phonons, thermal expansion, thermal conductivity, specific heat, and lattice enthalpy to thermodynamic characteristics.

Over the whole range of the composition parameters of x and y, the binary compounds InSb, InAs, and InP form a continuous sequence of alloys represented by InP_xAs_ySb_1–x–y. The data available for the binary materials that make up these quaternary alloys are used to examine them. The alloy InP_xAs_ySb_1–x–y is a potential of great importance in many industrial applications specially thermo-photovoltaic devices. The investigation of the optical, mechanical, thermal properties and lattice vibrations of this alloy is critical, because it gives us control over the planning high-performance electronic systems [10, 14,15,16,17,18,19,20]. Two distinct substrates, InAs and GaSb, can be lattice-matched to the quaternary InP_xAs_ySb_1–x–y alloy [21].

The current computations use the (EPM) with (VCA). The lattice constant and the pseudo-potential from factors of the quaternary alloy can be calculated in terms of those of its binary constituent elements. Knowledge of the fundamental energy bandgap, the calculations can be done to obtain the index of refraction$n$, high-frequency dielectric constant $\varepsilon_{\infty }$, static dielectric constant $\varepsilon_{{\text{s}}}$. The polarity $\alpha_{{\text{p}}}$ of a semiconductor can be calculated from the symmetric and anti-symmetric form factors at G (1,1,1) [22] and using them in calculating the elastic constants $c_{11} ,c_{12} ,c_{44}$ and elastic moduli bulk $B_{{\text{u}}}$, shear $C_{{\text{s}}}$, young $Y_{{\text{o}}}$.The longitudinal and transverse phonon frequencies $\omega_{{{\text{LO}}}} , \omega_{{{\text{TO}}}}$ and the Debye temperature $\theta_{{\text{D}}}$ could be successfully determined.

2 Theory and calculation

Using the EPM technique [23,24,25], in which the symmetric and anti-symmetric pseudo-potential form factors have been adjusted to fit the experimental band gap energies of parent compounds of the studied alloy, namely InP, InAs, and InSb at selected high symmetry points (Γ, X, L) in the first Brillouin zone. In this work, some of the optical, mechanical, and thermal properties of the quaternary alloy InP_xAs_ySb_1–x–y lattice-matched to InAs as a substrate have been calculated. The general form of the lattice matching condition is $x = ay + b$ [21], where:

$$a = \frac{{a_{{{\text{InAs}}}} - a_{{{\text{InSb}}}} }}{{a_{{{\text{InP}}}} - a_{{{\text{InSb}}}} }}$$

(1)

$$b = \frac{{a_{{{\text{Substrate}}}} - a_{{{\text{InSb}}}} }}{{a_{{{\text{InP}}}} - a_{{{\text{InSb}}}} }}.$$

(2)

For InAs as a substrate, we find the lattice match condition between x and y to be:

$$x = 0.68933 - 0.68933 y.$$

(3)

The study of InP_xAs_ySb_1–x–y alloy relies on the physical properties of the binary compounds that constitute it. The calculations are first performed for the binary compounds using (EPM), where a linear superposition of atomic potentials represents the crystal pseudo-potential as:

$$W\left( G \right) = W^{{\text{s}}} \left( G \right)\cos \left( {{\mathbf{G}} \cdot {{\varvec{\uptau}}}} \right) + iW^{{\text{a}}} \left( {\mathbf{G}} \right)\sin \left( {{\mathbf{G}} \cdot {{\varvec{\uptau}}}} \right).$$

(4)

The energy eigenvalues can be found using pseudo-potential form factors and numerical approaches to solve the secular determinant [26,27,28].

$$\left\| {\left( {\frac{1}{2}\left| {{\mathbf{k}} + \acute{ {\mathbf{G}} }} \right|^{2} - E_{{n{\mathbf{k}}}} } \right)\delta_{{{\mathbf{G}}\acute{ {\mathbf{G}} }}} + \mathop \sum \limits_{{{\mathbf{G}} \ne {\acute{\mathbf{G}}}}} V\left( {\left| {\Delta {\mathbf{G}}} \right|} \right)} \right\| = 0.$$

(5)

The energy band gaps might be calculated using the obtained energy eigenvalues and. More information on this method can be found in the references [26,27,28]. To start the EPM calculations for the quaternary InP_xAs_ySb_1–x–y alloy, we need to know its lattice constant $^{\prime}a^{\prime}$ and the pseudo-potential form factors, which could be obtained in terms of those of the binary materials according to the relations reported by Adachi [21], where

$$a\left( {x,y} \right) = xa_{{{\text{InP}}}} + ya_{{{\text{InAs}}}} + \left( {1 - x - y} \right)a_{{{\text{InSb}}}}$$

(6)

$$W\left( {x,y} \right) = xW_{{{\text{InP}}}} + yW_{{{\text{InAs}}}} + \left( {1 - x - y} \right)W_{{{\text{InSb}}}} .$$

(7)

The polarity $\alpha$_p of the quaternary alloy is calculated according to Vogl’s relation [22] as:

$$\alpha_{{\text{p}}} = - \frac{{W_{3}^{{\text{a}}} }}{{W_{3}^{{\text{s}}} }}.$$

(8)

Knowledge of the polarities, the elastic parameters C₁₁, C₁₂, C_44, $B_{{\text{u}}} , Y_{{\text{o}}}$ and $C_{{\text{s}}}$ of the studied alloys could be determined [18, 29, 30]. The elastic constants of the investigated material are determined using Baranowski’s improved description [31,32,33].

$$C_{11} = \frac{\sqrt 3 }{{4d^{5} }}\left[ {4.37\frac{{\hbar^{2} }}{m}(5 + \lambda )\left( {1 - \alpha_{{\text{p}}}^{2} } \right)^{\frac{3}{2}} - 0.60751\left( {1 - \alpha_{{\text{p}}}^{2} } \right)^{\frac{1}{2}} \frac{{\hbar^{2} }}{m}} \right]$$

(9)

$$C_{12} = \frac{\sqrt 3 }{{4d^{5} }}\left[ {4.37\frac{{\hbar^{2} }}{m}(3 - \lambda )\left( {1 - \alpha_{{\text{p}}}^{2} } \right)^{\frac{3}{2}} + 0.60751\left( {1 - \alpha_{{\text{p}}}^{2} } \right)^{\frac{1}{2}} \frac{{\hbar^{2} }}{m}} \right]$$

(10)

$$C_{44} = \frac{{3(C_{11} + 2C_{12} )(C_{11} - C_{12} )}}{{(7C_{11} + 2C_{12} )}},$$

(11)

where $d = \frac{{\sqrt {3\,} a}}{4}$ is the nearest-neighbor distance, $\lambda$ is a dimensionless parameter which has a constant value of 0.738 [29]. The determination of $C_{11}$, $C_{12}$ and $C_{44}$ makes it is possible to proceed with their related parameters. The bulk modulus $B_{{\text{u}}}$ which describes the material’s response to uniform pressure related to the elastic constants by the expression [34]

$$B_{{\text{u}}} = \frac{{C_{11} + 2C_{12} }}{3}.$$

(12)

The shear modulus $C_{s}$ which describes the material’s response to shearing strains related to the elastic constants by the equation [34]

$$C_{{\text{s}}} = \frac{{C_{11} - C_{12} }}{2}.$$

(13)

The young’s modulus $Y_{0}$ which is a measure of stiffness of a given material related to the elastic constants by the expression [35].

$$Y_{0} = \frac{{(C_{11} + 2C_{12} )(C_{11} - C_{12} )}}{{C_{11} + C_{12} }}.$$

(14)

The energy bandgap ${E}_{\Gamma }$ of the InP_xAs_ySb_1–x–y alloy are calculated and used to determine its refractive index ‘n’ . This can be done through many empirical formulae [36,37,38] and in this work, we adopted Vandamme’s formula [38]. The calculated refractive index is used to determine the high frequency and the static dielectric constants $\varepsilon_{\infty }$, $\varepsilon_{{\text{s}}}$, respectively, using the following formulae [39, 40].

$$\varepsilon_{\infty } = n^{2}$$

(15)

$$\varepsilon_{{\text{s}}} = \left\{ {\left[ {1 + \frac{{ \propto_{{\text{p}}}^{2} \left( {1 + 2\alpha_{c}^{2} } \right)}}{{2\alpha_{{\text{c}}}^{4} }}} \right]\left[ {\varepsilon_{\infty } - 1} \right]} \right\} + 1,$$

(16)

where $\alpha_{{\text{c}}}$, is the covalency factor which is defined as:

$$\alpha_{{\text{c}}} = \sqrt {1 - \alpha_{{\text{p}}}^{2} } .$$

(17)

The optical phonon frequencies ${\upomega }_{{{\text{LO}}}}$ and ${\upomega }_{{{\text{TO}}}}$ could be obtained by solving the Lyddane–Sachs–Teller relation [41, 42].

$$\frac{{\omega_{{{\text{TO}}}}^{2} }}{{\omega_{{{\text{LO}}}}^{2} }} = \frac{{\varepsilon_{\infty } }}{{\varepsilon_{{\text{s}}} }},$$

(18)

with the relation [41, 42]:

$$\omega_{{{\text{LO}}}}^{2} - \omega_{{{\text{TO}}}}^{2} = \frac{{4\pi e_{{\text{T}}}^{*2} e^{2} }}{{M{\Omega }_{{\text{o}}} \varepsilon_{\infty } }},$$

(19)

where $M$ $\Omega_{{\text{o}}}$ are twice of reduced mass and the volume occupied by one atom.

Finally, knowing the longitudinal phonon frequencies $\omega_{{{\text{LO}}}} ,$ the Debye temperature $\theta_{D}$ could be successfully determined [43, 44].

$$\theta_{{\text{D}}} = \frac{{\hbar \omega_{{{\text{LO}}}} }}{k}$$

(20)

$$C_{{\text{p}}} \sim C_{{\text{V}}} = 3R\left( {\frac{T}{{\theta_{{\text{D}}} }}} \right)^{3} \mathop \smallint \limits_{0}^{{\theta_{{\text{D}}} /T}} \frac{{3x^{4} e^{x} }}{{\left( {e^{x} - 1} \right)^{2} }}{\text{d}}x,$$

(21)

where $R$ is the universal gas constant $R = 8.314 \;{\text{J/Mol.K}}$, where the quantity $\left( {\frac{T}{{\theta_{{\text{D}}} }}} \right)^{3} \int_{0}^{{\theta_{{\text{D}}} /T}} {\frac{{3x^{4} e^{x} }}{{\left( {e^{x} - 1} \right)^{2} }}{\text{d}}x}$ called the Debye function $F(\theta_{D} /T$)

$$F\left( {\frac{{\theta_{D} }}{T}} \right) = \left( {\frac{T}{{\theta_{{\text{D}}} }}} \right)^{3} \mathop \smallint \limits_{0}^{{\theta_{{\text{D}}} /T}} \frac{{3x^{4} e^{x} }}{{\left( {e^{x} - 1} \right)^{2} }}{\text{d}}x.$$

(22)

No table of contents entries found.

3 Results and discussion

Table 1 shows the calculated direct and indirect energy band gaps of the binary compounds InSb, InAs, and InP which establish the InP_xAs_ySb_1–x–y alloy. The calculated energy band gaps are matched with the available experimental data and displayed good agreement. To calculate the bandgap energies of the InP_xAs_ySb_1–x–y alloys, we required its compositional lattice constants and its form factors. The calculated band gap energies for different values of ‘As’ concentration at standard temperature and pressure are recorded in Table 2 and exhibited in Fig. 1. The calculated results showed that InP_xAs_ySb_1–x–y alloys are direct bandgap semiconductors over the whole region of Arsenide concentration ‘y’. The bandgap energies of the quaternary alloy are almost linearly decreased with enhancing the compositional parameter ‘y’. InP_xAs_ySb_1–x–y alloy becomes a binary material (InAs) when y = 1 and its energy gaps give excellent accord with the experimental ones [43, 45].

Table 1 The bandgap energies of the binary compounds

Table 2 The bandgap energies of InP_xAs_ySb_1–x–y/InAs system for various values of ‘As’ concentration

Fig. 1

Direct and indirect energy band Gaps of InP_xAs_ySb_1–x–y/InAs system as function of the compositional parameter y

Table 3 and Fig. 2 show the variation of the elastic constants C₁₁, C_12, and C₄₄ as a function of As concentration for InP_xAs_ySb_1–x–y lattice-matched to InAs substrate. We note that C₁₁ is slightly increased with increasing ‘As’ content on going from InP to InAs, however, C₁₂ and C₄₄ are slightly affected with As concentration. The values of the elastic constants in Table 3 satisfy the stability conditions C₁₁–C₁₂ > 0, C₁₁ > 0, C₄₄ > 0, C₁₁ + 2C₁₂ > 0 [48], which indicating that InP_xAs_ySb_1–x–y alloys are mechanically stable in their structure over the whole region of As concentration. The calculated elastic constants for y = 1 are matched with the published results and present good agreement.

Table 3 The elastic constants of InP_xAs_ySb_1–x–y/InAs system for various concentrations

Fig. 2

The elastic constants for InP_xAs_ySb_1–x–y /InAs as function of composition

The obtained elastic constants have permitted us to determine the B_u, Y₀, and C_s moduli of the studied alloy for different values of compositional parameter y as shown in Table 4 and Fig. 3. It is being observed that all quantities are slightly increased with increasing the compositional parameter y. Since, the bulk modulus of a crystalline substance is a measurement of its hardness, so the InP_xAs_ySb_1–x–y becomes harder as the composition y increases. Likewise, the increase of shear modulus C_s with increasing As concentration gives high lattice stability. Also, the enhancement of Young’s modulus Y₀ with increasing y increases the stiffness of the studied material [6, 50, 51]. The calculated ${B}_{\mathrm{u}}/{C}_{\mathrm{s}}$ ratio for InP_xAs_ySb_1–x–y/InAs system is lie between 2.18 and 2.19 which larger than 1.75, which indicates that the studied alloy is in the ductile manner [48].

Table 4 The elastic moduli of InP_xAs_ySb_1–x–y/InAs system for various concentrations

Fig. 3

The elastic Moduli of InP_xAs_ySb_1–x–y/InAs system as a function of composition

The accurate knowledge of the n and its related dielectric constants of a semiconductor is a significant part of the strategy and investigation of micro-cavities, solar cells, and injection lasers [52]. In the current work, the compositional dependences of the $n$ that calculated from the Vandamme’s principle [38], the ${\varepsilon }_{\infty }$ and ${\varepsilon }_{\mathrm{s}}$ are determined and recorded in Table 7 and demonstrated in Fig. 4. The refractive index is somewhat enhanced with enhancing y; however, the dielectric constants are enhanced with the same rate by increasing the compositional parameter y.

Table 7 The index of refraction $n$, ${\varepsilon }_{\infty }$ and ${\varepsilon }_{\mathrm{s}}$ of InP_xAs_ySb_1–x–y/InAs system for various concentrations

Fig. 4

Compositional dependence of $\varepsilon_{\infty }$, $\varepsilon_{{\text{s}}}$ and n of InP_xAs_ySb_1–x–y/InAs system

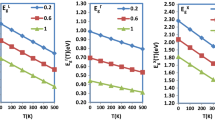
Table 8 displays the compositional dependence of the phonon frequencies, Longitudinal $\omega_{{{\text{LO}}}}$, transverse $\omega_{{{\text{TO}}}}$, and the Debye temperature $\theta_{{\text{D}}}$ of InP_xAs_ySb_1–x–y/InAs system. The calculated values of them versus As concentration y are plotted in Figs. 5 and 6, respectively. Both phonon frequencies and the Debye temperature are decreased nonlinearly with increasing the compositional parameter ‘y’. Generally, all calculated results regarding the quaternary alloy of interest for y = 1 are compared to publicly available data and found to be in good accord which gives credibility to our findings for InP_xAs_ySb_1–x–y /InAs system.

Table 8 Longitudinal ${\omega }_{\mathrm{LO}}$ and transverse ${\omega }_{\mathrm{TO}}$ and ${\theta }_{\mathrm{D}}$ of InP_xAs_ySb_1–x–y/InAs system for various concentrations

Fig. 5

Compositional dependence of the $\omega_{{{\text{LO}}}}$ and $\omega_{{{\text{TO}}}}$ of InP_xAs_ySb_1–x–y/InAs system

Fig. 6

Debye temperature of InP_xAs_ySb_1–x–y/InAs system versus As concentration

4 Conclusion

Using the (EPM) under the (VCA), the energy band gaps of the InP_xAs_ySb_1–x–y/InAs system in the composition range 0 < y < 1 were calculated. The polarities of the quaternary alloys are obtained through Vogl’s relation and used in determining the elastic parameters C_ij and (${B}_{\mathrm{u}}$), (${C}_{\mathrm{s}}$) and (${Y}_{0}$) for different values of ‘As’ concentration in InP_xAs_ySb_1–x–y/InAs system. The compositional dependence of the $n$, ${\varepsilon }_{\infty }$ and ${\varepsilon }_{\mathrm{s}}$ of ${\mathrm{InP}}_{x}{\mathrm{As}}_{y}{\mathrm{Sb}}_{1-x-y}$ /InAs were determined. Also, the longitudinal ${\omega }_{\mathrm{LO}}$, the transverse ${\omega }_{\mathrm{TO}}$ phonon frequencies and the ${\theta }_{\mathrm{D}}$ of the studied alloy for different values of compositional parameter y have been examined. The majority of our findings in this article are predictions and can be used as a guide for future research. The studied properties could be beneficial in optoelectronic devices.